Deriválás - Alapműveletek vektorokkal
A Fizipedia wikiből
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Deriválás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Adottak az alábbi vektorok.
-
![\[\mathbf{v}_{1}=\left[\begin{array}{c} 1 \\ 2 \\ -1 \end{array}\right]\qquad\qquad\mathbf{v}_{2}=\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]\]](/images/math/c/9/7/c9790a0215a98942995b7e3b46bfefe5.png)
- a) Határozzuk meg az
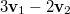 vektort!
vektort!
- b) Mekkora a vektorok normája (nagysága)?
- c) Mekkora szöget zár be a két vektor?
- d) Adjuk meg a
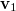 vektor
vektor 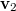 irányába eső komponensét!
irányába eső komponensét!
-
Megoldás
- a)
![\[ 3\mathbf{v}_{1}-2\mathbf{v}_{2}= 3 \left[\begin{array}{c} 1 \\ 2 \\ -1 \end{array}\right]- 2 \left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]= \left[\begin{array}{c} 3 \\ 6 \\ -3 \end{array}\right]- \left[\begin{array}{c} 0 \\ 2 \\ 2 \end{array}\right]= \left[\begin{array}{c} 3 \\ 4 \\ -5 \end{array}\right]\]](/images/math/3/e/f/3efaca08c151b99db0f569bcec1da448.png)
- b)
![\[|\mathbf{v}_{1}|^{2}=1^{2}+2^{2}+(-1)^{2}=6\qquad\Rightarrow\qquad |\mathbf{v}_{1}|=\sqrt{6}\]](/images/math/6/4/a/64ae8794ddd544aa99185d95df34498f.png)
![\[|\mathbf{v}_{2}|^{2}=0^{2}+1^{2}+1^{2}=2\qquad\Rightarrow\qquad |\mathbf{v}_{2}|=\sqrt{2}\]](/images/math/5/b/d/5bde7fe03adb483b10912347a81afcd8.png)
- c) Bármely két vektor esetén ahol
![\[\mathbf{v}_{1}\cdot\mathbf{v}_{2}=|\mathbf{v}_{1}||\mathbf{v}_{2}|\cos\alpha\,,\]](/images/math/6/0/6/606fc9ec1545e8a6081adc2dd89bf85e.png)
 a vektorok skaláris szorzását jelöli és
a vektorok skaláris szorzását jelöli és  a két vektor által bezárt szög. Ebben a feladatban tehát
a két vektor által bezárt szög. Ebben a feladatban tehát![\[\mathbf{v}_{1}\cdot\mathbf{v}_{2}=1\cdot 0+ 2\cdot 1+ -1\cdot 1=1\,,\]](/images/math/5/b/6/5b603bf79ada96dcbc86e982f7f83ffe.png)
![\[1=\sqrt{6}\sqrt{2}\cos\alpha\qquad\Rightarrow\qquad \alpha=73,2\,^{\circ}\]](/images/math/d/5/3/d5382063d946b62cf34e8ddf78223adf.png)
- d) A
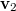 vektor irányába mutató egység vektor Ezzel az egységvektorral a
vektor irányába mutató egység vektor Ezzel az egységvektorral a![\[\mathbf{n}_{2}=\frac{\mathbf{v}_{2}}{|\mathbf{v}_{2}|}=\frac{1}{\sqrt{2}}\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]\,.\]](/images/math/4/7/a/47a0c2883324f5543b79f5b3c4d845ed.png)
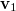 vektor
vektor 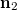 irányába mutató komponense
irányába mutató komponense ![\[\mathbf{v}_{12}=\mathbf{n}_{2}(\mathbf{n}_{2}\cdot\mathbf{v}_{1})=\frac{1}{2}\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]\,.\]](/images/math/4/f/2/4f26d9ceda96ce249fd9eecead34e0b4.png)
- a)