Elektrosztatika
Tartalomjegyzék |
A Coulomb törvény és nyugvó ponttöltés tere
Ebben a fejezetben kiderül, hogy miért használnak villámhárítót és az hogyan tudja megvédeni az épületeket a bennük található elektronikus berendezésekkel együtt. Megtudjuk, hogy miért burkolják a számítógépes termek járófelületét elektrosztatikus padlóval. A CRT monitor és a számítógépes billentyűzet működési elve is könnyen megérthető az elektrosztatika törvényeinek alkalmazásával. Választ kaphatunk arra a kérdésre is, hogy a számítógép háza miért készül fémből.
Töltések
A középkorban, sőt már az ókorban is ismert volt néhány dörzselektromos jelenség . Az egyik csaknem mindenki által ismert kísérletben üvegrudat bőrrel dörzsölve azt tapasztalhatjuk, hogy egy cérnaszálra függesztett alufólia darabkát a rúd először vonz, majd érintkezés után taszít. A kísérlet természetesen elvégezhető más anyagokkal is: dörzsölhetünk gyapjúval ebonitrudat vagy egy műanyag vonalzót textillel és alufólia helyett használhatunk kis papírdarabkákat. (Testek elektromos jellegének vizsgálatához elektroszkópot használnak.) A dörzsöléssel sajátos elektromos állapotba hozott két ebonitrúd taszítja egymást. Ugyanez elmondható két bőrrel dörzsölt üvegrúdra is. Azonban az ebonitrúd és az üvegrúd vonzzák egymást. Ugyanezt a kísérletet más anyagdarabokkal megismételve azt tapasztalták, hogy az elektromos állapotba hozott testek között taszító vagy vonzó jellegű kölcsönhatás lép fel. A jelenség magyarázata a következő: a dörzsölés hatására elektromos töltések jutnak át az egyik szigetelőről a másikra az érintkezési pontokban. A kísérletek alapján megállapították, hogy kétféle elektromos töltés van, tehát a testek pozitív ill. negatív töltéssel lettek feltöltve. Megállapodás alapján a bőrrel dörzsölt üvegrúd töltését pozitívnak mondjuk. Az is egyértelműen kiderült, hogy az egynemű töltések taszítják egymást, míg a különböző nemű töltések között vonzó jellegű kölcsönhatás lép fel, azaz a pozitív töltések taszítják egymást; ugyanígy a negatív töltések között is taszítás alakul ki, azonban a pozitív és a negatív töltések vonzzák egymást. Az elektromosan fel nem töltött testet semlegesnek nevezzük, benne ill. rajta a pozitív és negatív töltések száma megegyezik. Kapcsolódó videó: Töltések elhelyezkedése vezető felületén
Coulomb törvény
Az elektrosztatikában nyugalomban lévő töltött részecskék közötti kölcsönhatást, a töltés(ek) terét, a töltésrendszer energiáját, stb. vizsgáljuk. Az elektrosztatikus erő vizsgálatára először C. A. Coulomb két kisméretű – pontszerűnek tekinthető - töltött test közötti erőhatást torziós mérleggel mérve a következő megállapításokra jutott.
Két töltött, pontszerű részecske közötti elektrosztatikus erőhatás nagysága a közöttük lévő távolság négyzetével fordítva arányos.
Az elektrosztatikus erők esetében is érvényes a kölcsönhatás törvénye (erő-ellenerő).
A töltött részecskék közötti erőhatás mértéke a két pontszerű töltés szorzatával arányos.
Az eredmények alapján Coulomb 1783-ban matematikai formában is megadta a két töltött, pontszerűnek tekinthető részecske közötti elektrosztatikus erő nagyságát, így a róla elnevezett Coulomb törvény:
![\[ {\ F} = k \frac{Q_1 Q_2}{r^2} \]](/images/math/f/6/1/f61bee848f71a7be339e8498ef4c9748.png) |
(1.2.1) |
ahol 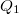 és
és 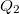 a két töltött részecske töltése,
a két töltött részecske töltése,  a közöttük lévő távolság és
a közöttük lévő távolság és  arányossági tényező. Az elektromos töltés mértékegysége a
arányossági tényező. Az elektromos töltés mértékegysége a  (Coulomb). A távolság méterben mérendő. Az arányossági tényező pedig
(Coulomb). A távolság méterben mérendő. Az arányossági tényező pedig 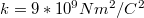 . Ezt az arányossági tényezőt szokás még a következő alakban is megadni:
. Ezt az arányossági tényezőt szokás még a következő alakban is megadni:
![\[ {\ k} = \frac{1}{4\pi\varepsilon_0} \]](/images/math/4/0/f/40fc77eee0fdeffdad2de23810ed1b06.png)
ahol 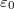 a vákuum permittivitása és értéke
a vákuum permittivitása és értéke 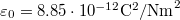 .
Ma már tudjuk, hogy az atomok és molekulák semleges neutronokat, pozitív töltésű protonokat és negatív töltéssel rendelkező elektronokat tartalmaznak. Az elektron és a proton töltésének nagysága megegyezik. Ebből az is következik, hogy minden töltött test töltésének nagysága az elektron vagy a proton töltésének egész számú többszöröse. Az elektron töltésének meghatározására először 1910-ben Millikan épített kísérleti elrendezést. Az azóta megvalósított pontosabb kísérletek alapján az elektron töltése:
.
Ma már tudjuk, hogy az atomok és molekulák semleges neutronokat, pozitív töltésű protonokat és negatív töltéssel rendelkező elektronokat tartalmaznak. Az elektron és a proton töltésének nagysága megegyezik. Ebből az is következik, hogy minden töltött test töltésének nagysága az elektron vagy a proton töltésének egész számú többszöröse. Az elektron töltésének meghatározására először 1910-ben Millikan épített kísérleti elrendezést. Az azóta megvalósított pontosabb kísérletek alapján az elektron töltése:
![\[ {q_e = 1.6*10^{-19} C} \]](/images/math/4/4/4/444f886ff494462a9907bc8ee0665c7b.png)
(az elektron és a proton ill. a neutron tömege és egyéb állandók a függelékben találhatók.)
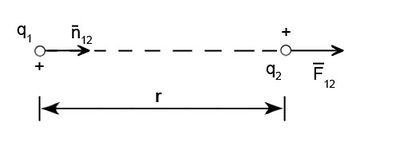
Két ponttöltés kölcsönhatásaként fellépő elektrosztatikus erő vektoriális alakban is megadható:
![\[{\vec F} = k \frac{Q_1 Q_2}{r^2} {\vec n_{12}} \]](/images/math/a/5/6/a56a68bda85682ea9b4d4780ded9890f.png) |
(1.2.2) |
| 1. ábra |
ahol az 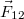 erő a
erő a 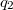 töltésre hat és
töltésre hat és 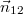 a
a 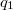 töltéstől a
töltéstől a 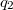 töltés felé mutató egységvektor. A kölcsönhatási törvény érvényesülése – egy egyszerű matematikai módszerrel – indexcserével megvalósul, tehát a
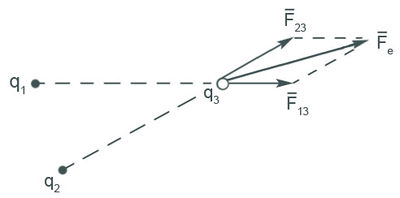
töltés felé mutató egységvektor. A kölcsönhatási törvény érvényesülése – egy egyszerű matematikai módszerrel – indexcserével megvalósul, tehát a 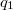 töltésre ható erő is egyszerűen meghatározható. Ha egy ponttöltés néhány másik ponttöltés környezetében található, akkor a töltésre ható eredő erő az egyes elektrosztatikus kölcsönhatásokból származtatható erők vektoriális összege, azaz alkalmazható a szuperpozíció elve.
töltésre ható erő is egyszerűen meghatározható. Ha egy ponttöltés néhány másik ponttöltés környezetében található, akkor a töltésre ható eredő erő az egyes elektrosztatikus kölcsönhatásokból származtatható erők vektoriális összege, azaz alkalmazható a szuperpozíció elve.
| 2. ábra |
Elektromos erőtér
Az előzőekben láttuk tehát, hogy két - egymástól akár nagyobb távolságban lévő - töltés között is erőhatás lép fel. Kérdés, hogy ez hogyan lehetséges. A ponttöltések közötti erő nagyságát megadó Coulomb törvény alakja formailag igen hasonlít a tömegvonzás formulájára, amelynek használata során feltesszük (a klasszikus mechanikában), hogy mozgó tömegpontok esetén is alkalmazható. Ez a tömegvonzás esetében azt jelenteni, hogy van egy olyan – minden közvetítő nélkül működő - távolhatás, amely minden időpontban csak a tömegpontok pillanatnyi helyzetétől függ, azaz ennek a hatásnak végtelen gyorsan kell terjednie. Mai szemléletünk alapján azonban a végtelen gyorsan, közvetítő közeg nélkül terjedő távolhatás eszméje a fizikában nem elfogadható. Felfogásunk szerint minden elektromosan töltött testnek vagy részecskének van elektromos tere (ezt elektromos mezőnek is nevezik). Az elektromos tér közvetíti az elektrosztatikus erőhatást két töltött részecske között. Ennek a jelentése a következő: ha egy töltés egy másik töltés erőterében van, akkor arra a másik töltés elektromos tere erőhatást gyakorol és fordítva. Felvetődik a kérdés, hogy egy töltött részecskére hogyan hat a saját erőtere. Ezt a problémát itt nem tárgyaljuk részletesen; egyszerűen fogadjuk el, hogy egy töltött részecske – például az elektron – a saját elektromos erőterét "nem érzi". Tehát egy töltött részecskére egy másik töltés elektromos terében erő hat. Ezt a hatást írja le a Coulomb törvény nyugvó részecskék esetében. Ennek segítségével egyszerűen meghatározhatjuk egy ponttöltés elektromos terét. Formailag átalakítva a Coulomb törvény vektoriális alakját (1.2.2 képlet) a következőt kapjuk:
![\[{\vec F} = k \frac{Q}{r^2} {\vec n_{12}{\cdot}{q}} \]](/images/math/2/8/1/2814e04da6f82b18462da305870ec259.png) |
(1.3.1) |
ahol 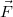 erő a Q töltés terében a q töltésre hat. (Az
erő a Q töltés terében a q töltésre hat. (Az 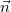 a Q töltéstől a q töltés irányába mutató egységvektor.)
A kölcsönhatás – mint az látható - megadható az
a Q töltéstől a q töltés irányába mutató egységvektor.)
A kölcsönhatás – mint az látható - megadható az 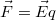 alakban, ahol
alakban, ahol 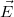 a Q ponttöltés elektromos erőtere:
a Q ponttöltés elektromos erőtere:
![\[{\vec E} = k \frac{Q}{r^2} {\vec n_{12}} \]](/images/math/4/6/5/465cab591d812322d451ed130885a62a.png) |
(1.3.2) |
Mondhatjuk tehát, hogy egy Q ponttöltés elektromos tere megadható az
![\[{\vec E} = k \frac{Q}{r^2} {\vec n} = k \frac{Q}{r^3} {\vec r} \]](/images/math/9/9/2/9928710376e383a7c2214fe721a9cf59.png) |
(1.3.3) |
általánosabb formában, ahol 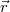 a ponttöltésből a tér adott pontjába mutató vektor, és az azzal párhuzamos egységvektor az
a ponttöltésből a tér adott pontjába mutató vektor, és az azzal párhuzamos egységvektor az 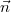 .
.
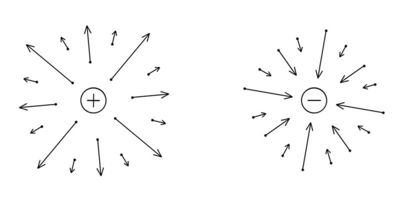
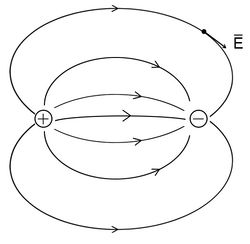
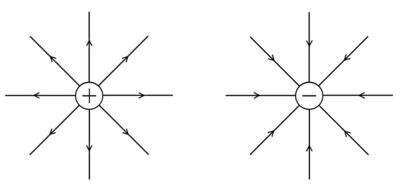
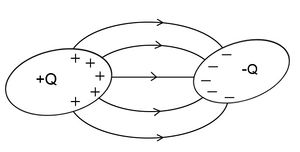
Egy pozitív és egy negatív töltés elektromos terét szemlélteti a 3. ábra.
| 3. ábra |
Minthogy az egy töltésre ható elektrosztatikus erő egy töltésrendszer terében az egyes töltésekkel fennálló kölcsönhatás következtében fellépő erők vektoriális összege, ezért mondhatjuk, hogy az eredő elektromos térerősség meghatározásához is használhatjuk a szuperpozíció elvét, azaz 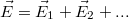 (4. ábra).
(4. ábra).
| 4. ábra |
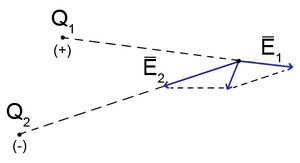
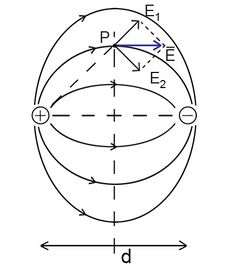
A előbbiek szemléltetésére jó példa az elektromos dipólus, amely egymástól bizonyos távolságban lévő 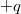 és egy
és egy 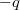 töltésekből áll. Az elektromos dipólus terét szemlélteti a következő két ábra:
töltésekből áll. Az elektromos dipólus terét szemlélteti a következő két ábra:
| 5.a ábra | 5.b ábra |
A P pontban (5.b ábra) az 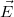 eredő elektromos térerősség a
eredő elektromos térerősség a 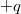 töltés
töltés 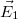 és a
és a 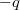 töltés
töltés 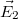 térerősségének vektori összege. Az elrendezés szimmetriájából adódik, hogy a két töltést összekötő szakasz felezőpontjára merőleges síkra a térerősség vonalak merőlegesek.
térerősségének vektori összege. Az elrendezés szimmetriájából adódik, hogy a két töltést összekötő szakasz felezőpontjára merőleges síkra a térerősség vonalak merőlegesek.
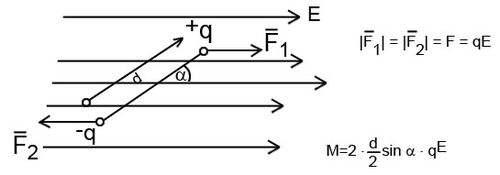
Az is fontos kérdés, hogy mi történik, ha egy dipólt elektromos térbe helyezünk. Könnyű belátni, hogy egy elektromos dipólusra homogén elektromos erőtérben ható eredő erő zérus, hiszen a 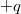 és a
és a 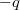 töltésekre ható
töltésekre ható 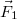 és
és 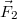 erők (6.ábra) kioltják egymást, hiszen
erők (6.ábra) kioltják egymást, hiszen 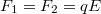 .
.
| 6. ábra |
Igaz ugyan, hogy a dipólra kapott eredő erő homogén térben eltűnik, azonban forgatónyomaték hat rá, amelynek nagysága – az ábra jelöléseit felhasználva – könnyen kiszámítható:
![\[{M = qdE \sin({\alpha})= pE \sin({\alpha})} \]](/images/math/4/7/7/4777de08c78c8c9dae0c2f099ba0abc7.png) |
(1.3.4) |
ahol  a két töltés távolsága és
a két töltés távolsága és 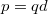 az elektromos dipólmomentum vektorának abszolút értéke; a
az elektromos dipólmomentum vektorának abszolút értéke; a 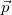 a
a 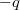 töltéstől a
töltéstől a 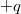 felé mutat. Az elektromos dipólra ható forgatónyomaték vektoriális alakban is megadható:
felé mutat. Az elektromos dipólra ható forgatónyomaték vektoriális alakban is megadható:
![\[{\vec M} = {\vec p}{\times} {\vec E} \]](/images/math/d/2/8/d28100af17ecaf560d2ad8f0edb03b10.png) |
(1.3.5) |
Az elektromos dipólra inhomogén erőtérben nem csak forgatónyomaték, hanem erő is hat. A precíz bizonyítás helyett ezt könnyen beláthatjuk egy leegyszerűsített modell segítségével. Legyen az elektromos erőtér párhuzamos az x tengellyel annak a pontnak a közelében, ahol a kisméretű dipól található. A tér inhomogén, azaz 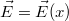 . A dipól két töltése (vagy két töltéssúlypontja) közötti távolság
. A dipól két töltése (vagy két töltéssúlypontja) közötti távolság 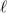 . Ekkor a két töltésre ható erő eredőjének nagysága:
. Ekkor a két töltésre ható erő eredőjének nagysága:
![\[{F = q[E(x+\Delta x)-E(x)]} \]](/images/math/5/c/f/5cf6cf25015d8cf2dd7a324f6f11a76a.png) |
(1.3.6) |
Ebből elsőrendű közelítéssel és kihasználva, hogy 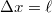 - amennyiben az elektromos dipól beállt az elektromos erőtér irányába - és
- amennyiben az elektromos dipól beállt az elektromos erőtér irányába - és 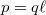 , kapjuk a dipólra ható erő nagyságát:
, kapjuk a dipólra ható erő nagyságát:
![\[{F = q \frac{{\rm d}E}{{\rm d}x}\Delta x = \frac{{\rm d}E}{{\rm d}x}p} \]](/images/math/0/c/a/0ca86aa4ddfae558eb27a0c69967c903.png) |
(1.3.7) |
Egy ponttöltésre ható elektrosztatikus erő - mint azt már láttuk - az 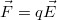 alakban adható meg. Amennyiben egy töltéssel rendelkező részecske csak az elektromos térrel van kölcsönhatásban, akkor a töltött részecske gyorsulása a mechanika módszereinek felhasználásával meghatározható, azaz:
alakban adható meg. Amennyiben egy töltéssel rendelkező részecske csak az elektromos térrel van kölcsönhatásban, akkor a töltött részecske gyorsulása a mechanika módszereinek felhasználásával meghatározható, azaz:
![\[{\vec a} = \frac{q \vec E}{m} \]](/images/math/c/8/7/c87e770226a08d61b38172e75e6b3e88.png) |
(1.3.8) |
Most már érthető, hogy töltött részecskéket miért lehet elektromos tér alkalmazásával gyorsítani. Jó példa erre - az igen nagyszámú egyéb alkalmazás mellett - a lineáris részecskegyorsító, amelynek segítségével csaknem fénysebességre lehet elektronokat, protonokat, ionokat stb. gyorsítani.
Az elektromos teret nem csak a töltött részecskék illetve részecskék nyalábjának (pl. egy elektronnyaláb) gyorsítására, hanem irányának megváltoztatásához, eltérítéséhez is lehet használni. Ezen az effektuson alapul a CRT monitor (pl. televízió képcsöve) működési elve (1.3.6 fejezet).
Töltéssűrűség
Amennyiben nem csak ponttöltéseket vizsgálunk, hanem egy ill. többdimenziós tartományon elosztott töltéseket, akkor definiálhatunk lineáris, felületi és térfogati töltéssűrűséget.
Ha egy  hosszúságú szakaszon
hosszúságú szakaszon  töltés helyezkedik el, akkor a lineáris töltéssűrűség:
töltés helyezkedik el, akkor a lineáris töltéssűrűség:
![\[{\lambda} = \frac{Q}{\ell} \qquad {\rm ill.} \qquad {\lambda} = \mathop{\rm{lim}}_{\Delta \ell \longrightarrow 0} \frac{\Delta Q}{\Delta \ell}\]](/images/math/3/d/f/3df0e6f0d868064669ed538262abea6e.png) |
(1.4.1) |
Hasonlóképpen a felületi töltéssűrűség:
![\[{\sigma} = \frac{Q}{A} \qquad {\rm ill.} \qquad {\sigma} =\mathop{\rm{lim}}_{\Delta A\longrightarrow 0} \frac{\Delta Q}{\Delta A}\]](/images/math/3/a/b/3abe392486dbc742055e6f6decbd3474.png) |
(1.4.2) |
ahol  a felület nagysága, melyen
a felület nagysága, melyen  töltés található.
A térfogati töltéssűrűség:
töltés található.
A térfogati töltéssűrűség:
![\[{\rho} = \frac{Q}{V} \qquad {\rm ill.} \qquad {\rho} =\mathop{\rm{lim}}_{\Delta V\longrightarrow 0} \frac{\Delta Q}{\Delta V}\]](/images/math/7/1/9/71916a7967c6f0499d6a8424d40f6bfe.png) |
(1.4.3) |
ahol  a térfogat, amelyben
a térfogat, amelyben  töltés van.
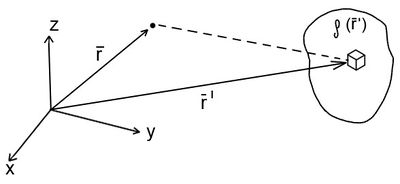
Adott töltéssűrűségek esetén is kiszámítható a tér egy pontjában az eredő elektromos tér a szuperpozíció elvét felhasználva. Például ismert térfogati töltéssűrűség környezetében az eredő elektromos térerősség
töltés van.
Adott töltéssűrűségek esetén is kiszámítható a tér egy pontjában az eredő elektromos tér a szuperpozíció elvét felhasználva. Például ismert térfogati töltéssűrűség környezetében az eredő elektromos térerősség
![\[{\vec E (\vec r)} = \int\limits_{V'} \frac{1}{4\pi\varepsilon_0} \frac{\rho(\vec r')}{\left| \vec r - \vec r' \right|^3} (\vec r - \vec r') {\rm d}V' \]](/images/math/f/8/3/f83573d9734469ce9686298e0c01b01d.png) |
(1.4.4) |
ahol a töltésrendszert magába foglaló 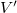 térfogatra kell integrálni (7. ábra).
térfogatra kell integrálni (7. ábra).
| 7. ábra |
Ugyanez a módszer alkalmazható felületi és lineáris töltéssűrűségre, azonban ott értelemszerűen az adott felületre ill. vonaldarabra kell integrálni.
A Gauss-törvény
Az elektromos térerősség ábrázolása – elektromos erővonalak
Az elektromos erőtér egy vektormező, amelynek grafikus ábrázolása – a valóságban nem létező – de igen szemléletes erőtérvonalakkal (hallgatólagosan már eddig is használtuk a fogalmat, építve az előtanulmányok ismereteire) is ábrázolható pl. magányos ponttöltések esetében (8.ábra).
| 8. ábra |
Az erővonalak általában nem egyenesek. Jó példa erre a két, egymás közelében elhelyezkedő pozitív és negatív töltés együttes terét szemléltető erővonal-kép (3.ábra).
Az erővonal egy pontjában az elektromos térerősség vektora érintőirányú. Az elektromos térerősség-vonalak kísérleti szemléltetése is lehetséges.
A erővonalkép alkalmas arra is, hogy az erőteret jellemezzük. Az előző két ábrán is látható, hogy a nagyobb elektromos térerősség nagyobb erővonal-sűrűséget jelent. Tegyük fel, hogy egy ponttöltésből kiindul N db erővonal. A töltéstől r távolságban a térerősség nagysága, mint azt láttuk:
![\[E = k \frac{Q}{r^2} \]](/images/math/7/0/c/70cb89ed031255b5d57b39fdddd19dfd.png) |
(1.5.1) |
Ekkor a töltést koncentrikusan körülvevő,  sugarú gömbfelület nagysága
sugarú gömbfelület nagysága 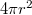 és a rajta átmenő erővonalak sűrűsége:
és a rajta átmenő erővonalak sűrűsége:
![\[n = \frac{N}{4{\pi}{r^2}} \]](/images/math/e/6/e/e6efbaa234a1b757ed4b9076fb434767.png) |
(1.5.2) |
Az (1.5.1) és (1.5.2) formulák alapján mondhatjuk, hogy a térerősség nagysága arányos az erővonal-sűrűséggel.
Az elektromos fluxus
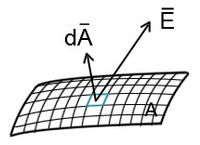
Valamely vektortér – pl. elektromos térerősség – fluxusát egy felületre a következőképpen definiálhatjuk (lásd az 9. ábra jelöléseit):
![\[{\Phi} = \int\limits_{A} \vec E \ {\rm d}\vec A \]](/images/math/1/e/0/1e099facda54e42bd9663519c940fd97.png) |
(1.5.3) |
| 9. ábra |
ahol 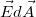 az infinitezimális felületelem vektor és a térerősség vektor skaláris szorzata és ezt kell az adott felületre integrálni. A felületelem vektora merőleges a felületre, nagysága a felületelem mértékével (felületével) egyezik meg és zárt felület esetén kifelé mutat (a zárt térrészből).
az infinitezimális felületelem vektor és a térerősség vektor skaláris szorzata és ezt kell az adott felületre integrálni. A felületelem vektora merőleges a felületre, nagysága a felületelem mértékével (felületével) egyezik meg és zárt felület esetén kifelé mutat (a zárt térrészből).
Gauss törvény
Az előzőek után könnyen belátható, hogy a ponttöltést koncentrikusan körülvevő r sugarú gömbfelületre az elektromos fluxus (ebben az egyszerű példában a térerősség nagysága és a felület szorzata):
![\[{\Phi} = \int\limits_{A} \vec E \ {\rm d}\vec A = \frac{1}{4\pi\varepsilon_0} \frac{Q}{r^2} \cdot 4{\pi}{r^2} = \frac{Q}{\varepsilon_0} \]](/images/math/7/2/e/72ec31a8f81138e66bf65f40a88ce675.png) |
(1.5.4) |
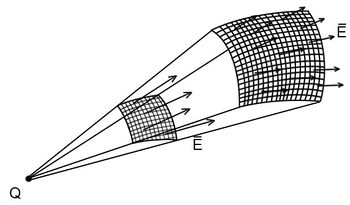
Szemléletesen megmutatható az is, hogy nem csak koncentrikus gömbfelületek esetében kapjuk ugyanazt az értéket a fluxusra egy ponttöltés esetén. Tekintsük a következő ábrán látható két gömbsüveget a Q töltés terében:
| 10. ábra |
A gömbsüveg darabkák felülete 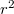 - tel, és a rá mindenhol merőleges a térerősség nagysága
- tel, és a rá mindenhol merőleges a térerősség nagysága 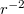 – nal arányos; ebből következik, hogy a fluxus értéke az adott térszögre állandó. Egy egyszeresen összefüggő felület felületelemei viszont nem biztos, hogy merőlegesek az elektromos térerősségvonalakra.
– nal arányos; ebből következik, hogy a fluxus értéke az adott térszögre állandó. Egy egyszeresen összefüggő felület felületelemei viszont nem biztos, hogy merőlegesek az elektromos térerősségvonalakra.
Ebben az esetben azonban az elemi felületelemre számítható fluxust meghatározó 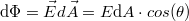 kifejezésben a
kifejezésben a 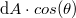 éppen a felületelem térerősségre merőleges
éppen a felületelem térerősségre merőleges 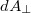 vetületét adja. Megállapíthatjuk tehát, hogy az adott - infinitezimális -
vetületét adja. Megállapíthatjuk tehát, hogy az adott - infinitezimális - 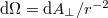 térszögre kapott fluxus értéke valóban állandó érték és nagysága:
térszögre kapott fluxus értéke valóban állandó érték és nagysága:
![\[{{\rm d}\Phi} = \frac{Q}{4\pi\varepsilon_0} {{\rm d}\Omega} \]](/images/math/8/3/1/83153ed046340115521f64696292486e.png) |
(1.5.5) |
Az előzőek alapján könnyen belátható, hogy egy  töltést tartalmazó zárt felületre - azaz
töltést tartalmazó zárt felületre - azaz 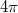 térszögre - a fluxus értéke
térszögre - a fluxus értéke 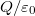 , a felület alakjától függetlenül.
, a felület alakjától függetlenül.
Ha a tér – melyben több töltés is található - egy pontjában az eredő térerősséget szeretnénk meghatározni, akkor a szuperpozíció elvét alkalmazhatjuk, azaz az adott pontban az egyes töltések elektromos terét kell vektoriálisan összeadni. Minthogy az 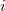 -ik töltést körülvevő zárt felületre a fluxus
-ik töltést körülvevő zárt felületre a fluxus 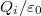 , így tehát a szuperpozíció elvének alkalmazásával megkapjuk a Gauss törvény matematikai alakját, azaz egy töltésrendszert magába foglaló zárt felületre a fluxus:
, így tehát a szuperpozíció elvének alkalmazásával megkapjuk a Gauss törvény matematikai alakját, azaz egy töltésrendszert magába foglaló zárt felületre a fluxus:
![\[{\Phi} = \int\limits_{A} \vec E \ {\rm d}\vec A = \frac{\sum_{i} Q_i}{\varepsilon_0} \]](/images/math/9/5/4/9540b7fb4fbe6588c49f3a5ccc2b6c1b.png) |
(1.5.6) |
ahol természetesen a 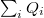 a zárt felületen belüli össztöltést jelenti.
a zárt felületen belüli össztöltést jelenti.
A Gauss-törvény használatával szimmetrikus töltéselrendezés esetében általában jóval könnyebb az elektromos erőtér nagyságát meghatározni, mint a szuperpozíció elvének - pl. az (1.4.4) formula - felhasználásával.
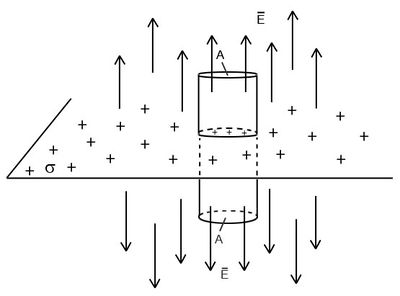
Lássunk erre egy példát! Határozzuk meg egy végtelen nagy, 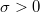 , azaz pozitív, állandó felületi töltéssűrűségű lemez környezetében az elektromos térerősség nagyságát. Az elrendezés szimmetriájából adódik (transzlációs szimmetria), hogy az elektromos erőtér csak a lemezre merőleges lehet és nagysága mindenhol ugyanakkora, azaz homogén erőtér van a lemez két oldalán. (A térerősség vektorok a lemez két oldalán ellentétes irányúak.) A 11. ábrán látható Gauss-dobozra – mint zárt felületre - felírhatjuk a Gauss-törvényt.
, azaz pozitív, állandó felületi töltéssűrűségű lemez környezetében az elektromos térerősség nagyságát. Az elrendezés szimmetriájából adódik (transzlációs szimmetria), hogy az elektromos erőtér csak a lemezre merőleges lehet és nagysága mindenhol ugyanakkora, azaz homogén erőtér van a lemez két oldalán. (A térerősség vektorok a lemez két oldalán ellentétes irányúak.) A 11. ábrán látható Gauss-dobozra – mint zárt felületre - felírhatjuk a Gauss-törvényt.
| 11. ábra |
A fluxus megadásához elegendő figyelembe venni a doboz két véglapját, hiszen az oldalfalon nem megy át elektromos erőtérvonal. Legyen mindkét véglap területe  , ekkor a Gauss-törvény alkalmazása igen egyszerű, hiszen a bezárt töltés
, ekkor a Gauss-törvény alkalmazása igen egyszerű, hiszen a bezárt töltés 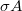 , tehát:
, tehát:
![\[\int\limits_{A} \vec E \ {\rm d}\vec A = 2EA = \frac{\sigma A}{\varepsilon_0}\]](/images/math/e/9/c/e9ce5807ec63dd5a60ae180c9cfa09fe.png) |
(1.5.7) |
Ebből az elektromos térerősség nagysága kifejezhető:
![\[E = \frac{\sigma}{2 \varepsilon_0}\]](/images/math/4/a/0/4a0ac2696787ca5f09092bce66ba1e4c.png) |
(1.5.8) |
Ez a számítás jó közelítéssel használható egy igen nagyméretű töltött lemez esetében is, amennyiben a pont - ahol a térerősséget szeretnénk meghatározni - jóval távolabb van a lemez széleitől, mint magától a lemeztől.
Vezetők és szigetelők
Az anyagokat csoportosíthatjuk aszerint is, hogy mennyire jól vezetik az elektromosságot, azaz bennük, ill. rajtuk mennyire könnyen mozdulhatnak el a töltések. Ezen tulajdonságuk alapján beszélhetünk vezetőkről, szigetelőkről és félvezetőkről. A szilárd testek általában rácsszerkezettel rendelkeznek. A bennük lévő ionok (azaz az atommagok és a vezetésben nem résztvevő elektronok) töltése pozitív és a rácsban az egymástól mért távolságuk állandó. A körülöttük lévő elektronok semlegesítik az atommagok illetve az ionok terét. Ez egy igen leegyszerűsített kép; a szilárdtestek szerkezetéről, tulajdonságairól a modern fizika tárgyban lesz szó.
Elektromos vezetők
A fémes vezetőkben az elektronok egy része könnyen – úgy is mondhatjuk, hogy szabadon – el tud mozdulni. Ezeket a szabad elektronokat nevezzük vezetési elektronoknak, amelyek – mint ahogy a nevük is utal rá – felelősek a fémek jó vezetőképességéért (később pontosan definiáljuk a vezetőképességet). A különböző fémes vezetők vezetőképessége általában eltérő. Jó vezető az arany, az ezüst, a réz, stb.
Szigetelők
A szigetelőkben az elektronok helye a rácsban kötött, ezért töltésvezető tulajdonságuk gyenge. Ez természetesen nem azt jelenti, hogy a szigetelők egyáltalán nem vezetik az áramot, azonban a fémes vezetőkhöz képest töltésvezető képességük akár húsz nagyságrenddel is kisebb lehet. Ha egy szigetelő anyag felületére elektromos töltést helyezünk, akkor az hosszú időn keresztül ott is marad.
Félvezetők
Vezetőképességüket tekintve a félvezető anyagok a fémes vezetők és a szigetelők között helyezkednek el. A félvezető kristályok – például a szilícium vagy a germánium - általában a fémekhez viszonyítva rosszul vezetik az elektromosságot, azonban a szigetelőkhöz képest jó vezetők. Fontos megjegyezni azonban, hogy a félvezető anyagot más atomokkal "szennyezve" annak vezetőképessége nagyságrendekkel megváltoztatható. Bizonyos anyagok vezetőképessége például megvilágítás hatására növekszik meg (photoconductor).
Vezető anyag elektrosztatikus erőtérben
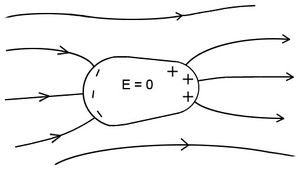
Amennyiben egy jó vezetőből készült anyagdarabot olyan térrészbe helyezünk, ahol az időben állandó elektromos térerősség nem zérus, akkor a vezető elektronjainak egy része igen gyorsan kialakít egy olyan elrendeződést – felületi töltéssűrűséget – amely leárnyékolja a külső teret (12. ábra), azaz a vezetőn belül az elektromos térerősség zérus.
| 12. ábra |
Az ábrán az is látszik, hogy az eredetileg semleges test - amely semmilyen elektromos tulajdonságot nem mutatott – a külső elektromos erőtér hatására ellentétes előjelű töltéseket halmoz fel a felület különböző részein. (Az össztöltés természetesen a továbbiakban is nulla.) Ezt a jelenséget nevezzük töltésmegosztásnak. Az is könnyen belátható, hogy a vezető felület közelében a térerősség a felületre merőleges, hiszen ha a felülettel párhuzamos komponense is lenne, akkor a felület közelében lévő elektronokra elektrosztatikus erő hatna és az elektronok ennek hatására elmozdulnának. Az elektronok a jó vezetőben viszont mindaddig mozognak, amíg elektromos erő hat rájuk, azaz amíg a töltött részecskék új elrendezése ki nem oltja az elektromos erőteret az anyagon belül és mindaddig, amíg a felülettel párhuzamos elektromos térerősség komponens nem lesz zérus.
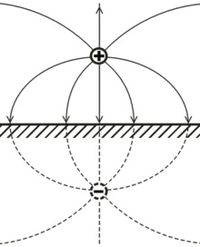
Jól példázza az előbb említett két feltétel - azaz, hogy a vezetőben a térerősség nulla és a téresősség-vektor merőleges a felületre - teljesülését a következő példa. Legyen  töltés
töltés 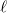 távolságban egy
távolságban egy 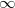 (nagyon nagy) vezető síktól (13. ábra). Kérdés, hogy hogyan lehet meghatározni az elektromos tér szerkezetét a
(nagyon nagy) vezető síktól (13. ábra). Kérdés, hogy hogyan lehet meghatározni az elektromos tér szerkezetét a  töltést tartalmazó, a sík által határolt féltérben. Erre a választ egy igen egyszerű módszer segítségével kaphatjuk meg. Tételezzük fel, hogy egy
töltést tartalmazó, a sík által határolt féltérben. Erre a választ egy igen egyszerű módszer segítségével kaphatjuk meg. Tételezzük fel, hogy egy 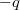 ún. tükörtöltés jelenik meg a sík másik oldalán - attól éppen
ún. tükörtöltés jelenik meg a sík másik oldalán - attól éppen 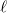 távolságban - az eredeti töltés síkra tükrözött helyzetében. Az ábrán jól látszik, hogy a gondolatban odaképzelt virtuális
távolságban - az eredeti töltés síkra tükrözött helyzetében. Az ábrán jól látszik, hogy a gondolatban odaképzelt virtuális 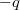 töltéssel együtt az eredeti
töltéssel együtt az eredeti  töltés együtt egy elektromos dipólt képez és ennek térerőssége - a q töltést tartalmazó féltérben - éppen megfelel az említett feltételeknek. Természetesen a
töltés együtt egy elektromos dipólt képez és ennek térerőssége - a q töltést tartalmazó féltérben - éppen megfelel az említett feltételeknek. Természetesen a 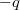 töltés nem a tükörhelyzetben jelenik meg, hanem el van osztva a fémvezető felületén. A vezető lap felszínén a felületi töltéssűrűség kiszámítható az (1.5.8) formula segítségével. (Könnyen ellenőrizhető, hogy jól számoltunk-e, hiszen
töltés nem a tükörhelyzetben jelenik meg, hanem el van osztva a fémvezető felületén. A vezető lap felszínén a felületi töltéssűrűség kiszámítható az (1.5.8) formula segítségével. (Könnyen ellenőrizhető, hogy jól számoltunk-e, hiszen  -t kiintegrálva a felületre
-t kiintegrálva a felületre 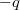 -t kell kapnunk).
-t kell kapnunk).
Azt, hogy a szigetelők hogyan viselkednek külső elektromos erőtérben, majd később mutatjuk meg (4.6. fejezet). A félvezetők tulajdonságait, vezetőképességét, stb. a modern fizika rész tárgyalja.
Az elektromos potenciál és energia
Töltött részecskén végzett munka elektrosztatikus térben
Amennyiben egy q töltésű részecskét az 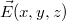 elektromos térben az
elektromos térben az  pontból lassan a
pontból lassan a  pontba mozgatunk, akkor a tér által végzett munka:
pontba mozgatunk, akkor a tér által végzett munka:
![\[W = \int\limits_A^B \vec F \ {\rm d}\vec s = \int\limits_A^B q\vec E \ {\rm d}\vec s \]](/images/math/8/f/2/8f2e09858b3af2959d2408cf3d8f0535.png) |
(3.1.1) |
Ha a töltést egy kísérletező személy mozgatta, akkor az általa a töltésen végzett munka – mint az könnyen belátható - a tér munkájának a 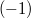 – szerese. A kísérletező munkája viszont a töltött részecske potenciális energiáját növelte. A töltött részecske potenciális energiájának változása tehát:
– szerese. A kísérletező munkája viszont a töltött részecske potenciális energiáját növelte. A töltött részecske potenciális energiájának változása tehát:
![\[\Delta E_p = - \int\limits_A^B q\vec E \ {\rm d}\vec s \]](/images/math/b/4/2/b4251579676bc1c277383f9a8152145c.png) |
(3.1.2) |
Az elektromos potenciálkülönbség
Látható tehát (3.1.2), hogy a potenciális energia változása arányos a mozgatott részecske töltésével. Ha azonban inkább magát a teret szeretnénk jellemezni, akkor célszerű elosztani a potenciális energiaváltozást a részecske töltésével, így megkapjuk a tér két pontja között az elektromos potenciálkülönbséget:
![\[\Delta U_{AB} = \frac {\Delta E_p}{q} = - \int\limits_A^B \vec E \ {\rm d}\vec s \]](/images/math/5/d/1/5d1babe8ca19abb355f2858ea0e933ff.png) |
(3.2.1) |
Érdemes még emlékezni a 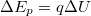 összefüggésre is. Homogén elektromos térben két pont között a potenciálkülönbség egyszerűbben is megadható:
összefüggésre is. Homogén elektromos térben két pont között a potenciálkülönbség egyszerűbben is megadható:
![\[\Delta U_{AB} = - \vec E \vec s \]](/images/math/8/a/d/8ade18762c3feacc60b3ae52ce87e174.png) |
(3.2.2) |
ahol 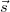 természetesen az
természetesen az  és a
és a  pontok közötti elmozdulás-vektor. Az eredmény nem függ attól, hogy milyen úton jutottunk el az
pontok közötti elmozdulás-vektor. Az eredmény nem függ attól, hogy milyen úton jutottunk el az  pontból a
pontból a  -be, hiszen a térre merőleges elmozdulások nem okoznak potenciálváltozást. Az elmozdulásnak tehát csak az elektromos erőtér irányába eső komponensét kell figyelembe venni; az
-be, hiszen a térre merőleges elmozdulások nem okoznak potenciálváltozást. Az elmozdulásnak tehát csak az elektromos erőtér irányába eső komponensét kell figyelembe venni; az 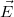 és
és 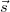 skalárszorzata ezt biztosítja.
Az elektromos teret jellemző
skalárszorzata ezt biztosítja.
Az elektromos teret jellemző 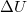 mennyiséget elektromos feszültségnek is nevezik, mértékegysége:
mennyiséget elektromos feszültségnek is nevezik, mértékegysége: 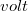 , jele:
, jele:  . Szemléletes jelentése a következő: amennyiben
. Szemléletes jelentése a következő: amennyiben 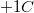 töltést az elektromos tér két olyan pontja között mozgatunk, amelyek között a feszültség
töltést az elektromos tér két olyan pontja között mozgatunk, amelyek között a feszültség 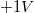 , akkor a részecske potenciális energiáját
, akkor a részecske potenciális energiáját 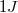 -lal növeltük; vagy fordítva: ha a
-lal növeltük; vagy fordítva: ha a 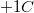 töltésű részecske egy olyan tartományon halad át, ahol a potenciálesés
töltésű részecske egy olyan tartományon halad át, ahol a potenciálesés 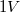 , akkor a tér által a részecskén végzett munka
, akkor a tér által a részecskén végzett munka 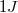 . Így tehát az elektromos tér által végzett munka:
. Így tehát az elektromos tér által végzett munka:
![\[ W_{t\acute{e}r} = - q\Delta U_{AB} \]](/images/math/2/1/0/210301b460f555f73198109b85031ab4.png) |
(3.2.3) |
A munkatétel alkalmazásával hasznos formulát kaphatunk, amelynek segítségével akár a tér által gyorsított részecske mozgási energiájának megváltozása és ebből a töltött részecske sebessége is kiszámítható:
![\[ W_{t\acute{e}r} = \Delta E_k \qquad {\rm ill.} \qquad - q\Delta U_{AB} = \frac {1}{2}mv^{2}_B - \frac {1}{2}mv^{2}_A \]](/images/math/d/9/5/d95980603a402bd89b9f14049b40b762.png) |
(3.2.4) |
Alkalmazásként tekintsük néhány egyszerű töltéselrendezés terének elektromos potenciálját!
Ponttöltés terének elektromos potenciálja meghatározható a következőképpen: a Q ponttöltés terét megadó (1.3.2) formulát behelyettesíthetjük az elektromos potenciálkülönbség definíciójába:
![\[\Delta U_{AB} = - \int\limits_A^B \vec E \ {\rm d}\vec s = \int\limits_A^B k\frac {Q}{r^2} \vec n \ {\rm d} \vec s \]](/images/math/e/7/f/e7fc7cf2bbc49f9d1fd52dcba37cfca5.png) |
(3.2.5) |
Innen integrálással kapjuk (könnyen belátható, hogy feszültség csak a radiális irányú elmozdulásra adódik, így a számítás egyszerűsödik):
![\[\Delta U_{AB} = kQ \left(\frac{1}{r_B} - \frac{1}{r_A}\right) \]](/images/math/f/a/6/fa67f049e5ecb48f77fd55f5fcf39042.png) |
(3.2.6) |
ahol 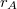 és
és 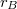 a két pont helyzetét megadó helyvektor abszolút értéke. Ha az
a két pont helyzetét megadó helyvektor abszolút értéke. Ha az  pont a
pont a  -ben (nagyon távol;
-ben (nagyon távol; 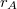 >>
>> 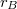 ) van, akkor a tér egy pontjának elektromos potenciálja a
) van, akkor a tér egy pontjának elektromos potenciálja a  töltés terében, attól
töltés terében, attól  távolságban:
távolságban:
![\[\ U(r) = k\frac{Q}{r} \]](/images/math/6/d/b/6db0a7b8979a5026cd3d37df13c56108.png) |
(3.2.7) |
alakba írható. Itt most magától értetődően adódott, hogy a 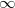 távoli pont potenciálja zérus:
távoli pont potenciálja zérus: 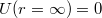 .
.
Ponttöltések rendszerének elektromos potenciálja is meghatározható az előzőek segítségével. A szuperpozíció elvéből következik, hogy 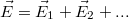 , ahol
, ahol 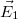 és
és 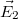 jelenti a
jelenti a 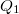 ,
, 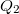 stb. töltések terét. A potenciálkülönbség definícióját felhasználva:
stb. töltések terét. A potenciálkülönbség definícióját felhasználva:
![\[\Delta U_{AB} = - \int\limits_A^B \vec E \ d\vec s = - \int\limits_A^B (\vec E_1 + \vec E_2 + ...) \ {\rm d}\vec s = - \int\limits_A^B \vec E_1\ {\rm d}\vec s - \int\limits_A^B \vec E_2 \ {\rm d}\vec s - ...\]](/images/math/2/b/3/2b360d12ab0611892b51d60720a2996b.png) |
(3.2.8) |
Vagyis a tér két pontja közötti potenciálkülönbség az egyes töltések terében számítható potenciálkülönbségek összege. Megállapíthatjuk tehát, hogy ponttöltések esetében - amennyiben a potenciál értékét a 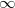 – ben
– ben  -nak választjuk – a tér egy meghatározott pontjában, amely a
-nak választjuk – a tér egy meghatározott pontjában, amely a  töltéstől
töltéstől 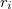 , távolságban van, az elektromos potenciál a ponttöltések potenciáljainak összege:
, távolságban van, az elektromos potenciál a ponttöltések potenciáljainak összege:
![\[ U(r) = \sum_{i} U_i = \sum_{i} k\frac{Q_i}{r_i} \]](/images/math/c/8/5/c85316903f064ff5f3413b4b2623e117.png) |
(3.2.9) |
Ezután már könnyen általánosíthatjuk a (3.2.9) formulát folytonos töltéseloszlások terében a potenciál meghatározásához:
![\[ U(\vec r) = \int\limits_{V'} \frac{1}{4\pi\varepsilon_0} \frac{\rho(\vec r')}{\left| \vec r - \vec r' \right|} {\rm d}V' \]](/images/math/b/7/a/b7a5730c3ba81b00d66eb1749ab0ea80.png) |
(3.2.10) |
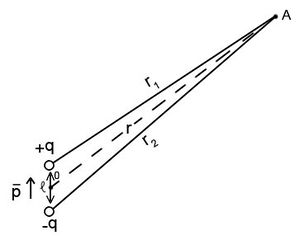
A (3.2.9) eredmény alkalmazására jó példa az elektromos dipólus potenciáljának közelítő számítása a dipólustól nagy távolságban 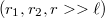 .
.
| 14. ábra |
A dipólust alkotó két töltés potenciálja - a 14. ábrán lévő jelöléseket alkalmazva – a következőféleképpen adható meg:
![\[ U (\vec r) = kq \left(\frac{1}{r_1} - \frac{1}{r_2}\right) = kq \frac {r_2 - r_1}{r_1 r_2} \]](/images/math/3/a/0/3a0133c1f1b7b7ec4055ab8c5c2b4b82.png) |
(3.2.11) |
Kihasználva a közelítés adta lehetőségeket - azaz, ha 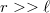 , akkor
, akkor 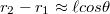 és
és 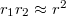 - meghatározható az elektromos dipólus terében egy pont potenciálja:
- meghatározható az elektromos dipólus terében egy pont potenciálja:
![\[ U (\vec r ) = k \frac{q \ell cos \theta}{r^2} = k \frac {p cos \theta}{r^2} = k \frac {\vec p\cdot \vec r}{r^3} \]](/images/math/e/6/f/e6f21b66155cc7af426be6c79f91ab22.png) |
(3.2.12) |
ahol  a
a 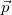 és az O pontból az A pontba mutató
és az O pontból az A pontba mutató 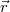 közötti szög.
közötti szög.
Töltésrendszer elektrosztatikus energiája
Az előzőek alapján – (3.2.1) és (3.2.7) felhasználásával - most már meg tudjuk határozni, hogy egy egyszerű, két töltött részecskéből álló rendszernek mennyi az elektrosztatikus energiája. A 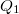 töltés terének elektromos potenciálja, mint láttuk:
töltés terének elektromos potenciálja, mint láttuk:
![\[ U(r) = k\frac{Q_1}{r} \]](/images/math/8/7/b/87b58f853a58e00a0743074f7f910a0a.png) |
(3.3.1) |
A 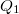 töltés terében, attól
töltés terében, attól  távolságban lévő
távolságban lévő 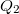 töltés potenciális energiája:
töltés potenciális energiája:
![\[ E_p(r) = Q_2 U(r) = k\frac{Q_1 Q_2}{r} \]](/images/math/e/4/0/e4020d2f4e162c6b875fb1c3f718c771.png) |
(3.3.2) |
Ez egyrészt azt jelenti, hogy ennyi munkát kell végeznünk, hogy a  töltést a
töltést a 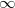 -ből a
-ből a 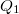 töltés közelébe mozgassuk attól
töltés közelébe mozgassuk attól  távolságra. Másrészt azonban ezt úgy is értelmezhetjük, hogy az általunk végzett munka a töltésrendszer energiáját növelte, azaz
távolságra. Másrészt azonban ezt úgy is értelmezhetjük, hogy az általunk végzett munka a töltésrendszer energiáját növelte, azaz 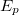 a
a 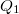 és
és 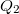 töltéspár elektrosztatikus energiáját adja.
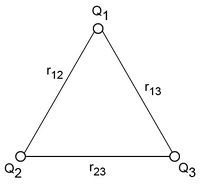
Egy töltésrendszer több részecskéből is állhat. Az egyszerűség kedvéért először tekintsünk egy három részecskéből álló elrendezést (15.ábra)!
töltéspár elektrosztatikus energiáját adja.
Egy töltésrendszer több részecskéből is állhat. Az egyszerűség kedvéért először tekintsünk egy három részecskéből álló elrendezést (15.ábra)!
| 15. ábra |
A 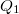 töltés helyén a potenciál :
töltés helyén a potenciál :
![\[ U_{Q_1} = k\frac{Q_2}{r_{12}} + k\frac{Q_3}{r_{13}} \]](/images/math/f/5/9/f596902ec61d5b0da0401a31492b642f.png) |
(3.3.3) |
Tehát a 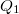 töltés potenciális energiája a
töltés potenciális energiája a 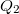 és
és 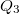 töltés terében, azaz a
töltés terében, azaz a 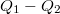 valamint a
valamint a 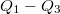 töltéspár elektrosztatikus energiája:
töltéspár elektrosztatikus energiája:
![\[ Q_1 U_{Q_1} = k\frac{Q_1 Q_2}{r_{12}} + k\frac{Q_1 Q_3}{r_{13}} \]](/images/math/6/3/c/63c680d64ebb3c3a1327b18263c05a00.png) |
(3.3.4) |
Megkapjuk a három töltésből álló rendszer energiáját, ha a kapott eredményhez hozzáadhatjuk még a 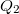 és
és 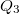 töltések kölcsönhatási energiáját is:
töltések kölcsönhatási energiáját is:
![\[ E_p = k\frac{Q_1 Q_2}{r_{12}} + k\frac{Q_1 Q_3}{r_{13}} + k\frac{Q_2 Q_3}{r_{23}} \]](/images/math/2/4/8/24847db64ccebba80f3f04013d0a1c74.png) |
(3.3.5) |
Általánosíthatjuk a kapott formulát N számú töltött részecskére, tehát ponttöltések rendszerének elektrosztatikus energiája:
![\[ E_p = \frac {1}{2}\sum_{i,j=1}^{N} k\frac{Q_i Q_j}{r_{ij}} \qquad {\rm ahol} \qquad i \neq j \]](/images/math/4/e/d/4ede3e14740cc5de9dea8fa22d1a69e7.png) |
(3.3.6) |
Töltéssűrűséggel megadott töltéselrendezés potenciális energiája is megadható az előző összefüggés integrális alakjával:
![\[ E_p = \frac {1}{2} \int\limits_{V} \rho (\vec r) U(\vec r) {\rm d}V \]](/images/math/1/1/7/11756715696805f226d0d55866ab6cf6.png) |
(3.3.7) |
ahol természetesen az adott térrészre kell integrálni, amelyben a töltések elhelyezkednek.
Elektromos erőtér származtatása az elektromos potenciálból
A fentiekben láttuk, hogy töltött részecskék elektromos terében bármely pont elektromos potenciálja meghatározható. Felmerül a kérdés, hogy az 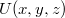 potenciál segítségével ki tudjuk-e számítani az elektromos térerősség komponenseit. Ehhez adjuk meg két olyan pont közötti potenciálkülönbséget, amelyek igen közel (annyira közel, hogy
potenciál segítségével ki tudjuk-e számítani az elektromos térerősség komponenseit. Ehhez adjuk meg két olyan pont közötti potenciálkülönbséget, amelyek igen közel (annyira közel, hogy 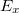 állandónak vehető) helyezkednek el egymáshoz az
állandónak vehető) helyezkednek el egymáshoz az  tengelyen:
tengelyen:
![\[ {\rm d}U = - E_x {\rm d}x \]](/images/math/9/d/c/9dca973bd9f8344dff55a6e49f415211.png) |
(3.4.1) |
Innen 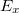 kifejezhető:
kifejezhető:
![\[ E_x = - \frac {{\rm d}U}{{\rm d}x} \]](/images/math/3/3/f/33f7bef069edf5ee00551a2c1afa4a05.png) |
(3.4.2) |
Hasonló módon 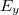 és
és 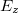 is meghatározható, így általánosan írható:
is meghatározható, így általánosan írható:
![\[ \vec E = - {\rm grad}U(x,y,z) \]](/images/math/4/c/7/4c76ee5f8e56f354d8480b303cbb904b.png) |
(3.4.3) |
Ebből a fontos eredményből következik, hogy az elektromos potenciál zéruspontját tetszőlegesen választhatom meg, hiszen ha a potenciálfüggvényt egy konstans hozzáadásával megváltoztatom, attól még a belőle számítható elektromos erőtér ugyanaz marad.
Az előzőekben bemutatott példák esetében (ponttöltés tere, homogén elektromos erőtér) láttuk, hogy két pont közötti elektromos feszültség meghatározásához mindössze a két pont ( és
és  pontok) helyzetére volt szükség. Ebből azt szűrhetjük le, hogy a potenciálkülönbség nem függ attól, hogy milyen úton jutunk el az egyik pontból a másikba. Ennek bizonyítására az a tény szolgál, hogy az elektrosztatikus erőtér örvénymentes, azaz:
pontok) helyzetére volt szükség. Ebből azt szűrhetjük le, hogy a potenciálkülönbség nem függ attól, hogy milyen úton jutunk el az egyik pontból a másikba. Ennek bizonyítására az a tény szolgál, hogy az elektrosztatikus erőtér örvénymentes, azaz:
![\[ \oint\vec E {\rm d}\vec s = 0 \qquad {\rm, mert} \qquad {\rm rot}(\vec E) = {\rm rot} ( {\rm grad}(U(\vec r))) = 0 \]](/images/math/e/2/b/e2b9ebba5f9f70b7fbbff31fd517e392.png) |
(3.4.4) |
Innen már adódik az állítás. Ezt egyébként szemléletesen is beláthatjuk. Valamely töltéselrendezés terében azon pontok összességét, amelyekben a elektromos potenciál értéke ugyanaz és amelyek felületet alkotnak, ekvipotenciális felületnek nevezzük. Az ekvipotenciális felület mentén történő elmozdulás nem okoz potenciálváltozást, mindössze a rá merőleges elmozdulás-komponenssel kell számolnunk, azaz a tér két pontja közötti potenciálkülönbség a két pontot magába foglaló ekvipotenciális felület potenciálértékének különbségéből számítható. Ezzel be is bizonyítottuk az állítást. (Nem minden esetben része feltétlenül egy pont egy ekvipotenciális felületnek, de ez a magyarázat lényegét nem érinti.) Amennyiben egy pontból az elektrosztatikus térben elmozdulok egy másik pontba és aztán vissza az eredeti, kiindulási pozícióba, akkor a visszaúton ugyanakkora volt a elektromos potenciálváltozás nagysága, de az előjele ellentétes; így tehát könnyen érthető, hogy egy zárt hurkon körbehaladva a teljes feszültség zérus.
A (3.2.12) és a (3.4.3)-es formulák segítségével egy elektromos dipól térerősségének távolságfüggése becsülhető a távoltérben. A pontos számítás helyett tekintsük most a dipól potenciálját megadó (3.2.12) formulát. Ebből a (3.4.3) segítségével beláthatjuk, hogy az elektromos térerősség komponensek nagysága 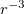 -nal arányos (hiszen a térerősség komponensek a potenciálból deriválással adódnak). Ezért van az, hogy az elektromos dipólok közötti kölcsönhatás erőssége jóval gyengébb, mint a ponttöltések közötti elektrosztatikus erő, melynek távolságfüggése
-nal arányos (hiszen a térerősség komponensek a potenciálból deriválással adódnak). Ezért van az, hogy az elektromos dipólok közötti kölcsönhatás erőssége jóval gyengébb, mint a ponttöltések közötti elektrosztatikus erő, melynek távolságfüggése 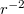 jellegű. Jó példa erre a víz; a
jellegű. Jó példa erre a víz; a 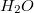 molekuláknak van pozitív és negatív töltés-súlypontjuk, azaz rendelkeznek dipólmomentummal.
molekuláknak van pozitív és negatív töltés-súlypontjuk, azaz rendelkeznek dipólmomentummal.
Az 1.2.4. fejezetben részletesen bemutattuk, hogy az elektromos tér fémes vezetőben zérus értéket vesz fel és a felület mentén az elektromos térerősség vektora merőleges a felületre (12. ábra). Ebből következik (3.4.3) alapján, hogy a vezetőn belül és a vezető felületén az elektromos potenciál értéke állandó. A vezető felülete természetesen - a fentiekben elmondottak szerint - ekvipotenciális felület. Az előzőekből következik, hogy a fémes burkolattal ellátott berendezések védettek a külső elektromos tér zavaró hatásától. Akár egy szerver-szoba elektromos védelme is megoldható az un. Faraday kalitka segítségével, amely gyakorlatilag egy sűrű szövésű fémhálóból kialakított zárt burkolat.
Az előzőeket támasztja alá az a tény is, miszerint az autóban ülő utasok általában megmenekülnek, ha villám csap a járműbe. Az autó fémburkolata ilyenkor Faraday kalitkaként funkcionál.
Most már érthető, hogy a számítógépek burkolata miért készül fémlemezből. A különböző fémes vezetők ill. műszerek fémburkolata különböző feszültségértéken lehet. Természetesen ez problémát okozhat, hiszen közöttük elektromos kisülés jöhet létre elektromos zavarokat okozva. Ennek a problémának egyszerű megoldását adja a földelés. Különböző földelési rendszerek vannak; most elég csak annyit megérteni, hogy az egységes földelést jelentő, igen nagy fémes vezetőkből álló hálózat minden tagján ugyanakkora a feszültségérték. A földelési rendszer és a földelt berendezések feszültségét nullának vehetjük, hiszen az elektromos potenciál zéruspontját tetszőlegesen választhatjuk meg. Ennek ellenére egy számítógépes laborban a földelt konnektorhoz csatlakoztatott berendezések még veszélyben lehetnek az ott dolgozó személyzet miatt, hiszen a műszálas ruhák, gumitalpú cipők stb. a dörzselektromosság révén feltöltődhetnek. Ezt a problémát orvosolják az eletrosztatikus padlóval, amelyben vezető fémszálak vagy grafit van finoman elosztva és a padlót is leföldelik.
A csúcshatás
Legyen két, egymástól távol lévő vezető gömb sugara  és
és  . A gömbökön
. A gömbökön 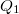 ill.
ill. 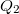 töltés van egyenletesen elosztva (elfogadjuk, hogy a gömbökön lévő töltések tere nem okoz töltésmegosztást a közöttük lévő nagy távolság miatt). Tegyük fel, hogy mindkét gömb felületén az elektromos potenciál ugyanazt az értéket veszi fel, azaz
töltés van egyenletesen elosztva (elfogadjuk, hogy a gömbökön lévő töltések tere nem okoz töltésmegosztást a közöttük lévő nagy távolság miatt). Tegyük fel, hogy mindkét gömb felületén az elektromos potenciál ugyanazt az értéket veszi fel, azaz
![\[ k\frac{Q_1}{R_{1}} = k\frac{Q_2}{R_{2}} \]](/images/math/f/d/9/fd9846c5979afdbaacd71f488fbf53cd.png) |
(3.5.1) |
A vezető gömbök felületének közelében viszont az elektromos térerősség nagysága:
![\[ E_1 = k \frac{Q_1}{R^{2}_1} \qquad {\rm ill.} \qquad E_2 = k \frac{Q_2}{R^{2}_2} \]](/images/math/7/2/2/72248315921f3dc55c2b1127dd0d4e0f.png) |
(3.5.2) |
Ebből kapható, hogy 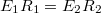 , tehát:
, tehát:
![\[ \frac{E_1}{E_2} = \frac{R_2}{R_1} \]](/images/math/8/d/b/8dba44eafd1c9bd233628f452f389571.png) |
(3.5.3) |
Ez az eredmény általánosítható szabálytalan alakú vezetők esetére is. Minthogy a vezető felülete ekvipotenciális felület, ebből következik, hogy a legkisebb görbületi sugarú csúcs közelében lesz az elektromos térerősség értéke a legnagyobb.
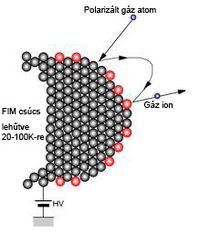
A csúcshatás alkalmazásán alapul a térion mikroszkóp működési elve. Egy alacsony nyomású gáztérbe, amelyben hélium (He) vagy neon (Ne) atomok vannak benyúlik egy pozitív nagyfeszültségű, alacsony hőmérsékletű (20 - 80 K), igen hegyes fémtű. A kis görbületi sugarú tűhegy közelében az elektromos tér igen erős és inhomogén. A tű hegyének közelébe kerülő atomok polarizálódnak és így rájuk vonzóerő hat. A tű hegyébe becsapódva az atomok ionizálódnak, elektront veszítenek, majd az így létrejövő pozitív iont a tű elektromos tere - gyakorlatilag a tű hegyét határoló felületre merőlegesen - gyorsítja (16. ábra). Ezek az ionok a tű hegyétől sugárirányban kifelé mozognak, majd becsapódva a szcintillációs ernyőbe láthatóvá teszik a tű hegyét alkotó atomokat, mint ahogy az alábbi - egy térion mikroszkóp (FIM) - ernyőjéről készült képen (17. ábra) látszik (egy-egy sötét folt egy-egy atomot jelez, a jelenség részletes tárgyalása a modern fizika témakörébe tartozik).
A villámhárító egyrészt jó vezetőképességének köszönhetően, másrészt a csúcshatás (azaz csúcs közelében az előzőekben már leírt módon kialakuló ionizált, jó vezetőképességű gázok) segítségével "vonzza" megához a villámot és vezeti le a földbe megvédve ezzel az épületeket, az elektromos és a számítógépes hálózatokat.
Főként zivatar ill. vihar előtt szokott előfordulni a Szent-Elmo tüzének is nevezett igen ritka jelenség, amely valójában koronakisülés; ez szintén a csúcshatáson alapul. Az éles csúcsok ill. élek közelében a térerősség elég nagy értéket (nagyobbat, mint az átütési szilárdság, lásd később) vesz fel ahhoz, hogy a levegő molekulái ionizálódjanak. Ez az ionizációs folyamat azért következik be, mert a kozmikus sugárzás hatásaként a levegőben általában jelenlévő kis számú ion a tér hatására gyorsulni kezd, majd elég nagy sebességet elérve már rendelkezik annyi az energiával, hogy újabb és újabb atomokat ill. molekulákat ionizáljon. Ilyenkor ú.n. hideg plazma jön létre, amelyben elektronok és pozitív ionok vannak. A plazmában lévő ionok újra rekombinálódva fényt bocsátanak ki. Ennek következtében hegyes tárgyak (általában vezetők) csúcsa körül fényjelenség látható. Tengerészek számoltak be arról, hogy vihar előtt néha az árboc csúcsa körül fényes pamacs látható. Megemlítendő, hogy a koronakisülés létrejöttéhez kisebb gáznyomáson kisebb elektromos térerősség is elegendő; így például a normál légköri nyomáson (1 atm) jól működő áramkörökben zavar keletkezhet kisebb légnyomás esetén.
| 17. ábra |
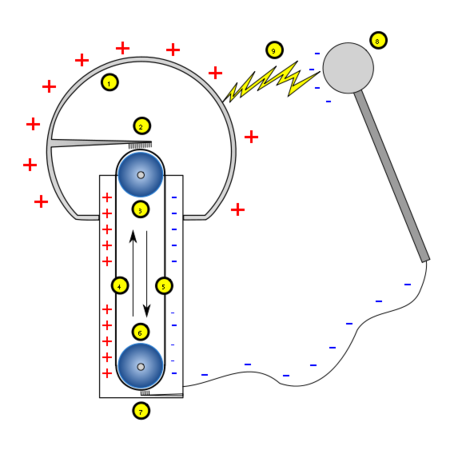
Szintén a csúcshatáson alapuló, a részecske és magfizikai kutatásban is alkalmazott eszköz a Van de Graaff generátor. A berendezés segítségével több millió volt feszültséget is létre lehet hozni, ezért részecskegyorsítóként használható. A 18. ábrán látható a Van de Graaff generátor elvi felépítése. A szigetelő szalag - gyakran gumiszalag - szállítja a töltéseket. (Van de Graaff az általa épített első berendezésben selyemszalagot használt.) Az alsó, fémből készült és a földhöz képest pozitív potenciálra kapcsolt fémgörgő forgatja a szalagot. A felső görgő általában műanyagból készül. Az alsó görgőnél található fésűszerű elektróda a csúcshatás következtében elszívja a negatív töltéseket a szalagról, ez az elektróda többnyire a földeléshez van csatlakoztatva. A felső elektróda pedig a pozitív töltéseket szedi le a szigetelő szalagról. A felső fémgömb belsejében az elektromos térerősség csaknem zérus, így könnyen eljutnak a pozitív töltések a gömbfelszínre növelve annak elektromos potenciálját. A 19. ábrán látható a Simonyi Károly által épített - az ELTE épületében kiállított - berendezés. Kapcsolódó videók: Elektromos csúcshatás I., Elektromos csúcshatás II.
| 18.ábra | 19.ábra |
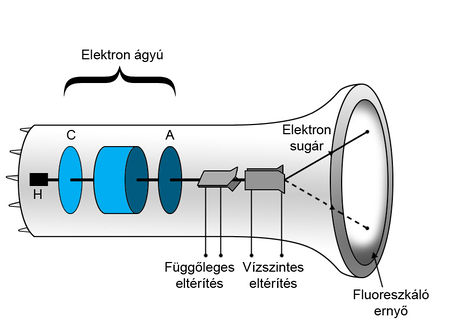
A CRT monitor fizikai alapjai
A régebbi típusú TV készülékek és monitorok - amelyeket CRT (cathode ray tube) monitornak hívnak - működési elve könnyen megérthető az eddig tanultak alapján. Tekintsük a 20. ábrán látható egyszerű elrendezést!
| 20. ábra |
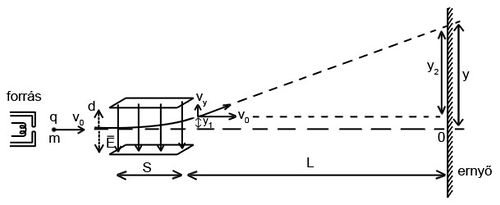
A baloldali forrásból kilépő elektronok sebessége 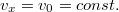 , és ha a két fémlemez között az elektromos erőtér elhanyagolható, akkor az elektronok az ernyő közepébe csapódnak (a fluoreszcens festéknek köszönhetően kis fénypontot képezve). Ha azonban a lemezek közötti térerősség nem zérus – jelöljük
, és ha a két fémlemez között az elektromos erőtér elhanyagolható, akkor az elektronok az ernyő közepébe csapódnak (a fluoreszcens festéknek köszönhetően kis fénypontot képezve). Ha azonban a lemezek közötti térerősség nem zérus – jelöljük  -vel a nagyságát – akkor a részecskére ható erő nagysága
-vel a nagyságát – akkor a részecskére ható erő nagysága 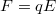 , és a gyorsulása:
, és a gyorsulása:
![\[ a_y = \frac{qE}{m} \]](/images/math/6/4/6/646a691bbe5a3bb203630590b9a452c6.png) |
(3.6.1) |
ahol  az elektron töltése és
az elektron töltése és  a tömege. Minthogy az elektron a lemezek között
a tömege. Minthogy az elektron a lemezek között
![\[ t_1 = \frac{s}{v_0} \]](/images/math/d/4/2/d42f9f941bdf17a0fb5af9af1f826182.png) |
(3.6.2) |
ideig tartózkodik (nem foglalkozunk a lemezpár szélén megjelenő szórt térrel), így könnyen kiszámíthatjuk az elektronnyaláb eltolódását:
![\[ y_1 = \frac{1}{2} a_y t^{2}_1 = \frac{1}{2} \frac{qE}{m} \left(\frac{s}{v_0} \right)^2 \]](/images/math/4/e/a/4ea1246ed536114f4773ba83adfd45b5.png) |
(3.6.3) |
és sebességének y komponensét:
![\[ v_y = a_y t_1 = \frac{qE}{m} \frac{s}{v_0} \]](/images/math/d/8/2/d8217b7fb04c9ccbca6a27e4dfa5e808.png) |
(3.6.4) |
Az elektron – miután kilépett az eltérítő lemezpár elektromos teréből – egyenesvonalú egyenletes mozgással halad az ernyőig. Az ehhez szükséges időtartam:
![\[ t_2 = \frac{\ell}{v_0} \]](/images/math/d/9/e/d9e570108b705a272138e6f43d3c41dc.png) |
(3.6.5) |
és az elektron ezen időtartam alatti  irányú eltolódása:
irányú eltolódása:
![\[ y_2 = v_y t_2 = \frac{qE}{m} \frac{s}{v_0} \frac{\ell}{v_0} \]](/images/math/3/c/5/3c54a96712424a31642f963b2c5a8e7d.png) |
(3.6.6) |
Most már megadhatjuk az elektronnyaláb teljes eltolódását, azaz deflexióját:
![\[ y = y_1 + y_2 = \frac{1}{2} \frac{qE}{m} \left(\frac{s}{v_0} \right)^2 + \frac{qE}{m} \frac{s}{v_0} \frac{\ell}{v_0} = \left[ \frac {q}{m} \frac {s}{v^{2}_0} \left(\frac{s}{2} + \ell \right) \right] E \]](/images/math/0/1/9/019dae387629adcf9ac1c0f924421c12.png) |
(3.6.7) |
Az elektromos térerősség nagysága viszont a lemezpárra kapcsolt elektromos feszültséggel arányos:
![\[ E = \frac{U}{d} \]](/images/math/6/c/6/6c64b49c4497090ba51bbe70c70ea899.png) |
(3.6.8) |
ahol  a lemezek közötti távolág. Megállapíthatjuk tehát, hogy az elektronnyaláb a középponttól a lemezpárra kapcsolt feszültséggel arányos távolságban ütközik az ernyőnek. Természetesen a TV készülékek, oszcilloszkóp képernyők, monitorok stb. esetében nem elég csak a függőleges irányú nyalábeltérítés, ezért egy másik lemezpárt is alkalmaznak a vízszintes irányú eltérítéshez (21.ábra).
a lemezek közötti távolág. Megállapíthatjuk tehát, hogy az elektronnyaláb a középponttól a lemezpárra kapcsolt feszültséggel arányos távolságban ütközik az ernyőnek. Természetesen a TV készülékek, oszcilloszkóp képernyők, monitorok stb. esetében nem elég csak a függőleges irányú nyalábeltérítés, ezért egy másik lemezpárt is alkalmaznak a vízszintes irányú eltérítéshez (21.ábra).
| 21. ábra |
Az elektromos mező energiája
Az előző fejezetben láttuk, hogy - általában - munkát kell végeznünk, ha egy töltött részecskét elektromos térben mozgatunk. Amennyiben munkavégzés történt, akkor a töltött részecskéből, az elektromos térből, stb. álló rendszer energiáját növeltük. Kérdés, hogy hol, illetve milyen formában raktározza a rendszer az energiát? Erre a kérdésre a választ néhány igen egyszerű, de szemléletes modell vizsgálatával kapjuk, és menet közben egy pár fontos definíciót és összefüggést is megismerhetünk.
Kapacitás
Tekintsük a következő igen egyszerű elrendezést: van két, elektromosan semleges vezető test egymástól bizonyos távolságra. Ezután az egyik testről a másikra, egyszerre mindig csak kis mennyiségű töltést (akár elektronokat egyenként) lassan mozgatva végül is elérjük, hogy az egyik vezetőn 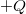 , míg a másikon
, míg a másikon 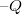 töltés lesz (22. ábra).
töltés lesz (22. ábra).
| 22. ábra |
Természetesen a töltések mozgatásához munkavégzésre volt szükség és így most újra felvethető, hogy hová is lett az energia. Most egy kicsit felejtsük el ezt a kérdést és közelítsünk a problémához más oldalról. Tételezzük fel, hogy valaki egy elektromos feszültségmérővel megméri a  elektromos potenciálkülönbséget a két vezető között. Egy adott elrendezés esetében kétszer nagyobb töltéshez kétszer nagyobb feszültség tartozik, hiszen kétszer nagyobb töltés esetén a térerősség nagysága is megduplázódik és az elektromos potenciálkülönbség definíciójából (3.2.5) már adódik az állítás. Beláttuk tehát, hogy
elektromos potenciálkülönbséget a két vezető között. Egy adott elrendezés esetében kétszer nagyobb töltéshez kétszer nagyobb feszültség tartozik, hiszen kétszer nagyobb töltés esetén a térerősség nagysága is megduplázódik és az elektromos potenciálkülönbség definíciójából (3.2.5) már adódik az állítás. Beláttuk tehát, hogy  arányos a
arányos a  -val. A két mennyiség hányadosaként kaphatjuk az elrendezés kapacitását:
-val. A két mennyiség hányadosaként kaphatjuk az elrendezés kapacitását:
![\[ C = \frac{Q}{U} \]](/images/math/5/9/9/5996e4248156123b229edf1eb57015da.png) |
(4.1.1) |
Ez az érték – a kapacitás – mindössze az elrendezés geometriájától függ és mértékegysége a 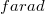 , jele
, jele  . (Mint az a (4.1.1.) – ből következik:
. (Mint az a (4.1.1.) – ből következik: 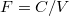 ). A kapacitás ill. egy kondenzátor áramköri jelölése:
). A kapacitás ill. egy kondenzátor áramköri jelölése:  .
.
Kondenzátorok
Az egyik legegyszerűbb geometriájú elrendezés a síkkondenzátor, amely két azonos méretű, egymással párhuzamos vezető lapból áll (23.ábra). A lapok felülete  és egymástól
és egymástól  távolságban vannak.
távolságban vannak.
| 23. ábra |
Előzőleg láttuk (1.5.8), hogy egy végtelen, konstans töltéssűrűségű lap elektromos terének nagysága állandó, és értéke
![\[ E = \frac{\sigma}{2\varepsilon_0} \]](/images/math/b/c/1/bc1f23beaae4f05bad6592b7696c94ab.png) |
(4.2.1) |
Ezt az eredményt most alkalmazzuk a feltöltött síkkondenzátor lemezei közötti elektromos erőtér nagyságának kiszámításához. Ha a lemezek közötti távolság jóval – mondjuk nagyságrendekkel – kisebb, mint a lemezek oldaléleinek hossza, akkor az elektromos erőtér szerkezete hasonló lesz a végtelen töltött sík teréhez, hiszen ekkor a lemezek széleinél szóródó tér elhanyagolható. Könnyen belátható, hogy a  és a
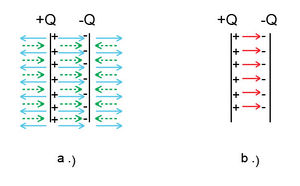
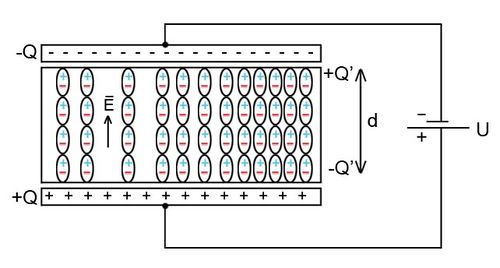
és a 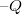 töltéssel egyenletesen feltöltött lemezpár között az elektromos tér nagysága kétszerese a (4.2.1)-ben megadott értéknek, a lemezeken kívül viszont a tér nagysága zérus, amint azt a 24.a és 24.b ábra szemlélteti. (A pozitív és a negatív töltések terét kék ill. zöld színnel jelöltük, míg az eredő teret a 24.b ábrán pirossal.)
töltéssel egyenletesen feltöltött lemezpár között az elektromos tér nagysága kétszerese a (4.2.1)-ben megadott értéknek, a lemezeken kívül viszont a tér nagysága zérus, amint azt a 24.a és 24.b ábra szemlélteti. (A pozitív és a negatív töltések terét kék ill. zöld színnel jelöltük, míg az eredő teret a 24.b ábrán pirossal.)
| 24. ábra |
A lemezek közötti homogén elektromos tér nagysága tehát:
![\[ E = \frac{\sigma}{\varepsilon_0} \qquad {\rm , mivel} \qquad \sigma = \frac {Q}{A} \qquad \longrightarrow \qquad E = \frac{Q}{\varepsilon_0 A} \]](/images/math/0/8/2/08291734e40bd653fbd73f74d9176252.png) |
(4.2.2) |
Minthogy a tér nagysága állandó, a két lemez közötti potenciálkülönbséget a (3.2.2) segítségével határozhatjuk meg (Síkkondenzátor I.):
![\[ U = Ed = \frac{Qd}{\varepsilon_0 A} \]](/images/math/d/7/9/d799c2f09a7df5328e18604ba5153f94.png) |
(4.2.3) |
Ebből már a 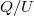 hányados, azaz a síkkondenzátor kapacitása egyszerűen megadható (Síkkondenzátor III.):
hányados, azaz a síkkondenzátor kapacitása egyszerűen megadható (Síkkondenzátor III.):
![\[ C = \frac {Q}{U} = \frac{\varepsilon_0 A}{d} \]](/images/math/d/b/2/db2fcfead5ea56f5be1f5ccbdef2757a.png) |
(4.2.4) |
Természetesen más elrendezések, kondenzátortípusok kapacitása is kiszámítható, még ha nem is olyan egyszerűen, mint a síkkondenzátoré. A nevezetesebbek, pl. a gömbkondenzátor és a hengerkondenzátor kapacitása is meghatározható a bemutatott módszer segítségével, mindössze a matematikai leírás egy kissé bonyolultabb.
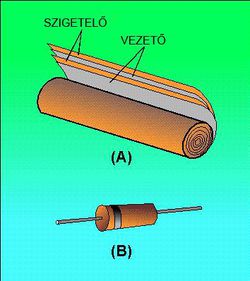
A leggyakrabban előforduló síkkondenzátorok technikai megvalósítása általában úgy történik, hogy a két igen vékony, hajlítható, belső oldalukon fémréteggel (pl. alufólia) ellátott szigetelők közé megfelelő vastagságú dielektrikumot helyeznek és ezt a szendvicsszerkezetet hengerformára feltekerik.
Ha egy kondenzátor geometriája változik, akkor természetesen a kapacitása is más értéket vesz fel (4.2.4.). Ez ad lehetőséget arra, hogy kondenzátorokat érzékelőként is alkalmazzunk. Nyomás(megváltozás)érzékelésre is használják a kapacitív érzékelőket. A mindennapi életben gyakran találkozhatunk műszaki alkalmazásukkal, mint pl. az érintőképernyő ill. a számítógépes billentyűzet. A kondenzátor kapacitásváltozását felhasználhatjuk elmozdulás mérésére is.
Kondenzátor energiája
Tegyük fel, hogy van egy kondenzátor (vagy akár egy, a 22. árbán bemutatott általános elrendezés), amelynek a kapacitása  és amelyet szeretnénk feltölteni. A lemezek feltöltését végezzük az előzőekben már leírt módon, azaz az eredetileg semleges vezetődarabok egyikéről kis adagokban töltéseket viszünk át a másikra, míg végül is az egyik vezetőn
és amelyet szeretnénk feltölteni. A lemezek feltöltését végezzük az előzőekben már leírt módon, azaz az eredetileg semleges vezetődarabok egyikéről kis adagokban töltéseket viszünk át a másikra, míg végül is az egyik vezetőn 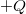 , a másikon
, a másikon 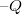 töltés jelenik meg. Ezen folyamat közben legyen az egyik vezetőn
töltés jelenik meg. Ezen folyamat közben legyen az egyik vezetőn 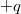 , a másikon
, a másikon 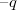 töltés és ezután
töltés és ezután 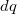 töltést mozgatunk az egyik vezetőről a másikra. Az ehhez szükséges munkavégzés:
töltést mozgatunk az egyik vezetőről a másikra. Az ehhez szükséges munkavégzés:
![\[ {\rm d}W = U{\rm d}q \]](/images/math/e/8/4/e8475f3d4c5cf5e256dc978c44cfee70.png) |
(4.3.1) |
A kondenzátor fegyverzetei közötti feszültség értéke 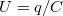 , így:
, így:
![\[ {\rm d}W = \frac {1}{C}q{\rm d}q \]](/images/math/e/9/e/e9e9903818b46b4a111ff5865194a6bd.png) |
(4.3.2) |
A kondenzátor feltöltéséhez szükséges teljes munkát, azaz a kondenzátor energiáját integrálással kapjuk:
![\[ W = \frac {1}{C} \int\limits_0^Q q{\rm d}q = \frac {1}{2} \frac {Q^2}{C} \]](/images/math/4/8/d/48da29bbebc71feebecc3b30ed29d827.png) |
(4.3.3) |
Természetesen a 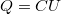 összefüggés felhasználásával az előző formula más alakban is megadható, azaz a kondenzátor energiája:
összefüggés felhasználásával az előző formula más alakban is megadható, azaz a kondenzátor energiája:
![\[ W = \frac {1}{2} \frac {Q^2}{C} = \frac {1}{2} QU = \frac {1}{2} CU^2 \]](/images/math/7/4/4/744a4b6e87095d2b96a54d7ad05fd90a.png) |
(4.3.4) |
Kapcsolódó videó: Síkkondenzátor II.
Az elektromos mező energiája
Az előző három alfejezet – bár mindegyik önmagában is fontos tudnivalókat tartalmaz – főként azt a célt szolgálja, hogy az eredetileg feltett kérdésre, hogy hol raktározódik el az energia, megadhassuk a választ. Azt már tudjuk, hogy egy kondenzátor energiája megadható a
![\[ W = \frac {1}{2} \frac {Q^2}{C} \]](/images/math/4/1/0/41085ebbb6e9886b7b879d83a8099d00.png) |
(4.4.1) |
alakban. Az egyszerűség kedvéért tekintsünk egy síkkondenzátort, melynek lemezei  távolságban vannak egymástól és
távolságban vannak egymástól és  a felületük. A (4.2.2)-ben megmutattuk, hogy egy síkkondenzátor lemezei között az elektromos tér nagysága
a felületük. A (4.2.2)-ben megmutattuk, hogy egy síkkondenzátor lemezei között az elektromos tér nagysága
![\[ E = \frac{Q}{\varepsilon_0 A} \]](/images/math/d/4/4/d447be391930b7f8b66ebe299a25965c.png) |
(4.4.2) |
Ebből adódik, hogy 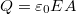 és felhasználhatjuk még a síkkondenzátor kapacitását megadó (4.2.4) formulát, hogy megkapjuk a kondenzátor energiáját. Azonban most nem erre vagyunk kíváncsiak. Tudjuk azonban, hogy a fegyverzetek közötti elektromos tér homogén, azaz a nagysága állandó. Ha most feltételezzük azt, hogy az energia a térben van valahogyan elraktározva, akkor – felhasználva a tér homogenitását, valamint, hogy
és felhasználhatjuk még a síkkondenzátor kapacitását megadó (4.2.4) formulát, hogy megkapjuk a kondenzátor energiáját. Azonban most nem erre vagyunk kíváncsiak. Tudjuk azonban, hogy a fegyverzetek közötti elektromos tér homogén, azaz a nagysága állandó. Ha most feltételezzük azt, hogy az energia a térben van valahogyan elraktározva, akkor – felhasználva a tér homogenitását, valamint, hogy 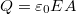 - a kondenzátor energiáját elosztva a kondenzátor
- a kondenzátor energiáját elosztva a kondenzátor 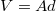 térfogatával adódik az elektromos tér energiasűrűsége:
térfogatával adódik az elektromos tér energiasűrűsége:
![\[ \varepsilon_E = \frac {1}{2} \varepsilon_0 E^2 \]](/images/math/7/3/2/732eb1a9704ba3b9a73d21af59150c2f.png) |
(4.4.3) |
Ezt az eredményt természetesen a későbbiekben tárgyalandó Maxwell egyenletekből is le lehet vezetni az itt bemutatott szemléletes modell vizsgálatánál egzaktabb formában. Most az elektromos tér energiasűrűségének alakját abból a feltételezésből kaptuk, hogy az energia a térben van elosztva. Azonban könnyen meggyőződhetünk arról, hogy az (4.4.3) formula segítségével más, egyszerűen is kiszámítható elrendezések, kondenzátortípusok - pl. hengerkondenzátor, gömbkondenzátor stb. - energiája is kiszámítható annak ellenére, hogy bennük a tér nem homogén. Belátható tehát, hogy feltételezésünk jónak bizonyult, azaz egy elektrosztatikus rendszer energiája a elektromos térben van elraktározva és energiasűrűsége valóban megadható a (4.4.3) alakban. Amennyiben egy (töltés)elrendezés esetén ismerjük a tér minden pontjában az elektromos erőtér nagyságát, akkor az energiasűrűség formulájának segítségével a rendszer elektrosztatikus energiája is kiszámítható:
![\[ W = \int\limits_V \varepsilon_E {\rm d}V \]](/images/math/a/0/d/a0d583a69c1520d844b6e79d91a1c206.png) |
(4.4.4) |
Ezután joggal merülhet fel az a kérdés, hogy ennek segítségével megadható-e egy ponttöltés energiája. Sajnos erre a kérdésre nem lehet egyszerű választ adni és el kell fogadnunk, hogy ennek a problémának a kezelése kivezet az elektrosztatika keretei közül. Ez nem jelenti azt, hogy a ponttöltés fogalmát el kell felejtenünk, de az energia kiszámítását a kellő gondossággal kell elvégezni, pl. (3.3.6) vagy (4.4.3) felhasználásával.
Sorosan és párhuzamosan kötött kondenzátorok
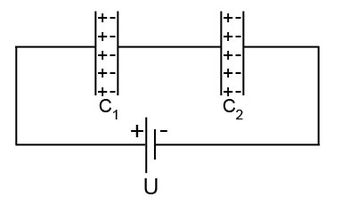
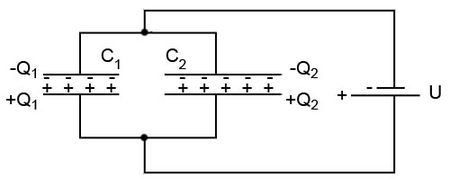
Az előző fejezetben láttuk, hogy egy kondenzátorban energiát lehet raktározni. Ha több kondenzátort összekapcsolunk, akkor természetesen több energiát vagy töltést lehet esetenként elraktározni, azonban ezzel a lehetőséggel most nem foglalkozunk. Érdekesebb inkább azt megvizsgálni, hogy egy kondenzátorokból összeállított kapcsolást hogyan lehet (ha egyáltalán lehet) helyettesíteni egyetlen kondenzátorral, amely elektromosan ugyanúgy viselkedik, azaz ugyanakkora feszültséget rákapcsolva ugyanakkora töltés jelenik meg rajta és ugyanannyi energiát raktároz el. Azt fogjuk megmutatni, hogy sorosan ill. párhuzamosan kötött kondenzátoroknak mekkora az eredő kapacitása. Ezeknek az eredményeknek a felhasználásával a bonyolultabb vagy összetettebb, kondenzátorokból álló kapcsolás elektromos tulajdonságai is meghatározhatók, mint pl. az eredő kapacitás vagy az egyes elemeken megjelenő töltés stb. Tekintsük először a 25. ábrán is látható egyszerű elrendezést, amelyben két kondenzátor van sorosan összekötve és a kondenzátorok szabad végeit vezető huzalokkal egy feszültségforráshoz (egy elemhez vagy egy akkumulátorhoz) kapcsoljuk. Egy vezetőn vagy az áramkör részének tekinthető vezetéken – minthogy statikus térről van szó - mindenhol ugyanakkora az elektromos potenciál értéke.
| 25. ábra |
A 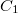 kapacitású kondenzátor fegyverzetein
kapacitású kondenzátor fegyverzetein 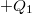 ill.
ill. 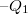 töltés jelenik meg, míg a
töltés jelenik meg, míg a 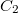 kapacitás lemezein
kapacitás lemezein 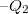 és
és 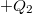 töltés. Az elrendezés középső részén, azaz a két kondenzátor összekapcsolt fegyverzetein a töltésmegosztással megjelenő töltések összege zérus, hiszen ez a rész nem áll semmilyen elektromos kapcsolatban a feszültségforrással, ezért arról elektromos töltés nem is vándorolhatott oda. Ebből következik, hogy
töltés. Az elrendezés középső részén, azaz a két kondenzátor összekapcsolt fegyverzetein a töltésmegosztással megjelenő töltések összege zérus, hiszen ez a rész nem áll semmilyen elektromos kapcsolatban a feszültségforrással, ezért arról elektromos töltés nem is vándorolhatott oda. Ebből következik, hogy 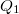 megegyezik
megegyezik 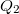 -vel, tehát mindkét kondenzátor fegyverzetein ugyanakkora pozitív és negatív töltés található; jelöljük ezt ezután Q-val. Az elektrosztatikus erőtér konzervatív (3.4.4), ebből következik, hogy a feszültségforrás két sarkán mérhető feszültség értéke megegyezik a két kondenzátoron eső feszültségérték összegével:
-vel, tehát mindkét kondenzátor fegyverzetein ugyanakkora pozitív és negatív töltés található; jelöljük ezt ezután Q-val. Az elektrosztatikus erőtér konzervatív (3.4.4), ebből következik, hogy a feszültségforrás két sarkán mérhető feszültség értéke megegyezik a két kondenzátoron eső feszültségérték összegével: 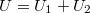 . A kapacitás definíciójából (4.1.1) viszont azonnal adódik, hogy
. A kapacitás definíciójából (4.1.1) viszont azonnal adódik, hogy 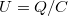 , tehát
, tehát
![\[ \frac {Q}{C_e} = \frac {Q}{C_1} + \frac {Q}{C_2} \qquad {\rm azaz} \qquad \frac {1}{C_e} = \frac {1}{C_1} + \frac {1}{C_2} \]](/images/math/0/2/3/0232cc995a7ea7b33a6e7d6c4f76059f.png) |
(4.5.1) |
Ahol 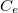 – vel jelöltük az eredő kapacitást. Amennyiben kettőnél több kondenzátor van sorba kötve, akkor ugyanezzel a gondolatmenettel könnyen belátható, hogy az eredő kapacitás:
– vel jelöltük az eredő kapacitást. Amennyiben kettőnél több kondenzátor van sorba kötve, akkor ugyanezzel a gondolatmenettel könnyen belátható, hogy az eredő kapacitás:
![\[ \frac {1}{C_e} = \sum_{i} \frac {1}{C_i} \]](/images/math/2/1/b/21bdddada29fb40dca1e4586c04cf8c9.png) |
(4.5.2) |
alakból számítható. Ezután határozzuk meg a párhuzamosan kötött kondenzátorok eredő kapacitását! Ehhez vizsgáljuk meg a 26. ábrán látható elrendezést.
Minthogy töltések nem mozognak (eltekintünk az egyensúly beállásáig tartó, általában igen rövid ideig tartó folyamatoktól), ezért a feszültségforrás jobb ill. baloldalán a feszültségérték a vezető huzalokon ill. a fegyverzeteken állandó. Ebből viszont az következik, hogy mindkét kondenzátorra ugyanakkora  feszültség esik. Ha a
feszültség esik. Ha a 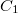 és
és 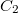 kapacitású kondenzátorokon megjelenő töltés
kapacitású kondenzátorokon megjelenő töltés 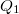 ill.
ill. 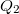 , akkor az elrendezés által tárolt össztöltés természetesen
, akkor az elrendezés által tárolt össztöltés természetesen 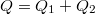 , minthogy az elrendezés egyik oldalán
, minthogy az elrendezés egyik oldalán 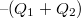 töltés, míg a másikon
töltés, míg a másikon 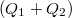 töltés van (27.ábra).
töltés van (27.ábra).
| 26.ábra | 27.ábra |
Az eredő kapacitásnak természetesen ugyanannyi töltéssel kell rendelkeznie, ha  feszültségforráshoz kapcsoljuk, azaz
feszültségforráshoz kapcsoljuk, azaz
![\[ Q = Q_1 + Q_2 \qquad \rightarrow \qquad UC_e = UC_1 + UC_2 \qquad {\rm azaz} \qquad C_e = C_1 + C_2 \]](/images/math/8/5/b/85b48e3de33ab99d2500ef35c79977dd.png) |
(4.5.3) |
Ha kettőnél több kondenzátor van párhuzamosan kötve, akkor hasonló okfejtéssel könnyen bebizonyítható, hogy az eredő kapacitás:
![\[ C_e = \sum_{i} C_i \]](/images/math/3/6/d/36db367c7001ff3f97972e39f022ddf3.png) |
(4.5.4) |
Dielektrikumok
Mindeddig hallgatólagosan feltételeztük, hogy a kondenzátor fegyverzetei között vákuum van. Ilyen kondenzátorokat azonban nemcsak hogy nehézkes és költséges lenne létrehozni, de nem is tűnik célszerűnek. Az alábbiakban kiderül majd, hogy ha a kondenzátor fegyverzetei közé valamilyen szigetelőt (papírt, üveget, műanyagot vagy akár paraffint, stb.) helyezünk, akkor a kapacitás értéke jelentősen megnövelhető és ráadásul az eszközre kapcsolható maximális feszültségérték is – akár nagyságrendekkel – nagyobb lehet.
Egy szigetelő vagy más néven dielektrikum elektromos tér hiányában (hacsak nem viszünk rá töltéseket) elektromosan semleges viselkedést mutat, és saját tere nincs. Amennyiben valamely dielektrikumot elektromos térbe helyezünk, akkor általában az anyag "válasza" erre a külső térre az, hogy polarizálódik, azaz benne pozitív ill. negatív töltéssúlypont alakul ki. A szigetelőket ezen tulajdonságuk alapján poláros ill. nempoláros dielektrikumokra oszthatjuk.
A poláros dielektrikumok molekuláinak van eredő dipólmomentuma, azonban külső tér hiányában főként a hőmérsékleti rendezetlenség miatt ezek orientációja véletlenszerű, így kifelé makroszkópikus polarizációs tulajdonságot nem mutatnak.
Az első fejezetben láttuk, hogy egy elektromos dipólra homogén elektromos térben forgatónyomaték hat. Ezt úgy is értelmezhetjük, hogy az elektromos tér "igyekszik" egy elektromos dipólmomentummal rendelkező molekulát a tér irányába befordítani. Természetesen egy sokaságot tekintve (egy makroszkópikus anyagdarab nagyságrendileg 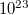 darab molekulát tartalmaz ) a tér nem képes az összes dipólt, azaz az összes molekulát tökéletesen a térrel párhuzamos irányba összerendezni, mert a hőmérsékleti rendezetlenség miatt nem lehet egyszerre az összes molekula a minimális energiájú állapotban (hivatk.). Azt azonban kijelenthetjük, és ez a szemléletből is adódik, hogy "minél erősebb a külső tér, annál inkább beállnak a molekulák a tér irányába". Ez azt jelenti, hogy az erősebb - intenzívebb - külső tér hatására a molekulák rendezettsége nő, tehát a polarizációs hatás is erősebb lesz.
darab molekulát tartalmaz ) a tér nem képes az összes dipólt, azaz az összes molekulát tökéletesen a térrel párhuzamos irányba összerendezni, mert a hőmérsékleti rendezetlenség miatt nem lehet egyszerre az összes molekula a minimális energiájú állapotban (hivatk.). Azt azonban kijelenthetjük, és ez a szemléletből is adódik, hogy "minél erősebb a külső tér, annál inkább beállnak a molekulák a tér irányába". Ez azt jelenti, hogy az erősebb - intenzívebb - külső tér hatására a molekulák rendezettsége nő, tehát a polarizációs hatás is erősebb lesz.
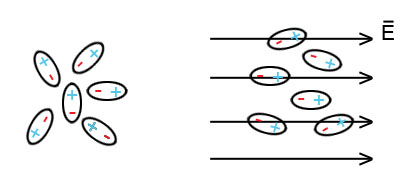
Poláros dielektrikum molekuláinak van eredő dipólmomentuma. Külső tér hiányában a molekulák rendezetlenül állnak, ellenben külső tér hatására többé-kevésbé igyekeznek bállni a tér irányába(28.ábra).
| 28. ábra |
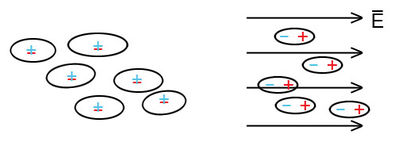
A nempoláros dielektrikum molekulái külső tér nélkül dipólmomentummal nem rendelkeznek. Azonban molekuláiban a külső elektromos tér a pozitív és a negatív töltéssúlypontok egymástól való különválását, eltávolodását okozza (29.ábra). Ez azt jelenti, hogy a molekulák elemi dipólmomentuma annál nagyobb értéket vesz fel, minél nagyobb az elektromos tér értéke. Ebből az is következik, hogy egy makroszkópikus szigetelő darab dipólmomentuma intenzívebb külső térben nagyobb értéket vesz fel.
| 29. ábra |
Az előbbieket összefoglalva tehát megállapíthatjuk, hogy mind a poláros, mind a nempoláros dielektrikum esetében az a tapasztalat, hogy a polarizációs hatás a külső elektromos térrel arányos. A mérések és - az itt nem részletezett - számítások azt mutatják, hogy nem túl intenzív tér esetében az anyagban kialakuló dipólmomentum-sűrűség (egyszerűbb esetben ez az anyag dipólmomentuma osztva az anyagdarab térfogatával), azaz az ún.  polarizáció a külső térrel egyenesen arányos:
polarizáció a külső térrel egyenesen arányos:
![\[ P = \varepsilon_0 \varkappa E \]](/images/math/6/8/7/6871bfb76759a27e3fd7d98f836b6209.png) |
(4.6.1) |
ahol 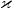 az adott anyagra jellemző szuszceptibilitás.
az adott anyagra jellemző szuszceptibilitás.
Néhány anyag szuszceptibiltásának értéke:
| Anyag | szuszceptibilitás |
|---|---|
| paraffin | 0.9 - 1.2 |
| csillám | 3 - 7 |
| üveg | 4 - 15 |
| porcelán | 5 |
| víz | 80 |
| etilalkohol | 20 |
| száraz levegő | 0.00059 |
Most vizsgáljuk meg, hogy mi történik, ha egy síkkondenzátor  felületű fegyverzetei közé – amelyek egymástól
felületű fegyverzetei közé – amelyek egymástól  távolságban vannak - dielektrikumot teszünk, amely teljesen kitölti a kondenzátor lemezei közötti teret. Legyen a lemezek közötti elektromos tér nagysága
távolságban vannak - dielektrikumot teszünk, amely teljesen kitölti a kondenzátor lemezei közötti teret. Legyen a lemezek közötti elektromos tér nagysága  . A tér hatására az anyag polarizálódik (30. ábra):
. A tér hatására az anyag polarizálódik (30. ábra):
| 30. ábra |
A molekulák láncokba rendeződnek és a láncvégeken lévő (kvázi)töltések felületi töltéssűrűséget hoznak létre. A polarizáció értéke amint azt láttuk: 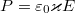 . Ebből a szigetelő dipólmomentuma
. Ebből a szigetelő dipólmomentuma 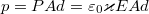 . Az anyagdarab végein megjelenő pozitív ill. negatív kvázitöltések nagysága a dipólmomentum definíciója alapján (1.3.fejezet):
. Az anyagdarab végein megjelenő pozitív ill. negatív kvázitöltések nagysága a dipólmomentum definíciója alapján (1.3.fejezet): 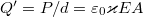 . Ha ezt elosztjuk a felület mértékével, akkor ebből adódik a dielektrikum felületi töltéssűrűsége:
. Ha ezt elosztjuk a felület mértékével, akkor ebből adódik a dielektrikum felületi töltéssűrűsége: 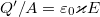 , amely megegyezik a
, amely megegyezik a  polarizáció nagyságával.
Tételezzük fel, hogy az
polarizáció nagyságával.
Tételezzük fel, hogy az  térerősség azért alakul ki a kondenzátor fegyverzetei között, mert
térerősség azért alakul ki a kondenzátor fegyverzetei között, mert  feszültséget kapcsoltunk a kondenzátorra. A két paraméter közötti összefüggés (3.2.2):
feszültséget kapcsoltunk a kondenzátorra. A két paraméter közötti összefüggés (3.2.2): 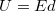 . Most tegyük fel, hogy a kondenzátor lemezein
. Most tegyük fel, hogy a kondenzátor lemezein 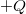 és
és 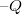 töltések vannak. Ekkor a síkkondenzátor kapacitásértékének meghatározásánál látott gondolatmenet (4.2.2) segítségével kapjuk, hogy:
töltések vannak. Ekkor a síkkondenzátor kapacitásértékének meghatározásánál látott gondolatmenet (4.2.2) segítségével kapjuk, hogy:
![\[ E = \frac {Q-Q'} {\varepsilon_0 A} \]](/images/math/2/6/4/2641aa0e57b9be333d7fa85d55324130.png) |
(4.6.2) |
Innen adódik: 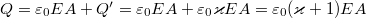 .
.
A dielektrikummal ellátott síkkondenzátor kapacitása ezután a kapacitás definíciójából kapható:
![\[ C = \frac {Q}{U} = \frac{\varepsilon_0 (\varkappa + 1)EA}{Ed} = \frac {\varepsilon_0 \varepsilon_r A} {d} \]](/images/math/b/b/e/bbe22a95faafa33faad6c5b6c686c07f.png) |
(4.6.3) |
ahol 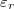 a szigetelő relatív dielektromos állandója (hivatalos megnevezése: relatív permittivitás) és
a szigetelő relatív dielektromos állandója (hivatalos megnevezése: relatív permittivitás) és 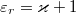 . A kapacitásra kapott (4.6.3) eredmény – amelyet egyébként a mérések is igazolnak - kvantitatív formában adja, amit a fejezet elején említettünk, azaz hogy egy kondenzátor kapacitását többszörösére növelhetjük, ha dielektrikummal töltjük ki a lemezek közötti teret (Síkkondenzátor IV.).
. A kapacitásra kapott (4.6.3) eredmény – amelyet egyébként a mérések is igazolnak - kvantitatív formában adja, amit a fejezet elején említettünk, azaz hogy egy kondenzátor kapacitását többszörösére növelhetjük, ha dielektrikummal töltjük ki a lemezek közötti teret (Síkkondenzátor IV.).
Említésre méltó még az a tény is, hogy a dielektrikumra - annak sérülése nélkül – jóval nagyobb elektromos tér kapcsolható, mintha a kondenzátor lemezei között légüres tér vagy levegő lenne. Az anyagtól függő maximális elektromos térerősséget átütési szilárdságnak (vagy dielektromos szilárdságnak) nevezik, lásd a következő táblázatot.
| Anyag | Átütési szilárdság
kV/cm |
|---|---|
| száraz levegő* | 21 |
| száraz papír | 25 - 40 |
| titán-dioxid | 20 - 100 |
| alumínium-oxid | 100 - 150 |
| PVC | 100 - 300 |
| polietilén | 200 |
| polisztirol | 220 - 500 |
(* normál állapotú)
A leggyakrabban alkalmazott kondenzátor a tekercselt kondenzátor – valójában síkkondenzátor, bár az alakja alapján nem erre gondolnánk - technikai megvalósítása általában a következőképpen történik. Két, igen vékony, hajlékony fémréteg (pl. alumínium fólia) közé megfelelő vastagságú dielektrikumot helyeznek, majd az egyik vezető lapot még kívülről ellátják egy vastagabb szigetelő réteggel és ezt a szendvicsszerkezetet – gyakran hengerformára - feltekerik (31. a és b ábra).
| 31.a ábra | 31.b ábra |
A dielektrikumok egyik csoportja az ún. elektrétek. Az elektromos dipólmomentummal rendelkező molekulákból álló anyagot elegendően erős elektromos térben megolvaszják majd hagyják kihűlni, így stabilizálódik az anyag polarizációs állapota. Az elektréteknek számos alkalmazási lehetősége van, ezek közül talán legismertebb az elektrétmikofon, amelyben az előfeszítést adja a remanens polarizációjú dielektrikum. Kapcsolódó videók: Dielektrikum mint energiatároló és Erővonalak dielektrikumban.
| Az elektrosztatikában használt jelölések, mértékegység és a fontosabb állandók |
|---|
| Megnevezés | Jelölés | Mértékegység |
|---|---|---|
| elektromos töltés | 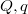
|
 (Coulomb) (Coulomb)
|
| elektromos tér | 
|
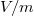 vagy vagy 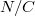
|
| lineáris töltéssűrűség | 
|
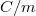
|
| felületi töltéssűrűség | 
|
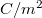
|
| térfogati töltéssűrűség | 
|
|
| potenciális energia | 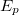
|
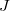 (Joule) (Joule)
|
| elektromos potenciál | 
|
 (Volt) (Volt)
|
| elektromos dipólmomentum | 
|
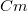
|
| kapacitás | 
|
 (Farad) (Farad)
|
| szuszceptibilitás | 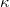
|
(nincs) |
| eltolási vektor | 
|
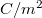
|
| polarizáció | 
|
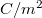
|
| elektromos tér energiasűrűsége | 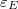
|
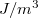
|
| elektromos fluxus | 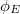
|
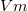
|
| relatív dielektromos állandó | 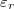
|
(nincs) |
| Megnevezés | Jelölés | Nagysága |
|---|---|---|
| elektron töltése | 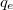
|
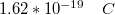
|
| elektron tömege | 
|
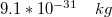
|
| proton tömege | 
|
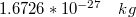
|
| neutron tömege | 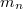
|
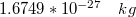
|
| vákuum permittivitása | 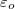
|
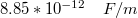
|