Elektrosztatika példák - Egyenletesen töltött gömbtérfogat energiája
Feladat
- Egy
 sugarú gömbben homogén
sugarú gömbben homogén  térfogati töltéssűrűség van. Határozzuk meg az elrendezés energiáját!
térfogati töltéssűrűség van. Határozzuk meg az elrendezés energiáját!
Megoldás
A töltéselrendezés energiájához ismernünk kell a térerősséget a tér minden pontjában. Először a gömbön belül határozzuk meg a teret. Felveszünk egy 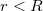 sugarú gömbfelületet, melynek centruma egybe esik a töltött gömbével. Meghatározzuk, mekkora töltést zár magába az
sugarú gömbfelületet, melynek centruma egybe esik a töltött gömbével. Meghatározzuk, mekkora töltést zár magába az  sugarú zárt felület:
sugarú zárt felület:
![\[Q=\dfrac{4}{3}r^3 \pi \rho\]](/images/math/7/3/e/73e922a7b73266b299b9f07118abba74.png)
A zárt felületre felírjuk a Gauss törvényt:
![\[\dfrac{Q}{\varepsilon_0}=\dfrac{4r^3\pi \rho}{3 \varepsilon_0}=\oint \overline{EdA}\]](/images/math/6/3/8/638a87a5a173aa3fc732856d4bee4d7d.png)
A rendszer gömbszimmetriája miatt az  sugarú felület minden pontjában azonos
sugarú felület minden pontjában azonos  nagyságú térerősséget mérhetünk, továbbá kijelenthetjük, hogy a térerősség vektorok minden pontban merőlegesek a felületre. Így a Gauss integrál jelentősen egyszerűsödik:
nagyságú térerősséget mérhetünk, továbbá kijelenthetjük, hogy a térerősség vektorok minden pontban merőlegesek a felületre. Így a Gauss integrál jelentősen egyszerűsödik:
![\[\dfrac{4r^3\pi \rho}{3 \varepsilon_0}=\oint \overline{EdA}=4r^2\pi E\]](/images/math/9/c/4/9c41ff2d3efe22214e68fdc04e004d0d.png)
Ebből kifejezve  -t, megkapjuk a térerősség nagyságát a gömb belsejében a centrumtól mért
-t, megkapjuk a térerősség nagyságát a gömb belsejében a centrumtól mért 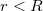 távolság függvényében:
távolság függvényében:
![\[E_{bent}=\dfrac{\rho}{3 \varepsilon_0}r\]](/images/math/3/6/9/369e0f7b193b4f7c2c36fedf99a76e46.png)
A gömbön kívüli teret (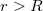 ) szintén a Gauss törvény segítségével határozhatjuk meg:
) szintén a Gauss törvény segítségével határozhatjuk meg:
![\[E_{kint}=\dfrac{Q}{4\pi \varepsilon_0}\dfrac{1}{r^2}\]](/images/math/8/9/e/89e9b31364d462f4f944950d168a54db.png)
Itt  a gömb teljes töltését jelenti:
a gömb teljes töltését jelenti:
![\[Q=\dfrac{4 R^3 \pi \rho}{3}\]](/images/math/3/b/6/3b6fb67f550b7f29184b43c61c4ac82e.png)
Tehát a gömbön kívüli tér nagysága:
![\[E_{kint}=\dfrac{\rho}{3 \varepsilon_0}\dfrac{R^3}{r^2}\]](/images/math/f/e/8/fe8abbf6ce2e7113bc4a244d811c6dca.png)
Az elektromos tér energiasűrűsége az alábbiak szerint definiálható:
![\[w=\dfrac{1}{2}\varepsilon_0 E^2\]](/images/math/0/d/8/0d86a1f37032bef873ff2aada30f7820.png)
A tér teljes energiája az energiasűrűség integrálja a teljes térre:
![\[W=\int w dV=\dfrac{\varepsilon_0}{2} \left( \int_0^R E_{bent}^2 4\pi r^2 dr + \int_R^{\infty} E_{kint}^2 4\pi r^2 dr \right)\]](/images/math/f/b/b/fbbc843d878398a48b0837cfd1359ec7.png)
![\[W=4\pi \dfrac{\varepsilon_0}{2} \left( \dfrac{\rho}{3\varepsilon_0} \right)^2 \left( \int_0^R r^2 r^2 dr + \int_R^{\infty} \left( \dfrac{R^3}{r^2} \right)^2 r^2 dr \right)\]](/images/math/2/e/2/2e2913f1ef00881544465d742705b181.png)
![\[W= \dfrac{2 \rho^2 \pi}{9 \varepsilon_0} \left( \int_0^R r^4 dr + \int_R^{\infty} \dfrac{R^6}{r^2} dr \right)= \dfrac{2 \rho^2 \pi}{9 \varepsilon_0} \left( \dfrac{R^5}{5} + \dfrac{R^6}{R} \right)\]](/images/math/2/1/e/21eccb7cdc33fb20d22eed7a1e0873f2.png)
![\[W=\dfrac{4 \rho^2 \pi R^5}{15 \varepsilon_0}\]](/images/math/4/c/9/4c9cb38d1d2f29cddb52eb3204968e09.png)