Elektrosztatika példák - Hengeres vezetékből és végtelen vezető síkból álló rendszer kapacitása
Feladat
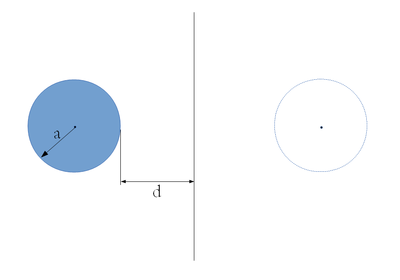
 hosszúságú egyenes hengeres vezeték párhuzamosan helyezkedik el egy végtelen vezető síkkal. A vezeték keresztmetszetének sugara
hosszúságú egyenes hengeres vezeték párhuzamosan helyezkedik el egy végtelen vezető síkkal. A vezeték keresztmetszetének sugara  , a távolság a vezeték síkhoz legközelebbi pontja és a sík között
, a távolság a vezeték síkhoz legközelebbi pontja és a sík között  . Mekkora a rendszer kapacitása? (
. Mekkora a rendszer kapacitása? (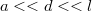 )
)
Megoldás
Induljunk ki az előző, Párhuzamos hengeres vezetékek kapacitása megoldásából. Ott kiszámítottuk, hogy két egymástól  távolságra levő párhuzamos,
távolságra levő párhuzamos,  sugarú,
sugarú,  hosszúságú fémhenger kapacitása:
hosszúságú fémhenger kapacitása:
![\[C^*=\dfrac{\pi l \varepsilon_0}{ln \left( \dfrac{b}{a} \right)}\]](/images/math/6/d/0/6d0f20230c4c3da1cce5324740eb4de0.png)
Válasszuk a hengerek távolságát 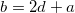 -nak (a
-nak (a  paraméter jelentését, lsd. 4. feladat ábráján). Ebben az esetben a kapacitás:\
paraméter jelentését, lsd. 4. feladat ábráján). Ebben az esetben a kapacitás:\
![\[C^*=\dfrac{\pi l \varepsilon_0}{ln \left( \dfrac{2d}{a} \right)}\]](/images/math/5/b/b/5bb9308a65dafa9d13a7b6d00e00b9c9.png)
Vegyük észre, hogy a párhuzamos hengerek 1. ábrán jelölt szimmetriasíkja egy ekvipotenciális felület. Ez könnyen belátható, hiszen ezt a síkot az elektromos tér erővonalai mindenütt merőlegesen döfik. Emiatt a síkban egy próbatöltést tetszőlegesen mozgathatunk munkavégzés nélkül, tehát a sík pontjai azonos potenciálon vannak.
S ha így van, egy vékony fémlapot is elhelyezhetünk ebben a síkban anélkül, hogy az elektromos tér változást szenvedne. Az így kapott elrendezés ekvivalens két sorba kapcsolt síklap-henger kondenzátorral, mely a jelen feladat kitűzésében szerepel. Gondolatkísérletünkkel tehát beláttuk, hogy a  kapacitású síklap-henger kondenzátor, és a fent hivatkozott
kapacitású síklap-henger kondenzátor, és a fent hivatkozott 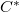 kapacitású henger-henger kondenzátor kapacitásaira igaz az alábbi összefüggés:
kapacitású henger-henger kondenzátor kapacitásaira igaz az alábbi összefüggés:
![\[\dfrac{1}{C^*}=\dfrac{1}{C}+\dfrac{1}{C}\]](/images/math/4/b/c/4bc39599f289f17b0320b715b2d0ff1e.png)
Ebből kifejezve  -t:
-t:
![\[C=2C^*=\dfrac{2 \pi l \varepsilon_0}{ln \left( \dfrac{2d}{a} \right)}\]](/images/math/8/c/d/8cd3115934f50c80549049f8c1d87c65.png)