Hullámjelenségek vizsgálata mikrohullámokkal
A mérés célja:
- a hullámjelenségekkel kapcsolatos ismeretek elmélyítése,
- hullámtani összefüggések kísérleti ellenőrzése,
- hullámoptikai jelenségek és eszközök modellezése.
A cél érdekében:
- összefoglaljuk a hullámjelenségekre vonatkozó alapvető ismereteket,
- megvizsgáljuk a mikrohullámok visszaverődését, törését, interferenciáját és elhajlását,
- összeállítunk néhány, a hullámok interferenciáján alapuló (optikában is használatos) mérési elrendezést, és megmérjük a használt mikrohullám hullámhosszát.
Tartalomjegyzék |
Elméleti összefoglaló
Kísérleteink során a hullámjelenségek tanulmányozására mikrohullámokat használunk. A mikrohullámok a fényhez hasonlóan elektromágneses hullámok, melyek hullámhossza nagyjából az 1 mm – 30 cm közötti sávba esik (frekvenciájuk ennek megfelelően 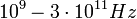 között van).
Az elektromágneses hullámok általános jellemzését ismételje át a Kísérleti Fizika tárgyban tanultak alapján.
között van).
Az elektromágneses hullámok általános jellemzését ismételje át a Kísérleti Fizika tárgyban tanultak alapján.
Hullámok polarizációja
Transzverzális hullámban a változó mennyiséget jellemző vektor mindig a hullám terjedési irányára merőleges síkban van, ezen belül azonban tetszőleges irányú lehet. Ha ebben a síkban kiválasztunk egy irányt, és a hullám útjába olyan akadályt helyezünk el, amely csak a kiválasztott irányú rezgést teszi lehetővé, akkor az akadályon túl olyan hullámot kapunk, amelyben a rezgések az akadály által kiválasztott irány és a terjedési irány által meghatározott síkban vannak. Az ilyen hullámot síkban polarizáltnak, az eljárást pedig a hullám polarizálásának nevezik. A kitüntetett sík a polarizáció síkja, a polarizált hullámot létrehozó akadály a polarizátor, a polarizátor által kiválasztott irányra pedig gyakran a polarizátor iránya vagy állása elnevezés használatos. Különböző jellegű hullámok polarizálására különböző módszerek használhatók, így pl. húrban vagy kötélen terjedő transzverzális hullámok egyszerű réssel, elektromágneses hullámok tükörrel vagy speciális anyagokból készült eszközökkel, a mikrohullámok egyszerű fémráccsal polarizálhatók. A polarizált hullámok jellegzetes tulajdonsága, hogy a polarizációs síkjukra merőleges polarizátorral kiolthatók (a rezgésnek nincs a polarizátor által kitüntetett irányban eső vetülete). Az elektromágneses hullámok esetén a polarizáció síkja a fenti definíció alapján nem egyértelmű, hiszen itt a terjedésre merőleges síkban két egymásra merőleges vektor van. Megállapodás szerint ebben az esetben a polarizáció síkja az elektromos térerősségvektort tartalmazó sík.
Hullám visszaverődése és törése
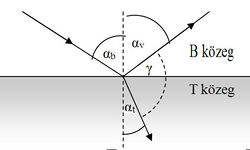
A hullámok mindig véges méretű közegekben terjednek, ezért előbb-utóbb elérik a közeg határát (elektromágneses hullámok esetén a közeg maga a légüres tér is lehet). A tapasztalat szerint a hullám a közeg határáról részben visszaverődik, részben pedig általában irányváltoztatással (töréssel) továbbhalad az új közegben. A visszaverődés és törés törvényeit a 1.ábra jelöléseivel a következőképpen fogalmazhatjuk meg.
Visszaverődésnél a beeső síkhullám haladási iránya ( ) és a visszaverő felület normálisa (
) és a visszaverő felület normálisa ( ) által bezárt ún. beesési szög (
) által bezárt ún. beesési szög (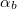 ) megegyezik a visszavert hullám haladási iránya (
) megegyezik a visszavert hullám haladási iránya ( ) és a beesési merőleges által bezárt ún. visszaverődési szöggel (
) és a beesési merőleges által bezárt ún. visszaverődési szöggel (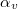 ):
):
![\[ \alpha_b = \alpha_v. \]](/images/math/2/a/7/2a7a86ffab16bc065fd949d60b95c1e3.png)
Szomszédos közegbe behatoló hullám haladási iránya a két közeg tulajdonságaitól és a beesési szögtől függ, s azt a
![\[ \frac{sin \alpha_b}{sin \alpha_t}= \frac{c_b}{c_t}=n_{tb}\]](/images/math/0/b/e/0be2bf35118cf5cccd501ebd8901a7a6.png)
ún. Snellius—Descartes-törvényből kaphatjuk meg. Itt 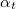 a megtört hullám haladási iránya (
a megtört hullám haladási iránya ( ) és a beesési merőleges által bezárt ún. törési szög.
) és a beesési merőleges által bezárt ún. törési szög. 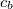 és
és 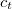 pedig a hullám terjedési sebessége a beeső hullámoldalán lévő közegben (az ábrán a
pedig a hullám terjedési sebessége a beeső hullámoldalán lévő közegben (az ábrán a  közeg) és a határon áthaladó (megtört) hullám oldalán lévő közegben (az ábrán
közeg) és a határon áthaladó (megtört) hullám oldalán lévő közegben (az ábrán  közeg). A terjedési sebességek fenti hányadosa külön jelölést (
közeg). A terjedési sebességek fenti hányadosa külön jelölést (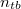 ) és nevet is kapott:
) és nevet is kapott: 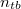 a
a  („törő”) közegnek a
(„törő”) közegnek a  („beesési”) közegre vonatkozó – ún. relatív – törésmutatója. Használatos még egy közegnek a vákuumra vonatkozó – ún. abszolút – törésmutatója is. Kimutatható, hogy a fenti két közeg abszolút törésmutatóját
(„beesési”) közegre vonatkozó – ún. relatív – törésmutatója. Használatos még egy közegnek a vákuumra vonatkozó – ún. abszolút – törésmutatója is. Kimutatható, hogy a fenti két közeg abszolút törésmutatóját 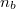 -vel, illetve
-vel, illetve 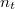 -vel jelölve, a relatív törésmutató még az alábbi módon is felírható:
-vel jelölve, a relatív törésmutató még az alábbi módon is felírható:
![\[ n_{tb} = \frac{n_t}{n_b}.\]](/images/math/1/6/b/16b244e1324114993e0144ab13eb0818.png)
Ha az 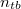 relatív törésmutató kisebb mint 1 (azaz
relatív törésmutató kisebb mint 1 (azaz 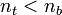 ), akkor a beesési szög növelésével előáll az az eset, hogy a törési szög eléri a
), akkor a beesési szög növelésével előáll az az eset, hogy a törési szög eléri a 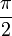 értéket. A beesési szöget tovább növelve ilyenkor a határfelület tükörként viselkedik, és a hullám a visszaverődés törvénye szerint gyakorlatilag teljesen visszaverődik. Ez a jelenség a teljes visszaverődés, az
értéket. A beesési szöget tovább növelve ilyenkor a határfelület tükörként viselkedik, és a hullám a visszaverődés törvénye szerint gyakorlatilag teljesen visszaverődik. Ez a jelenség a teljes visszaverődés, az 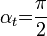 értéknek megfelelő beesési szög (
értéknek megfelelő beesési szög (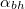 ) pedig a teljes visszaverődés határszöge, amelyre fennáll, hogy
) pedig a teljes visszaverődés határszöge, amelyre fennáll, hogy
![\[ sin \alpha_{bh} = n_{tb}.\]](/images/math/2/b/2/2b27a916652686556a1e578208e78895.png)
A visszaverődés vagy törés során megváltozhat a hullám fázisa, elektromágneses hullám esetén pedig a hullám polarizációja is. Gyakorlati szempontból is fontos tapasztalat, hogy egy bizonyos beesési szög esetén a visszavert elektromágneses hullám síkban polarizálttá válik. A visszavert hullám polarizációs síkja ilyenkor merőleges a beeső hullám és a visszavert hullám haladási iránya által meghatározott ún. beesési síkra (azaz az elektromos térerősség-vektor a visszavert hullámban párhuzamos a visszaverő felülettel). Kimutatható, hogy ez az eset akkor következik be, ha a visszavert és megtört hullám haladási iránya egymásra merőleges (vagyis a 1.ábrán 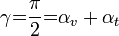 ), amiből következik, hogy ekkor a beesési szögre fennáll a
), amiből következik, hogy ekkor a beesési szögre fennáll a
![\[tg \alpha_{b,brewster}= n_{tb}\]](/images/math/2/c/e/2ce9034eb9a54a4b5c399f841c35f948.png)
összefüggés. Az összefüggést Brewster-törvénynek, az azt kielégítő 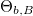 beesési szöget pedig Brewster-szögnek nevezik.
beesési szöget pedig Brewster-szögnek nevezik.
Hullámok interferenciája
A vizsgált térrészben egyidejűleg több hullám is terjedhet. Ilyenkor a tér egy pontjában a rezgési állapotot az esetek többségében a szuperpozíció elve alapján kaphatjuk meg. Eszerint a vizsgált helyen a hullámfüggvények pillanatnyi értékei egyszerűen összegződnek.
A hullámok összegződését interferenciának nevezik, amelynek eredménye a vizsgált pontban attól függ, hogy ott az összegződő hullámok milyen fázisban találkoznak. Az eredmény szélső esetben lehet például az amplitúdók összeadódása (maximális erősítés), ha a két hullám azonos fázisban találkozik, de lehet az amplitúdók kivonódása (maximális gyengítés), sőt azonos amplitúdók esetén teljes kioltás is, ha a hullámok ellenkező fázisban találkoznak. Ha a hullámforrások fázisa időben nem változik, és azonos frekvenciájú, megszakításmentes, szabályos haladóhullámokat vizsgálunk (koherens hullámok), akkor az összegződés helyén fennálló fáziskülönbséget két dolog határozza meg: a hullámforrások rezgései közötti fáziskülönbség és a hullámok által a találkozási helyig befutott utak különbsége. Koherens hullámok esetén eszerint a hullám amplitúdója bármely helyen időben állandó, ami egy állandósult térbeli amplitúdó-eloszlást – látható hullámok esetén szemmel is megfigyelhető állandósult interferenciaképet – eredményez. Így például azonos fázisban működő hullámforrások által keltett két harmonikus hullám interferenciájánál a fáziskülönbséget kizárólag az útkülönbség szabja meg. Könnyen belátható, hogy ha a hullámforrások távolsága a vizsgált ponttól 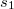 és
és 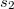 , akkor a hullámok maximálisan erősítik egymást minden olyan helyen, amelyre fennáll, hogy a
, akkor a hullámok maximálisan erősítik egymást minden olyan helyen, amelyre fennáll, hogy a 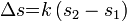 útkülönbség a hullámhossz egészszámú többszöröse
útkülönbség a hullámhossz egészszámú többszöröse
![\[ \Delta s_n = n \lambda \left( n=1,2,3,...\right).\]](/images/math/7/1/0/7104e56de4a3536c283ee800f959d3b4.png)
A maximális gyengítés pedig a
![\[ \Delta s_n = \left( 2n-1 \right) \frac{\lambda }{2} \left( n=1,2,3,...\right)\]](/images/math/8/f/a/8fac88f83111907d1d71bf0e24711bc1.png)
feltételnek megfelelő helyeken következik be.
Állóhullámok
A hullámok interferenciájának igen fontos speciális esete az állóhullámok kialakulása, amely annak a következménye, hogy egy közeg határán a hullám legalább részben visszaverődik. A határ felé haladó és az onnan visszaverődött hullámok interferenciája bizonyos feltételek teljesülése esetén sajátos, állandósult hullámalakzatot – ún. állóhullámot – eredményez. Ennek jellegzetessége az, hogy a közeg meghatározott tartományaiban lévő pontokban a rezgés azonos fázisban történik, a rezgés amplitúdója pedig csak a hely függvénye.
Állóhullám létrehozható pl. a harmonikus síkhullámot visszaverő, a hullám terjedési irányára merőleges két sík közötti térrészben, de csak akkor, ha a hullám hullámhossza (frekvenciája) bizonyos feltételeknek eleget tesz. A lehetséges állóhullám-hullámhosszakat a visszaverő felületek közötti  távolság és a visszaverődés helyein fennálló határfeltételek szabják meg. A határfelületen a fizikai feltételek lehetnek olyanok, hogy ott számottevő rezgés nem jöhet létre, (pl. egy rugalmas húr vége rögzített, egy rezgő légoszlop szilárd fallal határolt, de ugyanilyen hatású egy tükröző fémfelület az elektromágneses hullám elektromos összetevőjére). Más esetekben nincs, vagy alig van korlátozás a rezgés kialakulására a határon (pl. rugalmas kötél szabad végén, gázoszlop nyitott végén, az elektromágneses hullám mágneses összetevőjére tükröző fémfelületen).
Kimutatható, hogy ha a rezgés az
távolság és a visszaverődés helyein fennálló határfeltételek szabják meg. A határfelületen a fizikai feltételek lehetnek olyanok, hogy ott számottevő rezgés nem jöhet létre, (pl. egy rugalmas húr vége rögzített, egy rezgő légoszlop szilárd fallal határolt, de ugyanilyen hatású egy tükröző fémfelület az elektromágneses hullám elektromos összetevőjére). Más esetekben nincs, vagy alig van korlátozás a rezgés kialakulására a határon (pl. rugalmas kötél szabad végén, gázoszlop nyitott végén, az elektromágneses hullám mágneses összetevőjére tükröző fémfelületen).
Kimutatható, hogy ha a rezgés az  hosszúságú tartomány mindkét végén korlátozott, vagy, ha mindkét végen akadálytalan, akkor a lehetséges hullámhosszakat a
hosszúságú tartomány mindkét végén korlátozott, vagy, ha mindkét végen akadálytalan, akkor a lehetséges hullámhosszakat a
![\[ \lambda_n = \frac{2L}{n} \left( n=1,2,3,...\right)\]](/images/math/5/9/f/59f65f68ff6e0c6bbfa5956240848c1f.png)
összefüggés adja meg. Egyik végen korlátozott, másik végen szabad rezgés esetén pedig a
![\[ \lambda_n = \frac{4L}{2n-1} \left( n=1,2,3,...\right).\]](/images/math/a/e/7/ae74f9cc7e73e6b4b61bfff26315f094.png)
Egy ilyen állóhullámban a hullámterjedés iránya mentén az amplitúdó a hely függvényében szinusz (koszinusz) függvény szerint változik, és ennek megfelelően maximumokat (duzzadóhelyeket) és minimumokat (csomópontokat) tartalmazó amplitúdó-eloszlás jön létre, amelyben mind a csomópontok, mind pedig a duzzadóhelyek egymástól
![\[ d_n = \frac{\lambda_n}{2} \left( n=1,2,3,...\right)\]](/images/math/8/7/9/879316b4a68874750cf94a5729b61e32.png)
távolságra vannak.
Hullámok elhajlása (diffrakció)
Sajátos jelenségeket figyelhetünk meg, ha egy hullám a hullámhosszával összemérhető kiterjedésű inhomogenitásokat tartalmazó közegben terjed. Ilyen eset például az, amikor a hullám kisméretű, áthatolhatatlan akadállyal (akadályokkal) vagy áthatolhatatlan közeghatáron lévő, a hullám számára átjárható réssel (résekkel) találkozik. Ilyenkor az akadályon vagy résen való áthaladás után az eredetileg egyenletes térbeli intenzitáseloszlású síkhullám intenzitásában jellegzetes irányfüggés jelenik meg. Ezt a jelenséget a hullámok elhajlásának vagy diffrakciójának nevezik (az elnevezés arra utal, hogy a hullám eltér eredeti haladási irányától: pl. behatol az akadály mögötti térbe is).
Ha a hullám kisméretű (a hullámhosszával összemérhető) résen halad át, akkor a résen áthaladt hullámok interferencia révén bizonyos irányokban erősítik, más irányokban pedig gyengítik egymást. Ezért, ha a résen túl egy, a terjedési irányra merőleges egyenes ( ) mentén megmérjük a hullám
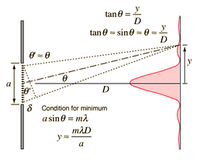
) mentén megmérjük a hullám 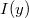 intenzitáseloszlását, akkor jellegzetes, váltakozó maximumokat és minimumokat tartalmazó görbét kapunk (2.ábra). Hasonló intenzitáseloszlás jön létre, csak még kifejezettebb maximumokkal és minimumokkal, kettős rés vagy egy rés-sorozat – ún. rács – esetén.
Az, hogy egy réselrendezésnél a maximumok, illetve minimumok milyen irányokban jönnek létre, a
intenzitáseloszlását, akkor jellegzetes, váltakozó maximumokat és minimumokat tartalmazó görbét kapunk (2.ábra). Hasonló intenzitáseloszlás jön létre, csak még kifejezettebb maximumokkal és minimumokkal, kettős rés vagy egy rés-sorozat – ún. rács – esetén.
Az, hogy egy réselrendezésnél a maximumok, illetve minimumok milyen irányokban jönnek létre, a  hullámhossztól, a rés méretétől (
hullámhossztól, a rés méretétől ( ), két rés vagy rács esetén a struktúra ismétlődési távolságától, az ún. rácsállandótól (
), két rés vagy rács esetén a struktúra ismétlődési távolságától, az ún. rácsállandótól ( ) függ.
Kimutatható, hogy az intenzitásminimumok irányát megadó
) függ.
Kimutatható, hogy az intenzitásminimumok irányát megadó 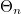 szögek (2.ábra) egyedülálló rés, kettős rés és rács esetén egyaránt a
szögek (2.ábra) egyedülálló rés, kettős rés és rács esetén egyaránt a
![\[ b \cdot sin \Theta_n = n \lambda \left( n = \pm 1, \pm 2, \pm 3,... \right) \]](/images/math/1/7/0/17041fdd1bcd26cb921d92ce32777f75.png)
összefüggésből kaphatóak meg, ahol  a rés (rések) mérete.
Az intenzitásmaximumok irányára egyetlen rés esetén nincs egyszerű összefüggés (természetesen ezek a minimumok között vannak, így a helyük (11) alapján durván megbecsülhető). Két rés és rács esetén a maximumok irányai az
a rés (rések) mérete.
Az intenzitásmaximumok irányára egyetlen rés esetén nincs egyszerű összefüggés (természetesen ezek a minimumok között vannak, így a helyük (11) alapján durván megbecsülhető). Két rés és rács esetén a maximumok irányai az
![\[ a \cdot sin \Theta_n = n \lambda \left(n =0, \pm 1, \pm 2, \pm 3,... \right) \]](/images/math/e/f/f/eff63957f323664c6f25b52c90a6b636.png)
összefüggésből számíthatók, ahol  a rácsstruktúra periódushossza (az
a rácsstruktúra periódushossza (az 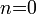 érték a hullám el nem térített részének megfelelő ún. főmaximum irányát adja meg).
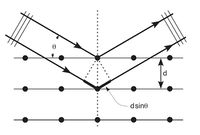
A közeg inhomogenitásai természetesen lehetnek bonyolultabbak is, mint a fenti esetben. Érdekes, és az anyagtudományban alapvető szerepet játszó eset elektromágneses hullámok elhajlása háromdimenziós periodikus struktúrán, térbeli rácson. Ilyen struktúrának tekinthető az összes kristályos anyag, amelyben a rácsot a periodikusan elhelyezkedő atomok képezik (3.ábra). Megfelelően kis hullámhosszú elektromágneses hullám (pl. röntgensugárzás) a kristályrácson áthaladva elhajlást szenved, s a létrejött intenzitáseloszlás a kristályrács jellegzetességeit tükrözi. Ilyen elhajlási kísérletek tehát a kristályszerkezet vizsgálatára alkalmasak.
Az elhajlási maximumok létrejöttét legegyszerűbben az alábbi módon képzelhetjük el. A kristályban az atomokat tartalmazó rácssík az elektromágneses hullámokat a visszaverődés törvényének megfelelően visszaveri (3b.ábra). A párhuzamos síkokról visszavert hullámok interferenciájuk során akkor erősítik egymást, ha útkülönbségük megfelel a (6) összefüggésnek. Ez olyan
érték a hullám el nem térített részének megfelelő ún. főmaximum irányát adja meg).
A közeg inhomogenitásai természetesen lehetnek bonyolultabbak is, mint a fenti esetben. Érdekes, és az anyagtudományban alapvető szerepet játszó eset elektromágneses hullámok elhajlása háromdimenziós periodikus struktúrán, térbeli rácson. Ilyen struktúrának tekinthető az összes kristályos anyag, amelyben a rácsot a periodikusan elhelyezkedő atomok képezik (3.ábra). Megfelelően kis hullámhosszú elektromágneses hullám (pl. röntgensugárzás) a kristályrácson áthaladva elhajlást szenved, s a létrejött intenzitáseloszlás a kristályrács jellegzetességeit tükrözi. Ilyen elhajlási kísérletek tehát a kristályszerkezet vizsgálatára alkalmasak.
Az elhajlási maximumok létrejöttét legegyszerűbben az alábbi módon képzelhetjük el. A kristályban az atomokat tartalmazó rácssík az elektromágneses hullámokat a visszaverődés törvényének megfelelően visszaveri (3b.ábra). A párhuzamos síkokról visszavert hullámok interferenciájuk során akkor erősítik egymást, ha útkülönbségük megfelel a (6) összefüggésnek. Ez olyan 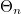 szögeknél teljesül, amelyekre fennáll, hogy
szögeknél teljesül, amelyekre fennáll, hogy
![\[ 2d \cdot sin \Theta_n = n \lambda \left(n =0, \pm 1, \pm 2, \pm 3,... \right). \]](/images/math/7/6/6/766e63d3a8779bb65c8993d4176b0709.png)
Itt 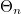 a beeső hullám iránya és a rácssík által bezárt szöget jelenti. Ez az ún. Bragg-egyenlet.
a beeső hullám iránya és a rácssík által bezárt szöget jelenti. Ez az ún. Bragg-egyenlet.
A mérőberendezés és használata
A berendezés alkotóelemei
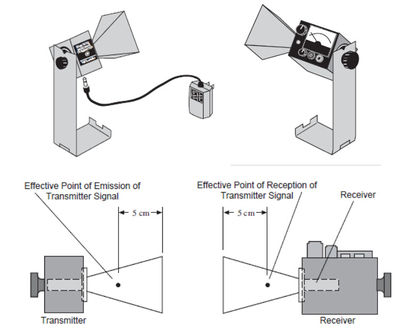
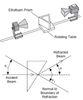
A kísérletek során a mikrohullámokat egy speciális mikrohullámú adóberendezéssel állítjuk elő (4a. ábra). Az adó a mikrohullámokat egy ún. Gunn-dióda segítségével hozza létre, s egy téglalap keresztmetszetű tölcséren át sugározza ki. A hullámok a dióda hossztengelyével párhuzamosan polarizáltak. Annak érdekében, hogy a kísérletekben a hullámok polarizációs síkját változtatni tudjuk, az adó a hátoldalán lévő csavar kilazítása után vízszintes tengely körül elforgatható, s az elfordulás szöge egy skálán leolvasható. Az adó bekapcsolt állapotát egy LED jelzi. A mikrohullámok észlelésére szolgáló vevőkészülék (4b.ábra) tölcsére a beeső hullámokat egy Schottky-diódára gyűjti össze, amely érzékeli a hullám intenzitását, és egyben a hossztengelyével egyirányú polarizátorként működik. A vevőn elhelyezett műszer kitérése nem túl nagy intenzitásoknál nagyjából (de nem pontosan) a hullám intenzitásával arányos. A vevő az adóhoz hasonlóan vízszintes tengely körül forgatható. Bekapcsolása az Intensity gombnak az OFF állásból a legkisebb „30x” feliratú állásba való átállításával történik. Ezután a működését jelző LED világít. Az erősítés úgy növelhető, hogy az Intensity gombot az egyre kisebb szorzószámú méréshatár állásokba kapcsoljuk. A mérési érték úgy kapható meg, hogy a műszeren leolvasott értéket megszorozzuk a használt méréshatár szorzószámával. Minden mérés elején célszerű beállítani a vevő érzékenységét. Ez úgy történik, hogy a vevőt a mérendő jel irányába állítjuk az adóval azonos tölcsérállással, és a Variable Sensitivity gombot addig állítjuk, amíg a műszer mutatója a skála közepére áll. Ha ez nem lehetséges a legkisebb erősítésnél („30x” állás), akkor az Intensity gombbal addig növeljük az erősítést (ez csökkenő szorzószámot jelent), amíg a mutató középre állítása sikerül. A mérés közben ezen a beállításon ne változtassunk! Az adón és a vevőn kívül a méréseknél számos segédeszközt használunk, melyeket a 5.ábra mutat be. A vevőn levő piros és fekete, Output feliratú banánhüvelyeken a mutatós műszer által jelzett áramértékkel arányos feszültség jelenik meg a 0 V - 2 V tartományban. A kimeneti jelet mérjük meg digitális multiméterrel, így a maximum és minimum értékek pontosabban leolvashatók és a maximum és minimum helyek is pontosabban megtalálhatók.
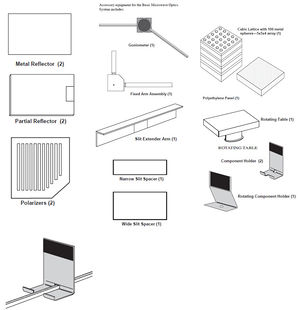
Mérési összeállítások
Az alábbiakban a berendezéssel végezhető legfontosabb mérési összeállításokat és azok működési elvét mutatjuk be, megadva az összeállítás vázlatos rajzát is. A rajzokon a 5.ábra számozását használjuk.
Visszaverődés vizsgálata
A mikrohullámok visszaverődését goniométer segítségével a 6.ábrán látható elrendezésben vizsgáljuk. A vevőt a goniométer elfordítható karjára, a fémtükröt a forgatható tárgytartóra tesszük. A beesési szöget a fémtükör elfordításával változtatjuk, a visszavert sugarat a vevőt tartó goniométer-kar elfordításával keressük meg. A szögeket a goniométeren lévő skálán olvashatjuk le.
Állóhullámok vizsgálata
Ennek a vizsgálatnak a vázlata a 7.ábrán látható. Ez a mérés annyiban tér el a többitől, hogy itt a hullám intenzitásának mérésére nem közvetlenül a vevőt, hanem egy speciális szondát (Sz) használunk. A szonda a vevőhöz csatlakoztatható, és az általa szolgáltatott jelet a vevő mutatós műszerén olvassuk le. Az állóhullámok az adó és a tükör között alakulnak ki, ha a távolságuk az állóhullám-feltételnek megfelel. Ilyen távolságot a tükör mozgatásával tudunk beállítani. Az amplitúdó helyfüggését a szonda mozgatásával mérhetjük ki. Ennek ismeretében (10) összefüggés alapján meghatározhatjuk a használt mikrohullám hullámhosszát. A hullámhosszmérésnél a nagyobb pontosság érdekében ne két szomszédos maximum, hanem az elsőnek megtalált és a tizenegyedik maximum közötti távolságot mérjük meg.
Törés prizmán
A mérési elrendezés a 8.ábrán látható. Előbb vizsgáljuk meg, hogy az üres prizma milyen hatással van a mikrohullámok terjedésére, majd a mellékelt, sztirol golyókkal megtöltött prizmán mérjük ki az eltérítést. Az egyszerűbb kiértékelés érdekében a prizmát a forgó asztal elfordításával állítsuk be úgy, hogy egyik lapja merőleges legyen a beeső hullám haladási irányára (9.ábra). A megtört sugarat a vevőt tartó goniométer-kar elforgatásával keressük meg. A prizmát kitöltő anyagnak a levegőre vonatkoztatott törésmutatóját, illetve a hullám terjedési sebességét a prizmában a (2) összefüggésből kaphatjuk meg.
Polarizáció vizsgálata
Ehhez a vizsgálathoz lényegében a szembeállított adót és vevőt használjuk (10a.ábra és 10b.ábra), s egyes vizsgálatoknál közéjük helyezzük el a polarizátorként működő fémrácsot. A polarizátor állásának hatását egy polarizált hullámra vizsgálhatjuk külön polarizátor nélkül is oly módon, hogy a vevőt vízszintes tengelye körül forgatjuk, hiszen a vevő egyben polarizátor is. Ezen kívül az elrendezéssel megvizsgálhatjuk az adó és vevő közé helyezett polarizátor hatását is annak különböző állásai esetén.
Elhajlás résen
Egy és két rés alkalmazásával megvizsgálhatjuk a hullámelhajlást a 11a.ábra és 11b.ábra szerinti összeállításban. Két résnél a és méretét kb. 1,5 cm-esre állítsuk be, egy rés kialakításához a résközt vegyük ki, és kb. 7 cm-es résmérettel dolgozzunk.
Lloyd-féle tükör
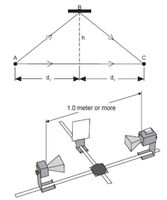
Ezzel az elrendezéssel azonos forrásból jövő, de különböző utakat (a 12.ábrán 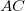 és
és 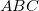 ) befutó hullámok interferenciájának vizsgálatával hullámhosszt mérhetünk. A mérésnél először a
) befutó hullámok interferenciájának vizsgálatával hullámhosszt mérhetünk. A mérésnél először a  tükröt közelítjük a goniométer tengelyéhez. Ekkor a vevő – attól függően, hogy a két hullám útkülönbsége
tükröt közelítjük a goniométer tengelyéhez. Ekkor a vevő – attól függően, hogy a két hullám útkülönbsége  -ben éppen a (6) vagy (7) feltételnek felel meg – egymást követő maximumokat és minimumokat detektál. Álljunk meg a goniométerhez legközelebb eső olyan helyen, ahol a jel maximális és mérjük meg a tükör helyzetét jellemző
-ben éppen a (6) vagy (7) feltételnek felel meg – egymást követő maximumokat és minimumokat detektál. Álljunk meg a goniométerhez legközelebb eső olyan helyen, ahol a jel maximális és mérjük meg a tükör helyzetét jellemző 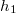 távolságot. Ezután a tükröt távolítsuk az
távolságot. Ezután a tükröt távolítsuk az 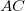 egyenestől addig, amíg újra maximális intenzitást kapunk, és mérjük meg az ehhez a pozícióhoz tartozó
egyenestől addig, amíg újra maximális intenzitást kapunk, és mérjük meg az ehhez a pozícióhoz tartozó 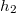 távolságot is. Ha még a vevő és adó távolságát is megmérjük, akkor a mért adatok segítségével az eredeti (
távolságot is. Ha még a vevő és adó távolságát is megmérjük, akkor a mért adatok segítségével az eredeti (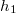 -hez tartozó) úthossz és az új (
-hez tartozó) úthossz és az új (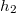 -höz tartozó) úthossz meghatározható. Mivel tudjuk, hogy ekkor a hullámok útkülönbsége (6) szerint éppen a
-höz tartozó) úthossz meghatározható. Mivel tudjuk, hogy ekkor a hullámok útkülönbsége (6) szerint éppen a  hullámhosszal egyenlő, a két úthossz különbsége közvetlenül a hullámhosszt adja. Ügyeljünk arra, hogy az adó és a vevő tengelye egy egyenesen legyen, az adó és vevő goniométer tengelyétől azonos távolságban helyezkedjen el, és egymástól mért távolságuk legalább 1 m legyen. A tükör síkja legyen párhuzamos az adó-vevő egyenessel. A távolságok meghatározásánál vegyük figyelembe a 4. ábrán bejelölt effektív pontok helyét!
hullámhosszal egyenlő, a két úthossz különbsége közvetlenül a hullámhosszt adja. Ügyeljünk arra, hogy az adó és a vevő tengelye egy egyenesen legyen, az adó és vevő goniométer tengelyétől azonos távolságban helyezkedjen el, és egymástól mért távolságuk legalább 1 m legyen. A tükör síkja legyen párhuzamos az adó-vevő egyenessel. A távolságok meghatározásánál vegyük figyelembe a 4. ábrán bejelölt effektív pontok helyét!
Michelson-interferométer
Ez az eszköz, amely a hullámhossz és elmozdulás mérésére használható, vázlatosan a 13.ábrán látható. Alapelve – a Lloyd-féle tükörhöz hasonlóan – az, hogy egy forrásból jövő hullámot két részre osztunk, és különböző utakon vezetve újra egyesítjük. Az egyesítésnél a hullámok interferálnak, s ennek eredménye (erősítés vagy gyengítés) a befutott utak különbségétől függ. Az ábrán látható esetben az adóból jövő hullám egy része a  tükör felé visszaverődik, másik része áthalad az
tükör felé visszaverődik, másik része áthalad az  tükör felé. Ezután a
tükör felé. Ezután a  -ről visszaverődő hullám egy része a
-ről visszaverődő hullám egy része a  lapon áthaladva, az
lapon áthaladva, az  tükörről visszaverődő hullám egy része pedig a
tükörről visszaverődő hullám egy része pedig a  lapról visszaverődve a vevőbe jut, amely a két hullám interferenciájának megfelelő jelet ad. Az interferáló két hullám útkülönbsége éppen
lapról visszaverődve a vevőbe jut, amely a két hullám interferenciájának megfelelő jelet ad. Az interferáló két hullám útkülönbsége éppen 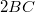 és
és 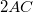 távolságok különbsége.
A mérés során először az A tükör elmozdításával megkeresünk egy olyan helyzetet, ahol a vevő maximális intenzitást mutat (vagyis az útkülönbségre teljesül a (6) feltétel), majd a tükröt ebből a helyzetből addig távolítjuk a
távolságok különbsége.
A mérés során először az A tükör elmozdításával megkeresünk egy olyan helyzetet, ahol a vevő maximális intenzitást mutat (vagyis az útkülönbségre teljesül a (6) feltétel), majd a tükröt ebből a helyzetből addig távolítjuk a  -től, amíg ismét maximális jelet kapunk. Az
-től, amíg ismét maximális jelet kapunk. Az  tükör két helyzete közti távolság ekkor éppen a hullámhossz fele (
tükör két helyzete közti távolság ekkor éppen a hullámhossz fele ( ), ugyanis az útkülönbség a kettes szorzó miatt éppen ekkor hullámhossznyi. A mérésnél a nagyobb pontosság érdekében 10 új maximumnak megfelelő távolságra mozdítsuk el a tükröt.
), ugyanis az útkülönbség a kettes szorzó miatt éppen ekkor hullámhossznyi. A mérésnél a nagyobb pontosság érdekében 10 új maximumnak megfelelő távolságra mozdítsuk el a tükröt.
Brewster-szög mérése
A mérést a 14.ábra szerint végezzük el. Az adót és vevőt először vízszintes polarizációra állítjuk be (90° a hátlapjaikon lévő skálán), a polietilén lapot pedig addig forgatjuk el, amíg az adóból jövő hullám beesési szöge kb. 20° lesz. A vevőt tartó goniométer-kart elforgatva a vevővel megkeressük a lapról visszavert hullámot (maximális intenzitás), és feljegyezzük a mért intenzitást. Az intenzitás mérését különböző beesési szögeknél megismételjük. Ugyanebben az állásban a mérést megismételjük úgy, hogy az adót és a vevőt függőleges polarizációjú helyzetbe fordítjuk át (0°-os állás). A Brewster-szögnél a vízszintesen polarizált hullám nem verődik vissza, mert ilyenkor a függőleges helyzetű lap a visszavert hullámra nézve függőleges irányú polarizátorként működik.
Bragg-elhajlás köbös rácson
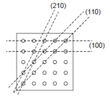
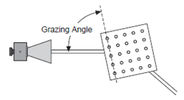
A mérési elrendezés a 15a.ábrán látható. A vizsgálat során különböző – függőleges helyzetű – rácssíkok esetén (15b.ábra) megkeressük a (13) Bragg-egyenletnek megfelelő 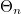 szögeket. Vigyázzunk, mert a (13) egyenletben szereplő szög nem a hullám beesési szöge, hanem a rácssíkkal bezárt szög (15c. ábra). (A rácssíkok jelölésére az ábrán használt számhármasok a síkok ún. Miller-indexei. Ezek a síkoknak a kocka éleivel párhuzamosan választott koordinátatengelyeken adott tengelymetszeteinek reciprokával arányos számok.)
A mérés menete az (
szögeket. Vigyázzunk, mert a (13) egyenletben szereplő szög nem a hullám beesési szöge, hanem a rácssíkkal bezárt szög (15c. ábra). (A rácssíkok jelölésére az ábrán használt számhármasok a síkok ún. Miller-indexei. Ezek a síkoknak a kocka éleivel párhuzamosan választott koordinátatengelyeken adott tengelymetszeteinek reciprokával arányos számok.)
A mérés menete az (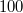 ) sík esetén a következő. Az adót és vevőt egymással szembeállítjuk, a rácsot úgy helyezzük a forgatható asztalra, hogy az (
) sík esetén a következő. Az adót és vevőt egymással szembeállítjuk, a rácsot úgy helyezzük a forgatható asztalra, hogy az (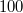 ) síkok párhuzamosak legyenek a beeső hullám haladási irányával, és feljegyezzük a mért intenzitást. Forgassuk el a rácsot a forgóasztal segítségével 1°-kal, a vevőt tartó goniométer-kart pedig 2°-kal az óramutató járásával egy irányban, írjuk fel a
) síkok párhuzamosak legyenek a beeső hullám haladási irányával, és feljegyezzük a mért intenzitást. Forgassuk el a rácsot a forgóasztal segítségével 1°-kal, a vevőt tartó goniométer-kart pedig 2°-kal az óramutató járásával egy irányban, írjuk fel a 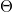 szöget és a mért intenzitást. Folytassuk a fenti elforgatásokat és méréseket, és ábrázoljuk a mért intenzitásokat a beesési szög függvényében. A Bragg-egyenletnek megfelelő szögeknél maximumot kell kapnunk. A mérés és a (13) egyenlet alapján meghatározhatjuk az (
szöget és a mért intenzitást. Folytassuk a fenti elforgatásokat és méréseket, és ábrázoljuk a mért intenzitásokat a beesési szög függvényében. A Bragg-egyenletnek megfelelő szögeknél maximumot kell kapnunk. A mérés és a (13) egyenlet alapján meghatározhatjuk az (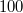 ) síkok egymástól mért távolságát. Hasonló módon járhatunk el a többi sík esetén is.
) síkok egymástól mért távolságát. Hasonló módon járhatunk el a többi sík esetén is.
Mérési feladatok
1. Prizma segítségével határozza meg a sztirolgolyók levegőre vonatkoztatott törésmutatóját és a hullám terjedési sebességét ebben a közegben. Az üres prizmát vízzel feltöltve határozza meg a víz levegőre vonatkoztatott törésmutatóját. Vigyázzon, hogy a víz ne folyjon ki!
2.1. Állítsa szembe az adót és vevőt azonos polarizációs állásban (pl. a műszerek hátoldalán lévő skálán 0°-os állás, más szóval a tölcsérek hossztengelye vízszintesen áll). Ezután a vevőt forgassa vízszintes tengelye körül, és mérje ki az intenzitás függését a vevő állását jellemző szögtől (10°-onként, 0°-tól 180°-ig). Értelmezze az eredményt!
2.2. Az adó és vevő függőleges polarizációjú (0°-os) állásánál tegye be a fémrács-polarizátort vízszintesen álló résekkel az adó és a vevő közé, és a vevő forgatásával ismét mérje ki az intenzitás szögfüggését. Ismételje meg a mérést úgy, hogy a polarizátor rései 22,5°, 45°, 67,5° és 90°-os szögeket zárnak be a vízszintessel. Értelmezze az eredményeket!
2.3. Állítsa az adót és vevőt egymásra merőleges polarizációjú állásba. Mérje meg az intenzitást a fémrács-polarizátor nélkül, majd tegye be a polarizátort és mérje meg a jelet, amikor a polarizátor rései vízszintesek, függőlegesek és 45°-os szöget zárnak be a vízszintessel. Értelmezze az eredményeket!
3. Állítsa össze a kettős résen történő elhajlásmérés elrendezését a keskeny résközzel, 1,5 cm-es résmérettel. Állítsa az adót és a vevőt egymással szembe, függőleges polarizációjú állásba (0°). Ezután a vevőt tartó goniométer-kart a vevővel együtt forgatva mérje ki és ábrázolja az intenzitás szögfüggését (5°-onként 0° és 85° között, a maximumértékek körül 2°-onként). A mérést ismételje meg a széles résközzel is (ekkor a vevőt állítsa kb. 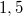 -szeres távolságba a réstől). Ellenőrizze a (12) összefüggést a maximumszögekre (a hullámhosszt számolja ki az adó egységen feltüntetett frekvenciából), és értelmezze az eltéréseket. Végezze el a mérést egyetlen réssel is 7 cm-es résmérettel és ellenőrizze a (11) összefüggést a minimumszögekre.
-szeres távolságba a réstől). Ellenőrizze a (12) összefüggést a maximumszögekre (a hullámhosszt számolja ki az adó egységen feltüntetett frekvenciából), és értelmezze az eltéréseket. Végezze el a mérést egyetlen réssel is 7 cm-es résmérettel és ellenőrizze a (11) összefüggést a minimumszögekre.
4. A Lloyd-féle tükörrel mérje meg az alkalmazott mikrohullám hullámhosszát két különböző adó-vevő távolságnál. Az eredményt hasonlítsa össze a 2. mérésnél kapott értékkel!
5. Michelson-interferométerrel mérje meg a használt mikrohullám hullámhosszát az  tükör két különböző kiinduló helyzete esetén. Az eredményeket vesse össze egymással és a korábbi hullámhosszmérések (2. és 4. mérési feladat) eredményével.
tükör két különböző kiinduló helyzete esetén. Az eredményeket vesse össze egymással és a korábbi hullámhosszmérések (2. és 4. mérési feladat) eredményével.
6. A Brewster-szög mérésére szolgáló elrendezésben mérje ki és ábrázolja a polietilén lapról visszavert mikrohullám intenzitásának szögfüggését. A beesési szöget változtassa 5°-onként 20° és 75° között. A mérést végezze el először úgy, hogy az adó és vevő polarizációja vízszintes, majd úgy, hogy az adó és vevő polarizációja függőleges. Értelmezze az eredményeket és határozza meg a Brewster-szöget!
7. A Bragg-elhajlás segítségével határozza meg a mellékelt köbös rácsban az (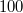 ) , (
) , (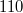 ) és (
) és (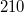 ) síkok távolságát és hasonlítsa össze az eredményeket a közvetlen hosszméréssel kapott értékekkel!
) síkok távolságát és hasonlítsa össze az eredményeket a közvetlen hosszméréssel kapott értékekkel!
Ha maradt ideje, végezze el az alábbi mérési feladatokat is:
8. Ellenőrizze a (3) visszaverődési törvényt mikrohullámok esetén. A mérést 10° és 90° közé eső beesési szögeknél 10°-onként végezze el. Készítsen táblázatot és értelmezze az esetleges eltéréseket a visszaverődési törvénytől!
9. Állítson elő állóhullámokat, és mérje meg a használt mikrohullám hullámhosszát. Számítsa ki a hullám frekvenciáját is (a terjedési sebesség adott). A mérést két különböző beállításnál végezze el!
Biztonsági tudnivalók
Fontos!
Mivel a mikrohullámoknak a környező tárgyakról való visszaverődése a mérést befolyásolhatja, a mérés során a mérőasztalról minden felesleges tárgyat (különösen a fémtárgyakat) távolítsuk el! A mikrohullámokat a testünk is visszaveri, ezért soha ne álljunk olyan helyzetben, hogy az adóról jövő hullámot a testünk a vevőbe reflektálhatja. Legjobb, ha a vevő tölcsérének síkja mögött állva végezzük a mérést. Bár az adók teljesítménye jóval a megengedett biztonsági érték alatt van, soha ne nézzünk közvetlenül az adó tölcsérébe, ha az működik. Nem valószínű, de előfordulhat, hogy a mikrohullámok zavarják egyes orvosi elektronikus készülékek – pl. szívritmus-szabályozó (pacemaker) – működését. Ha ilyen eszközt használ, jelezze a gyakorlatvezetőnek.
PDF formátum