Mechanika - Henger lejtőn

Feladat

1. (*3.3.16.) Egy $\setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0%$ hajlásszögű lejtőre $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű és $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú hengert helyezünk, majd magára hagyjuk.

   a) Hogyan fog a henger mozogni, ha a lejtő és a hengerfelület között nem lép fel súrlódás?

   b) Mekkora lesz az a minimális 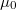$\setbox0\hbox{$\mu_0$}% \message{//depth:\the\dp0//}% \box0%$ súrlódási tényező, melynél a henger tisztán gördül a lejtőn? Határozza meg a tiszta gördülés esetén a mozgást jellemző mennyiségeket!

   c) Mekkora lesz a henger szögsebessége a $\setbox0\hbox{$h$}% \message{//depth:\the\dp0//}% \box0%$ magasságú lejtő alján?

   d) Írja le a henger mozgását olyan esetben, amikor $\setbox0\hbox{$\mu<\mu_0$}% \message{//depth:\the\dp0//}% \box0%$!

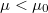Megoldás

1. a) A tömegközéppont mozgásegyenlete 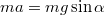$\setbox0\hbox{$ma=mg\sin{\alpha}$}% \message{//depth:\the\dp0//}% \box0%$, így az ennek megfelelően gyorsul. A henger kezdeti forgásmentes állapota nem változik meg, mert nincs nyomatékkal bíró erő a tömegközéppontra nézve, így a korong tisztán lecsúszik.

   b) Feltéve, hogy a henger tisztán gördül, a mozgásegyenletek az alábbiak

   $\[ma=mg\sin{\alpha}-F_s\]$

   és

   $\[\theta\beta=\frac12mR^2\cdot\frac aR=F_sR\]$

   Ezekből

   $\[a=\frac23g\sin{\alpha}\]$

   és

   $\[F_s=\frac{ma}2=\frac13mg\sin{\alpha}\leq\mu mg\cos{\alpha}\]$

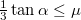   Ez utóbbiból $\setbox0\hbox{$\frac13\tan{\alpha}\leq\mu$}% \message{//depth:\the\dp0//}% \box0%$, tehát a legkisebb szükséges súrlódási együttható a csak a lejtő szögétől függ.

   c) A pillanatnyi forgáspontra felírt tehetetlenségi nyomatékkal a teljes mozgási energiát forgási energiaként írhatjuk fel, ezzel az energiamegmaradás

   $\[mgh=\frac12\left(\frac32mR^2\right)\omega^2,\]$

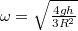   ebből $\setbox0\hbox{$\omega=\sqrt{\frac{4gh}{3R^2}}$}% \message{//depth:\the\dp0//}% \box0%$ Megjegyezzük, hogy tiszta gördülés esetén a tapadási súrlódás nem végez munkát, és nem azonos a gördülési ellenállással.

   d) Ekkor 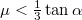$\setbox0\hbox{$\mu<\frac13\tan{\alpha}$}% \message{//depth:\the\dp0//}% \box0%$, és a csúszás miatt a gyorulás és a szöggyorulás (a két ismeretlen változó) független, így a két mozgásegyenlet is(!). A súrlódási erő csúszási, tehát 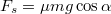$\setbox0\hbox{$F_s=\mu mg\cos{\alpha}$}% \message{//depth:\the\dp0//}% \box0%$ már nem ismeretlen. A gyorsulások

   $\[a=g(\sin{\alpha}-\mu\cos{\alpha})\]$

   és

   $\[\beta=\frac{2\mu g\cos{\alpha}}R\]$

   A súrlódási együttható relációjából belátható továbbá, hogy

   $\[2\mu\cos{\alpha}<\frac23\sin{\alpha}<\sin{\alpha}-\mu\cos{\alpha},\]$

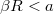   így $\setbox0\hbox{$\beta R<a$}% \message{//depth:\the\dp0//}% \box0%$, a henger csúszva gördül.