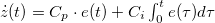Mérőkártya programozás, atomi méretű kontaktusok
A mérés célja atomi méretű kontaktusok vezetési tulajdonságainak vizsgálata a korábban megismert MyDAQ adatgyűjtőkártya segítségével.
Ennek érdekében nanokontaktusok vezetőképesség-görbéit rögzítjük a szétszakadás előtti pillanatokban, mikor csak pár atom köti össze a két oldalt. A számítógéppel beolvasott vezetőképesség görbéket statisztikailag vizsgáljuk vezetőképesség hisztogram segítségével.
Bevezetés: atomi méretű kontaktusok
Napjainkban a fizikai kutatások egyre jelentősebb és rohamosan növekvő területe a különböző nanoszerkezetek vizsgálata, melyek tipikus szélessége pár száz — vagy mint látni fogjuk akár egyetlen — atom. A nanométeres skálájú eszközökben számos meghökkentő kvantumfizikai folyamatot tapasztalunk, hiszen a rendszer mérete összemérhetővé válik az elektronok szabad úthosszával, vagy akár az elektron hullámhosszal is, az egészen kicsi, atomi mérető rendszereknél pedig az anyag atomi kvantáltságát is figyelembe kell venni. A nanoszerkezetek az alapkutatás számára érdekes kvantumfizikai jelenségek vizsgálatán túl az elektronikai eszközök miniatürizálásában és fejlesztésében is rohamosan növekvő szerepet kapnak. A legtöbb nanostruktúra előállítása komoly, elektron-sugár litográfiára épülő technikai hátteret igényel, és számos kvantumfizikai folyamat csak extrém alacsony hőmérsékleteken (4 K-10 mK) tanulmányozható. A mérési gyakorlaton egy olyan nanofizikai jelenséget vizsgálunk, mely szobahőmérsékleten, viszonylag egyszerű mérőrendszerrel is megfigyelhető, bár a vizsgált struktúra talán az egyik legkisebb nanoszerkezet, egy olyan kontaktus, melyben két elektródát egyetlen atom köt össze.
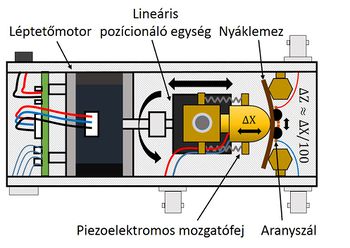
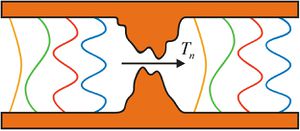
Egy egyatomos kontaktus meglepően egyszerűen létrehozható, hiszen egy fémszál szétszakításának utolsó pillanatában egyetlen atom köti össze a két oldalt. Komoly kihívás viszont a kontaktus stabilizálása, hiszen egy nanokontaktus tanulmányozásának elengedhetetlen feltétele, hogy a mérőberendezés mechanikai stabilitása jelentősen jobb legyen egy tipikus atom-atom távolságnál (~300 pm). Ilyen körülmények elérhetőek egy nagystabilitású alacsony hőmérsékleti alagútmikroszkóppal, de rendelkezésre áll egy másik eszköz is, az ún. MCBJ technika (Mechanically Controllable Break Junction technique). Ennek a módszernek a működését szemlélteti az 1. ábra. A kontaktust egy egyszerű fémszálból hozzuk létre, melyet két ragasztópöttyel egy laprugóra rögzítünk. A laprugó hajlításával a rögzítési pontok távolodnak egymástól, így a fémszál elszakítható. A műszer mechanikai elrendezéséből következik, hogy ha a laprugót középen egy finoman mozgatható tengely segítségével hajlítjuk, az elektródák relatív elmozdulása csak nagyjából 1/100-ad része a tengely elmozdulásának. Ha a méréseket extrém alacsony hőmérsékleten, folyékony hélium környezetben végezzük, és a rugó hajlításához finoman hangolható piezo mozgatót használunk, a pásztázó alagútmikroszkópnál nagyságrendekkel jobb, akár pár pm-es mechanikai stabilitás érhető el.
| 1. ábra. A mérésen használt MCBJ elrendezés vázlata. |
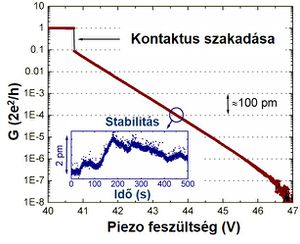
A rendszer stabilitását a kvantummechanikai alagúteffektus segítségével vizsgálhatjuk. Ha a fémszál szétszakítása után az elektródákat finoman közelítjük egymáshoz, a közvetlen kontaktus létrejötte előtt alagútáram folyik a két oldal között, melynek nagysága az elektródák távolságának exponenciális függvénye. Kiszámolható, hogy az alagútáram mintegy tízszeresére növekszik, ha az elektródákat 100 pm-rel közelítjük egymáshoz. Alacsony hőmérsékleti kísérletekben az exponenciális távolságfüggés mintegy hat nagyságrenden keresztül kimutatható (2. ábra), azaz a vezetőképesség mintegy egymilliószorosára nő, miközben az elektródákat csak 600 pm-rel (egy tipikus atom-atom távolság két-háromszorosával) közelítjük egymáshoz. Ez a jelenség az elektródák közötti távolság változásának nagyon érzékeny detektálását teszi lehetővé. A 2. ábra betétje mutatja, hogy rögzített piezo feszültségnél az elektródák távolsága tíz perc alatt csak 2 pm-rel változik, amely mintegy egyszázad része a tipikus atom-atom távolságnak.
| 2. ábra. Alagútáram és stabilitás mérése alacsony hőmérsékleti MCBJ mérőrendszerben. |
Az ábrán látható, hogy az elektródák közelítése közben egy adott ponton egy hirtelen ugrást tapasztalunk, melyet egy vezetőképesség plató követ. Ekkor egy közvetlen, fémes kontaktus jön létre, mely a legtöbb esetben egyetlen atomból áll.
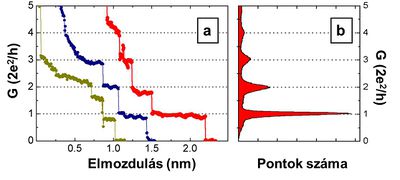
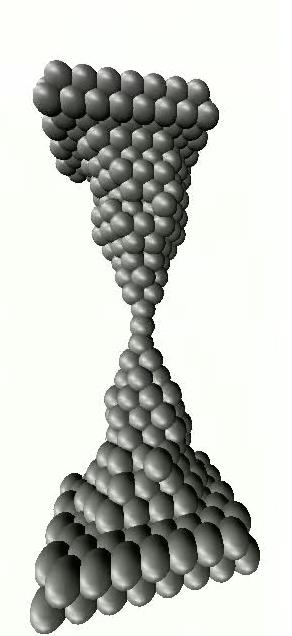
Most közelítsük meg az egyatomos kontaktus kialakulását a másik oldalról, és vizsgáljuk meg a vezetőképesség változását a fémszál szétszakítása közben. Ahogy a szál vékonyodik, először folytonosan csökkenő vezetőképességet tapasztalunk. Ha viszont a kontaktus átmérője már eléri a pár atomot, a vezetőképesség már nem tud folytonosan változni az atomi kvantáltság miatt. A 3/a. ábra bal oldali panelje nanokontaktusok szétszakítása közben felvett vezetőképesség-görbéket mutat. A kontaktus két oldalának széthúzása közben először az atomok csak rugalmasan mozdulnak el egymáshoz képest, miközben a vezetőképesség csak mérsékelten változik (platók). Egy bizonyos feszítés után viszont az atomok ugrásszerűen átrendeződnek, és egy kevesebb atomot tartalmazó, kedvezőbb konfiguráció jön létre. Az atomi átrendeződéseket a vezetőképesség ugrásszerű változása tükrözi. Mikor a teljes szétszakadás előtti utolsó platót látjuk, a két oldalt már csak egyetlen atom köti össze. Ha a szakítás után a két elektródát összenyomjuk, a szakítási felületen az atomok újra összekapcsolódnak, így a nanovezeték szakítását újra és újra megismételhetjük (3/c. ábra). Természetszerűleg, minden egyes nanokontaktus szétszakításakor a vezetőképesség-görbék máshogyan néznek ki, bár jellegre hasonlóak (lásd a 3/a. ábra különböző vezetőképesség-görbéit). Egy adott anyagból készült nanokontaktusok karakterisztikus jellemzőit statisztikai módszerrel térképezhetjük fel. Nagyszámú szétszakítás közben felvett vezetőképesség görbéből felrajzolhatunk egy hisztogramot, mely megmutatja hogy a szétszakítások közben egy adott vezetőképesség-értéket milyen gyakorisággal láthattunk (3/b. ábra). A hisztogramban kirajzolódó csúcsok megmutatják a stabil, nagy gyakorisággal létrejövő atomi konfigurációk vezetőképességét. A hisztogram első csúcsa az egyatomos kontaktus vezetőképességét adja meg. Érdemes megemlíteni, hogy bizonyos anyagokban, pl. aranyban egy egyatomos kontaktus a további széthúzás hatására még nem szakad szét, hanem akár hét atom hosszúságú, egyetlen atom átmérőjű atomlánc is képződhet, ahogy ez a 3/c. ábrán látható szimuláció is szemlélteti.
| 3/a-b. ábra. Atomi méretű arany nanovezetékek szakítás közben felvett vezetőképesség-görbéi (bal oldal). Az egymás utáni szakítások jellegre hasonló, de a részletekben különböző vezetőképsség-görbéket adnak. Sok szakítás vezetőképesség-görbéi alapján felrajzolhatunk egy vezetőképesség-hisztogramot (jobb oldal), melyben a csúcsok a gyakran kialakuló atomi konfigurációk vezetőképességeit adják meg. | 3/c. ábra. Fém nanovezeték ismételt szakítása (számítógépes szimuláció). |
Az egyatomos kontaktus vezetési mechanizmusának megértéséhez kvantummechanikai megközelítésre van szükség, hiszen a kontaktus átmérője azonos méretskálájú az elektronok hullámhosszával. A vezetés kvantált vezetési csatornákon keresztül történik, melyek vezetőképessége nem haladhatja meg a kvantumvezetőképesség-egységet, 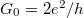 .
.
4. ábra Egy nanokontaktus vezetési tulajdonságait modellezhetjük két ideális (párhuzamos falú) kvantumvezeték közötti szórási tartománnyal, melyen a bal oldali n-edik vezetési csatornából a jobb oldali n-edik vezetési csatornába 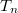 valószínűséggel transzmittálódnak az elektronok. valószínűséggel transzmittálódnak az elektronok.
|
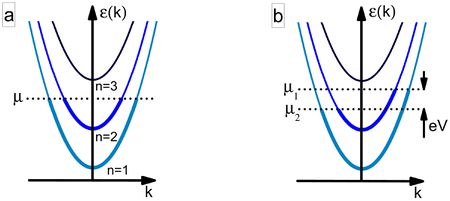
| 5. ábra (a) Diszperzós reláció ideális kvantumvezetékben. (b) Diszperzós reláció a mintára feszültséget kapcsolva. |
A vezetőképesség-kvantum megértéséhez vizsgáljunk meg egy ideális kvantumvezetéket. (Mindezekről részletesebb leírás található a nanofizika tudásbázisban!) Képzeljünk el egy két elektródát összekötő ballisztikus vezetéket, melyben nincsenek szórócentrumok, mint például a 4. ábra bal vagy jobb oldali, párhuzamos falú tartománya. Az elektronok mozgását a vezetékben a Schrödinger-egyenlet írja le, keresztirányban kvantált módusok alakulnak ki, hosszirányban pedig egydimenziós síkhullámként propagálnak az elektronhullámok. A diszperziós reláció 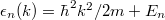 alakú, ahol
alakú, ahol 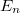 a keresztirányú módus energiája. Az egyes keresztmódusokhoz tartozó diszperziókat vezetési csatornának nevezzük. Nyitott csatornáról beszélünk, ha a diszperziós reláció metszi a kémiai potenciált,
a keresztirányú módus energiája. Az egyes keresztmódusokhoz tartozó diszperziókat vezetési csatornának nevezzük. Nyitott csatornáról beszélünk, ha a diszperziós reláció metszi a kémiai potenciált, 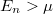 esetén viszont zárt a csatorna, azaz nem propagálnak benne elektronok. Számoljuk ki a kvantumvezeték vezetőképességét egyetlen vezetési csatorna esetén. Az elektródákra feszültséget kapcsolva a kémiai potenciálok eltolódnak
esetén viszont zárt a csatorna, azaz nem propagálnak benne elektronok. Számoljuk ki a kvantumvezeték vezetőképességét egyetlen vezetési csatorna esetén. Az elektródákra feszültséget kapcsolva a kémiai potenciálok eltolódnak 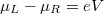 -vel, így a balról jobbra propagáló állapotok
-vel, így a balról jobbra propagáló állapotok 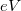 -vel magasabb energiáig vannak betöltve, mint a jobbról balra menő állapotok. A betöltések eltolódása miatt a pozitív és negatív irányú áram nem egyenlő, így a vezetékben
-vel magasabb energiáig vannak betöltve, mint a jobbról balra menő állapotok. A betöltések eltolódása miatt a pozitív és negatív irányú áram nem egyenlő, így a vezetékben 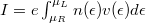 nettó áram folyik, ahol
nettó áram folyik, ahol 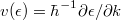 az elektronok sebessége,
az elektronok sebessége, 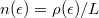 pedig az elektronsűrűség, ahol
pedig az elektronsűrűség, ahol  a vezeték hossza,
a vezeték hossza, 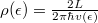 pedig az egydimenziós állapotsűrűség. Behelyettesítés után
pedig az egydimenziós állapotsűrűség. Behelyettesítés után 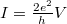 adódik, azaz az egy vezetési csatornának megfelelő vezetőképesség-kvantum
adódik, azaz az egy vezetési csatornának megfelelő vezetőképesség-kvantum 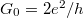 , amely 12906 Ω ellenállásnak felel meg. Az eredményt általánosíthatjuk, ha több vezetési csatornát is figyelembe veszünk, és minden csatornában megengedünk egy véges transzmissziós valószínűséget (4. ábra). A rendszert kezelhetjük egy megfelelő saját bázisban, melyben a bal oldali n-edik vezetési csatornából csak a jobb oldali n-edik vezetési csatornába szóródhatnak elektronok. Ez alapján egy tetszőleges nanokontaktus vezetőképességét az ún. Landauer-formula segítségével adhatjuk meg:
, amely 12906 Ω ellenállásnak felel meg. Az eredményt általánosíthatjuk, ha több vezetési csatornát is figyelembe veszünk, és minden csatornában megengedünk egy véges transzmissziós valószínűséget (4. ábra). A rendszert kezelhetjük egy megfelelő saját bázisban, melyben a bal oldali n-edik vezetési csatornából csak a jobb oldali n-edik vezetési csatornába szóródhatnak elektronok. Ez alapján egy tetszőleges nanokontaktus vezetőképességét az ún. Landauer-formula segítségével adhatjuk meg:
![\[G=\frac{2e^2}{h}\sum\limits_{n}{} T_n,\]](/images/math/d/5/6/d56db0d04c0942a7a2fc310e2d833b09.png)
ahol 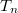 az
az  -edik csatorna transzmissziós valószínűsége. Egy adott nanokontaktus jól jellemezhető a vezetési csatornák számával, és az egyes csatornák transzmissziós valószínűségeivel, így a transzmissziós együtthatók halmazát gyakran a nanokontaktus mezoszkópikus PIN-kódjának hívják.
-edik csatorna transzmissziós valószínűsége. Egy adott nanokontaktus jól jellemezhető a vezetési csatornák számával, és az egyes csatornák transzmissziós valószínűségeivel, így a transzmissziós együtthatók halmazát gyakran a nanokontaktus mezoszkópikus PIN-kódjának hívják.
A 3. ábrán bemutatott vezetőképesség-görbéken ill. hisztogramon látjuk, hogy arany kontaktus szétszakításakor az egyatomos kontaktusnak megfelelő utolsó plató a 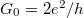 vezetőképesség-kvantumhoz közel helyezkedik el. Ebből szigorúan véve még nem következik, hogy egyetlen, tökéletesen transzmittáló csatorna adja-e a vezetést, hiszen véletlen egybeesésként több részlegesen részlegesen áteresztő vezetési csatorna együttes vezetőképessége is kiadhat
vezetőképesség-kvantumhoz közel helyezkedik el. Ebből szigorúan véve még nem következik, hogy egyetlen, tökéletesen transzmittáló csatorna adja-e a vezetést, hiszen véletlen egybeesésként több részlegesen részlegesen áteresztő vezetési csatorna együttes vezetőképessége is kiadhat 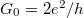 -nak megfelelő vezetőképességet. Ennek megállapításához további mérések szükségesek, melyek nem csak a transzmissziós együtthatók összegét mérik, hanem további információt nyújtanak a transzmissziós együtthatókról. Példaként említhetjük a sörétzaj mérését. Ha a vezetőképesség átlagértéke mellett a vezetőképesség időbeli fluktuációit is mérjük, a
-nak megfelelő vezetőképességet. Ennek megállapításához további mérések szükségesek, melyek nem csak a transzmissziós együtthatók összegét mérik, hanem további információt nyújtanak a transzmissziós együtthatókról. Példaként említhetjük a sörétzaj mérését. Ha a vezetőképesség átlagértéke mellett a vezetőképesség időbeli fluktuációit is mérjük, a 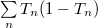 mennyiség is meghatározható. Látszik, hogy egyetlen tökéletesen transzmittáló csatorna esetén a sörétzaj eltűnik, míg több, részlegesen transzmittáló csatorna esetén véges zajt kapunk. Az arany kontaktuson végzett zajmérések egyértelműen megmutatták, hogy az egyatomos arany kontaktus
mennyiség is meghatározható. Látszik, hogy egyetlen tökéletesen transzmittáló csatorna esetén a sörétzaj eltűnik, míg több, részlegesen transzmittáló csatorna esetén véges zajt kapunk. Az arany kontaktuson végzett zajmérések egyértelműen megmutatták, hogy az egyatomos arany kontaktus 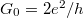 vezetőképességét 1 db tökéletesen áteresztő csatorna adja. Elméleti megfontolások alapján ez azzal hozható összefüggésbe, hogy aranyban csak az s elektronok vesznek részt a vezetésben. Például d-fémekben, ahol az egyatomos kontaktus vezetéséhez a d elektronok is hozzájárulnak akár 5 részleges transzmissziójú nyitott csatornát is megfigyelhetünk. Megjegyezzünk, hogy a jelenség különbözik a két dimenziós heterostruktúrákban megfigyelhető vezetőképesség kvantálástól vagy a kvantum Hall effektustól , ahol csak teljesen nyitott és zárt csatornák vannak jelen.
vezetőképességét 1 db tökéletesen áteresztő csatorna adja. Elméleti megfontolások alapján ez azzal hozható összefüggésbe, hogy aranyban csak az s elektronok vesznek részt a vezetésben. Például d-fémekben, ahol az egyatomos kontaktus vezetéséhez a d elektronok is hozzájárulnak akár 5 részleges transzmissziójú nyitott csatornát is megfigyelhetünk. Megjegyezzünk, hogy a jelenség különbözik a két dimenziós heterostruktúrákban megfigyelhető vezetőképesség kvantálástól vagy a kvantum Hall effektustól , ahol csak teljesen nyitott és zárt csatornák vannak jelen.
Mérési elrendezés
A laboratóriumi gyakorlaton egyatomos kontaktusok vezetését vizsgáljuk egy vékony fémszál ismételt elszakításával és összeérintésével. Mivel az egyatomos arany kontaktusok vezetőképessége közel van a vezetőképesség-kvantumhoz, illetve az összes fém közül az arany oxidálódik a legkevésbé, ezért méréseinket arany mintán végezzük. A kontaktus kontrollált mozgatása érdekében az MCBJ technikát használjuk. A laprugókra 100 μm átmérőjű nagytisztaságú aranyszálat rögzítettünk.
| 6. ábra. Nyáklapból készült rugalmas lapkára forrasztott fémszál |
A laprugó egy léptetőmotorral vezérelt lineáris mozgató, valamint egy piezoelektromos mozgató segítségével hajlítható. A mintára az MyDAQ kártya segítségével 100 mV nagyságrendű feszültséget adunk, a kontaktuson folyó áramot egy 105 erősítésű áramerősítővel mérjük.
Az 1.ábrának megfelelően egy alumínium konzolba rögzítve található a léptetőmotor, a piezomozgató és a rugalmas lapkára rögzített fémszál. A motorhoz egy tápegység tartozik. A motor és a piezomozgató vezérlését, illetve a vezetőképesség mérését teljes egészében egy számítógéphez csatlakoztatott MyDAQ kártyával végezzük. A méréshez szükséges kiegészítő áramkörök egy előre összeállított próbanyákon találhatóak.
A TRINAMIC - PD3-013-42 léptetőmotor az alumínium konzolra rögzített négypólusú mikrofoncsatlakozón keresztül vezérelhető. A négy pólusból háromra digitális jeleket küldünk a mérőkártyáról. Az egyik pólussal a motor ki és bekapcsolható (ENABLED), a másik pólussal a motor forgásiránya állítható (DIRECTION), a harmadik pólusra pedig egy rövid pulzust küldve a motor egy lépést tesz, azaz körülbelül 0.1 fokkal fordul el. A negyedik pólusra a digitális jelek földje (DGND) kerül. Az áramkörhöz csatlakoztatott kábel segítségével kötjük a motort a mérőkártyához. A kábel színkiosztása: ENABLED - Kék, DIRECTION - Zöld, STEP - Narancs, DGND - Barna. Az ENABLED, DIRECTION, STEP, DGND jeleket az összeállított áramkör csatlakozója a kártya DIO0, DIO1, DIO2 és DGND kimeneteivel köti össze.
A finom mozgatáshoz Piezomechanik PSt150/3.5x3.5/20 típusú piezomozgatót használunk, mely -30 - +150 V tartományban működtethető, a teljes feszültségtartomány 28 μm elmozdulásnak felel meg. A piezot nem vezérelhetjük közvetlenül a mérőkártyáról, hiszen az nem tudna elég nagy áramot kiadni, így egy erősítőt kell közbeiktatnunk. Ez az erősítő áramkör szintén az összeállított panelen helyezkedik el. A panel egy szabványos csatlakozóval köthető az adatgyűjtő kártyához.
A méréshez rendelkezésre áll egy mérőprogram, amiben a léptető motor vezérlését implementáltuk. Itt gombnyomássokkal lehet ki vagy befele tekerni a motort, illetve a lépések számát meghatározó pulzusok számát is meg lehet adni.
Mérési feladatok
1. Ismerjük meg és próbáljuk ki a kétpaneles MCBJ mérőprogramot, annak funkcióit, működését!
- A programnak a következőképp kell működni:
- -Timer ciklusonként kiad egy háromszög jelet
- - A mintára kiad egy konstans DC feszültséget. Méri a vezetőképességet a timer ciklusban (minden piezo feszültségnél)
- - Megjeleníti az adatokat, és gombnyomás esetén csak a pár
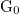 -s tartományt ábrázolja
-s tartományt ábrázolja
- - Megjeleníti az adatokat, és gombnyomás esetén csak a pár
- - Eltárolja az adatokat
- - Kiszámítja a hisztogramot és frissíti ciklusonként
A következő feladatok ezen lépésekben segítenek.
2. A Fizipédián található függvénygenerátor program alapján a MyDAQ ao1 kimenetén adjunk ki egy periódusnyi 10 V amplitúdójú háromszögjelet minden timer eseményben.
3. Szintén a Fizipédián található oszcilloszkóp program alapján írjuk meg az adatok beolvasását a MyDAQ ai0 bemenetén, minden timer eseményben olvassuk be, mentsük ki fájlba az összes adatot, valamint ábrázoljuk őket. A méréshez adjunk a mintára 100 mV DC feszültséget az ao0 csatornán.
4. Írjunk egy szoftveres triggert, majd egy kapcsolóval állíthatóan csak a megadott trigger szint utáni N pontot ábrázoljunk. A mérés közben a trigger szint legyen 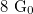 .
.
5. Írjunk egy rutint, mely az egymás után beolvasott görbék alapján hisztogramot készít, azaz kiszámolja a különböző feszültségértékek előfordulási gyakoriságát. Érdemes még a mérés előtt, felkészüléskor átgondolni, hogyan lehet hisztogram-készítő algoritmust megvalósítani. Mentsük ezt a hisztogramot a mérés végén/közben egy külön fájlba/változóba, hogy a jegyzőkönyv írásnál ez az adat rendelkezésre álljon.
6. Ábrázoljuk a paneleken a beolvasott vezetőképességet mellett a kumulált hisztogramot is! A vezetőképességet mindkét panelen 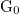 egységeben ábrázoljuk.
egységeben ábrázoljuk.
7. Állítsuk össze a mérési elrendezést atomi méretű kontaktusok vizsgálatához és teszteljük a kapcsolást egy 12900 Ω-os ellenállással! Ezen az ellenálláson teszteljük a hisztogramkészítő rutint. A rutint tesztelhetjük akár a kiadott háromszög jelen is (a hozzátartozó tömbön).
8. A mintaellenállás helyére kössük a laprugóra rögzített aranyszálat! Szakítsuk el a kontaktust a léptetőmotor segítségével, és vegyünk fel egyedi vezetőképesség görbéket! Tároljunk el pár görbét, melyek szépen mutatják a vezetőképesség platókat! A léptetőmotor és a piezoelektromos mozgató együttes vezérlésével a kontaktust újra meg újra elszakítva vegyünk fel legalább 100 görbét, és készítsünk vezetőképesség hisztogramot! Ezeket a görbéket mentsük el, hogy az otthoni adatelemzés lehetséges legyen!
Szorgalmi feladat 1: Vizsgáljuk az elszakított kontaktus összenyomását! Készítsünk olyan mérőfunkciót, amely rögzíti és ábrázolja a kontaktusok között folyó alagútáramot! Ábrázoljuk az alagútáramot logaritmikus skálán és vessük össze az irodalmi adattal!
Szorgalmi feladat 2: Az alagútáramot felhasználva szabályozzuk időben a két elektróda távolságát! Ehhez a közismert PI szabályozástechnikát alkalmazzuk. A finom mozgatást kizárólag a piezó segítségével valósítsuk meg. Teszteljük a stabilitást különböző külső hatásokkal (taps, hőforrás). Segítség:
A jegyzőkönyvbe
- -Absztrakt
- -Elméleti bevezető
- -Ábrázoljunk pár kiválasztott szakítási görbét!
- -A szétválogatott szakítási és összenyomási görbékről készítsünk egy-egy vezetőképesség hisztogram ábrát!
- -A különbségek és hasonlóságok a két hisztogram között.
- -Mi állhat a különbségek hátterében?
- -Vizsgáljuk meg az elektron alagutazási szakaszát egy görbének
- -Találjunk valamit, amit megtudunk határozni ennek segítségével (több jó megoldás is létezik)!
- -Szorgalmi: írjuk le a PI szabályozás lényegét és, hogy hogyan valósítottuk meg.
Segítség
Egy kiindulási program áll rendelkezésre a laborgyakorlathoz itt.
Egyéb
A korábbi mérésleírás itt található pdf formátumban.