„Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás” változatai közötti eltérés
(→Kvantumvezeték ellenállása) |
(→Kvantumvezeték ellenállása) |
||
| 60. sor: | 60. sor: | ||
Egy adott vezetési csatornára az elektronok sebességét, illetve az állapotsűrűséget a következőképpen írhatjuk: | Egy adott vezetési csatornára az elektronok sebességét, illetve az állapotsűrűséget a következőképpen írhatjuk: | ||
| − | $$v_n=\frac{1}{\hbar}\frac{\partial \varepsilon_n(k)}{\partial k},\ \ \ \ g_n=\frac{L}{2\pi}\left(\frac{\partial \varepsilon_n(k)}{\partial k}\right)^{-1}$$ | + | $$v_n=\frac{1}{\hbar}\frac{\partial \varepsilon_n(k)}{\partial k},\ \ \ \ g_n=\frac{L}{2\pi}\left(\frac{\partial \varepsilon_n(k)}{\partial k}\right)^{-1}.$$ |
| − | Az $eV$ energiasávban található elektronok sűrűségét $n_n=eV\cdot g_n/L$ képlettel számolhatjuk. | + | Az $eV$ energiasávban található elektronok sűrűségét $n_n=eV\cdot g_n/L$ képlettel számolhatjuk. A vezetékben folyó áram számolásához az elektrontöltés, a sebesség és az elektronsűrűség szorzatát kell képezni, illetve ezt összegezni a különböző vezetési csatornákra: |
| − | + | ||
| − | A vezetékben folyó áram számolásához az elektrontöltés, a sebesség és az elektronsűrűség szorzatát kell képezni, illetve ezt összegezni a különböző vezetési csatornákra: | + | |
$$I=2\sum_{n=1}^{M}e v_n n_n =\frac{2e^2}{h}MV,$$ | $$I=2\sum_{n=1}^{M}e v_n n_n =\frac{2e^2}{h}MV,$$ | ||
| − | ahol a kettes szorzó a spin szerinti degenerációnak felel meg. Mivel a sebesség és az elektronsűrűség szorzatában az energiadiszperzió deriváltja kiesik, a kvantumvezeték vezetőképessége egyszerűen a vezetőképesség-kvantum egész számú többszörösének adódik. Érdemes megjegyezni, hogy a hosszirányú | + | ahol a kettes szorzó a spin szerinti degenerációnak felel meg. Mivel a sebesség és az elektronsűrűség szorzatában az energiadiszperzió deriváltja kiesik, a kvantumvezeték vezetőképessége egyszerűen a $G_0=2e^2/h$ ''vezetőképesség-kvantum'' egész számú többszörösének adódik. Érdemes megjegyezni, hogy a hosszirányú transzláció-invariancia miatt az $x$ irányú impulzus megmarad, |
így az egyes csatornák között nem történhet átszóródás, mert az a $k$ hullámszám megváltozásával járna, azaz a vezetési csatornák áramjárulékát valóban tekinthetjük egymástól függetlennek. | így az egyes csatornák között nem történhet átszóródás, mert az a $k$ hullámszám megváltozásával járna, azaz a vezetési csatornák áramjárulékát valóban tekinthetjük egymástól függetlennek. | ||
A fenti számolásban abból indultunk ki, hogy csak az elektródák kémiai potenciálja alatt találunk betöltött állapotokat, azaz zérus hőmérsékletet tételezünk fel. Véges hőmérsékleten a kémiai potenciál $kT$ szélességű környezetében egyaránt találhatók betöltött és betöltetlen állapotok, az állapotok betöltöttségének valószínűségét a Fermi-függvény írja le: | A fenti számolásban abból indultunk ki, hogy csak az elektródák kémiai potenciálja alatt találunk betöltött állapotokat, azaz zérus hőmérsékletet tételezünk fel. Véges hőmérsékleten a kémiai potenciál $kT$ szélességű környezetében egyaránt találhatók betöltött és betöltetlen állapotok, az állapotok betöltöttségének valószínűségét a Fermi-függvény írja le: | ||
| − | $$f(\ | + | $$f(\varepsilon)=\frac{1}{e^{\frac{\varepsilon -\mu}{kT}}+1}.$$ |
| − | Az kvantumvezeték belsejében a $k>0$, bal oldali elektródából származó elektronállapotok betöltöttségét az 1-es elektróda $f_l(\ | + | Az kvantumvezeték belsejében a $k>0$, bal oldali elektródából származó elektronállapotok betöltöttségét az 1-es elektróda $f_l(\varepsilon)$ betöltési szám függvénye írja le, míg a $k<0$ állapotok a 2-es elektróda $f_2(\varepsilon)$ betöltési szám függvényével jellemezhetők, ahol $f_1$ és $f_2$ egymáshoz képest $eV$ energiával eltolt Fermi-függvények. Ez a leírás egyben az elektrontartályok tökéletességét is feltételezi, azaz a kvantumvezetékből az egyik elektródába érkező elektronok csak ''termalizálódás'' után szóródhatnak vissza a kvantumvezetékbe, így az elektródát elhagyó elektronok valóban az elektróda Fermi-függvénye szerinti energiaeloszlást követik. |
| − | A fentiek alapján véges hőmérsékleten a vezetékben pozitív illetve negatív irányba folyó áramot | + | A fentiek alapján véges hőmérsékleten a vezetékben pozitív illetve negatív irányba folyó áramot az |
| − | + | $$I^+=\frac{2 e}{L} \sum \limits_{k>0} v_k f_1(\varepsilon_k) = 2e \int \frac{\mathrm{d}k}{2 \pi}\frac{\partial \varepsilon_k}{\hbar \partial k} f_1(\varepsilon_k) = \frac{2 e}{h}\int \mathrm{d} \varepsilon f_1(\varepsilon),$$ | |
| − | $$I^+=\frac{2 e}{L} \sum \limits_{k>0} v_k f_1(\ | + | $$I^-=\frac{2 e}{L} \sum \limits_{k<0} v_k f_2(\varepsilon_k) = \frac{2 e}{h}\int \mathrm{d} \varepsilon f_2(\varepsilon)$$ |
| − | $$I^-=\frac{2 e}{L} \sum \limits_{k<0} v_k f_2(\ | + | |
képletek írják le, azaz az eredő áram: | képletek írják le, azaz az eredő áram: | ||
| − | $$I=I^+-I^-=\frac{2 e}{h} \int \mathrm{d} \ | + | $$I=I^+-I^-=\frac{2 e}{h} \int \mathrm{d} \varepsilon (f_1(\varepsilon)-f_2(\varepsilon))=\frac{2 e}{h}e V.$$ |
| − | Mivel $\int \mathrm{d} \ | + | Mivel $\int \mathrm{d} \varepsilon (f_1(\varepsilon)-f_2(\varepsilon))$ integrál tetszőleges hőmérsékleten $eV$-vel egyenlő, így egy egycsatornás ideális kvantumvezeték ellenállása tetszőleges hőmérsékleten a $G_0=\frac{2 e^2}{h}$ ''vezetőképesség-kvantum''. |
</wlatex> | </wlatex> | ||
A lap 2013. július 5., 14:04-kori változata
Tartalomjegyzék[elrejtés] |
Karakterisztikus méretskálák
Egy nanométeres skálájú objektum vezetési tulajdonságai több szempontból eltérnek a makroszkopikus skálán megszokott jelenségektől.
Makroszkopikus vezetékek ellenállása jól leírható az Ohm-törvénnyel: az áramsűrűség a fajlagos vezetőképesség és az elektromos tér szorzata, a vezetőképesség pedig arányos a vezeték keresztmetszetével és fordítottan arányos a hosszával:
![\[\vec{j}=\sigma \cdot \vec{E}, \ \ \ G=R^{-1}=\frac{A\cdot \sigma}{L}\]](/images/math/7/b/c/7bc09554c31016e9d495c03164518ac1.png)
Az Ohm-törvény egyszerűen magyarázható az elektromos vezetés Drude-modelljével. Az elektronok a kristályrácsban két ütközés közötti
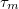 karakterisztikus idő alatt
karakterisztikus idő alatt 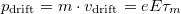 impulzust nyernek, majd a véletlen irányba történő szóródás hatására ezt elveszítik. Ennek megfelelően
impulzust nyernek, majd a véletlen irányba történő szóródás hatására ezt elveszítik. Ennek megfelelően  elektronsűrűség esetén az az áramsűrűség illetve fajlagos vezetőképesség:
elektronsűrűség esetén az az áramsűrűség illetve fajlagos vezetőképesség:
![\[\vec{j}=n\cdot e\cdot v_\mathrm{drift}\ \ \ \rightarrow \ \ \ \sigma=\frac{ne^2\tau_m}{m}.\]](/images/math/f/a/b/fab95ca33435af25c18d27f16f26f4af.png)
Az elektronok két ütközés között eltelt 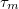 momentumrelaxációs idő alatt
momentumrelaxációs idő alatt 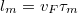 utat tesznek meg, ahol
utat tesznek meg, ahol 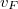 a
Fermi-sebesség. A Drude-modell értelmét veszti ha a vizsgált vezeték karakterisztikus mérete (
a
Fermi-sebesség. A Drude-modell értelmét veszti ha a vizsgált vezeték karakterisztikus mérete ( ) kisebb mint az ütközések skáláját jellemző
) kisebb mint az ütközések skáláját jellemző 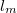 momentumrelaxációs szabadúthossz. Ezen feltétel alapján megkülönböztethetünk diffúzív vezetékeket (
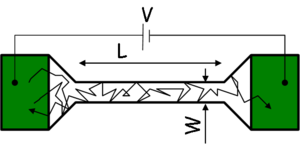
momentumrelaxációs szabadúthossz. Ezen feltétel alapján megkülönböztethetünk diffúzív vezetékeket (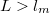 ), melyekben a elektronok sokszor szóródnak mialatt eljutnak az egyik elektródából a másikba (1/a. ábra), illetve ballisztikus nanovezetékeket (
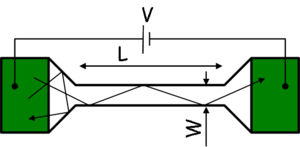
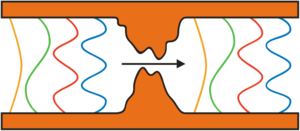
), melyekben a elektronok sokszor szóródnak mialatt eljutnak az egyik elektródából a másikba (1/a. ábra), illetve ballisztikus nanovezetékeket (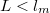 ), melyekben az elektronok csak a vezeték falán szóródnak, de a vezetéken belül nem (1/b. ábra).
), melyekben az elektronok csak a vezeték falán szóródnak, de a vezetéken belül nem (1/b. ábra).
| 1/a. ábra. Diffúzív vezeték | 1/b. ábra. Ballisztikus vezeték |
A két határeset között lényeges különbség jól szemléltethető az ellenállás hosszfüggésével: míg egy diffúzív vezeték ellenállása nő a vezeték hosszának növelésével, addig az 1/b. ábrán szemléltetett ballisztikus vezetékbe bejutó elektronok visszaszórás nélkül átjutnak a túloldalra, azaz az ellenállás nem függ a vezeték hosszától.
Az elektronok hullámtermészetét figyelembe véve azt is érdemes megvizsgálni, hogy a vizsgált rendszer méretének skáláján megőrződik-e az elektronhullámok fázisinformációja. Ha a minta mérete kisebb mint az 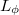 fázisrelaxációs hossz, akkor a vezetési tulajdonságok makroszkopikus skálán nem tapasztalható érdekes interferencia-jelenségeket mutatnak, melyeket az interferencia és dekoherencia nanoszerkezetekben fejezetben szemléltetünk.
fázisrelaxációs hossz, akkor a vezetési tulajdonságok makroszkopikus skálán nem tapasztalható érdekes interferencia-jelenségeket mutatnak, melyeket az interferencia és dekoherencia nanoszerkezetekben fejezetben szemléltetünk.
Szintén érdekes kérdés, hogy a vizsgált nanoszerkezetben megőrződik-e az elektronok spininformációja. Az ún. spindiffúziós hossznál (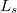 ) kisebb, mágnesesen rendezett tartományokat tartalmazó nanoszerkezetekben érdekes spintronikai jelenségeket tapasztalhatunk.
) kisebb, mágnesesen rendezett tartományokat tartalmazó nanoszerkezetekben érdekes spintronikai jelenségeket tapasztalhatunk.
További érdekes jelenségekkel találkozhatunk, ha a vezeték keresztmetszete a az elektronok Fermi-hullámhosszával összemérhetővé válik, 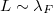 . Ezt a határesetet tárgyaljuk az alábbiakban.
. Ezt a határesetet tárgyaljuk az alábbiakban.
Kvantumvezeték ellenállása
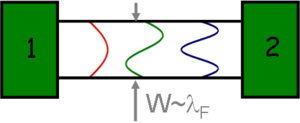
Az elektronok hullámhosszával összemérhető vezetékek tulajdonságait vizsgáljuk meg egy egyszerű modellel: két elektrontartályt kössünk össze egy kétdimenziós, párhuzamos falú ideális kvantumvezetékkel, melyben az elektronok szóródás nélkül haladnak (2. ábra).
| 2. ábra. Ideális kvantumvezeték |
Hard wall határfeltételt alkalmazva (azaz a bezáró potenciál a vezetéken belül ill. kívül zérus ill. végtelen) egyszerűen felírható az elektronok hullámfüggvénye:
![\[\Psi_{n,k}(x,y)=e^{ikx}\cdot \sin\left(\frac{n \pi y}{W} \right),\]](/images/math/c/b/b/cbb631029abef03f779de5d448cf7b17.png)
azaz hosszirányban ( ) síkhullám terjedést, keresztirányban pedig kvantált állóhullámokat kapunk. Ennek megfelelően az elektronok energiája:
) síkhullám terjedést, keresztirányban pedig kvantált állóhullámokat kapunk. Ennek megfelelően az elektronok energiája:
![\[\varepsilon_n(k)=\frac{\hbar^2k^2}{2 m} + \frac{\pi^2 \hbar^2}{2 m W^2}\cdot n^2,\]](/images/math/c/7/7/c772508502b24caf1faa4c68c5109a51.png)
ahol  az
az  -irányú síkhullám terjedéshez tartozó hullámszám,
-irányú síkhullám terjedéshez tartozó hullámszám,  pedig a kvantált keresztmódust (
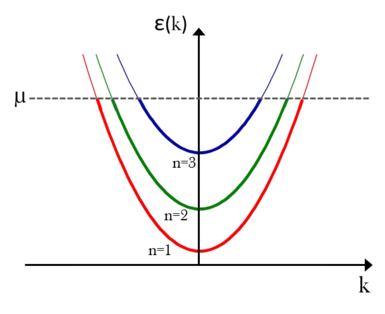
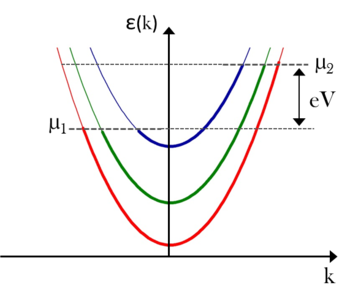
pedig a kvantált keresztmódust ( -irányú állóhullámot) jellemzi. Az energiakifejezés a 3/a. ábrán szemléltetett, egymáshoz képest a keresztirányú energiák szerint eltolt egydimenziós diszperziós relációknak felel meg. Értelemszerűen csak azon módusokon (ún. vezetési csatornákon) keresztül folyhat áram, melyekhez tartozó keresztirányú energia kisebb az elektródák Fermi-energiájánál, azaz a diszperziós reláció metszi a Fermi-szintet. Ezen feltételnek megfelelő módusokat nyitott vezetési csatornának nevezzük, a nyitott csatornák számát
-irányú állóhullámot) jellemzi. Az energiakifejezés a 3/a. ábrán szemléltetett, egymáshoz képest a keresztirányú energiák szerint eltolt egydimenziós diszperziós relációknak felel meg. Értelemszerűen csak azon módusokon (ún. vezetési csatornákon) keresztül folyhat áram, melyekhez tartozó keresztirányú energia kisebb az elektródák Fermi-energiájánál, azaz a diszperziós reláció metszi a Fermi-szintet. Ezen feltételnek megfelelő módusokat nyitott vezetési csatornának nevezzük, a nyitott csatornák számát  -el jelöljük.
-el jelöljük.
| 3/a. ábra. Diszperzós reláció ideális kvantumvezetékben | 3/b. ábra. Diszperzós reláció a mintára feszültséget kapcsolva |
Ha a két elektrontartály közé  feszültséget kapcsolunk akkor a nanovezeték elektronállapotai a 3/b. ábrán szemléltetett módon töltődnek be: a pozitív
feszültséget kapcsolunk akkor a nanovezeték elektronállapotai a 3/b. ábrán szemléltetett módon töltődnek be: a pozitív  -val rendelkező állapotok mind a bal oldali elektródából származnak, így ezek
-val rendelkező állapotok mind a bal oldali elektródából származnak, így ezek 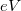 -vel magasabb energiáig vannak betöltve mint a jobb oldali elektródából származó, negatív
-vel magasabb energiáig vannak betöltve mint a jobb oldali elektródából származó, negatív  -val rendelkező állapotok. Áramot csak a
-val rendelkező állapotok. Áramot csak a 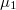 ás
ás 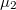 kémiai potenciál közötti tartományban levő pozitív
kémiai potenciál közötti tartományban levő pozitív  -jú állapotok szállítanak, hiszen
-jú állapotok szállítanak, hiszen 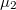 kémiai potenciál alatt a pozitív és negatív irányba haladó állapotok egyaránt betöltöttek, így eredő áramuk zérus lesz.
kémiai potenciál alatt a pozitív és negatív irányba haladó állapotok egyaránt betöltöttek, így eredő áramuk zérus lesz.
Egy adott vezetési csatornára az elektronok sebességét, illetve az állapotsűrűséget a következőképpen írhatjuk:
![\[v_n=\frac{1}{\hbar}\frac{\partial \varepsilon_n(k)}{\partial k},\ \ \ \ g_n=\frac{L}{2\pi}\left(\frac{\partial \varepsilon_n(k)}{\partial k}\right)^{-1}.\]](/images/math/f/4/f/f4f7ceadc88e3403d53b0023da1ad7c4.png)
Az 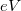 energiasávban található elektronok sűrűségét
energiasávban található elektronok sűrűségét 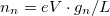 képlettel számolhatjuk. A vezetékben folyó áram számolásához az elektrontöltés, a sebesség és az elektronsűrűség szorzatát kell képezni, illetve ezt összegezni a különböző vezetési csatornákra:
képlettel számolhatjuk. A vezetékben folyó áram számolásához az elektrontöltés, a sebesség és az elektronsűrűség szorzatát kell képezni, illetve ezt összegezni a különböző vezetési csatornákra:
![\[I=2\sum_{n=1}^{M}e v_n n_n =\frac{2e^2}{h}MV,\]](/images/math/6/1/c/61ce1c2052a80ff9f33efa0b2b800ba5.png)
ahol a kettes szorzó a spin szerinti degenerációnak felel meg. Mivel a sebesség és az elektronsűrűség szorzatában az energiadiszperzió deriváltja kiesik, a kvantumvezeték vezetőképessége egyszerűen a 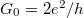 vezetőképesség-kvantum egész számú többszörösének adódik. Érdemes megjegyezni, hogy a hosszirányú transzláció-invariancia miatt az
vezetőképesség-kvantum egész számú többszörösének adódik. Érdemes megjegyezni, hogy a hosszirányú transzláció-invariancia miatt az  irányú impulzus megmarad,
így az egyes csatornák között nem történhet átszóródás, mert az a
irányú impulzus megmarad,
így az egyes csatornák között nem történhet átszóródás, mert az a  hullámszám megváltozásával járna, azaz a vezetési csatornák áramjárulékát valóban tekinthetjük egymástól függetlennek.
hullámszám megváltozásával járna, azaz a vezetési csatornák áramjárulékát valóban tekinthetjük egymástól függetlennek.
A fenti számolásban abból indultunk ki, hogy csak az elektródák kémiai potenciálja alatt találunk betöltött állapotokat, azaz zérus hőmérsékletet tételezünk fel. Véges hőmérsékleten a kémiai potenciál 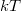 szélességű környezetében egyaránt találhatók betöltött és betöltetlen állapotok, az állapotok betöltöttségének valószínűségét a Fermi-függvény írja le:
szélességű környezetében egyaránt találhatók betöltött és betöltetlen állapotok, az állapotok betöltöttségének valószínűségét a Fermi-függvény írja le:
![\[f(\varepsilon)=\frac{1}{e^{\frac{\varepsilon -\mu}{kT}}+1}.\]](/images/math/5/a/a/5aae133ab52ed8c35f1826a9457cb79c.png)
Az kvantumvezeték belsejében a 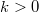 , bal oldali elektródából származó elektronállapotok betöltöttségét az 1-es elektróda
, bal oldali elektródából származó elektronállapotok betöltöttségét az 1-es elektróda 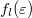 betöltési szám függvénye írja le, míg a
betöltési szám függvénye írja le, míg a 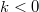 állapotok a 2-es elektróda
állapotok a 2-es elektróda 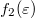 betöltési szám függvényével jellemezhetők, ahol
betöltési szám függvényével jellemezhetők, ahol 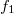 és
és 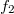 egymáshoz képest
egymáshoz képest 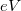 energiával eltolt Fermi-függvények. Ez a leírás egyben az elektrontartályok tökéletességét is feltételezi, azaz a kvantumvezetékből az egyik elektródába érkező elektronok csak termalizálódás után szóródhatnak vissza a kvantumvezetékbe, így az elektródát elhagyó elektronok valóban az elektróda Fermi-függvénye szerinti energiaeloszlást követik.
A fentiek alapján véges hőmérsékleten a vezetékben pozitív illetve negatív irányba folyó áramot az
energiával eltolt Fermi-függvények. Ez a leírás egyben az elektrontartályok tökéletességét is feltételezi, azaz a kvantumvezetékből az egyik elektródába érkező elektronok csak termalizálódás után szóródhatnak vissza a kvantumvezetékbe, így az elektródát elhagyó elektronok valóban az elektróda Fermi-függvénye szerinti energiaeloszlást követik.
A fentiek alapján véges hőmérsékleten a vezetékben pozitív illetve negatív irányba folyó áramot az
![\[I^+=\frac{2 e}{L} \sum \limits_{k>0} v_k f_1(\varepsilon_k) = 2e \int \frac{\mathrm{d}k}{2 \pi}\frac{\partial \varepsilon_k}{\hbar \partial k} f_1(\varepsilon_k) = \frac{2 e}{h}\int \mathrm{d} \varepsilon f_1(\varepsilon),\]](/images/math/3/1/c/31c4678e29410e7fa637f9687cb858a1.png)
![\[I^-=\frac{2 e}{L} \sum \limits_{k<0} v_k f_2(\varepsilon_k) = \frac{2 e}{h}\int \mathrm{d} \varepsilon f_2(\varepsilon)\]](/images/math/b/6/2/b62e9effa804bd451c8f5b37e453b7a3.png)
képletek írják le, azaz az eredő áram:
![\[I=I^+-I^-=\frac{2 e}{h} \int \mathrm{d} \varepsilon (f_1(\varepsilon)-f_2(\varepsilon))=\frac{2 e}{h}e V.\]](/images/math/e/8/0/e80de55ed30db22f813dd9ffdbc36397.png)
Mivel 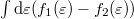 integrál tetszőleges hőmérsékleten
integrál tetszőleges hőmérsékleten 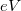 -vel egyenlő, így egy egycsatornás ideális kvantumvezeték ellenállása tetszőleges hőmérsékleten a
-vel egyenlő, így egy egycsatornás ideális kvantumvezeték ellenállása tetszőleges hőmérsékleten a 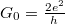 vezetőképesség-kvantum.
vezetőképesség-kvantum.
Landauer formula
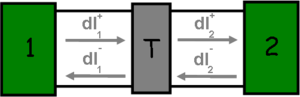
Most tekintsük azt az egyszerű modellt, amikor egy egycsatornás, ideális kvantumvezeték közepén egy szórócentrum található, melyen  valószínűséggel jutnak át az elektronok. Ebben az esetben az elektródák felől a szórócentrum felé haladó állapotok továbbra is a megfelelő elektródából származnak, és ennek az eloszlásfüggvényét követik (lásd a ?? ábrán a
valószínűséggel jutnak át az elektronok. Ebben az esetben az elektródák felől a szórócentrum felé haladó állapotok továbbra is a megfelelő elektródából származnak, és ennek az eloszlásfüggvényét követik (lásd a ?? ábrán a 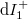 és
és 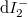 áramkomponenseket). A szórócentrumtól az elektródák felé haladó állapotok viszont kevertek, pl. a
áramkomponenseket). A szórócentrumtól az elektródák felé haladó állapotok viszont kevertek, pl. a 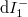 áramjáruléknál egyaránt figyelembe kell venni az 1-es elektródából induló és a szórócentrumon reflektálódó, illetve a 2-es elektródából induló és a szórócentrumon transzmittálódó elektronokat.
áramjáruléknál egyaránt figyelembe kell venni az 1-es elektródából induló és a szórócentrumon reflektálódó, illetve a 2-es elektródából induló és a szórócentrumon transzmittálódó elektronokat.
Zérus hőmérsékleten csak a 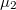 kémiai potenciál alatti állapotok származhatnak mindkét elektródából, azonban az
kémiai potenciál alatti állapotok származhatnak mindkét elektródából, azonban az 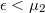 állapotok teljes árama értelemszerűen zérust ad, hiszen ez annak felel meg, mintha zérus feszültséget kapcsoltunk volna a rendszerre. Így a véges áramért továbbra is
állapotok teljes árama értelemszerűen zérust ad, hiszen ez annak felel meg, mintha zérus feszültséget kapcsoltunk volna a rendszerre. Így a véges áramért továbbra is 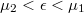 állapotok felelnek, melyek csak az 1-es elektródából származhatnak. Így a teljes áram könnyen számolható például a szórócentrum és a 2-es elektróda közötti vezetékdarabban. Itt a
állapotok felelnek, melyek csak az 1-es elektródából származhatnak. Így a teljes áram könnyen számolható például a szórócentrum és a 2-es elektróda közötti vezetékdarabban. Itt a 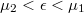 energiasávban levő elektronok
energiasávban levő elektronok 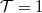 esetén a korábbiak alapján
esetén a korábbiak alapján 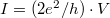 áramot adnának, ami
áramot adnának, ami 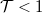 esetén értelemszerűen a transzmittálódó elektronok hányadával skálázódik, azaz
esetén értelemszerűen a transzmittálódó elektronok hányadával skálázódik, azaz 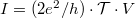 . Így egy egycsatornás,
. Így egy egycsatornás,  transzmisszós valószínűségű szórócentrumot tartalmazó nanovezeték vezetőképessége:
transzmisszós valószínűségű szórócentrumot tartalmazó nanovezeték vezetőképessége:
![\[G=\frac{2e^2}{h}\mathcal{T} .\]](/images/math/3/c/3/3c33c14c13478a7d5031d6b5b51ced23.png)
Vizsgáljuk meg, hogy ez az eredmény érvényes-e véges hőmérsékleten is. A 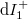 és
és 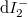 áramkomponensek kizárólag az 1-es illetve a 2-es elektródából származnak, így a korábbiak alapján egy
áramkomponensek kizárólag az 1-es illetve a 2-es elektródából származnak, így a korábbiak alapján egy 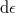 energiatartományban az áramjárulékuk:
energiatartományban az áramjárulékuk:
![\[\mathrm{d}I_1^+(\epsilon)=\frac{2 e}{h}\cdot f_1(\epsilon)\mathrm{d}\epsilon,\;\; \mathrm{d}I_2^-(\epsilon)=\frac{2 e}{h}\cdot f_2(\epsilon)\mathrm{d}\epsilon.\]](/images/math/2/f/6/2f6fb00ef30f83e32c2237831d31b794.png)
Ha az áramot a szórócentrum és az 1-es elektróda közötti vezetékdarabon akarjuk kiértékelni, akkor szükségünk van a 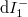 áramjárulékra is, mely
áramjárulékra is, mely  valószínűséggel a 2-es elektródából bejövő módus transzmissziójából,
valószínűséggel a 2-es elektródából bejövő módus transzmissziójából, 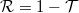 valószínűséggel pedig pedig a az 1-es elektródából bejövő módus reflexiójából származik:
valószínűséggel pedig pedig a az 1-es elektródából bejövő módus reflexiójából származik:
![\[\mathrm{d}I_1^-(\epsilon)=\mathrm{d}I_1^+(\epsilon)\cdot (1-\mathcal{T}) + \mathrm{d}I_2^-(\epsilon)\cdot \mathcal{T},\]](/images/math/6/9/c/69c605f538bd74a1115063a19928811a.png)
így a negatív és pozitív irányba haladó áramkomponensek együttes járuléka:
![\[\mathrm{d}I_1=\mathrm{d}I_1^+ - \mathrm{d}I_1^- = \frac{2 e}{h} \cdot \mathcal{T} \cdot [f_1(\epsilon)-f_2(\epsilon)]\mathrm{d}\epsilon.\]](/images/math/2/0/1/2012176fd0f3eee14c317be6d6b4a0c3.png)
A teljes áramot integrálással kapjuk meg:
![\[I=\frac{2 e}{h} \cdot \int \mathcal{T}\cdot [f_1(\epsilon)-f_2(\epsilon)]\mathrm{d}\epsilon.\]](/images/math/4/e/f/4efa33ab7245a0d1acbaa4f417e0ce90.png)
A két Fermi-függvény különbsége a 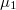 és
és 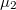 kémiai potenciálok közötti energiatartományban, illetve a két kémiai potenciál körüli
kémiai potenciálok közötti energiatartományban, illetve a két kémiai potenciál körüli 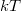 energiatartományban különbözik zérustól. Feltételezve hogy ebben a tartományban a
energiatartományban különbözik zérustól. Feltételezve hogy ebben a tartományban a  transzmisszós valószínűség energiafüggetlen, és kihasználva a
transzmisszós valószínűség energiafüggetlen, és kihasználva a 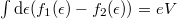 azonosságot a vezetőképességre véges hőmérsékleten is a
azonosságot a vezetőképességre véges hőmérsékleten is a
![\[G=\frac{2 e^2}{h}\cdot \mathcal{T}\]](/images/math/3/9/c/39c19c41cf54b36e17aafebf82ee4a19.png)
eredményt kapjuk. Ha a transzmissziós valószínűség nem tekinthető energiafüggetlennek, akkor  -t a releváns energiatartományra vett átlagos transzmissziós valószínűségnek kell tekinteni.
-t a releváns energiatartományra vett átlagos transzmissziós valószínűségnek kell tekinteni.
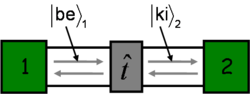
Több vezetési csatorna esetén a szórócentrum hatását egy komplex transzmissziós mátrixszal ( ) írhatjuk le, mely a bal oldalon az egyes csatornákban bejövő, azaz az elektródától a szórócentrum felé haladó illetve a jobb oldalon kimenő, azaz a szórócentrumtól az elektróda felé haladó módusok között teremt kapcsolatot
) írhatjuk le, mely a bal oldalon az egyes csatornákban bejövő, azaz az elektródától a szórócentrum felé haladó illetve a jobb oldalon kimenő, azaz a szórócentrumtól az elektróda felé haladó módusok között teremt kapcsolatot
![\[\left| \mathrm{ki} \right>_2=\hat{t} \left| \mathrm{be} \right>_1\]](/images/math/f/1/d/f1d28141f42e56c0e95f8262b76ba5e1.png)
Megmutatható, hogy a vezetőképesség ebben az esetben
![\[G = \frac{2 e^2}{h} \mathrm{Tr}(\hat{t}^\dagger \hat{t})\]](/images/math/7/3/1/731d25473a2b91fd02df762b3eef3887.png)
formában írható. A 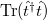 kifejezést átírhatjuk
kifejezést átírhatjuk 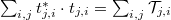 formában, ahol
formában, ahol 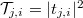 a bal oldali i-edik csatornából a jobb oldali j-edik vezetési csatornába történő átszórás valószínűségét adja meg. Ennek megfelelően a vezetőképesség
a bal oldali i-edik csatornából a jobb oldali j-edik vezetési csatornába történő átszórás valószínűségét adja meg. Ennek megfelelően a vezetőképesség
![\[G = \frac{2 e^2}{h} \sum \limits_{i,j} \mathcal{T}_{j,i}\]](/images/math/d/d/6/dd6a269bd64cb9e81b26fe13d09f4ea4.png)
formában írható. Megfelelő bázisban a probléma diagonalizálható, azaz elérhető hogy a jobb oldali i-edik csatornából csak a bal oldali i-edik csatornába tudjanak szóródni elektronok. Ekkor a rendszer a nyitott vezetési csatornák számának megfelelő  db. egymástól független egydimenziós vezetéknek tekinthető, melyek vezetőképesség-járulékát egyszerűen összegezhetjük:
db. egymástól független egydimenziós vezetéknek tekinthető, melyek vezetőképesség-járulékát egyszerűen összegezhetjük:
![\[G = \frac{2 e^2}{h} \sum \limits_{i=1..N} \mathcal{T}_i.\]](/images/math/b/5/d/b5ddacc209168c8bfd3c40d09bd11038.png)
A 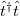 operátor sajátértékeinek megfelelő
operátor sajátértékeinek megfelelő 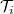 transzmissziós együtthatók az i-edik sajátcsatorna transzmissziós valószínűségét adják meg.
transzmissziós együtthatók az i-edik sajátcsatorna transzmissziós valószínűségét adják meg.
Vezetőképesség kvantálás kvantum pont-kontaktusban
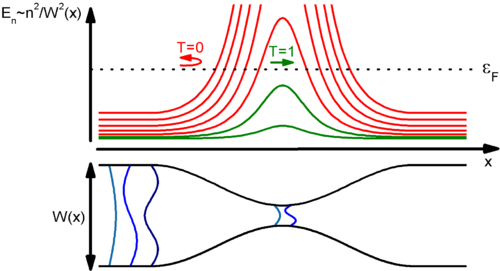
Vegyünk egy olyan kétdimenziós kvantumvezetéket, melyben nincsenek szórócentrumok, a vezeték 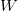 szélessége pedig lassan (adiabatikusan) változik a hossztengely mentén (?? ábra alsó panel). A lassan változó szélességnek köszönhetően a vezeték lokálisan mindenütt jól közelíthető egy párhuzamos falú vezetékdarabbal, és a hullámfüggvények leírhatók az adott szélességhez tartozó keresztirányú állóhullámokkal, illetve hosszirányú síkhullám terjedéssel. A ?? ábra felső panele a keresztirányú állóhullámokhoz tartozó energiát ábrázolja a vezeték mentén különböző vezetési csatornákra. Az egyértelmű, hogy azon vezetési csatornák tudnak csak átjutni a vezetéken (ú.n. kvantum-pontkontaktuson), melyek keresztirányú energiája a vezeték legkisebb keresztmetszeténél is a Fermi-energia alatt van.
szélessége pedig lassan (adiabatikusan) változik a hossztengely mentén (?? ábra alsó panel). A lassan változó szélességnek köszönhetően a vezeték lokálisan mindenütt jól közelíthető egy párhuzamos falú vezetékdarabbal, és a hullámfüggvények leírhatók az adott szélességhez tartozó keresztirányú állóhullámokkal, illetve hosszirányú síkhullám terjedéssel. A ?? ábra felső panele a keresztirányú állóhullámokhoz tartozó energiát ábrázolja a vezeték mentén különböző vezetési csatornákra. Az egyértelmű, hogy azon vezetési csatornák tudnak csak átjutni a vezetéken (ú.n. kvantum-pontkontaktuson), melyek keresztirányú energiája a vezeték legkisebb keresztmetszeténél is a Fermi-energia alatt van.
A ?? ábra a vezetékben kialakuló diszperziós relációkat mutatja a vezeték két közeli tartományában. A jobb oldali panel egy kicsit keskenyebb vezetékszakaszhoz tartozik mint a bal oldali, így a nagyobb keresztirányú energia miatt a parabolikus diszperziók felfele tolódnak. Mivel a vezeték lokálisan közel transzlációinvariáns, így a hosszirányú impulzus és a  hullámszám csak keveset változhat miközben az elektron egy adott tartományból eljut egy másik, közeli tartományba. Egy adot vezetési csatornán
hullámszám csak keveset változhat miközben az elektron egy adott tartományból eljut egy másik, közeli tartományba. Egy adot vezetési csatornán  hullámszámmal rendelkező állapot a vezeték keskenyedése során csak úgy tud mindig kis impulzusváltozással előre haladni, ha mindig ugyan abban a vezetési csatornában marad (lásd zöld nyíl). Más csatornába történő átszóródás, illetve visszaszóródás esetén
hullámszámmal rendelkező állapot a vezeték keskenyedése során csak úgy tud mindig kis impulzusváltozással előre haladni, ha mindig ugyan abban a vezetési csatornában marad (lásd zöld nyíl). Más csatornába történő átszóródás, illetve visszaszóródás esetén  jelentősen változna. Kicsit más a helyzet, ha az előrehaladás után az adott csatorna diszperziós relációjának alja a Fermi-energia fölé kerül, azaz az elektron nem tud továbbhaladni. Ebben az esetben az a legkisebb impolzusváltozással járó folyamat, ha nullához közeli de pozitív bejövő
jelentősen változna. Kicsit más a helyzet, ha az előrehaladás után az adott csatorna diszperziós relációjának alja a Fermi-energia fölé kerül, azaz az elektron nem tud továbbhaladni. Ebben az esetben az a legkisebb impolzusváltozással járó folyamat, ha nullához közeli de pozitív bejövő  -val rendelkező elektron ugyan azon csatorna
-val rendelkező elektron ugyan azon csatorna 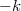 állapotába szóródik vissza.
állapotába szóródik vissza.
A fenti érvek alapján elmondható, hogy egy lassan változó szélességű kvantum-pontkontaktusban az összes olyan csatorna melyhez tartozó keresztirányú energia a legkisebb keresztmetszetben is a Fermi-energia alatt van 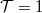 valószínűséggel transzmittálódik (lásd zöld görbék a ?? ábrán), az összes többi csatorna pedig
valószínűséggel transzmittálódik (lásd zöld görbék a ?? ábrán), az összes többi csatorna pedig 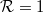 valószínűséggel reflektálódik, azaz a vezetőképesség a vezetőképesség-kvantum egész számú többszöröse:
valószínűséggel reflektálódik, azaz a vezetőképesség a vezetőképesség-kvantum egész számú többszöröse:
![\[G=\frac{2e^2}{h}M,\]](/images/math/a/5/a/a5af2626ce765f8c594e3b30ae49e615.png)
ahol  a legkisebb keresztmetszetben elférő keresztirányú módusok száma.
a legkisebb keresztmetszetben elférő keresztirányú módusok száma.
Ez a jelenség kísérletekben is megfigyelhető ha egy kétdimenziós elektrongázban két felső kapuelektróda segítségével egy keskeny csatornát alakítunk ki. Az elrendezést a ?? ábra bal oldali panele szemlélteti:
2DEG:
| 2. ábra - 2DEG pontkontaktus. |