„Alfa spektroszkópia” változatai közötti eltérés
| (egy szerkesztő 27 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | |||
| − | |||
| − | |||
| − | |||
<wlatex> | <wlatex> | ||
| 12. sor: | 8. sor: | ||
A hallgató az alábbi ismereteket sajátítja el a gyakorlat során: | A hallgató az alábbi ismereteket sajátítja el a gyakorlat során: | ||
| − | * alfa-spektrometriás módszer gyakorlati alkalmazása | + | * alfa-spektrometriás módszer megismerése és gyakorlati alkalmazása, továbbá ezen belül |
| − | * alfa-spektrométer felépítése, az egyes részegységek feladata, jellemzői | + | ** alfa-spektrométer felépítése, az egyes részegységek feladata, jellemzői |
| − | * felületi záróréteges Si detektorok fajtái, jellemzői | + | ** felületi záróréteges Si detektorok fajtái, jellemzői |
| − | * alfa-forrás formájának jelentősége | + | ** alfa-forrás formájának jelentősége |
| − | * alfa-spektrumok kiértékelése | + | ** alfa-spektrumok kiértékelése |
| − | * | + | ** a mérési módszer összehasonlítása más (pl. gamma-spektrometriás) módszerekkel |
| − | * a mérési módszer összehasonlítása más (pl. gamma-spektrometriás) módszerekkel | + | |
===A laboratóriumi gyakorlat célja=== | ===A laboratóriumi gyakorlat célja=== | ||
| 33. sor: | 28. sor: | ||
===Felületi záróréteges detektorok=== | ===Felületi záróréteges detektorok=== | ||
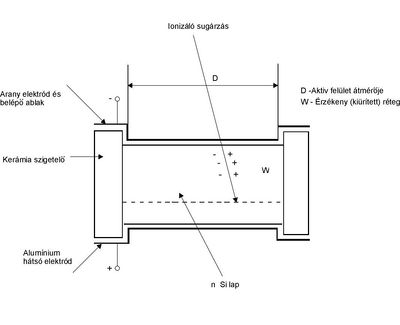
| − | Alfa-spektrometriai célokra leggyakrabban az ún. ''felületi záróréteges detektorokat'' alkalmazzák (1.ábra). Ezek alapanyaga nagy tisztaságú, ${n}$ típusú Si egykristályból készült lap. Ezt savas maratás után oxidációnak vetik alá. A felületen kialakuló nagyon vékony oxid réteg ${p}$ típusként szerepel. Így jön létre a ${p - n}$ ''átmenet''. Ezt követően a kristály egyik oldali sík felületére nagyon vékony arany réteget (kb. 50 | + | Alfa-spektrometriai célokra leggyakrabban az ún. ''felületi záróréteges detektorokat'' alkalmazzák (1.ábra). Ezek alapanyaga nagy tisztaságú, ${n}$ típusú Si egykristályból készült lap. Ezt savas maratás után oxidációnak vetik alá. A felületen kialakuló nagyon vékony oxid réteg ${p}$ típusként szerepel. Így jön létre a ${p - n}$ ''átmenet''. Ezt követően a kristály egyik oldali sík felületére nagyon vékony arany réteget (kb. 50 μg/cm<sup>2</sup>) visznek fel vákuumpárologtatással. Az arany réteg egyrészt elektromos kontaktusul szolgál, másrészt fényzáróként szerepel. Ez a detektor belépő ablaka. Az arany rétegnek azért kell minél vékonyabbnak lenni, hogy a kis hatótávolságú (nagy fajlagos ionizációval rendelkező) alfa-részecskék minél kisebb energiaveszteséggel léphessenek be a detektorba. A Si lap másik síkoldalára - rendszerint Al-ból készült elektród kerül. Az arany és alumínium elektródák közé ''záróirányú feszültséget'' kapcsolnak, mely tovább szélesíti a ${p - n}$ átmenetnél kialakult kiürített réteget. Ez a detektor ''érzékeny térfogata''. Ennek olyan vastagságúnak kell lenni, hogy a mérendő alfa-részecskék teljes energiájukat leadják azaz elnyelődjenek benne, (mivel az egyik feladat energiájuk meghatározása) létrehozva elektron – pozitív-lyuk töltéshordozó párokat. Az így keletkezett töltéshordozókat a detektorra kapcsolt feszültség összegyűjti és a kimeneten elektromos impulzusok jelennek meg. Az impulzus amplitúdója arányos az abszorbeált alfa részecske energiájával (energiamérés). |
Az újabb technológiával készült detektorokat PIPS ('''P'''assivated '''I'''mplanted '''P'''lanar '''S'''ilicon) típusúaknak nevezik. Az ilyen detektor belépő ablaka implantált réteggel van ellátva és ezért sokkal ellenállóbb mechanikus behatásokkal (pl. dekontaminálás) szemben, mint az előző típus. | Az újabb technológiával készült detektorokat PIPS ('''P'''assivated '''I'''mplanted '''P'''lanar '''S'''ilicon) típusúaknak nevezik. Az ilyen detektor belépő ablaka implantált réteggel van ellátva és ezért sokkal ellenállóbb mechanikus behatásokkal (pl. dekontaminálás) szemben, mint az előző típus. | ||
| − | [[Fájl: | + | {| |
| + | | <span id="fig:1">[[Fájl:FizLab4_ALFA_01.jpg|közép|bélyegkép|400px|1.ábra: Felületi záróréteges detektor szerkezete.]]</span> | ||
| + | |} | ||
A felületi záróréteges detektorokat három - a méréstechnika szempontjából fontos - paraméterrel szokás jellemezni: | A felületi záróréteges detektorokat három - a méréstechnika szempontjából fontos - paraméterrel szokás jellemezni: | ||
| 45. sor: | 42. sor: | ||
* kiürített réteg vastagság, | * kiürített réteg vastagság, | ||
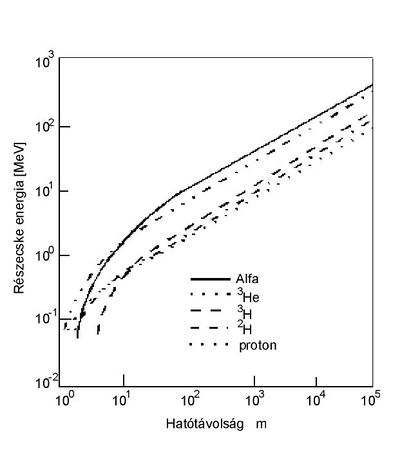
| − | Általában az ''energiafelbontás'' 20 keV körüli érték (5,5 MeV-es alfa-részecskékre). Adott detektor esetén elsősorban a sugárforrás vastagságától, valamint a detektor és sugárforrás közötti távolságtól függ. A ''belépő ablak felület'' általában 100 - 1000 mm<sup>2</sup> közötti. Ennek nagysága egyrészt a detektor hatásfokát szabja meg, de kihatással van az energia felbontásra is (elektronikus okokból: nagyobb térfogatból a kigyűjtött töltések mennyiségének statisztikus ingadozása nagyobb, mint kisebb térfogat esetén). A ''kiürített réteg vastagsága'' 100 - 5000 | + | Általában az ''energiafelbontás'' 20 keV körüli érték (5,5 MeV-es alfa-részecskékre). Adott detektor esetén elsősorban a sugárforrás vastagságától, valamint a detektor és sugárforrás közötti távolságtól függ. A ''belépő ablak felület'' általában 100 - 1000 mm<sup>2</sup> közötti. Ennek nagysága egyrészt a detektor hatásfokát szabja meg, de kihatással van az energia felbontásra is (elektronikus okokból: nagyobb térfogatból a kigyűjtött töltések mennyiségének statisztikus ingadozása nagyobb, mint kisebb térfogat esetén). A ''kiürített réteg vastagsága'' 100 - 5000 μm szokott lenni. Mint fentebb említettük, ez utóbbinak elégnek kell lenni a detektálni kívánt töltött részecskék teljes lefékezéséhez, ami nyilván részecskefajta és energiafüggő. Erről ad tájékoztatást a 2. ábra. |
| − | |||
| + | Az 1. táblázat néhány "közismert" alfa-sugárzó izotóp nukleáris adatait tartalmazza. | ||
| + | |||
| + | |||
| + | <div class="center" style="width:auto; margin-left:auto; margin-right:auto;">1. táblázat | ||
| + | </div> | ||
| + | |||
| + | {| border="1" cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: center; height: 50px" cellspacing="0" width="500" | ||
| + | |- | ||
| + | ! ${Z}$ || izotóp || ${t_{1/2}}$ || ${E_{\alpha}} \textrm{(MeV)}$ || ${k_{\alpha}}$ (%) | ||
| + | |- | ||
| + | | 86 || <sup>222</sup>Rn || 3,82d || 5,49 || 100 | ||
| + | |- | ||
| + | | 88 || <sup>226</sup>Ra || 1600y || 4,79; 4,6 || 94,5; 5,6 | ||
| + | |- | ||
| + | | 90 || <sup>232</sup>Th || 1,41${\times}$10<sup>10</sup>y || 4,01; 3,96 || 77; 23 | ||
| + | |- | ||
| + | | 92 || <sup>235</sup>U || 7,04${\times}$10<sup>8</sup>y || 4,6; 4,56; 4,39; 4,37; 4,22 || 4,6; 3,7; 57;74; 5,7 | ||
| + | |- | ||
| + | | 92 || <sup>238</sup>U || 4,47${\times}$10<sup>9</sup>y || 4,2; 4,15 || 77; 23 | ||
| + | |- | ||
| + | | 94 || <sup>239</sup>Pu || 2,41${\times}$10<sup>4</sup>y || 5,126; 5,14; 5,1 || 73,3; 15,1; 11,5 | ||
| + | |- | ||
| + | | 95 || <sup>241</sup>Am || 432y || 5,49; 5,44; 5,39 || 86; 12,7; 1,3 | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| | ||
| + | | <span id="fig:2">[[Fájl:FizLab4_ALFA_02.jpg|közép|bélyegkép|400px|2.ábra: Energia - hatótávolság görbék különböző töltött részecskékre Si-ban.]]</span> | ||
| + | |} | ||
===Mérőberendezés (alfa-spektrométer) blokkvázlata=== | ===Mérőberendezés (alfa-spektrométer) blokkvázlata=== | ||
| 54. sor: | 79. sor: | ||
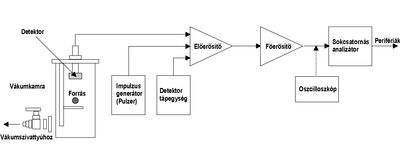
Egy alfa-spektrométer blokkvázlatát szemlélteti a 3. ábra. | Egy alfa-spektrométer blokkvázlatát szemlélteti a 3. ábra. | ||
| − | [[Fájl: | + | {| |
| + | | <span id="fig:3">[[Fájl:FizLab4_ALFA_03.jpg|közép|bélyegkép|400px|3.ábra: Alfa-spektrométer blokkvázlata.]]</span> | ||
| + | |} | ||
Tekintettel az alfa-részecskék nagy fajlagos ionizáló képességére (kis hatótávolságára), a detektort és a sugárforrást közös vákuum térbe kell helyezni, továbbá a sugárforrásnak minél vékonyabbnak kell lenni, hogy benne az alfa-részecskék abszorbciója - így energia szórásuk - minél kisebb legyen. | Tekintettel az alfa-részecskék nagy fajlagos ionizáló képességére (kis hatótávolságára), a detektort és a sugárforrást közös vákuum térbe kell helyezni, továbbá a sugárforrásnak minél vékonyabbnak kell lenni, hogy benne az alfa-részecskék abszorbciója - így energia szórásuk - minél kisebb legyen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
A detektor által szolgáltatott elektromos impulzusok jelformálás és erősítés céljából ''erősítő'' rendszerre kerülnek. Az erősítőkkel kapcsolatos szigorú kívánalom az igen jó ''jel/zaj'' viszony és a nagyfokú ''linearitás''. Az erősítőkből kilépő elektromos jelsorozatot sokcsatornás analizátor (MCA: MultiChannel Analyzer) dolgozza fel. A félvezető-detektoros alfa-spektrométerek MCA-ja - a detektor jó energia felbontása miatt - 1-2 ezer csatornás. | A detektor által szolgáltatott elektromos impulzusok jelformálás és erősítés céljából ''erősítő'' rendszerre kerülnek. Az erősítőkkel kapcsolatos szigorú kívánalom az igen jó ''jel/zaj'' viszony és a nagyfokú ''linearitás''. Az erősítőkből kilépő elektromos jelsorozatot sokcsatornás analizátor (MCA: MultiChannel Analyzer) dolgozza fel. A félvezető-detektoros alfa-spektrométerek MCA-ja - a detektor jó energia felbontása miatt - 1-2 ezer csatornás. | ||
| 67. sor: | 89. sor: | ||
Az impulzus generátor (pulser) és az oszcilloszkóp nem szoros tartozékai a spektrométernek, elsősorban a rendszer elektronikus vizsgálatához használatosak. | Az impulzus generátor (pulser) és az oszcilloszkóp nem szoros tartozékai a spektrométernek, elsősorban a rendszer elektronikus vizsgálatához használatosak. | ||
| + | |||
| + | '''Figyelmeztetések:''' | ||
| + | |||
| + | * Az alfa-sugárforrások aktív oldalát (de bármilyen más radioaktív sugárforrást sem) soha ne érintsük kézzel. Mindig a forrás tartó lemez szélét fogjuk meg csipesszel. | ||
| + | * A félvezető detektorok érzékeny felületét óvjuk a mechanikus hatásoktól, mert a felület megsérülhet, elszennyeződhet és a detektor tönkremehet. | ||
===Alfa-spektrométer főbb jellemzői=== | ===Alfa-spektrométer főbb jellemzői=== | ||
| 89. sor: | 116. sor: | ||
|} | |} | ||
| − | + | ahol | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[Fájl: | + | {| cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: left; |
| + | |- | ||
| + | | ${E}$ || = az alfa energia [keV] | ||
| + | |- | ||
| + | | ${m}$ || = az energiakalibrációs egyenes meredeksége [keV/csatorna] | ||
| + | |- | ||
| + | | ${CS}$ || = csatornaszám | ||
| + | |- | ||
| + | | ${b}$ || = a tengelymetszet [keV] | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | | <span id="fig:4">[[Fájl:FizLab4_ALFA_04.jpg|közép|bélyegkép|400px|4.ábra: Energia kalibráció.]]</span> | ||
| + | |} | ||
===Energiafelbontó-képesség meghatározása=== | ===Energiafelbontó-képesség meghatározása=== | ||
| 104. sor: | 141. sor: | ||
A berendezés energia felbontására jellemző félértékszélesség: | A berendezés energia felbontására jellemző félértékszélesség: | ||
| − | ${FWHM}$ [keV] = ${\Delta}$ ${CS}$ [csatornaszám] | + | ${FWHM}$ [keV] = ${\Delta}$ ${CS}$ [csatornaszám] ${\times}$ ${m}$[keV/csatornaszám] alapon számítható. |
| − | [[Fájl: | + | {| |
| + | | <span id="fig:5">[[Fájl:FizLab4_ALFA_05.jpg|közép|bélyegkép|400px|5.ábra: Az energiafelbontás definíciójához.]]</span> | ||
| + | |} | ||
Végezze el a fenti mérést és számítást úgy is, hogy a sugárforrás a detektortól távolabb (kb. 40 mm) van. Hasonlítsa össze a két mérésből kapott eredményeket és magyarázza meg az azok közötti eltérést. | Végezze el a fenti mérést és számítást úgy is, hogy a sugárforrás a detektortól távolabb (kb. 40 mm) van. Hasonlítsa össze a két mérésből kapott eredményeket és magyarázza meg az azok közötti eltérést. | ||
| 117. sor: | 156. sor: | ||
Határozza meg a spektrométer hatásfokát abban a mérési geometriában, amelyben az ismeretlen mintát mérte. A hatásfok kétféle módon nyerhető: | Határozza meg a spektrométer hatásfokát abban a mérési geometriában, amelyben az ismeretlen mintát mérte. A hatásfok kétféle módon nyerhető: | ||
| − | - az egyik egy durvább közelítés, amely olyan esetben is alkalmazható, amikor nem áll rendelkezésre (drága etalon) kalibráló sugárforrás. Ez a módszer azon a feltételezésen alapszik, hogy minden a detektorba jutó alfa-részecske regisztrálásra kerül a csúcs területben. Ekkor a sugárforrás - detektor távolság ( | + | - az egyik egy durvább közelítés, amely olyan esetben is alkalmazható, amikor nem áll rendelkezésre (drága etalon) kalibráló sugárforrás. Ez a módszer azon a feltételezésen alapszik, hogy minden a detektorba jutó alfa-részecske regisztrálásra kerül a csúcs területben. Ekkor a sugárforrás - detektor távolság (${H}$), valamint a detektor belépő ablak felszínének (${F}$) ismeretében a hatásfok a következő módon becsülhető: |
{| width = "100%" | {| width = "100%" | ||
| 136. sor: | 175. sor: | ||
|} | |} | ||
| − | + | ahol | |
| − | + | ||
| − | + | {| cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: left; | |
| − | + | |- | |
| − | + | | $k_{\alpha}$ || = az adott energiájú alfa-sugárzás gyakorisága (nukleáris állandó) | |
| + | |- | ||
| + | | $t_{m}$ || = a mérési idő [s] | ||
| + | |- | ||
| + | | $A_{st}$ || = a standard izotóp aktivitása [Bq] a mérés időpontjában (előfordulhat, hogy ehhez bomláskorrekciót kell alkalmazni, | ||
| + | |- | ||
| + | | || mert a standard aktivitása más időpontban adott!) | ||
| + | |} | ||
| + | |||
| + | |||
| + | A hatásfok szórása becsülhető a nettó csúcsterület szórásából. | ||
{| width = "100%" | {| width = "100%" | ||
| 149. sor: | 198. sor: | ||
|} | |} | ||
| + | ahol | ||
| + | |||
| + | {| cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: left; | ||
| + | |- | ||
| + | | ${N_{st}}$ || = standard sugárforrás nettó csúcsterülete | ||
| + | |- | ||
| + | | ${\sigma_{\eta}}$ || = hatásfok abszolút szórása | ||
| + | |- | ||
| + | | ${\sigma_{N}}$ || = nettó csúcsterület abszolút szórása | ||
| + | |} | ||
| + | |||
| + | |||
| + | A nettó csúcsterület abszolút szórása. | ||
| + | |||
| + | {| width = "100%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ \sigma_{N} = \sqrt{N+2B} \]</latex></div> | ||
| + | | align = "right" | <span id="eq2"> (5) </span> | ||
| + | |} | ||
| + | |||
| + | ahol | ||
| + | |||
| + | {| cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: left; | ||
| + | |- | ||
| + | | ${N}$ || = nettó csúcsterület | ||
| + | |- | ||
| + | | ${B}$ || = háttér csúcsterülete | ||
| + | |} | ||
===Ismeretlen izotóp(ok) aktivitásának meghatározása=== | ===Ismeretlen izotóp(ok) aktivitásának meghatározása=== | ||
| − | Vegyen fel alfa-spektrumot valamely ismeretlen radioaktív mintáról. A forrást olyan pozícióba helyezze a detektor elé, ahol ismert a hatásfok (akár előzetes meghatározásból, akár a gyakorlatvezetőtől). A spektrumban észlelt csúcsterület(ek) meghatározása után számítsa ki a minta | + | Vegyen fel alfa-spektrumot valamely ismeretlen radioaktív mintáról. A forrást olyan pozícióba helyezze a detektor elé, ahol ismert a hatásfok (akár előzetes meghatározásból, akár a gyakorlatvezetőtől). A spektrumban észlelt csúcsterület(ek) meghatározása után számítsa ki a minta alfa sugárzó izotópjának (izotópjainak) aktivitását (${A_{x}}$) és annak relatív statisztikus szórását ($^{\sigma_{A_{x}}}/A_{x}$ ) |
| + | a (6) és (7) összefüggések alapján: | ||
{| width = "100%" | {| width = "100%" | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ A_{x}[Bq]=\frac{ | + | | width = "80%" | <div class="texdisplay"><latex display >\[ A_{x}[Bq]=\frac{N_{x}}{k_{\alpha}t_{m}\eta} \]</latex></div> |
| − | | align = "right" | <span id="eq2"> ( | + | | align = "right" | <span id="eq2"> (6) </span> |
|} | |} | ||
| 165. sor: | 244. sor: | ||
| width = "10%" | | | width = "10%" | | ||
| width = "80%" | <div class="texdisplay"><latex display >\[ \sigma_{A_{x}}=\sqrt{{{\sigma^{2}}_{N}+\sigma^{2}}_{\eta}} \]</latex></div> | | width = "80%" | <div class="texdisplay"><latex display >\[ \sigma_{A_{x}}=\sqrt{{{\sigma^{2}}_{N}+\sigma^{2}}_{\eta}} \]</latex></div> | ||
| − | | align = "right" | <span id="eq2"> ( | + | | align = "right" | <span id="eq2"> (7) </span> |
|} | |} | ||
| + | ahol | ||
| + | |||
| + | {| cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: left; | ||
| + | |- | ||
| + | | $N_{x}$ || = az ismeretlen forrástól származó valamelyik alfa-csúcs területe [imp] | ||
| + | |- | ||
| + | | $t_{m}$ || = a mérés időtartama [s] | ||
| + | |- | ||
| + | | $\eta$ || = a hatásfok az adott mérési elrendezésben | ||
| + | |- | ||
| + | | $\sigma_{N}$|| = a csúcsterület statisztikus szórása | ||
| + | |- | ||
| + | | $\sigma_{\eta}$ || = a hatásfok hibája | ||
| + | |- | ||
| + | | $\sigma_{A}$ || = az aktivitás statisztikus hibája | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Az aktivitást számítsa ki mindkét, a 4. pontban ismertetett hatásfok meghatározás alapján. | Az aktivitást számítsa ki mindkét, a 4. pontban ismertetett hatásfok meghatározás alapján. | ||
| 181. sor: | 270. sor: | ||
==A méréshez szükséges eszközök és anyagok== | ==A méréshez szükséges eszközök és anyagok== | ||
| − | * félvezető-detektorral ellátott alfa-spektrométer | + | * félvezető-detektorral ellátott alfa-spektrométer |
| − | * standard sugárforrás | + | * standard sugárforrás |
| − | * ismeretlen összetételű alfa-sugárforrás | + | * ismeretlen összetételű alfa-sugárforrás |
* csipesz, tolómérő, stb. | * csipesz, tolómérő, stb. | ||
| − | == | + | '''Amiről beszélni kell''' (útmutató a gyakorlatvezetőnek): |
| + | * az alfa-sugárzás tulajdonságai (alfa-bomlás, alagút effektus, fajlagos ionizáció, hatótávolság) | ||
| + | * az alfa spektrum alakjának magyarázata | ||
| + | * az alfa- és gamma-spektrumok alakjának összehasonlítása | ||
| + | * mire használható az alfa-spektrometria | ||
| + | * érzékenység összehasonlítása az alfa- és gamma-spektrometria között | ||
| + | * milyen detektorok alkalmasak alfa-sugárzás intenzitásának mérésére és spektrometriájára | ||
| + | * milyen információk nyerhetők egy alfa-spektrumból | ||
| + | * az alfa-sugárforrás készítéssel szemben támasztott követelmények | ||
| + | * alfa-sugárforrás (spektrometriai célra) készítésének módszerei | ||
| + | * az alfa-sugárzás dozimetriai szempontból | ||
| + | |||
| + | ==Ellenőrző kérdések== | ||
| + | |||
| + | # Milyen alfa-sugárzó izotópokat ismer, ezek eredet ? (példák) | ||
| + | # Az alfa-sugárzás és az anyag közötti kölcsönhatások jellemzői. | ||
| + | # Alfa sugárzás mérésére alkalmazható félvezető-detektor felépítése, működési elve. | ||
| + | # Alfa-spektrométer felépítése, az egyes egységek funkciója, jellemzői. | ||
| + | # Az alfa-sugárforrás formájának jelentősége méréstechnikai szempontból. | ||
| + | # Miért szükséges a mérés kezdetekor az energia kalibráció elvégzése és ez hogyan történik? | ||
| + | # Energia felbontóképesség az alfa-spektrometriában. | ||
| + | # Mi a különbség és hasonlóság az alfa-, béta-, és gamma-sugárzások között? | ||
| + | |||
| + | ==Irodalomjegyzék== | ||
* Bódizs D.: Atommagsugárzások méréstechnikái, Typotex Kiadó Budapest, 2006 | * Bódizs D.: Atommagsugárzások méréstechnikái, Typotex Kiadó Budapest, 2006 | ||
| − | * Deme S.: Félvezető detektorok magsugárzás mérésére Műszaki Könyvkiadó Budapest, 1968 | + | * Deme S.: Félvezető detektorok magsugárzás mérésére, Műszaki Könyvkiadó Budapest, 1968 |
| − | * Nagy L.Gy.: Radiokémia és izotóptechnika (bizonyos fejezetei)Tankönyvkiadó Budapest, 1983 | + | * Nagy L.Gy.: Radiokémia és izotóptechnika (bizonyos fejezetei), Tankönyvkiadó Budapest, 1983 |
| − | * Applied Radiation and Isotopes Vol. 35 No. 4, 1984 | + | * Applied Radiation and Isotopes Vol. 35 No. 4, 1984, Alpha - Particle - Spectrometry Techniques and Applications |
| + | |||
| + | ==Külső hivatkozások== | ||
| + | |||
| + | Az Alfa spektroszkópia laborjegyzet forrása elérhető a [http://www.reak.bme.hu/uploads/media/04_Alfa_spektrum_merese_01.pdf] linken: | ||
A lap jelenlegi, 2013. július 30., 07:36-kori változata
Tartalomjegyzék |
Bevezetés
Az útmutató a Nukleáris méréstechnika c. tantárgy laboratóriumi gyakorlatához készült. A hallgató az alábbi ismereteket sajátítja el a gyakorlat során:
- alfa-spektrometriás módszer megismerése és gyakorlati alkalmazása, továbbá ezen belül
- alfa-spektrométer felépítése, az egyes részegységek feladata, jellemzői
- felületi záróréteges Si detektorok fajtái, jellemzői
- alfa-forrás formájának jelentősége
- alfa-spektrumok kiértékelése
- a mérési módszer összehasonlítása más (pl. gamma-spektrometriás) módszerekkel
A laboratóriumi gyakorlat célja
A gyakorlat elvégzésével az elméleti előadásokon hallott ismeretek elmélyítése és gyakorlatban való megismerése történik. A félvezető detektorok tulajdonságainak összehasonlítása, a felületi záróréteges Si detektor alkalmazása alfa-sugárzó minták azonosítására, aktivitásának és aktivitáskoncentrációjának meghatározására. A mérési eljárás alkalmazhatósága, előnyei, korlátai.
Elméleti összefoglalás
A Si vagy Ge alapanyagú félvezető detektorokat - amelyeket szilárd ionizációs kamráknak is neveznek - széles körben alkalmazzák a nukleáris méréstechnikában. Használhatók kb. 20 keV-es elektronenergiától 200 MeV-es nehéz ion (pl. alfa-részek) energiáig, valamint gamma-spektrometriai célokra.
Alfa-sugárzás mérésére a félvezető detektorok számos típusát fejlesztették ki. Egyik fajtájuk az ún. felületi záróréteges Si detektor. Ez igen jó energia felbontással, gyors felfutású impulzus alakkal (kb. 1 ns) rendelkezik, ezért jól alkalmazható pl. spektrometriában, valamint koincidencia mérésekben. Ezen detektorok megszólalási valószínűsége (azaz elektromos jel kiadása) azokra a töltött részecskékre, amelyek bejutottak a detektor érzékeny térfogatába, 100%, energiafelbontásuk széles tartományban állandó. Kis méretük miatt jól illeszthetők különböző mérési geometriákhoz, külső elektromos és mágneses terekre alig érzékenyek.
Felületi záróréteges detektorok
Alfa-spektrometriai célokra leggyakrabban az ún. felületi záróréteges detektorokat alkalmazzák (1.ábra). Ezek alapanyaga nagy tisztaságú, 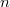 típusú Si egykristályból készült lap. Ezt savas maratás után oxidációnak vetik alá. A felületen kialakuló nagyon vékony oxid réteg
típusú Si egykristályból készült lap. Ezt savas maratás után oxidációnak vetik alá. A felületen kialakuló nagyon vékony oxid réteg 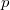 típusként szerepel. Így jön létre a
típusként szerepel. Így jön létre a 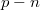 átmenet. Ezt követően a kristály egyik oldali sík felületére nagyon vékony arany réteget (kb. 50 μg/cm2) visznek fel vákuumpárologtatással. Az arany réteg egyrészt elektromos kontaktusul szolgál, másrészt fényzáróként szerepel. Ez a detektor belépő ablaka. Az arany rétegnek azért kell minél vékonyabbnak lenni, hogy a kis hatótávolságú (nagy fajlagos ionizációval rendelkező) alfa-részecskék minél kisebb energiaveszteséggel léphessenek be a detektorba. A Si lap másik síkoldalára - rendszerint Al-ból készült elektród kerül. Az arany és alumínium elektródák közé záróirányú feszültséget kapcsolnak, mely tovább szélesíti a
átmenet. Ezt követően a kristály egyik oldali sík felületére nagyon vékony arany réteget (kb. 50 μg/cm2) visznek fel vákuumpárologtatással. Az arany réteg egyrészt elektromos kontaktusul szolgál, másrészt fényzáróként szerepel. Ez a detektor belépő ablaka. Az arany rétegnek azért kell minél vékonyabbnak lenni, hogy a kis hatótávolságú (nagy fajlagos ionizációval rendelkező) alfa-részecskék minél kisebb energiaveszteséggel léphessenek be a detektorba. A Si lap másik síkoldalára - rendszerint Al-ból készült elektród kerül. Az arany és alumínium elektródák közé záróirányú feszültséget kapcsolnak, mely tovább szélesíti a 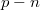 átmenetnél kialakult kiürített réteget. Ez a detektor érzékeny térfogata. Ennek olyan vastagságúnak kell lenni, hogy a mérendő alfa-részecskék teljes energiájukat leadják azaz elnyelődjenek benne, (mivel az egyik feladat energiájuk meghatározása) létrehozva elektron – pozitív-lyuk töltéshordozó párokat. Az így keletkezett töltéshordozókat a detektorra kapcsolt feszültség összegyűjti és a kimeneten elektromos impulzusok jelennek meg. Az impulzus amplitúdója arányos az abszorbeált alfa részecske energiájával (energiamérés).
átmenetnél kialakult kiürített réteget. Ez a detektor érzékeny térfogata. Ennek olyan vastagságúnak kell lenni, hogy a mérendő alfa-részecskék teljes energiájukat leadják azaz elnyelődjenek benne, (mivel az egyik feladat energiájuk meghatározása) létrehozva elektron – pozitív-lyuk töltéshordozó párokat. Az így keletkezett töltéshordozókat a detektorra kapcsolt feszültség összegyűjti és a kimeneten elektromos impulzusok jelennek meg. Az impulzus amplitúdója arányos az abszorbeált alfa részecske energiájával (energiamérés).
Az újabb technológiával készült detektorokat PIPS (Passivated Implanted Planar Silicon) típusúaknak nevezik. Az ilyen detektor belépő ablaka implantált réteggel van ellátva és ezért sokkal ellenállóbb mechanikus behatásokkal (pl. dekontaminálás) szemben, mint az előző típus.
A felületi záróréteges detektorokat három - a méréstechnika szempontjából fontos - paraméterrel szokás jellemezni:
- energiafelbontó képesség,
- belépő ablak felület nagysága,
- kiürített réteg vastagság,
Általában az energiafelbontás 20 keV körüli érték (5,5 MeV-es alfa-részecskékre). Adott detektor esetén elsősorban a sugárforrás vastagságától, valamint a detektor és sugárforrás közötti távolságtól függ. A belépő ablak felület általában 100 - 1000 mm2 közötti. Ennek nagysága egyrészt a detektor hatásfokát szabja meg, de kihatással van az energia felbontásra is (elektronikus okokból: nagyobb térfogatból a kigyűjtött töltések mennyiségének statisztikus ingadozása nagyobb, mint kisebb térfogat esetén). A kiürített réteg vastagsága 100 - 5000 μm szokott lenni. Mint fentebb említettük, ez utóbbinak elégnek kell lenni a detektálni kívánt töltött részecskék teljes lefékezéséhez, ami nyilván részecskefajta és energiafüggő. Erről ad tájékoztatást a 2. ábra.
Az 1. táblázat néhány "közismert" alfa-sugárzó izotóp nukleáris adatait tartalmazza.
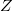 |
izotóp | 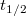 |
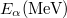 |
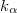 (%) (%)
|
|---|---|---|---|---|
| 86 | 222Rn | 3,82d | 5,49 | 100 |
| 88 | 226Ra | 1600y | 4,79; 4,6 | 94,5; 5,6 |
| 90 | 232Th | 1,41 1010y 1010y |
4,01; 3,96 | 77; 23 |
| 92 | 235U | 7,04 108y 108y |
4,6; 4,56; 4,39; 4,37; 4,22 | 4,6; 3,7; 57;74; 5,7 |
| 92 | 238U | 4,47 109y 109y |
4,2; 4,15 | 77; 23 |
| 94 | 239Pu | 2,41 104y 104y |
5,126; 5,14; 5,1 | 73,3; 15,1; 11,5 |
| 95 | 241Am | 432y | 5,49; 5,44; 5,39 | 86; 12,7; 1,3 |
Mérőberendezés (alfa-spektrométer) blokkvázlata
Egy alfa-spektrométer blokkvázlatát szemlélteti a 3. ábra.
Tekintettel az alfa-részecskék nagy fajlagos ionizáló képességére (kis hatótávolságára), a detektort és a sugárforrást közös vákuum térbe kell helyezni, továbbá a sugárforrásnak minél vékonyabbnak kell lenni, hogy benne az alfa-részecskék abszorbciója - így energia szórásuk - minél kisebb legyen.
A detektor által szolgáltatott elektromos impulzusok jelformálás és erősítés céljából erősítő rendszerre kerülnek. Az erősítőkkel kapcsolatos szigorú kívánalom az igen jó jel/zaj viszony és a nagyfokú linearitás. Az erősítőkből kilépő elektromos jelsorozatot sokcsatornás analizátor (MCA: MultiChannel Analyzer) dolgozza fel. A félvezető-detektoros alfa-spektrométerek MCA-ja - a detektor jó energia felbontása miatt - 1-2 ezer csatornás. A spektrum kiértékelés általában számítógéppel (PC) és megfelelő software felhasználásával történik. A kiértékelés főbb lépései: csúcskeresés, az energia kalibráció alapján energia meghatározás, izotópazonosítás, hatásfok alapján aktivitás, vagy aktivitáskoncentráció meghatározás.
Az impulzus generátor (pulser) és az oszcilloszkóp nem szoros tartozékai a spektrométernek, elsősorban a rendszer elektronikus vizsgálatához használatosak.
Figyelmeztetések:
- Az alfa-sugárforrások aktív oldalát (de bármilyen más radioaktív sugárforrást sem) soha ne érintsük kézzel. Mindig a forrás tartó lemez szélét fogjuk meg csipesszel.
- A félvezető detektorok érzékeny felületét óvjuk a mechanikus hatásoktól, mert a felület megsérülhet, elszennyeződhet és a detektor tönkremehet.
Alfa-spektrométer főbb jellemzői
Mint említettük, az alfa-spektrométerek legfontosabb jellemzői: az energiafelbontó-képesség és a hatásfok.
Az energiafelbontó-képesség szemléletesen, az a két legközelebbi energia, amit a berendezés még szét tud választani. Ennek mérőszáma az ún. félértékszélesség (ld. később). Ezt egyrészt a detektor tulajdonságai, másrészt az erősítők zaja határozza meg, de mint fentebb említettük, alfa-spektrometriában függ még a detektor - sugárforrás távolságtól is, valamint nagyban befolyásolja a sugárforrás "vékonysága". Megfelelő vékonyságú alfa-sugárforrás készítése általában igen bonyolult feladat és az alfa-spektrometria igen fontos lépése.
A hatásfok azt adja meg, hogy a sugárforrásból a 4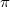 térszögbe emittált alfa-részecskékből mennyi ad impulzust a spektrum energia csúcsaiba. Ezt a detektor belépő ablakának mérete, másrészt mérési geometria (sugárforrás detektor távolság, forrás alak) határozzák meg.
térszögbe emittált alfa-részecskékből mennyi ad impulzust a spektrum energia csúcsaiba. Ezt a detektor belépő ablakának mérete, másrészt mérési geometria (sugárforrás detektor távolság, forrás alak) határozzák meg.
Mérési feladatok
Energiakalibráció
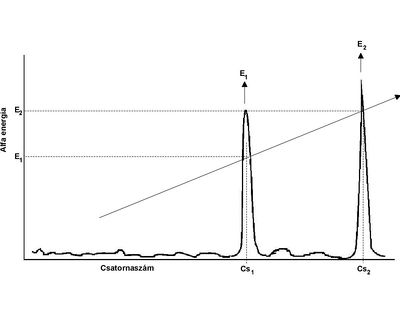
Ellenőrizze a spektrométer összeállítását és írja fel az egyes egységek típusát. A gyakorlatvezető útmutatása szerint állítsa be az egyes egységeken a mérési paramétereket és jegyezze fel azokat. Ismert energiájú alfa-részecskéket kibocsátó sugárforrást (etalon) helyezzen a detektor elé. A vákuumszivattyú bekapcsolása és a szükséges vákuum (néhány Pa) elérése után kapcsolja rá a detektorra az üzemi feszültséget (30-100 V - a gyakorlatvezető utasítása szerint). Vegyen fel alfa-spektrumot a sokcsatornás analizátorral. Az etalonhoz megadott energiák és az analizátorból a marker segítségével kiolvasott, a csúcsok maximum helyeihez tartozó csatornaszámok ismeretében végezze el az energia kalibrációt az adott erősítő beállítás mellett (4. ábra), azaz határozza meg az energiakalibrációs egyenes paramétereit: meredekség, tengelymetszet, más szóval írja fel egyenletét:
![\[ E=mCS+b \]](/images/math/c/5/f/c5fbb1e5d4bb8a862a99ff62cdf0a166.png) |
(1) |
ahol
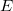 |
= az alfa energia [keV] |
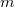 |
= az energiakalibrációs egyenes meredeksége [keV/csatorna] |
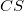 |
= csatornaszám |
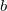 |
= a tengelymetszet [keV] |
Energiafelbontó-képesség meghatározása
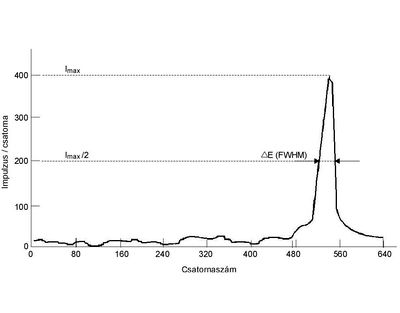
Helyezzen el ismert energiájú alfa-részecskéket kibocsátó sugárforrás(oka)t a detektor elé, egy közelebbi (kb. 5 mm) távolságra és vegyen fel spektrumot. A mérési idő megválasztásánál vegye figyelembe a statisztikus hibát! Határozza meg a spektrumban található energia csúcsok félértékszélességeit az 5. ábrának megfelelően.
(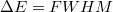 =
= 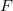 ull
ull 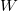 idth at
idth at 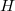 alf
alf 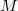 aximum)
aximum)
A berendezés energia felbontására jellemző félértékszélesség:
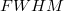 [keV] =
[keV] = 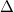
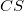 [csatornaszám]
[csatornaszám] 
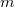 [keV/csatornaszám] alapon számítható.
[keV/csatornaszám] alapon számítható.
Végezze el a fenti mérést és számítást úgy is, hogy a sugárforrás a detektortól távolabb (kb. 40 mm) van. Hasonlítsa össze a két mérésből kapott eredményeket és magyarázza meg az azok közötti eltérést.
Ismeretlen alfa-sugárzó izotóp(ok) azonosítása
Ismeretlen összetételű alfa-sugárzó preparátummal vegyen fel spektrumot. Az energiacsúcsok maximum helyeinek (csatornaszám) kiolvasása és az energia kalibráció alapján számítsa ki az alfa-energiákat. Izotóp táblázat segítségével a kapott energia értékek ismeretében állapítsa meg a minta izotóp összetételét és jegyezze fel az izotópok főbb nukleáris adatát (pl. felezési idő, "valódi" alfa-energiák és alfa-gyakoriságok). A mérési időt úgy kell megválasztani – tekintettel a statisztikus szórásra - hogy a csúcs maximumban az impulzusszám ne legyen kevesebb, mint kb. 5000.
Hatásfok meghatározása
Határozza meg a spektrométer hatásfokát abban a mérési geometriában, amelyben az ismeretlen mintát mérte. A hatásfok kétféle módon nyerhető:
- az egyik egy durvább közelítés, amely olyan esetben is alkalmazható, amikor nem áll rendelkezésre (drága etalon) kalibráló sugárforrás. Ez a módszer azon a feltételezésen alapszik, hogy minden a detektorba jutó alfa-részecske regisztrálásra kerül a csúcs területben. Ekkor a sugárforrás - detektor távolság (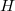 ), valamint a detektor belépő ablak felszínének (
), valamint a detektor belépő ablak felszínének (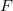 ) ismeretében a hatásfok a következő módon becsülhető:
) ismeretében a hatásfok a következő módon becsülhető:
![\[ \eta=\frac{F}{4H^{2}\pi} \]](/images/math/4/4/9/449143fc9da481cbf1ff6a0536ba871a.png) |
(2) |
Ennek a számításnak a hibája kb. 10%-nak vehető.
- a másik, lényegesen pontosabb eljárás, ismert aktivitású standard (etalon) alfa-sugárforrás alkalmazásával végezhető el. Ekkor a standard forrást ugyan abba a mérési pozícióba kell helyezni, amelyben az ismeretlen minta volt és felvenni az alfa-spektrumot. Ebből a spektrumból az energia csúcs területe (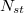 ) alapján:
) alapján:
![\[ \eta=\frac{N}{k_{\alpha}t_{m}A_{st}} \]](/images/math/3/e/4/3e4110601d0d347dfdcba90ba94bf38d.png) |
(3) |
ahol
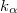 |
= az adott energiájú alfa-sugárzás gyakorisága (nukleáris állandó) |
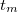 |
= a mérési idő [s] |
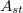 |
= a standard izotóp aktivitása [Bq] a mérés időpontjában (előfordulhat, hogy ehhez bomláskorrekciót kell alkalmazni, |
| mert a standard aktivitása más időpontban adott!) |
A hatásfok szórása becsülhető a nettó csúcsterület szórásából.
![\[ \sigma_{\eta} \approx \sigma_{N}=\sqrt{N_{st}} \]](/images/math/f/b/d/fbd9643f8a86b0f1c0d5ac462f819ff0.png) |
(4) |
ahol
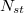 |
= standard sugárforrás nettó csúcsterülete |
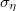 |
= hatásfok abszolút szórása |
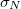 |
= nettó csúcsterület abszolút szórása |
A nettó csúcsterület abszolút szórása.
![\[ \sigma_{N} = \sqrt{N+2B} \]](/images/math/8/f/5/8f5eb19eb40e35929e15b659b2929292.png) |
(5) |
ahol
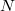 |
= nettó csúcsterület |
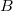 |
= háttér csúcsterülete |
Ismeretlen izotóp(ok) aktivitásának meghatározása
Vegyen fel alfa-spektrumot valamely ismeretlen radioaktív mintáról. A forrást olyan pozícióba helyezze a detektor elé, ahol ismert a hatásfok (akár előzetes meghatározásból, akár a gyakorlatvezetőtől). A spektrumban észlelt csúcsterület(ek) meghatározása után számítsa ki a minta alfa sugárzó izotópjának (izotópjainak) aktivitását (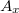 ) és annak relatív statisztikus szórását (
) és annak relatív statisztikus szórását (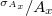 )
a (6) és (7) összefüggések alapján:
)
a (6) és (7) összefüggések alapján:
![\[ A_{x}[Bq]=\frac{N_{x}}{k_{\alpha}t_{m}\eta} \]](/images/math/6/d/6/6d6d43c1b3fa6cfad8ef0def0c93fae6.png) |
(6) |
![\[ \sigma_{A_{x}}=\sqrt{{{\sigma^{2}}_{N}+\sigma^{2}}_{\eta}} \]](/images/math/d/1/8/d183b7b72cbabf5e12079b227b06fc98.png) |
(7) |
ahol
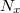 |
= az ismeretlen forrástól származó valamelyik alfa-csúcs területe [imp] |
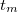 |
= a mérés időtartama [s] |
 |
= a hatásfok az adott mérési elrendezésben |
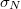 |
= a csúcsterület statisztikus szórása |
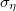 |
= a hatásfok hibája |
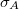 |
= az aktivitás statisztikus hibája |
Az aktivitást számítsa ki mindkét, a 4. pontban ismertetett hatásfok meghatározás alapján. Disszkutálja a kapott eredményeket és az azok közötti eltérést.
A méréshez szükséges eszközök és anyagok
- félvezető-detektorral ellátott alfa-spektrométer
- standard sugárforrás
- ismeretlen összetételű alfa-sugárforrás
- csipesz, tolómérő, stb.
Amiről beszélni kell (útmutató a gyakorlatvezetőnek):
- az alfa-sugárzás tulajdonságai (alfa-bomlás, alagút effektus, fajlagos ionizáció, hatótávolság)
- az alfa spektrum alakjának magyarázata
- az alfa- és gamma-spektrumok alakjának összehasonlítása
- mire használható az alfa-spektrometria
- érzékenység összehasonlítása az alfa- és gamma-spektrometria között
- milyen detektorok alkalmasak alfa-sugárzás intenzitásának mérésére és spektrometriájára
- milyen információk nyerhetők egy alfa-spektrumból
- az alfa-sugárforrás készítéssel szemben támasztott követelmények
- alfa-sugárforrás (spektrometriai célra) készítésének módszerei
- az alfa-sugárzás dozimetriai szempontból
Ellenőrző kérdések
- Milyen alfa-sugárzó izotópokat ismer, ezek eredet ? (példák)
- Az alfa-sugárzás és az anyag közötti kölcsönhatások jellemzői.
- Alfa sugárzás mérésére alkalmazható félvezető-detektor felépítése, működési elve.
- Alfa-spektrométer felépítése, az egyes egységek funkciója, jellemzői.
- Az alfa-sugárforrás formájának jelentősége méréstechnikai szempontból.
- Miért szükséges a mérés kezdetekor az energia kalibráció elvégzése és ez hogyan történik?
- Energia felbontóképesség az alfa-spektrometriában.
- Mi a különbség és hasonlóság az alfa-, béta-, és gamma-sugárzások között?
Irodalomjegyzék
- Bódizs D.: Atommagsugárzások méréstechnikái, Typotex Kiadó Budapest, 2006
- Deme S.: Félvezető detektorok magsugárzás mérésére, Műszaki Könyvkiadó Budapest, 1968
- Nagy L.Gy.: Radiokémia és izotóptechnika (bizonyos fejezetei), Tankönyvkiadó Budapest, 1983
- Applied Radiation and Isotopes Vol. 35 No. 4, 1984, Alpha - Particle - Spectrometry Techniques and Applications
Külső hivatkozások
Az Alfa spektroszkópia laborjegyzet forrása elérhető a [1] linken: