„Szcintillációs detektorok” változatai közötti eltérés
| (egy szerkesztő 11 közbeeső változata nincs mutatva) | |||
| 26. sor: | 26. sor: | ||
A szervetlen szcintillátor kristályok átlátszó, szigetelő anyagok, melyekben az ionizáló részecske gerjesztésének hatására elektronok jutnak a töltött sávból a vezetési sávba, elektron-lyuk párokat hozva létre a töltött és a vezetési sávban. Az elektron foton kibocsátás mellett visszajuthat a vezetési sávba (rekombináció), azonban ez pont a tiltott sáv energiájának megfelelő energia kibocsátással jár, így az a kristályban el is nyelődik. Ahhoz hogy a keletkező foton kijusson, szennyező (aktivátor) anyagra van szükség a kristályban. Megfelelő szennyezők ugyanis olyan módon perturbálhatják a kristály rácsszerkezetét, hogy lokálisan újabb energianívók jelennek meg a vezetési sáv alatt, valamint a töltött sáv fölött, vagyis a tiltott sáv leszűkül. Ilyen esetben az elektron-lyuk párok a kristályban vándorolva könnyen egy ilyen szennyezőnél köthetnek ki, mert ez energetikailag kedvezőbb. Ezért a legerjesztődés során is a tiltott sáv szélességénél kisebb energiájú foton bocsátódik ki, melyre a kristály csak korlátozottan elnyelő, így kijut a kristályból. Egy másik lehetséges folyamatban, az elektron-lyuk pár egy gyengén kötött rendszert, ún. exitont alkot. Ennek az energiaszintje szintén kisebb, mint E<sub>g</sub> és bomlásakor látható fényt bocsát ki. Tiszta kristályban exitonok csak alacsony hőmérsékleten jöhetnek létre, szobahőmérsékleten ehhez a folyamathoz is aktivátorra van szükség. | A szervetlen szcintillátor kristályok átlátszó, szigetelő anyagok, melyekben az ionizáló részecske gerjesztésének hatására elektronok jutnak a töltött sávból a vezetési sávba, elektron-lyuk párokat hozva létre a töltött és a vezetési sávban. Az elektron foton kibocsátás mellett visszajuthat a vezetési sávba (rekombináció), azonban ez pont a tiltott sáv energiájának megfelelő energia kibocsátással jár, így az a kristályban el is nyelődik. Ahhoz hogy a keletkező foton kijusson, szennyező (aktivátor) anyagra van szükség a kristályban. Megfelelő szennyezők ugyanis olyan módon perturbálhatják a kristály rácsszerkezetét, hogy lokálisan újabb energianívók jelennek meg a vezetési sáv alatt, valamint a töltött sáv fölött, vagyis a tiltott sáv leszűkül. Ilyen esetben az elektron-lyuk párok a kristályban vándorolva könnyen egy ilyen szennyezőnél köthetnek ki, mert ez energetikailag kedvezőbb. Ezért a legerjesztődés során is a tiltott sáv szélességénél kisebb energiájú foton bocsátódik ki, melyre a kristály csak korlátozottan elnyelő, így kijut a kristályból. Egy másik lehetséges folyamatban, az elektron-lyuk pár egy gyengén kötött rendszert, ún. exitont alkot. Ennek az energiaszintje szintén kisebb, mint E<sub>g</sub> és bomlásakor látható fényt bocsát ki. Tiszta kristályban exitonok csak alacsony hőmérsékleten jöhetnek létre, szobahőmérsékleten ehhez a folyamathoz is aktivátorra van szükség. | ||
| − | + | {| | |
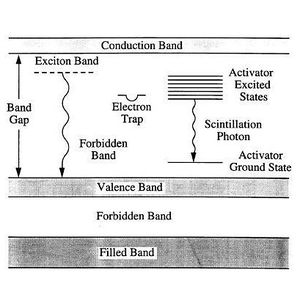
| + | | <span id="fig:1">[[Fájl:FizLab4_SZD_01.jpg|közép|bélyegkép|300px|1.ábra: Sávszerkezet szervetlen szcintillációs kristályban]]</span> | ||
| + | |} | ||
| − | Az ionizáló részecske 10 | + | Az ionizáló részecske 10<sup>-9</sup> s-on belül létrehozza az elektron-lyuk párokat, ezután azonban a fotonok kibocsátása a fenti folyamatokra jellemző hosszabb időskálán történik. Ezért a fénykibocsátás intenzitásának időbeli alakulása egy exponenciális (${\tau}$) időállandóval írható le: |
{| width = "100%" | {| width = "100%" | ||
| 42. sor: | 44. sor: | ||
1948-ban fedezték fel, hogy a kb. 0.1 mol% tallium-jodiddal (TlI) szennyezett NaI oldatból növesztett egykristályok minden akkor ismert szcintillátornál nagyobb intenzitású fénykibocsátást produkálnak. Egyszerű és olcsó előállíthatósága és megmunkálhatósága miatt a mai napig a legáltalánosabban alkalmazott szcintillátor anyag. | 1948-ban fedezték fel, hogy a kb. 0.1 mol% tallium-jodiddal (TlI) szennyezett NaI oldatból növesztett egykristályok minden akkor ismert szcintillátornál nagyobb intenzitású fénykibocsátást produkálnak. Egyszerű és olcsó előállíthatósága és megmunkálhatósága miatt a mai napig a legáltalánosabban alkalmazott szcintillátor anyag. | ||
| − | A szcintillációs folyamatok alapos megértéséhez tekintsük át mi történik egy NaI kristályban egy 1 MeV-os töltött részecske (pl. Compton-szórásban meglökött elektron) hatására. A töltött részecske lassulása során leadott energia részben a kristályrácsnak adódik át ( | + | A szcintillációs folyamatok alapos megértéséhez tekintsük át mi történik egy NaI kristályban egy 1 MeV-os töltött részecske (pl. Compton-szórásban meglökött elektron) hatására. A töltött részecske lassulása során leadott energia részben a kristályrácsnak adódik át (fonon keltés), részben pedig ionizációra, vagyis elektron-lyuk párok létrehozására fordítódik. Az ionizáció hatásfokára jellemző, hogy az egy keletkező elektron-lyuk párra eső leadott energiát a tiltott sáv szélességének háromszorosával lehet becsülni. Ez a NaI kristályban kb. 20 eV, így a keletkező elektron(e<sup>-</sup>)-lyuk(h<sup>+</sup>) párok száma kb. 50.000. Ezek több folyamaton keresztül juthatnak el a foton kibocsátásig. Mivel az e<sup>-</sup> transzportja a kristályban nagyságrendileg gyorsabb, ezért általában először az e<sup>-</sup> fogódik be egy Tl<sup>+</sup> ion által képzett lumineszcens centrumban Tl<sup>0</sup> atomot hozva létre. A Coulomb-potenciál hatására később a lassabban mozgó h<sup>+</sup> is befogódik ugyanitt és egy gerjesztett (Tl<sup>+</sup>)* iont keletkezik. Az is előfordulhat azonban, hogy a h<sup>+</sup> egy másik Tl<sup>+</sup>-nál fogódik be Tl<sup>++</sup>-t hozva létre. Ebben az esetben a rekombináció akkor jön létre, ha az e<sup>-</sup> a termikus gerjesztésnek köszönhetően kilép a Tl<sup>0</sup> csapdából és eljut a Tl<sup>++</sup> ionig. Mivel a NaI(Tl)-ban szobahőmérsékleten a Tl<sup>0</sup> állapot élettartama összevethető lyuk vándorlásához szükséges idővel ez a két folyamat azonos időskálán zajlik le. |
A gerjesztett (Tl<sup>+</sup>)* ion sugárzásos legerjesztődése szintén viszonylag lassabb folyamat, mert a közvetlen átmenet nem megengedett, ezért szintén termikus gerjesztés útján egy közbenső állapoton keresztül zajlik a fentiekhez hasonló időskálán. Ezen a folyamatok összessége adja a NaI(Tl) kristály viszonylag hosszú, $\tau$=230 ns-os időállandóját. | A gerjesztett (Tl<sup>+</sup>)* ion sugárzásos legerjesztődése szintén viszonylag lassabb folyamat, mert a közvetlen átmenet nem megengedett, ezért szintén termikus gerjesztés útján egy közbenső állapoton keresztül zajlik a fentiekhez hasonló időskálán. Ezen a folyamatok összessége adja a NaI(Tl) kristály viszonylag hosszú, $\tau$=230 ns-os időállandóját. | ||
| 70. sor: | 72. sor: | ||
* anód. | * anód. | ||
| − | + | {| | |
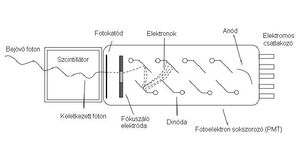
| + | | <span id="fig:2">[[Fájl:FizLab4_SZD_02.jpg|közép|bélyegkép|300px|2.ábra: A szcintillációs detektor felépítése]]</span> | ||
| + | |} | ||
| − | + | {| | |
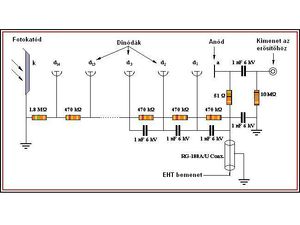
| + | | <span id="fig:3">[[Fájl:FizLab4_SZD_03.jpg|közép|bélyegkép|300px|3.ábra: Fotoelektron-sokszorozó áramköri kapcsolása]]</span> | ||
| + | |} | ||
==A szcintillációs detektorból kapott elektromos jel== | ==A szcintillációs detektorból kapott elektromos jel== | ||
| − | Folytatva | + | Folytatva az '''A NaI(TI) szcintillátor''' pontban megkezdett példát, ha feltételezzük, hogy a NaI(Tl) szcintillátorban keletkezett 38.000 db foton mind a fotokatódra jut, akkor kb. 25 %-os kvantumhatásokkal számolva mintegy 10.000 db fotoelektron keletkezik. d=5 szekunder elektron keltés és n=10 dinóda fokozat esetén a fotoelektron-sokszorozó erősítése 10<sup>7</sup>, vagyis 10<sup>11</sup> elektron ér az anódra. Az így kapott összesen Q=10<sup>11</sup>e töltésmennyiség a NaI(Tl) kristály ${\tau}$ időállandójának megfelelően exponenciálisan oszlik el, tehát az anódon megjelenő áram erőssége szintén exponenciálisan cseng le: |
{| width = "100%" | {| width = "100%" | ||
| 85. sor: | 91. sor: | ||
|} | |} | ||
| − | Tehát a fenti példában i(0)=10< | + | Tehát a fenti példában i(0)=10<sup>11</sup>x1,6x10<sup>-19</sup> C / 230 ns ${\approx}$ 69 mA, ami már egy jól mérhető jel. Az anódra azonban kb. 1000 V-nak megfelelő feszültséget kapcsolunk ezért egy megfelelően méretezett kicsatoló kondenzátor segítségével választjuk le a gyorsan változó jelet az egyenáramú tápfeszültségtől. A V(t) feszültség jel alakját a 4. ábra szerinti egyszerű áramköri modell segítségével érthetjük meg. A C kapacitás az anódhoz csatlakozó áramköri elemek szórt kapacitása az R ellenállás pedig a vezeték és csatlakozó ellenállások mellett az áramkör időállandójának állításához használt megfelelően méretezett ellenállás. V(t)-re így a következő differenciál egyenletet kapjuk: |
{| width = "100%" | {| width = "100%" | ||
| 94. sor: | 100. sor: | ||
|} | |} | ||
| − | + | {| | |
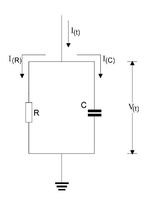
| + | | <span id="fig:4">[[Fájl:FizLab4_SZD_04.jpg|közép|bélyegkép|150px|4.ábra: Jelkicsatoló áramkör egyszerű modellje]]</span> | ||
| + | |} | ||
(2)-t behelyettesítve egy inhomogén elsőrendű differenciál-egyenletet kapunk, amelynek a megoldása a következő alakban adódik: | (2)-t behelyettesítve egy inhomogén elsőrendű differenciál-egyenletet kapunk, amelynek a megoldása a következő alakban adódik: | ||
| 112. sor: | 120. sor: | ||
A második esetben C értékét úgy szokták választani, hogy a fenti 1 MeV-es elektron 1-2 V közötti jel amplitúdót produkáljon. | A második esetben C értékét úgy szokták választani, hogy a fenti 1 MeV-es elektron 1-2 V közötti jel amplitúdót produkáljon. | ||
| − | + | {| | |
| + | | <span id="fig:5">[[Fájl:FizLab4_SZD_05.jpg|közép|bélyegkép|300px|5.ábra: A szcintillációs detektorból kapott jel alakja]]</span> | ||
| + | |} | ||
==A szcintillációs detektorok energia-felbontóképessége== | ==A szcintillációs detektorok energia-felbontóképessége== | ||
| − | A spektroszkópiai célokra használt detektorok egyik legfontosabb paramétere az energia-felbontóképesség, amely arra nézve ad felvilágosítást, hogy egymáshoz közel eső energiájú részecskéket mennyire tud a detektálás során megkülönböztetni. A detektorban leadott energia feszültségjel-amplitúdóvá konvertálása során egymást követő folyamatok ugyanis mind statisztikus jellegűek, így egy adott energiához egy jellemzően Gauss-eloszlással rendelkező kiszélesedett csúcs tartozik. A csúcs szélességét a csúcs maximumának feléhez tartozó pontok távolságával, a ${\ | + | A spektroszkópiai célokra használt detektorok egyik legfontosabb paramétere az energia-felbontóképesség, amely arra nézve ad felvilágosítást, hogy egymáshoz közel eső energiájú részecskéket mennyire tud a detektálás során megkülönböztetni. A detektorban leadott energia feszültségjel-amplitúdóvá konvertálása során egymást követő folyamatok ugyanis mind statisztikus jellegűek, így egy adott energiához egy jellemzően Gauss-eloszlással rendelkező kiszélesedett csúcs tartozik. A csúcs szélességét a csúcs maximumának feléhez tartozó pontok távolságával, a ${\Delta}$E félérték-szélességel (Full Width at Half Maximum, FWHM) szokás jellemezni. A gyakorlatban gyakran használjuk a relatív félérték-szélességet, amelyet a következőképpen definiálunk: |
{| width = "100%" | {| width = "100%" | ||
| 122. sor: | 132. sor: | ||
| width = "10%" | | | width = "10%" | | ||
| width = "80%" | <div class="texdisplay"><latex display >\[f=\frac{\Delta{E}}{E_{0}} \]</latex></div> | | width = "80%" | <div class="texdisplay"><latex display >\[f=\frac{\Delta{E}}{E_{0}} \]</latex></div> | ||
| − | | align = "right" | <span id="eq2"> ( | + | | align = "right" | <span id="eq2"> (5) </span> |
|} | |} | ||
| − | + | {| | |
| + | | <span id="fig:6">[[Fájl:FizLab4_SZD_06.jpg|közép|bélyegkép|300px|6.ábra: A ${\Delta}$E félérték-szélesség értelmezése]]</span> | ||
| + | |} | ||
| − | A szcintillációs detektorok fent ismertetett valamennyi folyamatát jó közelítéssel Poisson folyamatnak lehet tekinteni, vagyis a keletkezett részecskék (elektron-lyuk párok, fotonok, fotoelektronok, szekunder elektronok) számának szórását a várható érték négyzetgyöke adja meg. Így egy egyszerű alsó becslést adhatunk a kapott jel amplitúdó relatív szórására, ha megkeressük a legnagyobb relatív szórást a folyamatban. A | + | A szcintillációs detektorok fent ismertetett valamennyi folyamatát jó közelítéssel Poisson folyamatnak lehet tekinteni, vagyis a keletkezett részecskék (elektron-lyuk párok, fotonok, fotoelektronok, szekunder elektronok) számának szórását a várható érték négyzetgyöke adja meg. Így egy egyszerű alsó becslést adhatunk a kapott jel amplitúdó relatív szórására, ha megkeressük a legnagyobb relatív szórást a folyamatban. Az '''A szcintillációs detektorból kapott elektromos jel''' pontban folytatott példában láttuk, hogy a fotoelektronok száma mindössze 10000, tehát itt 1%-os relatív szórás jelentkezik. Gauss-eloszlást feltételezve ez 23,5 keV-os félérték-szélességet okoz az 1 MeV-os csúcsban, vagyis 2,35 %-os relatív félérték-szélességet. Ez az alsó becslés már jelzi, hogy a foton-elektron konverzió rossz hatásfoka miatt a szcintillációs detektorok felbontóképességben nem tudják felvenni a versenyt a félvezető detektorokkal. Valójában a NaI(Tl) detektorok felbontóképessége ezen az energián 5% körüli. |
| − | ==Az egycsatornás analizátor ( | + | ==Az egycsatornás analizátor (Single Channel Analyzer, SCA) működési elve== |
| − | A gamma-spektroszkópiában alkalmazott sokcsatornás analizátorok őse az ún. egycsatornás analizátor, vagy differenciál-diszkriminátor. A differenciál-diszkriminátor (DD) olyan berendezés, amely a beérkező jelsorozatból csak azokat a jeleket engedi át (vagyis csak azokra a jelekre szolgáltat kimenőjelet a számláló felé), amelyek amplitúdója két meghatározott feszültség közé esik. Ezt a feszültségintervallumot a diszkriminátor "ablaká"-nak szoktuk nevezni. Jóllehet a diszkriminátort feszültségben állítjuk be, ehelyett mindig részecskeenergiában gondolkodunk, és a diszkriminátor "ablaká"-t is energiára számoljuk át: az "ablak" így az E és E+${\ | + | A gamma-spektroszkópiában alkalmazott sokcsatornás analizátorok őse az ún. egycsatornás analizátor, vagy differenciál-diszkriminátor. A differenciál-diszkriminátor (DD) olyan berendezés, amely a beérkező jelsorozatból csak azokat a jeleket engedi át (vagyis csak azokra a jelekre szolgáltat kimenőjelet a számláló felé), amelyek amplitúdója két meghatározott feszültség közé esik. Ezt a feszültségintervallumot a diszkriminátor "ablaká"-nak szoktuk nevezni. Jóllehet a diszkriminátort feszültségben állítjuk be, ehelyett mindig részecskeenergiában gondolkodunk, és a diszkriminátor "ablaká"-t is energiára számoljuk át: az "ablak" így az E és E+${\Delta}$E közé eső energiájú részecskéket jelenti (ld. 7. ábra). A DD kimenetére egy számlálóegységet csatlakoztatunk, amellyel megmérhető a beütésszám egy adott energia-intervallumban. |
A DD a sokcsatornás analizátorok megjelenésével sem tűnt el, mert nem csak spektroszkópiai célokra használatos. Számtalan mérési elrendezésben szükséges, hogy csak egy meghatározott energiatartományban (pl. egy gamma-csúcs) számláljuk a beütéseket. DD használhatunk a háttér kiszűrésére, gamma-vonalak közötti koincidencia mérésére stb. | A DD a sokcsatornás analizátorok megjelenésével sem tűnt el, mert nem csak spektroszkópiai célokra használatos. Számtalan mérési elrendezésben szükséges, hogy csak egy meghatározott energiatartományban (pl. egy gamma-csúcs) számláljuk a beütéseket. DD használhatunk a háttér kiszűrésére, gamma-vonalak közötti koincidencia mérésére stb. | ||
| + | {| | ||
| + | | <span id="fig:7">[[Fájl:FizLab4_SZD_07.jpg|közép|bélyegkép|300px|7.ábra: A differenciál-diszkriminátor energia szintjei]]</span> | ||
| + | |} | ||
| + | |||
| + | A 11. ábrán az egycsatornás analizátor (differenciáldiszkriminátor, DD) blokkdiagramja látható. Az E alapszintet a Kl komparátoron az E potenciométerrel, a felső E+${\Delta}$E szintet pedig a K2 komparátoron az E+${\Delta}$E potenciométerrel állítjuk be. | ||
| − | + | {| | |
| − | + | | <span id="fig:8">[[Fájl:FizLab4_SZD_08.jpg|közép|bélyegkép|300px|8.ábra: Egycsatornás analizátor (differenciál-diszkriminátor, DD) blokkdiagramja]]</span> | |
| + | |} | ||
| + | Most belátjuk, hogy a 9. ábrán látható jelsorozatból csak a "b" jel hatására jelenik meg jel az antikoincidencia egység kimenetén. | ||
| + | * Az "a" jel amplitúdója nem éri el az E alapszintet, sem a K1, sem a K2 komparátor kimenetén nincs jel, így az antikoincidencia egység nem ad kimenő jelet. Az antikoincidencia egység akkor ad kimenő jelet, ha a két bemenete közül '''csak az egyiken''' van jel. Ez azt jelenti, hogy nincs kimenő jel, ha: (1) egyik bemeneten sincs jel, (2) mindkét bemeneten van jel. | ||
| + | * A "b" jel amplitúdója meghaladja az E értéket, de nem éri el az E+${\Delta}$E szintet. Ekkor a K1 komparátor kimenő jele a T<sub>1</sub> késleltetőn keresztül indítja a 2. jelformálót, melynek T<sub>3</sub> kimenete az antikoincidencia fokozatra kerül. (A késleltető szükségességéről később lesz szó.) Ugyanekkor a K2 komparátor felől nem érkezik jel az antikoincidencia fokozatra, ennek kimenő impulzusa indítja a 3. jelformálót, melynek T<sub>4</sub> kimenete egyben a DD uniformizált kimenő jele (számláló felé). | ||
| + | * A "c" jel amplitúdója meghaladja az E+${\Delta}$E komparátoron beállított szintet. Ebben az esetben mind K1, mind a K2 komparátor kimenetén megjelenik jel, tehát az antikoincidencia egység kimenetén nem kapunk jelet, ha a két komparátor kimenő jele egyszerre érkezik. A 12. ábrán látható, hogy az E+${\Delta}$E szintet a "c" jel később lépi át, mint az E szintet. Emiatt az antikoincidencia egység bemenetére nem egyszerre érkezik a két komparátor jele, tehát az megszólal, viszont a DD működési elve ennek az ellenkezőjét kívánja. Emiatt van szükség a T<sub>1</sub> késleltetőre: biztosítja a jelek egyidejű megérkezését. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Fontos megjegyezni, hogy a DD kimenetén már szabványos 5V magasságú négyszögjel jelenik meg. | Fontos megjegyezni, hogy a DD kimenetén már szabványos 5V magasságú négyszögjel jelenik meg. | ||
| − | + | {| | |
| − | 9. ábra A differenciál-diszkriminátor folyamatábrája | + | | <span id="fig:9">[[Fájl:FizLab4_SZD_09.jpg|közép|bélyegkép|300px|9.ábra: A differenciál-diszkriminátor folyamatábrája]]</span> |
| + | |} | ||
| − | + | ==A MÉRÉSI ELRENDEZÉS== | |
A méréshez használt eszközök: | A méréshez használt eszközök: | ||
| − | + | * <sup>137</sup>Cs és <sup>90</sup>Sr etalon források | |
| − | + | * ólomtorony mintatartóval | |
| − | + | * szcintillációs mérőfej gamma- és béta-sugárzás mérésére | |
| − | + | * NIM (Nuclear Instrumentation Module) bin a következő egységekkel | |
| − | + | ** szcintillációs mérőfej csatlakozó modul | |
| − | + | ** nagyfeszültségű tápegység (High Voltage Supply) | |
| − | + | ** spektroszkópiai erősítő (Amplifier) | |
| − | + | ** egycsatornás analizátor (SCA) | |
| − | + | ** számláló, időzítő egység (Counter Timer) | |
| − | + | ** Multiport-II sokcsatornás analizátor (MCA) | |
| − | + | * számítógép GENIE-2000 analizátor szoftverrel | |
| − | + | * oszcilloszkóp | |
| − | Az elrendezés összeállítása előtt meg kell győződni róla, hogy a tápegység nagyfeszültséget állító potmétere 0-ra van tekerve és a tápegység ki van kapcsolva. A mérés megkezdése előtt a | + | |
| − | + | Az elrendezés összeállítása előtt meg kell győződni róla, hogy a tápegység nagyfeszültséget állító potmétere 0-ra van tekerve és a tápegység ki van kapcsolva. A mérés megkezdése előtt a <sup>137</sup>Cs mintát el kell helyezni az ólomtoronyban, a mintatartó 6. polcán. A γ-mérőfejet felülről, óvatosan az ólomtoronyban kiképzett helyére csúsztatjuk. A 7+1 pólusú csatlakozó dugaszt a NIM binben található csatlakozó modulba kell dugni. Ezen az egységen keresztül kapja a mérőfej a tápfeszültséget és innen kapjuk a mért jelet is a BNC csatlakozón keresztül. A jelet BNC kábellel az erősítő bemenetére kötjük. Az erősítő unipoláris kimenetét az egycsatornás analizátor bementére, valamint (egy elosztó segítségével) a Multiport-II bemenetére. Az egycsatornás analizátor kimenetét a számláló egység bemenetére kötjük. A számítógép egy USB kábellel csatlakozik a Multiport-II-höz. A számítógépen a Gamma Acqusition programot kell elindítani, majd a File / Open datasource... menüben a Source: Detector jelölése után lehet a megfelelő egységet a | |
| − | A mérések során tett megfigyeléseket rögzítsük a jegyzőkönyvben. A feladatokban feltett kérdésekre adott rövid válaszok feltétlenül szerepeljenek a jegyzőkönyvben. A mért adatokat rögzíteni és részletesen kiértékelni ott kell, ahol ezt a feladat külön kéri. | + | számítógéphez rendelni. |
| − | + | ||
| + | ==MÉRÉSI FELADATOK== | ||
| + | |||
| + | A mérések során tett megfigyeléseket rögzítsük a jegyzőkönyvben. A feladatokban feltett kérdésekre adott rövid válaszok feltétlenül szerepeljenek a jegyzőkönyvben. A mért adatokat rögzíteni és részletesen kiértékelni ott kell, ahol ezt a feladat külön kéri. | ||
| + | |||
| + | ===A szintillációs detektor jelének vizsgálata=== | ||
| + | |||
A tápfeszültséget lassan növeljük 750 V-ra. A szcintillációs detektor jelét kössük közvetlenül az oszcilloszkópra. A feszültség- és időosztás, valamint a trigger-szint állításával keressük meg az 5. ábra szerinti jelet. Milyen a jel polaritása és miért? | A tápfeszültséget lassan növeljük 750 V-ra. A szcintillációs detektor jelét kössük közvetlenül az oszcilloszkópra. A feszültség- és időosztás, valamint a trigger-szint állításával keressük meg az 5. ábra szerinti jelet. Milyen a jel polaritása és miért? | ||
| − | Az oszcilloszkóp kurzorai segítségével mérjük meg a | + | |
| − | + | Az oszcilloszkóp kurzorai segítségével mérjük meg a <sup>137</sup>Cs 662 keV-os csúcsához tartozó jel magasságát. Vegyünk fel 3-4 pontot az exponenciálisan lecsengő szakaszon és illesztéssel határozzuk meg az RC időállandót! Mérjük meg a maximumhelyhez tartozó időt! (3)-ból vezessük le a maximumhely képletét és fejezzük ki a kristály ${\tau}$ időállandóját. A kapott transzendens egyenlet numerikus megoldásával határozzuk meg az időállandót és az eredményt vessük össze az irodalmi adattal! | |
| + | |||
| + | ===Az erősítőből kapott jel vizsgálata=== | ||
| + | |||
Kössük az oszcilloszkópot az erősítő kimenetére és keressük meg a jelet. A Coarse Gaint a legalacsonyabb értékre vegyük, Fine Gain pedig maradjon egységnyi erősítésen. Keressük meg a legmagasabb jelet eredményező jelformálási időt! Figyeljük meg, hogy hogyan függ össze eredeti jel és az erősített jel magassága különböző erősítéseknél! Ellenőrizzük, hogy az erősítés változtatásával a jel amplitúdó valóban lineárisan változik. | Kössük az oszcilloszkópot az erősítő kimenetére és keressük meg a jelet. A Coarse Gaint a legalacsonyabb értékre vegyük, Fine Gain pedig maradjon egységnyi erősítésen. Keressük meg a legmagasabb jelet eredményező jelformálási időt! Figyeljük meg, hogy hogyan függ össze eredeti jel és az erősített jel magassága különböző erősítéseknél! Ellenőrizzük, hogy az erősítés változtatásával a jel amplitúdó valóban lineárisan változik. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Glenn F. Knoll: Radiation Detection and Measurement; John Wiley and Sons, New York, (2000) | + | ===A spektrum vizsgálata sokcsatornás analizátoron=== |
| − | Bódizs Dénes: Atommagsugárzások méréstechnikái; Typotex, Budapest, (2006) | + | |
| + | Figyeljük meg a Genie2000-ben kialakuló spektrumot. Magyarázzuk meg a spektrumon látható csúcsokat. A mérésvezető segítségével vegyünk fel két további spektrumot: először úgy, hogy a detektort a levegőben tartjuk, a forrást pedig csipesszel alatta. Utána a forrást közvetlenül a padló felett tartsuk és fölötte a detektort. Milyen különbségeket látunk a három esetben? Mentsük el mindhárom spektrumot és a jegyzőkönyvben magyarázzuk meg a különbségeket. A spektrumból határozzuk meg a <sup>137</sup>Cs csúcsához tartozó félérték-szélességet. Hogyan viszonyul ez a félvezető detektoroknál tapasztaltakhoz? | ||
| + | |||
| + | ===A fotoelektron-sokszorozó erősítésének vizsgálata=== | ||
| + | |||
| + | Határozzuk meg a detektorból kapott feszültségjel amplitúdóját (V<sub>jel</sub>) a <sup>137</sup>Cs teljesenergia csúcsára a tápfeszültség (V<sub>táp</sub>) függvényében 700 V-tól 1000 V-ig 50 V-os lépésekben. Elegendő, ha az analizátoron határozzuk meg a csúcshoz tartozó csatornaszámhoz és a V<sub>jel</sub>-et a 4.1-ben megmért értékhez arányítjuk az ahhoz tartozó csatornaszám függvényében. A mérés során szüksége lehet az erősítés változtatására, ezt is vegyük figyelemben. A kapott pontokra illesszünk V<sub>jel</sub>=aV<sub>táp</sub><sup>b</sup> függvényt, hogy meghatározzuk, hogy a PMT erősítése milyen hatvány szerint függ a tápfeszültségtől. | ||
| + | |||
| + | ===Spektrum felvétele egycsatornás analizátorral=== | ||
| + | |||
| + | Az erősítő kimenetét kössük az egycsatornás analizátor bemenetére. Az analizátor kimenetét pedig a számláló bemenetére. Az egycsatornás analizátoron (az ún. aszimetrikus ablak üzemmódban) egy potméterrel lehet állítani az ablak alsó szintjét 10 teljes fordulattal 0 és 10 V között. Egy másik potméter pedig az ablak szélességét állítja 10 fordulattal 0 és 1 V között. Először 1 V-os ablakkal "térképezzük fel" a spektrumot, keressük meg a teljesenergia-csúcsot, majd 0,1 V-os ablakkal vegyük fel a csúcsot részletesen. Határozzuk meg a csúcshoz tartozó feszültséget és vessük össze az oszcilloszkópon mért értékkel. | ||
| + | |||
| + | ===béta- és gamma-mérőfejek összehasonlítása=== | ||
| + | |||
| + | A csatlakozó egység másik bemenetére csatlakoztassunk egy béta-mérőfejet (ehhez először tekerjük le 0-ra a tápfeszültséget és kapcsoljuk ki). Vegyük fel a <sup>137</sup>Cs spektrumát a béta-mérőfejjel, majd a <sup>90</sup>Sr spektrumát a béta- és a gamma-mérőfejjel. A spektrumokat mentsük el, és a jegyzőkönyvben magyarázzuk meg miben különböznek. | ||
| + | |||
| + | ==IRODALOM== | ||
| + | |||
| + | * Glenn F. Knoll: Radiation Detection and Measurement; John Wiley and Sons, New York, (2000) | ||
| + | * Bódizs Dénes: Atommagsugárzások méréstechnikái; Typotex, Budapest, (2006) | ||
| + | |||
| + | ==Külső hivatkozások== | ||
| + | |||
| + | A Szcintillációs detektorok laborjegyzet forrása elérhető a [http://www.reak.bme.hu/uploads/media/02_szcintillacios_detektorok_SzM.pdf] linken: | ||
A lap jelenlegi, 2013. augusztus 6., 18:13-kori változata
BEVEZETÉS
Az egyik legrégibb nukleáris detektortípus a szcintillációs detektor. Az első szcintillációs számlálók üveglapra szórt cinkszulfid (ZnS) porból álltak, amelyen mikroszkóppal figyelték a radioaktív sugárzások okozta felvillanásokat. Tömeges elterjedésüket a nagy fényhozamú és hatásfokú szcintillátorok felfedezése, valamint a nagy érzékenységű fotoelektron-sokszorozók kifejlesztése tette lehetővé. Megjelenésük óta beszélhetünk gamma-spektroszkópiáról. Spektroszkópiai célokra ma már jellemzőbb a félvezető detektorok használata, de szcintillációs detektorokat továbbra is számtalan célra alkalmaznak.
A MÉRÉS ELVE
Szcintillációs detektorok
A szcintilláló anyagok töltött részecskék mozgási energiáját fényfelvillanássá alakítják át. Fontos tulajdonságuk, hogy az ionizáló részecskék energiájával arányos a felvillanás intenzitása, tehát spektroszkópiai célra is használhatók. A sugárzásnak fényenergiává való átalakítása közvetlenül valósul meg gyors töltött részecskék (pl.: protonok, alfa-részecskék és elektronok) esetében. Az elektromosan semleges gamma-fotonokból álló gamma-sugárzás hatására azonban közvetlenül nem keletkeznek detektálható fényjelek. Ezért a gamma-sugárzás detektálása a különböző folyamatok során (fotoeffektus, Compton-szórás, párkeltés) az általa keltett elektronok révén lehetséges.
A szcintillációs detektor két fő részből áll:
- Szcintillátor: az ionizáló sugárzás hatására fényvillanásokat produkál. Lehet szilárd, folyadék vagy gáz.
- Fotoelektromos sokszorozó (photomultiplier): a szcintillátorhoz optikailag csatolt fotoelektromos eszköz, amely a fényjelet elektromos jellé alakítja és felerősíti. A katódjára jutott fényimpulzus intenzitásával arányos nagyságú elektromos impulzust szolgáltat. Újabb alkalmazásokban időnként fotodióda helyettesíti.
Szcintillátorok
Aktivált szervetlen kristályok
Az aktivált szervetlen kristályokban lezajló szcintillációs folyamat az elektronszerkezet sávelméletével magyarázható. Ismeretes, hogy különálló atomok elektronhéjain (például gázban) az elektronok csak diszkrét energiaértékeket vehetnek fel. Szilárd anyagokban (kristályokban) a szomszédos atomok kölcsönhatására ezek a diszkrét energianívók felhasadnak és sávok jönnek létre, mivel több elektron nem tölthet be azonos állapotot. Kristályos anyagokban az atommagok között kialakuló potenciálgátnál nagyobb energiával rendelkező sávokon ott elhelyezkedő elektronok már nem az atommaghoz, hanem az egész rácshoz vannak kötve. Ha egy ilyen külső sáv csak részben betöltött, akkor az elektronok a kristályrácsban vándorolhatnak, tehát az anyag vezető és a sávot vezetési sávnak nevezzük. Ha azonban a sávban minden energianívó betöltött (töltött sáv), akkor az anyag szigetelő. A töltött sáv és a (szigetelőkben betöltetlen) vezetési sáv között az ún. tiltott sáv helyezkedik el, amelynek szélessége Eg szigetelőkben legalább 3 eV.
A szervetlen szcintillátor kristályok átlátszó, szigetelő anyagok, melyekben az ionizáló részecske gerjesztésének hatására elektronok jutnak a töltött sávból a vezetési sávba, elektron-lyuk párokat hozva létre a töltött és a vezetési sávban. Az elektron foton kibocsátás mellett visszajuthat a vezetési sávba (rekombináció), azonban ez pont a tiltott sáv energiájának megfelelő energia kibocsátással jár, így az a kristályban el is nyelődik. Ahhoz hogy a keletkező foton kijusson, szennyező (aktivátor) anyagra van szükség a kristályban. Megfelelő szennyezők ugyanis olyan módon perturbálhatják a kristály rácsszerkezetét, hogy lokálisan újabb energianívók jelennek meg a vezetési sáv alatt, valamint a töltött sáv fölött, vagyis a tiltott sáv leszűkül. Ilyen esetben az elektron-lyuk párok a kristályban vándorolva könnyen egy ilyen szennyezőnél köthetnek ki, mert ez energetikailag kedvezőbb. Ezért a legerjesztődés során is a tiltott sáv szélességénél kisebb energiájú foton bocsátódik ki, melyre a kristály csak korlátozottan elnyelő, így kijut a kristályból. Egy másik lehetséges folyamatban, az elektron-lyuk pár egy gyengén kötött rendszert, ún. exitont alkot. Ennek az energiaszintje szintén kisebb, mint Eg és bomlásakor látható fényt bocsát ki. Tiszta kristályban exitonok csak alacsony hőmérsékleten jöhetnek létre, szobahőmérsékleten ehhez a folyamathoz is aktivátorra van szükség.
Az ionizáló részecske 10-9 s-on belül létrehozza az elektron-lyuk párokat, ezután azonban a fotonok kibocsátása a fenti folyamatokra jellemző hosszabb időskálán történik. Ezért a fénykibocsátás intenzitásának időbeli alakulása egy exponenciális ( ) időállandóval írható le:
) időállandóval írható le:
![\[I(t)=I_{0}\mathrm{e}^{-\frac{t}{\tau}} \]](/images/math/0/0/3/003bf403671fe66fab1c1c3006ee04c1.png) |
(1) |
Előfordulhat, hogy az elektron-lyuk pár olyan állapotokba kerül (ún. elektroncsapda), amelyek között nincsen megengedett átmenet, így a rekombináció nem jöhet létre. Az ilyen metastabil állapotokból a hőmozgás hatására bekövetkező kis gerjesztés után tudnak kikerülni, és így történhet meg a legerjesztődés. Ez bizonyos időbe telik, ezért az ilyen kristályokban egy sokkal lassabban bomló komponens is megjelenhet a fénykibocsátásban (utánvilágítási idő, "afterglow"). Ezt okozhatják rácshibák, vagy nem kívánt szennyezők is.
A NaI(Tl) szcintillátor
1948-ban fedezték fel, hogy a kb. 0.1 mol% tallium-jodiddal (TlI) szennyezett NaI oldatból növesztett egykristályok minden akkor ismert szcintillátornál nagyobb intenzitású fénykibocsátást produkálnak. Egyszerű és olcsó előállíthatósága és megmunkálhatósága miatt a mai napig a legáltalánosabban alkalmazott szcintillátor anyag. A szcintillációs folyamatok alapos megértéséhez tekintsük át mi történik egy NaI kristályban egy 1 MeV-os töltött részecske (pl. Compton-szórásban meglökött elektron) hatására. A töltött részecske lassulása során leadott energia részben a kristályrácsnak adódik át (fonon keltés), részben pedig ionizációra, vagyis elektron-lyuk párok létrehozására fordítódik. Az ionizáció hatásfokára jellemző, hogy az egy keletkező elektron-lyuk párra eső leadott energiát a tiltott sáv szélességének háromszorosával lehet becsülni. Ez a NaI kristályban kb. 20 eV, így a keletkező elektron(e-)-lyuk(h+) párok száma kb. 50.000. Ezek több folyamaton keresztül juthatnak el a foton kibocsátásig. Mivel az e- transzportja a kristályban nagyságrendileg gyorsabb, ezért általában először az e- fogódik be egy Tl+ ion által képzett lumineszcens centrumban Tl0 atomot hozva létre. A Coulomb-potenciál hatására később a lassabban mozgó h+ is befogódik ugyanitt és egy gerjesztett (Tl+)* iont keletkezik. Az is előfordulhat azonban, hogy a h+ egy másik Tl+-nál fogódik be Tl++-t hozva létre. Ebben az esetben a rekombináció akkor jön létre, ha az e- a termikus gerjesztésnek köszönhetően kilép a Tl0 csapdából és eljut a Tl++ ionig. Mivel a NaI(Tl)-ban szobahőmérsékleten a Tl0 állapot élettartama összevethető lyuk vándorlásához szükséges idővel ez a két folyamat azonos időskálán zajlik le.
A gerjesztett (Tl+)* ion sugárzásos legerjesztődése szintén viszonylag lassabb folyamat, mert a közvetlen átmenet nem megengedett, ezért szintén termikus gerjesztés útján egy közbenső állapoton keresztül zajlik a fentiekhez hasonló időskálán. Ezen a folyamatok összessége adja a NaI(Tl) kristály viszonylag hosszú,  =230 ns-os időállandóját.
=230 ns-os időállandóját.
A mérések szerint 1 MeV leadott energia hatására 38.000 db, a Tl gerjesztési nívójának megfelelő, kb. 3 eV-os (415 nm) foton lép ki a kristályból. Az elektron-lyuk párok lumineszcens centrumban való befogódásának és sugárzásos legerjesztődésének hatásfoka tehát elég magas, csak kevés elektron-lyuk pár rekombinálódik kisugárzásmentes átmeneten keresztül, vagy a kristályban elnyelődő UV-fotont kibocsátva (ezeket a foton kibocsátás nélküli folyamatokat hívjuk kioltásnak, „quenching”-nek). Összességében azonban csak a leadott energia kb. 12%-a távozik fotonok formájában, mivel – mint láttuk – a töltött részecske által leadott energiának csak kb. harmada fordítódik elektron-lyuk párok létrehozására, továbbá a lumineszcens centrumokban történő rekombinációnál kibocsátott foton energiája kevesebb, mint fele a tiltott sáv szélességének.
Szerves szcintillátorok
A szerves szcintillátorok működése az összetett molekulák különböző konfigurációi közötti átmeneteken alapul. Az ionizáló sugárzás itt a molekulákat gerjeszti, egy magasabb energiaszintű konfigurációba juttatva. A konfigurációk között jelentős (3-4 eV) különbség lehet, amely a termikus gerjesztés hatására nem áthidalható. Az egyes konfigurációkhoz viszont tized eV nagyságrendű vibrációs gerjesztett állapotok tartoznak. Az ionizáló sugárzás által okozott gerjesztés során általában a magasabb energiaszintű konfiguráció valamelyik vibrációs gerjesztett állapota jön létre. Ez először hőkibocsátással a konfiguráció alapállapotába bomlik, majd onnan fotonkibocsátással az alapkonfiguráció egyik gerjesztett állapotába. Így a kibocsátott foton hullámhossza nagyobb, mint az adott anyagra jellemző gerjesztési hullámhossz, és nem nyelődik el.
A szerves szcintillátoroknak a fentiekből fakadó fontos tulajdonsága, hogy szcintillációs tulajdonságuk csak a molekulához kötődik és bármilyen halmazállapotban, anyagi minőségben fennáll. Így előfordulhatnak kristályos formában, polimerizálva plasztikként vagy oldatban. Az ún. folyadék szcintillátorok speciális alkalmazása, hogy a radioaktív mintát feloldva benne alfa- és béta-sugárzás nagy hatásfokú mérésére alkalmas.
A szerves szcintillátorok előnye a szervetlenekhez képest, hogy időállandójuk sokkal rövidebb, néhány ns körüli. Hátrányuk, hogy fényhozamuk kb. egy nagyságrenddel kisebb, valamint hogy kisebb sűrűségük és az alkotóelemek alacsonyabb rendszáma miatt gamma-sugárzás detektálására kisebb a hatásfokuk.
Fotoelektron-sokszorozók (photo-multiplier tube, PMT)
A fotoelektron-sokszorozók két elektronemissziós jelenségen alapulnak:
- Fotoeffektus: fény hatására fémekből, ötvözetekből elektronok lépnek ki. Ezeket fotoelektronoknak nevezzük. A folyamatban a fénykvantum h
 energiát ad át az elektronnak, amelynek fedeznie az elektron eljutását a felületre és a kilépési munkát.
energiát ad át az elektronnak, amelynek fedeznie az elektron eljutását a felületre és a kilépési munkát.
- Szekunder emisszió: fémekre, ötvözetekre becsapódó elektronok újabb elektronokat váltanak ki, melyeknek száma a becsapódó elektronok energiájától függ. Ezek a szekunder elektronok.
A fotoeffektus a fotoelektron-sokszorozó cső fotokatódján játszódik le. Annak érdekében, hogy a szcintillációs kristályban keletkező foton a fotokatódra jusson, a kristály és a fotokatód között – a külső fény kizárásával – optikai csatolást kell létesíteni. Ez legtöbb esetben kontakt csatolás, ahol az illesztés olyan olajjal (illetve ragasztással) történik, melynek az optikai törésmutatója az üveg törésmutatójához hasonló. Megfelelő optikai csatolással és a kristályt körülvevő tükröző felületek segítségével garantálható, hogy a fotonon köze 100%-a a fotokatódra jusson. Fotokatódnak lehetővé kell tennie, hogy a keletkező fotoelektronok kilépjenek a vákuumba. Azonban az elektron az anyagban nagyon gyorsan veszít az energiájából és a maximális mélység, ahonnan egy fotoelektron még ki tud jutni fémekben mindössze néhány nm, félvezetőkben pedig kb. 25nm. Tehát a fotokatód csak egy nagyon vékony réteg lehet, amelyet a gyakorlatban a PMT-t magában foglaló vákuumcső belső felületére visznek fel. Ilyen vékony réteg viszont még áttetsző, a beérkező fénynek kevesebb, mint felét nyeli el. Így nem meglepő, hogy a fotokatódok ún. kvantum hatásfoka (vagyis a kilépő fotoelektronok és a beérkező fotonok aránya) csak 20-30% körüli. Tipikus fotókatód anyagok az ún. multialkáli anyagok, mint pl.: KCs, Na2KSb, stb. A fotokatódból kilépő fotoelektronokat gyorsító feszültség juttatja a szekunder emissziós felületre (dinódára). A becsapódó elektron energiája fedezi az elektronok gerjesztéséhez szükséges 2-3 eV energiát, vagyis a tipikusan 100 V körüli feszültség akár 30 gerjesztett elektront is eredményezhet. Ezek azonban gyakorlatilag izotróp irányeloszlással rendelkeznek és még a felszín felé haladóknak is csak töredéke tud kilépni a felületről. Így ezen a feszültségszinten tipikusan 4-6 szekunder elektron lép ki a dinóda felületéről. Ezeket hasonló gyorsító feszültség segítségével a következő dinóda fokozat felé irányítjuk. Fontos, hogy a szekunder elektronok a dinódának ugyanazon az oldalán lépnek ki, mint ahol a primer elektron belép. Ezért a dinóda fokozatok speciális kialakítása és elrendezése szükséges, hogy a kilépő elektronokat a következő dinóda fokozat felé irányíthassuk. Ha a szekunder elektronok (átlagos) számát d-vel jelöljük, akkor nyilvánvaló, hogy n db dinóda fokozat alkalmazása esetén egy fotoelektronból M=dn elektron jut az anódra. M a fotoelektron-sokszorozó erősítési tényezője. Mivel d függ a primer elektron energiájától, M is függ a fotoelektron sokszorozóra kapcsolt V tápfeszültségtől. Ha feltételezzük, hogy a tápfeszültséget egyenletesen osztjuk fel a dinóda fokozatok között, és hogy a d függése a gyorsító feszültségtől lineáris, akkor M is az n-edik hatvány szerint függne V-től. Valójában a d valamilyen tört hatvány szerint függ a feszültségtől így M ~ V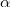 , ahol
, ahol 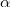 az adott cső fontos paramétere és általában 6 és 9 között van.
az adott cső fontos paramétere és általában 6 és 9 között van.
A fotomultiplier fő részei tehát, amelyeket természetesen vákuumcsőben kell elhelyezni (ld. 2. ábra):
- fotokatód
- dinódák
- anód.
A szcintillációs detektorból kapott elektromos jel
Folytatva az A NaI(TI) szcintillátor pontban megkezdett példát, ha feltételezzük, hogy a NaI(Tl) szcintillátorban keletkezett 38.000 db foton mind a fotokatódra jut, akkor kb. 25 %-os kvantumhatásokkal számolva mintegy 10.000 db fotoelektron keletkezik. d=5 szekunder elektron keltés és n=10 dinóda fokozat esetén a fotoelektron-sokszorozó erősítése 107, vagyis 1011 elektron ér az anódra. Az így kapott összesen Q=1011e töltésmennyiség a NaI(Tl) kristály  időállandójának megfelelően exponenciálisan oszlik el, tehát az anódon megjelenő áram erőssége szintén exponenciálisan cseng le:
időállandójának megfelelően exponenciálisan oszlik el, tehát az anódon megjelenő áram erőssége szintén exponenciálisan cseng le:
![\[i(t)=\frac{Q}{\tau}e^\frac{t}{\tau} \]](/images/math/8/8/3/88363d7e2a105b86b8ba48deba5a99ac.png) |
(2) |
Tehát a fenti példában i(0)=1011x1,6x10-19 C / 230 ns 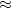 69 mA, ami már egy jól mérhető jel. Az anódra azonban kb. 1000 V-nak megfelelő feszültséget kapcsolunk ezért egy megfelelően méretezett kicsatoló kondenzátor segítségével választjuk le a gyorsan változó jelet az egyenáramú tápfeszültségtől. A V(t) feszültség jel alakját a 4. ábra szerinti egyszerű áramköri modell segítségével érthetjük meg. A C kapacitás az anódhoz csatlakozó áramköri elemek szórt kapacitása az R ellenállás pedig a vezeték és csatlakozó ellenállások mellett az áramkör időállandójának állításához használt megfelelően méretezett ellenállás. V(t)-re így a következő differenciál egyenletet kapjuk:
69 mA, ami már egy jól mérhető jel. Az anódra azonban kb. 1000 V-nak megfelelő feszültséget kapcsolunk ezért egy megfelelően méretezett kicsatoló kondenzátor segítségével választjuk le a gyorsan változó jelet az egyenáramú tápfeszültségtől. A V(t) feszültség jel alakját a 4. ábra szerinti egyszerű áramköri modell segítségével érthetjük meg. A C kapacitás az anódhoz csatlakozó áramköri elemek szórt kapacitása az R ellenállás pedig a vezeték és csatlakozó ellenállások mellett az áramkör időállandójának állításához használt megfelelően méretezett ellenállás. V(t)-re így a következő differenciál egyenletet kapjuk:
![\[i(t)=C\frac{d}{dt}V(t)+\frac{V(t)}{R} \]](/images/math/d/f/6/df625b16aff425b87bd39e5e3818ed59.png) |
(3) |
(2)-t behelyettesítve egy inhomogén elsőrendű differenciál-egyenletet kapunk, amelynek a megoldása a következő alakban adódik:
![\[V(t)={\frac{RC\tau}{RC-\tau}}\frac{Q}{\tau{C}}\bigg(e^{-\frac{t}{{RC}}}-e^{-\frac{t}{{\tau}}}\bigg) \]](/images/math/5/e/0/5e0cfc13809e5655802fa3378f484b3d.png) |
(4) |
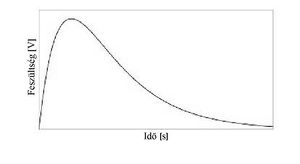
Vagyis a jel egy rövidebb időállandó szerinti emelkedő és hosszabb időállandó szerinti lecsengő szakaszból áll (ld. 5. ábra). Az R és C értékek megfelelő megválasztásával két eset lehetséges:
- RC<<
 : Ebben az esetben a jel lecsengését a szcintillátor időállandója határozza meg, így a lehető legrövidebb jel érhető el. Előnyös nagy számlálási sebességnél, a holtidő csökkentésére, de jel amplitúdója kicsi, ami az energia felbontóképességet rontja.
: Ebben az esetben a jel lecsengését a szcintillátor időállandója határozza meg, így a lehető legrövidebb jel érhető el. Előnyös nagy számlálási sebességnél, a holtidő csökkentésére, de jel amplitúdója kicsi, ami az energia felbontóképességet rontja.
-
 <<RC : A jel lecsengését az RC időállandó határozza meg. A jel amplitúdója közel lesz a maximális Q/C értékhez, jelalak hosszabb. A gyakorlatban és jelen mérésben is inkább ezt a beállítást alkalmazzuk.
<<RC : A jel lecsengését az RC időállandó határozza meg. A jel amplitúdója közel lesz a maximális Q/C értékhez, jelalak hosszabb. A gyakorlatban és jelen mérésben is inkább ezt a beállítást alkalmazzuk.
A második esetben C értékét úgy szokták választani, hogy a fenti 1 MeV-es elektron 1-2 V közötti jel amplitúdót produkáljon.
A szcintillációs detektorok energia-felbontóképessége
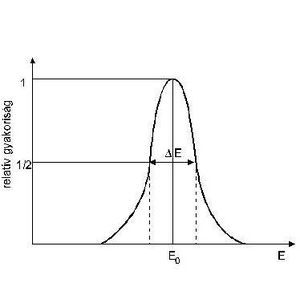
A spektroszkópiai célokra használt detektorok egyik legfontosabb paramétere az energia-felbontóképesség, amely arra nézve ad felvilágosítást, hogy egymáshoz közel eső energiájú részecskéket mennyire tud a detektálás során megkülönböztetni. A detektorban leadott energia feszültségjel-amplitúdóvá konvertálása során egymást követő folyamatok ugyanis mind statisztikus jellegűek, így egy adott energiához egy jellemzően Gauss-eloszlással rendelkező kiszélesedett csúcs tartozik. A csúcs szélességét a csúcs maximumának feléhez tartozó pontok távolságával, a 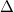 E félérték-szélességel (Full Width at Half Maximum, FWHM) szokás jellemezni. A gyakorlatban gyakran használjuk a relatív félérték-szélességet, amelyet a következőképpen definiálunk:
E félérték-szélességel (Full Width at Half Maximum, FWHM) szokás jellemezni. A gyakorlatban gyakran használjuk a relatív félérték-szélességet, amelyet a következőképpen definiálunk:
![\[f=\frac{\Delta{E}}{E_{0}} \]](/images/math/f/1/2/f12cdbee1461af5cfa7f2b51e30e4e41.png) |
(5) |
A szcintillációs detektorok fent ismertetett valamennyi folyamatát jó közelítéssel Poisson folyamatnak lehet tekinteni, vagyis a keletkezett részecskék (elektron-lyuk párok, fotonok, fotoelektronok, szekunder elektronok) számának szórását a várható érték négyzetgyöke adja meg. Így egy egyszerű alsó becslést adhatunk a kapott jel amplitúdó relatív szórására, ha megkeressük a legnagyobb relatív szórást a folyamatban. Az A szcintillációs detektorból kapott elektromos jel pontban folytatott példában láttuk, hogy a fotoelektronok száma mindössze 10000, tehát itt 1%-os relatív szórás jelentkezik. Gauss-eloszlást feltételezve ez 23,5 keV-os félérték-szélességet okoz az 1 MeV-os csúcsban, vagyis 2,35 %-os relatív félérték-szélességet. Ez az alsó becslés már jelzi, hogy a foton-elektron konverzió rossz hatásfoka miatt a szcintillációs detektorok felbontóképességben nem tudják felvenni a versenyt a félvezető detektorokkal. Valójában a NaI(Tl) detektorok felbontóképessége ezen az energián 5% körüli.
Az egycsatornás analizátor (Single Channel Analyzer, SCA) működési elve
A gamma-spektroszkópiában alkalmazott sokcsatornás analizátorok őse az ún. egycsatornás analizátor, vagy differenciál-diszkriminátor. A differenciál-diszkriminátor (DD) olyan berendezés, amely a beérkező jelsorozatból csak azokat a jeleket engedi át (vagyis csak azokra a jelekre szolgáltat kimenőjelet a számláló felé), amelyek amplitúdója két meghatározott feszültség közé esik. Ezt a feszültségintervallumot a diszkriminátor "ablaká"-nak szoktuk nevezni. Jóllehet a diszkriminátort feszültségben állítjuk be, ehelyett mindig részecskeenergiában gondolkodunk, és a diszkriminátor "ablaká"-t is energiára számoljuk át: az "ablak" így az E és E+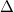 E közé eső energiájú részecskéket jelenti (ld. 7. ábra). A DD kimenetére egy számlálóegységet csatlakoztatunk, amellyel megmérhető a beütésszám egy adott energia-intervallumban.
E közé eső energiájú részecskéket jelenti (ld. 7. ábra). A DD kimenetére egy számlálóegységet csatlakoztatunk, amellyel megmérhető a beütésszám egy adott energia-intervallumban.
A DD a sokcsatornás analizátorok megjelenésével sem tűnt el, mert nem csak spektroszkópiai célokra használatos. Számtalan mérési elrendezésben szükséges, hogy csak egy meghatározott energiatartományban (pl. egy gamma-csúcs) számláljuk a beütéseket. DD használhatunk a háttér kiszűrésére, gamma-vonalak közötti koincidencia mérésére stb.
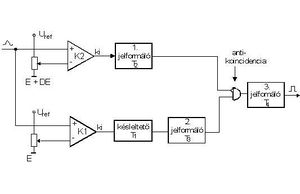
A 11. ábrán az egycsatornás analizátor (differenciáldiszkriminátor, DD) blokkdiagramja látható. Az E alapszintet a Kl komparátoron az E potenciométerrel, a felső E+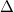 E szintet pedig a K2 komparátoron az E+
E szintet pedig a K2 komparátoron az E+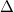 E potenciométerrel állítjuk be.
E potenciométerrel állítjuk be.
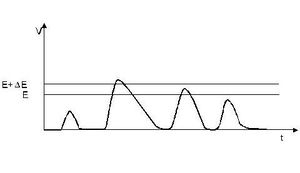
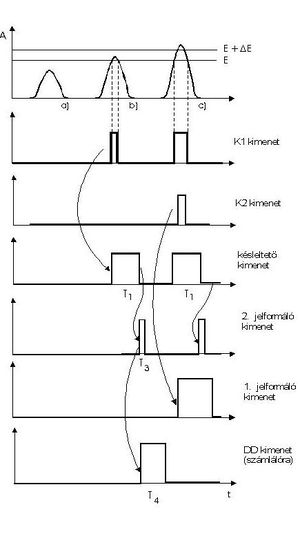
Most belátjuk, hogy a 9. ábrán látható jelsorozatból csak a "b" jel hatására jelenik meg jel az antikoincidencia egység kimenetén.
- Az "a" jel amplitúdója nem éri el az E alapszintet, sem a K1, sem a K2 komparátor kimenetén nincs jel, így az antikoincidencia egység nem ad kimenő jelet. Az antikoincidencia egység akkor ad kimenő jelet, ha a két bemenete közül csak az egyiken van jel. Ez azt jelenti, hogy nincs kimenő jel, ha: (1) egyik bemeneten sincs jel, (2) mindkét bemeneten van jel.
- A "b" jel amplitúdója meghaladja az E értéket, de nem éri el az E+
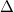 E szintet. Ekkor a K1 komparátor kimenő jele a T1 késleltetőn keresztül indítja a 2. jelformálót, melynek T3 kimenete az antikoincidencia fokozatra kerül. (A késleltető szükségességéről később lesz szó.) Ugyanekkor a K2 komparátor felől nem érkezik jel az antikoincidencia fokozatra, ennek kimenő impulzusa indítja a 3. jelformálót, melynek T4 kimenete egyben a DD uniformizált kimenő jele (számláló felé).
E szintet. Ekkor a K1 komparátor kimenő jele a T1 késleltetőn keresztül indítja a 2. jelformálót, melynek T3 kimenete az antikoincidencia fokozatra kerül. (A késleltető szükségességéről később lesz szó.) Ugyanekkor a K2 komparátor felől nem érkezik jel az antikoincidencia fokozatra, ennek kimenő impulzusa indítja a 3. jelformálót, melynek T4 kimenete egyben a DD uniformizált kimenő jele (számláló felé).
- A "c" jel amplitúdója meghaladja az E+
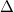 E komparátoron beállított szintet. Ebben az esetben mind K1, mind a K2 komparátor kimenetén megjelenik jel, tehát az antikoincidencia egység kimenetén nem kapunk jelet, ha a két komparátor kimenő jele egyszerre érkezik. A 12. ábrán látható, hogy az E+
E komparátoron beállított szintet. Ebben az esetben mind K1, mind a K2 komparátor kimenetén megjelenik jel, tehát az antikoincidencia egység kimenetén nem kapunk jelet, ha a két komparátor kimenő jele egyszerre érkezik. A 12. ábrán látható, hogy az E+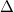 E szintet a "c" jel később lépi át, mint az E szintet. Emiatt az antikoincidencia egység bemenetére nem egyszerre érkezik a két komparátor jele, tehát az megszólal, viszont a DD működési elve ennek az ellenkezőjét kívánja. Emiatt van szükség a T1 késleltetőre: biztosítja a jelek egyidejű megérkezését.
E szintet a "c" jel később lépi át, mint az E szintet. Emiatt az antikoincidencia egység bemenetére nem egyszerre érkezik a két komparátor jele, tehát az megszólal, viszont a DD működési elve ennek az ellenkezőjét kívánja. Emiatt van szükség a T1 késleltetőre: biztosítja a jelek egyidejű megérkezését.
Fontos megjegyezni, hogy a DD kimenetén már szabványos 5V magasságú négyszögjel jelenik meg.
A MÉRÉSI ELRENDEZÉS
A méréshez használt eszközök:
- 137Cs és 90Sr etalon források
- ólomtorony mintatartóval
- szcintillációs mérőfej gamma- és béta-sugárzás mérésére
- NIM (Nuclear Instrumentation Module) bin a következő egységekkel
- szcintillációs mérőfej csatlakozó modul
- nagyfeszültségű tápegység (High Voltage Supply)
- spektroszkópiai erősítő (Amplifier)
- egycsatornás analizátor (SCA)
- számláló, időzítő egység (Counter Timer)
- Multiport-II sokcsatornás analizátor (MCA)
- számítógép GENIE-2000 analizátor szoftverrel
- oszcilloszkóp
Az elrendezés összeállítása előtt meg kell győződni róla, hogy a tápegység nagyfeszültséget állító potmétere 0-ra van tekerve és a tápegység ki van kapcsolva. A mérés megkezdése előtt a 137Cs mintát el kell helyezni az ólomtoronyban, a mintatartó 6. polcán. A γ-mérőfejet felülről, óvatosan az ólomtoronyban kiképzett helyére csúsztatjuk. A 7+1 pólusú csatlakozó dugaszt a NIM binben található csatlakozó modulba kell dugni. Ezen az egységen keresztül kapja a mérőfej a tápfeszültséget és innen kapjuk a mért jelet is a BNC csatlakozón keresztül. A jelet BNC kábellel az erősítő bemenetére kötjük. Az erősítő unipoláris kimenetét az egycsatornás analizátor bementére, valamint (egy elosztó segítségével) a Multiport-II bemenetére. Az egycsatornás analizátor kimenetét a számláló egység bemenetére kötjük. A számítógép egy USB kábellel csatlakozik a Multiport-II-höz. A számítógépen a Gamma Acqusition programot kell elindítani, majd a File / Open datasource... menüben a Source: Detector jelölése után lehet a megfelelő egységet a számítógéphez rendelni.
MÉRÉSI FELADATOK
A mérések során tett megfigyeléseket rögzítsük a jegyzőkönyvben. A feladatokban feltett kérdésekre adott rövid válaszok feltétlenül szerepeljenek a jegyzőkönyvben. A mért adatokat rögzíteni és részletesen kiértékelni ott kell, ahol ezt a feladat külön kéri.
A szintillációs detektor jelének vizsgálata
A tápfeszültséget lassan növeljük 750 V-ra. A szcintillációs detektor jelét kössük közvetlenül az oszcilloszkópra. A feszültség- és időosztás, valamint a trigger-szint állításával keressük meg az 5. ábra szerinti jelet. Milyen a jel polaritása és miért?
Az oszcilloszkóp kurzorai segítségével mérjük meg a 137Cs 662 keV-os csúcsához tartozó jel magasságát. Vegyünk fel 3-4 pontot az exponenciálisan lecsengő szakaszon és illesztéssel határozzuk meg az RC időállandót! Mérjük meg a maximumhelyhez tartozó időt! (3)-ból vezessük le a maximumhely képletét és fejezzük ki a kristály  időállandóját. A kapott transzendens egyenlet numerikus megoldásával határozzuk meg az időállandót és az eredményt vessük össze az irodalmi adattal!
időállandóját. A kapott transzendens egyenlet numerikus megoldásával határozzuk meg az időállandót és az eredményt vessük össze az irodalmi adattal!
Az erősítőből kapott jel vizsgálata
Kössük az oszcilloszkópot az erősítő kimenetére és keressük meg a jelet. A Coarse Gaint a legalacsonyabb értékre vegyük, Fine Gain pedig maradjon egységnyi erősítésen. Keressük meg a legmagasabb jelet eredményező jelformálási időt! Figyeljük meg, hogy hogyan függ össze eredeti jel és az erősített jel magassága különböző erősítéseknél! Ellenőrizzük, hogy az erősítés változtatásával a jel amplitúdó valóban lineárisan változik.
A spektrum vizsgálata sokcsatornás analizátoron
Figyeljük meg a Genie2000-ben kialakuló spektrumot. Magyarázzuk meg a spektrumon látható csúcsokat. A mérésvezető segítségével vegyünk fel két további spektrumot: először úgy, hogy a detektort a levegőben tartjuk, a forrást pedig csipesszel alatta. Utána a forrást közvetlenül a padló felett tartsuk és fölötte a detektort. Milyen különbségeket látunk a három esetben? Mentsük el mindhárom spektrumot és a jegyzőkönyvben magyarázzuk meg a különbségeket. A spektrumból határozzuk meg a 137Cs csúcsához tartozó félérték-szélességet. Hogyan viszonyul ez a félvezető detektoroknál tapasztaltakhoz?
A fotoelektron-sokszorozó erősítésének vizsgálata
Határozzuk meg a detektorból kapott feszültségjel amplitúdóját (Vjel) a 137Cs teljesenergia csúcsára a tápfeszültség (Vtáp) függvényében 700 V-tól 1000 V-ig 50 V-os lépésekben. Elegendő, ha az analizátoron határozzuk meg a csúcshoz tartozó csatornaszámhoz és a Vjel-et a 4.1-ben megmért értékhez arányítjuk az ahhoz tartozó csatornaszám függvényében. A mérés során szüksége lehet az erősítés változtatására, ezt is vegyük figyelemben. A kapott pontokra illesszünk Vjel=aVtápb függvényt, hogy meghatározzuk, hogy a PMT erősítése milyen hatvány szerint függ a tápfeszültségtől.
Spektrum felvétele egycsatornás analizátorral
Az erősítő kimenetét kössük az egycsatornás analizátor bemenetére. Az analizátor kimenetét pedig a számláló bemenetére. Az egycsatornás analizátoron (az ún. aszimetrikus ablak üzemmódban) egy potméterrel lehet állítani az ablak alsó szintjét 10 teljes fordulattal 0 és 10 V között. Egy másik potméter pedig az ablak szélességét állítja 10 fordulattal 0 és 1 V között. Először 1 V-os ablakkal "térképezzük fel" a spektrumot, keressük meg a teljesenergia-csúcsot, majd 0,1 V-os ablakkal vegyük fel a csúcsot részletesen. Határozzuk meg a csúcshoz tartozó feszültséget és vessük össze az oszcilloszkópon mért értékkel.
béta- és gamma-mérőfejek összehasonlítása
A csatlakozó egység másik bemenetére csatlakoztassunk egy béta-mérőfejet (ehhez először tekerjük le 0-ra a tápfeszültséget és kapcsoljuk ki). Vegyük fel a 137Cs spektrumát a béta-mérőfejjel, majd a 90Sr spektrumát a béta- és a gamma-mérőfejjel. A spektrumokat mentsük el, és a jegyzőkönyvben magyarázzuk meg miben különböznek.
IRODALOM
- Glenn F. Knoll: Radiation Detection and Measurement; John Wiley and Sons, New York, (2000)
- Bódizs Dénes: Atommagsugárzások méréstechnikái; Typotex, Budapest, (2006)
Külső hivatkozások
A Szcintillációs detektorok laborjegyzet forrása elérhető a [1] linken: