„Nanoszerkezetek előállítási és vizsgálati technikái” változatai közötti eltérés

A Fizipedia wikiből
(→‎Nanofabrikálás eszköztára)
(→‎Elektronsugár litográfia (E-beam lithography))
 
(4 szerkesztő 167 közbeeső változata nincs mutatva)
1. sor: 1. sor:
−
== Nanofabrikálás eszköztára ==
+
A nanotechnológia jelentősen hozzájárult az elektronika fejlődéséhez. Gordon E. Moore, az Intel cég egyik alapítója 1965-ben azt a megfigyelését tette közzé, miszerint egy integrált áramkörben lévő tranzisztorok száma két évenként megduplázódik. Ez a megfigyelés egészen napjainkig teljesülni látszik, ennek megfelelően a tranzisztorok mérete szintén exponenciálisan csökkent az elmúlt évtizedekben (1. ábra). Manapság egy tranzisztor aktív tartománya mindössze ~10 nm széles. Ez a méret elméletileg még két nagyságrenddel csökkenthető, amíg elérjük az elképzelhető legkisebb, egyetlen atomból álló tranzisztorokat. A további méretcsökkentés azonban számtalan technológiai problémát vet fel, így a jelenleginél kisebb, vagy más működési elvet követő információtárolási és feldolgozási technológiák kidolgozása világszerte intenzív kutatások tárgyát képezi. Ennek megfelelően a nanofizikai kutatások túlmutatnak az érdekes jelenségek feltérképezésén, és alapvetően hozzájárulnak a jövő technológiáinak kidolgozásához.
−
<wlatex>
+
−
Hogyan készítsünk nanoszerkezeteket, és utána hogyan "nézzük" meg őket?
+
  
−
=== Nanofabrikálás eszköztára ===
+
{|  cellpadding="5" cellspacing="0" align="center"
−
<wlatex>
+
|-
−
* Pásztázó alagútmikroszkóp (STM)
+
| [[Fájl:Moore.png|közép|400px|]]
−
* Atomi erő mikroszkóp (AFM)
+
|-
−
* Pásztázó és transzmissziós elektronmikroszkóp (SEM, TEM)
+
| align="center"|1. ábra. ''Tipikus méretskálák és a DRAM generációk exponenciális méretcsökkenését szemléltető Moore-törvény.''
−
* Elektronsugár litográfia (példa: InAs nanoáramkörök készítése)
+
|}
−
* Fókuszált ionsugár (FIB, He ion microscope)
+
−
* Párologtatási módszerek, molecular beam epitaxy (MBE) (példa: 2DEG készítése)
+
−
* Split gate technika
+
−
* AFM litográfia(példa: Aharonov Bohm gyűrű)
+
−
* Önszerveződő növesztés
+
−
</wlatex>
+
  
−
=== Nanofizikai "objektumok" ===
+
A következőkben rövid betekintést nyújtunk a nanoáramkörök illetve különböző nanoszerkezetek készítésének és vizsgálatának eszköztárába.
−
<wlatex>
+
−
* Kvantum pont-kontaktusok (QPC)(Kvantumvezeték, vezetőképesség kvantálás, Landauer formula, sörét zaj)
+
−
* Kvantum pöttyök (quandum dot)(Coulomb blokád, kinetikus energiaszintek, egy-elektron tranzisztor)
+
−
* Aharonov Bohm gyűrű(interferencia, dekoherencia, Thouless energia)
+
−
* Mach Zehnder interferométer elektronokkal(Quantum Hall élállapotok)
+
−
* Hibrid nanoszerkezetek
+
−
</wlatex>
+
  
−
=== Pásztázó alagútmikroszkóp (Scanning tunneling microscope, STM ===
+
== Pásztázó alagútmikroszkóp (Scanning Tunneling Microscope - STM) ==
 
<wlatex>
 
<wlatex>
−
* Egy 3D piezo mozgató segítségével egy hegyes tűt mozgatunk egy fémes felület fölött.
+
Már az ókori görögök is azt feltételezték, hogy az anyag atomokból épül fel. Ezt a feltételezést a 20. század elején számos kísérlettel sikerült bizonyítani, azonban ahhoz, hogy képet tudjunk készíteni egy anyag felületén lévő atomokról egészen 1981-ig kellett várni, amikor is Gerd Binnig és Heinrich Rohrer megépítették az első pásztázó alagútmikroszkópot. Találmányukért fizikai Nobel-díjat kaptak 1986-ban. Azóta az alagútmikroszkóp széleskörben elterjedt, manapság a nanofizikai kutatások egyik alapvető vizsgálati eszközei közé tartozik.
−
* Konstans feszültségnél a minta és a tű közötti alagútáramot mérjük. XY irányú "pásztázás" közben Z irányban úgy mozgatjuk a tűt, hogy az alagútáram konstans maradjon. A Z(XY) függés a minta felületi topográfiáját adja meg akár atomi felbontással.
+
−
* Akár egy ollóval elvágott PtIr vagy W tűvel is készíthetünk jó STM képet
+
−
* Az STM tű segítségével atomokat tologathatunk a felszínen ("Quantum corral")
+
−
** 48 kört alkotó Fe atom egy Cu felületen. A kör belsejében állóhullámok látszanak.
+
−
** 36 ellipszist alkotó Co atom, + 1 Co atom az egyik fókuszpontban, aminek a hatása a másik fókuszpontban is látszik. (Manoharan et al., in Nature, 2000)
+
−
</wlatex>
+
  
−
=== Atomi erő mikroszkóp (Atomic Force Microscope, AFM)===
+
Működésének elve az alagúteffektuson alapul: egy hegyes tűt nm-es távolságra pozícionálunk a vizsgált minta felületéhez, a tűre feszültséget kapcsolunk, ennek hatására alagútáram folyik a tű és a minta között:
−
<wlatex>
+
−
* Egy 3D piezo mozgató segítségével egy finom cantilever (laprugó) végén levő hegyes tűt mozgatunk a vizsgált felület fölött. A cantilever "meghajlását" általában a cantileverről visszavert lézersugár és egy fotodetektor segítségével mérjük.
+
−
* "Non-contact mode": a cantilevert a minta fölött a sajátfrekvenciája környékén rezgetjük. A minta és a tű közötti erőgradiens hatására a sajátfrekvencia elhangolódik. Az XY szkennelés közben a tűt Z irányban úgy mozgatjuk, hogy a rezgés amplitúdója (v. fázisa) konstans maradjon. A Z(XY) függés megadja a felület topográfiáját, akár atomi felbontással.
+
−
* "Contact mode": a cantilevert folyamatosan a mintához nyomjuk. XY mozgatás közben a Z pozíciót úgy változtatjuk, hogy a cantilever meghajlása (és így a minta és a tű közötti taszító erő) konstans maradjon.
+
−
* AFM-el nem fémes felületek is tanulmányozhatók!
+
−
</wlatex>
+
  
−
=== Pásztázó és transzmissziós elektron mikroszkóp (Scanning electron microscope, SEM / Transmission electron microscope, TEM) ===
+
$$I \propto V_b \cdot \mathrm{Exp}\left\{-A\cdot  d\cdot \sqrt{\Phi} \right\},$$
−
<wlatex>
+
−
* SEM: fókuszált elektronnyalábbal pásztázzuk a mintát, és a visszaszórt elektronokat, másodlagos elektronokat, a keltett röntgen sugárzást v. fényt detektáljuk. 1-5 nm felbontás érhető el. A minta felülete elektromosan vezető kell, hogy legyen a töltésfelhalmozódás elkerülése végett. (Szigetelőkön vékony fémes bevonatot kell létrehozni)
+
−
* TEM: egy elektronsugár egy ultra vékony mintán transzmittálódik, a transzmittált nyaláb képét nagyítás után egy képernyőre / CCD kamerára vetítjük. Akár atomi felbontás is elérhető.
+
−
</wlatex>
+
  
−
=== Elektronsugár litográfia (E-beam lithography) ===
+
ahol $V_b$ a tű és a minta közé kapcsolt feszültség, $d$ a minta-tű távolság, $\Phi$ a kilépési munka valamint $A=1.025\;\mathrm{\AA\;}^{-1}eV^{-1/2}$ egy állandó. Az alagútáram exponenciális függése a minta-tű távolságtól rendkívül pontos mérést tesz lehetővé: ha mindössze $1\;\AA$-el, azaz körülbelül fél atomnyi távolsággal, megnöveljük a minta-tű távolságot, az áram a tizedére csökken.
−
<wlatex>
+
−
Egy pásztázó elektronmikroszkópot egy író egységgel egészítünk ki, mely az egyszerű raszter-szkennelés helyett tetszőleges, általunk tervezett pálya mentén mozgatja az elektronsugarat.
+
  
−
# A hordozóra (pl. Si lapka) fotoreziszt anyagot viszünk fel (pl. PMMA).
 
−
# A tervek alapján végigpásztázzuk a rezisztet elektronnyalábbal.
 
−
# A rezisztben megvilágítás hatására megváltoznak a kötések, így a megvilágított rész az előhívóval könnyen feloldható és eltávoltítható. (Negatív reziszt esetén a meg nem világított rész oldódik az előhívóban)
 
−
# Előhívás után fémet párologtatunk a felületre. A megvilágított részeken a fém a hordozóra, amúgy a reziszt tetejére kerül.
 
−
# Megfelelő anyaggal a megmaradt rezisztet, és így a tetején levő fém réteget is  eltávolítjuk, így csak a megvilágított helyeken maradnak fém nanostruktúrák.
 
  
−
Felbontás, InAs nanoáramkörök gyártása:
+
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:STM_approach.ogv|bélyegkép|közép|800px|thumbtime=0:08]]
 +
|-
 +
| align="center"|2. ábra. ''STM tű közelítése a felülethez, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.''
 +
|}
  
−
Ugyan az elektronsugarat pár nm átmérőre fókuszálhatjuk, a rezisztben keltett másodlagos elektronok diffúziójuk során további kötéseket törnek fel a rezisztben. Emiatt az elektronsugár mikroszkópia felbontásánál a litográfia felbontása egy nagyságrenddel rosszabb (>20nm).
+
A mérés kezdetén a 2. ábrán látható módon addig közelítjük a tűt a minta felületéhez, míg az alagútáram el nem éri a - tipikusan $nA$-es nagyságrendű - kívánt értéket. Alagútmikroszkóppal két különböző módon végezhetünk méréseket. A konstans áram üzemmódot használják leggyakrabban (3. ábra), ehhez a minta felületével párhuzamosan pásztázunk a tűvel miközben egy szabályozó áramkört használva úgy mozgatjuk a tűt a felületre merőleges irányban, hogy mindig állandó legyen a mért alagútáram, azaz a tű közel azonos távolságban mozogjon a minta felületéhez képest. Ilyen módon akár atomi felbontással letapogatható a minta topográfiája.
  
−
Példa:
+
{|  cellpadding="5" cellspacing="0" align="center"
−
# InAs nanovezetékek növesztése
+
|-
−
# A nanovezetékeket terítjük a hordozón
+
| [[Fájl:STM_feedback.ogv|bélyegkép|közép|800px|thumbtime=0:17]]
−
# Fénymikroszkóppal meghatározzuk a kontaktálni kívánt nanovezetékeket a hordozón előre létrehozott markerekhez viszonyítva
+
|-
−
# Megtervezzük, és az ismertetett módszerrel legyártjuk a nanoáramköröket. A markerek segítségével illesztünk.
+
| align="center"|3. ábra. ''Pásztázás a minta felett: topográfia felvétele konstans áram üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.''
−
</wlatex>
+
|}
  
−
=== Fókuszált ion sugár (Focused ion beam, FIB) ===
+
A másik üzemmód a konstans magasság üzemmód (4. ábra), ehhez a szabályozást kikapcsolva, a tűt állandó magasságban tartva pásztázunk a felület felett. A mért alagútáramból meghatározható a minta topográfiája. Ez az üzemmód gyors pásztázási sebességet tesz lehetővé, ami többek között akkor lehet hasznos, ha valamilyen lassú időbeli változást - például hőtágulás miatti csúszást - kell kiküszöbölni. Ahhoz, hogy ezt a mérési módot alkalmazhassuk, a mintának kellőképpen simának kell lennie és a tűt elegendően távol kell tartanunk, hogy ne ütközzön a felületbe.
−
<wlatex>
+
 
−
* A mintát fókuszált ionokkal (általában Ga+,  5-50 keV energia) bombázzuk, aminek hatására a felületet másodlagos ionok vagy semleges atomok, illetve elektronok hagyják el. A módszert használhatjuk anyagmegmunkálásra (>10 nm felbontás) illetve a másodlagos ionok és elektronok detektálásával képet is készíthetünk a felületről.
+
{|  cellpadding="5" cellspacing="0" align="center"
−
* Nem vezető minta esetén érdemes elektronokkal is bombázni a felületet a töltések semlegesítésére. Ezzel a módszerrel szigetelő mintákat is vizsgálhatunk a felület fémes bevonása nélkül (lásd SEM).
+
|-
−
* Erősen destruktív módszer, a felületről atomokat távolít el, és a Ga be is épülhet a felületbe.
+
| [[Fájl:STM_scan_noFeedback.ogv|bélyegkép|közép|800px|thumbtime=0:07]]
 +
|-
 +
| align="center"|4. ábra. ''Pásztázás a minta felett: topográfia felvétele konstans magasság üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.''
 +
|}
 +
 
 +
Az alagútáram exponenciális távolságfüggése lehetővé teszi, hogy akár egy ollóval hegyezett tűvel is készíthetünk jó minőségű STM képet. Az alábbi ábrák egy grafit minta felületének valamint egy szén nanocsőnek az atomi felbontású képét mutatják be.
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:HOPG_atomic.png|közép|500px]]
 +
|-
 +
| align="center"|5. ábra. ''Atomi felbontású STM kép grafit minta felületéről, forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013.''
 +
|}
 +
 
 +
{| cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:Chiraltube.gif|közép|300px]]
 +
|-
 +
| align="center"|6. ábra. ''Szén nanocső atomi felbontású képe, forrás: [http://en.wikipedia.org/wiki/File:Chiraltube.gif Wikipedia]''
 +
|}
 +
 
 +
 
 +
Az STM tű nem csak a képalkotásra, hanem a minta felületének atomi felbontású manipulációjára is alkalmas: a tű segítségével atomokat lehet mozgatni a felületen. Ezzel a technikával hozták létre a 7. ábrán látható kör alakzatot, amit 48 vas atom alkot egy réz felületen. Az alagútmikroszkópos felvételen jól megfigyelhetőek a kör belsejében kialakuló állóhullámok ("Quantum corral").
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:Quantum_corral.jpg|közép|300px]]
 +
|-
 +
| align="center"|7. ábra. ''Elektron-állóhullámok egy atomokból kirakott kör belsejében, forrás: [http://en.wikipedia.org/wiki/File:The_Well_(Quantum_Corral).jpg Wikipedia]''
 +
|}
 +
 
 +
Egy másik, hasonló kísérlet során 36 kobalt atomból álló ellipszist hoztak létre, aminek az egyik fókuszpontjába egy kobalt atomot helyeztek. Az elektronok hullámtermészetének köszönhetően az ellipszis másik fókuszpontjában is mérhető a kobalt atom hatása.<sup> [http://www.nature.com/nature/journal/v403/n6769/abs/403512a0.html 1]</sup>
 +
 
 +
Az STM legnagyobb hátránya, hogy csak elektromosan vezető felületeket vizsgálhatunk vele. Szigetelő felületek vizsgálatára fejlesztették ki az atomerő mikroszkópot.
 
</wlatex>
 
</wlatex>
  
−
=== További felhasználások ===
+
== Atomerő mikroszkóp (Atomic Force Microscope - AFM)==
 
<wlatex>
 
<wlatex>
−
* FIB-assisted chemical vapor deposition(pl. W(CO)6 molekulákkal volfrám felvitele a felületre. Pt, Co, Au, C szintén felvihető)
+
Az atomerő mikroszkóp érzékelője az úgynevezett kantilever: egy laprugó a végén egy hegyes tűvel. Az alagútmikroszkóppal ellentétben az alagútáram helyett a minta és a tű közötti erőhatást mérik, amihez a kantilever lehajlását detektálják. Ezt a leggyakrabban a 8. ábrán vázolt elven: a laprugóról visszavert lézersugár és egy fotodetektor segítségével végzik.
−
* Gas assisted FIB-etching
+
 
−
* He ion mikroszkóp(kevésbé destruktív, jobb felbontás)
+
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:Atomic_force_microscope.png|közép|300px]]
 +
|-
 +
| align="center"|8. ábra. ''Tipikus atomerő mikroszkóp működési elve, forrás [http://en.wikipedia.org/wiki/File:Atomic_force_microscope_block_diagram.svg Wikipedia]''
 +
|}
 +
 
 +
Az atomerő mikroszkóp hátránya az alagútmikroszkóphoz képest, hogy míg az alagútmikroszkóp esetén a távolsággal exponenciálisan változó alagútáramot mérve nagyon pontosan detektálható a minta-tű távolság változása, addig az atomerő mikroszkóp esetén a minta atomjai és a tű között fellépő - tipikusan nN nagyságrendű - erő  sokkal kevésbé érzékeny a minta-tű távolságra valamint nem is monoton módon változik. A tűvel a felülethez közeledve először az indukált dipólus-dipólus kölcsönhatásból származó, nagy hatótávolságú, vonzó ''van der Waals'' erő jelenik meg. Tovább közeledve a rövidebb hatótávolságú, kémiai kötésekből származó erő kezd dominálni, mely először vonzó, majd taszító hatást fejt ki a tűre (9. ábra).
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:afm_pot.png|közép|300px]]
 +
|-
 +
| align="center"|9. ábra. ''Potenciál a minta-tű távolság függvényében.''
 +
|}
 +
 
 +
A minta és a tű közötti erő mérése alapvetően két különböző elven, statikus illetve dinamikus üzemmódban valósítható meg. Statikus üzemmódban a tűt a minta felületéhez nyomják, az erő közvetlenül a laprugó lehajlásából határozható meg. Dinamikus üzemmódban a laprugót a rezonancia-frekvenciáján rezgetik, a minta és a tű közötti erőhatás következtében megváltozik a rezgés frekvenciája, fázisa, amplitúdója ezek egyikéből meghatározható az erő nagysága.
 +
 
 +
Az atomerőmikroszkóp mérési üzemmódjai tovább csoportosíthatóak aszerint, hogy a 9. ábrán vázolt potenciál melyik szakaszán végzik a mérést: a kisebb minta-tű távolsághoz tartozó taszító erőhatású tartományon mérve kontakt, a nagyobb minta-tű távolsághoz tartozó, vonzó erőhatással jellemezhető tartományon mérve nem kontakt üzemmódról beszélhetünk.
 +
 
 +
Statikus üzemmódban pásztázás közben úgy mozgatják a tűt, hogy a laprugó lehajlása állandó legyen. A minta és a tű közötti erőhatás annál pontosabban határozható meg, minél kisebb a laprugó rugóállandója. Azonban a felület közvetlen közelében nagy vonzó erő hat a tűre, ami azt a felületre rántja. Ezért statikus üzemmódot alkalmazva szinte mindig kontakt üzemmódban mérnek.
 +
 
 +
Nem kontakt üzemmódban a laprugót a rezonanciafrekvenciáján gerjesztik, a rezgés amplitúdója 10 nm-nél kisebb, akár néhány pm is lehet. A tűre ható erő elhangolja a rezonancia-frekvenciát, pásztázás közben úgy mozgatják a tűt, hogy mindig állandó legyen a frekvencia-eltolódás (10. ábra).
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:AFM_dyn.ogv|bélyegkép|közép|500px|thumbtime=0:01]]
 +
|-
 +
| align="center"|10. ábra. ''Atomerő  mikroszkóp működése nem kontakt, dinamikus üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.''
 +
|}
 +
 
 +
Szobahőmérsékleten mérve a legtöbb minta felszínén egy vékony folyadék film képződik, ami megnehezíti a nem kontakt üzemmódban történő mérést, erre a célra fejlesztették ki az úgynevezett tapping üzemmódot. Ebben az esetben a laprugót a rezonancia-frekvenciájához közel gerjesztik, a rezgés amplitúdója tipikusan 100-200 nm. A minta és a tű közötti erőhatás egyre csökkenti a rezgés amplitúdóját, ahogyan a tű közeledik a minta felületéhez. Pásztázás közben a laprugó rezgési amplitúdójára szabályozva mindig úgy mozgatják a tűt, hogy az amplitúdó állandó legyen.
 +
 
 +
A 11. ábrán látható egy polimerláncról készült felvétel, tapping üzemmódban mérve.
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:Single-Molecule-Under-Water-AFM-Tapping-Mode.jpg|közép|300px]]
 +
|-
 +
| align="center"|11. ábra. ''Polimerlánc atomerőmikroszkópos képe, forrás: [http://en.wikipedia.org/wiki/File:Single-Molecule-Under-Water-AFM-Tapping-Mode.jpg Wikipedia]''
 +
|}
 +
 
 +
A kereskedelmi forgalomban kapható atomerő mikroszkópok esetén leggyakrabban az előbbiekben ismertetett kantilevert használják érzékelőként. Speciális körülmények - például alacsony hőmérsékleten történő mérés esetén - problémát jelenthet a laprugó lehajlásának lézeres detektálása, sokkal kézenfekvőbb megoldás egy olyan érzékelő, amivel elektromos elven mérhetjük a minta és a tű között fellépő erőt. A hagyományos AFM kantilever helyett egy speciális, piezoelektromos elven működő érzékelő készíthető a kvarc órákban is használt hangvilla alakú kvarcoszcillátort alkalmazva (12. ábra).
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| align="center"|[[Fájl:TF_photo.jpg|center|280px]]
 +
| align="center"|[[Fájl:TF_res.png|center|400px]]
 +
|-
 +
| colspan="2" align="center"|12. ábra. ''Kvarcórákban használt hangvilla alakú kvarcoszcillátor (bal oldal) és annak rezonancia-görbéje (jobb oldal), forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013.''
 +
|}
 +
 
 +
A hangvilla alakú kvarcoszcillátort kvarcórákban, elektronikai áramkörökben használják órajel előállítására, olcsón beszerezhető - körülbelül 20 Ft/db. Az oszcillátor egy hangvilla alakú kvarc (Tuning Fork vagy röviden TF-nek is szokták nevezni), a legfontosabb jellemzője a rezonancia-frekvenciájának az értéke, névlegesen 32,768kHz. A kvarcot kontaktáló fém elektródák úgy vannak kialakítva, hogy elektromosan mind gerjeszteni mind a rezgést detektálni csak egyetlen rezgési módusban lehet: amikor az ágak a hangvilla síkjában, tükörszimmetrikusan rezegnek. A kontaktusokra váltakozó feszültséget kapcsolva, a kristály periodikusan deformálódik, rezgésbe jön. Amikor a rákapcsolt
 +
váltakozó feszültség frekvenciája megegyezik a kvarckristály anyagától és méreteitől függő rezonancia-frekvenciájával, a rezgési amplitúdó sokszorosára nő. A rezgés detektálásához a kvarcoszcillátoron folyó áramot mérjük, ami a hangvilla ágainak sebességével arányos, a rezonancia-frekvenciánál maximuma van (12. ábra, jobb oldal). Minél kisebb a csúcsnak a félérték-szélessége, annál pontosabban mérhető a rezonancia-frekvencia.
 +
 
 +
Az AFM érzékelőhöz a kvarcoszcillátor egyik ágára egy hegyes tűt ragasztunk, ez az érzékelő dinamikus módban történő mérést tesz lehetővé. A kvarcoszcillátort a rezonancia-frekvenciáján gerjesztjük, a tűt a felülethez közelítve a rezonancia-frekvencia eltolódik. Pásztázás közben úgy mozgatjuk a tűt a felületre merőlegesen, hogy a frekvencia-eltolódás mindig a kívánt minta-tű távolságnak megfelelő frekvencia-eltolódással egyezzen meg.
 +
 
 +
Mivel a minta és a tű közötti erőhatás lassan változik a minta-tű távolság függvényében, ezért atomerő mikroszkóppal nehezebb jó felbontást elérni mint alagútmikroszkóppal mérve. Ehhez jóval hegyesebb tűre van szükség, például elektrokémiai marásos eljárással hegyezhetünk tűt erre a célra.
 +
 
 +
A 13. ábrán látható egy elektronsugaras litográfiával készült majd arannyal bevont felületű nanoszerkezeten történő mérés alagútmikroszkóp üzemmódban - az alagútáramra szabályozva, majd ezt követően ugyanazon a helyen atomerő mikroszkóp üzemmódban - a kvarcoszcillátor frekvencia-eltolódására, azaz a minta és a tű között fellépő erőre szabályozva. Mindkét esetben pár száz nm széles, párhuzamos csíkok láthatóak. Az alagútmikroszkóp felvételén a litográfiával készült csíkokon kívül finomabb struktúrák is megfigyelhetőek: párszor 10 nm méretű dombok, ezeket az atomerő mikroszkóp nem volt képes felbontani.
 +
 
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| align="center"|[[Fájl:STM_stripes.png|bal|450px]]
 +
| align="center"|[[Fájl:AFM_stripes.png|png|450px]]
 +
|}
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| align="center"|13. ábra. ''Elektronsugaras litográfiával készült nanoszerkezeten történő mérés STM majd AFM üzemmódban, forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013.''
 +
|}
 
</wlatex>
 
</wlatex>
  
−
=== Párologtatási módszerek, MBE ===
+
== Pásztázó és transzmissziós elektron mikroszkóp (Scanning electron microscope, SEM / Transmission electron microscope, TEM) ==
 
<wlatex>
 
<wlatex>
−
*Fizikai gőzfázisú leválasztás (Physical Vapour Deposition, PVD). A forrásanyagot nagy vákuumban párologtatással vagy porlasztással a gőztérbe viszik, és leválasztják a szubsztrátumra.
+
Az 1986-ban kiosztott Nobel-díj a pásztázó alagútmikroszkóp feljesztői mellett Ernst Ruska-t is díjazta az első elektronmikroszkóp elkészítéséért. Az STM mellett az elektronmikroszkóp azóta is a nanofizikai kutatások alapvető eszközei közé tartozik.
−
* Ahhoz, hogy a leválasztott anyag az energetikailag kedvező helyeket megtalálja a szubsztrát fűtésére van szükség.
+
 
−
* Forrásanyag párologtatása: ellenállásfűtéssel, v. elektronsugárral (e-gun evaporation), vagy lézerimpulzussal (laser ablation PVD)
+
Működési elvük alapján megkülönböztethetünk transzmissziós elektronmikroszkópot (transmission electron microscope, TEM), illetve pásztázó elektronmikroszkópot (scanning electron microscope, SEM).  
−
* Forrásanyag porlasztása (sputtering) pl. Ar+ ionokkal
+
 
−
* Molekulasugaras epitaxiális rétegnövesztés (Molecular Beam Epitaxy, MBE)
+
A transzmissziós elektronmikroszkóp alapelve közel áll egy optikai mikroszkópéhoz, hiszen vékony mintán transzmittálódik az elektronnyaláb, majd a transzmittált nyaláb képét nagyítás után egy képernyőre / CCD kamerára vetítik. (Természetesen az elektronnyalábot leképező ''optikák'' fejlesztése komoly feladat volt, ezt külön említik Ernst Ruska Nobel-díjának indoklásában. Manapság a legjobb felbontású transzmissziós elektronmikroszkópokkal akár atomi felbontás is elérhető.<sup>[http://www.sciencemag.org/content/323/5922/1705.abstract 2]</sup>
−
**Igen tiszta körülmények (<10-10 mbar nyomás) + fűtött hordozó + forrásanyag jól kontrolált leválasztása (e-gun) -> egykristályos epitaxiális rétegek növeszthetők ~1 réteg/s sebességgel. Rétegek in situ számlálása nagyenergiájú reflexiós elektrondiffrakcióval (Reflected High Energy Electron Diffraction, RHEED)
+
 
−
* Kémiai gőzfázisú leválasztás (Chemical Vapor Deposition, CVD): gázfázisba vitt anyagokból valamilyen kémiai reakcióval választják le a hordozó felületére a rétegépítő anyagot.
+
Pásztázó elektronmikroszkóp esetén az elektronágyúval előállított és megfelelő energiára gyorsított elektronnyalábot mágneses tekercsekkel kis (akár pár nanométer) átmérőre fókuszálják.
 +
A fókuszált elektronnyalábbal pásztázzák a mintát, és a visszaszórt elektronokat, másodlagos elektronokat, a keltett röntgen sugárzást v. fényt detektálják, ezen információk alapján alkotnak képet, vagy nyernek spektroszkópiai információt a mintáról. A minta felülete elektromosan vezető kell, hogy legyen a töltésfelhalmozódás elkerülése végett, így szigetelőkön vékony fémes bevonatot kell létrehozni. Pásztázó elektronmikroszkóppal pár nanométeres felbontás érhető el.
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| align="center"|[[Fájl:Jeol.png|center|400px]]
 +
|-
 +
| align="center"|14. ábra ''JEOL típusú pásztázó elektronmikroszkóp fényképe a BME Fizika Tanszék és az MFA közös laboratóriumában.''
 +
|}
 
</wlatex>
 
</wlatex>
  
−
=== Példa: 2D elektron gáz Ga<sub>x</sub>Al<sub>1-x</sub>As heteroszerkezetekben ===
+
== Elektronsugár litográfia (E-beam lithography) ==
 
<wlatex>
 
<wlatex>
−
A GaAs és az AlAs tiltott sávja jelentősen eltér, viszont a rácsállandójuk <0.15% pontossággal megegyezik, így kristályhibák nélkül, epitaxiálisan növeszthetők egymásra. Ga<sub>x</sub>Al<sub>1-x</sub>As növesztése esetén a tiltott sáv x értékével folytonosan változtatható (band engineering).
+
A pásztázó elektronmikroszkópot nanoszerkezetek készítésére is használhatjuk. Ehhez az elektronmikroszkópot egy író egységgel egészítjünk ki, mely az egyszerű raszter-szkennelés helyett tetszőleges, általunk tervezett pálya mentén mozgatja az elektronsugarat. Először egy hordozóra (pl. Si lapka) egy vékony polimer réteget viszünk fel, az un. rezisztet (pl. PMMA). Ezután a tervek alapján végigpásztázzuk a rezisztet az elektronnyalábbal. A megvilágítás hatására a reziszt hosszú szénláncai felhasadnak rövidebbekre, így a megvilágított rész az előhívóval könnyen feloldható és eltávoltítható (ill. negatív reziszt esetén a meg nem világított rész oldódik az előhívóban). Ezután fémet párologtatunk a felületre. A megvilágított részeken a fém a hordozóra, amúgy a reziszt tetejére kerül. Végül megfelelő anyaggal a megmaradt rezisztet, és így a tetején levő fém réteget is  eltávolítjuk, így csak a megvilágított helyeken maradnak fém nanostruktúrák.
 +
Az elektronsugár-litográfia fenti lépéseit a 15. ábra videója szemlélteti. A fém elektródák párologtatásához különböző módszerek állnak rendelkezésre, erről a [[vékonyréteg leválasztás]] fejezetben adunk részletes leírást.
  
−
AlGaAs és GaAs rétegeket növesztük egymásra. A két anyag kilépési munkája és kémiai potenciálja eltér, viszont érintkezésükkor töltésátrendeződések után a kémiai potenciálok kiegyenlítődnek. Ekkor a sávok "elhajlása" miatt a határfelületen kialakul egy szabadon mozgó elektronokat tartalmazó 2D réteg a határfelületen, az úgynevezett 2D elektron gáz, 2DEG.  
+
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:Litography_anim.ogv]]
 +
|-
 +
| align="center"|15. ábra. ''Elektronsugaras litográfia.''
 +
|}
  
−
A dópolást a határfelülettől távolabb végzik (remote v. d- doping) így a szennyező atomok (pl. Si) potenciálja kevésbe zavarja az elektronok mozgását a 2DEG-ben. Ennek, és az epitaxiális növesztésnek köszönhetően az elektronok szabad úthossza kiemelkedően nagy lehet (alacsony hőmérsékleten akár 0.25mm!)
+
Elektronsugár-litográfia segítségével különböző nanofizikai objektumokat (pl. grafén darabka, szén nanocső, félvezető nanovezeték, stb.) könnyedén kontaktálhatunk vékony fém elektródákkal, így kialakíthatjuk az általunk megtervezett nanoáramkört, a 16. ábra erre mutat példát.
  
−
Alkalmazás: High Electron Mobility Transistor 600GHz-es max. frekvencia
+
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:Nanoáramkorok.jpg|közép|300 px]]
 +
|-
 +
| align="center"|16. ábra. ''Cooper-pár feltörő nanoáramkör: InAs nanovezeték normál és szupravezető elektródákkal, illetve számos kapuelektródával. Forrás: a BME Fizika Tanszék és a Bázeli Egyetem együttműködésében folyó kutatások.''
 +
|}
 +
 
 +
 
 +
Ugyan az elektronsugarat pár nm átmérőre fókuszálhatjuk, a rezisztben keltett másodlagos elektronok diffúziójuk során további kötéseket törnek fel a rezisztben (17. ábra). Emiatt az elektronsugár-mikroszkópia felbontásánál a litográfia felbontása egy nagyságrenddel rosszabb (>20nm).
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:Electron_beam_scattering.jpg|közép|300 px]]
 +
|-
 +
| align="center"|17. ábra. ''Bejövő elektron által keltett másodlagos elektronok diffúziója a rezisztben, forrás: [http://en.wikipedia.org/wiki/File:Electron_beam_scattering.jpg Wikipedia].''
 +
|}
 
</wlatex>
 
</wlatex>
−
=== Kontaktusok és kapu elektródák létrehozása ===
+
 
 +
==Kétdimenziós elektrongáz Ga<sub>x</sub>Al<sub>1-x</sub>As heteroszerkezetekben ==
 
<wlatex>
 
<wlatex>
−
==== Kapu elektródák – Schottky kontaktus ====
+
Mind a nanofizikai kutatásokban, mind a nanofizika alkalmazásában kiemelt szerepet tölt be egy speciális anyagcsalád, a Ga<sub>x</sub>Al<sub>1-x</sub>As heteroszerkezetek, illetve az ezekben kialakuló kétdimenziós elektrongáz rendszerek. Mind a GaAs mind az AlAs félvezető anyagok, jelentősen eltérő tiltott sáv szélességgel (gap-el). A két anyag rácsszerkezete azonban megegyezik, és rácsállandójuk is szinte teljesen azonos (az eltérés kissebb mint 0.15%). Ennek köszönhetően egy GaAs egykristályra szinte kristályhiba nélkül ránöveszthető egy AlAs egykristály, sőt különböző koncentrációjú Ga<sub>x</sub>Al<sub>1-x</sub>As kristály is, azaz $x$ megfelelő megválasztásával széles tartományban változtathatjuk az egymásra növesztett félvezető rétegek tiltott sávjának szélességét. A [[vékonyréteg leválasztás]]
−
* A fém és a félvezető között egy kiürített réteg alakul ki, melyen csak termikus gerjesztéssel vagy alagutazással juthatnak át az elektronok
+
c. fejezetben ismertetett epitaxiális rétegleválasztási módszer (Molecular Beam Epitaxy, MBE) segítségével valósítható meg az, hogy a különböző tiltott sávú rétegeket epitaxiálisan, azaz a kristályrendet követve növesszük egymásra.  
−
* A kapuelektródára adott feszültséggel szabályozhatjuk a 2DEG elektronsűrűségét:
+
−
$$d = \sqrt{\frac{2 \epsilon \Phi_b}{e^2 N_D}}$$
+
−
==== Ohmikus kontaktus ====
+
−
* Erős dópolással lecsökkentjük a kiürített réteg vastagságát
+
−
* Gyakori módszer tiszta félvezető felület utólagos kontaktálására:
+
−
==== „Split gate” technika ====
+
−
* Foto v. elektronsugár litográfiával készült elektródákra adott feszültségekkel struktúrálják a 2DEG-et
+
−
</wlatex>
+
−
=== AFM litográfia ===
+
−
<wlatex>
+
−
* A félvezető felületén szobahőmérsékleten egy vékony víz réteg képződik (páratartalom precíz kontrolálása!)
+
−
* Dópolt Si tű + nagy feszültség -> oxidvonalak húzhatók a felületen (Szélesség: <100nm, magasság 20-30nm)
+
−
* Az oxidvonalak alatt kiszorul a 2DEG, így különválasztott tartományokra szabdalható
+
−
</wlatex>
+
−
=== Önszerveződő nanoszerkezetek, kémiai növesztés ===
+
−
<wlatex>
+
−
* A felületek gyakran átrendeződnek jól definiált struktúrájú alakzatokba (surface reconstruction) 
+
−
* Molekulákból önszerveződő rétegeket képezhetünk. Pl. arany felületre a tiol csoport (SH) szeret kötődni, így egyik végükön tiol csoporttal rendelkező molekulák egy arany felületen önszerveződő monoréteget (self-assambled monolayer, SAM) alkothatnak
+
−
* Bizonyos anyagok szakítás során szeretnek atomi láncokat képezni
+
−
* Grafén nanoszalagok létrehozása oxidációval. SiO2 hordozón elhelyezett grafén réteget először oxigén légkörben oxidálunk (~500 OC), aminek hatására kör alakú lyukak jönnek létre. Ezeket 700 OC-os argon atmoszférában hőkezeljük, miközben jól definiált irányú hatszögek jönnek létre. (Reakció: SiO2+C -> SiO + CO) Forrás: Magda Gábor, Dr. Bíró László Péter (MFA) 
+
−
</wlatex>
+
  
 +
A 18. ábrán szemléltetett rétegszerkezetben jobb oldalon egy GaAs réteg található, melyhez bal oldalon egy Si-al dópolt Ga<sub>x</sub>Al<sub>1-x</sub>As réteg csatlakozik. A két anyag kilépési munkája és kémiai potenciálja eltér, viszont érintkezésükkor töltésátrendeződések után a kémiai potenciálok kiegyenlítődnek. Ekkor a sávok "elhajlása" miatt a határfelületen kialakul egy szabadon mozgó elektronokat tartalmazó kétdimenziós réteg, az úgynevezett 2D elektron gáz, 2DEG.
 +
A kétdimenziós elektrongáz potenciálja a Ga<sub>x</sub>Al<sub>1-x</sub>As rétegre párologtatott fémes kapuelektróda segítségével változtatható, megfelelő feszültséggel a kétdimenziós elektrongáz ki is üríthető. A szinte tökéletes kristályrendet követő határfelületnek köszönhetően az elektronok szabadon, kevés szóródással mozoghatnak a kétdimenziós elektrongázban, azaz nagy lesz az elektronok szabadúthossza, illetve mobilitása. A határfelület tökéletességét tovább növeli, hogy az adalékoló Si atomokat nem közvetlenül a határfelület tartományában, hanem attól távolabb helyezik el (remote doping, v. delta doping), így az elektronok az adalékoló atomokon sem szóródnak jelentős mértékben. Alacsony hőmérsékleten a 2DEG-ben mozgó elektronok szabad úthossza akár milliméteres nagyságrendű is lehet.
  
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:2DEG_band.svg|közép|400px|]]
 +
|-
 +
| align="center"|18. ábra. ''Kétdimenziós elektrongáz Ga<sub>x</sub>Al<sub>1-x</sub>As heteroszerkezetben, forrás: [http://en.wikipedia.org/wiki/File:HEMT-scheme-en.svg Wikipedia]''
 +
|}
  
 +
A Ga<sub>x</sub>Al<sub>1-x</sub>As heteroszerkezetekből készült nagy mobilitású tranzisztorok (High Electron Mobility Transistor, HEMT, lásd 19. ábra) tették lehetővé a mobil kommunikációt, és a félvezető lézerek is általában Ga<sub>x</sub>Al<sub>1-x</sub>As heteroszerkezetekből készülnek, azaz ez a félvezető anyagcsalád kiemelkedő jelentőségű a technikai alkalmazások szempontjából.
 +
A félvezető heteroszerkezetek fejlesztéséért Zhores I. Alferov és Herbert Kroemer 2000-ben Nobel-díjat kapott.
 +
 +
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:HEMT.svg|közép|400px|]]
 +
|-
 +
| align="center"|19. ábra. ''Nagy elektronmobilitású tranzisztor, forrás: [http://en.wikipedia.org/wiki/File:HEMT-scheme-en.svg Wikipedia]''
 +
|}
 +
 +
A 2DEG rendszerek a nanofizikai kutatásokban is alapvető szerepet játszanak. A heteroszerkezet tetejére párologtatott fém elektródák és a heteroszerkezet között Schottky gát alakul ki, így az elektródákra kapcsolt kapcsolt feszültség csak a heteroszerkezet potenciálját hangolja, de az elektródából nem jutnak át elektronok a heteroszerkezetbe. Az ilyen típusú elektródákat kapuelektródának nevezzük. A 2DEG fölé helyezett, megfelelően kialakított kapuelektródákkal a 2DEG elektronjait az általunk kívánt tartományba kényszeríthetjük. Ilyen 2DEG-ből kialakított struktúrákra a [[kvantum pöttyök]] illetve a [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Vezetőképesség-kvantálás kvantum-pontkontaktusban|vezetőképesség-kvantálás]] fejezetekben látunk példákat.
 +
 +
A 2DEG kontaktálásához (pl. a forrás és nyelő elektróda kialakításához) fémes, ohmikus kontaktusokra van szükség. Ha a fémes elektróda alatt a félvezető struktúrát erősen dópoljuk, akkor nagyon lecsökken a Schottky gát szélessége, így gyakorlatilag ohmikus kontaktus alakul ki.
 
</wlatex>
 
</wlatex>
 +
 +
==Hivatkozások==
 +
 +
===Fent hivatkozott szakcikkek===
 +
[1] [http://www.nature.com/nature/journal/v403/n6769/abs/403512a0.html H. C. Manoharan, C. P. Lutz & D. M. Eigler: ''Quantum mirages formed by coherent projection of electronic structure'', '''Nature 403''' p512-515 (2000)]
 +
 +
[2] [http://www.sciencemag.org/content/323/5922/1705.abstract C. Ö. Girit et. al: ''Graphene at the Edge: Stability and Dynamics'', '''Science 323''' p1705-1708 (2009)]
 +
 +
===Ajánlott könyvek és összefoglaló cikkek===
 +
*[http://books.google.hu/books/about/Electronic_Transport_in_Mesoscopic_Syste.html?id=28BC-ofEhvUC&redir_esc=y S. Datta: ''Electronic Transport in Mesoscopic Systems'', Cambridge University Press (1997)]
 +
*[http://books.google.hu/books/about/Semiconductor_Nanostructures.html?id=qD6623gfAZgC&redir_esc=y Thomas Ihn: ''Semiconducting nanosctructures'', OUP Oxford (2010)]
 +
*[http://books.google.hu/books?id=YNr4OcCExUcC&printsec=frontcover&dq=Nazarov+quantum+transport&hl=hu&sa=X&ei=2SzZUfGCMYna4ASDq4DQBQ&ved=0CDIQ6AEwAA Yuli V. Nazarov, Yaroslav M. Blanter: ''Quantum Transport: Introduction to Nanoscience'', Cambridge University Press (2009)]
 +
 +
===Ajánlott kurzusok===
 +
*[[Új kísérletek a nanofizikában|''Új kísérletek a nanofizikában'', Halbritter András és Csonka Szabolcs, BME Fizika Tanszék]]
 +
*[[Transzport komplex nanoszerkezetekben|''Transzport komplex nanoszerkezetekben'', Halbritter András, Csonka Szabolcs, Csontos Miklós, Makk Péter, BME Fizika Tanszék]]
 +
*[[Alkalmazott szilárdtestfizika|''Alkalmazott szilárdtestfizika'', Mihály György, BME Fizika Tanszék]]
 +
*[[Fizika 3 - Villamosmérnöki mesterszak|''Fizika 3'', Mihály György, BME Fizika Tanszék (mérnök hallgatóknak)]]
 +
*[http://www.phy.bme.hu/~zarand/mezoszkopia.html ''Mezoszkopikus rendszerek fizikája'', Zaránd Gergely, BME Elméleti Fizika Tanszék]
 +
*''Mezoszkopikus rendszerek fizikája'', Cserti József, ELTE Komplex Rendszerek Fizikája Tanszék

A lap jelenlegi, 2013. szeptember 16., 20:35-kori változata

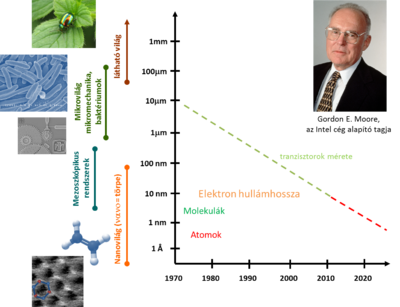
A nanotechnológia jelentősen hozzájárult az elektronika fejlődéséhez. Gordon E. Moore, az Intel cég egyik alapítója 1965-ben azt a megfigyelését tette közzé, miszerint egy integrált áramkörben lévő tranzisztorok száma két évenként megduplázódik. Ez a megfigyelés egészen napjainkig teljesülni látszik, ennek megfelelően a tranzisztorok mérete szintén exponenciálisan csökkent az elmúlt évtizedekben (1. ábra). Manapság egy tranzisztor aktív tartománya mindössze ~10 nm széles. Ez a méret elméletileg még két nagyságrenddel csökkenthető, amíg elérjük az elképzelhető legkisebb, egyetlen atomból álló tranzisztorokat. A további méretcsökkentés azonban számtalan technológiai problémát vet fel, így a jelenleginél kisebb, vagy más működési elvet követő információtárolási és feldolgozási technológiák kidolgozása világszerte intenzív kutatások tárgyát képezi. Ennek megfelelően a nanofizikai kutatások túlmutatnak az érdekes jelenségek feltérképezésén, és alapvetően hozzájárulnak a jövő technológiáinak kidolgozásához.

Moore.png
1. ábra. Tipikus méretskálák és a DRAM generációk exponenciális méretcsökkenését szemléltető Moore-törvény.

A következőkben rövid betekintést nyújtunk a nanoáramkörök illetve különböző nanoszerkezetek készítésének és vizsgálatának eszköztárába.

Tartalomjegyzék

Pásztázó alagútmikroszkóp (Scanning Tunneling Microscope - STM)


Már az ókori görögök is azt feltételezték, hogy az anyag atomokból épül fel. Ezt a feltételezést a 20. század elején számos kísérlettel sikerült bizonyítani, azonban ahhoz, hogy képet tudjunk készíteni egy anyag felületén lévő atomokról egészen 1981-ig kellett várni, amikor is Gerd Binnig és Heinrich Rohrer megépítették az első pásztázó alagútmikroszkópot. Találmányukért fizikai Nobel-díjat kaptak 1986-ban. Azóta az alagútmikroszkóp széleskörben elterjedt, manapság a nanofizikai kutatások egyik alapvető vizsgálati eszközei közé tartozik.

Működésének elve az alagúteffektuson alapul: egy hegyes tűt nm-es távolságra pozícionálunk a vizsgált minta felületéhez, a tűre feszültséget kapcsolunk, ennek hatására alagútáram folyik a tű és a minta között:

\[I \propto V_b \cdot \mathrm{Exp}\left\{-A\cdot d\cdot \sqrt{\Phi} \right\},\]

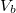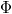ahol \setbox0\hbox{$V_b$}% \message{//depth:\the\dp0//}% \box0% a tű és a minta közé kapcsolt feszültség, \setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0% a minta-tű távolság, \setbox0\hbox{$\Phi$}% \message{//depth:\the\dp0//}% \box0% a kilépési munka valamint 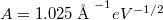\setbox0\hbox{$A=1.025\;\mathrm{\AA\;}^{-1}eV^{-1/2}$}% \message{//depth:\the\dp0//}% \box0% egy állandó. Az alagútáram exponenciális függése a minta-tű távolságtól rendkívül pontos mérést tesz lehetővé: ha mindössze 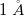\setbox0\hbox{$1\;\AA$}% \message{//depth:\the\dp0//}% \box0%-el, azaz körülbelül fél atomnyi távolsággal, megnöveljük a minta-tű távolságot, az áram a tizedére csökken.


STM approach.ogv
2. ábra. STM tű közelítése a felülethez, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.

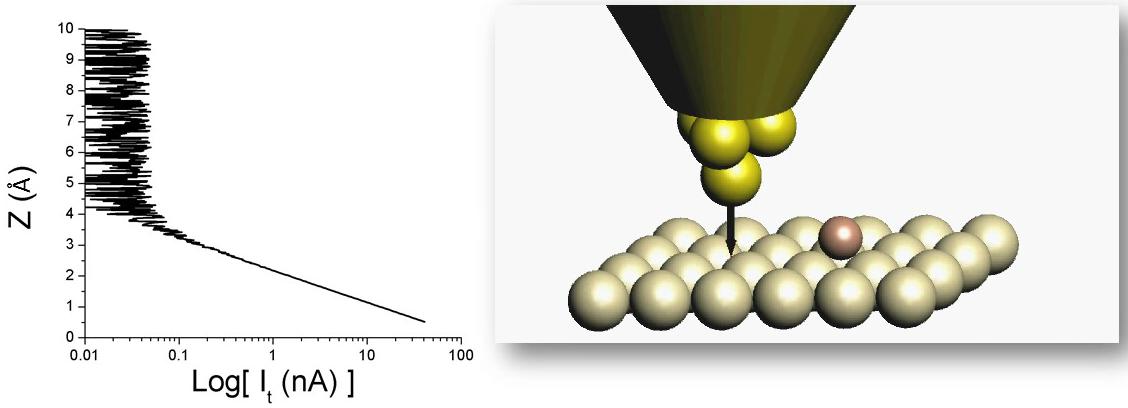
A mérés kezdetén a 2. ábrán látható módon addig közelítjük a tűt a minta felületéhez, míg az alagútáram el nem éri a - tipikusan 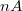\setbox0\hbox{$nA$}% \message{//depth:\the\dp0//}% \box0%-es nagyságrendű - kívánt értéket. Alagútmikroszkóppal két különböző módon végezhetünk méréseket. A konstans áram üzemmódot használják leggyakrabban (3. ábra), ehhez a minta felületével párhuzamosan pásztázunk a tűvel miközben egy szabályozó áramkört használva úgy mozgatjuk a tűt a felületre merőleges irányban, hogy mindig állandó legyen a mért alagútáram, azaz a tű közel azonos távolságban mozogjon a minta felületéhez képest. Ilyen módon akár atomi felbontással letapogatható a minta topográfiája.

STM feedback.ogv
3. ábra. Pásztázás a minta felett: topográfia felvétele konstans áram üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.

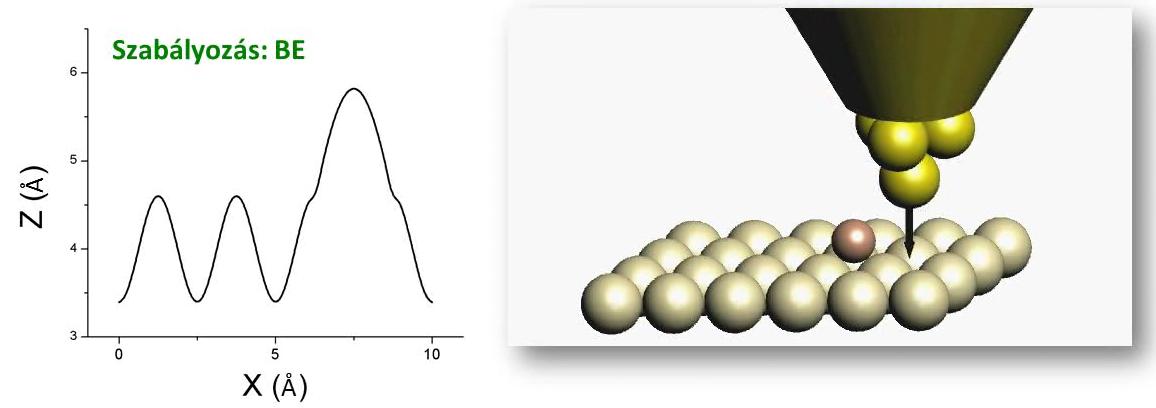
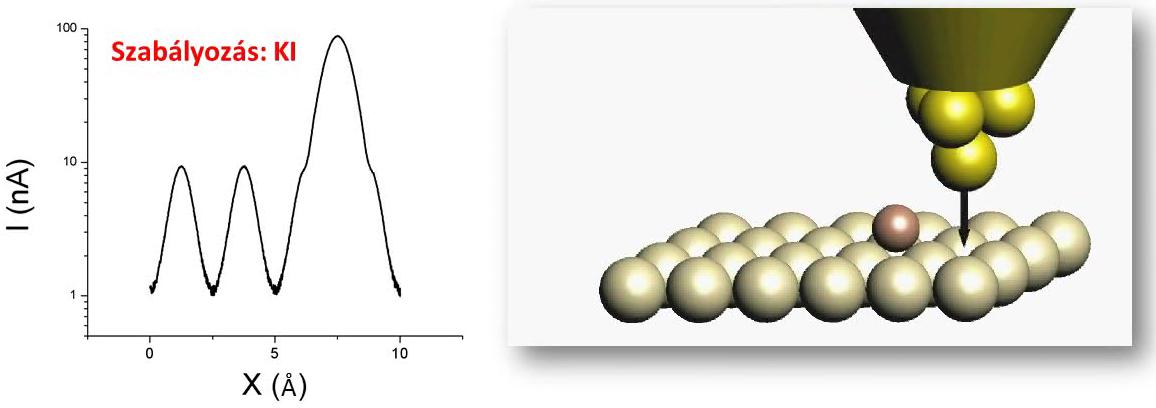
A másik üzemmód a konstans magasság üzemmód (4. ábra), ehhez a szabályozást kikapcsolva, a tűt állandó magasságban tartva pásztázunk a felület felett. A mért alagútáramból meghatározható a minta topográfiája. Ez az üzemmód gyors pásztázási sebességet tesz lehetővé, ami többek között akkor lehet hasznos, ha valamilyen lassú időbeli változást - például hőtágulás miatti csúszást - kell kiküszöbölni. Ahhoz, hogy ezt a mérési módot alkalmazhassuk, a mintának kellőképpen simának kell lennie és a tűt elegendően távol kell tartanunk, hogy ne ütközzön a felületbe.

STM scan noFeedback.ogv
4. ábra. Pásztázás a minta felett: topográfia felvétele konstans magasság üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.

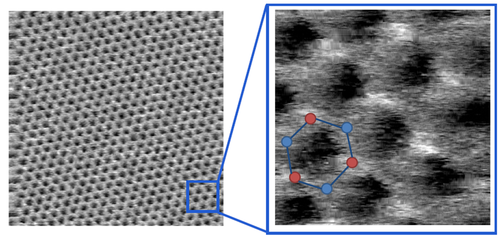
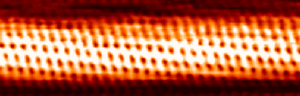
Az alagútáram exponenciális távolságfüggése lehetővé teszi, hogy akár egy ollóval hegyezett tűvel is készíthetünk jó minőségű STM képet. Az alábbi ábrák egy grafit minta felületének valamint egy szén nanocsőnek az atomi felbontású képét mutatják be.

HOPG atomic.png
5. ábra. Atomi felbontású STM kép grafit minta felületéről, forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013.
Chiraltube.gif
6. ábra. Szén nanocső atomi felbontású képe, forrás: Wikipedia


Az STM tű nem csak a képalkotásra, hanem a minta felületének atomi felbontású manipulációjára is alkalmas: a tű segítségével atomokat lehet mozgatni a felületen. Ezzel a technikával hozták létre a 7. ábrán látható kör alakzatot, amit 48 vas atom alkot egy réz felületen. Az alagútmikroszkópos felvételen jól megfigyelhetőek a kör belsejében kialakuló állóhullámok ("Quantum corral").

Quantum corral.jpg
7. ábra. Elektron-állóhullámok egy atomokból kirakott kör belsejében, forrás: Wikipedia

Egy másik, hasonló kísérlet során 36 kobalt atomból álló ellipszist hoztak létre, aminek az egyik fókuszpontjába egy kobalt atomot helyeztek. Az elektronok hullámtermészetének köszönhetően az ellipszis másik fókuszpontjában is mérhető a kobalt atom hatása. 1

Az STM legnagyobb hátránya, hogy csak elektromosan vezető felületeket vizsgálhatunk vele. Szigetelő felületek vizsgálatára fejlesztették ki az atomerő mikroszkópot.

Atomerő mikroszkóp (Atomic Force Microscope - AFM)


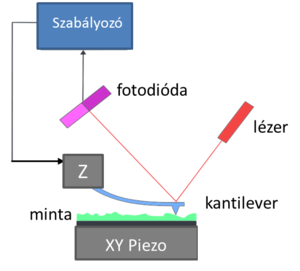
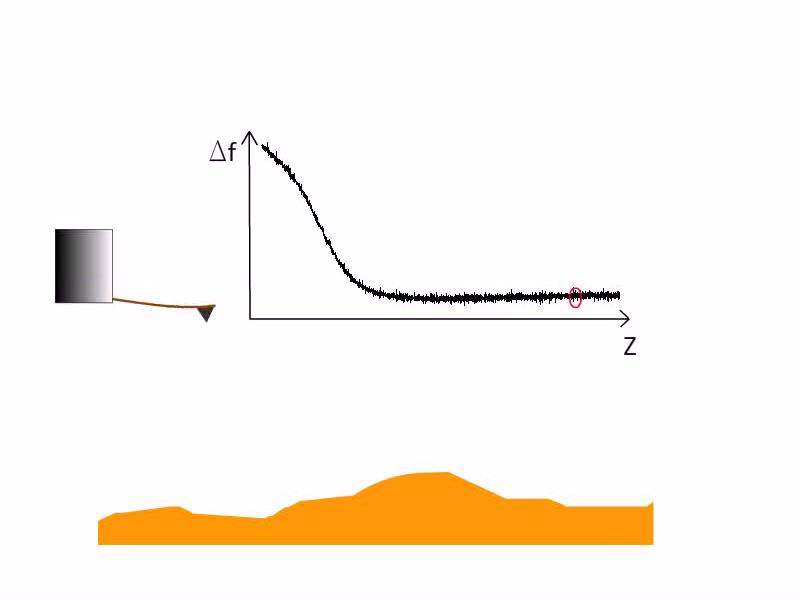
Az atomerő mikroszkóp érzékelője az úgynevezett kantilever: egy laprugó a végén egy hegyes tűvel. Az alagútmikroszkóppal ellentétben az alagútáram helyett a minta és a tű közötti erőhatást mérik, amihez a kantilever lehajlását detektálják. Ezt a leggyakrabban a 8. ábrán vázolt elven: a laprugóról visszavert lézersugár és egy fotodetektor segítségével végzik.

Atomic force microscope.png
8. ábra. Tipikus atomerő mikroszkóp működési elve, forrás Wikipedia

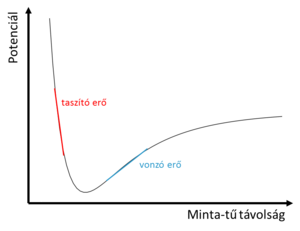
Az atomerő mikroszkóp hátránya az alagútmikroszkóphoz képest, hogy míg az alagútmikroszkóp esetén a távolsággal exponenciálisan változó alagútáramot mérve nagyon pontosan detektálható a minta-tű távolság változása, addig az atomerő mikroszkóp esetén a minta atomjai és a tű között fellépő - tipikusan nN nagyságrendű - erő sokkal kevésbé érzékeny a minta-tű távolságra valamint nem is monoton módon változik. A tűvel a felülethez közeledve először az indukált dipólus-dipólus kölcsönhatásból származó, nagy hatótávolságú, vonzó van der Waals erő jelenik meg. Tovább közeledve a rövidebb hatótávolságú, kémiai kötésekből származó erő kezd dominálni, mely először vonzó, majd taszító hatást fejt ki a tűre (9. ábra).

Afm pot.png
9. ábra. Potenciál a minta-tű távolság függvényében.

A minta és a tű közötti erő mérése alapvetően két különböző elven, statikus illetve dinamikus üzemmódban valósítható meg. Statikus üzemmódban a tűt a minta felületéhez nyomják, az erő közvetlenül a laprugó lehajlásából határozható meg. Dinamikus üzemmódban a laprugót a rezonancia-frekvenciáján rezgetik, a minta és a tű közötti erőhatás következtében megváltozik a rezgés frekvenciája, fázisa, amplitúdója ezek egyikéből meghatározható az erő nagysága.

Az atomerőmikroszkóp mérési üzemmódjai tovább csoportosíthatóak aszerint, hogy a 9. ábrán vázolt potenciál melyik szakaszán végzik a mérést: a kisebb minta-tű távolsághoz tartozó taszító erőhatású tartományon mérve kontakt, a nagyobb minta-tű távolsághoz tartozó, vonzó erőhatással jellemezhető tartományon mérve nem kontakt üzemmódról beszélhetünk.

Statikus üzemmódban pásztázás közben úgy mozgatják a tűt, hogy a laprugó lehajlása állandó legyen. A minta és a tű közötti erőhatás annál pontosabban határozható meg, minél kisebb a laprugó rugóállandója. Azonban a felület közvetlen közelében nagy vonzó erő hat a tűre, ami azt a felületre rántja. Ezért statikus üzemmódot alkalmazva szinte mindig kontakt üzemmódban mérnek.

Nem kontakt üzemmódban a laprugót a rezonanciafrekvenciáján gerjesztik, a rezgés amplitúdója 10 nm-nél kisebb, akár néhány pm is lehet. A tűre ható erő elhangolja a rezonancia-frekvenciát, pásztázás közben úgy mozgatják a tűt, hogy mindig állandó legyen a frekvencia-eltolódás (10. ábra).

AFM dyn.ogv
10. ábra. Atomerő mikroszkóp működése nem kontakt, dinamikus üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.

Szobahőmérsékleten mérve a legtöbb minta felszínén egy vékony folyadék film képződik, ami megnehezíti a nem kontakt üzemmódban történő mérést, erre a célra fejlesztették ki az úgynevezett tapping üzemmódot. Ebben az esetben a laprugót a rezonancia-frekvenciájához közel gerjesztik, a rezgés amplitúdója tipikusan 100-200 nm. A minta és a tű közötti erőhatás egyre csökkenti a rezgés amplitúdóját, ahogyan a tű közeledik a minta felületéhez. Pásztázás közben a laprugó rezgési amplitúdójára szabályozva mindig úgy mozgatják a tűt, hogy az amplitúdó állandó legyen.

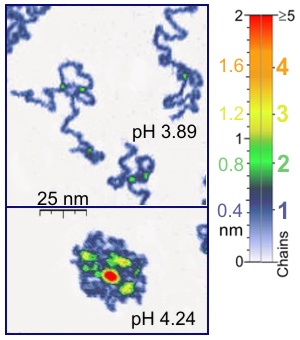
A 11. ábrán látható egy polimerláncról készült felvétel, tapping üzemmódban mérve.

Single-Molecule-Under-Water-AFM-Tapping-Mode.jpg
11. ábra. Polimerlánc atomerőmikroszkópos képe, forrás: Wikipedia

A kereskedelmi forgalomban kapható atomerő mikroszkópok esetén leggyakrabban az előbbiekben ismertetett kantilevert használják érzékelőként. Speciális körülmények - például alacsony hőmérsékleten történő mérés esetén - problémát jelenthet a laprugó lehajlásának lézeres detektálása, sokkal kézenfekvőbb megoldás egy olyan érzékelő, amivel elektromos elven mérhetjük a minta és a tű között fellépő erőt. A hagyományos AFM kantilever helyett egy speciális, piezoelektromos elven működő érzékelő készíthető a kvarc órákban is használt hangvilla alakú kvarcoszcillátort alkalmazva (12. ábra).

TF photo.jpg
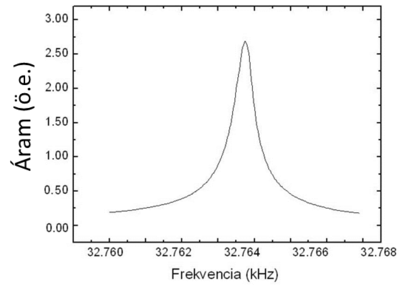
TF res.png
12. ábra. Kvarcórákban használt hangvilla alakú kvarcoszcillátor (bal oldal) és annak rezonancia-görbéje (jobb oldal), forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013.

A hangvilla alakú kvarcoszcillátort kvarcórákban, elektronikai áramkörökben használják órajel előállítására, olcsón beszerezhető - körülbelül 20 Ft/db. Az oszcillátor egy hangvilla alakú kvarc (Tuning Fork vagy röviden TF-nek is szokták nevezni), a legfontosabb jellemzője a rezonancia-frekvenciájának az értéke, névlegesen 32,768kHz. A kvarcot kontaktáló fém elektródák úgy vannak kialakítva, hogy elektromosan mind gerjeszteni mind a rezgést detektálni csak egyetlen rezgési módusban lehet: amikor az ágak a hangvilla síkjában, tükörszimmetrikusan rezegnek. A kontaktusokra váltakozó feszültséget kapcsolva, a kristály periodikusan deformálódik, rezgésbe jön. Amikor a rákapcsolt váltakozó feszültség frekvenciája megegyezik a kvarckristály anyagától és méreteitől függő rezonancia-frekvenciájával, a rezgési amplitúdó sokszorosára nő. A rezgés detektálásához a kvarcoszcillátoron folyó áramot mérjük, ami a hangvilla ágainak sebességével arányos, a rezonancia-frekvenciánál maximuma van (12. ábra, jobb oldal). Minél kisebb a csúcsnak a félérték-szélessége, annál pontosabban mérhető a rezonancia-frekvencia.

Az AFM érzékelőhöz a kvarcoszcillátor egyik ágára egy hegyes tűt ragasztunk, ez az érzékelő dinamikus módban történő mérést tesz lehetővé. A kvarcoszcillátort a rezonancia-frekvenciáján gerjesztjük, a tűt a felülethez közelítve a rezonancia-frekvencia eltolódik. Pásztázás közben úgy mozgatjuk a tűt a felületre merőlegesen, hogy a frekvencia-eltolódás mindig a kívánt minta-tű távolságnak megfelelő frekvencia-eltolódással egyezzen meg.

Mivel a minta és a tű közötti erőhatás lassan változik a minta-tű távolság függvényében, ezért atomerő mikroszkóppal nehezebb jó felbontást elérni mint alagútmikroszkóppal mérve. Ehhez jóval hegyesebb tűre van szükség, például elektrokémiai marásos eljárással hegyezhetünk tűt erre a célra.

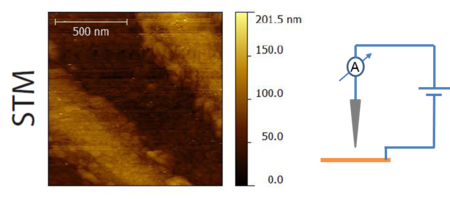
A 13. ábrán látható egy elektronsugaras litográfiával készült majd arannyal bevont felületű nanoszerkezeten történő mérés alagútmikroszkóp üzemmódban - az alagútáramra szabályozva, majd ezt követően ugyanazon a helyen atomerő mikroszkóp üzemmódban - a kvarcoszcillátor frekvencia-eltolódására, azaz a minta és a tű között fellépő erőre szabályozva. Mindkét esetben pár száz nm széles, párhuzamos csíkok láthatóak. Az alagútmikroszkóp felvételén a litográfiával készült csíkokon kívül finomabb struktúrák is megfigyelhetőek: párszor 10 nm méretű dombok, ezeket az atomerő mikroszkóp nem volt képes felbontani.


STM stripes.png
 png
13. ábra. Elektronsugaras litográfiával készült nanoszerkezeten történő mérés STM majd AFM üzemmódban, forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013.

Pásztázó és transzmissziós elektron mikroszkóp (Scanning electron microscope, SEM / Transmission electron microscope, TEM)


Az 1986-ban kiosztott Nobel-díj a pásztázó alagútmikroszkóp feljesztői mellett Ernst Ruska-t is díjazta az első elektronmikroszkóp elkészítéséért. Az STM mellett az elektronmikroszkóp azóta is a nanofizikai kutatások alapvető eszközei közé tartozik.

Működési elvük alapján megkülönböztethetünk transzmissziós elektronmikroszkópot (transmission electron microscope, TEM), illetve pásztázó elektronmikroszkópot (scanning electron microscope, SEM).

A transzmissziós elektronmikroszkóp alapelve közel áll egy optikai mikroszkópéhoz, hiszen vékony mintán transzmittálódik az elektronnyaláb, majd a transzmittált nyaláb képét nagyítás után egy képernyőre / CCD kamerára vetítik. (Természetesen az elektronnyalábot leképező optikák fejlesztése komoly feladat volt, ezt külön említik Ernst Ruska Nobel-díjának indoklásában. Manapság a legjobb felbontású transzmissziós elektronmikroszkópokkal akár atomi felbontás is elérhető.2

Pásztázó elektronmikroszkóp esetén az elektronágyúval előállított és megfelelő energiára gyorsított elektronnyalábot mágneses tekercsekkel kis (akár pár nanométer) átmérőre fókuszálják. A fókuszált elektronnyalábbal pásztázzák a mintát, és a visszaszórt elektronokat, másodlagos elektronokat, a keltett röntgen sugárzást v. fényt detektálják, ezen információk alapján alkotnak képet, vagy nyernek spektroszkópiai információt a mintáról. A minta felülete elektromosan vezető kell, hogy legyen a töltésfelhalmozódás elkerülése végett, így szigetelőkön vékony fémes bevonatot kell létrehozni. Pásztázó elektronmikroszkóppal pár nanométeres felbontás érhető el.

Jeol.png
14. ábra JEOL típusú pásztázó elektronmikroszkóp fényképe a BME Fizika Tanszék és az MFA közös laboratóriumában.

Elektronsugár litográfia (E-beam lithography)


A pásztázó elektronmikroszkópot nanoszerkezetek készítésére is használhatjuk. Ehhez az elektronmikroszkópot egy író egységgel egészítjünk ki, mely az egyszerű raszter-szkennelés helyett tetszőleges, általunk tervezett pálya mentén mozgatja az elektronsugarat. Először egy hordozóra (pl. Si lapka) egy vékony polimer réteget viszünk fel, az un. rezisztet (pl. PMMA). Ezután a tervek alapján végigpásztázzuk a rezisztet az elektronnyalábbal. A megvilágítás hatására a reziszt hosszú szénláncai felhasadnak rövidebbekre, így a megvilágított rész az előhívóval könnyen feloldható és eltávoltítható (ill. negatív reziszt esetén a meg nem világított rész oldódik az előhívóban). Ezután fémet párologtatunk a felületre. A megvilágított részeken a fém a hordozóra, amúgy a reziszt tetejére kerül. Végül megfelelő anyaggal a megmaradt rezisztet, és így a tetején levő fém réteget is eltávolítjuk, így csak a megvilágított helyeken maradnak fém nanostruktúrák. Az elektronsugár-litográfia fenti lépéseit a 15. ábra videója szemlélteti. A fém elektródák párologtatásához különböző módszerek állnak rendelkezésre, erről a vékonyréteg leválasztás fejezetben adunk részletes leírást.

Litography anim.ogv
15. ábra. Elektronsugaras litográfia.

Elektronsugár-litográfia segítségével különböző nanofizikai objektumokat (pl. grafén darabka, szén nanocső, félvezető nanovezeték, stb.) könnyedén kontaktálhatunk vékony fém elektródákkal, így kialakíthatjuk az általunk megtervezett nanoáramkört, a 16. ábra erre mutat példát.

Nanoáramkorok.jpg
16. ábra. Cooper-pár feltörő nanoáramkör: InAs nanovezeték normál és szupravezető elektródákkal, illetve számos kapuelektródával. Forrás: a BME Fizika Tanszék és a Bázeli Egyetem együttműködésében folyó kutatások.


Ugyan az elektronsugarat pár nm átmérőre fókuszálhatjuk, a rezisztben keltett másodlagos elektronok diffúziójuk során további kötéseket törnek fel a rezisztben (17. ábra). Emiatt az elektronsugár-mikroszkópia felbontásánál a litográfia felbontása egy nagyságrenddel rosszabb (>20nm).

Electron beam scattering.jpg
17. ábra. Bejövő elektron által keltett másodlagos elektronok diffúziója a rezisztben, forrás: Wikipedia.

Kétdimenziós elektrongáz GaxAl1-xAs heteroszerkezetekben


Mind a nanofizikai kutatásokban, mind a nanofizika alkalmazásában kiemelt szerepet tölt be egy speciális anyagcsalád, a GaxAl1-xAs heteroszerkezetek, illetve az ezekben kialakuló kétdimenziós elektrongáz rendszerek. Mind a GaAs mind az AlAs félvezető anyagok, jelentősen eltérő tiltott sáv szélességgel (gap-el). A két anyag rácsszerkezete azonban megegyezik, és rácsállandójuk is szinte teljesen azonos (az eltérés kissebb mint 0.15%). Ennek köszönhetően egy GaAs egykristályra szinte kristályhiba nélkül ránöveszthető egy AlAs egykristály, sőt különböző koncentrációjú GaxAl1-xAs kristály is, azaz \setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0% megfelelő megválasztásával széles tartományban változtathatjuk az egymásra növesztett félvezető rétegek tiltott sávjának szélességét. A vékonyréteg leválasztás c. fejezetben ismertetett epitaxiális rétegleválasztási módszer (Molecular Beam Epitaxy, MBE) segítségével valósítható meg az, hogy a különböző tiltott sávú rétegeket epitaxiálisan, azaz a kristályrendet követve növesszük egymásra.

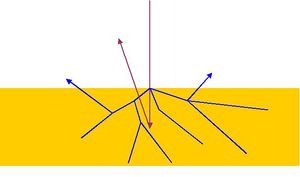
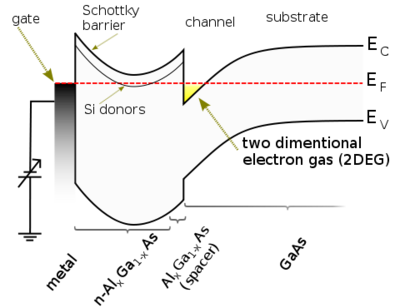
A 18. ábrán szemléltetett rétegszerkezetben jobb oldalon egy GaAs réteg található, melyhez bal oldalon egy Si-al dópolt GaxAl1-xAs réteg csatlakozik. A két anyag kilépési munkája és kémiai potenciálja eltér, viszont érintkezésükkor töltésátrendeződések után a kémiai potenciálok kiegyenlítődnek. Ekkor a sávok "elhajlása" miatt a határfelületen kialakul egy szabadon mozgó elektronokat tartalmazó kétdimenziós réteg, az úgynevezett 2D elektron gáz, 2DEG. A kétdimenziós elektrongáz potenciálja a GaxAl1-xAs rétegre párologtatott fémes kapuelektróda segítségével változtatható, megfelelő feszültséggel a kétdimenziós elektrongáz ki is üríthető. A szinte tökéletes kristályrendet követő határfelületnek köszönhetően az elektronok szabadon, kevés szóródással mozoghatnak a kétdimenziós elektrongázban, azaz nagy lesz az elektronok szabadúthossza, illetve mobilitása. A határfelület tökéletességét tovább növeli, hogy az adalékoló Si atomokat nem közvetlenül a határfelület tartományában, hanem attól távolabb helyezik el (remote doping, v. delta doping), így az elektronok az adalékoló atomokon sem szóródnak jelentős mértékben. Alacsony hőmérsékleten a 2DEG-ben mozgó elektronok szabad úthossza akár milliméteres nagyságrendű is lehet.

2DEG band.svg
18. ábra. Kétdimenziós elektrongáz GaxAl1-xAs heteroszerkezetben, forrás: Wikipedia

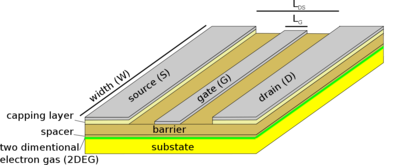
A GaxAl1-xAs heteroszerkezetekből készült nagy mobilitású tranzisztorok (High Electron Mobility Transistor, HEMT, lásd 19. ábra) tették lehetővé a mobil kommunikációt, és a félvezető lézerek is általában GaxAl1-xAs heteroszerkezetekből készülnek, azaz ez a félvezető anyagcsalád kiemelkedő jelentőségű a technikai alkalmazások szempontjából. A félvezető heteroszerkezetek fejlesztéséért Zhores I. Alferov és Herbert Kroemer 2000-ben Nobel-díjat kapott.


HEMT.svg
19. ábra. Nagy elektronmobilitású tranzisztor, forrás: Wikipedia

A 2DEG rendszerek a nanofizikai kutatásokban is alapvető szerepet játszanak. A heteroszerkezet tetejére párologtatott fém elektródák és a heteroszerkezet között Schottky gát alakul ki, így az elektródákra kapcsolt kapcsolt feszültség csak a heteroszerkezet potenciálját hangolja, de az elektródából nem jutnak át elektronok a heteroszerkezetbe. Az ilyen típusú elektródákat kapuelektródának nevezzük. A 2DEG fölé helyezett, megfelelően kialakított kapuelektródákkal a 2DEG elektronjait az általunk kívánt tartományba kényszeríthetjük. Ilyen 2DEG-ből kialakított struktúrákra a kvantum pöttyök illetve a vezetőképesség-kvantálás fejezetekben látunk példákat.

A 2DEG kontaktálásához (pl. a forrás és nyelő elektróda kialakításához) fémes, ohmikus kontaktusokra van szükség. Ha a fémes elektróda alatt a félvezető struktúrát erősen dópoljuk, akkor nagyon lecsökken a Schottky gát szélessége, így gyakorlatilag ohmikus kontaktus alakul ki.

Hivatkozások

Fent hivatkozott szakcikkek

[1] H. C. Manoharan, C. P. Lutz & D. M. Eigler: Quantum mirages formed by coherent projection of electronic structure, Nature 403 p512-515 (2000)

[2] C. Ö. Girit et. al: Graphene at the Edge: Stability and Dynamics, Science 323 p1705-1708 (2009)

Ajánlott könyvek és összefoglaló cikkek

Ajánlott kurzusok

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Nanoszerkezetek_előállítási_és_vizsgálati_technikái&oldid=12568”