„Kvantumpöttyök” változatai közötti eltérés
(→Kvantum pöttyök, energia skálák) |
|||
| (3 szerkesztő 72 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<wlatex> | <wlatex> | ||
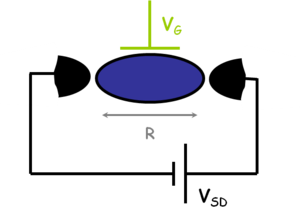
| − | Korábban láttunk páldákat olyan nanoszerkezetekre, ahol az elektronok mozgása csak két illetve egy dimenzióban megengedett (GaAs/AlGaAs határfelületen létrejövő | + | Korábban láttunk páldákat olyan nanoszerkezetekre, ahol az elektronok mozgása csak két illetve egy dimenzióban megengedett (GaAs/AlGaAs határfelületen létrejövő kétdimenziós elektrongázok ill. pontkontaktusok). Ezen alacsony dimenziós szerkezetek olyan érdekes jelenségek megfigyelését teszik lehetővé, mint a [[Kvantált Hall-jelenség|kvantált Hall-effektus]] vagy a [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Vezetőképesség-kvantálás kvantum-pontkontaktusban|vezetőképesség-kvantálás]]. Ebben a fejezetben egy további alacsony dimenziós nanoszerkezet-családdal fogunk foglalkozni, az ún. kvantumpöttyökkel (kvantum-dotokkal), ahol az elektronok mozgását mind a három dimenzió mentén megszorítjuk. Ezen nulla dimenziós szerkezetek egy mesterséges szigetet jelentenek az elektronok számára, amik tipikus sugara $R \approx 1\mu m - 1nm$ (lásd 1. ábra). Kvantumpöttyöket gyakran a térvezérelt tranzisztorokhoz hasonló áramkörökbe építik: két elektródát kapcsolnak a szigethez (forrás/source és nyelő/drain), amikből elektronok juthatnak a szigetre és távozhatnak onnét. Ezt egy harmadik, ún. kapu/gate elektróda egészíti ki, ami a sziget elektromos potenciájának változtatását teszi lehetővé. A továbbiakban ilyen térvezérelt geometriájú kvantumpöttyöket fogunk tárgyalni. |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 15. sor: | 6. sor: | ||
| [[Fájl:QD_1.png|közép|300px|]] | | [[Fájl:QD_1.png|közép|300px|]] | ||
|- | |- | ||
| − | | align="center"|1. ábra Kvantum pötty/dot áramkörbe építve. Egy $R$ sugarú sziget, forrás/source és nyelő/drain | + | | align="center"|1. ábra. ''Kvantum pötty/dot áramkörbe építve. Egy $R$ sugarú sziget, forrás/source és nyelő/drain elektródák között (fekete) illetve egy kapu/gate elektródához csatolva (zöld).'' |
|} | |} | ||
| − | + | ==Megvalósítás== | |
| − | + | Kvantumpöttyöket különböző módszerekkel lehet létrehozni. Ezekre lássunk néhány példát: | |
| − | + | * Egy kétdimenziós elektrongázra kapuelektródákat téve, az elektródákra adott negatív feszültséggel a kapuelektródák alól az elektronok kiszorulnak. A kapukat megfelelően elrendezve létre lehet hozni szigeteket az elektrongázból, amik kvantumpöttyként viselkednek (lásd. 2a ábra). Például az egyik kapura adott $V_G$ feszültség változtatásával a pötty potenciálja hangolható. | |
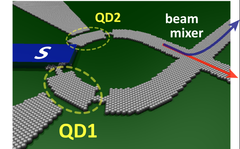
| − | + | * Kvantumpöttyök készíthetőek változatos nanoszerkezetekből: szén nanocsövekből, félvezető nanopálcákból, grafénból. A 2b. ábra mutat egy példát grafén kvantumpöttyre. Plazmamarással egy szigetet vágunk ki a szén síkból, ami elvékonyított részekkel kapcsolódhat az elektródákhoz. | |
| − | * Egy kétdimenziós | + | * Elektródák közé juttatott nagyobb molekula (pl. fullerén) is mutathat kvantumpötty viselkedést (lásd. 2c ábra). A molekulák kis méretéből adódóan ($R \approx 1$nm) a három elektróda elhelyezése problémás. |
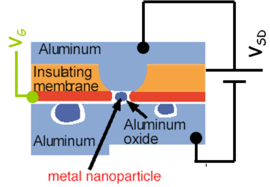
| − | * | + | * Kvantumpöttyként működnek kis fémes szemcsék is. Ha ezeket szigetelő rétegbe ágyazzuk, és fém elekródákat hozunk létre mellettük, a szokásos forrást, nyelőt és kapu elektródát tartalmazó geometria létrehozható (lásd. 2d ábra). |
| − | * Elektródák közé juttatott nagyobb molekula (pl. fullerén) is mutathat | + | |
| − | * | + | |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 34. sor: | 23. sor: | ||
| [[Fájl:QD_Peldak_01.png|közép|270px|]] | | [[Fájl:QD_Peldak_01.png|közép|270px|]] | ||
|- | |- | ||
| − | | align="center"| | + | | align="center"|2a. ábra. ''2DEG-ban kapuelektródákkal létrehozott kvantumpötty. A fekete körvonalú szürke területek a kapuelektródák, a rájuk kapcsolt negatív feszültség hozza létre az elektronok csapdázó potenciálját. A zölddel jelölt elektródára adott feszültség szolgál a potenciálgödör hangolására. Elektronok a sárga tartományban vannak.''<sup>[http://books.google.hu/books/about/Electron_Transport_in_Quantum_Dots.html?id=dP_RuhA_77IC&redir_esc=y 1]</sup> |
| − | | align="center"| | + | | align="center"|2b. ábra. ''Grafénből kimart szerkezet két kvantumpöttyel (QD1 és QD2).'' |
| − | | align="center"| | + | | align="center"|2c. ábra. ''Molekulán alapuló kvantum pötty.''<sup>[http://www.sciencedirect.com/science/journal/03701573/345/2-3 2]</sup> |
| − | | align="center"| | + | | align="center"|2d. ábra. ''Oxidba ágyazott alumínium nanoszemcsén alapuló kvantumpötty.''<sup>[http://www.sciencedirect.com/science/journal/03701573/345/2-3 2]</sup> |
|} | |} | ||
| − | ==== | + | ==Energiaskálák== |
| + | Kvantumpöttyre helyezett elektronok viselkedését a sziget bezáró potenciálja, az elektronok közötti taszitó kölcsönhatás, illetve a szigeten töltött átlagos idő jelentősen befolyásolja. Tekintsük át az ezekhez kapcsolódó energiaskálákat: | ||
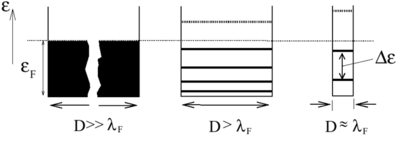
| + | * Szinttávolság (level spacing, $\Delta$): Ha a kvantumpötty mérete nem sokkal nagyobb, mint a Fermi-hullámhossz, azaz $R \sim \lambda_F$, az elektronok hullámtermészetét figyelembe kell venni. Az elektronok a sziget bezáró potenciálja által meghatározott hullámfüggvényeket tölthetik be, melyekhez a folytonos energiaspektrum helyett diszkrét energiaszintek tartoznak, ha a pötty mérete elegendően kicsi (lásd 3a. ábra). A diszkrét energiaszintek átlagos távolságát hívjuk szinttávolságanak, $\Delta$. A szinttávolság például kétdimenziós kvantumpötty esetén $\Delta \sim 1/R^2$. Tipikus értéke $R \approx 1\mu m$ esetén $\Delta \approx 10 \mu eV$. | ||
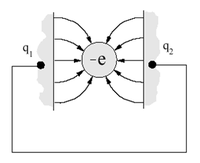
| + | * Elektrosztatikus energia (charging energy, $E_C$): Az elektronok között fellépő Coulomb-taszítás miatt energiaköltséggel jár, ha újabb és újabb elektronokat akarunk helyezni a kvantumpöttyre. Egyszerű elektrosztatikus képben (lásd 3b. ábra) ezt a többletenergiát a pötty és a környezete közötti kapacitás, $(C_\Sigma)$ határozza meg: $E_C = e^2/2C_\Sigma$ (ahol $e$ az elektrontöltés). A szigetet $R$ sugarú gömbbel közelítve $C_\Sigma \approx 4 \pi \epsilon_0 \epsilon_r R$ alapján $E_C \sim 1/R$ függést kapunk. Maradva a kétdimenziós elektrongázból kialakított pötty példájánál, egy $R \approx 1\mu m$ sugarú pötty esetében: $E_C \approx 300u$eV. | ||
| + | * Kvantum-fluktuációk energia-bizonytalansága: Mivel a kvantumpötty alagútátmeneteken keresztül csatolva van az elektródákhoz, a pöttyre helyezett elektronok véges valószínűséggel távozhatnak a pöttyről, ami a sziget eneriaszintjeinek a kiszélesedéséhez vezet. A kiszélesedés mértéke: $\delta E \approx h/ \delta t$, ahol $h$ a Plank-állandó $\delta t$ pedig az átlagos idő, amit az elektron a pöttyön tartózkodik. Az utóbbit megbecsülhetjük az alagútátmenet ellenállása ($R_T$) és kapacitása ($C$) alapján: $\delta t \approx R_T C$. Ahhoz, hogy a kvantumpötty-viselkedést a fluktuációk ne mossák el, megköveteljük, hogy $\delta E \ll E_C$ legyen. $E_C \approx e^2/2C$-t kihasználva az alagútátmenet ellenállására a következő megszorítást kapjuk: $2h/e^2 \ll R_T$. Az $R_0 = 1/G_0$ ellenálláskvantumot bevezetve, ahol $G_0 = 2 e^2/h$ a [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás|korábban definiált vezetőképesség kvantum]], a feltételt átírhatjuk $R_0 \ll R_T$ alakra. Azaz az alagútátmenet ellenállását nagyobbra kell választani az ellenálláskvantumnál, hogy a kvantumpötty-viselkedés megfigyelhető legyen. | ||
| − | + | A kapott számok alapján látható, hogy egy $1 \mu m$ körüli átmérőjű kvantumpöttynél az elektrosztatikus energia lényegesen nagyobb, mint a szinttávolság. Ugyanakkor, ha a kvantumpötty méretét csökkentjük, a szinttávolság erősebb méretfüggéséből adódóan a két skála azonos nagyságúvá válhat. Ha tekintjük a legkisebb kvantumpöttyöket, egyetlen atomot vagy molekulát, ott már a szinttávolság a domináns energiaskála. Az atomok elektronszerkezetét (azaz a periódusos rendszert) elsődlegesen a mag vonzó potenciáljában kialakuló hullámfüggvényekhez tartozó diszkrét energiaszintek határozzák meg, és az elektronok közötti Coulomb-kölcsönhatás csak korrekciót ad ehhez. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | A kapott számok alapján látható, hogy egy $1 \mu | + | |
| 57. sor: | 44. sor: | ||
| [[Fájl:QD_EnergiaSkala_02.png|közép|200px|]] | | [[Fájl:QD_EnergiaSkala_02.png|közép|200px|]] | ||
|- | |- | ||
| − | | align="center"| | + | | align="center"|3a. ábra ''Kvantumbezártságból adódó energiaszintek.''<sup>[http://books.google.hu/books/about/Electron_Transport_in_Quantum_Dots.html?id=dP_RuhA_77IC&redir_esc=y 1]</sup> |
| − | | align="center"| | + | | align="center"|3b. ábra ''Kvatumpöttyre helyezett elektron elektrosztatikus energiája.''<sup>[http://books.google.hu/books/about/Electron_Transport_in_Quantum_Dots.html?id=dP_RuhA_77IC&redir_esc=y 1]</sup> |
|} | |} | ||
| + | ==Kvantumpöttyök leírása elektrosztatikus képben== | ||
| + | Kvantumpöttybe zárt elektronok eneregiája az elektronok kinetikus energiájából, és az elektronok között fellépő elektron-elektron kölcsönhatásból adódik össze. Az elektronok közötti taszításból származó többletenergiát egyszerűen közelíhetjük elektrosztatikus képben a kvantumpötty és a környezete közötti kapacitások figyelembevételével. Az előző részben kapott becslések alapján láttuk, hogy egy átlagos méretű kvantumpötty esetén a kinetikus energiát és a bezáró potenciált együttesen jellemző szinttávolság lényegesen kisebb, mint a kapacitások alapján becsült elektrosztatikus energia, így a következőkben kizárólag az elektrosztatikus energiatagot megtartva adunk leírást a kvantumpöttyök viselékedésére. Látni fogjuk, hogy a kvantumpöttyök alapvető jelenségei (mint például a Coulomb-blokád, Coulomb-gyémánt szerkezet, egy elektron tranzisztor viselkedés ...) már ebben az egyszerű képben is megérthetőek. | ||
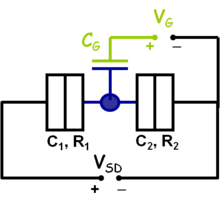
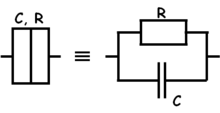
| − | + | Az 1. ábrán látható áramkörbe épített kvantumpöttyöt elektrosztatikus képben a 4. ábrán látható módon helyettesíthetjük. A pötty területe (kék) két alagútátmeneten keresztül kapcsolődik a forrás és a nyelő oldal közé kapcsolt $V_{SD}$ feszültségforráshoz. Az alagútátmeneteket párhuzamosan kapcsolt kapacitással ($C$) és ellenállással modellezhetjük ($R$). A kapacitás fegyverzeteit az alagútátmenet által elválasztott két közeli felület adja, a tipikusan nagy ellennállás érték pedig az alagútátmeneten történő átjutást jellemzi. A kvantumpötty közelében található kapuelektródát (zöld) a sziget és az elektróda közötti kapacitással irhatjuk le ($C_G$). A kapuelektródára kapcsolt $V_G$ feszültség segítségével lehet majd a pötty betöltöttségét hangolni. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | Az 1. ábrán látható áramkörbe épített | + | |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 73. sor: | 58. sor: | ||
| [[Fájl:QD_CoulombEnergia_02.png|közép|220px|]] | | [[Fájl:QD_CoulombEnergia_02.png|közép|220px|]] | ||
|- | |- | ||
| − | | align="center"|4a. ábra | + | | align="center"|4a. ábra. ''Kvantumpötty elektrosztatikus helyettestő képe'' |
| − | | align="center"|4b. ábra Az elektródákat elválasztó alagútátmenetek helyettesítő képe | + | | align="center"|4b. ábra. ''Az elektródákat elválasztó alagútátmenetek helyettesítő képe'' |
|} | |} | ||
| − | Elektrosztatikus közelítésben a | + | Elektrosztatikus közelítésben a kvantumpötty energiáját a pöttyöt körbehatároló kapacitások segítségével a következőképpen irhatjuk fel: |
$$E_C (N, V_{SD}=0, V_G = 0) = (Ne)^2/2C_{\Sigma}$$, | $$E_C (N, V_{SD}=0, V_G = 0) = (Ne)^2/2C_{\Sigma}$$, | ||
| − | ahol $N$ a | + | ahol $N$ a kvantumpöttyön lévő elektronok száma, $C_{\Sigma}$ pedig a pötty és a környezete közötti összkapacitás: $C_{\Sigma}=C_{S}+C_{D}+C_{G}$. |
| − | $E_C$ kifejezése alapján | + | $E_C$ kifejezése alapján ha az elektronok számát növelni akarjuk eggyel, az a következő többlet energiába kerül: $\Delta E_C = E_C(N+1)-E_C(N) \approx N e^2/C_{\Sigma}$. |
Véges kapufeszültség esetén vigyázni kell az energia felírásakor, hiszen az elektronok pöttyre helyezése során a kapu telepe is munkát végez, ami csökkenti a feltöltéshez szükséges energiát. Ha a pöttyre helyezett töltés $-eN$, akkor a párhuzamosan kapcsolt kapacitások miatt a kapu elektróda fegyverzetén $Q_{G}=-eN C_G/ C_{\Sigma}$ töltés lesz. A pötty energiáját a telep | Véges kapufeszültség esetén vigyázni kell az energia felírásakor, hiszen az elektronok pöttyre helyezése során a kapu telepe is munkát végez, ami csökkenti a feltöltéshez szükséges energiát. Ha a pöttyre helyezett töltés $-eN$, akkor a párhuzamosan kapcsolt kapacitások miatt a kapu elektróda fegyverzetén $Q_{G}=-eN C_G/ C_{\Sigma}$ töltés lesz. A pötty energiáját a telep | ||
| − | $W_{ | + | $W_{GTelep}=\int_{felt\ddot{o}lt \acute{e}s}{I_{G \acute{a}gban} V_G dt}= -Q_G V_G$ munkavégzésével korrigálva kapjuk: $E_C= E_C(V_G=0)-W_{Gtelep}$. Mindezek alapján: |
| − | + | $$E_C (N, V_{SD}=0, V_G) = 1/2C_{\Sigma}(Ne-V_G C_G)^2 + \alpha$$, | |
| − | + | ahol $\alpha$ egy $N$-től független mennyiség. A fentiek alapján a kapufeszültség hatása egy $Q_0=V_G C_G$ ún. offset-töltéssel azonos. | |
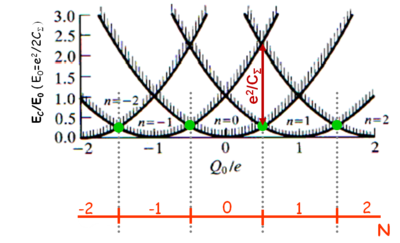
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | $E_C (N, V_{SD}=0, V_G) = 1/2C_{\Sigma}(Ne-V_G C_G)^2 + \alpha$, | + | |
| − | + | ||
| − | ahol $\alpha$ $N$ független | + | |
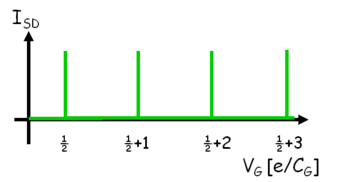
| + | Az elektrosztatikus energiára kapott $E_C$ kifejezés az 5a- ábrán látható az offset-töltés függvényében különböző $N$ elektronszámok mellett. Az ábra alapján minden egyes $Q_0$ értékre könnyen meghatározható, hogy milyen elektronszám fogja minimalizálnia a kvantum pötty energiáját. A piros tengelyen a pötty alapállapotához tartozó elektronszám van feltüntetve. Az ábrán jelölt zöld pontokban a kvantum pötty alapállapota degenerált. Például a $Q_0/e=1/2$ helyen az $N=0$ és $N=1$ állapotok energiája azonos. Ezekben a speciális pontokban az egyik elektródáról egy elektron be tud ugrani a kvantumpöttyre energiaköltség nélkül és az elektron ki tud ugrani a másik elektródára. Ezen szekvenciális elektron alagutazási folyamaton keresztül áram tud folyni a kvantumpöttyön keresztül ha kis $V_{SD}$ feszültséget kapcsolunk a két elektróda közé. Az 5b. ábra mutatja a kvantumpöttyön átfolyó áramot az offset-töltéssel arányos kapufeszültség függvényében (kis $V_{SD}$ mellett). Az áram a $V_G$ paramétertér nagyrészében nulla leszámítva egymástól egyenlő távolságban található pontokat, ahol az áram csúcsszerűen megnő. Ezeket hívjuk ún. Coulomb-csúcsoknak. Véges áramot csak ezen degenerációs pontokban kapunk, közöttük az elektronok átjutása a pöttyön blokkolva van. Ezt a jelenséget hívják ún. Coulomb-blokádnak, ami a kvantumpöttyök egyik fontos tulajdonsága. A Coulomb-blokád az elektronok közötti taszító Coulomb-kölcsönhatás és az elektromos töltés kvantáltságának a következménye. A kvantumpöttyön az elektronszám jól meghatározott, és ennek következtében áram nem tud a pöttyön keresztül folyni egészen addig, amíg az offset-töltés változtatásával degenerációs pontba nem hangoljuk az elektron szigetet. (A degenerációs pontok távolsága $\Delta Q_0/e=1$). | ||
| 105. sor: | 81. sor: | ||
| [[Fájl:QD_CoulombEnergia_04.png|közép|350px|]] | | [[Fájl:QD_CoulombEnergia_04.png|közép|350px|]] | ||
|- | |- | ||
| − | | align="center"|5a. ábra | + | | align="center"|5a. ábra. ''Kvantumpötty elektrosztatikus energiája különböző elektronszámnál (N). A zöld pontokban az alapállapot degenerált, és ezzel a pöttyön az elektronszám nem jól meghatározott. Az alapállapoti elektronszámok pirossal vannak feltüntetve.'' |
| − | | align="center"|5b. ábra Coulomb blokád jelensége | + | | align="center"|5b. ábra. ''Coulomb-blokád jelensége: a kvantumpöttyön keresztül csak $\Delta V_G = e/C_G$ távolságra eső kapufeszültségek mellett folyik áram, mikor a pöttyön az elektronszám nem meghatározott.'' |
|} | |} | ||
| + | |||
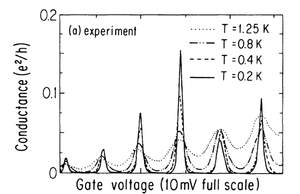
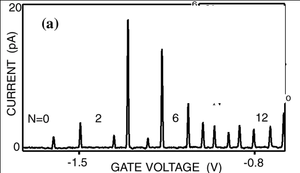
| + | A kapott elméleti várakozásokat vessük össze kvantumpöttyökön mért tipikus kísérleti eredményekkel. A 6. ábrán láthatóak vezetőképesség-mérések ($G=I/V_{SD}$) a kapufeszültség függvényében (kis $V_{SD}$ mellett). Alacsony hőmérsékleten éles csúcsok jelentkeznek, amiket nulla vezetőképességű tartományok határolnak el a Coulomb-blokádnak megfelelően. A 6a. ábrán a csúcsok egyenletesen helyezkednek el a $V_G$ tengely mentén az elektrosztatikus képben kapott eredményekkel összhangban. A hőmérséklet növelésével a csúcsok elmosódnak, és a köztes völgyekben az áram egyre nagyobbra nő. Ez a termikus elmosódás akkor válik jelentőssé, ha a pötty hőmérséklete összemérhetővé válik az elektrosztatikus energiaskálával: $k_B T \approx E_C$. A 6b. ábrán is egy hasonló mérés látható. A Coulomb-csúcsok itt is megjelennek, ugyanakkor a csúcsok távolsága nem egyenletes, ahogyan az egyszerű modellünkből várnánk. Ennek megértéséhez már az elektrosztatikus képen túl kell lépni, és figyelembe kell venni a pötty bezáró potenciáljában kialakuló diszkrét elektronállapotokat is. Az egyenletlen csúcstávolság egészen kis méretű kvantum pöttyök esetén jelentkezik, ahol $\Delta \approx E_C$ (lásd energiaskáláknál). | ||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 114. sor: | 92. sor: | ||
| [[Fájl:QD CoulombBlokad 02.png|közép|300px|]] | | [[Fájl:QD CoulombBlokad 02.png|közép|300px|]] | ||
|- | |- | ||
| − | | align="center"|6a. ábra | + | | align="center"|6a. ábra. ''Kvantumpöttyök Coulomb-csúcsai kísérletben.''<sup>[http://prl.aps.org/abstract/PRL/v66/i23/p3048_1 3]</sup> |
| − | | align="center"|6b. ábra Coulomb-csúcsok nem ekvidisztans poziciókban | + | | align="center"|6b. ábra. ''Coulomb-csúcsok nem ekvidisztans poziciókban.''<sup>[http://prl.aps.org/abstract/PRL/v77/i17/p3613_1 4]</sup> |
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| + | ==Coulomb-energiaszintek== | ||
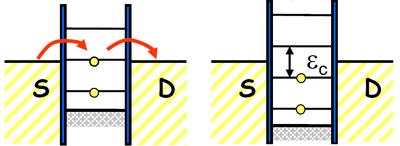
| − | + | Állítsuk a kvantumpötty kapufeszültségét $Q_0=1/2 + N$ értékre. Ilyenkor az $N+1$-ik elektoron számára éppen energetikailag kedvező, hogy bekerüljön a pöttyre. Ezt modellezhetjük úgy, hogy egy diszkrét energianívót feltételezünk a pöttyön az elektródák Fermi-energiáival azonos energián, amire ''egyetlen'' elektron helyezhető. Az egyik elektródából elektron ugorhat erre a diszkrét energiaszintre, majd a másik elektródára kiugorva áram tud folyni a pöttyön keresztül (lásd. 7. ábra bal panel). Továbbra is $Q_0=1/2 + N$ kapufeszültség értéknél maradva a következő ($N+2$-ik) elektron pöttyre helyezéséhez további $\epsilon _ C = e^2/C_{\Sigma}$ energiára van szükség (lásd 5a. ábra), ami megadja a következő diszkrét energianívó távolságát a Fermi-energiától. Az előzőeket ismételve egy kvantumpötty energiaszerkezetét leírhatjuk egymástól $\epsilon_C$ távolságra elhelyezett diszkrét energiaszintekkel, amikre ''egy-egy'' elektront lehet ráhelyezni. Ezeket az energiaszinteket szokás Coulomb-energiaszinteknek is nevezni. Az így kialakuló létra jellegű energiaszerkezet helyzetét a forrás ($S$) és a nyelő ($D$) Fermi-energiájához képest a $V_G$ kapufeszültség segítségével lehet hangolni. A 7. ábra bal paneljéhez képest a jobb panelen növeltük a kapufeszültséget. Ezáltal az energiaszintek lejjebb tolódtak, és a kvantumpötty Coulomb-blokádba került. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | [[Fájl: | + | | [[Fájl:QD_Coulomb_Energiaszint.png|közép|400px|]] |
|- | |- | ||
| − | | align="center"| | + | | align="center"|7. ábra. ''Kvantumpötty leírása Coulomb-energiaszintekkel: A függőleges az energiatengely, a forrás $S$ és a nyelő $D$ oldalon a Fermi-szintig betöltött elektronállapotok vannak jelölve sárgával. Az alagútátmenetek (kék) között a Coulomb-energiaszintek láthatóak $\epsilon_C$ távolságokra egymástól. A bal oldali ábrán az az eset látható, mikor az $N=2$ betöltés éppen megengedetté válik, az energiaszint rezonanciája miatt áram tud folyni a kvantumpöttyön keresztül. A jobb oldali ábra egy Coulomb-blokádolt esetet mutat, ahol az alsó két Coulomb-energiaszint betöltött, de a harmadik nívó még energetikailag nem érhető el.'' |
|} | |} | ||
| − | + | A 8. ábra videója szemlélteti, hogy miközben a Coulomb energiaszinteket a $V_G$ kapufeszültséggel eltoljuk, a kvantumpötty csak diszkrét tartományokban mutat véges vezetőképességet, pontosan akkor, amikor egy Coulomb energiaszint a Fermi-energiánál található. | |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | [[Fájl: | + | | [[Fájl:QDot.ogv|bélyegkép|közép|800px|thumbtime=0:17]] |
| − | + | ||
|- | |- | ||
| − | | align="center"| | + | | align="center"|8. ábra. ''Coulomb csúcsok megjelenése a Coulomb-energiaszintek hangolása közben'' |
| − | + | ||
|} | |} | ||
| − | + | ==Coulomb-gyémántok== | |
| − | + | A Coulomb-energiaszintek bevezetése segít az $S$ és $D$ oldal közé kapcsolt véges $V_{SD}$ hatásának megértésében. | |
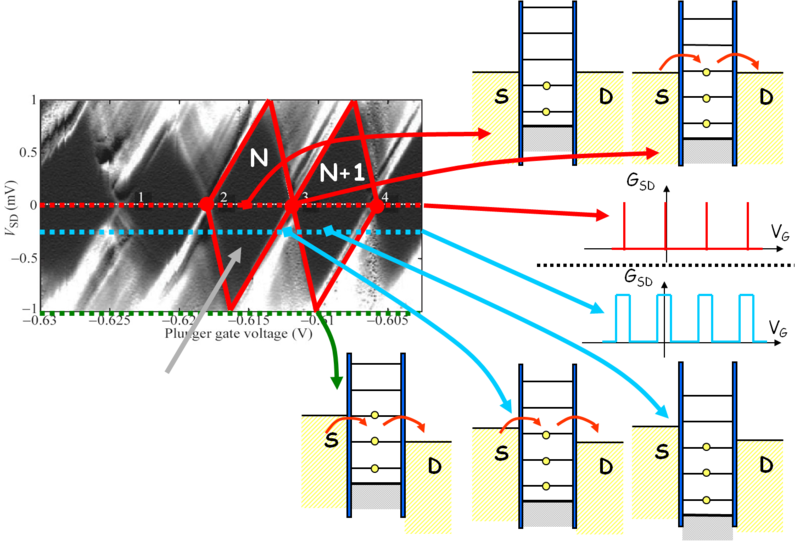
| + | A 9. ábra bal odalán látható kísérleti eredmény egy kvantumpötty vezetőképességét mutatja $V_{SD}$ illetve $V_G$ függvényében. A szürkeárnyalatos térképen nagyobb vezetőképességhez fehérebb szín tartozik. Zérus $V_{SD}$ esetén (lásd piros pontozott vonal, illetve piros nyíllal jelölt ábrarészletek) a 6. illetve 8. ábrán már bemutatott Coulomb-csúcsokat láthatjuk diszkrét $V_G$ értékeknél. Véges $V_{SD}$ esetén (kék pontozott vonal) azonban véges szélességű $V_G$ tartományban látunk áramot, egészen addig, amíg egy Coulomb-energiaszint $S$ és $D$ kémiai potenciálja között tartózkodik (lásd kék nyíllal jelölt ábrarészletek). $V_{SD} > \epsilon_C$ esetén (zöld pontozott vonal) $S$ és $D$ kémiai potenciálja között biztosan található legalább egy Coulomb-energiaszint, így tetszőleges $V_G$-nél véges vezetőképességet mérünk (lásd zöld nyíllal jelölt ábrarészlet). Ennek megfelelően megmutatható, hogy a $V_G - V_{SD}$ síkon rombusz alakú tartományokban találhatóak azak a részek, ahol nem esik Coulomb-energiaszint az $S$ és $D$ kémiai potenciáljai közé, azaz zérus a kvantumpötty vezetőképessége. A 9. ábrán jól láthatóak a fekete rombusz alakú tartományok, piros vonal szemlélteti a szélüket. Ezeket hívjuk Coulomb-gyémántoknak (-rombuszoknak), az angol Coulomb-diamond nyomán. A rombuszokon belül jól meghatározott a kvantumpöttyön tartózkodó elektronok száma, a szomszédos rombuszok egyel nagyobb (ill. kisebb) elektronszámhoz tartoznak. | ||
| − | |||
| − | |||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | [[Fájl: | + | | [[Fájl:QD CoulombBlokad 04.png|közép|800px|]] |
|- | |- | ||
| − | | align="center"| | + | | align="center"|9. ábra. ''Coulomb-gyémánt mintázat. A kvantumpötty energiaszintjei a gyémántmintázat különböző részein.'' |
|} | |} | ||
| + | Mivel egy kvantumpötty paramétereinek hangolásával úgy lehet áramot ki és bekapcsolni, hogy közben egyetlen elektronnal változik a pöttyön tartózkodó elektronok száma, így a kvantumpöttyből kialakított térvezérelt tranzisztort egyelektron-tranzisztornak is szokták nevezni. Megfelelő elrendezésben ráadásul annyira ki lehet üríteni a kvantumpöttyöt, hogy ténylegesen egyetlen vezetésben résztvevő elektron tartózkodjon rajta. | ||
| − | + | Összefoglalva a fentieket, a kvantumpöttyök viselkedését egy leegyszerűsített model keretében tárgyaltuk, ami a kvantumpöttyön az elektronok között fellépő Coulomb-taszítást vette figyelembe, ezt is egyszerű elektrosztatikus közelítésen keresztül a pötty és a környezetében található elektródák közötti kapacitások figyelembe vételével. Már ebben az egyszerű elektrosztatikis képben a kvantumpöttyök alapvető elektromos vezetési tulajdonságai, úgy mint a Coulomb-blokád jelensége vagy a Coulomb-gyémánt mintázatok megérthetőek. | |
| − | + | ==Hivatkozások== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ===Fent hivatkozott szakcikkek=== | |
| + | [1] [http://books.google.hu/books/about/Electron_Transport_in_Quantum_Dots.html?id=dP_RuhA_77IC&redir_esc=y Jonathan P Bird: ''Electron transport in quantum dots'', Kluwer Academic Publishers (2003)] | ||
| − | + | [2] [http://www.sciencedirect.com/science/journal/03701573/345/2-3 Jan von Delft and D. C. Ralph: ''Spectroscopy of Discrete Energy Levels in Ultrasmall Metallic Grains'', '''Physics Reports 345''', p61 (2001)] | |
| − | + | [3] [http://prl.aps.org/abstract/PRL/v66/i23/p3048_1 Y. Meir et al., ''Transport through a strongly interacting electron system: Theory of periodic conductance oscillations'', '''Phys. Rev. Lett. 66''', 3048 (1991)] | |
| − | + | ||
| − | + | [4] [http://prl.aps.org/abstract/PRL/v77/i17/p3613_1 S. Tarucha et al., ''Shell Filling and Spin Effects in a Few Electron Quantum Dot'', '''Phys. Rev. Lett. 77''', 3613 (1996)] | |
| − | + | ===Ajánlott könyvek és összefoglaló cikkek=== | |
| + | *[http://books.google.hu/books/about/Electronic_Transport_in_Mesoscopic_Syste.html?id=28BC-ofEhvUC&redir_esc=y S. Datta: ''Electronic Transport in Mesoscopic Systems'', Cambridge University Press (1997)] | ||
| + | *[http://books.google.hu/books/about/Semiconductor_Nanostructures.html?id=qD6623gfAZgC&redir_esc=y Thomas Ihn: ''Semiconducting nanosctructures'', OUP Oxford (2010)] | ||
| + | *[http://books.google.hu/books?id=YNr4OcCExUcC&printsec=frontcover&dq=Nazarov+quantum+transport&hl=hu&sa=X&ei=2SzZUfGCMYna4ASDq4DQBQ&ved=0CDIQ6AEwAA Yuli V. Nazarov, Yaroslav M. Blanter: ''Quantum Transport: Introduction to Nanoscience'', Cambridge University Press (2009)] | ||
| + | ===Ajánlott kurzusok=== | ||
| + | *[[Új kísérletek a nanofizikában|''Új kísérletek a nanofizikában'', Halbritter András és Csonka Szabolcs, BME Fizika Tanszék]] | ||
| + | *[[Transzport komplex nanoszerkezetekben|''Transzport komplex nanoszerkezetekben'', Halbritter András, Csonka Szabolcs, Csontos Miklós, Makk Péter, BME Fizika Tanszék]] | ||
| + | *[[Alkalmazott szilárdtestfizika|''Alkalmazott szilárdtestfizika'', Mihály György, BME Fizika Tanszék]] | ||
| + | *[[Fizika 3 - Villamosmérnöki mesterszak|''Fizika 3'', Mihály György, BME Fizika Tanszék (mérnök hallgatóknak)]] | ||
| + | *[http://www.phy.bme.hu/~zarand/mezoszkopia.html ''Mezoszkopikus rendszerek fizikája'', Zaránd Gergely, BME Elméleti Fizika Tanszék] | ||
| + | *''Mezoszkopikus rendszerek fizikája'', Cserti József, ELTE Komplex Rendszerek Fizikája Tanszék | ||
</wlatex> | </wlatex> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
A lap jelenlegi, 2013. szeptember 17., 17:21-kori változata
Korábban láttunk páldákat olyan nanoszerkezetekre, ahol az elektronok mozgása csak két illetve egy dimenzióban megengedett (GaAs/AlGaAs határfelületen létrejövő kétdimenziós elektrongázok ill. pontkontaktusok). Ezen alacsony dimenziós szerkezetek olyan érdekes jelenségek megfigyelését teszik lehetővé, mint a kvantált Hall-effektus vagy a vezetőképesség-kvantálás. Ebben a fejezetben egy további alacsony dimenziós nanoszerkezet-családdal fogunk foglalkozni, az ún. kvantumpöttyökkel (kvantum-dotokkal), ahol az elektronok mozgását mind a három dimenzió mentén megszorítjuk. Ezen nulla dimenziós szerkezetek egy mesterséges szigetet jelentenek az elektronok számára, amik tipikus sugara 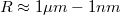 (lásd 1. ábra). Kvantumpöttyöket gyakran a térvezérelt tranzisztorokhoz hasonló áramkörökbe építik: két elektródát kapcsolnak a szigethez (forrás/source és nyelő/drain), amikből elektronok juthatnak a szigetre és távozhatnak onnét. Ezt egy harmadik, ún. kapu/gate elektróda egészíti ki, ami a sziget elektromos potenciájának változtatását teszi lehetővé. A továbbiakban ilyen térvezérelt geometriájú kvantumpöttyöket fogunk tárgyalni.
(lásd 1. ábra). Kvantumpöttyöket gyakran a térvezérelt tranzisztorokhoz hasonló áramkörökbe építik: két elektródát kapcsolnak a szigethez (forrás/source és nyelő/drain), amikből elektronok juthatnak a szigetre és távozhatnak onnét. Ezt egy harmadik, ún. kapu/gate elektróda egészíti ki, ami a sziget elektromos potenciájának változtatását teszi lehetővé. A továbbiakban ilyen térvezérelt geometriájú kvantumpöttyöket fogunk tárgyalni.
1. ábra. Kvantum pötty/dot áramkörbe építve. Egy  sugarú sziget, forrás/source és nyelő/drain elektródák között (fekete) illetve egy kapu/gate elektródához csatolva (zöld). sugarú sziget, forrás/source és nyelő/drain elektródák között (fekete) illetve egy kapu/gate elektródához csatolva (zöld).
|
Megvalósítás
Kvantumpöttyöket különböző módszerekkel lehet létrehozni. Ezekre lássunk néhány példát:
- Egy kétdimenziós elektrongázra kapuelektródákat téve, az elektródákra adott negatív feszültséggel a kapuelektródák alól az elektronok kiszorulnak. A kapukat megfelelően elrendezve létre lehet hozni szigeteket az elektrongázból, amik kvantumpöttyként viselkednek (lásd. 2a ábra). Például az egyik kapura adott
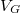 feszültség változtatásával a pötty potenciálja hangolható.
feszültség változtatásával a pötty potenciálja hangolható.
- Kvantumpöttyök készíthetőek változatos nanoszerkezetekből: szén nanocsövekből, félvezető nanopálcákból, grafénból. A 2b. ábra mutat egy példát grafén kvantumpöttyre. Plazmamarással egy szigetet vágunk ki a szén síkból, ami elvékonyított részekkel kapcsolódhat az elektródákhoz.
- Elektródák közé juttatott nagyobb molekula (pl. fullerén) is mutathat kvantumpötty viselkedést (lásd. 2c ábra). A molekulák kis méretéből adódóan (
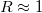 nm) a három elektróda elhelyezése problémás.
nm) a három elektróda elhelyezése problémás.
- Kvantumpöttyként működnek kis fémes szemcsék is. Ha ezeket szigetelő rétegbe ágyazzuk, és fém elekródákat hozunk létre mellettük, a szokásos forrást, nyelőt és kapu elektródát tartalmazó geometria létrehozható (lásd. 2d ábra).
| 2a. ábra. 2DEG-ban kapuelektródákkal létrehozott kvantumpötty. A fekete körvonalú szürke területek a kapuelektródák, a rájuk kapcsolt negatív feszültség hozza létre az elektronok csapdázó potenciálját. A zölddel jelölt elektródára adott feszültség szolgál a potenciálgödör hangolására. Elektronok a sárga tartományban vannak.1 | 2b. ábra. Grafénből kimart szerkezet két kvantumpöttyel (QD1 és QD2). | 2c. ábra. Molekulán alapuló kvantum pötty.2 | 2d. ábra. Oxidba ágyazott alumínium nanoszemcsén alapuló kvantumpötty.2 |
Energiaskálák
Kvantumpöttyre helyezett elektronok viselkedését a sziget bezáró potenciálja, az elektronok közötti taszitó kölcsönhatás, illetve a szigeten töltött átlagos idő jelentősen befolyásolja. Tekintsük át az ezekhez kapcsolódó energiaskálákat:
- Szinttávolság (level spacing,
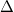 ): Ha a kvantumpötty mérete nem sokkal nagyobb, mint a Fermi-hullámhossz, azaz
): Ha a kvantumpötty mérete nem sokkal nagyobb, mint a Fermi-hullámhossz, azaz 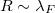 , az elektronok hullámtermészetét figyelembe kell venni. Az elektronok a sziget bezáró potenciálja által meghatározott hullámfüggvényeket tölthetik be, melyekhez a folytonos energiaspektrum helyett diszkrét energiaszintek tartoznak, ha a pötty mérete elegendően kicsi (lásd 3a. ábra). A diszkrét energiaszintek átlagos távolságát hívjuk szinttávolságanak,
, az elektronok hullámtermészetét figyelembe kell venni. Az elektronok a sziget bezáró potenciálja által meghatározott hullámfüggvényeket tölthetik be, melyekhez a folytonos energiaspektrum helyett diszkrét energiaszintek tartoznak, ha a pötty mérete elegendően kicsi (lásd 3a. ábra). A diszkrét energiaszintek átlagos távolságát hívjuk szinttávolságanak, 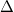 . A szinttávolság például kétdimenziós kvantumpötty esetén
. A szinttávolság például kétdimenziós kvantumpötty esetén 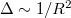 . Tipikus értéke
. Tipikus értéke 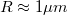 esetén
esetén 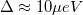 .
.
- Elektrosztatikus energia (charging energy,
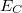 ): Az elektronok között fellépő Coulomb-taszítás miatt energiaköltséggel jár, ha újabb és újabb elektronokat akarunk helyezni a kvantumpöttyre. Egyszerű elektrosztatikus képben (lásd 3b. ábra) ezt a többletenergiát a pötty és a környezete közötti kapacitás,
): Az elektronok között fellépő Coulomb-taszítás miatt energiaköltséggel jár, ha újabb és újabb elektronokat akarunk helyezni a kvantumpöttyre. Egyszerű elektrosztatikus képben (lásd 3b. ábra) ezt a többletenergiát a pötty és a környezete közötti kapacitás, 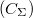 határozza meg:
határozza meg: 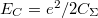 (ahol
(ahol  az elektrontöltés). A szigetet
az elektrontöltés). A szigetet  sugarú gömbbel közelítve
sugarú gömbbel közelítve 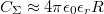 alapján
alapján 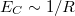 függést kapunk. Maradva a kétdimenziós elektrongázból kialakított pötty példájánál, egy
függést kapunk. Maradva a kétdimenziós elektrongázból kialakított pötty példájánál, egy 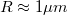 sugarú pötty esetében:
sugarú pötty esetében: 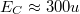 eV.
eV.
- Kvantum-fluktuációk energia-bizonytalansága: Mivel a kvantumpötty alagútátmeneteken keresztül csatolva van az elektródákhoz, a pöttyre helyezett elektronok véges valószínűséggel távozhatnak a pöttyről, ami a sziget eneriaszintjeinek a kiszélesedéséhez vezet. A kiszélesedés mértéke:
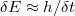 , ahol
, ahol  a Plank-állandó
a Plank-állandó 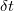 pedig az átlagos idő, amit az elektron a pöttyön tartózkodik. Az utóbbit megbecsülhetjük az alagútátmenet ellenállása (
pedig az átlagos idő, amit az elektron a pöttyön tartózkodik. Az utóbbit megbecsülhetjük az alagútátmenet ellenállása (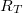 ) és kapacitása (
) és kapacitása ( ) alapján:
) alapján: 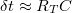 . Ahhoz, hogy a kvantumpötty-viselkedést a fluktuációk ne mossák el, megköveteljük, hogy
. Ahhoz, hogy a kvantumpötty-viselkedést a fluktuációk ne mossák el, megköveteljük, hogy 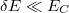 legyen.
legyen. 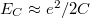 -t kihasználva az alagútátmenet ellenállására a következő megszorítást kapjuk:
-t kihasználva az alagútátmenet ellenállására a következő megszorítást kapjuk: 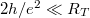 . Az
. Az 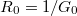 ellenálláskvantumot bevezetve, ahol
ellenálláskvantumot bevezetve, ahol 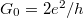 a korábban definiált vezetőképesség kvantum, a feltételt átírhatjuk
a korábban definiált vezetőképesség kvantum, a feltételt átírhatjuk 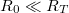 alakra. Azaz az alagútátmenet ellenállását nagyobbra kell választani az ellenálláskvantumnál, hogy a kvantumpötty-viselkedés megfigyelhető legyen.
alakra. Azaz az alagútátmenet ellenállását nagyobbra kell választani az ellenálláskvantumnál, hogy a kvantumpötty-viselkedés megfigyelhető legyen.
A kapott számok alapján látható, hogy egy 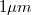 körüli átmérőjű kvantumpöttynél az elektrosztatikus energia lényegesen nagyobb, mint a szinttávolság. Ugyanakkor, ha a kvantumpötty méretét csökkentjük, a szinttávolság erősebb méretfüggéséből adódóan a két skála azonos nagyságúvá válhat. Ha tekintjük a legkisebb kvantumpöttyöket, egyetlen atomot vagy molekulát, ott már a szinttávolság a domináns energiaskála. Az atomok elektronszerkezetét (azaz a periódusos rendszert) elsődlegesen a mag vonzó potenciáljában kialakuló hullámfüggvényekhez tartozó diszkrét energiaszintek határozzák meg, és az elektronok közötti Coulomb-kölcsönhatás csak korrekciót ad ehhez.
körüli átmérőjű kvantumpöttynél az elektrosztatikus energia lényegesen nagyobb, mint a szinttávolság. Ugyanakkor, ha a kvantumpötty méretét csökkentjük, a szinttávolság erősebb méretfüggéséből adódóan a két skála azonos nagyságúvá válhat. Ha tekintjük a legkisebb kvantumpöttyöket, egyetlen atomot vagy molekulát, ott már a szinttávolság a domináns energiaskála. Az atomok elektronszerkezetét (azaz a periódusos rendszert) elsődlegesen a mag vonzó potenciáljában kialakuló hullámfüggvényekhez tartozó diszkrét energiaszintek határozzák meg, és az elektronok közötti Coulomb-kölcsönhatás csak korrekciót ad ehhez.
| 3a. ábra Kvantumbezártságból adódó energiaszintek.1 | 3b. ábra Kvatumpöttyre helyezett elektron elektrosztatikus energiája.1 |
Kvantumpöttyök leírása elektrosztatikus képben
Kvantumpöttybe zárt elektronok eneregiája az elektronok kinetikus energiájából, és az elektronok között fellépő elektron-elektron kölcsönhatásból adódik össze. Az elektronok közötti taszításból származó többletenergiát egyszerűen közelíhetjük elektrosztatikus képben a kvantumpötty és a környezete közötti kapacitások figyelembevételével. Az előző részben kapott becslések alapján láttuk, hogy egy átlagos méretű kvantumpötty esetén a kinetikus energiát és a bezáró potenciált együttesen jellemző szinttávolság lényegesen kisebb, mint a kapacitások alapján becsült elektrosztatikus energia, így a következőkben kizárólag az elektrosztatikus energiatagot megtartva adunk leírást a kvantumpöttyök viselékedésére. Látni fogjuk, hogy a kvantumpöttyök alapvető jelenségei (mint például a Coulomb-blokád, Coulomb-gyémánt szerkezet, egy elektron tranzisztor viselkedés ...) már ebben az egyszerű képben is megérthetőek.
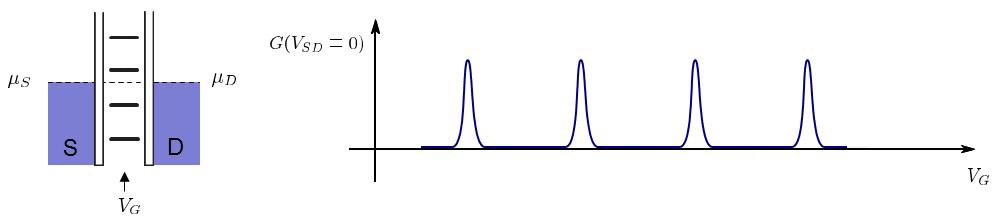
Az 1. ábrán látható áramkörbe épített kvantumpöttyöt elektrosztatikus képben a 4. ábrán látható módon helyettesíthetjük. A pötty területe (kék) két alagútátmeneten keresztül kapcsolődik a forrás és a nyelő oldal közé kapcsolt 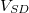 feszültségforráshoz. Az alagútátmeneteket párhuzamosan kapcsolt kapacitással (
feszültségforráshoz. Az alagútátmeneteket párhuzamosan kapcsolt kapacitással ( ) és ellenállással modellezhetjük (
) és ellenállással modellezhetjük ( ). A kapacitás fegyverzeteit az alagútátmenet által elválasztott két közeli felület adja, a tipikusan nagy ellennállás érték pedig az alagútátmeneten történő átjutást jellemzi. A kvantumpötty közelében található kapuelektródát (zöld) a sziget és az elektróda közötti kapacitással irhatjuk le (
). A kapacitás fegyverzeteit az alagútátmenet által elválasztott két közeli felület adja, a tipikusan nagy ellennállás érték pedig az alagútátmeneten történő átjutást jellemzi. A kvantumpötty közelében található kapuelektródát (zöld) a sziget és az elektróda közötti kapacitással irhatjuk le (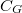 ). A kapuelektródára kapcsolt
). A kapuelektródára kapcsolt 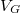 feszültség segítségével lehet majd a pötty betöltöttségét hangolni.
feszültség segítségével lehet majd a pötty betöltöttségét hangolni.
| 4a. ábra. Kvantumpötty elektrosztatikus helyettestő képe | 4b. ábra. Az elektródákat elválasztó alagútátmenetek helyettesítő képe |
Elektrosztatikus közelítésben a kvantumpötty energiáját a pöttyöt körbehatároló kapacitások segítségével a következőképpen irhatjuk fel:
![\[E_C (N, V_{SD}=0, V_G = 0) = (Ne)^2/2C_{\Sigma}\]](/images/math/6/2/1/621721a5f701d76365a6bd2da5fcf35d.png)
ahol  a kvantumpöttyön lévő elektronok száma,
a kvantumpöttyön lévő elektronok száma, 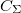 pedig a pötty és a környezete közötti összkapacitás:
pedig a pötty és a környezete közötti összkapacitás: 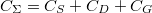 .
.
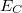 kifejezése alapján ha az elektronok számát növelni akarjuk eggyel, az a következő többlet energiába kerül:
kifejezése alapján ha az elektronok számát növelni akarjuk eggyel, az a következő többlet energiába kerül: 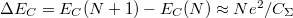 .
.
Véges kapufeszültség esetén vigyázni kell az energia felírásakor, hiszen az elektronok pöttyre helyezése során a kapu telepe is munkát végez, ami csökkenti a feltöltéshez szükséges energiát. Ha a pöttyre helyezett töltés 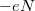 , akkor a párhuzamosan kapcsolt kapacitások miatt a kapu elektróda fegyverzetén
, akkor a párhuzamosan kapcsolt kapacitások miatt a kapu elektróda fegyverzetén 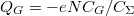 töltés lesz. A pötty energiáját a telep
töltés lesz. A pötty energiáját a telep
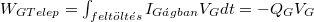 munkavégzésével korrigálva kapjuk:
munkavégzésével korrigálva kapjuk: 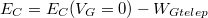 . Mindezek alapján:
. Mindezek alapján:
![\[E_C (N, V_{SD}=0, V_G) = 1/2C_{\Sigma}(Ne-V_G C_G)^2 + \alpha\]](/images/math/d/a/b/dab58959ce356b9dd6071a745607c6f2.png)
ahol  egy
egy  -től független mennyiség. A fentiek alapján a kapufeszültség hatása egy
-től független mennyiség. A fentiek alapján a kapufeszültség hatása egy 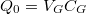 ún. offset-töltéssel azonos.
ún. offset-töltéssel azonos.
Az elektrosztatikus energiára kapott 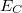 kifejezés az 5a- ábrán látható az offset-töltés függvényében különböző
kifejezés az 5a- ábrán látható az offset-töltés függvényében különböző  elektronszámok mellett. Az ábra alapján minden egyes
elektronszámok mellett. Az ábra alapján minden egyes 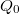 értékre könnyen meghatározható, hogy milyen elektronszám fogja minimalizálnia a kvantum pötty energiáját. A piros tengelyen a pötty alapállapotához tartozó elektronszám van feltüntetve. Az ábrán jelölt zöld pontokban a kvantum pötty alapállapota degenerált. Például a
értékre könnyen meghatározható, hogy milyen elektronszám fogja minimalizálnia a kvantum pötty energiáját. A piros tengelyen a pötty alapállapotához tartozó elektronszám van feltüntetve. Az ábrán jelölt zöld pontokban a kvantum pötty alapállapota degenerált. Például a 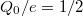 helyen az
helyen az 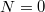 és
és 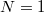 állapotok energiája azonos. Ezekben a speciális pontokban az egyik elektródáról egy elektron be tud ugrani a kvantumpöttyre energiaköltség nélkül és az elektron ki tud ugrani a másik elektródára. Ezen szekvenciális elektron alagutazási folyamaton keresztül áram tud folyni a kvantumpöttyön keresztül ha kis
állapotok energiája azonos. Ezekben a speciális pontokban az egyik elektródáról egy elektron be tud ugrani a kvantumpöttyre energiaköltség nélkül és az elektron ki tud ugrani a másik elektródára. Ezen szekvenciális elektron alagutazási folyamaton keresztül áram tud folyni a kvantumpöttyön keresztül ha kis 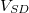 feszültséget kapcsolunk a két elektróda közé. Az 5b. ábra mutatja a kvantumpöttyön átfolyó áramot az offset-töltéssel arányos kapufeszültség függvényében (kis
feszültséget kapcsolunk a két elektróda közé. Az 5b. ábra mutatja a kvantumpöttyön átfolyó áramot az offset-töltéssel arányos kapufeszültség függvényében (kis 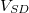 mellett). Az áram a
mellett). Az áram a 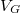 paramétertér nagyrészében nulla leszámítva egymástól egyenlő távolságban található pontokat, ahol az áram csúcsszerűen megnő. Ezeket hívjuk ún. Coulomb-csúcsoknak. Véges áramot csak ezen degenerációs pontokban kapunk, közöttük az elektronok átjutása a pöttyön blokkolva van. Ezt a jelenséget hívják ún. Coulomb-blokádnak, ami a kvantumpöttyök egyik fontos tulajdonsága. A Coulomb-blokád az elektronok közötti taszító Coulomb-kölcsönhatás és az elektromos töltés kvantáltságának a következménye. A kvantumpöttyön az elektronszám jól meghatározott, és ennek következtében áram nem tud a pöttyön keresztül folyni egészen addig, amíg az offset-töltés változtatásával degenerációs pontba nem hangoljuk az elektron szigetet. (A degenerációs pontok távolsága
paramétertér nagyrészében nulla leszámítva egymástól egyenlő távolságban található pontokat, ahol az áram csúcsszerűen megnő. Ezeket hívjuk ún. Coulomb-csúcsoknak. Véges áramot csak ezen degenerációs pontokban kapunk, közöttük az elektronok átjutása a pöttyön blokkolva van. Ezt a jelenséget hívják ún. Coulomb-blokádnak, ami a kvantumpöttyök egyik fontos tulajdonsága. A Coulomb-blokád az elektronok közötti taszító Coulomb-kölcsönhatás és az elektromos töltés kvantáltságának a következménye. A kvantumpöttyön az elektronszám jól meghatározott, és ennek következtében áram nem tud a pöttyön keresztül folyni egészen addig, amíg az offset-töltés változtatásával degenerációs pontba nem hangoljuk az elektron szigetet. (A degenerációs pontok távolsága 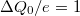 ).
).
| 5a. ábra. Kvantumpötty elektrosztatikus energiája különböző elektronszámnál (N). A zöld pontokban az alapállapot degenerált, és ezzel a pöttyön az elektronszám nem jól meghatározott. Az alapállapoti elektronszámok pirossal vannak feltüntetve. | 5b. ábra. Coulomb-blokád jelensége: a kvantumpöttyön keresztül csak 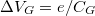 távolságra eső kapufeszültségek mellett folyik áram, mikor a pöttyön az elektronszám nem meghatározott. távolságra eső kapufeszültségek mellett folyik áram, mikor a pöttyön az elektronszám nem meghatározott.
|
A kapott elméleti várakozásokat vessük össze kvantumpöttyökön mért tipikus kísérleti eredményekkel. A 6. ábrán láthatóak vezetőképesség-mérések (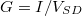 ) a kapufeszültség függvényében (kis
) a kapufeszültség függvényében (kis 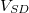 mellett). Alacsony hőmérsékleten éles csúcsok jelentkeznek, amiket nulla vezetőképességű tartományok határolnak el a Coulomb-blokádnak megfelelően. A 6a. ábrán a csúcsok egyenletesen helyezkednek el a
mellett). Alacsony hőmérsékleten éles csúcsok jelentkeznek, amiket nulla vezetőképességű tartományok határolnak el a Coulomb-blokádnak megfelelően. A 6a. ábrán a csúcsok egyenletesen helyezkednek el a 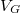 tengely mentén az elektrosztatikus képben kapott eredményekkel összhangban. A hőmérséklet növelésével a csúcsok elmosódnak, és a köztes völgyekben az áram egyre nagyobbra nő. Ez a termikus elmosódás akkor válik jelentőssé, ha a pötty hőmérséklete összemérhetővé válik az elektrosztatikus energiaskálával:
tengely mentén az elektrosztatikus képben kapott eredményekkel összhangban. A hőmérséklet növelésével a csúcsok elmosódnak, és a köztes völgyekben az áram egyre nagyobbra nő. Ez a termikus elmosódás akkor válik jelentőssé, ha a pötty hőmérséklete összemérhetővé válik az elektrosztatikus energiaskálával: 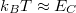 . A 6b. ábrán is egy hasonló mérés látható. A Coulomb-csúcsok itt is megjelennek, ugyanakkor a csúcsok távolsága nem egyenletes, ahogyan az egyszerű modellünkből várnánk. Ennek megértéséhez már az elektrosztatikus képen túl kell lépni, és figyelembe kell venni a pötty bezáró potenciáljában kialakuló diszkrét elektronállapotokat is. Az egyenletlen csúcstávolság egészen kis méretű kvantum pöttyök esetén jelentkezik, ahol
. A 6b. ábrán is egy hasonló mérés látható. A Coulomb-csúcsok itt is megjelennek, ugyanakkor a csúcsok távolsága nem egyenletes, ahogyan az egyszerű modellünkből várnánk. Ennek megértéséhez már az elektrosztatikus képen túl kell lépni, és figyelembe kell venni a pötty bezáró potenciáljában kialakuló diszkrét elektronállapotokat is. Az egyenletlen csúcstávolság egészen kis méretű kvantum pöttyök esetén jelentkezik, ahol 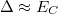 (lásd energiaskáláknál).
(lásd energiaskáláknál).
| 6a. ábra. Kvantumpöttyök Coulomb-csúcsai kísérletben.3 | 6b. ábra. Coulomb-csúcsok nem ekvidisztans poziciókban.4 |
Coulomb-energiaszintek
Állítsuk a kvantumpötty kapufeszültségét 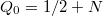 értékre. Ilyenkor az
értékre. Ilyenkor az 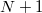 -ik elektoron számára éppen energetikailag kedvező, hogy bekerüljön a pöttyre. Ezt modellezhetjük úgy, hogy egy diszkrét energianívót feltételezünk a pöttyön az elektródák Fermi-energiáival azonos energián, amire egyetlen elektron helyezhető. Az egyik elektródából elektron ugorhat erre a diszkrét energiaszintre, majd a másik elektródára kiugorva áram tud folyni a pöttyön keresztül (lásd. 7. ábra bal panel). Továbbra is
-ik elektoron számára éppen energetikailag kedvező, hogy bekerüljön a pöttyre. Ezt modellezhetjük úgy, hogy egy diszkrét energianívót feltételezünk a pöttyön az elektródák Fermi-energiáival azonos energián, amire egyetlen elektron helyezhető. Az egyik elektródából elektron ugorhat erre a diszkrét energiaszintre, majd a másik elektródára kiugorva áram tud folyni a pöttyön keresztül (lásd. 7. ábra bal panel). Továbbra is 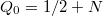 kapufeszültség értéknél maradva a következő (
kapufeszültség értéknél maradva a következő (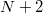 -ik) elektron pöttyre helyezéséhez további
-ik) elektron pöttyre helyezéséhez további 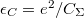 energiára van szükség (lásd 5a. ábra), ami megadja a következő diszkrét energianívó távolságát a Fermi-energiától. Az előzőeket ismételve egy kvantumpötty energiaszerkezetét leírhatjuk egymástól
energiára van szükség (lásd 5a. ábra), ami megadja a következő diszkrét energianívó távolságát a Fermi-energiától. Az előzőeket ismételve egy kvantumpötty energiaszerkezetét leírhatjuk egymástól 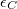 távolságra elhelyezett diszkrét energiaszintekkel, amikre egy-egy elektront lehet ráhelyezni. Ezeket az energiaszinteket szokás Coulomb-energiaszinteknek is nevezni. Az így kialakuló létra jellegű energiaszerkezet helyzetét a forrás (
távolságra elhelyezett diszkrét energiaszintekkel, amikre egy-egy elektront lehet ráhelyezni. Ezeket az energiaszinteket szokás Coulomb-energiaszinteknek is nevezni. Az így kialakuló létra jellegű energiaszerkezet helyzetét a forrás ( ) és a nyelő (
) és a nyelő ( ) Fermi-energiájához képest a
) Fermi-energiájához képest a 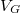 kapufeszültség segítségével lehet hangolni. A 7. ábra bal paneljéhez képest a jobb panelen növeltük a kapufeszültséget. Ezáltal az energiaszintek lejjebb tolódtak, és a kvantumpötty Coulomb-blokádba került.
kapufeszültség segítségével lehet hangolni. A 7. ábra bal paneljéhez képest a jobb panelen növeltük a kapufeszültséget. Ezáltal az energiaszintek lejjebb tolódtak, és a kvantumpötty Coulomb-blokádba került.
7. ábra. Kvantumpötty leírása Coulomb-energiaszintekkel: A függőleges az energiatengely, a forrás  és a nyelő és a nyelő  oldalon a Fermi-szintig betöltött elektronállapotok vannak jelölve sárgával. Az alagútátmenetek (kék) között a Coulomb-energiaszintek láthatóak oldalon a Fermi-szintig betöltött elektronállapotok vannak jelölve sárgával. Az alagútátmenetek (kék) között a Coulomb-energiaszintek láthatóak 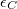 távolságokra egymástól. A bal oldali ábrán az az eset látható, mikor az távolságokra egymástól. A bal oldali ábrán az az eset látható, mikor az 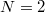 betöltés éppen megengedetté válik, az energiaszint rezonanciája miatt áram tud folyni a kvantumpöttyön keresztül. A jobb oldali ábra egy Coulomb-blokádolt esetet mutat, ahol az alsó két Coulomb-energiaszint betöltött, de a harmadik nívó még energetikailag nem érhető el. betöltés éppen megengedetté válik, az energiaszint rezonanciája miatt áram tud folyni a kvantumpöttyön keresztül. A jobb oldali ábra egy Coulomb-blokádolt esetet mutat, ahol az alsó két Coulomb-energiaszint betöltött, de a harmadik nívó még energetikailag nem érhető el.
|
A 8. ábra videója szemlélteti, hogy miközben a Coulomb energiaszinteket a 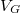 kapufeszültséggel eltoljuk, a kvantumpötty csak diszkrét tartományokban mutat véges vezetőképességet, pontosan akkor, amikor egy Coulomb energiaszint a Fermi-energiánál található.
kapufeszültséggel eltoljuk, a kvantumpötty csak diszkrét tartományokban mutat véges vezetőképességet, pontosan akkor, amikor egy Coulomb energiaszint a Fermi-energiánál található.
| 8. ábra. Coulomb csúcsok megjelenése a Coulomb-energiaszintek hangolása közben |
Coulomb-gyémántok
A Coulomb-energiaszintek bevezetése segít az  és
és  oldal közé kapcsolt véges
oldal közé kapcsolt véges 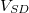 hatásának megértésében.
A 9. ábra bal odalán látható kísérleti eredmény egy kvantumpötty vezetőképességét mutatja
hatásának megértésében.
A 9. ábra bal odalán látható kísérleti eredmény egy kvantumpötty vezetőképességét mutatja 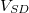 illetve
illetve 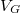 függvényében. A szürkeárnyalatos térképen nagyobb vezetőképességhez fehérebb szín tartozik. Zérus
függvényében. A szürkeárnyalatos térképen nagyobb vezetőképességhez fehérebb szín tartozik. Zérus 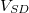 esetén (lásd piros pontozott vonal, illetve piros nyíllal jelölt ábrarészletek) a 6. illetve 8. ábrán már bemutatott Coulomb-csúcsokat láthatjuk diszkrét
esetén (lásd piros pontozott vonal, illetve piros nyíllal jelölt ábrarészletek) a 6. illetve 8. ábrán már bemutatott Coulomb-csúcsokat láthatjuk diszkrét 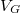 értékeknél. Véges
értékeknél. Véges 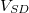 esetén (kék pontozott vonal) azonban véges szélességű
esetén (kék pontozott vonal) azonban véges szélességű 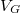 tartományban látunk áramot, egészen addig, amíg egy Coulomb-energiaszint
tartományban látunk áramot, egészen addig, amíg egy Coulomb-energiaszint  és
és  kémiai potenciálja között tartózkodik (lásd kék nyíllal jelölt ábrarészletek).
kémiai potenciálja között tartózkodik (lásd kék nyíllal jelölt ábrarészletek). 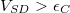 esetén (zöld pontozott vonal)
esetén (zöld pontozott vonal)  és
és  kémiai potenciálja között biztosan található legalább egy Coulomb-energiaszint, így tetszőleges
kémiai potenciálja között biztosan található legalább egy Coulomb-energiaszint, így tetszőleges 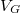 -nél véges vezetőképességet mérünk (lásd zöld nyíllal jelölt ábrarészlet). Ennek megfelelően megmutatható, hogy a
-nél véges vezetőképességet mérünk (lásd zöld nyíllal jelölt ábrarészlet). Ennek megfelelően megmutatható, hogy a 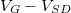 síkon rombusz alakú tartományokban találhatóak azak a részek, ahol nem esik Coulomb-energiaszint az
síkon rombusz alakú tartományokban találhatóak azak a részek, ahol nem esik Coulomb-energiaszint az  és
és  kémiai potenciáljai közé, azaz zérus a kvantumpötty vezetőképessége. A 9. ábrán jól láthatóak a fekete rombusz alakú tartományok, piros vonal szemlélteti a szélüket. Ezeket hívjuk Coulomb-gyémántoknak (-rombuszoknak), az angol Coulomb-diamond nyomán. A rombuszokon belül jól meghatározott a kvantumpöttyön tartózkodó elektronok száma, a szomszédos rombuszok egyel nagyobb (ill. kisebb) elektronszámhoz tartoznak.
kémiai potenciáljai közé, azaz zérus a kvantumpötty vezetőképessége. A 9. ábrán jól láthatóak a fekete rombusz alakú tartományok, piros vonal szemlélteti a szélüket. Ezeket hívjuk Coulomb-gyémántoknak (-rombuszoknak), az angol Coulomb-diamond nyomán. A rombuszokon belül jól meghatározott a kvantumpöttyön tartózkodó elektronok száma, a szomszédos rombuszok egyel nagyobb (ill. kisebb) elektronszámhoz tartoznak.
| 9. ábra. Coulomb-gyémánt mintázat. A kvantumpötty energiaszintjei a gyémántmintázat különböző részein. |
Mivel egy kvantumpötty paramétereinek hangolásával úgy lehet áramot ki és bekapcsolni, hogy közben egyetlen elektronnal változik a pöttyön tartózkodó elektronok száma, így a kvantumpöttyből kialakított térvezérelt tranzisztort egyelektron-tranzisztornak is szokták nevezni. Megfelelő elrendezésben ráadásul annyira ki lehet üríteni a kvantumpöttyöt, hogy ténylegesen egyetlen vezetésben résztvevő elektron tartózkodjon rajta.
Összefoglalva a fentieket, a kvantumpöttyök viselkedését egy leegyszerűsített model keretében tárgyaltuk, ami a kvantumpöttyön az elektronok között fellépő Coulomb-taszítást vette figyelembe, ezt is egyszerű elektrosztatikus közelítésen keresztül a pötty és a környezetében található elektródák közötti kapacitások figyelembe vételével. Már ebben az egyszerű elektrosztatikis képben a kvantumpöttyök alapvető elektromos vezetési tulajdonságai, úgy mint a Coulomb-blokád jelensége vagy a Coulomb-gyémánt mintázatok megérthetőek.
Hivatkozások
Fent hivatkozott szakcikkek
[1] Jonathan P Bird: Electron transport in quantum dots, Kluwer Academic Publishers (2003)
Ajánlott könyvek és összefoglaló cikkek
- S. Datta: Electronic Transport in Mesoscopic Systems, Cambridge University Press (1997)
- Thomas Ihn: Semiconducting nanosctructures, OUP Oxford (2010)
- Yuli V. Nazarov, Yaroslav M. Blanter: Quantum Transport: Introduction to Nanoscience, Cambridge University Press (2009)
Ajánlott kurzusok
- Új kísérletek a nanofizikában, Halbritter András és Csonka Szabolcs, BME Fizika Tanszék
- Transzport komplex nanoszerkezetekben, Halbritter András, Csonka Szabolcs, Csontos Miklós, Makk Péter, BME Fizika Tanszék
- Alkalmazott szilárdtestfizika, Mihály György, BME Fizika Tanszék
- Fizika 3, Mihály György, BME Fizika Tanszék (mérnök hallgatóknak)
- Mezoszkopikus rendszerek fizikája, Zaránd Gergely, BME Elméleti Fizika Tanszék
- Mezoszkopikus rendszerek fizikája, Cserti József, ELTE Komplex Rendszerek Fizikája Tanszék