„Akusztooptikai fénydiffrakció vizsgálata” változatai közötti eltérés
Lenk (vitalap | szerkesztései) a |
Lenk (vitalap | szerkesztései) a |
||
| 186. sor: | 186. sor: | ||
==PDF formátum== | ==PDF formátum== | ||
| − | [[Media: | + | [[Media:akusztooptikaL.pdf|Akusztooptikai fénydiffrakció vizsgálata]] |
</wlatex> | </wlatex> | ||
<!--Utolso szerkesztes:2013.09.25--> | <!--Utolso szerkesztes:2013.09.25--> | ||
A lap jelenlegi, 2013. szeptember 27., 09:27-kori változata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Bevezetés
A Brillouin által megjósolt akuszto-optikai kölcsönhatást 1932-ben mutatta ki Debye és Sears. Az effektus felhasználását, vagyis akuszto-optikai elven működő eszközök kifejlesztését és ezek alkalmazását a kollimált, monokromatikus fényforrások, a lézerek elterjedése tette lehetővé. Akuszto-optikai eszközök működnek lézeres sornyomtatóban, nagyfelbontású fénymásoló berendezésekben, egyes spektrométerekben, és olyan analóg műveletvégző optikai rendszerekben, amelyek nagysebességű (a digitálisnál gyorsabb) Fourier-transzformáció, illetve konvolúció képzésre alkalmasak.
A továbbiakban megismerkedünk az akuszto-optikai eszközök működésének megértéséhez szükséges alapfogalmakkal, és az akuszto-optikai kölcsönhatás néhány tulajdonságával.
Elméleti alapok
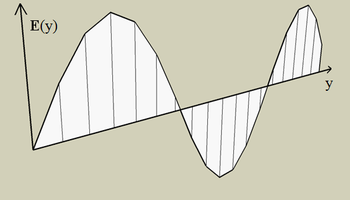
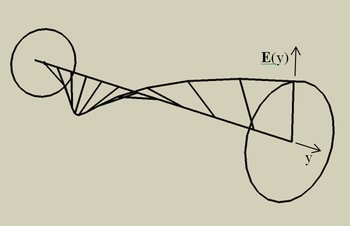
A fény elektromágneses hullám, melyben az E elektromos térerősség és a B mágneses indukcióvektor periodikus változása a terjed. Ezek (vákuumban) a terjedési irányra egyenként és egymásra is merőlegesek. Lineárisan polarizált hullámról akkor beszélünk, ha a térerősség vektor a terjedési irány mentén végig egy meghatározott síkban marad (1. ábra). Polarizációs iránynak az elektromos térerősség vektor irányát nevezzük. Két egymásra merőlegesen polarizált hullám egymástól függetlenül terjed. Cirkulárisan poláros nyalábnak azt nevezzük, ha a térerősség amplitúdója állandó, de a végpontja a nyaláb mentén és időben is a terjedési irány körül forog (2. ábra). Általános esetben a nyaláb se nem lineáris, se nem cirkulárisan poláros, hanem elliptikusan poláros (a vektor forog, és az amplitúdója is változik), illetve lehet polarizálatlan is (ez az állapot pl. végtelen sok, véletlen kezdőfázisú lineárisan polarizált nyaláb összegeként képzelhető el).
Egy tetszőlegesen polarizált nyaláb leírható két jól megválasztott fázisú és amplitúdójú, egymásra merőleges lineáris polarizációjú nyaláb összegeként (pl. a cirkulárisan polarizált hullám két azonos amplitúdójú 90° fáziskülönbségű lineárisan polarizált nyaláb összege). Ugyanígy bázisként használható két ellentétes irányba forgó cirkulárisan polarizált hullám (pl. lineárisan poláros hullám két azonos amplitúdójú jobbra és balra cirkulárisan poláros hullám összege). A fényt a továbbiakban síkhullámnak tekintjük (ez legalábbis esetünkben elfogadható közelítés).
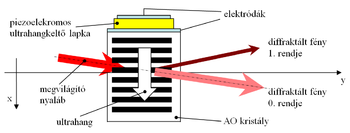
Akusztikus hullám esetén a közeg egyes pontjainak periodikus elmozdulása terjed tova, ami szintén vektormennyiség, és iránya az elmozdulás irányát, nagysága az elmozdulás nagyságát adja meg. Az elmozdulásvektor hely szerinti deriváltját (a közeg dV térfogatelemeinek relatív méretváltozását) nevezzük mechanikai deformációnak. A mérésben használt eszközben az akusztikus hullám transzverzális, amely az ultrahangkeltő és a kristály orientálásától, azaz a kristály lapjainak és a kristálytani tengelyek szögétől függ. Az ultrahang hullámot piezoelektromos egykristály lapkával hozzuk létre, amelyben a rákapcsolt nagyfrekvenciás (45 MHz, néhány volt amplitúdójú) feszültséggel arányos méretváltozás jön létre. Az ultrahangkeltő felépítése a 3. ábrán látható. A lapka által a generátorból felvett elektromos teljesítmény egyenlő az akusztikus hullám teljesítményével, ezért az ultrahang hullám teljesítményét a meghajtó áramkör elektromosan szabályozni tudja.
A két hullám (akusztikus-fény) a fotorugalmassági effektus révén hat kölcsön, melynek lényege, hogy a mechanikai deformáció törésmutató változást (Δn) hoz létre:
![\[\Delta n = \frac{1}{2}n^3pS\]](/images/math/8/f/4/8f4a2f46a9351fd2b861610132cba601.png)
ahol „n” a közeg törésmutatója, „p” a fotorugalmassági állandó és „S” a mechanikai deformáció (relatív méretváltozás).
Akusztikus hullámok esetén a mechanikai deformáció periodikus a közegben:
![\[S = S_0\sin \Omega\left(t-\frac{x}{v}\right)\]](/images/math/2/9/9/2990cde29ca6785e5444c985fc517865.png)
ahol „ ” az akusztikus hullám körfrekvenciája
” az akusztikus hullám körfrekvenciája 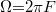 , „v” a hang terjedési sebessége, S0 az amplitúdója és „F” a frekvenciája. Ekkor az (1) egyenletnek megfelelően:
, „v” a hang terjedési sebessége, S0 az amplitúdója és „F” a frekvenciája. Ekkor az (1) egyenletnek megfelelően:
![\[\Delta n = n_0\sin \Omega\left(t-\frac{x}{v}\right)\]](/images/math/f/c/4/fc420e13da3ab3df9378e0f927343ca7.png)
Vagyis egy, az x irányban haladó, az akusztikus hullám sebességével terjedő törésmutató változás hullámot kapunk: egy mozgó, szinuszosan modulált fázisrácsot (ld. következő fejezet).
Akuszto-optikai fénydiffrakció
Terjedjen a 3. ábrán látható közegben az akusztikus hullámra merőleges y-irányban egy elektromágneses hullám:
![\[\mathbf{E} = \mathbf{E}_0\sin \omega\left(t - \frac{yn}{c}\right) \]](/images/math/8/4/2/8422ae812a141ab0bbf86af5c9a7972a.png)
ahol „E” az elektromos térerősség, „c” a fénysebesség vákuumban, és „n” a közeg törésmutatója az elektromágneses hullám frekvenciáján. Látható, hogy a hullám fázisa:
![\[\varphi = \omega \left(t-\frac {y\cdot n(x)}{c}\right) = \omega t -\omega y\frac{n_0 \sin \Omega (t-\frac{x}{v}) }{c}\]](/images/math/2/5/3/25352e419b3c7308e8cab18f634b2c77.png)
függ a közeg törésmutatójától, vagyis a közegben terjedő akusztikus hullám a fotorugalmassági effektus következtében megváltoztatja az elektromágneses hullám fázisát. A fázisváltozás következtében a fényhullám elhajlik az akusztikus hullámon, amit akuszto-optikai fénydiffrakciónak nevezünk. Ennek egy speciális esete a Bragg-diffrakció, amikor a hanghullám (ill. a fázisrács) a fény terjedési irányában jóval szélesebb, mint az alkalmazott fény hullámhossza: ekkor az irányváltoztatás nélkül áthaladó megvilágító nyaláb (nulladrend) mellett csak egy diffrakciós rendet tapasztalunk, ami formálisan úgy írható le mintha a beeső fénynyaláb az akusztikus hullám fázisfelületeiről reflektálódna. Viszont ha a rács „vékony” (a hullámhosszakhoz viszonyítva) akkor megjelennek ±1, ±2, … rendek is. Az akuszto-optikai fénydiffrakció általános tárgyalása messze túlmutat a mérés anyagán, ezért a továbbiakban csak az akuszto-optikai Bragg-diffrakcióval foglalkozunk. Bragg-diffrakció tehát akkor jön létre, ha a) az akusztikus hullám y-irányban sokkal „vastagabb”, mint a kölcsönhatásban résztvevő hullámok hullámhossza, b) a beesés szögére (α) teljesül az ún. Bragg-feltétel:
![\[2\Lambda \sin \alpha = \lambda \]](/images/math/3/4/e/34e4144fc3a5e6a3f77d832dcca99cb3.png)
ahol „ ” a fény hullámhossza a kristályban, „
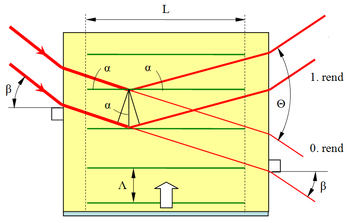
” a fény hullámhossza a kristályban, „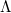 ” az ultrahang hullámhossza, „α” nyaláb és a fázissík által bezárt szög (ld. 4. ábra). Ezt átrendezve kapjuk:
” az ultrahang hullámhossza, „α” nyaláb és a fázissík által bezárt szög (ld. 4. ábra). Ezt átrendezve kapjuk:
![\[\sin \alpha = \frac {\lambda}{2\Lambda} \]](/images/math/d/1/3/d134b25fd6e259c43b9d27e3f5142f37.png)
Ez a feltétel abból adódik, hogy a szomszédos fázisfelületekről a tükrözési törvénynek megfelelően visszaverődő nyalábok konstruktívan interferáljanak, azaz az úthosszkülönbség épp az optikai hullámhossz legyen. A jelenség megértéséhez a 4. ábrán látható az akusztikus hullámból két szomszédos fázissíkról történő fényvisszaverődés.
A fény f frekvenciája nem változik meg a kristályba való belépéskor, ám megváltozik az akuszto-optikai diffrakció során, mégpedig az F akusztikus frekvenciával (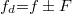 ). Mivel azonban F<<f, így
). Mivel azonban F<<f, így 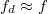 , a hullámhossz a kristályban a következőképpen számolható:
, a hullámhossz a kristályban a következőképpen számolható:
![\[\frac{c}{n} = \lambda f \qquad \Rightarrow \qquad \lambda = \frac{\lambda_0}{n}\]](/images/math/6/7/7/677da302ed45dacfc86bb555eea20e43.png)
ahol „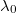 ” a vákuumbeli hullámhossz. Így az eltérülési szög szinusza:
” a vákuumbeli hullámhossz. Így az eltérülési szög szinusza:
![\[\sin \alpha = \frac{1}{2}\cdot \frac{\lambda_0}{n\Lambda} \]](/images/math/c/4/3/c438ff8602bc979d9398da8af4742194.png)
A fény a diffrakció után a kristályból kilépve még meg is törik. Mivel ennek a kilépő nyalábnak a szintén kilépő nulladrendhez viszonyított szöge (Θ) a legjobban mérhető mennyiség, fejezzük ki ennek kapcsolatát α-val, ill. az akusztikus hullámhosszal, Λ-val:
![\[\Theta= 2\beta = 2\cdot arcsin(n\cdot \sin \alpha) = 2\cdot arcsin\left(\frac{\lambda_0}{2\Lambda}\right)\]](/images/math/f/0/0/f0021c87b62cec415100f74eb692ea77.png)
ahol „β” a bejövő nyaláb beesési szöge (ld. 4. ábra). A levezetés mellőzésével a diffraktált optikai nyaláb Id intenzitása:
![\[I_d = I_0\sin^2\left(A\sqrt{P_aL}\right) \]](/images/math/d/b/6/db6746f1016e2a4edb49048686a697dc.png)
ahol „I0” a 0. rendű nyaláb intenzitása kikapcsolt akusztikus jel esetén (azaz a diffrakció mentesen áthaladó megvilágító nyalábé), „Pa” az akusztikus hullám teljesítménye, „L” az akusztikus hullám „y” irányú kiterjedése (kölcsönhatási hossz) és „A” egy hullámhossztól, anyagtól függő állandó. Az Id/I0 hányadost η-val jelöljük, a neve pedig diffrakciós hatásfok. A (11) összefüggést grafikusan az 5. ábra szemlélteti. A (10) és (11) összefüggésekből látszik, hogy az akuszto-optikai eszközt alapvetően kétféleképpen lehet használni:
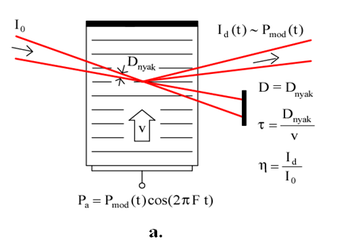
- Modulátorként: az ultrahang Pa teljesítményét változtatva, Pa = Pmod(t), a diffraktált rendbe jutó fényintenzitás szabályozható (6.a. ábra): Id(t) ~ Pmod(t).
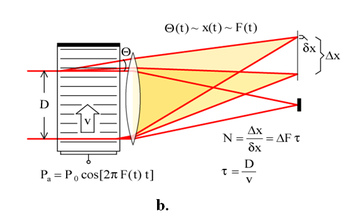
- Deflektorként: az ultrahang F = v/Λ frekvenciájának változtatásával, F=F(t), az eltérített fény Θ szögét lehet befolyásolni (6.b. ábra): Θ(t) ~ F(t).
Modulátor esetén a (12) egyenlettel adott tr felfutási idő csökkentése, deflektor esetén a felbontás (N) növelése a cél. Ez utóbbi a 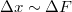 eltérítési tartomány növelésével, illetve a
eltérítési tartomány növelésével, illetve a 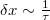 fókuszfolt méretének csökkentésével (azaz a nyalábátmérő növelésével) érhető el.
fókuszfolt méretének csökkentésével (azaz a nyalábátmérő növelésével) érhető el.
Optikailag anizotróp anyagokban a törésmutató (így a terjedési sebesség is) függ a hullám terjedési irányától, polarizációjától. A mérésben használt TeO2 (tellúr-dioxid) egykristályban, az általunk használt irányban a jobbról és balról cirkulárisan polarizált hullámok különböző sebességgel (ill. hullámhosszal) terjednek, így csak az egyikre teljesülhet a (7) szerinti Bragg-feltétel. A mérésben fényforrásként lézert használunk, amely λ = 633 nm hullámhosszúságú lineárisan poláros fényt sugároz. Lineárisan polarizált fény alkalmazása esetén a belépő hullám a bevezetőben említetteknek megfelelően felbontható egy jobbról és egy balról cirkulárisan poláros nyaláb összegére, amelyek tehát különböző sebességgel terjednek. A (7) Bragg-feltétel csak az egyikre teljesül, így az ultrahang csak az egyiket fogja diffraktálni. A lineárisan poláros hullámnak fele a jobbról, fele a balról cirkuláris hullám, így a diffraktált nyaláb intenzitása lineárisan poláros fényre a fele a cirkulárisan poláros fényre mérhetőnek. Emiatt a mérési elrendezés tartalmaz egy λ/4-es fázistoló lemezt, ami megfelelő beállítás esetén a lézerforrás lineárisan polarizált fényét cirkulárisan polárossá alakítja.
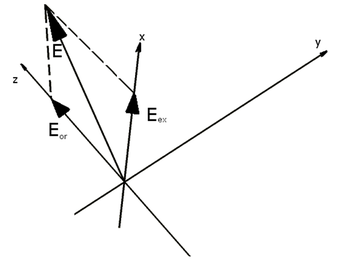
A fázistoló lemez egy olyan kvarc lapka, amelyben az y irányban terjedő, z irányban polarizált (ordinárius), és x irányban polarizált (extraordinárius) fénynyaláb terjedési sebessége különböző. Az eltérő terjedési sebességek miatt áthaladás után fáziskülönbség lép fel az ordinárius és extraordinárius nyalábok között. A λ/4-es vastagságát úgy állították be, hogy az általa okozott fáziskésleltetés éppen 90°, azaz λ/4. Az olyan lineárisan polarizált nyaláb, amely y irányban esik a lapkára, és a polarizációja az x-z síkban 45°-os szöget zár be az x-tengellyel, azonos amplitudójú ordinárius és egy extraordinárius nyalábokra bontható (ld. 7. ábra). A bevezetőben említetteknek megfelelően ebben az esetben a kilépő nyaláb cirkulárisan polarizált lesz.
A (11) összefüggésből látható; hogy az ultrahanghullám teljesítményével modulálható a diffraktált nyaláb intenzitása (ld. modulátor üzemmód, 6.a. ábra). Négyszögjel moduláció esetén (ami a meghajtó jel teljesítmény gyors ki-be kapcsolásának felel meg), a diffraktált nyaláb intenzitása a meghajtó elektromos négyszögjel frekvenciájának megfelelő négyszögjel lesz, s felfutási ideje (tr) arányos azzal az idővel, amíg az ultrahang áthalad a fénynyalábon ( ):
):
![\[t_r = \frac{\tau}{1,5}\]](/images/math/0/6/8/068e78a90f901b92467becfd46ae444a.png)
![\[\tau = \frac{D}{v}\]](/images/math/7/b/0/7b08c4c62d82e35248a29db1ebd0f5f1.png)
ahol „D” az optikai nyaláb átmérője és „v” az ultrahang terjedési sebessége (esetünkben 620 m/s). A diffraktált nyaláb impulzusfelfutási ideje tehát úgy csökkenthető, ha csökkentjük a nyalábátmérőt (pl. fókuszálással, ekkor a nyalábátmérő az 6.a. ábra Dnyak ún. „nyalábnyak” méretével adható meg).
A mérési elrendezés
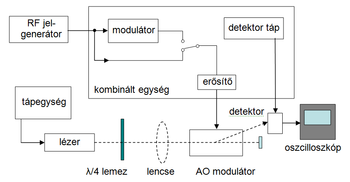
A mérési összeállítás a 8. ábrán látható, a felhasznált eszközök az alábbiak:
- Lézer: 5 mW fényteljesítményű, 633 nm hullámhosszúságú He-Ne gázlézer, tápegységgel. A nyalábba nézni tilos!
- λ/4 lemez: Megfelelően orientált kvarc egykristály lapka állítható tartóban, optikai tengelye (z) a lapka síkjában van. A belépő lineárisan polarizált fény polarizációjának az optikai tengelytől mért optimális szögét (45°) a lapka y tengely körüli elforgatásával érjük el, ezáltal a kilépő fény cirkulárisan polarizált állapotú lesz.
- Lencse: Egy darab 100 mm-es fókusztávolságú gyűjtőlencse a fénynyaláb cellára fókuszálására (ld. 4. sz. mérési feladat).
- AO modulátor: Akuszto-optikai modulátor. TeO2 egykristályból készült elektronikusan vezérelhető fényintenzitás modulátor (hőelvezetést és mechanikai védelmet biztosító fémházba építve).
- Detektor: Egy áramgenerátorként működő gyors fotodiódából áll, a kapcsolás 12 V-os tápfeszültséget igényel. A fotodióda árama a vele sorba kapcsolt ellenálláson feszültséget ejt, mely oszcilloszkóppal mérhető.
- Modulátor: 1-10-100-500-2000 kHz-es négyszögjelek előállítására alkalmas, segítségével az AO modulátor nagyfrekvenciás meghajtó jele ki- bekapcsolható (digitális moduláció).
- Erősítő: A nagyfrekvenciás (RF) jelgenerátor kisszintű kimenőjelét erősíti az AO modulátor meghajtásához szükséges teljesítményre. Az erősítő kimenő szintje határolt, a maximális torzítatlan kimenő teljesítmény 1 W (30 dBm).
- Detektor táp: A fotodetektor 12 V-os tápfeszültségét biztosítja.
- RF jelgenerátor: HT gyártmányú jelgenerátor, mely az AO modulátor meghajtásához szükséges nagyfrekvenciás szinuszos jelet biztosítja. A generátor alkalmas amplitúdó- és frekvencia-moduláció megvalósítására, továbbá időben változó frekvenciájú (sweep) jel előállítására.
- Oszcilloszkóp: Kétcsatornás digitális oszcilloszkóp.
Mérési feladatok
- 1. A diffraktált nyaláb intenzitásának vizsgálata a belépő fény polarizációjának függvényében
Kapcsolja be a lézert! Helyezze a fotodetektort az AO modulátor után a nyalábba és csatlakoztassa a fénymérő bemenetére (DET INP). A műszer alatti potméterrel állítsa be a műszer mutatóját a 100-as értékre. Kapcsolja be az RF jelgenerátort (állandó kimenő teljesítmény: CW üzemmód!). A generátor frekvenciáját állítsa be 47-50 MHz közötti frekvenciára (TUNING és FINE TUNE), a kimenő jelszintet pedig 1 W-ra (ld. 1. táblázat), Csatlakoztassa az RF jelgenerátor kimenetét (RF OUT) az erősítő fokozat bemenetére (RF IN), annak kimenetét (RF OUT) pedig az AO modulátor bemenetére (az erősítő modulátorát állítsa MOD: OUT-ra). Helyezze a diffraktált nyaláb 1. rendjébe a fotodetektort. A lézer és az AO modulátor dőlésszögének, ill. utóbbi pozíciójának finom állításával keresse meg a jelmaximumot. Forgassa el lassan a modulátor elé helyezett cirkuláris polarizátort a lézernyaláb által meghatározott tengely körül (polarizátor y-tengely). Figyelje a fényintenzitás változását és értelmezze a jelenséget!
- 2. A diffraktált nyaláb intenzitásának vizsgálata a meghajtó teljesítmény függvényében
Állítsa a cirkuláris polarizátort olyan állásba, hogy a diffraktált nyaláb intenzitása maximális legyen. Változtassa az RF jelgenerátor kimenő jelszintjét; az akusztikus teljesítményt az 1. táblázatból lehet leolvasni. Vegye fel a bemenő teljesítmény - diffraktált intenzitás értékeket, úgy, hogy a jelszintet innentől az oszcillószkóp segítségével határozza meg! Normalizálja az intenzitásértékeket I0-al (ehhez le kell mérni a diffraktálatlan 0. rend intenzitását az AO modulátor kikapcsolt állapotában). A mérési pontokat ábrázolja I-P karakterisztikán! Határozza meg a diffrakciós hatásfokra megismert (11) összefüggésben szereplő (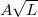 ) állandót, majd ennek segítségével ábrázolja az ideális karakterisztikát és hasonlítsa össze a mért karakterisztikával, Határozza meg a cella maximális diffrakciós hatásfokához tartozó optimális meghajtó teljesítményt!
) állandót, majd ennek segítségével ábrázolja az ideális karakterisztikát és hasonlítsa össze a mért karakterisztikával, Határozza meg a cella maximális diffrakciós hatásfokához tartozó optimális meghajtó teljesítményt!
| kapcsoló állás | - 3 dB | P_a |
|---|---|---|
| 1 | ki | 1.06 W |
| 1 | be | 0,94 W |
| 2 | ki | 0.87 W |
| 2 | be | 0.42 W |
| 3 | ki | 0.25 W |
| 3 | be | 0.10 W |
| 4 | ki | 60 mW |
| 4 | be | 30 mW |
| 5 | ki | 12 mW |
| 5 | be | 6 mW |
- 3. A hangsebesség mérése
Állítsa be az RF jelgenerátort 30 MHz-re! Vegye ki a fotodetektort a nyalábból és jelölje meg a diffraktált nyaláb helyét a modulátor mögötti ernyőn (mm-papíron). Ismételje meg ezt 10 MHz-enként 60 MHz-ig. Mérje meg a pontok távolságát a nulladrendű nyalábtól, ill. az AO modulátor távolságát a mm-papírtól. Ábrázolja a mérési pontokat! A diffrakció szögét (Θ) meghatározó (10) képlet szerint határozza meg a modulátor TeO2 kölcsönhatási közegében az ultrahang terjedési sebességét (λ az optikai, Λ az akusztikus hullámhossz a közegben, α a diffrakció félszöge a közegben; a közeg törésmutatója n = 2,26 és a lézer vákuumbeli hullámhossza λ0 = 633 nm)! A kapott értéket vesse össze a megadott értékkel! Hasonlítsa össze ezt az adatot más anyagokban mérhető hangsebességekkel. Kapcsolja be a frekvencia sweep-et (SWEEP: WIDE). Változtassa. a sweep szélességét (SWEEP WIDTH) és hosszát (SWEEP RATE). Az ernyőn figyelje a jelenséget, tapasztalatait írja le!
- 4. Impulzusfelfutási idő mérése
Állítson be a négyszögjel generátoron 100 kHz-et! Kapcsolja be a négyszögjel generátort (MOD: IN állás). Helyezze a nyalábba a fotodetektort, és jelét jelenítse meg az oszcilloszkópon! Olvassa le a 10-90%-os Intenzitású pontok között definiált impulzusfelfutási időt! A felfutási időre megismert (12) összefüggés alapján határozza meg a nyalábátmérőt! Helyezze a lencséket a fényútba, és ismételje meg a fenti mérést és számítást! Ismertesse tapasztalatait!
- 5. A cella túlvezérlésének vizsgálata
A fotodetektor jelét jelenítse meg oszcilloszkópon. Kapcsolja be a szinuszos jellel történő amplitúdó modulációt (AM), a moduláció sebessége legyen 400 Hz (MOD SIGNAL). A modulációs torzítás kiküszöbölése érdekében állítsa be a modulációs mélységet 90 %-ra (MODULATION). Változtassa az AO modulátor meghajtó teljesítményét a 2. feladatban meghatározott optimális teljesítményszint környékén. Rajzolja le a kapott jelalakokat és értelmezze őket a 5. ábra alapján!
PDF formátum
Akusztooptikai fénydiffrakció vizsgálata
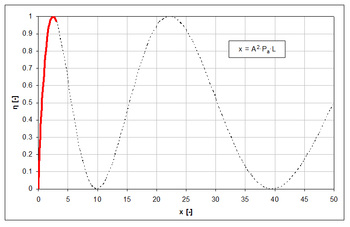
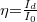 akusztikus teljesítmény (Pa) függése. A vastagon kiemelt piros rész a mérésben szereplő tartományt mutatja.
akusztikus teljesítmény (Pa) függése. A vastagon kiemelt piros rész a mérésben szereplő tartományt mutatja.