„Gamma spektroszkópia” változatai közötti eltérés
| (egy szerkesztő 75 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | |||
| − | |||
| − | |||
| − | |||
<wlatex> | <wlatex> | ||
__TOC__ | __TOC__ | ||
| − | + | ==Bevezetés== | |
| − | == | + | |
A gamma-spektrometria az atommagból valamilyen magfolyamat következtében (radioaktív bomlás, mesterséges vagy természetes magreakció) kilépő gamma sugárzás energiájának, intenzitásának, szögeloszlásának mérésével foglalkozik. A jelen laborgyakorlat lehetővé teszi az elméleti előadásokon hallott nukleáris méréstechnikai ismeretek elmélyítését és azok gyakorlati alkalmazásainak készségszintű elsajátítását. A gyakorlaton részt vevők betekintést nyernek a félvezető detektorra alapozott gamma-spektrometria alapjaiba, megismerik annak fontosabb eszközeit és a gamma-spektrumok kiértékelésének elemi lépéseit. | A gamma-spektrometria az atommagból valamilyen magfolyamat következtében (radioaktív bomlás, mesterséges vagy természetes magreakció) kilépő gamma sugárzás energiájának, intenzitásának, szögeloszlásának mérésével foglalkozik. A jelen laborgyakorlat lehetővé teszi az elméleti előadásokon hallott nukleáris méréstechnikai ismeretek elmélyítését és azok gyakorlati alkalmazásainak készségszintű elsajátítását. A gyakorlaton részt vevők betekintést nyernek a félvezető detektorra alapozott gamma-spektrometria alapjaiba, megismerik annak fontosabb eszközeit és a gamma-spektrumok kiértékelésének elemi lépéseit. | ||
| 24. sor: | 19. sor: | ||
* mérési adatok feldolgozása, azok bizonytalanságának becslése | * mérési adatok feldolgozása, azok bizonytalanságának becslése | ||
| − | == | + | ==Elméleti összefoglaló== |
'''Fotoeffektus, szórás, párkeltés, emisszió és abszorpció:''' | '''Fotoeffektus, szórás, párkeltés, emisszió és abszorpció:''' | ||
| − | Az atommagok alfa- és béta-bomlásai, a maghasadás valamint a magreakciók gyakran a leánymag gerjesztett állapotához vezetnek. A magfolyamat során keletkezett atommag a gerjesztett állapotból általában egy vagy több gamma foton kibocsátásával tér vissza az alapállapotába. A radioaktív atommag bomlása során emittált gamma fotonok energiája, intenzitása vagy szögeloszlása információt hordoz a sugárzó atommag belső felépítéséről, szerkezetéről. Egy | + | Az atommagok alfa- és béta-bomlásai, a maghasadás valamint a magreakciók gyakran a leánymag gerjesztett állapotához vezetnek. A magfolyamat során keletkezett atommag a gerjesztett állapotból általában egy vagy több gamma foton kibocsátásával tér vissza az alapállapotába. A radioaktív atommag bomlása során emittált gamma fotonok energiája, intenzitása vagy szögeloszlása információt hordoz a sugárzó atommag belső felépítéséről, szerkezetéről. Egy atommagnak több legerjesztődési folyamata is lehet, amit az ún. bomlássémával szoktak ábrázolni (1. ábra). Az 1. ábrán egy '''A''' tömegű és '''Z''' rendszámú atommag energianívóit a függőleges tengelyen, míg a vízszintes tengelyen a rendszámot ábrázoltuk. |
| − | + | {| | |
| + | | <span id="fig:1">[[Fájl:FizLab4_GAMMA_01.jpg|közép|bélyegkép|300px|1.ábra: <sup>60</sup>Co bomlási sémája.]]</span> | ||
| + | |} | ||
A különböző bomlási útvonalakhoz más-más átmeneti valószínűség tartozik, amit az adott béta vagy gamma-emisszió gyakoriságának nevezünk. A gyakorisági értékek az adott atommagra jellemző olyan nukleáris állandók, amik azt adják meg, hogy ha az adott magból 100 db elbomlik, akkor nagy valószínűséggel hány esetben emittál a mag adott energiájú béta-részecskét vagy gamma-fotont. A gamma-sugárzás és az anyag kölcsönhatása három alapvető folyamattal jellemezhető: '''fotoeffektus''', '''Compton-szórás''' és '''párkeltés'''. Ezt a három alapvető fizikai folyamatot más elméleti tárgyak már részletesen elemezték ezért a jelen leírásban csak egy rövid áttekintést adunk. | A különböző bomlási útvonalakhoz más-más átmeneti valószínűség tartozik, amit az adott béta vagy gamma-emisszió gyakoriságának nevezünk. A gyakorisági értékek az adott atommagra jellemző olyan nukleáris állandók, amik azt adják meg, hogy ha az adott magból 100 db elbomlik, akkor nagy valószínűséggel hány esetben emittál a mag adott energiájú béta-részecskét vagy gamma-fotont. A gamma-sugárzás és az anyag kölcsönhatása három alapvető folyamattal jellemezhető: '''fotoeffektus''', '''Compton-szórás''' és '''párkeltés'''. Ezt a három alapvető fizikai folyamatot más elméleti tárgyak már részletesen elemezték ezért a jelen leírásban csak egy rövid áttekintést adunk. | ||
| − | A fotoeffektus során a gamma-foton átadja a '''teljes energiáját''' egy atom valamelyik kötött elektronjának, amely szabaddá válik, miközben az elektronburokban egy elektronhiányos állapot jön létre. A detektor anyagában lejátszódó fotoeffektus hatására a félvezető belsejében olyan elektronok lesznek jelen, amelyek elegendő energiával rendelkeznek | + | A '''fotoeffektus''' során a gamma-foton átadja a '''teljes energiáját''' egy atom valamelyik kötött elektronjának, amely szabaddá válik, miközben az elektronburokban egy elektronhiányos állapot jön létre. A detektor anyagában lejátszódó fotoeffektus hatására a félvezető belsejében olyan elektronok lesznek jelen, amelyek elegendő energiával rendelkeznek ahhoz, hogy részt vegyenek az elektromos vezetési folyamatban. A jelenség hatáskeresztmetszete az alábbi (1) formulával írható le, ahol '''Z''' az anyag rendszáma, '''N''' az anyag atomsűrűsége: |
{| width = "100%" | {| width = "100%" | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \ | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \sigma_{f} \sim NZ^{5}(E_{\gamma})^{-3,5} \]</latex></div> |
| align = "right" | <span id="eq2"> (1) </span> | | align = "right" | <span id="eq2"> (1) </span> | ||
|} | |} | ||
| − | A Compton-szórás során a foton az energiájának ( | + | A '''Compton-szórás''' során a foton az energiájának (E<sub>${\gamma}$</sub>) csak egy részét adja át a szabad vagy az E<sub>${\gamma}$</sub> energiához képest kis kötési energiával rendelkező atomi elektronnak. A folyamat során a foton energiája és iránya megváltozik. A szórt foton energiájának nagyságát a (2) egyenlet írja le, ahol 0 < ${\vartheta}$ < 180° a szórt foton iránya a primer foton irányához képest, ''m'' az elektron nyugalmi tömege, ''c'' a fénysebesség. |
| + | |||
| + | {| width = "100%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ E_{\gamma} = \frac {E_{\gamma}} {\frac {E_{\gamma}}{mc^2}}(1-cos\vartheta)+1 \]</latex></div> | ||
| + | | align = "right" | <span id="eq2"> (2) </span> | ||
| + | |} | ||
| + | |||
A folyamat hatáskeresztmetszetét a Klein-Nishina formula írja le a (3) egyenlet szerint. | A folyamat hatáskeresztmetszetét a Klein-Nishina formula írja le a (3) egyenlet szerint. | ||
| − | A fenti szórási folyamatban a meglökött elektron energiája egy meghatározott | + | |
| − | energiatartományba esik | + | {| width = "100%" |
| − | spektrumokban | + | |- |
| − | 1333 keV energiájú fotonhoz tartozó Compton-él energiája 1119 keV. | + | | width = "10%" | |
| − | A párkeltés folyamata során egy gamma-foton a detektor anyaga egy atommagjának | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \sigma_{KN} \sim \frac {NZ} {E_{\gamma}} \ln (\frac {2E_{\gamma}}{mc^2}+0,5) \]</latex></div> |
| − | + | | align = "right" | <span id="eq2"> (3) </span> | |
| − | mint a | + | |} |
| − | nagyobb, mint a két részecske nyugalmi tömegeinek összege, akkor a foton maradék | + | |
| − | energiája az elektron és pozitron kinetikus energiájára fordítódik. A pozitron | + | A fenti szórási folyamatban a meglökött elektron energiája egy meghatározott energiatartományba esik a ${\vartheta}$ szög értékétől függően, aminek következménye a gamma spektrumokban megjelenő Compton-él és plató. Például a <sup>60</sup>Co bomlása során keletkező 1333 keV energiájú fotonhoz tartozó Compton-él energiája 1119 keV. |
| − | egy elektronnal, aminek eredményeképpen annihiláció következik be. A folyamat során két | + | |
| − | 0.511 MeV energiájú foton jelenik meg a detektorban. A párkeltés hatáskeresztmetszete az | + | A '''párkeltés''' folyamata során egy gamma-foton a detektor anyaga egy atommagjának erőterében elektron-pozitron párrá alakulhat abban az esetben, ha a foton energiája nagyobb, mint a 2''mc''<sup>2</sup> = 1.022 MeV. Ha E<sub>${\gamma}$</sub> > 1.022 MeV feltétel teljesül, azaz a foton energiája nagyobb, mint a két részecske nyugalmi tömegeinek összege, akkor a foton maradék energiája az elektron és pozitron kinetikus energiájára fordítódik. A pozitron később egyesül egy elektronnal, aminek eredményeképpen '''annihiláció''' következik be. A folyamat során két 0.511 MeV energiájú foton jelenik meg a detektorban. A párkeltés hatáskeresztmetszete az alábbi (4) kifejezéssel arányos: |
| − | alábbi (4) kifejezéssel arányos: | + | |
| − | A fenti három alapvet_ kölcsönhatási folyamat eredménye a gamma sugárzás abszorpciója, | + | {| width = "100%" |
| − | aminek egy gamma nyaláb intenzitására gyakorolt hatását az (5) egyenlettel írhatjuk le, ahol | + | |- |
| − | + | | width = "10%" | | |
| − | abszorbens réteg elhagyása utáni intenzitás. | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \sigma_{p} \sim NZ^{2}({E_{\gamma}} - 2mc^{2}) \]</latex></div> |
| − | A leggyakrabban alkalmazott | + | | align = "right" | <span id="eq2"> (4) </span> |
| − | fenti három | + | |} |
| − | a fotonenergia függvényében. | + | |
| − | + | A fenti három alapvet_ kölcsönhatási folyamat eredménye a gamma sugárzás abszorpciója, aminek egy gamma nyaláb intenzitására gyakorolt hatását az (5) egyenlettel írhatjuk le, ahol ${\mu}$ az ''abszorpciós együttható'', ''x'' az abszorbeáló anyag rétegvastagsága, ${I_{0}}$ a kezdeti, ${I}$ az abszorbens réteg elhagyása utáni intenzitás. | |
| − | értékben változik, ellentétben a Compton-szórás hatáskeresztmetszetével. Mindhárom | + | |
| − | folyamat eredménye olyan elektronok megjelenése a detektor anyagában, amelyek | + | {| width = "100%" |
| − | energiával rendelkeznek, | + | |- |
| − | + | | width = "10%" | | |
| − | feszültség- vagy áramimpulzus jelenik meg, melynek amplitúdója arányos az abszorbeált | + | | width = "80%" | <div class="texdisplay"><latex display >\[ I = I_{0}e^{-\mu x} \]</latex></div> |
| − | gamma-foton energiájával. A spektrométer elektronikus és digitalizáló egységeinek feladata | + | | align = "right" | <span id="eq2"> (5) </span> |
| − | ezen impulzusok paramétereinek | + | |} |
| − | energia-eloszlásának megjelenítése. | + | |
| − | + | A leggyakrabban alkalmazott félvezető-detektor alapanyagok a Ge és Si, ezért a 2. ábrán a fenti három alapvető fizikai folyamat hatáskeresztmetszetét ezekre az anyagokra adjuk meg a fotonenergia függvényében. | |
| − | Detektor | + | |
| − | A nukleáris spektroszkópiában két fajta | + | Megfigyelhető, hogy a fotoeffektus és a párkeltés hatáskeresztmetszete több nagyságrend értékben változik, ellentétben a Compton-szórás hatáskeresztmetszetével. Mindhárom folyamat eredménye olyan elektronok megjelenése a detektor anyagában, amelyek elegendő energiával rendelkeznek ahhoz, hogy az elektromos vezetési folyamatban részt vegyenek. Összegyűjtve az így létrehozott töltéshordozókat a detektor elektromos kimenetén feszültség- vagy áramimpulzus jelenik meg, melynek amplitúdója arányos az abszorbeált |
| − | alapanyagú egykristályok. A Si detektorok | + | gamma-foton energiájával. A spektrométer elektronikus és digitalizáló egységeinek feladata ezen impulzusok paramétereinek számszerűsítése és ezáltal a detektált gamma spektrum energia-eloszlásának megjelenítése. |
| − | mérésére alkalmasak. Az egykristályos Ge anyagban kb. 3 eV abszorbeált energia szükséges | + | |
| − | egy elektron-lyuk pár létrehozásához. Ez az érték kb. tizede a | + | {| |
| − | századrésze a szcintillációs detektorok hasonló értékeihez képest. Így, azonos energia | + | | <span id="fig:2">[[Fájl:FizLab4_GAMMA_02.jpg|közép|bélyegkép|300px|2.ábra: Alapvető foton-atom folyamatok hatáskeresztmetszetének változása a foton-energia függvényében Si és Ge elemekre.]]</span> |
| − | átadásával a | + | |} |
| − | két detektorban. Mivel a nagyobb számú töltéshordozó számának relatív ingadozása | + | |
| − | lényegesen kisebb, ami a detektoranyagban abszorbeált foton-energia meghatározását sokkal | + | ==A gamma-spektrometria eszközei== |
| − | pontosabbá teheti. Ez azt eredményezi, hogy a | + | |
| − | energiafelbontást lehet elérni, mint az egyéb detektortípusokkal. A kis | + | '''Detektor''' |
| − | relatíve kevés detektoranyagot tartalmazó | + | |
| − | + | A nukleáris spektroszkópiában két fajta félvezető-detektor a legelterjedtebb, a Ge és a Si alapanyagú egykristályok. A Si detektorok elsősorban béta és nehéz töltött részecskék mérésére alkalmasak. Az egykristályos Ge anyagban kb. 3 eV abszorbeált energia szükséges egy elektron-lyuk pár létrehozásához. Ez az érték kb. tizede a gáztöltésű detektor és századrésze a szcintillációs detektorok hasonló értékeihez képest. Így, azonos energia átadásával a félvezető-detektorban lényegesen több töltéshordozó keletkezik, mint a másik két detektorban. Mivel a nagyobb számú töltéshordozó számának relatív ingadozása lényegesen kisebb, ami a detektoranyagban abszorbeált foton-energia meghatározását sokkal pontosabbá teheti. Ez azt eredményezi, hogy a félvezető detektorokkal lényegesen jobb energiafelbontást lehet elérni, mint az egyéb detektortípusokkal. A kis sűrűségű, illetve relatíve kevés detektoranyagot tartalmazó gáztöltésű detektorok hatásfoka gamma-sugárzásra alacsony, míg a Ge nagyobb rendszáma és sűrűsége nagyobb detektálási hatásfokot eredményez, ami ideálissá teszi a gamma-sugárzás detektálására. A Si rendszáma kisebb, ezért elsősorban alacsony energiájú (3-60 keV) gamma- ill. Röntgen-sugárzás érzékelésére alkalmazzák. | |
| − | + | ||
| − | + | A fentiekben részletezett méréstechnikai tulajdonság oka a félvezetőkben lejátszódó szilárdtestfizikai folyamatokkal magyarázható. Egy félvezető egykristályban az atomokhoz kötött elektronok által betöltött legfelső energia-sáv az u. n. ''valencia sáv'', míg az atomokhoz nem kötött, szilárd félvezető belsejében szabadon mozogni képes elektronok energiasávja az u. n. ''vezetési sáv'' között található a ''tiltott sáv'', amelyben nincs elektronállapot. | |
| − | + | ||
| − | sugárzásra alacsony, míg a Ge nagyobb rendszáma és | + | A tiltott sáv szélessége a félvezető anyagokban 1-2 eV. Radioaktív sugárzás, hő vagy fény hatására a valencia sáv egyes elektronjai átkerülhetnek a vezetési sávba és így részt vehetnek az elektromos vezetésben. Ha egy gamma-foton kölcsönhatásba lép a kristály elektronjaival, akkor átadja azoknak energiáját, ezáltal az elektronok a valencia sávból a vezetési sávba kerülnek. A gerjesztett elektronok egy elektronhiányos állapotot hagynak maguk után a valenciasávban. Egy ilyen elektron-lyuk pár keltéséhez Ge-ban kb. 2.8 eV, Si-ban 3.6 eV energia szükséges. |
| − | hatásfokot eredményez, ami ideálissá teszi a gamma-sugárzás detektálására. A Si rendszáma | + | |
| − | kisebb, ezért | + | A detektorra kapcsolt feszültség hatására létrejövő kb. 1000 V/cm-es elektromos térerősség a töltéshordozók egyirányú áramlását idézi elő a detektor elektródáira. Az így létrejövő töltésekből álló impulzust a detektorhoz kapcsolt áramkörök alakítják tovább. Fontos, hogy az alkalmazott félvezetők anyagának fajlagos ellenállása kb 10<sup>8</sup> ${\Omega}$cm, mivel ellenkező esetben a saját áramból eredő zaj igen nagy lenne. Mivel elektronok eljuthatnak a vezetési sávba úgy is, hogy energiájukat véletlenszerűen, a környezetből abszorbeált termikus fotonokból nyerik, ezáltal növelhetik a spektrométer áramát olyan módon, hogy annak oka nem gamma fotonok detektálása, azaz a jelenség zajt eredményez. A ''termikus zaj'' csökkentése érdekében a félvezető detektorokat alacsony hőmérsékleten (kb. 77°K) cseppfolyós nitrogénnel hűtve kell üzemeltetni. Ma már vannak Peltier-effektust alkalmazó hűtéssel felszerelt, valamint szobahőmérsékleten működő félvezető detektorok is (SDD = Silicon Drift Detector). A HPGe detektorok technikai-geometriai kialakítására számos egyedi megoldást dolgoztak ki a felhasználás céljától függően. A leggyakrabban alkalmazott geometriai elrendezések a 3. ábrán láthatóak. További részleteket a témával foglalkozó, idézett irodalomban illetve a ''Nukleáris méréstechnika'' tárgy keretein belül lehet találni. A |
| − | érzékelésére alkalmazzák. | + | |
| − | A fentiekben részletezett méréstechnikai tulajdonság oka a | + | |
| − | szilárdtestfizikai folyamatokkal magyarázható. Egy | + | |
| − | kötött elektronok által betöltött | + | |
| − | nem kötött, szilárd | + | |
| − | u. n. vezetési sáv között található a tiltott sáv, amelyben nincs elektronállapot. | + | |
| − | A tiltott sáv szélessége a | + | |
| − | hatására a valencia sáv egyes elektronjai átkerülhetnek a vezetési sávba és így részt vehetnek | + | |
| − | az elektromos vezetésben. Ha egy gamma-foton kölcsönhatásba lép a kristály elektronjaival, | + | |
| − | akkor átadja azoknak energiáját, ezáltal az elektronok a valencia sávból a vezetési sávba | + | |
| − | kerülnek. A gerjesztett elektronok egy elektronhiányos állapotot hagynak maguk után a | + | |
| − | valenciasávban. Egy ilyen elektron-lyuk pár keltéséhez Ge-ban kb. 2.8 eV, Si-ban 3.6 eV | + | |
| − | energia szükséges. | + | |
| − | A detektorra kapcsolt feszültség hatására | + | |
| − | a töltéshordozók egyirányú áramlását idézi | + | |
| − | + | ||
| − | az alkalmazott | + | |
| − | esetben a saját áramból | + | |
| − | sávba úgy is, hogy energiájukat | + | |
| − | fotonokból nyerik, | + | |
| − | nem gamma fotonok detektálása, azaz a jelenség zajt eredményez. A termikus zaj | + | |
| − | csökkentése érdekében a | + | |
| − | cseppfolyós nitrogénnel | + | |
| − | + | ||
| − | Silicon Drift Detector). A HPGe detektorok technikai-geometriai kialakítására számos | + | |
| − | egyedi megoldást dolgoztak ki a felhasználás céljától | + | |
| − | geometriai elrendezések a 3. ábrán láthatóak. További részleteket a témával foglalkozó, | + | |
| − | + | ||
| − | + | ||
| − | idézett irodalomban illetve a Nukleáris méréstechnika tárgy keretein belül lehet találni. A | + | |
jelen gyakorlat során egy p-típusú koaxiális detektort fogunk használni. | jelen gyakorlat során egy p-típusú koaxiális detektort fogunk használni. | ||
| − | Elektronikus jelfeldolgozó egységek | + | |
| − | A gamma-spektrométerek egyes elektronikus egységeinek kiválasztását az adott nukleáris | + | {| |
| − | detektálási feladat szabja meg. Az | + | | <span id="fig:3">[[Fájl:FizLab4_GAMMA_03.jpg|közép|bélyegkép|300px|3.ábra: Ge típusú detektorok.]]</span> |
| − | illesztés illetve a jel | + | |} |
| − | + | ||
| − | és | + | '''Elektronikus jelfeldolgozó egységek''' |
| − | sebességek esetén | + | |
| − | Az expander (nyújtó) | + | A gamma-spektrométerek egyes elektronikus egységeinek kiválasztását az adott nukleáris detektálási feladat szabja meg. Az '''előerősítő''' feladata a detektor és a főerősítő közötti illesztés illetve a jel erősítése annak továbbítása előtt oly módon, hogy a jel/zaj arány minél kedvezőbb legyen. A '''főerősítő'''vel szemben támasztott követelmény a nagyfokú linearitás és időbeni stabilitás. Az '''alapszint helyreállító''' (base line restorer) nagy számlálási sebességek esetén fellépő alapszint-csökkenés mértékét (jelamplitúdó-változást) mérsékli. Az '''expander''' (nyújtó) '''erősítő''' a spektrum bizonyos részének széthúzását teszi lehetővé, abban az esetben, ha a spektrum struktúrájának részletesebb vizsgálatára van szükség. A '''stretcher''' (jelnyújtó) az analizátor bemenetének (ADC: analóg digital converter) egy elektronikailag kedvezőbb jelformát biztosít. A '''pulser''' vagy impulzusgenerátor egy stabil frekvenciával és amplitúdóval rendelkező impulzus-generátor a jelalak vizsgálathoz, illetve az automatikus holtidő-korrekcióhoz használatos. A '''sokcsatornás amplitúdó-analizátor'''t két különböző típusú ADC-vel szokták alkalmazni: a lassúbb változat a Wilkinson típusú ADC, míg a gyorsabb a jelanalízis szukcesszív approximációján alapszik. A '''nagyfeszültségű tápegység''' biztosítja a detektor működéséhez szükséges feszültséget (2-5000 V). Félvezető-detektorok esetében nem kívánalom a nagy stabilitás, csak az alacsony elektronikus zaj. A '''kisfeszültségű tápegység''' (${\pm}$6, ${\pm}$12, ${\pm}$24 V) a különböző elektronikus egységek (erősítők, stb.) tápfeszültség forrása. A jelen gyakorlat során egy DSP jelfeldolgozó egységet használunk, amely elvégzi a fentiekben felsorolt funkciókon kívül az analóg jelek digitalizálását és az egyes csatornatartalmakat közvetlenül a PC memóriájába tölti. |
| − | abban az esetben, ha a spektrum struktúrájának részletesebb vizsgálatára van szükség. A | + | |
| − | stretcher (jelnyújtó) az analizátor bemenetének (ADC: analóg digital converter) egy | + | ==A gamma-spektrumok kiértékelése== |
| − | elektronikailag | + | |
| − | frekvenciával és amplitúdóval | + | A 4. ábrán egy monoenergetikus gamma-sugárzásról felvett spektrum elvi alakja látható. A teljesenergia-csúcs megjelenése elsősorban a fotoeffektus révén következik be, ezért fotocsúcsnak is szokták nevezni. Az 511 keV energiánál jelentkező ún. annihilációs csúcs vagy a párkeltési folyamat következménye, vagy egy pozitív béta-bomló izotóptól származik. A visszaszórási csúcs a detektor burkolatán, a mérőhely árnyékolásának belső falán szóródott fotonok detektálásának következménye. A gamma spektrumokban a csúcsok alatt található |
| − | az automatikus | + | folytonos háttér nagysága, és ezzel egy adott izotóp kimutathatósági határa csökkenthető a szóró felületek távolabb helyezésével és az anyaguk rendszámának csökkentésével. A visszaszórási-, annihilációs-, stb. csúcsok a Compton kölcsönhatás miatt kialakuló ún. Compton tartományra szuperponálódnak. |
| − | két | + | |
| − | ADC, míg a gyorsabb a jelanalízis szukcesszív approximációján alapszik. A | + | A spektrum kiértékelésének alapvető célja az, hogy a ''teljesenergia-csúcsok'' területét meghatározzuk. Ehhez a következő lépéseket kell tenni: |
| − | + | ||
| − | + | * a spektrum energia-kalibrációja | |
| − | + | * csúcskeresés | |
| − | + | * a csúcsokhoz tartozó izotópok azonosítása egy izotópkönyvtár alapján | |
| − | + | * az átlapoló csúcsok matematikai szétválasztása és a spektrum matematikai függvényekkel történő illesztése | |
| − | + | * csúcsterületek kiszámítása | |
| − | + | * az egyes csúcsokhoz tartozó izotópok aktivitásának/fajlagos aktivitásának számítása | |
| − | + | ||
| − | 5000 V). | + | A fenti feladatokat, a mérést vezérlő '''Genie-2000''' szoftverrel végezzük, amely alapvető funkcióinak rövid útmutatója és használata a jelen jegyzethez mellékelt leírásban található. |
| − | elektronikus zaj. A | + | |
| − | egységek ( | + | {| |
| − | jelfeldolgozó egységet használunk, amely elvégzi | + | | <span id="fig:4">[[Fájl:FizLab4_GAMMA_04.jpg|közép|bélyegkép|300px|4.ábra: HPGe detektorral felvett gamma-spektrum szerkezete.]]</span> |
| − | az analóg jelek digitalizálását és az egyes csatornatartalmakat közvetlenül a PC | + | |} |
| − | memóriájába tölti. | + | |
| − | + | '''A gamma-spektrumok kiértékeléséhez szükséges fogalmak és azok számítása''' | |
| − | A 4. ábrán egy monoenergetikus gamma-sugárzásról felvett spektrum elvi alakja látható. A | + | |
| − | teljesenergia-csúcs megjelenése | + | A gamma-spektrométerek kvantitatív jellemzéséhez néhány alapvető paramétert kell definiálni. A detektor energia-felbontóképessége egy olyan, a gammafotonok energiától függő paraméter, amely megadja egy adott energiájú gamma csúcs félértékszélességét (FWHM= Full Width at Half Maximum) a csúcs centrumához tartozó energia függvényében. A gamma csúcsokat matematikailag egy Gauss-függvénnyel lehet leírni a (6) egyenlet |
| − | is szokták nevezni. Az 511 keV energiánál | + | szerint. A görbe kiszélesedését jellemezni lehet a maximum érték feléhez tartozó csúcsszélességgel (FWHM). |
| − | a párkeltési folyamat következménye, vagy egy pozitív | + | |
| − | visszaszórási csúcs a detektor burkolatán, a | + | {| width = "100%" |
| − | fotonok detektálásának következménye. A gamma spektrumokban a csúcsok alatt található | + | |- |
| − | folytonos háttér nagysága, és ezzel egy adott izotóp kimutathatósági határa | + | | width = "10%" | |
| − | szóró felületek távolabb helyezésével és az anyaguk rendszámának csökkentésével. A | + | | width = "80%" | <div class="texdisplay"><latex display >\[ y_{i}= \frac{y_{0}}{\sigma \sqrt {2\pi}} exp \Bigg(-\frac {(E-E_{0})^{2}}{2\sigma^{2}}\Bigg) \]</latex></div> |
| − | visszaszórási-, annihilációs-, stb. csúcsok a Compton kölcsönhatás miatt kialakuló ún. | + | | align = "right" | <span id="eq2"> (6) </span> |
| − | Compton tartományra szuperponálódnak. | + | |} |
| − | A spektrum kiértékelésének | + | |
| − | meghatározzuk. Ehhez a | + | A csúcsok kiszélesedésének több oka is van, amelyek közül a jelentősebb járulékot adó tag a detektorban lejátszódó fizikai folyamatok, illetve a jelfeldolgozó elektronikus egységek által keltett zaj miatt következik be. Az ${\Large{f}}$ értéke egy adott detektor esetén függ a gamma-energiától (annak növekedésével javul) és valamelyest a számlálási sebességtől (ennek növekedésével romlik). Ge detektorok esetében a ${\Delta}$''E'' ${\approx}$ 1.8 - 2.7 keV közötti értékű 1333 keV (<sup>60</sup>Co) gamma energiánál. |
| − | + | ||
| − | + | A félértékszélesség energiafüggését számos tényező befolyásolja, aminek eredményeképpen az FWHM az alábbi összefüggésben van a detektált gamma-fotonok energiájával. Az FWHM értékét befolyásoló folyamatokról bővebb ismereteket az [1] és [2] irodalomban lehet megtalálni. A félértékszélesség energiafüggését a Genie-2000 szoftver a (7) összefüggéssel közelíti | |
| − | + | ||
| − | + | {| width = "100%" | |
| − | függvényekkel | + | |- |
| − | + | | width = "10%" | | |
| − | + | | width = "80%" | <div class="texdisplay"><latex display >\[ FWHM = a+b \sqrt{E} \]</latex></div> | |
| − | számítása | + | | align = "right" | <span id="eq2"> (7) </span> |
| − | + | |} | |
| − | + | ||
| − | A fenti feladatokat, a mérést | + | ahol az ''a'' és ''b'' konstansok és ''E'' a gamma-fotonok energiája. |
| − | funkcióinak rövid útmutatója és használata a jelen jegyzethez mellékelt leírásban található. | + | |
| − | A gamma-spektrumok kiértékeléséhez szükséges fogalmak és azok számítása | + | Az ''abszolút vagy teljesenergia-csúcs hatásfok értéke'' azt adja meg, hogy a sugárforrásból kibocsátott, adott energiájú összes gamma fotonból hányat regisztrál a detektor a teljesenergia-csúcsban. A hatásfok számszerű definícióját a (8) összefüggéssel lehet megadni, ahol ''N'' a teljesenergia-csúcs területe, amit egy, a mérés időpontjában az ''A'' aktivitású sugárforrás gamma-sugárzásának detektálásával kaptunk, ${t_{m}}$ a mérés időtartama és ${k}$ a gamma-gyakoriság értéke. |
| − | A gamma-spektrométerek kvantitatív jellemzéséhez néhány | + | |
| − | definiálni. A detektor energia-felbontóképessége egy olyan, a gammafotonok energiától | + | {| width = "100%" |
| − | + | |- | |
| − | (FWHM= | + | | width = "10%" | |
| − | A gamma csúcsokat matematikailag egy Gauss-függvénnyel lehet leírni a (6) egyenlet | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \eta = \frac{N}{t_{m}Ak} \]</latex></div> |
| − | szerint. A görbe kiszélesedését jellemezni lehet a maximum érték feléhez tartozó | + | | align = "right" | <span id="eq2"> (8) </span> |
| − | csúcsszélességgel (FWHM). | + | |} |
| − | + | ||
| − | + | Az ''abszolút hatásfok'' értéke csökken a gamma sugárzás energiájának növekedésével, növekszik a detektor térfogatával és jelentősen befolyásolják a mérési geometria paraméterei: forrás-detektor távolság, forrás alakja, kiterjedtsége és a forrás anyaga. A félvezető-detektorokat gyártó cégek megadják az u. n. ''relatív hatásfokot'', amely egy 25 cm távolságban elhelyezett <sup>60</sup>Co pontforrás 1333 KeV vonalának intenzitására vonatkozik a (9) egyenletnek megfelelően | |
| − | + | ||
| − | + | {| width = "100%" | |
| − | + | |- | |
| − | + | | width = "10%" | | |
| − | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \eta_{rel} = \frac{\eta_{Ge}}{\eta_{Nal}} \]</latex></div> | |
| − | + | | align = "right" | <span id="eq2"> (9) </span> | |
| − | 0 | + | |} |
| − | 2 | + | |
| − | exp | + | ahol ${\eta_{Nal}}$ = 1.2 ${\times}$ 10<sup>-3</sup> a fentiek szerinti geometriában, egy 75${\times}$75 mm méretű Nal(TI) szcintillációs kristály abszolut teljesenergia-csúcs hatásfoka. |
| − | + | ||
| − | + | '''Mérés alatti bomlás korrekciója''' | |
| − | + | ||
| − | + | Ha a mérendő izotóp felezési ideje rövid a mérés időtartamához viszonyítva, azaz összemérhető a minta mérési idejével, akkor az aktivitás meghatározása során figyelembe kell venni a mérés alatt bekövetkező bomlásokat is. A radioaktív bomlás időfüggése alapján felírható a (10) egyenlet, ahol ''${\Large{\lambda}}$'' az izotóp bomlási állandója és ''t<sub>m</sub>'' a mérés időtartama, ''N<sub>0</sub>'' a radioaktív preparátum aktivitása a mérés kezdő időpontjában és ''N<sub>m</sub>'' a mérés teljes időtartama alatt mért aktivitás. | |
| − | + | ||
| − | + | {| width = "100%" | |
| − | + | |- | |
| − | + | | width = "10%" | | |
| − | + | | width = "80%" | <div class="texdisplay"><latex display >\[ N_{0} = \frac{N_{m}}{\int_{0}^{t_{m}}e^{-\lambda t}dt} = \frac {N_{m} \lambda t_{m}}{1-e^{-\lambda t_{m}}} \]</latex></div> | |
| − | + | | align = "right" | <span id="eq2"> (10) </span> | |
| − | + | |} | |
| − | + | ||
| − | + | ===Valódi koincidencia és a mintaösszetétel miatti korrekciók=== | |
| − | + | ||
| − | + | A gyakorlati gamma-spektroszkópiai méréseknél szükség lehet még további két különböző korrekció alkalmazására is. Az egyik ilyen jelenség a ''valódi-koincidencia'', amely akkor jön létre, ha a mérendő mintában olyan izotóp található, amely ''kaszkád bomlással'' több fotont emittál a spektrométer holtidején belüli időtartamban (ilyen a <sup>60</sup>Co, <sup>152</sup>Eu izotópok). Az effektus valószínűsége növekszik a detektortérfogattal és a minta-detektor távolság csökkenésével de független a minta aktivitásától. A valódi koincidencia miatt a spektrumban megjelennek az ''összegcsúcsok'', ami két valódi teljesenergia-csúcs összegéből áll elő, ezzel együtt a teljesenergia csúcsok területe kisebb lesz. A valódi koincidencia korrekcióba vétele általában bonyolult számítást jelent, amire a gyakorlat során alkalmazott | |
| − | + | Genie-2000 kiértékelő szoftver fel van készítve. | |
| − | + | ||
| − | + | A nagy térfogatú minták mérése során a mintában bekövetkező ''önabszorpció'' jelentős intenzitásváltozást okozhat. Ez akkor következik be, ha a detektortól távolabbi mintarészekből emittált fotonok csak a minta anyagán keresztül tudnak a detektorkristályba jutni. Ekkor a minta abszorbciós tulajdonságaitól függően csökken a detektált fotonok száma. Ennek a jelenségnek a figyelmen kívül hagyása kis energiájú (kb. 150 keV alatti) gamma-sugárzások mérésénél jelentős mértékű hibát okozhat. Az önabszorbció korrekciójának | |
| − | + | meghatározásához a hatásfok-kalibrációhoz használt forrásokat egy, a mintához hasonló abszorbciós tulajdonságú anyagba kevert izotópokkal kell elkészíteni. Megoldást jelenthet az is, ha a minta összetétele ismeretében a korrekció mértékét elméleti számításokkal megbecsüljük. | |
| − | + | ||
| − | + | ===A csúcsterületek számítása:=== | |
| − | + | ||
| − | A csúcsok kiszélesedésének több oka is van, amelyek közül a | + | A gyakorlat során a Genie-2000 kiértékelő szoftvert használjuk, ami a csúcsterület és annak hibája számítását automatikusan végzi a következő algoritmus szerint. |
| − | a detektorban lejátszódó fizikai folyamatok, illetve a jelfeldolgozó elektronikus egységek | + | |
| − | által keltett zaj miatt következik be. Az f értéke egy adott detektor esetén függ a | + | {| |
| − | (annak növekedésével javul) és valamelyest a számlálási | + | | <span id="fig:5">[[Fájl:FizLab4_GAMMA_05.jpg|közép|bélyegkép|300px|5.ábra: A gamma csúcsok kiértékelésének elemei, ahol ''N'' a nettó csúcsterület, ${\sigma_{N}}$ a csúcsterület statisztikus hibája.]]</span> |
| − | növekedésével romlik). Ge detektorok esetében a | + | |} |
| − | keV ( | + | |
| − | A félértékszélesség energiafüggését számos | + | A kiértékelő szoftverrel átlapoló csúcsokból álló együttesek is kiértékelhetőek. Ekkor a megfelelő spektrumrészletre több matematikai függvényből álló összetett alakot illesztünk, amely eredményéből a csúcsok alatti nettó terület meghatározható. |
| − | eredményeképpen az FWHM az alábbi összefüggésben van a detektált gamma-fotonok | + | |
| − | energiájával. Az FWHM értékét befolyásoló folyamatokról | + | ==Mérési feladatok== |
| − | irodalomban lehet megtalálni. A félértékszélesség energiafüggését a Genie-2000 szoftver a | + | |
| − | (7) összefüggéssel | + | ===Energiakalibráció=== |
| − | FWHM | + | |
| − | ahol a | + | Az energia-kalibráció elvégzéséhez helyezzen el a detektor elé ismert gamma-energiákat sugárzó, pontszerű, etalon sugárforrásokat (<sup>60</sup>Co, <sup>137</sup>Cs)! Vegyen fel egy gamma-spektrumot! A teljesenergia-csúcsok helyének megkeresésével, az energiák ismeretében határozza meg a gamma-energia-csatornaszám függvényt! Gyakorlatban a mért adatpárokra első- vagy másodfokú függvény illesztése szokásos. Ehhez a feladathoz használja a Genie-2000 szoftver energia-kalibrációra vonatkozó menüpontját ('''Calibrate''' menüpont). Legegyszerűbb esetben legyen két ismert kalibráló energia E<sub>1</sub> és E<sub>2</sub>, a hozzájuk tartozó csatornaszámok ''Cs<sub>1</sub>'' és ''Cs<sub>2</sub>''. Feltételezve, hogy a berendezés lineáris, a szoftver az alábbi két ponton átmenő egyenes alapján számítja ki a kalibrációs egyenes meredekségét. |
| − | Az abszolút vagy teljesenergia-csúcs hatásfok értéke azt adja meg, hogy a sugárforrásból | + | |
| − | kibocsátott, adott energiájú összes gamma fotonból hányat regisztrál a detektor a | + | |
| − | teljesenergia-csúcsban. A hatásfok | + | |
| − | megadni, ahol N a teljesenergia-csúcs területe, amit egy, a mérés | + | |
| − | aktivitású sugárforrás gamma-sugárzásának detektálásával kaptunk, m | + | |
| − | és k a gamma-gyakoriság értéke. | + | |
| − | + | ||
| − | + | ||
| − | m | + | |
| − | + | ||
| − | Az abszolút hatásfok értéke csökken a gamma sugárzás energiájának növekedésével, | + | |
| − | növekszik a detektor térfogatával és | + | |
| − | paraméterei: forrás-detektor távolság, forrás alakja, kiterjedtsége és a forrás anyaga. A | + | |
| − | + | ||
| − | távolságban elhelyezett | + | |
| − | egyenletnek | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | rel | + | |
| − | + | ||
| − | ahol | + | |
| − | szcintillációs kristály | + | |
| − | Mérés alatti bomlás korrekciója | + | |
| − | Ha a | + | |
| − | + | ||
| − | kell venni a mérés alatt | + | |
| − | felírható a (10) egyenlet, ahol | + | |
| − | a radioaktív preparátum aktivitása a mérés | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | m | + | |
| − | e | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | 1 | + | |
| − | + | ||
| − | + | ||
| − | Valódi koincidencia és a mintaösszetétel miatti korrekciók | + | |
| − | A gyakorlati gamma-spektroszkópiai méréseknél szükség lehet még további két | + | |
| − | korrekció alkalmazására is. Az egyik ilyen jelenség a valódi-koincidencia, amely akkor jön | + | |
| − | létre, ha a | + | |
| − | emittál a spektrométer holtidején belüli | + | |
| − | effektus | + | |
| − | csökkenésével de független a minta aktivitásától. A valódi koincidencia miatt a | + | |
| − | spektrumban megjelennek az összegcsúcsok, ami két valódi teljesenergia-csúcs | + | |
| − | áll | + | |
| − | korrekcióba vétele általában bonyolult számítást jelent, amire a gyakorlat során alkalmazott | + | |
| − | Genie-2000 | + | |
| − | A nagy térfogatú minták mérése során a mintában | + | |
| − | intenzitásváltozást okozhat. Ez akkor következik be, ha a detektortól távolabbi | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | jutni. Ekkor a minta abszorbciós tulajdonságaitól | + | |
| − | száma. Ennek a | + | |
| − | sugárzások mérésénél | + | |
| − | meghatározásához a hatásfok-kalibrációhoz használt forrásokat egy, a mintához hasonló | + | |
| − | abszorbciós tulajdonságú anyagba kevert izotópokkal kell elkészíteni. Megoldást jelenthet | + | |
| − | az is ha a minta összetétele ismeretében a korrekció mértékét elméleti számításokkal | + | |
| − | megbecsüljük. | + | |
| − | A csúcsterületek számítása: | + | |
| − | A gyakorlat során a Genie-2000 | + | |
| − | hibája | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | csúcsterület statisztikus hibája. | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Mérési feladatok | + | |
| − | + | ||
| − | Az energia-kalibráció elvégzéséhez helyezzen el a detektor elé ismert gamma-energiákat | + | |
| − | sugárzó, | + | |
| − | A teljesenergia-csúcsok helyének megkeresésével, az energiák ismeretében | + | |
| − | határozza meg a gamma-energia-csatornaszám függvényt! Gyakorlatban a mért adatpárokra | + | |
| − | + | ||
| − | 2000 szoftver energia-kalibrációra vonatkozó menüpontját (Calibrate | + | |
| − | + | ||
| − | csatornaszámok | + | |
| − | két ponton | + | |
| − | + | {| width = "100%" | |
| − | + | |- | |
| − | + | | width = "10%" | | |
| − | + | | width = "80%" | <div class="texdisplay"><latex display >\[ m = \frac{E_{2}-E_{1}}{Cs_{2}-Cs_{1}} \hspace{0.5cm} \Bigg(\frac {keV}{csat} \Bigg) \]</latex></div> | |
| − | + | | align = "right" | <span id="eq2"> (11) </span> | |
| − | + | |} | |
| − | + | ||
| − | + | Ahol ${m}$ az energia-kalibráció egyenesének meredeksége, amely két csatorna közötti intervallum energia értékét adja meg az adott erősítés esetén. A (11) egyenletet célszerű átrendezni a következő formára, ahol ${b}$ a kalibrációs egyenes tengelymetszete. | |
| − | + | ||
| − | m | + | {| width = "100%" |
| − | 2 1 | + | |- |
| − | 2 1 (11) | + | | width = "10%" | |
| − | Ahol | + | | width = "80%" | <div class="texdisplay"><latex display >\[ E = MCs+b \]</latex></div> |
| − | intervallum energia értékét adja meg az adott | + | | align = "right" | <span id="eq2"> (12) </span> |
| − | átrendezni a | + | |} |
| − | E | + | |
| − | Az energia-kalibráció elvégzéséhez használja az Calibrate/Energy Only Calibration | + | Az energia-kalibráció elvégzéséhez használja az '''Calibrate/Energy Only Calibration''' menüpontot, ahol a kalibrációhoz használt izotópok egyes vonalaira vonatkozóan be kell írni a vonal energiáját és a maximuma helyének csatornaszámát. A fenti művelethez használja fel a kalibráló gamma-forrásokra vonatkozó, az 1. táblázatban található adatokat! Mérje meg néhány, a gyakorlatvezetőtől kapott etalon sugárforrás gamma-spektrumát! Ellenőrizze a kiszámolt energia-kalibrációs görbét, a gyakorlatvezetőtől kapott források ismert energiájú vonalai felhasználásával! A méréseket úgy végezze el, hogy az egyes etalonokat mérés közben cserélje ki, ezáltal egy olyan kevert spektrumot kap, ami tartalmazza az összes mért izotóp vonalait! A szükséges mérési időt úgy válassza meg, hogy a gamma-csúcsok területének statisztikus hibája 1-3%-nál ne legyen nagyobb! |
| − | menüpontot, ahol a kalibrációhoz használt izotópok egyes vonalaira vonatkozóan be kell | + | Ügyeljen a holtidő nagyságára is, amit a minta-detektor távolság helyes megválasztásával tud elérni: 0, 10, 50, 150 mm! A mérések során a holtidő ne legyen nagyobb, mint 1-2%. |
| − | írni a vonal energiáját és a maximuma helyének csatornaszámát. A fenti | + | |
| − | használja fel a kalibráló | + | |
| − | Mérje meg néhány, a | + | {| border="1" cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: center; height: 350px" cellspacing="0" width="450" |
| − | + | |- | |
| − | kapott források ismert energiájú vonalai felhasználásával | + | ! colspan="6" | 1. feladat: Energia-kalibráció meghatározása |
| − | hogy az egyes etalonokat mérés közben cserélje ki | + | |- |
| − | kap, ami tartalmazza az összes mért izotóp vonalait | + | | width="30%" style="text-align: center;" colspan="2" | Izotóp |
| − | meg, hogy a | + | | width="10%" style="text-align: center;" | Energia (keV) |
| − | + | | width="20%" style="text-align: center;" | Csatornaszám | |
| − | + | | width="20%" style="text-align: center;" | m | |
| − | Ügyeljen a | + | | width="20%" style="text-align: center;" | b |
| − | tud elérni: 0, 10, 50, 150 mm | + | |- |
| − | 1. feladat: Energia-kalibráció meghatározása | + | | 1. || <sup>133</sup>Ba || 81.0 || || || | |
| − | Izotóp Energia (keV) Csatornaszám m b | + | |- |
| − | 1. | + | | 2. || <sup>57</sup>Co || 122.1 || || || | |
| − | 2. | + | |- |
| − | 3. | + | | 3. || <sup>133</sup>Ba || 276.4 || || || | |
| − | 4. | + | |- |
| − | 5. | + | | 4. || <sup>133</sup>Ba || 356.0 || || || | |
| − | 6. | + | |- |
| − | 7. | + | | 5. || <sup>137</sup>Cs || 661.7 || || || | |
| − | Ismert sugárforrások vonalainak energiái | + | |- |
| − | Izotóp | + | | 6. || <sup>60</sup>Co || 1173.2 || || || | |
| − | Energia (keV) | + | |- |
| − | (táblázat alapján) | + | | 7. || <sup>60</sup>Co || 1332.5 || || || | |
| − | Energia (keV) | + | |} |
| − | (energiakalibráció alapján) | + | |
| − | 1. | + | |
| − | 2. | + | {| border="1" cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: center; height: 300px" cellspacing="0" width="400" |
| − | 3. | + | |- |
| − | + | ! colspan="4" | Ismert sugárforrások vonalainak energiái | |
| − | 4. | + | |- |
| − | 5. | + | | width="10%" style="text-align: center;" colspan="2" | Izotóp |
| − | 6. | + | | width="15%" style="text-align: center;" | Energia (keV) (táblázat alapján) |
| − | A feladattal kapcsolatos adatokat a részfeladathoz tartozó táblázatba jegyezze fel | + | | width="15%" style="text-align: center;" | Energia (keV) (energiakalibráció alapján) |
| − | árnyékolt | + | |- |
| − | tetejére kell elhelyezni az etalon-forrásokat. A plexi mintatartó magasságbeli helyzetét | + | | 1. || <sup>241</sup>Am || || |
| − | változtatva | + | |- |
| − | tartozó detektor-minta távolságok az adott pozíción fel vannak tüntetve. A Genie-2000 által | + | | 2. || <sup>22</sup>Na || || |
| − | + | |- | |
| − | + | | 3. || rowspan="4" | <sup>152</sup>Eu || || | |
| − | kiszámított paramétereket és az illesztett kalibrációs görbét a Calibrate/Energy show | + | |- |
| − | menüpont alatt találja. | + | | 4. <!-- column 3 occupied by cell <sup>152</sup>Eu --> |
| − | + | | || | |
| − | Ehhez a feladathoz használja az | + | |- |
| − | ismert csúcsokkal | + | | 5. <!-- column 3 occupied by cell <sup>152</sup>Eu --> |
| − | adatokat illessze rá a FWHM | + | | || |
| − | 2. feladat: A spektrométer energia-felbontásának meghatározása | + | |- |
| − | Izotóp Energia (keV) FWHM (keV) a b | + | | 6. <!-- column 3 occupied by cell <sup>152</sup>Eu --> |
| − | 1. | + | | || |
| − | 2. | + | |} |
| − | 3. | + | |
| − | 4. | + | |
| − | 5. | + | A feladattal kapcsolatos adatokat a részfeladathoz tartozó táblázatba jegyezze fel! Az árnyékolt mérőkamrában talál egy plexi állványt és egy mintatartó plexi lapot, amelynek tetejére kell elhelyezni az etalon-forrásokat. A plexi mintatartó magasságbeli helyzetét változtatva különböző minta-detektor távolság állítható be. Az egyes pozíciók helyzetéhez tartozó detektor-minta távolságok az adott pozíción fel vannak tüntetve. A Genie-2000 által kiszámított paramétereket és az illesztett kalibrációs görbét a '''Calibrate/Energy show''' menüpont alatt találja. |
| − | 6. | + | |
| − | 7. | + | ===A spektrométer energiafelbontásának meghatározása=== |
| − | 3. A detektor abszolút hatásfok függvényének meghatározása | + | |
| − | Helyezzen ismert aktivitású és energiájú etalon pontforrásokat a detektor elé úgy, hogy | + | Ehhez a feladathoz használja az előző pontban már felvett és tárolt "mix" spektrumot az ismert csúcsokkal! Határozza meg az egyes csúcsok FWHM értékét, majd ábrázolja az adatokat illessze rá a ${FWHM = a+b}\sqrt{E}$ függvényt az energia függvényében! |
| − | mérés közben a | + | |
| − | források | + | |
| − | során végig azonos minta-detektor távolságot használjon! | + | {| border="1" cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: center; height: 320px" cellspacing="0" width="470" |
| − | A mért spektrumokat értékelje ki a Genie-2000 segítségével és számítsa ki a teljesenergiacsúcs | + | |- |
| − | integrálját (N), majd határozza meg a hatásfok értékeit | + | ! colspan="6" | 2. feladat: A spektrométer energia-felbontásának meghatározása |
| − | a (8) összefüggés felhasználásával N | + | |- |
| − | + | | width="30%" style="text-align: center;" colspan="2" | Izotóp | |
| − | + | | width="10%" style="text-align: center;" | Energia (keV) | |
| − | 3. feladat: A detektor abszolút hatásfoka energiafüggésének meghatározása | + | | width="20%" style="text-align: center;" | FWHM (keV) |
| − | A mintatartó magassági | + | | width="20%" style="text-align: center;" | a |
| − | Izotóp | + | | width="20%" style="text-align: center;" | b |
| − | Gamma | + | |- |
| − | energia | + | | 1. || <sup>133</sup>Ba || 81.0 || || || | |
| − | (keV) | + | |- |
| − | k | + | | 2. || <sup>57</sup>Co || 122.1 || || || | |
| − | 1. | + | |- |
| − | 2. | + | | 3. || <sup>133</sup>Ba || 276.4 || || || | |
| − | 3. | + | |- |
| − | 4. | + | | 4. || <sup>133</sup>Ba || 356.0 || || || | |
| − | 5. | + | |- |
| − | 6. | + | | 5. || <sup>137</sup>Cs || 661.7 || || || | |
| − | 7. | + | |- |
| − | Az | + | | 6. || <sup>60</sup>Co || 1173.2 || || || | |
| − | a b c d | + | |- |
| − | Ábrázolja a számított hatásfok értékeit ( | + | | 7. || <sup>60</sup>Co || 1332.5 || || || | |
| − | formában! A mért hatásfokadatokra a (13) szerinti polinom függvényt | + | |} |
| − | ahol | + | |
| − | + | ||
| − | Az | + | ===3. A detektor abszolút hatásfok függvényének meghatározása=== |
| − | számítsa ki a detektált izotópok aktivitását! Határozza meg a detektor hatásfokfüggvényét | + | |
| − | az adott távolságra vonatkozó pontforrás geometriára. | + | Helyezzen ismert aktivitású és energiájú etalon pontforrásokat a detektor elé úgy, hogy mérés közben a holtidő minden esetben kisebb legyen, mint 5%! Mérje meg az egyes izotóp források gamma-spektrumát! Mivel a hatásfok függ a geometriai elrendezéstől, a mérések során végig azonos minta-detektor távolságot használjon! |
| − | + | ||
| − | Határozza meg egy, a | + | A mért spektrumokat értékelje ki a Genie-2000 segítségével és számítsa ki a teljesenergiacsúcs integrálját ''(N)'', majd határozza meg a hatásfok értékeit (${\eta}$) a mért csúcsok energiáinál a (8) összefüggés felhasználásával ${\eta = N/t_{m}Ak}$! |
| − | számítása a (8) | + | |
| − | csúcsterület [imp], | + | |
| − | Gamma- | + | {| border="1" cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: center; height: 400px" cellspacing="0" width="800" |
| + | |- | ||
| + | ! colspan="9" | 3. feladat: A detektor abszolút hatásfoka energiafüggésének meghatározása | ||
| + | |- | ||
| + | ! colspan="9" | A mintatartó magassági poziciója: <font color="white"> .................... </font> mm | ||
| + | |- | ||
| + | | width="15%" style="text-align: center;" colspan="2" | Izotóp | ||
| + | | width="10%" style="text-align: center;" | t<sub>m</sub>(S) | ||
| + | | width="10%" style="text-align: center;" | A (Bq) | ||
| + | | width="15%" style="text-align: center;" | Dátum | ||
| + | | width="15%" style="text-align: center;" | Gamma energia (keV) | ||
| + | | width="10%" style="text-align: center;" | ''k'' | ||
| + | | width="10%" style="text-align: center;" | ${\eta_{sz\acute{a}mitott}}$ | ||
| + | | width="10%" style="text-align: center;" | ${\eta_{illesztett}}$ | ||
| + | |- | ||
| + | | 1. || <sup>133</sup>Ba || || || ||81.0 || || || | | ||
| + | |- | ||
| + | | 2. || <sup>57</sup>Co || || || || 122.1 || || || | | ||
| + | |- | ||
| + | | 3. || <sup>133</sup>Ba || || || || 276.4 || || || | | ||
| + | |- | ||
| + | | 4. || <sup>133</sup>Ba || || || || 356.0 || || || | | ||
| + | |- | ||
| + | | 5. || <sup>137</sup>Cs || || || || 661.7 || || || | | ||
| + | |- | ||
| + | | 6. || <sup>60</sup>Co || || || || 1173.2 || || || | | ||
| + | |- | ||
| + | | 7. || <sup>60</sup>Co || || || || 1332.5 || || || | | ||
| + | |- | ||
| + | ! colspan="9" | Az illesztett hatásfok paraméter értékei | ||
| + | |- | ||
| + | | a | ||
| + | | colspan="2" | | ||
| + | | b || || c || || d || | | ||
| + | |} | ||
| + | |||
| + | |||
| + | Ábrázolja a számított hatásfok értékeit (${{\eta}_{sz\acute{a}mitott}}$) az energia függvényében log-log formában! A mért hatásfokadatokra a (13) szerinti polinom függvényt célszerű illeszteni, ahol ${\eta}$ az ''E'' energiánál a fenti táblázat szerint számított hatásfok értéke. | ||
| + | |||
| + | {| width = "100%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ \ln\eta = a+b\ln E + c(\ln E)^{2}+d(\ln E)^{3} \]</latex></div> | ||
| + | | align = "right" | <span id="eq2"> (13) </span> | ||
| + | |} | ||
| + | |||
| + | Az illesztésből határozza meg az ''a,b,c,d,'' paramétereket. A hatásfokok ismeretében számítsa ki a detektált izotópok aktivitását! Határozza meg a detektor hatásfokfüggvényét az adott távolságra vonatkozó pontforrás geometriára. | ||
| + | |||
| + | ===Pontszerű radioaktív forrás aktivitásának meghatározása=== | ||
| + | |||
| + | Határozza meg egy, a gyakorlatvezető által megadott forrás aktivitását. Az aktivitás számítása a (8) összefüggésből származtatott (14) formula alapján történik, ahol ''N'' a nettó csúcsterület [imp], t<sub>m</sub> a minta mérési időtartama, ''k'' az adott gamma-vonal gyakorisága. | ||
| + | |||
| + | {| width = "100%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ A = \frac{N}{t_{m}\eta k} (Bq) \]</latex></div> | ||
| + | | align = "right" | <span id="eq2"> (14) </span> | ||
| + | |} | ||
| + | |||
| + | Becsülje meg a kapott eredmény hibáját a (14) összefüggés felhasználásával, ahol ${\sigma_{A}}$ | ||
| + | |||
| + | {| width = "100%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ \frac {\sigma_{A}}{A} \approx \frac {\sigma_{N}}{N} = \pm \frac{(N+2B)^{1/2}}{N} \]</latex></div> | ||
| + | | align = "right" | <span id="eq2"> (15) </span> | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| border="1" cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: center; height: 300px" cellspacing="0" width="800" | ||
| + | |- | ||
| + | ! colspan="10" | 4. feladat: Pontszerű radioaktív forrás aktivitásának meghatározása | ||
| + | |- | ||
| + | ! colspan="10" | A mintatartó magassági poziciója: <font color="white"> .................... </font> mm | ||
| + | |- | ||
| + | | width="10%" style="text-align: center;" colspan="2" | Izotóp | ||
| + | | width="10%" style="text-align: center;" | ''t<sub>m</sub>(S)'' | ||
| + | | width="10%" style="text-align: center;" | ''N (cps)'' | ||
| + | | width="10%" style="text-align: center;" | ${\eta}$ | ||
| + | | width="10%" style="text-align: center;" | Gamma vonal energiája (keV) | ||
| + | | width="10%" style="text-align: center;" | ''k'' | ||
| + | | width="10%" style="text-align: center;" | ${A_{sz\acute{a}mitott}}$ (Bq) | ||
| + | | width="10%" style="text-align: center;" | ${\sigma_{A}}$ (Bq) | ||
| + | | width="10%" style="text-align: center;" | ${A_{t\acute{e}nyleges}}$ (Bq) | ||
| + | |- | ||
| + | | 1. || rowspan="4" | <sup>152</sup>Eu || || || || 121.8 || 28.6 || || || | | ||
| + | |- | ||
| + | | 2. <!-- column 3 occupied by cell <sup>152</sup>Eu --> | ||
| + | | || || || 344.3 || 26.5 || || || | | ||
| + | |- | ||
| + | | 3. <!-- column 3 occupied by cell <sup>152</sup>Eu --> | ||
| + | | || || || 964.1 || 14.6 || || || | | ||
| + | |- | ||
| + | | 4. <!-- column 3 occupied by cell <sup>152</sup>Eu --> | ||
| + | | || || || 1408.0 || 21.0 || || || | | ||
| + | |} | ||
| + | |||
| + | |||
| + | ==Irodalom== | ||
| + | |||
| + | # G. F. Knoll, Radiation detection and measurement, John Wiley & Sonns, 2001. | ||
| + | # Bódizs D., Atommagsugárzások méréstechnikái, Typotex Kiadó Budapest, 2006 | ||
| + | # Deme S., Félvezető detektorok magsugárzás mérésére, Műszaki Könyvkiadó Budapest, 1968 | ||
| + | # Nagy L. Gy., Radiokémia és izotóptechnika, Tankönyvkiadó Budapest, 1983 | ||
| + | #C.M. Lederer, J.M. Hollander, I. Perlman, Table of Isotopes, Wiley, New York, 1984 | ||
| + | # K. Debertin, R.G. Helmer, Gamma- and X-ray spectrometry with semiconductor detectors, North Holland P.C. Amsterdam, 1988. | ||
| + | |||
| + | ==Kérdések== | ||
| + | |||
| + | # Soroljon fel 5 db gamma-sugárzó izotópot és bomlási módjukat! | ||
| + | # Ismertesse a gamma-sugárzás és az anyag atomjai között fellépő fontosabb kölcsönhatásokat és jellemzőiket! | ||
| + | # Mi a jelentése a radioaktív izotópok bomlássémájának? | ||
| + | # Hogyan működik a gamma-sugárzás mérésére alkalmazott HPGe detektor? | ||
| + | # Ismertesse egy gamma-spektrométer felépítését és az egyes egységeinek funkcióját, legfontosabb méréstechnikai jellemzőit! | ||
| + | # Milyen méréstechnikai jelentősége van a gamma-sugárforrás geometriai alakjának a hatásfok és az önabszorpció szempontjából? | ||
| + | # Miért szükséges a gamma-spektrométerek energia-kalibrációja és hogyan kell ezt elvégezni? | ||
| + | # Mit jelent az energia-felbontóképesség a gamma-spektroszkópiában és hogyan változik egy HPGe detektor felbontóképessége az energia függvényében? | ||
| + | # Mit jelent a spektrométer abszolút hatásfoka és hogyan lehet pontforrás esetén meghatározni? | ||
| + | # Hogyan lehet figyelembe venni a háttérsugárzást a gamma spektrumok kiértékelése során? | ||
| + | |||
| + | |||
| + | {| border="1" cellpadding="2" style="margin-left:auto; margin-right:auto; text-align: center; height: 50px" cellspacing="0" width="600" | ||
| + | |- | ||
| + | !colspan="6" | Kalibrálásra használt gamma etalon sugárforrások adatai | ||
| + | |- | ||
| + | ! rowspan="2" | Izotóp | ||
| + | ! colspan="5" |Gamma vonal energiája (keV) | ||
| + | |- | ||
| + | ! colspan="5" |Gamma vonal hozama (%) | ||
| + | |- | ||
| + | | rowspan="2" | <sup>22</sup>Na | ||
| + | | 1274.53 || || || || | ||
| + | |- | ||
| + | | 99.95 || || || || | ||
| + | |- | ||
| + | | rowspan="2" | <sup>57</sup>Co | ||
| + | | 122.06 || 136.47 || || || | ||
| + | |- | ||
| + | | 85.60 || 10.68 || || || | ||
| + | |- | ||
| + | | rowspan="2" | <sup>60</sup>Co | ||
| + | | 1332.50 || 1173.24 || || || | ||
| + | |- | ||
| + | | 99.99 || 99.97 || || || | ||
| + | |- | ||
| + | | rowspan="2" | <sup>133</sup>Ba | ||
| + | | 356.02 || 81.00 || 302.85 || 383.85 || 276.40 | ||
| + | |- | ||
| + | | 62.05 || 34.06 || 18.33 || 8.49 || 7.16 | ||
| + | |- | ||
| + | | rowspan="2" | <sup>137</sup>Cs | ||
| + | | 661.66 || || || || | ||
| + | |- | ||
| + | | 85.1 || || || || | ||
| + | |- | ||
| + | | rowspan="2" | <sup>241</sup>Am | ||
| + | | 59.54 || 26.345 || || || | ||
| + | |- | ||
| + | | 35.9 || 2.40 || || || | ||
| + | |- | ||
| + | | rowspan="9" | <sup>152</sup>Eu | ||
| + | |- | ||
| + | | 121.8 || 344.3 || 778.9 || 1408.0 || 1112.1 | ||
| + | |- | ||
| + | | 28.6 || 26.5 || 12.9 || 21.0 || 13.6 | ||
| + | |- | ||
| + | | 1085.9 || 964.1 || 867.4 || 78.9 || 244.7 | ||
| + | |- | ||
| + | | 10.2 || 14.6 || 4.3 || 12.9 || 7.6 | ||
| + | |- | ||
| + | | 411.1 || 443.9 || 919.3 || 1089.7 || 1212.9 | ||
| + | |- | ||
| + | | 2.2 || 2.8 || 0.43 || 1.73 || 1.4 | ||
| + | |- | ||
| + | | 1299.1 || 1457.6 || 1084.0 || 1005.3 || 488.7 | ||
| + | |- | ||
| + | | 1.62 || 0.50 || 0.25 || 0.65 || 0.42 | ||
| + | |} | ||
| + | |||
| + | |||
| + | ==Külső hivatkozások== | ||
| − | [ | + | A Gamma spektroszkópia laborjegyzet forrása elérhető a |
| − | + | [http://fizipedia.bme.hu/images/c/cb/Gammaspektrometria.pdf] linken: | |
A lap jelenlegi, 2013. szeptember 30., 10:55-kori változata
Tartalomjegyzék[elrejtés] |
Bevezetés
A gamma-spektrometria az atommagból valamilyen magfolyamat következtében (radioaktív bomlás, mesterséges vagy természetes magreakció) kilépő gamma sugárzás energiájának, intenzitásának, szögeloszlásának mérésével foglalkozik. A jelen laborgyakorlat lehetővé teszi az elméleti előadásokon hallott nukleáris méréstechnikai ismeretek elmélyítését és azok gyakorlati alkalmazásainak készségszintű elsajátítását. A gyakorlaton részt vevők betekintést nyernek a félvezető detektorra alapozott gamma-spektrometria alapjaiba, megismerik annak fontosabb eszközeit és a gamma-spektrumok kiértékelésének elemi lépéseit.
A gyakorlat alapvető mérőeszköze egy HPGe (High Purity Germanium) félvezető detektor, amely különböző mintákban lévő gamma-sugárzó izotópok azonosítására, azok abszolút és fajlagos aktivitásának meghatározására használható. A gamma spektrometria gyakorlati jelentőségét az adja, hogy számos területen alkalmazható a gamma-sugárzó izotópokkal kapcsolatos valamilyen analitikai vagy magfizikai probléma megoldásában. A magfizikai vonatkozású tudományos kutatásban a leggyakrabban az atommag energianívói energiájának és élettartamának meghatározására, izotópok bomlási sémáinak felderítésére, a belső konverziós együttható értékének mérésére, gamma-gamma szögkorreláció vizsgálatára stb. szokták alkalmazni.
A közvetlen gyakorlati célú hasznosítási területek a neutronaktivációs analízis, orvosi-, ipari-, mezőgazdasági nukleáris vonatkozású vizsgálatok a természetes és mesterséges radioizotópok analízisére, a környezet- és sugárvédelem gamma spektroszkópiai mérésekkel vizsgálható problémáinak megoldásában.
A gamma-spektrometriai gyakorlat során az alábbiakkal lehet megismerkedni:
- gamma-sugárzás és az anyag közötti kölcsönhatások megfigyelése
- gamma-spektrométer felépítése, az egyes részegységek spektroszkópiai jellemzői
- HPGe detektorok jelfeldolgozó elektronika alkalmazása a gamma-spektrometriában
- gamma-spektrumok kvantitatív kiértékelése
- mérési adatok feldolgozása, azok bizonytalanságának becslése
Elméleti összefoglaló
Fotoeffektus, szórás, párkeltés, emisszió és abszorpció:
Az atommagok alfa- és béta-bomlásai, a maghasadás valamint a magreakciók gyakran a leánymag gerjesztett állapotához vezetnek. A magfolyamat során keletkezett atommag a gerjesztett állapotból általában egy vagy több gamma foton kibocsátásával tér vissza az alapállapotába. A radioaktív atommag bomlása során emittált gamma fotonok energiája, intenzitása vagy szögeloszlása információt hordoz a sugárzó atommag belső felépítéséről, szerkezetéről. Egy atommagnak több legerjesztődési folyamata is lehet, amit az ún. bomlássémával szoktak ábrázolni (1. ábra). Az 1. ábrán egy A tömegű és Z rendszámú atommag energianívóit a függőleges tengelyen, míg a vízszintes tengelyen a rendszámot ábrázoltuk.
A különböző bomlási útvonalakhoz más-más átmeneti valószínűség tartozik, amit az adott béta vagy gamma-emisszió gyakoriságának nevezünk. A gyakorisági értékek az adott atommagra jellemző olyan nukleáris állandók, amik azt adják meg, hogy ha az adott magból 100 db elbomlik, akkor nagy valószínűséggel hány esetben emittál a mag adott energiájú béta-részecskét vagy gamma-fotont. A gamma-sugárzás és az anyag kölcsönhatása három alapvető folyamattal jellemezhető: fotoeffektus, Compton-szórás és párkeltés. Ezt a három alapvető fizikai folyamatot más elméleti tárgyak már részletesen elemezték ezért a jelen leírásban csak egy rövid áttekintést adunk.
A fotoeffektus során a gamma-foton átadja a teljes energiáját egy atom valamelyik kötött elektronjának, amely szabaddá válik, miközben az elektronburokban egy elektronhiányos állapot jön létre. A detektor anyagában lejátszódó fotoeffektus hatására a félvezető belsejében olyan elektronok lesznek jelen, amelyek elegendő energiával rendelkeznek ahhoz, hogy részt vegyenek az elektromos vezetési folyamatban. A jelenség hatáskeresztmetszete az alábbi (1) formulával írható le, ahol Z az anyag rendszáma, N az anyag atomsűrűsége:
![\[ \sigma_{f} \sim NZ^{5}(E_{\gamma})^{-3,5} \]](/images/math/6/c/c/6cc702f676d20e4dfcb86c7864860dce.png) |
(1) |
A Compton-szórás során a foton az energiájának (E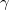 ) csak egy részét adja át a szabad vagy az E
) csak egy részét adja át a szabad vagy az E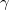 energiához képest kis kötési energiával rendelkező atomi elektronnak. A folyamat során a foton energiája és iránya megváltozik. A szórt foton energiájának nagyságát a (2) egyenlet írja le, ahol 0 <
energiához képest kis kötési energiával rendelkező atomi elektronnak. A folyamat során a foton energiája és iránya megváltozik. A szórt foton energiájának nagyságát a (2) egyenlet írja le, ahol 0 < 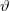 < 180° a szórt foton iránya a primer foton irányához képest, m az elektron nyugalmi tömege, c a fénysebesség.
< 180° a szórt foton iránya a primer foton irányához képest, m az elektron nyugalmi tömege, c a fénysebesség.
![\[ E_{\gamma} = \frac {E_{\gamma}} {\frac {E_{\gamma}}{mc^2}}(1-cos\vartheta)+1 \]](/images/math/0/e/0/0e08c542a679219d192ceeefac1628fc.png) |
(2) |
A folyamat hatáskeresztmetszetét a Klein-Nishina formula írja le a (3) egyenlet szerint.
![\[ \sigma_{KN} \sim \frac {NZ} {E_{\gamma}} \ln (\frac {2E_{\gamma}}{mc^2}+0,5) \]](/images/math/0/2/f/02fef8151218534ed5be5a1e1739fe51.png) |
(3) |
A fenti szórási folyamatban a meglökött elektron energiája egy meghatározott energiatartományba esik a 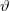 szög értékétől függően, aminek következménye a gamma spektrumokban megjelenő Compton-él és plató. Például a 60Co bomlása során keletkező 1333 keV energiájú fotonhoz tartozó Compton-él energiája 1119 keV.
szög értékétől függően, aminek következménye a gamma spektrumokban megjelenő Compton-él és plató. Például a 60Co bomlása során keletkező 1333 keV energiájú fotonhoz tartozó Compton-él energiája 1119 keV.
A párkeltés folyamata során egy gamma-foton a detektor anyaga egy atommagjának erőterében elektron-pozitron párrá alakulhat abban az esetben, ha a foton energiája nagyobb, mint a 2mc2 = 1.022 MeV. Ha E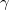 > 1.022 MeV feltétel teljesül, azaz a foton energiája nagyobb, mint a két részecske nyugalmi tömegeinek összege, akkor a foton maradék energiája az elektron és pozitron kinetikus energiájára fordítódik. A pozitron később egyesül egy elektronnal, aminek eredményeképpen annihiláció következik be. A folyamat során két 0.511 MeV energiájú foton jelenik meg a detektorban. A párkeltés hatáskeresztmetszete az alábbi (4) kifejezéssel arányos:
> 1.022 MeV feltétel teljesül, azaz a foton energiája nagyobb, mint a két részecske nyugalmi tömegeinek összege, akkor a foton maradék energiája az elektron és pozitron kinetikus energiájára fordítódik. A pozitron később egyesül egy elektronnal, aminek eredményeképpen annihiláció következik be. A folyamat során két 0.511 MeV energiájú foton jelenik meg a detektorban. A párkeltés hatáskeresztmetszete az alábbi (4) kifejezéssel arányos:
![\[ \sigma_{p} \sim NZ^{2}({E_{\gamma}} - 2mc^{2}) \]](/images/math/4/4/c/44c1be89edbae4c94e116a50c003d732.png) |
(4) |
A fenti három alapvet_ kölcsönhatási folyamat eredménye a gamma sugárzás abszorpciója, aminek egy gamma nyaláb intenzitására gyakorolt hatását az (5) egyenlettel írhatjuk le, ahol 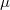 az abszorpciós együttható, x az abszorbeáló anyag rétegvastagsága,
az abszorpciós együttható, x az abszorbeáló anyag rétegvastagsága, 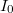 a kezdeti,
a kezdeti, 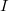 az abszorbens réteg elhagyása utáni intenzitás.
az abszorbens réteg elhagyása utáni intenzitás.
![\[ I = I_{0}e^{-\mu x} \]](/images/math/6/a/c/6ac5f07c1303b60fec27a00e45eaeaed.png) |
(5) |
A leggyakrabban alkalmazott félvezető-detektor alapanyagok a Ge és Si, ezért a 2. ábrán a fenti három alapvető fizikai folyamat hatáskeresztmetszetét ezekre az anyagokra adjuk meg a fotonenergia függvényében.
Megfigyelhető, hogy a fotoeffektus és a párkeltés hatáskeresztmetszete több nagyságrend értékben változik, ellentétben a Compton-szórás hatáskeresztmetszetével. Mindhárom folyamat eredménye olyan elektronok megjelenése a detektor anyagában, amelyek elegendő energiával rendelkeznek ahhoz, hogy az elektromos vezetési folyamatban részt vegyenek. Összegyűjtve az így létrehozott töltéshordozókat a detektor elektromos kimenetén feszültség- vagy áramimpulzus jelenik meg, melynek amplitúdója arányos az abszorbeált gamma-foton energiájával. A spektrométer elektronikus és digitalizáló egységeinek feladata ezen impulzusok paramétereinek számszerűsítése és ezáltal a detektált gamma spektrum energia-eloszlásának megjelenítése.
A gamma-spektrometria eszközei
Detektor
A nukleáris spektroszkópiában két fajta félvezető-detektor a legelterjedtebb, a Ge és a Si alapanyagú egykristályok. A Si detektorok elsősorban béta és nehéz töltött részecskék mérésére alkalmasak. Az egykristályos Ge anyagban kb. 3 eV abszorbeált energia szükséges egy elektron-lyuk pár létrehozásához. Ez az érték kb. tizede a gáztöltésű detektor és századrésze a szcintillációs detektorok hasonló értékeihez képest. Így, azonos energia átadásával a félvezető-detektorban lényegesen több töltéshordozó keletkezik, mint a másik két detektorban. Mivel a nagyobb számú töltéshordozó számának relatív ingadozása lényegesen kisebb, ami a detektoranyagban abszorbeált foton-energia meghatározását sokkal pontosabbá teheti. Ez azt eredményezi, hogy a félvezető detektorokkal lényegesen jobb energiafelbontást lehet elérni, mint az egyéb detektortípusokkal. A kis sűrűségű, illetve relatíve kevés detektoranyagot tartalmazó gáztöltésű detektorok hatásfoka gamma-sugárzásra alacsony, míg a Ge nagyobb rendszáma és sűrűsége nagyobb detektálási hatásfokot eredményez, ami ideálissá teszi a gamma-sugárzás detektálására. A Si rendszáma kisebb, ezért elsősorban alacsony energiájú (3-60 keV) gamma- ill. Röntgen-sugárzás érzékelésére alkalmazzák.
A fentiekben részletezett méréstechnikai tulajdonság oka a félvezetőkben lejátszódó szilárdtestfizikai folyamatokkal magyarázható. Egy félvezető egykristályban az atomokhoz kötött elektronok által betöltött legfelső energia-sáv az u. n. valencia sáv, míg az atomokhoz nem kötött, szilárd félvezető belsejében szabadon mozogni képes elektronok energiasávja az u. n. vezetési sáv között található a tiltott sáv, amelyben nincs elektronállapot.
A tiltott sáv szélessége a félvezető anyagokban 1-2 eV. Radioaktív sugárzás, hő vagy fény hatására a valencia sáv egyes elektronjai átkerülhetnek a vezetési sávba és így részt vehetnek az elektromos vezetésben. Ha egy gamma-foton kölcsönhatásba lép a kristály elektronjaival, akkor átadja azoknak energiáját, ezáltal az elektronok a valencia sávból a vezetési sávba kerülnek. A gerjesztett elektronok egy elektronhiányos állapotot hagynak maguk után a valenciasávban. Egy ilyen elektron-lyuk pár keltéséhez Ge-ban kb. 2.8 eV, Si-ban 3.6 eV energia szükséges.
A detektorra kapcsolt feszültség hatására létrejövő kb. 1000 V/cm-es elektromos térerősség a töltéshordozók egyirányú áramlását idézi elő a detektor elektródáira. Az így létrejövő töltésekből álló impulzust a detektorhoz kapcsolt áramkörök alakítják tovább. Fontos, hogy az alkalmazott félvezetők anyagának fajlagos ellenállása kb 108  cm, mivel ellenkező esetben a saját áramból eredő zaj igen nagy lenne. Mivel elektronok eljuthatnak a vezetési sávba úgy is, hogy energiájukat véletlenszerűen, a környezetből abszorbeált termikus fotonokból nyerik, ezáltal növelhetik a spektrométer áramát olyan módon, hogy annak oka nem gamma fotonok detektálása, azaz a jelenség zajt eredményez. A termikus zaj csökkentése érdekében a félvezető detektorokat alacsony hőmérsékleten (kb. 77°K) cseppfolyós nitrogénnel hűtve kell üzemeltetni. Ma már vannak Peltier-effektust alkalmazó hűtéssel felszerelt, valamint szobahőmérsékleten működő félvezető detektorok is (SDD = Silicon Drift Detector). A HPGe detektorok technikai-geometriai kialakítására számos egyedi megoldást dolgoztak ki a felhasználás céljától függően. A leggyakrabban alkalmazott geometriai elrendezések a 3. ábrán láthatóak. További részleteket a témával foglalkozó, idézett irodalomban illetve a Nukleáris méréstechnika tárgy keretein belül lehet találni. A
jelen gyakorlat során egy p-típusú koaxiális detektort fogunk használni.
cm, mivel ellenkező esetben a saját áramból eredő zaj igen nagy lenne. Mivel elektronok eljuthatnak a vezetési sávba úgy is, hogy energiájukat véletlenszerűen, a környezetből abszorbeált termikus fotonokból nyerik, ezáltal növelhetik a spektrométer áramát olyan módon, hogy annak oka nem gamma fotonok detektálása, azaz a jelenség zajt eredményez. A termikus zaj csökkentése érdekében a félvezető detektorokat alacsony hőmérsékleten (kb. 77°K) cseppfolyós nitrogénnel hűtve kell üzemeltetni. Ma már vannak Peltier-effektust alkalmazó hűtéssel felszerelt, valamint szobahőmérsékleten működő félvezető detektorok is (SDD = Silicon Drift Detector). A HPGe detektorok technikai-geometriai kialakítására számos egyedi megoldást dolgoztak ki a felhasználás céljától függően. A leggyakrabban alkalmazott geometriai elrendezések a 3. ábrán láthatóak. További részleteket a témával foglalkozó, idézett irodalomban illetve a Nukleáris méréstechnika tárgy keretein belül lehet találni. A
jelen gyakorlat során egy p-típusú koaxiális detektort fogunk használni.
Elektronikus jelfeldolgozó egységek
A gamma-spektrométerek egyes elektronikus egységeinek kiválasztását az adott nukleáris detektálási feladat szabja meg. Az előerősítő feladata a detektor és a főerősítő közötti illesztés illetve a jel erősítése annak továbbítása előtt oly módon, hogy a jel/zaj arány minél kedvezőbb legyen. A főerősítővel szemben támasztott követelmény a nagyfokú linearitás és időbeni stabilitás. Az alapszint helyreállító (base line restorer) nagy számlálási sebességek esetén fellépő alapszint-csökkenés mértékét (jelamplitúdó-változást) mérsékli. Az expander (nyújtó) erősítő a spektrum bizonyos részének széthúzását teszi lehetővé, abban az esetben, ha a spektrum struktúrájának részletesebb vizsgálatára van szükség. A stretcher (jelnyújtó) az analizátor bemenetének (ADC: analóg digital converter) egy elektronikailag kedvezőbb jelformát biztosít. A pulser vagy impulzusgenerátor egy stabil frekvenciával és amplitúdóval rendelkező impulzus-generátor a jelalak vizsgálathoz, illetve az automatikus holtidő-korrekcióhoz használatos. A sokcsatornás amplitúdó-analizátort két különböző típusú ADC-vel szokták alkalmazni: a lassúbb változat a Wilkinson típusú ADC, míg a gyorsabb a jelanalízis szukcesszív approximációján alapszik. A nagyfeszültségű tápegység biztosítja a detektor működéséhez szükséges feszültséget (2-5000 V). Félvezető-detektorok esetében nem kívánalom a nagy stabilitás, csak az alacsony elektronikus zaj. A kisfeszültségű tápegység ( 6,
6,  12,
12,  24 V) a különböző elektronikus egységek (erősítők, stb.) tápfeszültség forrása. A jelen gyakorlat során egy DSP jelfeldolgozó egységet használunk, amely elvégzi a fentiekben felsorolt funkciókon kívül az analóg jelek digitalizálását és az egyes csatornatartalmakat közvetlenül a PC memóriájába tölti.
24 V) a különböző elektronikus egységek (erősítők, stb.) tápfeszültség forrása. A jelen gyakorlat során egy DSP jelfeldolgozó egységet használunk, amely elvégzi a fentiekben felsorolt funkciókon kívül az analóg jelek digitalizálását és az egyes csatornatartalmakat közvetlenül a PC memóriájába tölti.
A gamma-spektrumok kiértékelése
A 4. ábrán egy monoenergetikus gamma-sugárzásról felvett spektrum elvi alakja látható. A teljesenergia-csúcs megjelenése elsősorban a fotoeffektus révén következik be, ezért fotocsúcsnak is szokták nevezni. Az 511 keV energiánál jelentkező ún. annihilációs csúcs vagy a párkeltési folyamat következménye, vagy egy pozitív béta-bomló izotóptól származik. A visszaszórási csúcs a detektor burkolatán, a mérőhely árnyékolásának belső falán szóródott fotonok detektálásának következménye. A gamma spektrumokban a csúcsok alatt található folytonos háttér nagysága, és ezzel egy adott izotóp kimutathatósági határa csökkenthető a szóró felületek távolabb helyezésével és az anyaguk rendszámának csökkentésével. A visszaszórási-, annihilációs-, stb. csúcsok a Compton kölcsönhatás miatt kialakuló ún. Compton tartományra szuperponálódnak.
A spektrum kiértékelésének alapvető célja az, hogy a teljesenergia-csúcsok területét meghatározzuk. Ehhez a következő lépéseket kell tenni:
- a spektrum energia-kalibrációja
- csúcskeresés
- a csúcsokhoz tartozó izotópok azonosítása egy izotópkönyvtár alapján
- az átlapoló csúcsok matematikai szétválasztása és a spektrum matematikai függvényekkel történő illesztése
- csúcsterületek kiszámítása
- az egyes csúcsokhoz tartozó izotópok aktivitásának/fajlagos aktivitásának számítása
A fenti feladatokat, a mérést vezérlő Genie-2000 szoftverrel végezzük, amely alapvető funkcióinak rövid útmutatója és használata a jelen jegyzethez mellékelt leírásban található.
A gamma-spektrumok kiértékeléséhez szükséges fogalmak és azok számítása
A gamma-spektrométerek kvantitatív jellemzéséhez néhány alapvető paramétert kell definiálni. A detektor energia-felbontóképessége egy olyan, a gammafotonok energiától függő paraméter, amely megadja egy adott energiájú gamma csúcs félértékszélességét (FWHM= Full Width at Half Maximum) a csúcs centrumához tartozó energia függvényében. A gamma csúcsokat matematikailag egy Gauss-függvénnyel lehet leírni a (6) egyenlet szerint. A görbe kiszélesedését jellemezni lehet a maximum érték feléhez tartozó csúcsszélességgel (FWHM).
![\[ y_{i}= \frac{y_{0}}{\sigma \sqrt {2\pi}} exp \Bigg(-\frac {(E-E_{0})^{2}}{2\sigma^{2}}\Bigg) \]](/images/math/f/1/d/f1d9f4159182d613166c455797b182ef.png) |
(6) |
A csúcsok kiszélesedésének több oka is van, amelyek közül a jelentősebb járulékot adó tag a detektorban lejátszódó fizikai folyamatok, illetve a jelfeldolgozó elektronikus egységek által keltett zaj miatt következik be. Az 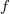 értéke egy adott detektor esetén függ a gamma-energiától (annak növekedésével javul) és valamelyest a számlálási sebességtől (ennek növekedésével romlik). Ge detektorok esetében a
értéke egy adott detektor esetén függ a gamma-energiától (annak növekedésével javul) és valamelyest a számlálási sebességtől (ennek növekedésével romlik). Ge detektorok esetében a 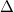 E
E 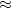 1.8 - 2.7 keV közötti értékű 1333 keV (60Co) gamma energiánál.
1.8 - 2.7 keV közötti értékű 1333 keV (60Co) gamma energiánál.
A félértékszélesség energiafüggését számos tényező befolyásolja, aminek eredményeképpen az FWHM az alábbi összefüggésben van a detektált gamma-fotonok energiájával. Az FWHM értékét befolyásoló folyamatokról bővebb ismereteket az [1] és [2] irodalomban lehet megtalálni. A félértékszélesség energiafüggését a Genie-2000 szoftver a (7) összefüggéssel közelíti
![\[ FWHM = a+b \sqrt{E} \]](/images/math/4/1/c/41cf89db97c49393892b18a5a078c1ab.png) |
(7) |
ahol az a és b konstansok és E a gamma-fotonok energiája.
Az abszolút vagy teljesenergia-csúcs hatásfok értéke azt adja meg, hogy a sugárforrásból kibocsátott, adott energiájú összes gamma fotonból hányat regisztrál a detektor a teljesenergia-csúcsban. A hatásfok számszerű definícióját a (8) összefüggéssel lehet megadni, ahol N a teljesenergia-csúcs területe, amit egy, a mérés időpontjában az A aktivitású sugárforrás gamma-sugárzásának detektálásával kaptunk, 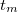 a mérés időtartama és
a mérés időtartama és 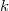 a gamma-gyakoriság értéke.
a gamma-gyakoriság értéke.
![\[ \eta = \frac{N}{t_{m}Ak} \]](/images/math/4/5/f/45fe8f6c1742e1af6945483458bf9136.png) |
(8) |
Az abszolút hatásfok értéke csökken a gamma sugárzás energiájának növekedésével, növekszik a detektor térfogatával és jelentősen befolyásolják a mérési geometria paraméterei: forrás-detektor távolság, forrás alakja, kiterjedtsége és a forrás anyaga. A félvezető-detektorokat gyártó cégek megadják az u. n. relatív hatásfokot, amely egy 25 cm távolságban elhelyezett 60Co pontforrás 1333 KeV vonalának intenzitására vonatkozik a (9) egyenletnek megfelelően
![\[ \eta_{rel} = \frac{\eta_{Ge}}{\eta_{Nal}} \]](/images/math/0/3/a/03a270b6697627d09fb367fef1b63094.png) |
(9) |
ahol 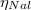 = 1.2
= 1.2  10-3 a fentiek szerinti geometriában, egy 75
10-3 a fentiek szerinti geometriában, egy 75 75 mm méretű Nal(TI) szcintillációs kristály abszolut teljesenergia-csúcs hatásfoka.
75 mm méretű Nal(TI) szcintillációs kristály abszolut teljesenergia-csúcs hatásfoka.
Mérés alatti bomlás korrekciója
Ha a mérendő izotóp felezési ideje rövid a mérés időtartamához viszonyítva, azaz összemérhető a minta mérési idejével, akkor az aktivitás meghatározása során figyelembe kell venni a mérés alatt bekövetkező bomlásokat is. A radioaktív bomlás időfüggése alapján felírható a (10) egyenlet, ahol 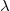 az izotóp bomlási állandója és tm a mérés időtartama, N0 a radioaktív preparátum aktivitása a mérés kezdő időpontjában és Nm a mérés teljes időtartama alatt mért aktivitás.
az izotóp bomlási állandója és tm a mérés időtartama, N0 a radioaktív preparátum aktivitása a mérés kezdő időpontjában és Nm a mérés teljes időtartama alatt mért aktivitás.
![\[ N_{0} = \frac{N_{m}}{\int_{0}^{t_{m}}e^{-\lambda t}dt} = \frac {N_{m} \lambda t_{m}}{1-e^{-\lambda t_{m}}} \]](/images/math/4/7/3/473e3d92bb356c78592ba64ff292ce37.png) |
(10) |
Valódi koincidencia és a mintaösszetétel miatti korrekciók
A gyakorlati gamma-spektroszkópiai méréseknél szükség lehet még további két különböző korrekció alkalmazására is. Az egyik ilyen jelenség a valódi-koincidencia, amely akkor jön létre, ha a mérendő mintában olyan izotóp található, amely kaszkád bomlással több fotont emittál a spektrométer holtidején belüli időtartamban (ilyen a 60Co, 152Eu izotópok). Az effektus valószínűsége növekszik a detektortérfogattal és a minta-detektor távolság csökkenésével de független a minta aktivitásától. A valódi koincidencia miatt a spektrumban megjelennek az összegcsúcsok, ami két valódi teljesenergia-csúcs összegéből áll elő, ezzel együtt a teljesenergia csúcsok területe kisebb lesz. A valódi koincidencia korrekcióba vétele általában bonyolult számítást jelent, amire a gyakorlat során alkalmazott Genie-2000 kiértékelő szoftver fel van készítve.
A nagy térfogatú minták mérése során a mintában bekövetkező önabszorpció jelentős intenzitásváltozást okozhat. Ez akkor következik be, ha a detektortól távolabbi mintarészekből emittált fotonok csak a minta anyagán keresztül tudnak a detektorkristályba jutni. Ekkor a minta abszorbciós tulajdonságaitól függően csökken a detektált fotonok száma. Ennek a jelenségnek a figyelmen kívül hagyása kis energiájú (kb. 150 keV alatti) gamma-sugárzások mérésénél jelentős mértékű hibát okozhat. Az önabszorbció korrekciójának meghatározásához a hatásfok-kalibrációhoz használt forrásokat egy, a mintához hasonló abszorbciós tulajdonságú anyagba kevert izotópokkal kell elkészíteni. Megoldást jelenthet az is, ha a minta összetétele ismeretében a korrekció mértékét elméleti számításokkal megbecsüljük.
A csúcsterületek számítása:
A gyakorlat során a Genie-2000 kiértékelő szoftvert használjuk, ami a csúcsterület és annak hibája számítását automatikusan végzi a következő algoritmus szerint.
A kiértékelő szoftverrel átlapoló csúcsokból álló együttesek is kiértékelhetőek. Ekkor a megfelelő spektrumrészletre több matematikai függvényből álló összetett alakot illesztünk, amely eredményéből a csúcsok alatti nettó terület meghatározható.
Mérési feladatok
Energiakalibráció
Az energia-kalibráció elvégzéséhez helyezzen el a detektor elé ismert gamma-energiákat sugárzó, pontszerű, etalon sugárforrásokat (60Co, 137Cs)! Vegyen fel egy gamma-spektrumot! A teljesenergia-csúcsok helyének megkeresésével, az energiák ismeretében határozza meg a gamma-energia-csatornaszám függvényt! Gyakorlatban a mért adatpárokra első- vagy másodfokú függvény illesztése szokásos. Ehhez a feladathoz használja a Genie-2000 szoftver energia-kalibrációra vonatkozó menüpontját (Calibrate menüpont). Legegyszerűbb esetben legyen két ismert kalibráló energia E1 és E2, a hozzájuk tartozó csatornaszámok Cs1 és Cs2. Feltételezve, hogy a berendezés lineáris, a szoftver az alábbi két ponton átmenő egyenes alapján számítja ki a kalibrációs egyenes meredekségét.
![\[ m = \frac{E_{2}-E_{1}}{Cs_{2}-Cs_{1}} \hspace{0.5cm} \Bigg(\frac {keV}{csat} \Bigg) \]](/images/math/7/9/9/799a7523c4cc10b4934658086219e6a5.png) |
(11) |
Ahol 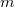 az energia-kalibráció egyenesének meredeksége, amely két csatorna közötti intervallum energia értékét adja meg az adott erősítés esetén. A (11) egyenletet célszerű átrendezni a következő formára, ahol
az energia-kalibráció egyenesének meredeksége, amely két csatorna közötti intervallum energia értékét adja meg az adott erősítés esetén. A (11) egyenletet célszerű átrendezni a következő formára, ahol 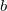 a kalibrációs egyenes tengelymetszete.
a kalibrációs egyenes tengelymetszete.
![\[ E = MCs+b \]](/images/math/a/4/7/a476b014550ab0d0728f35db989bd8a7.png) |
(12) |
Az energia-kalibráció elvégzéséhez használja az Calibrate/Energy Only Calibration menüpontot, ahol a kalibrációhoz használt izotópok egyes vonalaira vonatkozóan be kell írni a vonal energiáját és a maximuma helyének csatornaszámát. A fenti művelethez használja fel a kalibráló gamma-forrásokra vonatkozó, az 1. táblázatban található adatokat! Mérje meg néhány, a gyakorlatvezetőtől kapott etalon sugárforrás gamma-spektrumát! Ellenőrizze a kiszámolt energia-kalibrációs görbét, a gyakorlatvezetőtől kapott források ismert energiájú vonalai felhasználásával! A méréseket úgy végezze el, hogy az egyes etalonokat mérés közben cserélje ki, ezáltal egy olyan kevert spektrumot kap, ami tartalmazza az összes mért izotóp vonalait! A szükséges mérési időt úgy válassza meg, hogy a gamma-csúcsok területének statisztikus hibája 1-3%-nál ne legyen nagyobb! Ügyeljen a holtidő nagyságára is, amit a minta-detektor távolság helyes megválasztásával tud elérni: 0, 10, 50, 150 mm! A mérések során a holtidő ne legyen nagyobb, mint 1-2%.
| 1. feladat: Energia-kalibráció meghatározása | |||||
|---|---|---|---|---|---|
| Izotóp | Energia (keV) | Csatornaszám | m | b | |
| 1. | 133Ba | 81.0 | |||
| 2. | 57Co | 122.1 | |||
| 3. | 133Ba | 276.4 | |||
| 4. | 133Ba | 356.0 | |||
| 5. | 137Cs | 661.7 | |||
| 6. | 60Co | 1173.2 | |||
| 7. | 60Co | 1332.5 | |||
| Ismert sugárforrások vonalainak energiái | |||
|---|---|---|---|
| Izotóp | Energia (keV) (táblázat alapján) | Energia (keV) (energiakalibráció alapján) | |
| 1. | 241Am | ||
| 2. | 22Na | ||
| 3. | 152Eu | ||
| 4. | |||
| 5. | |||
| 6. | |||
A feladattal kapcsolatos adatokat a részfeladathoz tartozó táblázatba jegyezze fel! Az árnyékolt mérőkamrában talál egy plexi állványt és egy mintatartó plexi lapot, amelynek tetejére kell elhelyezni az etalon-forrásokat. A plexi mintatartó magasságbeli helyzetét változtatva különböző minta-detektor távolság állítható be. Az egyes pozíciók helyzetéhez tartozó detektor-minta távolságok az adott pozíción fel vannak tüntetve. A Genie-2000 által kiszámított paramétereket és az illesztett kalibrációs görbét a Calibrate/Energy show menüpont alatt találja.
A spektrométer energiafelbontásának meghatározása
Ehhez a feladathoz használja az előző pontban már felvett és tárolt "mix" spektrumot az ismert csúcsokkal! Határozza meg az egyes csúcsok FWHM értékét, majd ábrázolja az adatokat illessze rá a 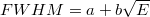 függvényt az energia függvényében!
függvényt az energia függvényében!
| 2. feladat: A spektrométer energia-felbontásának meghatározása | |||||
|---|---|---|---|---|---|
| Izotóp | Energia (keV) | FWHM (keV) | a | b | |
| 1. | 133Ba | 81.0 | |||
| 2. | 57Co | 122.1 | |||
| 3. | 133Ba | 276.4 | |||
| 4. | 133Ba | 356.0 | |||
| 5. | 137Cs | 661.7 | |||
| 6. | 60Co | 1173.2 | |||
| 7. | 60Co | 1332.5 | |||
3. A detektor abszolút hatásfok függvényének meghatározása
Helyezzen ismert aktivitású és energiájú etalon pontforrásokat a detektor elé úgy, hogy mérés közben a holtidő minden esetben kisebb legyen, mint 5%! Mérje meg az egyes izotóp források gamma-spektrumát! Mivel a hatásfok függ a geometriai elrendezéstől, a mérések során végig azonos minta-detektor távolságot használjon!
A mért spektrumokat értékelje ki a Genie-2000 segítségével és számítsa ki a teljesenergiacsúcs integrálját (N), majd határozza meg a hatásfok értékeit ( ) a mért csúcsok energiáinál a (8) összefüggés felhasználásával
) a mért csúcsok energiáinál a (8) összefüggés felhasználásával 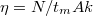 !
!
| 3. feladat: A detektor abszolút hatásfoka energiafüggésének meghatározása | ||||||||
|---|---|---|---|---|---|---|---|---|
| A mintatartó magassági poziciója: .................... mm | ||||||||
| Izotóp | tm(S) | A (Bq) | Dátum | Gamma energia (keV) | k | 
|
| |
| 1. | 133Ba | 81.0 | ||||||
| 2. | 57Co | 122.1 | ||||||
| 3. | 133Ba | 276.4 | ||||||
| 4. | 133Ba | 356.0 | ||||||
| 5. | 137Cs | 661.7 | ||||||
| 6. | 60Co | 1173.2 | ||||||
| 7. | 60Co | 1332.5 | ||||||
| Az illesztett hatásfok paraméter értékei | ||||||||
| a | b | c | d | |||||
Ábrázolja a számított hatásfok értékeit (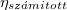 ) az energia függvényében log-log formában! A mért hatásfokadatokra a (13) szerinti polinom függvényt célszerű illeszteni, ahol
) az energia függvényében log-log formában! A mért hatásfokadatokra a (13) szerinti polinom függvényt célszerű illeszteni, ahol 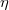 az E energiánál a fenti táblázat szerint számított hatásfok értéke.
az E energiánál a fenti táblázat szerint számított hatásfok értéke.
![\[ \ln\eta = a+b\ln E + c(\ln E)^{2}+d(\ln E)^{3} \]](/images/math/2/c/7/2c7da7d3f0b82b8ce56e76ffd864083a.png) |
(13) |
Az illesztésből határozza meg az a,b,c,d, paramétereket. A hatásfokok ismeretében számítsa ki a detektált izotópok aktivitását! Határozza meg a detektor hatásfokfüggvényét az adott távolságra vonatkozó pontforrás geometriára.
Pontszerű radioaktív forrás aktivitásának meghatározása
Határozza meg egy, a gyakorlatvezető által megadott forrás aktivitását. Az aktivitás számítása a (8) összefüggésből származtatott (14) formula alapján történik, ahol N a nettó csúcsterület [imp], tm a minta mérési időtartama, k az adott gamma-vonal gyakorisága.
![\[ A = \frac{N}{t_{m}\eta k} (Bq) \]](/images/math/a/c/9/ac971bbd2af791193d6893861c706ff5.png) |
(14) |
Becsülje meg a kapott eredmény hibáját a (14) összefüggés felhasználásával, ahol 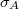
![\[ \frac {\sigma_{A}}{A} \approx \frac {\sigma_{N}}{N} = \pm \frac{(N+2B)^{1/2}}{N} \]](/images/math/6/0/3/60359fdfa4b082a6f8aac2a6a352c388.png) |
(15) |
| 4. feladat: Pontszerű radioaktív forrás aktivitásának meghatározása | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| A mintatartó magassági poziciója: .................... mm | |||||||||
| Izotóp | tm(S) | N (cps) | 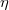
|
Gamma vonal energiája (keV) | k | 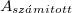 (Bq) (Bq)
|
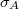 (Bq) (Bq)
|
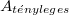 (Bq) (Bq)
| |
| 1. | 152Eu | 121.8 | 28.6 | ||||||
| 2. | 344.3 | 26.5 | |||||||
| 3. | 964.1 | 14.6 | |||||||
| 4. | 1408.0 | 21.0 | |||||||
Irodalom
- G. F. Knoll, Radiation detection and measurement, John Wiley & Sonns, 2001.
- Bódizs D., Atommagsugárzások méréstechnikái, Typotex Kiadó Budapest, 2006
- Deme S., Félvezető detektorok magsugárzás mérésére, Műszaki Könyvkiadó Budapest, 1968
- Nagy L. Gy., Radiokémia és izotóptechnika, Tankönyvkiadó Budapest, 1983
- C.M. Lederer, J.M. Hollander, I. Perlman, Table of Isotopes, Wiley, New York, 1984
- K. Debertin, R.G. Helmer, Gamma- and X-ray spectrometry with semiconductor detectors, North Holland P.C. Amsterdam, 1988.
Kérdések
- Soroljon fel 5 db gamma-sugárzó izotópot és bomlási módjukat!
- Ismertesse a gamma-sugárzás és az anyag atomjai között fellépő fontosabb kölcsönhatásokat és jellemzőiket!
- Mi a jelentése a radioaktív izotópok bomlássémájának?
- Hogyan működik a gamma-sugárzás mérésére alkalmazott HPGe detektor?
- Ismertesse egy gamma-spektrométer felépítését és az egyes egységeinek funkcióját, legfontosabb méréstechnikai jellemzőit!
- Milyen méréstechnikai jelentősége van a gamma-sugárforrás geometriai alakjának a hatásfok és az önabszorpció szempontjából?
- Miért szükséges a gamma-spektrométerek energia-kalibrációja és hogyan kell ezt elvégezni?
- Mit jelent az energia-felbontóképesség a gamma-spektroszkópiában és hogyan változik egy HPGe detektor felbontóképessége az energia függvényében?
- Mit jelent a spektrométer abszolút hatásfoka és hogyan lehet pontforrás esetén meghatározni?
- Hogyan lehet figyelembe venni a háttérsugárzást a gamma spektrumok kiértékelése során?
| Kalibrálásra használt gamma etalon sugárforrások adatai | |||||
|---|---|---|---|---|---|
| Izotóp | Gamma vonal energiája (keV) | ||||
| Gamma vonal hozama (%) | |||||
| 22Na | 1274.53 | ||||
| 99.95 | |||||
| 57Co | 122.06 | 136.47 | |||
| 85.60 | 10.68 | ||||
| 60Co | 1332.50 | 1173.24 | |||
| 99.99 | 99.97 | ||||
| 133Ba | 356.02 | 81.00 | 302.85 | 383.85 | 276.40 |
| 62.05 | 34.06 | 18.33 | 8.49 | 7.16 | |
| 137Cs | 661.66 | ||||
| 85.1 | |||||
| 241Am | 59.54 | 26.345 | |||
| 35.9 | 2.40 | ||||
| 152Eu | |||||
| 121.8 | 344.3 | 778.9 | 1408.0 | 1112.1 | |
| 28.6 | 26.5 | 12.9 | 21.0 | 13.6 | |
| 1085.9 | 964.1 | 867.4 | 78.9 | 244.7 | |
| 10.2 | 14.6 | 4.3 | 12.9 | 7.6 | |
| 411.1 | 443.9 | 919.3 | 1089.7 | 1212.9 | |
| 2.2 | 2.8 | 0.43 | 1.73 | 1.4 | |
| 1299.1 | 1457.6 | 1084.0 | 1005.3 | 488.7 | |
| 1.62 | 0.50 | 0.25 | 0.65 | 0.42 | |
Külső hivatkozások
A Gamma spektroszkópia laborjegyzet forrása elérhető a [1] linken:
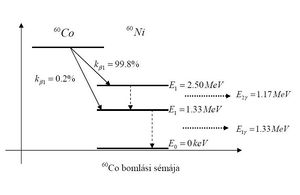
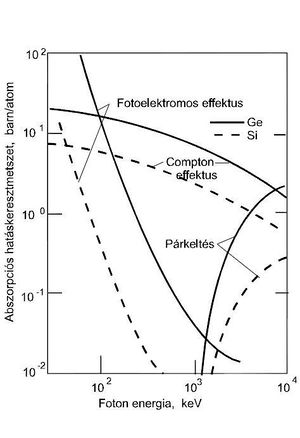
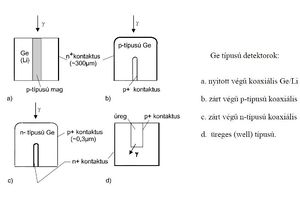
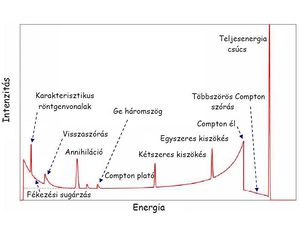
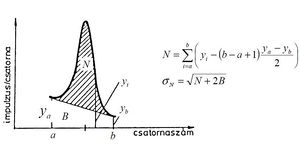
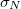 a csúcsterület statisztikus hibája.
a csúcsterület statisztikus hibája.