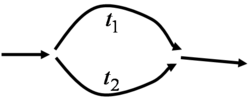„Interferencia és dekoherencia nanoszerkezetekben” változatai közötti eltérés

A Fizipedia wikiből
(→‎Vezetőképesség-fluktuációk)
(→‎Környezet miatti koherenciavesztés)
 
(egy szerkesztő 58 közbeeső változata nincs mutatva)
10. sor: 10. sor:
 
|}
 
|}
  
−
A modern fizika fejlődésével az interferencia-kísérletek újabb értelmezést kaptak, hiszen jól demonstrálták a részecske hullám dualitást. Ha az 1. ábrán szemléltetett kísérletben nagyon kis fényintenzitást, és nagyon érzékeny ernyőt használunk, akkor először véletlenszerű felvillanásokat látunk az ernyő különböző pontjain, mely a fény részecske-természetét támasztja alá. Ha viszont sokat várunk, akkor a véletlenszerű felvillanásokból kirajzolódik a jól ismert interferencia-kép (lásd 2. ábra).
+
A modern fizika fejlődésével az interferencia-kísérletek újabb értelmezést kaptak, hiszen jól demonstrálták a részecske-hullám dualitást. Ha az 1. ábrán szemléltetett kísérletben nagyon kis fényintenzitást, és nagyon érzékeny ernyőt használunk, akkor először véletlenszerű felvillanásokat látunk az ernyő különböző pontjain, mely a fény részecske-természetét támasztja alá. Ha viszont sokat várunk, akkor a véletlenszerű felvillanásokból kirajzolódik a jól ismert interferencia-kép (lásd 2. ábra).
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
27. sor: 27. sor:
 
==Fáziskoherencia-hossz==
 
==Fáziskoherencia-hossz==
 
<wlatex>
 
<wlatex>
−
A [[Transzport_nanovezetékekben:_Landauer-formula,_vezetőképesség-kvantálás|nanovezetékek tárgyalásánál]] már említettük, hogy egy nanoáramkörben akkor tapasztalhatunk interferencia-jelenséget, ha annak mérete kisebb a fáziskoferencia-hossznál. Próbáljuk ezt a karakterisztikus méretskálát egy kicsit pontosabban definiálni.
+
A [[Transzport_nanovezetékekben:_Landauer-formula,_vezetőképesség-kvantálás|nanovezetékek tárgyalásánál]] már említettük, hogy egy nanoáramkörben akkor tapasztalhatunk interferencia-jelenséget, ha annak mérete kisebb a fáziskoherencia-hossznál. Próbáljuk ezt a karakterisztikus méretskálát egy kicsit pontosabban definiálni.
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
37. sor: 37. sor:
 
Ha egy elektronhullámot egy adott pontban szétválasztunk, és feltételezzük, hogy a két parciális hullám két különböző trajektórián keresztül jut el egy másik pontba, ahol újra egyesülnek (3. ábra), akkor ebben a pontban a hullám intenzitását
 
Ha egy elektronhullámot egy adott pontban szétválasztunk, és feltételezzük, hogy a két parciális hullám két különböző trajektórián keresztül jut el egy másik pontba, ahol újra egyesülnek (3. ábra), akkor ebben a pontban a hullám intenzitását
 
$$
 
$$
−
T=\left| t_1 \right|^2 + \left| t_2 \right|^2 + 2\left| t_1t_2 \right| \exp\left(-\tau_L/\tau_\phi \right)
+
T=\left| t_1 \right|^2 + \left| t_2 \right|^2 + 2\left| t_1t_2 \right|\cos\left(\phi\right) \exp\left(-\tau_L/\tau_\phi \right)
 
$$
 
$$
−
alakban írhatjuk, ahol $t_1$ és $t_2$ az egyik illetve a másik trajektóriához tartozó komplex amplitúdó, $\tau_L$ pedig az egyik pontból a másik pontba történő eljutáshoz szükséges karakterisztikus idő.  
+
alakban írhatjuk, ahol $t_1$ és $t_2$ az egyik illetve a másik trajektóriához tartozó komplex amplitúdó, $\phi$ a két komplex amplitúdó közötti fáziskülönbség, $\tau_L$ pedig az egyik pontból a másik pontba történő eljutáshoz szükséges karakterisztikus idő.  
 
A két trajektória mentén az elektronok szóródásokat szenvednek. Rugalmas (pl. rácshibákon, szennyezőkön, történő) szóródás esetén egy időben konstans fázistolás lép fel, de ez nem befolyásolja az interferencia-képességet, legfeljebb azt, hogy a parciális hullámok találkozásakor erősítést vagy gyengítést tapasztalunk. Ha viszont az elektronhullám az egyik trajektória mentén egy rugalmatlan szórást szenved (pl. elektron-fonon kölcsönhatás), akkor megváltozik az energiája, és így a hullámok egyesítésekor egy időben fluktuáló, kiátlagolódó interferenciaképet kapunk. A fenti képletben $\tau_\phi$ ezen, rugalmatlan szórásoknak köszönhető koherenciavesztés karakterisztikus időskáláját adja meg. Ennél az időnél lényegesen hosszabb skálán a parciális hullámok egyesítésekor egyszerűen az intenzitások adódnak össze, és a fázisviszonyoktól függő interferenciatag (a fenti képlet utolsó tagja) elvész.  
 
A két trajektória mentén az elektronok szóródásokat szenvednek. Rugalmas (pl. rácshibákon, szennyezőkön, történő) szóródás esetén egy időben konstans fázistolás lép fel, de ez nem befolyásolja az interferencia-képességet, legfeljebb azt, hogy a parciális hullámok találkozásakor erősítést vagy gyengítést tapasztalunk. Ha viszont az elektronhullám az egyik trajektória mentén egy rugalmatlan szórást szenved (pl. elektron-fonon kölcsönhatás), akkor megváltozik az energiája, és így a hullámok egyesítésekor egy időben fluktuáló, kiátlagolódó interferenciaképet kapunk. A fenti képletben $\tau_\phi$ ezen, rugalmatlan szórásoknak köszönhető koherenciavesztés karakterisztikus időskáláját adja meg. Ennél az időnél lényegesen hosszabb skálán a parciális hullámok egyesítésekor egyszerűen az intenzitások adódnak össze, és a fázisviszonyoktól függő interferenciatag (a fenti képlet utolsó tagja) elvész.  
  
52. sor: 52. sor:
 
eltávolodást eredményez a kiindulási ponttól, ahol $D$ a diffúziós állandó, mely a momentumrelaxációs időből két dimenzióban $D=v_F^2\tau_m/2$ képlettel számolható.
 
eltávolodást eredményez a kiindulási ponttól, ahol $D$ a diffúziós állandó, mely a momentumrelaxációs időből két dimenzióban $D=v_F^2\tau_m/2$ képlettel számolható.
 
</wlatex>
 
</wlatex>
 +
 
== Aharonov-Bohm gyűrű ==
 
== Aharonov-Bohm gyűrű ==
 
<wlatex>
 
<wlatex>
−
Nanoáramkörökben az interferencia-jelenségeket nem tudjuk a ernyő mentén detektálni, olyan elrendezést kell találni, melyben például az áramkör két (vagy pár) kontaktusán keresztül feszültséget adunk a mintára, és a mért áramban jelenik meg az interfernecia valamilyen hangolható paraméter függvényében. Erre talán a legjobb példa a nanogyűrűkben tapasztalható Aharonov-Bohm jelenség.  
+
Nanoáramkörökben az interferencia-jelenségeket nem tudjuk egy ernyő mentén detektálni, olyan elrendezést kell találni, melyben például az áramkör két (vagy pár) kontaktusán keresztül feszültséget adunk a mintára, és a mért áramban jelenik meg az interfernecia valamilyen hangolható paraméter függvényében. Erre talán a legjobb példa a nanogyűrűkben tapasztalható Aharonov-Bohm jelenség.  
  
 
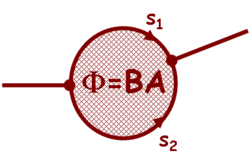
Az egyik kontaktusból bejövő elektronhullámot egy kör alakú gyűrű két ága mentén két részre osztjuk, és a gyűrű másik oldalára helyezett kontaktuson keresztül egyesül a két parciális hullám (4. ábra). Zérus mágneses térben az elektronok a felső ágon $k_F s_1$, míg az alsó ágon $k_F s_2$ fázist vesznek fel, ahol $k_F$ a Fermi-hullámszám, $s_1$ és $s_2$ pedig a két kontaktus közötti trajektóriahossz a felső illetve az alsó ág mentén (lásd 4. ábra). Ennek megfelelően az interferenciatag $\cos(k_F(s_1-s_2))$-vel arányos.
 
Az egyik kontaktusból bejövő elektronhullámot egy kör alakú gyűrű két ága mentén két részre osztjuk, és a gyűrű másik oldalára helyezett kontaktuson keresztül egyesül a két parciális hullám (4. ábra). Zérus mágneses térben az elektronok a felső ágon $k_F s_1$, míg az alsó ágon $k_F s_2$ fázist vesznek fel, ahol $k_F$ a Fermi-hullámszám, $s_1$ és $s_2$ pedig a két kontaktus közötti trajektóriahossz a felső illetve az alsó ág mentén (lásd 4. ábra). Ennek megfelelően az interferenciatag $\cos(k_F(s_1-s_2))$-vel arányos.
62. sor: 63. sor:
 
| align="center"|[[Fájl:AB_gyuru.png|közép|250px|]]
 
| align="center"|[[Fájl:AB_gyuru.png|közép|250px|]]
 
|-
 
|-
−
| align="center"|4. ábra ''Aharonov-Bohm gyűrű''.
+
| align="center"|4. ábra ''Aharonov-Bohm gyűrű''  
 
|}
 
|}
  
71. sor: 72. sor:
 
ahol $\Phi=B\cdot A$ a gyűrű által körbezárt mágneses fluxus, $\Phi_0=e/h$ pedig az úgynevezett fluxuskvantum. Látszik, hogy a vezetőképesség a fluxus változtatásával a fluxuskvantum periódusa szerint oszcillál. Ezt az oszcillációt először Webb és társai mutatták ki mezoszkopikus arany gyűrűn.<sup>[http://link.aps.org/doi/10.1103/PhysRevLett.54.2696 1]</sup>
 
ahol $\Phi=B\cdot A$ a gyűrű által körbezárt mágneses fluxus, $\Phi_0=e/h$ pedig az úgynevezett fluxuskvantum. Látszik, hogy a vezetőképesség a fluxus változtatásával a fluxuskvantum periódusa szerint oszcillál. Ezt az oszcillációt először Webb és társai mutatták ki mezoszkopikus arany gyűrűn.<sup>[http://link.aps.org/doi/10.1103/PhysRevLett.54.2696 1]</sup>
  
−
A 4. ábrán szándékosan különbözőnek jelöltük a felső és alsó ág hosszát, hiszen egy valós rendszerben nem lehet garantálni, hogy mindkét ág mentén pontosan ugyan olyan hosszú trajektória mentén haladjanak az elektronok. Ráadásul, ha a gyűrű két ága egy-egy szélesebb vezeték, akkor mindkét ágon több, különböző hosszúságú trajektória mentén juthat el az elektron az egyik kontaktusból a másikba, és ha ezek a trajektórahosszok túlzottan eltérnek,  akkor a szabad elektron terjedésből adódó $k_F\cdot s$ fázisok kiátlagolódnak, a koherencia elvész.
+
A 4. ábrán szándékosan különbözőnek jelöltük a felső és alsó ág hosszát, hiszen egy valós rendszerben nem lehet garantálni, hogy mindkét ág mentén pontosan ugyan olyan hosszú trajektória mentén haladjanak az elektronok. Ráadásul, ha a gyűrű két ága egy-egy szélesebb vezeték, akkor mindkét ágon több, különböző hosszúságú trajektória mentén juthat el az elektron az egyik kontaktusból a másikba, és ha ezek a trajektóriahosszok túlzottan eltérnek,  akkor a szabad elektron terjedésből adódó $k_F\cdot s$ fázisok kiátlagolódnak, a koherencia elvész.
  
−
Tanulságos az Aharonov-Bohm gyűrűben reflexiót számolva megnézni a releváns folyamatokat. A legalapvetőbb (nulladrendű) folyamat, ha az elektronok be se jutnak a gyűrűbe, hanem a gyűrű elején reflektálódnak (5. ábra, bal oldal). A következő, első rendben az elektronok úgy tudnak reflektálódni, hogy bejutnak a gyűrűbe, és jobbról vagy balról egyszer megkerülik azt, majd a bal oldali kontaktuson keresztül elhagyják a gyűrűt (5. ábra, középső és jobb oldali panel). Az Aharonov-Bohm effektus a nulladrendű, illetve az elsőrendű folyamatok interferenciájából adódik, melyek között a mágneses térből felvett fázis $2 \pi \Phi/\Phi_0$. Azonban széles vezetékek esetén a $k_F\cdot s$ fázisok kiátlagolódnak.
+
Tanulságos az Aharonov-Bohm gyűrűben reflexiót számolva megnézni a releváns folyamatokat. A legalapvetőbb (nulladrendű) folyamat, ha az elektronok be se jutnak a gyűrűbe, hanem a gyűrű elején reflektálódnak (5. ábra, bal oldal). A következő, első rendben az elektronok úgy tudnak reflektálódni, hogy bejutnak a gyűrűbe, és jobbról vagy balról egyszer megkerülik azt, majd a bal oldali kontaktuson keresztül elhagyják a gyűrűt (5. ábra, középső és jobb oldali panel). Az Aharonov-Bohm effektus a nulladrendű, illetve az elsőrendű folyamatok interferenciájából adódik, melyek között a mágneses térből felvett fáziskülönbség $2 \pi \Phi/\Phi_0$. Azonban széles vezetékek esetén a $k_F\cdot s$ fázisok kiátlagolódnak.
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
82. sor: 83. sor:
 
|}
 
|}
  
−
Érdemes megvizsgálni, a két elsőrendű folyamat interferenciáját, azaz amikor az elektronok balról illetve jobbról kerülik a gyűrűt. E két folyamat között a mágneses tér hatására $4 \pi \Phi/\Phi_0$ fáziskülönbség lép fel, azaz a vezetőképesség a fluxuskvantum fele szerinti periódussal oszcillál. Két tetszőleges trajektória közötti $k_F\cdot s$ fázisok itt is kiátlagolódhatnak, azonban minden egyes ''balról kerülő'' trajektóriához találunk egy időtükrözött ''jobbról kerülő'' trajektóriát, azaz egy trajektóriapárt, melyen pontosan ugyan azon a trajektórián, de ellentétes irányban halad az elektron. Az időtükrözött trajektóriapárok között a $k_F \cdot s$ fázisok különbsége pontosan zérus, így nulla mágneses térben mindig konstruktív interferenciát látunk, illetve véges mágneses térben a fluxuskvantum felének periódusával oszcillál a vezetőképesség. Ezt hívják Altshuler-Aronov-Spivak oszcillációnak.
+
Érdemes megvizsgálni a két elsőrendű folyamat interferenciáját, azaz amikor az elektronok balról illetve jobbról kerülik a gyűrűt. E két folyamat között a mágneses tér hatására $4 \pi \Phi/\Phi_0$ fáziskülönbség lép fel, azaz a vezetőképesség a fluxuskvantum fele szerinti periódussal oszcillál. Két tetszőleges trajektória közötti $k_F\cdot s$ fázisok itt is kiátlagolódhatnak, azonban minden egyes ''balról kerülő'' trajektóriához találunk egy időtükrözött ''jobbról kerülő'' trajektóriát, azaz egy trajektóriapárt, melyen pontosan ugyan azon a trajektórián, de ellentétes irányban halad az elektron. Az időtükrözött trajektóriapárok között a $k_F \cdot s$ fázisok különbsége pontosan zérus, így nulla mágneses térben mindig konstruktív interferenciát látunk, illetve véges mágneses térben a fluxuskvantum felének periódusával oszcillál a vezetőképesség. Ezt hívják Altshuler-Aronov-Spivak oszcillációnak.
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
102. sor: 103. sor:
 
| align="center"|[[Fájl:Vezetokepesseg_fluktuaciok1.png|közép|300px|]]
 
| align="center"|[[Fájl:Vezetokepesseg_fluktuaciok1.png|közép|300px|]]
 
|-
 
|-
−
| align="center"|7. ábra. ''A nanovezetékben az elektronok különböző diffúzív trajketóriák mentén juthatnak el az egyik kontaktusból a másikba''
+
| align="center"|7. ábra. ''A nanovezetékben az elektronok különböző diffúzív trajektóriák mentén juthatnak el az egyik kontaktusból a másikba''
 
|}
 
|}
  
−
Egy megfelelő szélességű és hosszúságú (a momentumrelaxációs szabadúthossznál hosszabb, de a fáziskoherencia hossznál rövidebb) nanovezetékben az elektronok számtalan különböző diffúzív trajketória mentén juthatnak el az egyik kontaktusból a másikba (8. ábra). A kis méret miatt ($L<L_\phi $) ezek a diffúzív trajektóriák interferálnak egymással. A mágneses térrel hangolhatjuk az egyes trajektóriákhoz tartozó fázist, így változtathatjuk az interferenciafeltételeket, de mivel nagyon sok véletlen trajektória interferenciajárulékáról van szó, ezért a mágneses tér függvényében a vezetőképesség nem periodikus oszcillációt, hanem egy véletlenszerű fluktuációt mutat (lásd 9. ábra). Fontos azonban megjegyezni, hogy ha a mágneses teret oda-vissza változtatjuk, akkor ez a véletlenszerű vezetőképesség-fluktuáció pontosan reprodukál, hiszen a vezetéken belül a mérés során nem változik a szórócentrumok helye, így a sok trajektória interferenciájából adódó vezetőképesség-korrekció a mágneses tér egyértelmű függvénye. Ha viszont felmelegítjük, és újra lehűtjük a nanovezetéket, akkor a rácshibák pozíciója megváltozik, és így jellegre hasonló, de a részletekben a korábbitól teljesen eltérő vezetőképesség fluktuációt kapunk a mágneses tér függvényében.
+
Egy megfelelő szélességű és hosszúságú (a momentumrelaxációs szabadúthossznál hosszabb, de a fáziskoherencia hossznál rövidebb) nanovezetékben az elektronok számtalan különböző diffúzív trajketória mentén juthatnak el az egyik kontaktusból a másikba (7. ábra). A kis méret miatt ($L<L_\phi $) ezek a diffúzív trajektóriák interferálnak egymással. A mágneses térrel hangolhatjuk az egyes trajektóriákhoz tartozó fázist, így változtathatjuk az interferenciafeltételeket, de mivel nagyon sok véletlen trajektória interferenciajárulékáról van szó, ezért a mágneses tér függvényében a vezetőképesség nem periodikus oszcillációt, hanem egy véletlenszerű fluktuációt mutat (lásd 8. ábra). Fontos azonban megjegyezni, hogy ha a mágneses teret oda-vissza változtatjuk, akkor ez a véletlenszerű vezetőképesség-fluktuáció pontosan reprodukál, hiszen a vezetéken belül a mérés során nem változik a szórócentrumok helye, így a sok trajektória interferenciájából adódó vezetőképesség-korrekció a mágneses tér egyértelmű függvénye. Ha viszont felmelegítjük, és újra lehűtjük a nanovezetéket, akkor a rácshibák pozíciója megváltozik, és így jellegre hasonló, de a részletekben a korábbitól teljesen eltérő vezetőképesség-fluktuációt kapunk a mágneses tér függvényében.
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
121. sor: 122. sor:
 
==Gyenge lokalizáció==
 
==Gyenge lokalizáció==
 
<wlatex>
 
<wlatex>
 +
Az 5. ábra vonatkozásában láttuk, hogy ha a forráskontaktusból indulva egy adott irányban megkerüli az elektron az Aharonov-Bohm gyűrűt és visszajut a forráskontaktusba, akkor ehhez a folyamathoz társíthatunk egy időtükrözött folyamatot, melyhez pontosan ugyan az $k_F\cdot s$ fázis tartozik, így az időtükrözött trajektóriapárok interferenciájának konstruktív vagy destruktív jellege csak  az Aharonov-Bohm fázistól, azaz a gyűrű területén megjelenő mágneses fluxustól függ. Ennek köszönhető, hogy egy hosszú, de kis átmérőjű fém hengerben is megjelenhetnek a mágneses térben periodikus interferenciaoszcillációk az időtükrözött trajektóriapárok interferenciájának köszönhetően.
 +
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
|[[Fájl:Gyenge_lokalizacio1.png|közép|300px|]]
+
| align="center"|[[Fájl:Gyenge_lokalizacio0.png|közép|300px|]]
 
|-
 
|-
−
| align="center"|1. ábra. Vezetőképesség fluktuációk
+
| align="center"|9. ábra. ''Az időtükrözött trajektóriapárok konstruktív interferenciája miatt zérus mágneses térben megnő a kiindulási pontba történő visszaszóródás valószínűsége''
 
|}
 
|}
  
 +
Zérus mágneses térben azonban nem jelenik meg Aharonov-Bohm fázis, így a fázisdiffúziós hosszon belüli időtükrözött trajektóriapárok mindig konstruktívan interferálnak a körbezárt területtől függetlenül. Ennek köszönhetően az időtükrözött trajektóriapároknak köszönhető interferencia-járulék nem csak a 6. ábrán szemléltetett hengeres geometriában, hanem tetszőleges mintán megfigyelhető. Egy A pontból egy B pontba sok különböző trajektórián eljuthat az elektron, így a sok trajektória interferenciajáruléka kiátlagolódik (9. ábra, bal oldal). Ha viszont a diffúzív mozgás során az A pontól az A pontba visszajut egy tetszőleges trajektórián az elektron, akkor a megfelelő időtükrözött trajektórián zérus mágneses térben ugyan azt a fázist veszi fel, azaz a kiindulási pontba történő visszajutás esetén az időtükrözött trajektóriapár konstruktívan interferál (9. ábra, jobb oldal). Ez azt jelenti, hogy megnő a forráselektródába történő visszaszóródás valószínűsége, azaz megnő a minta ellenállása. Ezt a jelenséget hívjuk ''gyenge lokalizációnak''. A mágneses tér bekapcsolásával azonban a különböző fluxust bezáró időtükrözött trajektóriapárok interferencia-járuléka kiátlagolódik az eltérő Aharonov-Bohm fázis miatt, azaz az ellenállás visszacsökken az interferencia-járulék nélküli értékre. Ezt a jelenséget szemlélteti a 10. ábrán látható tipikus kísérleti görbe, melynek illesztéséből a fázisdiffúziós hossz meghatározható.
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
|[[Fájl:Gyenge_lokalizacio2.png|közép|250px|]]
+
| align="center"|[[Fájl:Gyenge_lokalizacio2.png|közép|250px|]]
 
|-
 
|-
−
| align="center"|1. ábra. Vezetőképesség fluktuációk
+
| align="center"|10. ábra. ''Egy vékonyréteg minta ellenállása zérus mágneses térben a gyenge lokalizáció miatt maximumot mutat''
 
|}
 
|}
−
</wlatex>
 
−
 
−
 
−
 
−
=== Hőmérsékleti miatti koherenciavesztés ===
 
−
 
 
   
 
   
−
Alacsony hőméréskleten látszik az oszcilláció a mágneses tér függvényében, magasabb hőmérsékleten azonban elmosódik.
+
A gyenge lokalizáció jelensége nem csak elektronokra, hanem tetszőleges diffúzív közegben terjedő hullámra jelentkezhet: ha a közegbe egy adott irányból érkezik a hullám, és a visszavert hullám intenzitását mérjük különboző irányokban, akkor az időtükrözött trajektóriák interferenciájának köszönhetően a bejövő hullámmal ellentétes irányban visszavert hullám intenzitása megnő bármilyen más irányban visszevert hullámintenzitáshoz képest (11. ábra). Ezt a jelenséget felhőben terjedő radarhullámokra is megfigyelték.
−
 
+
−
Az interferenciakép eltűnésének az okai:
+
−
* Környezet miatti dekoherencia
+
−
* Hőmérsékleti miatti fázis kiátlagolódás
+
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
|[[Fájl:Fazisvesztes1.png|közép|180px|]]
+
| align="center"|[[Fájl:Gyenge_lokalizacio1.png|közép|300px|]]
−
|[[Fájl:Fazisvesztes2.png|közép|250px|]]
+
 
|-
 
|-
−
| align="center"|1. ábra.
+
| align="center"|11. ábra. ''Időtükrözött trajektóriapárok interferenciájának köszönhetően megnő a bejövő hullámmal ellentétes irányba visszaszórt hullám intenzitása''
−
| align="center"|1. ábra.  
+
 
|}
 
|}
 +
</wlatex>
  
 +
==Koherenciavesztés==
 +
<wlatex>
 +
Az eddigiekben nanoszerkezetekben jelentkező interferencia-jelenségeket vizsgáltunk. Most nézzük meg részletesebben, hogy milyen tényezők okozhatják a fent ismertetett interferencia-jelenségek megszűnését.
 +
</wlatex>
 +
=== Hőmérséklet miatti koherenciavesztés ===
 +
<wlatex>
 +
A fentiekben az elektronhullámokat monokromatikusnak tekintettük, azaz feltételeztük, hogy jól definiált energiával rendelkeznek. Ez teljesül nagyon alacsony hőmérsékleten, és nagyon kicsi mérőfeszültség mellett, hiszen ekkor gyakorlatilag csak a Fermi-szintnél levő elektronok adnak járulékot a vezetőképességhez. Véges hőmérsékleten azonban a Fermi-energia körüli véges $kT$ energiatartományban levő elektronok adnak járulékot a transzporthoz, így a különböző energiájú (és különböző hullámhosszal rendelkező) elektronok interferenciajáruléka kiátlagolódhat. Egy $E$ energiájú elektron által $t$ idő alatt felvett fázis $\phi=Et/\hbar$. Ha a transzportban résztvevő elektronok között $\Delta E=kT$ energiakülönbség lehet, akkor az azonos fázissal indított elektronhullámok között nagyságrendileg $\tau_\phi\approx \hbar/kT$ idő alatt akkora fáziskülönbség lép fel, hogy a különböző energiájú elektronokhoz tartozó fázis már teljesen kiátlagolódik (12. ábra, jobb oldal). Ennek megfelelően interferencia-jelenséget akkor láthatunk ha a nanoszerkezeten történő áthaladáshoz szükséges $\tau_c$ idő (12. ábra, bal oldal) kisebb $\tau_\phi$-nél.
  
−
Véges hőmérsékleten a Fermi energia körüli kT tartományban különböző energiájú elektronok propagálnak. Koherens összeadás esetén is a fázisok kiátlagolódnak!
+
{|  cellpadding="5" cellspacing="0" align="center"
−
$$\sim \int \limits_{E_F-kT/2}^{E_F+kT/2} e^{i E t / \hbar} \mathrm{d}E$$
+
|-
 +
| align="center"|[[Fájl:Fazisvesztes1.png|közép|180px|]]
 +
| align="center"|[[Fájl:Fazisvesztes2.png|közép|250px|]]
 +
|-
 +
| align="center"|12/a. ábra. ''A nanoszerkezeten az elektronok $\tau_c$ idő alatt haladnak át''
 +
| align="center"|12/b. ábra. ''Azonos fázissal induló különböző hullámhosszal rendelkező hullámok együttes járuléka $\tau_\phi$ idő után kiátlagolódik'' 
 +
|}
  
−
A nanoszerkezeten az elektronok átlagosan $\tau_c$ idő alatt haladnak át. Az ehhez tartozó karakterisztikus energia: Thouless energia, $E_T=\hbar/\tau_c$ $\longrightarrow$ $\sim kT > E_T$ hőmérsékleten lesz jelentős ez a kiátlagolódás
+
Egy nanoszerkezetet jellemezhetünk az ún. Thouless energiával, mely az elektronok nanoszerkezeten belül eltöltött $\tau_c$ idejének megfeleltetett $E_T=\hbar/\tau_c$ energia. Ezen definíció alapján egyszerűen azt mondhatjuk, hogy az adott nanoszerkezetben $kT>E_T$ esetén a hőmérsékleti kiszélesedés miatt elmosódnak az interferenciajelenségek.
  
−
=== Környezet miatti koherenciavesztés ===
+
A fázisok hőmérséklet miatti kiátlagolódása hasonló jelenség a fehér fénnyel végzett interferncia-kísérlethez: az interferenciakép a különböző hullámhosszúságú komponensek keveredése miatt mosódik el. Ez viszont nem jelenti azt, hogy az elektronok (vagy a fény) ''interferencia-képessége'', koherenciája megszűnne, hiszen ha a mérőrendszerben ki tudunk választani egy adott energiához tartozó részecskéket (pl. színszűrővel), akkor ezekre  megjelenik az interferenciakép. Ennek megfelelően a fázisok fent részletezett kiátlagolódását nem koherenciavesztésnek (decoherence) hanem fázisvesztésnek (dephasing) szokták nevezni.
 +
</wlatex>
 +
 
 +
===Környezet miatti koherenciavesztés===
 +
<wlatex>
 +
A [[#Interferencia-kísérletek hat nagyságrenddel kisebb skálán|kétrés kísérlet tárgyalásánál]] említettük, hogy ha tudjuk detektálni, hogy a részecskék melyik résen haladnak át, akkor megszűnik az interferencia-képesség. Ezt a jelenséget általánosabban is megfogalmazhatjuk. Az Aharonov-Bohm gyűrű példájával élve a forrás kontaktusból érkező elektronok haladhatnak a felső ágon (13. ábra, bal oldal), amit jelöljünk az $|1\rangle$ kvantummechanikai állapottal, és haladhatnak az alsó ágon (13. ábra, jobb oldal), amit jelöljünk a $|2\rangle$ állapottal.
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
 
|[[Fájl:Kornyezeti_dekoherencia.png|közép|400px|]]
 
|[[Fájl:Kornyezeti_dekoherencia.png|közép|400px|]]
 
|-
 
|-
−
| align="center"|1. ábra.  
+
| align="center"|13. ábra. ''Az alsó és a felső ágon haladó elektron különböző nyomot hagy a környezetben''
 
|}
 
|}
  
 +
Interferencia esetén a rendszer szuperponált állapotban van, a teljes hullámfüggvény:
 +
$$|\psi\rangle = \alpha|1\rangle + \beta|2\rangle.$$ 
 +
Ha az elektronok kölcsönhatnak a környezetükkel (pl. rácsrezgések), akkor a teljes hullámfüggvényben a környezet hullámfüggvényét ($|\Phi_\mathrm{env}\rangle$) is figyelembe kell venni. Kezdetben (a kölcsönhatás bekapcsolása előtt) a teljes hullámfüggvényt írhatjuk az elektron-hullámfüggvény és a környezeti hullámfüggvény szorzataként. Ha viszont a kölcsönhatás következtében a környezet hullámfüggvénye különbözővé válik aszerint hogy az elektron alul vagy felül halad, akkor a teljes hullámfüggvényt már nem lehet szorzat alakban írni, azaz az elektronállapot ''összefonódik'' a környezet állapotával:
 +
$$|\Psi\rangle = (\alpha|1\rangle + \beta|2\rangle)|\Phi_\mathrm{env}\rangle\;\;\longrightarrow\;\;\alpha|1\rangle|\Phi_\mathrm{env1}\rangle + \beta|2\rangle|\Phi_\mathrm{env2}\rangle.$$
  
−
* Alsó ágon haladó eletronhullám: $|1\rangle$
+
Ha valamilyen, csak az elektronokra vonatkozó fizikai mennyiséget (például az Aharonov-Bohm gyűrű transzmisszióját) mérjük, akkor a $\hat{T}$ operátorral jellemezhető mennyiség várható értékére:
−
* Felső ágon haladó eletronhullám: $|2\rangle$
+
$$\langle \Psi |\hat{T} |\Psi \rangle = |\alpha |^2 \langle 1 |\hat{T}|1\rangle + |\beta|^2 \langle 2|\hat{T}|2\rangle + \alpha^*\beta \langle 1|\hat{T}|2\rangle \langle \Phi_\mathrm{env1}|\Phi_\mathrm{env2}\rangle + \beta^*\alpha \langle 2|\hat{T}|1\rangle \langle \Phi_\mathrm{env2}|\Phi_\mathrm{env1}\rangle$$
 +
adódik, ahol figyelembe vettük, hogy a $\hat{T}$ operátor csak az elektron-hullámfüggvényre hat. Az első két tag a felső illetve az alsó ágon haladó nyalábok intenzitásának az összege, mely akkor is megjelenik, ha nem koherens a rendszerünk. A két ágon haladó hullám interferenciáját az utolsó két tag írja le. Ha a környezet hullámfüggvénye változatlan marad, $\langle \Phi_\mathrm{env1}|\Phi_\mathrm{env2}\rangle =1$, akkor nincsen koherenciavesztés. Azonban $\langle \Phi_\mathrm{env1}|\Phi_\mathrm{env2}\rangle \rightarrow 0$ esetén elveszik az interferencia, azaz ha a felül és alul haladó parciális elektronhullám ''különböző nyomot hagy a környezetben'' (13. ábra), akkor nem látunk interferenciát. Ebben az esetben ténylegesen elvész az interferenciakészség, ''koherenciavesztés történik''.
  
−
Teljes hullámfügvény:
+
Nanoáramkörökben a koherenciavesztés egyik fontos forrása ez elektron-fonon kölcsönhatás, aminek az erőssége függ a hőmérséklettől.
−
$$|\Psi\rangle = (\alpha|1\rangle + \beta|2\rangle)|\Phi_{env}\rangle\;\;\longrightarrow\;\;\alpha|1\rangle|\Phi_{env1} + \beta|2\rangle|\Phi_{env2}$$
+
</wlatex>
  
−
Transzmissziót mérünk:
+
===Környezetben hagyott nyom és dekoherencia közötti kapcsolat bemutatása egy szemléletes példán===
−
(T operátor csak az elektron hullámfüggvényekre hat, a környezetre nem!)
+
<wlatex>
−
$$\langle\Psi|T|\Psi\rangle = |\alpha|^2 \langle 1|T|1\rangle + |\beta|^2 \langle 2|T|2\rangle + \alpha^*\beta \langle 1|T|2\rangle \langle \Phi_{env1}|T|\Phi_{env2}\rangle + \beta^*\alpha \langle 2|T|1\rangle \langle \Phi_{env2}|T|\Phi_{env1}\rangle$$
+
A környezetben hagyott nyom és a interferenciakészség közti szoros kapcsolat jól szemléltethetó Stern, Aharonov és Imry gondolatkísérletével.<sup>[http://pra.aps.org/abstract/PRA/v41/i7/p3436_1 3]</sup> Egy szétválasztott elektronnyaláb két résen, vagy az Aharonov-Bohm gyűrű két ágán keresztül haladhat, a felül haladó elektron hullámfüggvénye $u_1(x)$, az alul haladóé pedig $u_2(x)$ (14. ábra). Egy töltött részecske segítségével szeretnénk detektálni, hogy hol halad az elektron. A töltött részecske hullámfüggvénye $\chi(q)$, melyhez $\Delta q$ helybizonytalanság tartozik. A töltött részecske és az elektron közötti Coulomb-potenciál $V(q-x)$, a kölcsönhatás csak az alsó ágon haladó elektronnal számottevő, a felső ágon haladó elektronnal vett kölcsönhatást elhanyagolhatónak tekintjük.
−
 
+
−
Ha $\langle \Phi_{env1}|\Phi_{env2}\rangle \rightarrow 0$, akkor elveszik az interferencia!
+
−
* Azaz ha a felül és alul haladó parciális elektronhullám különböző nyomot hagy a környezetben, akkor nem látunk interferenciát. Erre jó példa a fonon szórás, mely a hőmérséklet növelésével egyre jelentősebb dekoherenciához vezet.
+
−
 
+
−
=== Egyszerű példa (Stern, Aharonov, Imry) ===
+
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
191. sor: 202. sor:
 
|[[Fájl:Ketres_dekoherencia.png|közép|200px|]]
 
|[[Fájl:Ketres_dekoherencia.png|közép|200px|]]
 
|-
 
|-
−
| align="center"|1. ábra. Vezetőképesség fluktuációk
+
| align="center"|14. ábra. ''Az alsó résen áthaladó elektront (piros) egy töltött részecskével (kék) próbáljuk detektálni''
 
|}
 
|}
  
−
Az alsó ágon haladó részecske hullámfügvénye megváltozik a kölcsönhatás miatt: $|u_2(x)|\cdot e^{-i(E+V(q-x))\cdot t/\hbar}$
+
Először nézzük meg, hogy mi a feltétele annak, hogy a töltött részecske segítségével detektálni tudjunk egy alsó ágon haladó elektront. Ha alul halad az elektron, a töltött részecske gyorsul a Coulomb erő hatására. Kölcsönhatás ideje (t) alatt az impulzusváltozás: $\delta p = t\cdot \partial V/\partial q$. Ha az impulzusváltozás nagyobb az impulzus $\Delta p \approx \hbar / \Delta q$ bizonytalanságnál, akkor a detektáló részecske állapotából kiolvashatjuk, hogy az alsó ágon elhaladt egy elektron:
−
* A kölcsönhatás ideje alatt felszedett fázis: $\Phi$.
+
$$\delta p > \Delta p \Leftrightarrow \frac{\partial V}{\partial q}\cdot t > \frac{\hbar}{\Delta q}$$
−
* q bizonytalansága miatt a fázis is bizonytalan: $\Delta \Phi = \frac{1}{\hbar} \frac{\partial V}{\partial q} \cdot \Delta q \cdot t$
+
−
* Ha a fázisbizonytalanság nagy lesz, elveszik az interferencia:
+
−
$$\Delta \Phi > 1 \Leftrightarrow \frac{\partial V}{\partial q} \cdot t > \frac{\hbar}{\Delta q}$$
+
  
−
Töltött részecske, mely csak az alsó ágon áthaladó elektronnal hat kölcsön (a felső ágon haladó elektronnal elhanyagolható a kölcsönhatás). Helykoordináta: $q$, helybizonytalanság: $\Delta q$
+
Most nézzük meg azt, hogy az elektron és a töltött részecske kölcsönhatása hogyan befolyásolja az elektron interferencia-készségét.
 +
Az alsó ágon haladó elektron hullámfüggvénye megváltozik a kölcsönhatás miatt, az időfüggő hullámfüggvényben az elektron energiája a kölcsönhatási energiával módosul: $|u_2(x)|\cdot e^{-i(E+V(q-x))\cdot t/\hbar}$. A kölcsönhatás ideje alatt az alsó ágon haladó elektron $\phi$ fázist vesz fel. A detektáló részecske $\Delta q$ helybizonytalansága miatt azonban ez a fázis is bizonytalan:
 +
$\Delta \phi = \frac{1}{\hbar} \frac{\partial V}{\partial q} \cdot \Delta q \cdot t$. Kellően nagy fázisbizonytalanság esetén elveszik az interferencia:  
 +
$$\Delta \phi > 1 \Leftrightarrow \frac{\partial V}{\partial q} \cdot t > \frac{\hbar}{\Delta q}.$$
  
−
* Ha alul halad az elektron, a töltött részecske gyorsul az erő hatására. Kölcsönhatás ideje (t) alatt az impulzusváltozás: $\delta p = \frac{\partial V}{\partial q}\cdot t$
+
Vegyük észre, hogy pontosan ugyan az a feltétel írja le az interferenciakészség elvesztését, és a detektáló részecske megfigyelhető állapotváltozását. Azaz ez a gondolatkísérlet is alátámasztja, hogy két ág közötti interferencia pontosan akkor szűnik meg, amikor a két ágon haladó nyaláb egymástól megkülönböztethető nyomot hagy a környezetben.
 +
</wlatex>
  
−
* Ha az impulzus változás nagyobb az impulzus bizonytalanságnál,akkor a részecske tárolta az "útinformációt":
+
===Környezet miatti koherenciavesztés kísérleti demonstrációja===
−
$$\delta p > \Delta p \Leftrightarrow \frac{\partial V}{\partial q}\cdot t > \frac{\hbar}{\Delta q} \Leftrightarrow \langle\chi_1|\chi_2\rangle<<1$$
+
<wlatex>
 +
A környezet miatti koherenciavesztés kísérletileg is demonstrálható nanoszerkezetekben, például a 15. ábrán szemléltetett elrendezésben.<sup>[http://www.nature.com/nature/journal/v391/n6670/full/391871a0.html 4]</sup>
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| align="center"|[[Fájl:ABring_QPC.png|közép|200px|]]
 +
|-
 +
| align="center"|15. ábra. ''Aharonov-Bohm gyűrű a két ágba helyezett kvantumpöttyökkel, és a jobb oldali ág áramát érzékelő kvantum-pontkontaktussal''
 +
|}
 +
A forrás (S1) és nyelő (D1) elektródák között egy Aharonov-Bohm gyűrű található. A gyűrű mindkét ágában egy [[kvantumpöttyök|kvantumpöttyön]] keresztül haladnak az elektronok, azaz a gyűrű mindkét ágán található egy kisméretű vezető ’’sziget’’, mely kvantummechanikai alagutazással csatolódik a szomszédos vezetékdarabokhoz. Ezen kvantumpöttyök kis mérete miatt jelentős elektrosztatikus energiát kell befektetni ahhoz, hogy a szigetre további elektronokat helyezzünk el. A kvantumpöttyök potenciálja és ezen keresztül a kvantumpöttyökön található elektronok száma a G1 kapuelektróda segítségével hangolható. Az Aharonov-Bohm  gyűrű mellett egy [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Vezetőképesség-kvantálás kvantum-pontkontaktusban|kvantum-pontkontaktus]], azaz egy nagyon keskeny nanovezeték helyezkedik el az S2 forrás és D2 nyelő elektródák között. A G2 kapuelektródával a kvantumpontkontaktus szélessége olyan tartományba hangolható, ahol a vezetőképesség érzékenyen változik a kvantum-pontkontaktus szélességének a függvényében.
 +
A jobb oldali kvantumpöttyön található elektronok potenciálja kismértékben megváltoztatja a kvantum-pontkontaktus szélességét, így a kvantum-pontkontaktus vezetőképességének pontos mérésével megállapítható, hogy mikor halad át egy elektron a jobb oldali kvantumpöttyön. A kvantum-pontkontaktus áramának növelésével egyre pontosabban detektálhatjuk az Aharonov-Bohm gyűrű jobb oldali ágában haladó elektronokat, az egyre pontosabb mérés azonban koherenciavesztéshez vezet. A kísérletek valóban azt mutatják, hogy a kvantum-pontkontaktus áramának növelésével az Aharonov-Bohm oszcillációk láthatósága csökken. (A kísérleti elrendezés részletesebb megértéséhez érdemes elolvasni a [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás|kvantum-pontkontaktusokról]] és a [[Kvantumpöttyök|kvantumpöttyökről]] szóló fejezeteket.)
  
−
Ugyan az a két feltétel! Ugyanakkor veszik el az interferencia, amikor a környezet állapota megkülönbözethetővé válik alul illetve felül haladó elektron esetén!
+
</wlatex>
  
−
=== Környezet miatti koherenciavesztés Aharonov Bohm gyűrűben ===
+
==Hivatkozások==
−
Ha a kétrés kísérletben megmondható, hogy az elektron melyik résen haladt át (nyomot hagy a környezetében) $\rightarrow$ interferencia megszűnik.
+
  
−
Interferométer: Aharonov - Bohm elrendezés QDot-tal az egyik ágban.
+
===Fent hivatkozott szakcikkek===
 +
[1] [http://prl.aps.org/abstract/PRL/v54/i25/p2696_1 R. A. Webb, S. Washburn, C. P. Umbach, and R. B. Laibowitz: ''Observation of h/e Aharonov-Bohm Oscillations in Normal-Metal Rings'', '''Phys. Rev. Lett. 54''' p2696–2699 (1985)]
  
−
„Útvonal” detektor = QDot + mellette kvantum vezeték (QPC): a Dotban lévő elektron  visszaszórást okoz QPC-ben, minél több e-t szór vissza a QPC-ban, annál nagyobb nyomot hagy a környezetén.
+
[2] [http://rmp.aps.org/abstract/RMP/v59/i3/p755_1 A. G. Aronov, Yu. V. Sharvin: ''Magnetic flux effects in disordered conductors'', '''Rev. Mod. Phys. 59''' p755–779 (1987)]
  
−
Környezet miatti koherenciavesztés: a környezetben minnél nagyobb nyomot hagy az $e \rightarrow |\langle \Phi_{env1}|\Phi_{env2}\rangle|$ csökken $\rightarrow$ az interferencia láthatósága csökken (láthatóság: $\nu = Ampl/Avg$)  
+
[3] [http://pra.aps.org/abstract/PRA/v41/i7/p3436_1 Ady Stern, Yakir Aharonov, Yoseph Imry: ''Phase uncertainty and loss of interference: A general picture'', '''Phys. Rev. A 41'''p3436–3448 (1990)]
  
−
* Detektor „érzékenységét” QPC-ra adott ($V_d$) feszültség növelésével javíthatjuk: $I_{QPC}$ nő, több elektront tud visszaszórni.
+
[4] [http://www.nature.com/nature/journal/v391/n6670/full/391871a0.html E. Buks, R. Schuster, M. Heiblum, D. Mahalu, V. Umansky: ''Dephasing in electron interference by a 'which-path' detector'', '''Nature 391''' p871-874 (1998)]
  
−
* A detektor érzékenységének a növelésével az interferencia láthatósága csökken!
+
===Ajánlott könyvek és összefoglaló cikkek===
 +
*[http://books.google.hu/books/about/Electronic_Transport_in_Mesoscopic_Syste.html?id=28BC-ofEhvUC&redir_esc=y S. Datta: ''Electronic Transport in Mesoscopic Systems'', Cambridge University Press (1997)]
 +
*[http://books.google.hu/books/about/Semiconductor_Nanostructures.html?id=qD6623gfAZgC&redir_esc=y Thomas Ihn: ''Semiconducting nanosctructures'', OUP Oxford (2010)]
 +
*[http://books.google.hu/books?id=YNr4OcCExUcC&printsec=frontcover&dq=Nazarov+quantum+transport&hl=hu&sa=X&ei=2SzZUfGCMYna4ASDq4DQBQ&ved=0CDIQ6AEwAA Yuli V. Nazarov, Yaroslav M. Blanter: ''Quantum Transport: Introduction to Nanoscience'', Cambridge University Press (2009)]
  
−
 
+
===Ajánlott kurzusok===
−
 
+
*[[Új kísérletek a nanofizikában|''Új kísérletek a nanofizikában'', Halbritter András és Csonka Szabolcs, BME Fizika Tanszék]]
−
 
+
*[[Transzport komplex nanoszerkezetekben|''Transzport komplex nanoszerkezetekben'', Halbritter András, Csonka Szabolcs, Csontos Miklós, Makk Péter, BME Fizika Tanszék]]
−
 
+
*[[Alkalmazott szilárdtestfizika|''Alkalmazott szilárdtestfizika'', Mihály György, BME Fizika Tanszék]]
−
 
+
*[[Fizika 3 - Villamosmérnöki mesterszak|''Fizika 3'', Mihály György, BME Fizika Tanszék (mérnök hallgatóknak)]]
−
</wlatex>
+
*[http://www.phy.bme.hu/~zarand/mezoszkopia.html ''Mezoszkopikus rendszerek fizikája'', Zaránd Gergely, BME Elméleti Fizika Tanszék]
 +
*''Mezoszkopikus rendszerek fizikája'', Cserti József, ELTE Komplex Rendszerek Fizikája Tanszék

A lap jelenlegi, 2014. január 13., 17:38-kori változata

Tartalomjegyzék

Interferencia-kísérletek hat nagyságrenddel kisebb skálán


A fizikában régóta ismertek az interferencia-kísérletek, melyeknek egy emblematikus példája az 1. ábrán szemléltetett kétrés kísérlet. Ha fény két közeli résen halad keresztül, a rések mögé helyezett ernyőn interferencia-képet látunk, azaz az ernyőn látható intenzitásprofil nem egyezik meg az egyik illetve a másik rés kitakarásakor kapott intenzitások összegével, hanem azon tartományokban, ahova a két résen keresztül azonos fázissal érkezik a hullám erősítést, ahol pedig ellentétes (180 fokkal eltolt) fázissal, ott kioltást tapasztalunk. Természetesen ugyanez a jelenség a legkülönbözőbb közegekben megfigyelhető a vízhullámoktól a hanghullámokig.

Interferencia.png
1. ábra. Kétrés kísérlet fénnyel

A modern fizika fejlődésével az interferencia-kísérletek újabb értelmezést kaptak, hiszen jól demonstrálták a részecske-hullám dualitást. Ha az 1. ábrán szemléltetett kísérletben nagyon kis fényintenzitást, és nagyon érzékeny ernyőt használunk, akkor először véletlenszerű felvillanásokat látunk az ernyő különböző pontjain, mely a fény részecske-természetét támasztja alá. Ha viszont sokat várunk, akkor a véletlenszerű felvillanásokból kirajzolódik a jól ismert interferencia-kép (lásd 2. ábra).

Egyfoton interferencia.ogv
2. ábra. Interferencia-kép kialakulása egyedi fotonbecsapódásokból

További érdekesség, hogy ha a két rés mellé detektorokat helyezünk, és próbáljuk megállapítani, hogy a fényt alkotó fotonok éppen melyik résen haladnak keresztül, akkor azt tapasztaljuk, hogy minél pontosabban detektáljuk a résen áthaladó fotonokat, annál inkább elvész az interferenciakép. Azaz akár egyetlen foton is képes mindkét résen áthaladva önmagával interferálni, viszont ha megmérjük, hogy merre ment a foton, akkor az interferencia megszűnik.

Az elmúlt évtizedekben a nanofizika fejlődésének köszönhetően a kétrés kísérlethez hasonlóan izgalmas interferencia-kísérleteket mintegy 6 nagyságrenddel kisebb méretskálájú nanoáramkörökben is sikerült megvalósítani, ebbe a témakörbe nyújtunk betekintést a következőkben.

Fáziskoherencia-hossz


A nanovezetékek tárgyalásánál már említettük, hogy egy nanoáramkörben akkor tapasztalhatunk interferencia-jelenséget, ha annak mérete kisebb a fáziskoherencia-hossznál. Próbáljuk ezt a karakterisztikus méretskálát egy kicsit pontosabban definiálni.

Koherencia ido.png
3. ábra.

Ha egy elektronhullámot egy adott pontban szétválasztunk, és feltételezzük, hogy a két parciális hullám két különböző trajektórián keresztül jut el egy másik pontba, ahol újra egyesülnek (3. ábra), akkor ebben a pontban a hullám intenzitását

\[ T=\left| t_1 \right|^2 + \left| t_2 \right|^2 + 2\left| t_1t_2 \right|\cos\left(\phi\right) \exp\left(-\tau_L/\tau_\phi \right) \]

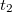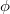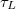alakban írhatjuk, ahol \setbox0\hbox{$t_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$t_2$}% \message{//depth:\the\dp0//}% \box0% az egyik illetve a másik trajektóriához tartozó komplex amplitúdó, \setbox0\hbox{$\phi$}% \message{//depth:\the\dp0//}% \box0% a két komplex amplitúdó közötti fáziskülönbség, \setbox0\hbox{$\tau_L$}% \message{//depth:\the\dp0//}% \box0% pedig az egyik pontból a másik pontba történő eljutáshoz szükséges karakterisztikus idő. A két trajektória mentén az elektronok szóródásokat szenvednek. Rugalmas (pl. rácshibákon, szennyezőkön, történő) szóródás esetén egy időben konstans fázistolás lép fel, de ez nem befolyásolja az interferencia-képességet, legfeljebb azt, hogy a parciális hullámok találkozásakor erősítést vagy gyengítést tapasztalunk. Ha viszont az elektronhullám az egyik trajektória mentén egy rugalmatlan szórást szenved (pl. elektron-fonon kölcsönhatás), akkor megváltozik az energiája, és így a hullámok egyesítésekor egy időben fluktuáló, kiátlagolódó interferenciaképet kapunk. 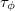A fenti képletben \setbox0\hbox{$\tau_\phi$}% \message{//depth:\the\dp0//}% \box0% ezen, rugalmatlan szórásoknak köszönhető koherenciavesztés karakterisztikus időskáláját adja meg. Ennél az időnél lényegesen hosszabb skálán a parciális hullámok egyesítésekor egyszerűen az intenzitások adódnak össze, és a fázisviszonyoktól függő interferenciatag (a fenti képlet utolsó tagja) elvész.

Ha két rugalmatlan szórás között nem történik rugalmas szórás, azaz 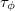\setbox0\hbox{$\tau_\phi$}% \message{//depth:\the\dp0//}% \box0% összemérhető a momentum relaxáció 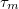\setbox0\hbox{$\tau_m$}% \message{//depth:\the\dp0//}% \box0% karakterisztikus idejével, akkor az a távolságskála melyen belül interferenciát tapasztalunk egyszerűen

\[ L_\phi=v_F \tau_\phi, \]

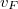ahol \setbox0\hbox{$v_F$}% \message{//depth:\the\dp0//}% \box0% az elektronok Fermi-sebessége. Ha viszont két rugalmatlan ütközés között számos rugalmas ütközés történik, akkor az elektronok diffúzív trajektóriák mentén mozognak. Ebben az esetben is 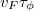\setbox0\hbox{$v_F \tau_\phi$}% \message{//depth:\the\dp0//}% \box0% trajektóriahossz után vész el az interferencia-készség, azonban ez a trajektóriahossz a diffúzív mozgás miatt térben csak

\[ L_\phi=\sqrt{D\tau_\phi} \]

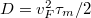eltávolodást eredményez a kiindulási ponttól, ahol \setbox0\hbox{$D$}% \message{//depth:\the\dp0//}% \box0% a diffúziós állandó, mely a momentumrelaxációs időből két dimenzióban \setbox0\hbox{$D=v_F^2\tau_m/2$}% \message{//depth:\the\dp0//}% \box0% képlettel számolható.

Aharonov-Bohm gyűrű


Nanoáramkörökben az interferencia-jelenségeket nem tudjuk egy ernyő mentén detektálni, olyan elrendezést kell találni, melyben például az áramkör két (vagy pár) kontaktusán keresztül feszültséget adunk a mintára, és a mért áramban jelenik meg az interfernecia valamilyen hangolható paraméter függvényében. Erre talán a legjobb példa a nanogyűrűkben tapasztalható Aharonov-Bohm jelenség.

Az egyik kontaktusból bejövő elektronhullámot egy kör alakú gyűrű két ága mentén két részre osztjuk, és a gyűrű másik oldalára helyezett kontaktuson keresztül egyesül a két parciális hullám (4. ábra). 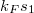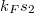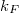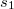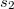Zérus mágneses térben az elektronok a felső ágon \setbox0\hbox{$k_F s_1$}% \message{//depth:\the\dp0//}% \box0%, míg az alsó ágon \setbox0\hbox{$k_F s_2$}% \message{//depth:\the\dp0//}% \box0% fázist vesznek fel, ahol \setbox0\hbox{$k_F$}% \message{//depth:\the\dp0//}% \box0% a Fermi-hullámszám, \setbox0\hbox{$s_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$s_2$}% \message{//depth:\the\dp0//}% \box0% pedig a két kontaktus közötti trajektóriahossz a felső illetve az alsó ág mentén (lásd 4. ábra). Ennek megfelelően az interferenciatag 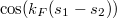\setbox0\hbox{$\cos(k_F(s_1-s_2))$}% \message{//depth:\the\dp0//}% \box0%-vel arányos.

AB gyuru.png
4. ábra Aharonov-Bohm gyűrű

Véges mágneses térben azonban a fenti fázisok mellett az elektronok 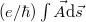\setbox0\hbox{$(e/\hbar ) \int \vec{A} \mathrm{d}\vec{s}$}% \message{//depth:\the\dp0//}% \box0% ún. Aharonov-Bohm fázist is felvesznek, ahol 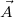\setbox0\hbox{$\vec{A}$}% \message{//depth:\the\dp0//}% \box0% a vektorpotenciál, az integrálást pedig az elektronok trajektóriája mentén kell elvégezni. A gyűrű felső és alsó ágának járulékát összegezve:

\[G\sim T = |t_1+t_2|^2 = \left| e^{i k_F s_1 + \frac{i e}{\hbar} \int \limits_1 \vec{A} \mathrm{d}\vec{s}} + e^{i k_F s_2 + \frac{i e}{\hbar} \int \limits_2 \vec{A} \mathrm{d}\vec{s}}\right|^2 = \]
\[2+2\cdot cos\left(k_F(s_1-s_2)+\frac{e}{\hbar} \oint \vec{A} \mathrm{d} \vec{s}\right) = 2+2\cdot cos(\delta_0 + 2 \pi \Phi/\Phi_0),\]

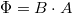ahol \setbox0\hbox{$\Phi=B\cdot A$}% \message{//depth:\the\dp0//}% \box0% a gyűrű által körbezárt mágneses fluxus, 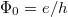\setbox0\hbox{$\Phi_0=e/h$}% \message{//depth:\the\dp0//}% \box0% pedig az úgynevezett fluxuskvantum. Látszik, hogy a vezetőképesség a fluxus változtatásával a fluxuskvantum periódusa szerint oszcillál. Ezt az oszcillációt először Webb és társai mutatták ki mezoszkopikus arany gyűrűn.1

A 4. ábrán szándékosan különbözőnek jelöltük a felső és alsó ág hosszát, hiszen egy valós rendszerben nem lehet garantálni, hogy mindkét ág mentén pontosan ugyan olyan hosszú trajektória mentén haladjanak az elektronok. Ráadásul, ha a gyűrű két ága egy-egy szélesebb vezeték, akkor mindkét ágon több, különböző hosszúságú trajektória mentén juthat el az elektron az egyik kontaktusból a másikba, és ha ezek a trajektóriahosszok túlzottan eltérnek, akkor a szabad elektron terjedésből adódó 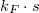\setbox0\hbox{$k_F\cdot s$}% \message{//depth:\the\dp0//}% \box0% fázisok kiátlagolódnak, a koherencia elvész.

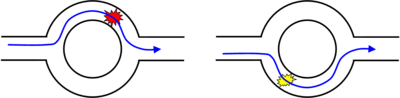
Tanulságos az Aharonov-Bohm gyűrűben reflexiót számolva megnézni a releváns folyamatokat. A legalapvetőbb (nulladrendű) folyamat, ha az elektronok be se jutnak a gyűrűbe, hanem a gyűrű elején reflektálódnak (5. ábra, bal oldal). A következő, első rendben az elektronok úgy tudnak reflektálódni, hogy bejutnak a gyűrűbe, és jobbról vagy balról egyszer megkerülik azt, majd a bal oldali kontaktuson keresztül elhagyják a gyűrűt (5. ábra, középső és jobb oldali panel). Az Aharonov-Bohm effektus a nulladrendű, illetve az elsőrendű folyamatok interferenciájából adódik, melyek között a mágneses térből felvett fáziskülönbség 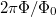\setbox0\hbox{$2 \pi \Phi/\Phi_0$}% \message{//depth:\the\dp0//}% \box0%. 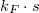Azonban széles vezetékek esetén a \setbox0\hbox{$k_F\cdot s$}% \message{//depth:\the\dp0//}% \box0% fázisok kiátlagolódnak.

AB gyuru2.png
5. ábra. Reflexióhoz járulékot adó alapvető folyamatok Aharonov-Bohm gyűrűben

Érdemes megvizsgálni a két elsőrendű folyamat interferenciáját, azaz amikor az elektronok balról illetve jobbról kerülik a gyűrűt. E két folyamat között a mágneses tér hatására 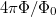\setbox0\hbox{$4 \pi \Phi/\Phi_0$}% \message{//depth:\the\dp0//}% \box0% fáziskülönbség lép fel, azaz a vezetőképesség a fluxuskvantum fele szerinti periódussal oszcillál. Két tetszőleges trajektória közötti 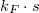\setbox0\hbox{$k_F\cdot s$}% \message{//depth:\the\dp0//}% \box0% fázisok itt is kiátlagolódhatnak, azonban minden egyes balról kerülő trajektóriához találunk egy időtükrözött jobbról kerülő trajektóriát, azaz egy trajektóriapárt, melyen pontosan ugyan azon a trajektórián, de ellentétes irányban halad az elektron. Az időtükrözött trajektóriapárok között a 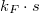\setbox0\hbox{$k_F \cdot s$}% \message{//depth:\the\dp0//}% \box0% fázisok különbsége pontosan zérus, így nulla mágneses térben mindig konstruktív interferenciát látunk, illetve véges mágneses térben a fluxuskvantum felének periódusával oszcillál a vezetőképesség. Ezt hívják Altshuler-Aronov-Spivak oszcillációnak.

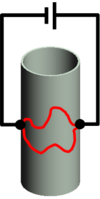
AAS oszcilláciok.png
6. ábra. Altshuler-Aronov-Spivak oszcillációk hosszú, de kis átmérőjű fémhengerben is megfigyelhetők

Az időtükrözött párok interferencia-járuléka vastag vezetékek esetén sem átlagolódik ki. Erre a legjobb példa Sharvin és Sharvin eredeti kísérlete, melyben egy kis átmérőjű (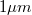\setbox0\hbox{$~1\mu m$}% \message{//depth:\the\dp0//}% \box0%) szigetelő drótra vékony magnéziumréteget vittek fel, és a drót két oldala között mértek vezetőképességet (6. ábra). Ebben az elrendezésben nyilvánvaló, hogy az elektronok teljesen különböző hosszúságú trajektóriák mentén juthatnak el ez egyik kontaktusból a másikra, így a 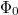\setbox0\hbox{$\Phi_0$}% \message{//depth:\the\dp0//}% \box0% periódusú Aharonov-Bohm oszcillációk kiátlagolódnak. Ezzel szemben az időtükrözött trajektóriák interferenciájából adódó 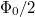\setbox0\hbox{$\Phi_0/2$}% \message{//depth:\the\dp0//}% \box0% periódusú Altshuler-Aronov-Spivak oszcillációk megmaradnak, és kísérletileg is kimutathatók, lásd A.G.Aronov és Yu.V.Sharvin összefoglaló cikke, 7. ábra. 2

Vezetőképesség-fluktuációk


Említettük, hogy túl széles vezetékkel készített Aharonov-Bohm gyűrűben a 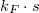\setbox0\hbox{$k_F\cdot s$}% \message{//depth:\the\dp0//}% \box0% fázisok kiátlagolódnak. Ez volt az oka annak, hogy az első próbálkozások Aharonov-Bohm oszcillációk kimutatására nanoszerkezetekben nem sikerültek, illetve a periodikus oszcillációk helyett a vezetőképesség a mágneses tér függvényében egy véletlenszerű fluktuációt mutatott. Később kiderült, hogy a vezetőképesség fluktuációja nanoszerkezetekben egy általános interferencia-jelenség.

Vezetokepesseg fluktuaciok1.png
7. ábra. A nanovezetékben az elektronok különböző diffúzív trajektóriák mentén juthatnak el az egyik kontaktusból a másikba

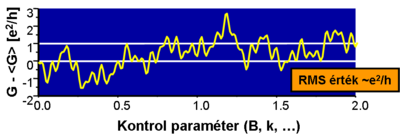
Egy megfelelő szélességű és hosszúságú (a momentumrelaxációs szabadúthossznál hosszabb, de a fáziskoherencia hossznál rövidebb) nanovezetékben az elektronok számtalan különböző diffúzív trajketória mentén juthatnak el az egyik kontaktusból a másikba (7. ábra). A kis méret miatt (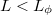\setbox0\hbox{$L<L_\phi $}% \message{//depth:\the\dp0//}% \box0%) ezek a diffúzív trajektóriák interferálnak egymással. A mágneses térrel hangolhatjuk az egyes trajektóriákhoz tartozó fázist, így változtathatjuk az interferenciafeltételeket, de mivel nagyon sok véletlen trajektória interferenciajárulékáról van szó, ezért a mágneses tér függvényében a vezetőképesség nem periodikus oszcillációt, hanem egy véletlenszerű fluktuációt mutat (lásd 8. ábra). Fontos azonban megjegyezni, hogy ha a mágneses teret oda-vissza változtatjuk, akkor ez a véletlenszerű vezetőképesség-fluktuáció pontosan reprodukál, hiszen a vezetéken belül a mérés során nem változik a szórócentrumok helye, így a sok trajektória interferenciájából adódó vezetőképesség-korrekció a mágneses tér egyértelmű függvénye. Ha viszont felmelegítjük, és újra lehűtjük a nanovezetéket, akkor a rácshibák pozíciója megváltozik, és így jellegre hasonló, de a részletekben a korábbitól teljesen eltérő vezetőképesség-fluktuációt kapunk a mágneses tér függvényében.

Vezetokepesseg fluktuaciok2.png
8. ábra. Vezetőképesség-fluktuációk

Megmutatható, hogy sok nyitott vezetési csatornával rendelkező (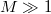\setbox0\hbox{$M\gg 1$}% \message{//depth:\the\dp0//}% \box0%), diffúzív (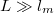\setbox0\hbox{$L\gg l_m$}% \message{//depth:\the\dp0//}% \box0%) de még fáziskoherens (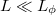\setbox0\hbox{$L\ll L_\phi$}% \message{//depth:\the\dp0//}% \box0%) nanovezetékben a vezetőképesség-fluktuációk nagysága univerzális, a fluktuációk szórása a vezetőképesség értékétől függetlenül 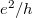\setbox0\hbox{$e^2/h$}% \message{//depth:\the\dp0//}% \box0% (lásd 8. ábra).

Érdemes megjegyezni, hogy a diffúzív trajektóriák közötti fázisviszonyok nem csak a mágneses térből adódó Aharonov-Bohm fázis segítségével hangolhatók, hanem az elektronok Fermi-hullámhosszának változtatásával is, amit a mintára tett feszültséggel, vagy egy szomszédos kapuelektróda potenciáljának változtatásával érhetünk el.

Gyenge lokalizáció


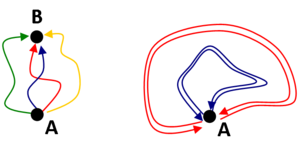
Az 5. ábra vonatkozásában láttuk, hogy ha a forráskontaktusból indulva egy adott irányban megkerüli az elektron az Aharonov-Bohm gyűrűt és visszajut a forráskontaktusba, akkor ehhez a folyamathoz társíthatunk egy időtükrözött folyamatot, melyhez pontosan ugyan az 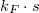\setbox0\hbox{$k_F\cdot s$}% \message{//depth:\the\dp0//}% \box0% fázis tartozik, így az időtükrözött trajektóriapárok interferenciájának konstruktív vagy destruktív jellege csak az Aharonov-Bohm fázistól, azaz a gyűrű területén megjelenő mágneses fluxustól függ. Ennek köszönhető, hogy egy hosszú, de kis átmérőjű fém hengerben is megjelenhetnek a mágneses térben periodikus interferenciaoszcillációk az időtükrözött trajektóriapárok interferenciájának köszönhetően.

Gyenge lokalizacio0.png
9. ábra. Az időtükrözött trajektóriapárok konstruktív interferenciája miatt zérus mágneses térben megnő a kiindulási pontba történő visszaszóródás valószínűsége

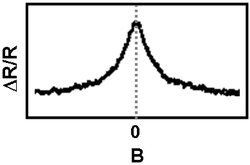
Zérus mágneses térben azonban nem jelenik meg Aharonov-Bohm fázis, így a fázisdiffúziós hosszon belüli időtükrözött trajektóriapárok mindig konstruktívan interferálnak a körbezárt területtől függetlenül. Ennek köszönhetően az időtükrözött trajektóriapároknak köszönhető interferencia-járulék nem csak a 6. ábrán szemléltetett hengeres geometriában, hanem tetszőleges mintán megfigyelhető. Egy A pontból egy B pontba sok különböző trajektórián eljuthat az elektron, így a sok trajektória interferenciajáruléka kiátlagolódik (9. ábra, bal oldal). Ha viszont a diffúzív mozgás során az A pontól az A pontba visszajut egy tetszőleges trajektórián az elektron, akkor a megfelelő időtükrözött trajektórián zérus mágneses térben ugyan azt a fázist veszi fel, azaz a kiindulási pontba történő visszajutás esetén az időtükrözött trajektóriapár konstruktívan interferál (9. ábra, jobb oldal). Ez azt jelenti, hogy megnő a forráselektródába történő visszaszóródás valószínűsége, azaz megnő a minta ellenállása. Ezt a jelenséget hívjuk gyenge lokalizációnak. A mágneses tér bekapcsolásával azonban a különböző fluxust bezáró időtükrözött trajektóriapárok interferencia-járuléka kiátlagolódik az eltérő Aharonov-Bohm fázis miatt, azaz az ellenállás visszacsökken az interferencia-járulék nélküli értékre. Ezt a jelenséget szemlélteti a 10. ábrán látható tipikus kísérleti görbe, melynek illesztéséből a fázisdiffúziós hossz meghatározható.

Gyenge lokalizacio2.png
10. ábra. Egy vékonyréteg minta ellenállása zérus mágneses térben a gyenge lokalizáció miatt maximumot mutat

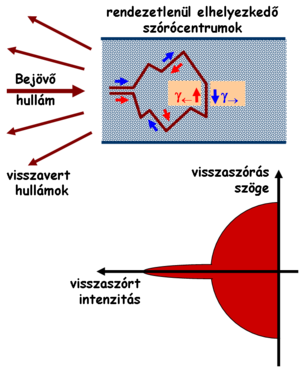
A gyenge lokalizáció jelensége nem csak elektronokra, hanem tetszőleges diffúzív közegben terjedő hullámra jelentkezhet: ha a közegbe egy adott irányból érkezik a hullám, és a visszavert hullám intenzitását mérjük különboző irányokban, akkor az időtükrözött trajektóriák interferenciájának köszönhetően a bejövő hullámmal ellentétes irányban visszavert hullám intenzitása megnő bármilyen más irányban visszevert hullámintenzitáshoz képest (11. ábra). Ezt a jelenséget felhőben terjedő radarhullámokra is megfigyelték.

Gyenge lokalizacio1.png
11. ábra. Időtükrözött trajektóriapárok interferenciájának köszönhetően megnő a bejövő hullámmal ellentétes irányba visszaszórt hullám intenzitása

Koherenciavesztés


Az eddigiekben nanoszerkezetekben jelentkező interferencia-jelenségeket vizsgáltunk. Most nézzük meg részletesebben, hogy milyen tényezők okozhatják a fent ismertetett interferencia-jelenségek megszűnését.

Hőmérséklet miatti koherenciavesztés


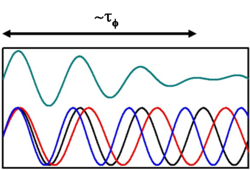
A fentiekben az elektronhullámokat monokromatikusnak tekintettük, azaz feltételeztük, hogy jól definiált energiával rendelkeznek. Ez teljesül nagyon alacsony hőmérsékleten, és nagyon kicsi mérőfeszültség mellett, hiszen ekkor gyakorlatilag csak a Fermi-szintnél levő elektronok adnak járulékot a vezetőképességhez. Véges hőmérsékleten azonban a Fermi-energia körüli véges 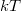\setbox0\hbox{$kT$}% \message{//depth:\the\dp0//}% \box0% energiatartományban levő elektronok adnak járulékot a transzporthoz, így a különböző energiájú (és különböző hullámhosszal rendelkező) elektronok interferenciajáruléka kiátlagolódhat. 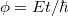Egy \setbox0\hbox{$E$}% \message{//depth:\the\dp0//}% \box0% energiájú elektron által \setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0% idő alatt felvett fázis \setbox0\hbox{$\phi=Et/\hbar$}% \message{//depth:\the\dp0//}% \box0%. Ha a transzportban résztvevő elektronok között 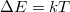\setbox0\hbox{$\Delta E=kT$}% \message{//depth:\the\dp0//}% \box0% energiakülönbség lehet, akkor az azonos fázissal indított elektronhullámok között nagyságrendileg 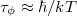\setbox0\hbox{$\tau_\phi\approx \hbar/kT$}% \message{//depth:\the\dp0//}% \box0% idő alatt akkora fáziskülönbség lép fel, hogy a különböző energiájú elektronokhoz tartozó fázis már teljesen kiátlagolódik (12. ábra, jobb oldal). Ennek megfelelően interferencia-jelenséget akkor láthatunk ha a nanoszerkezeten történő áthaladáshoz szükséges 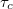\setbox0\hbox{$\tau_c$}% \message{//depth:\the\dp0//}% \box0% idő (12. ábra, bal oldal) kisebb 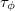\setbox0\hbox{$\tau_\phi$}% \message{//depth:\the\dp0//}% \box0%-nél.

Fazisvesztes1.png
Fazisvesztes2.png
12/a. ábra. A nanoszerkezeten az elektronok 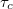\setbox0\hbox{$\tau_c$}% \message{//depth:\the\dp0//}% \box0% idő alatt haladnak át 12/b. ábra. Azonos fázissal induló különböző hullámhosszal rendelkező hullámok együttes járuléka 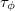\setbox0\hbox{$\tau_\phi$}% \message{//depth:\the\dp0//}% \box0% idő után kiátlagolódik

Egy nanoszerkezetet jellemezhetünk az ún. Thouless energiával, mely az elektronok nanoszerkezeten belül eltöltött 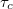\setbox0\hbox{$\tau_c$}% \message{//depth:\the\dp0//}% \box0% idejének megfeleltetett 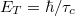\setbox0\hbox{$E_T=\hbar/\tau_c$}% \message{//depth:\the\dp0//}% \box0% energia. Ezen definíció alapján egyszerűen azt mondhatjuk, hogy az adott nanoszerkezetben 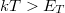\setbox0\hbox{$kT>E_T$}% \message{//depth:\the\dp0//}% \box0% esetén a hőmérsékleti kiszélesedés miatt elmosódnak az interferenciajelenségek.

A fázisok hőmérséklet miatti kiátlagolódása hasonló jelenség a fehér fénnyel végzett interferncia-kísérlethez: az interferenciakép a különböző hullámhosszúságú komponensek keveredése miatt mosódik el. Ez viszont nem jelenti azt, hogy az elektronok (vagy a fény) interferencia-képessége, koherenciája megszűnne, hiszen ha a mérőrendszerben ki tudunk választani egy adott energiához tartozó részecskéket (pl. színszűrővel), akkor ezekre megjelenik az interferenciakép. Ennek megfelelően a fázisok fent részletezett kiátlagolódását nem koherenciavesztésnek (decoherence) hanem fázisvesztésnek (dephasing) szokták nevezni.

Környezet miatti koherenciavesztés


A kétrés kísérlet tárgyalásánál említettük, hogy ha tudjuk detektálni, hogy a részecskék melyik résen haladnak át, akkor megszűnik az interferencia-képesség. Ezt a jelenséget általánosabban is megfogalmazhatjuk. Az Aharonov-Bohm gyűrű példájával élve a forrás kontaktusból érkező elektronok haladhatnak a felső ágon (13. ábra, bal oldal), amit jelöljünk az 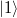\setbox0\hbox{$|1\rangle$}% \message{//depth:\the\dp0//}% \box0% kvantummechanikai állapottal, és haladhatnak az alsó ágon (13. 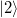ábra, jobb oldal), amit jelöljünk a \setbox0\hbox{$|2\rangle$}% \message{//depth:\the\dp0//}% \box0% állapottal.

Kornyezeti dekoherencia.png
13. ábra. Az alsó és a felső ágon haladó elektron különböző nyomot hagy a környezetben

Interferencia esetén a rendszer szuperponált állapotban van, a teljes hullámfüggvény:

\[|\psi\rangle = \alpha|1\rangle + \beta|2\rangle.\]

Ha az elektronok kölcsönhatnak a környezetükkel (pl. rácsrezgések), akkor a teljes hullámfüggvényben a környezet hullámfüggvényét (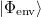\setbox0\hbox{$|\Phi_\mathrm{env}\rangle$}% \message{//depth:\the\dp0//}% \box0%) is figyelembe kell venni. Kezdetben (a kölcsönhatás bekapcsolása előtt) a teljes hullámfüggvényt írhatjuk az elektron-hullámfüggvény és a környezeti hullámfüggvény szorzataként. Ha viszont a kölcsönhatás következtében a környezet hullámfüggvénye különbözővé válik aszerint hogy az elektron alul vagy felül halad, akkor a teljes hullámfüggvényt már nem lehet szorzat alakban írni, azaz az elektronállapot összefonódik a környezet állapotával:

\[|\Psi\rangle = (\alpha|1\rangle + \beta|2\rangle)|\Phi_\mathrm{env}\rangle\;\;\longrightarrow\;\;\alpha|1\rangle|\Phi_\mathrm{env1}\rangle + \beta|2\rangle|\Phi_\mathrm{env2}\rangle.\]

Ha valamilyen, csak az elektronokra vonatkozó fizikai mennyiséget (például az Aharonov-Bohm gyűrű transzmisszióját) mérjük, akkor a 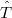\setbox0\hbox{$\hat{T}$}% \message{//depth:\the\dp0//}% \box0% operátorral jellemezhető mennyiség várható értékére:

\[\langle \Psi |\hat{T} |\Psi \rangle = |\alpha |^2 \langle 1 |\hat{T}|1\rangle + |\beta|^2 \langle 2|\hat{T}|2\rangle + \alpha^*\beta \langle 1|\hat{T}|2\rangle \langle \Phi_\mathrm{env1}|\Phi_\mathrm{env2}\rangle + \beta^*\alpha \langle 2|\hat{T}|1\rangle \langle \Phi_\mathrm{env2}|\Phi_\mathrm{env1}\rangle\]

adódik, ahol figyelembe vettük, hogy a 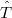\setbox0\hbox{$\hat{T}$}% \message{//depth:\the\dp0//}% \box0% operátor csak az elektron-hullámfüggvényre hat. Az első két tag a felső illetve az alsó ágon haladó nyalábok intenzitásának az összege, mely akkor is megjelenik, ha nem koherens a rendszerünk. A két ágon haladó hullám interferenciáját az utolsó két tag írja le. Ha a környezet hullámfüggvénye változatlan marad, 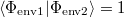\setbox0\hbox{$\langle \Phi_\mathrm{env1}|\Phi_\mathrm{env2}\rangle =1$}% \message{//depth:\the\dp0//}% \box0%, akkor nincsen koherenciavesztés. Azonban 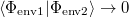\setbox0\hbox{$\langle \Phi_\mathrm{env1}|\Phi_\mathrm{env2}\rangle \rightarrow 0$}% \message{//depth:\the\dp0//}% \box0% esetén elveszik az interferencia, azaz ha a felül és alul haladó parciális elektronhullám különböző nyomot hagy a környezetben (13. ábra), akkor nem látunk interferenciát. Ebben az esetben ténylegesen elvész az interferenciakészség, koherenciavesztés történik.

Nanoáramkörökben a koherenciavesztés egyik fontos forrása ez elektron-fonon kölcsönhatás, aminek az erőssége függ a hőmérséklettől.

Környezetben hagyott nyom és dekoherencia közötti kapcsolat bemutatása egy szemléletes példán


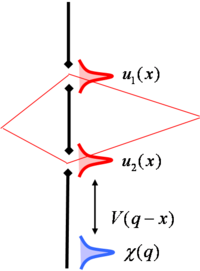
A környezetben hagyott nyom és a interferenciakészség közti szoros kapcsolat jól szemléltethetó Stern, Aharonov és Imry gondolatkísérletével.3 Egy szétválasztott elektronnyaláb két résen, vagy az Aharonov-Bohm gyűrű két ágán keresztül haladhat, a felül haladó elektron hullámfüggvénye 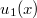\setbox0\hbox{$u_1(x)$}% \message{//depth:\the\dp0//}% \box0%, az alul haladóé pedig 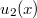\setbox0\hbox{$u_2(x)$}% \message{//depth:\the\dp0//}% \box0% (14. ábra). Egy töltött részecske segítségével szeretnénk detektálni, hogy hol halad az elektron. A töltött részecske hullámfüggvénye 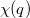\setbox0\hbox{$\chi(q)$}% \message{//depth:\the\dp0//}% \box0%, melyhez 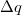\setbox0\hbox{$\Delta q$}% \message{//depth:\the\dp0//}% \box0% helybizonytalanság tartozik. A töltött részecske és az elektron közötti Coulomb-potenciál 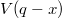\setbox0\hbox{$V(q-x)$}% \message{//depth:\the\dp0//}% \box0%, a kölcsönhatás csak az alsó ágon haladó elektronnal számottevő, a felső ágon haladó elektronnal vett kölcsönhatást elhanyagolhatónak tekintjük.

Ketres dekoherencia.png
14. ábra. Az alsó résen áthaladó elektront (piros) egy töltött részecskével (kék) próbáljuk detektálni

Először nézzük meg, hogy mi a feltétele annak, hogy a töltött részecske segítségével detektálni tudjunk egy alsó ágon haladó elektront. Ha alul halad az elektron, a töltött részecske gyorsul a Coulomb erő hatására. Kölcsönhatás ideje (t) alatt az impulzusváltozás: 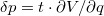\setbox0\hbox{$\delta p = t\cdot \partial V/\partial q$}% \message{//depth:\the\dp0//}% \box0%. Ha az impulzusváltozás nagyobb az impulzus 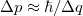\setbox0\hbox{$\Delta p \approx \hbar / \Delta q$}% \message{//depth:\the\dp0//}% \box0% bizonytalanságnál, akkor a detektáló részecske állapotából kiolvashatjuk, hogy az alsó ágon elhaladt egy elektron:

\[\delta p > \Delta p \Leftrightarrow \frac{\partial V}{\partial q}\cdot t > \frac{\hbar}{\Delta q}\]

Most nézzük meg azt, hogy az elektron és a töltött részecske kölcsönhatása hogyan befolyásolja az elektron interferencia-készségét. Az alsó ágon haladó elektron hullámfüggvénye megváltozik a kölcsönhatás miatt, az időfüggő hullámfüggvényben az elektron energiája a kölcsönhatási energiával módosul: 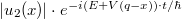\setbox0\hbox{$|u_2(x)|\cdot e^{-i(E+V(q-x))\cdot t/\hbar}$}% \message{//depth:\the\dp0//}% \box0%. A kölcsönhatás ideje alatt az alsó ágon haladó elektron 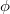\setbox0\hbox{$\phi$}% \message{//depth:\the\dp0//}% \box0% fázist vesz fel. A detektáló részecske 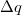\setbox0\hbox{$\Delta q$}% \message{//depth:\the\dp0//}% \box0% helybizonytalansága miatt azonban ez a fázis is bizonytalan: 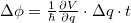\setbox0\hbox{$\Delta \phi = \frac{1}{\hbar} \frac{\partial V}{\partial q} \cdot \Delta q \cdot t$}% \message{//depth:\the\dp0//}% \box0%. Kellően nagy fázisbizonytalanság esetén elveszik az interferencia:

\[\Delta \phi > 1 \Leftrightarrow \frac{\partial V}{\partial q} \cdot t > \frac{\hbar}{\Delta q}.\]

Vegyük észre, hogy pontosan ugyan az a feltétel írja le az interferenciakészség elvesztését, és a detektáló részecske megfigyelhető állapotváltozását. Azaz ez a gondolatkísérlet is alátámasztja, hogy két ág közötti interferencia pontosan akkor szűnik meg, amikor a két ágon haladó nyaláb egymástól megkülönböztethető nyomot hagy a környezetben.

Környezet miatti koherenciavesztés kísérleti demonstrációja


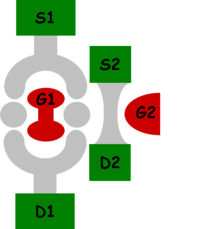
A környezet miatti koherenciavesztés kísérletileg is demonstrálható nanoszerkezetekben, például a 15. ábrán szemléltetett elrendezésben.4

ABring QPC.png
15. ábra. Aharonov-Bohm gyűrű a két ágba helyezett kvantumpöttyökkel, és a jobb oldali ág áramát érzékelő kvantum-pontkontaktussal

A forrás (S1) és nyelő (D1) elektródák között egy Aharonov-Bohm gyűrű található. A gyűrű mindkét ágában egy kvantumpöttyön keresztül haladnak az elektronok, azaz a gyűrű mindkét ágán található egy kisméretű vezető ’’sziget’’, mely kvantummechanikai alagutazással csatolódik a szomszédos vezetékdarabokhoz. Ezen kvantumpöttyök kis mérete miatt jelentős elektrosztatikus energiát kell befektetni ahhoz, hogy a szigetre további elektronokat helyezzünk el. A kvantumpöttyök potenciálja és ezen keresztül a kvantumpöttyökön található elektronok száma a G1 kapuelektróda segítségével hangolható. Az Aharonov-Bohm gyűrű mellett egy kvantum-pontkontaktus, azaz egy nagyon keskeny nanovezeték helyezkedik el az S2 forrás és D2 nyelő elektródák között. A G2 kapuelektródával a kvantumpontkontaktus szélessége olyan tartományba hangolható, ahol a vezetőképesség érzékenyen változik a kvantum-pontkontaktus szélességének a függvényében. A jobb oldali kvantumpöttyön található elektronok potenciálja kismértékben megváltoztatja a kvantum-pontkontaktus szélességét, így a kvantum-pontkontaktus vezetőképességének pontos mérésével megállapítható, hogy mikor halad át egy elektron a jobb oldali kvantumpöttyön. A kvantum-pontkontaktus áramának növelésével egyre pontosabban detektálhatjuk az Aharonov-Bohm gyűrű jobb oldali ágában haladó elektronokat, az egyre pontosabb mérés azonban koherenciavesztéshez vezet. A kísérletek valóban azt mutatják, hogy a kvantum-pontkontaktus áramának növelésével az Aharonov-Bohm oszcillációk láthatósága csökken. (A kísérleti elrendezés részletesebb megértéséhez érdemes elolvasni a kvantum-pontkontaktusokról és a kvantumpöttyökről szóló fejezeteket.)


Hivatkozások

Fent hivatkozott szakcikkek

[1] R. A. Webb, S. Washburn, C. P. Umbach, and R. B. Laibowitz: Observation of h/e Aharonov-Bohm Oscillations in Normal-Metal Rings, Phys. Rev. Lett. 54 p2696–2699 (1985)

[2] A. G. Aronov, Yu. V. Sharvin: Magnetic flux effects in disordered conductors, Rev. Mod. Phys. 59 p755–779 (1987)

[3] Ady Stern, Yakir Aharonov, Yoseph Imry: Phase uncertainty and loss of interference: A general picture, Phys. Rev. A 41p3436–3448 (1990)

[4] E. Buks, R. Schuster, M. Heiblum, D. Mahalu, V. Umansky: Dephasing in electron interference by a 'which-path' detector, Nature 391 p871-874 (1998)

Ajánlott könyvek és összefoglaló cikkek

Ajánlott kurzusok

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Interferencia_és_dekoherencia_nanoszerkezetekben&oldid=13862”