„Zajjelenségek nanoszerkezetekben” változatai közötti eltérés

A Fizipedia wikiből
(→‎Elektronok sörétzaja)
(→‎Termikus zaj)
 
(2 szerkesztő 55 közbeeső változata nincs mutatva)
1. sor: 1. sor:
−
===Az áram időbeli fluktuációja===
+
==Az áram időbeli fluktuációja==
 
<wlatex>
 
<wlatex>
−
 
+
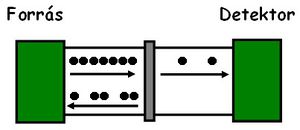
A [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Landauer-formula|korábbiakban láttuk]], hogy egy egycsatornás kvantumvezeték vezetőképessége $G=2e^2\mathcal{T}/h$, ahol $\mathcal{T}$ a vezeték közepén elhelyezett szórócentrum transzmissziós valószínűsége. Ez a vezetőképesség abból adódik, hogy a bejövő elektronhullám parciálisan transzmittálódik illetve reflektálódik. [[Interferencia és dekoherencia nanoszerkezetekben#Interferencia-kísérletek hat nagyságrenddel kisebb skálán|A fotonokkal végzett kétrés kísérlethez hasonlóan]] ha megmérjük, hogy egy elektron áthaladt vagy visszaverődött a szórócentrumon, akkor csak azt kaphatjuk, hogy vagy az egész elektron áthaladt vagy az egész elektron visszaverődött, parciális töltés transzmisszióját nem mérhetjük. Így a mért áram (ill. vezetőképesség) abból adódik, hogy az elektronok $\mathcal{T}$-ed része teljesen transzmittálódik, $\mathcal{R}=1-\mathcal{T}$-ed része pedig reflektálódik (1. ábra). Innen már rögtön látszik, hogy a véletlenszerűen transzmittálódó töltéscsomagok árama a várható érték körül fluktuálni fog.  
−
A korábbiakban láttuk, hogy egy egycsatornás kvantumvezeték vezetőképessége $G=2e^2T/h$, ahol $T$ a vezeték közepén elhelyezett szórócentrum transzmissziós valószínűsége. Ez a vezetőképesség abból adódik, hogy a bejövő elektronhullám parciálisan transzmittálódik illetve reflektálódik. [[A fotonokkal végzett kétrés kísérlethez hasonlóan]] ha megmérjük, hogy egy elektron áthaladt vagy visszaverődött a szórócentrumon, akkor csak azt kaphatjuk, hogy vagy az egész elektron áthaladt vagy az egész elektron visszaverődött, parciális töltés transzmisszióját nem mérhetjük. Így a mért áram (ill. vezetőképesség) abból adódik, hogy az elektronok $T$-ed része teljesen transzmittálódik, $1-T$-ed része pedig reflektálódik. Innen már rögtön látszik, hogy a véletlenszerűen transzmittálódó töltéscsomagok árama a várható érték körül fluktuálni fog.  
+
 
   
 
   
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Zaj_mint_jel_barrier.jpg|közép|300px|]]
+
| align="center"|[[Fájl:Zaj_mint_jel_barrier.jpg|közép|300px|]]
 
|-
 
|-
−
| align="center"|1. ábra
+
| align="center"|1. ábra. ''A bejövő elektronoknak csak egy része jut át a szórócentrumon, így az áramban zajt tapasztalunk''
 
|}
 
|}
  
  
−
Egy elektronra vonatkoztatva az áthaladt töltés $T$ valószínűséggel $e$, $1-T$ valószínűséggel pedig $0$, így várhatóértékben  
+
Egy elektronra vonatkoztatva az áthaladt töltés $\mathcal{T}$ valószínűséggel $e$, $1-\mathcal{T}$ valószínűséggel pedig $0$, így várhatóértékben  
−
$$<Q>=T\cdot e+(1-T)\cdot 0=T\cdot e,$$
+
$$\left< Q\right>=\mathcal{T}\cdot e+(1-\mathcal{T})\cdot 0=\mathcal{T}\cdot e,$$
−
azaz a Landauer formulának megfelelően az áram $T$-vel arányos. Hasonlóan kiszámolhatjuk az áthaladt töltés szórásnégyzetét:
+
azaz a [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Landauer-formula|Landauer-formulának]] megfelelően az áram $\mathcal{T}$-vel arányos. Hasonlóan kiszámolhatjuk az áthaladt töltés szórásnégyzetét:
−
$$<(\Delta Q)^2>=<Q^2>-<Q>^2=T\cdot e^2 - (T\cdot e)^2=T(1-T)e^2,$$
+
$$\left< (\Delta Q)^2\right>=\left< Q^2\right> -\left< Q\right> ^2=\mathcal{T}\cdot e^2 - (\mathcal{T}\cdot e)^2=\mathcal{T}(1-\mathcal{T})e^2,$$
−
azaz az áram szórásnégyzete $T(1-T)$-vel arányos, ami $T=0$ és $T=1$ kivételével mindig véges, azaz egy részlegesen transzmittáló nanovezeték mindig véges áramfluktuációt, véges ''zajt'' mutat.
+
azaz az áram szórásnégyzete $\mathcal{T}(1-\mathcal{T})$-vel arányos, ami $\mathcal{T}=0$ és $\mathcal{T}=1$ kivételével mindig véges, azaz egy részlegesen transzmittáló nanovezeték mindig véges áramfluktuációt, véges ''zajt'' mutat.
−
 
+
−
A zaj, azaz egy mennyiség várható érték körüli fluktuációja sok esetben lényeges többlet információt hordozhat a várható értékhez (pl. vezetőképességhez) képest, amire a későbbiekben pár egyszerű példát mutatunk. Mindenek előtt azonban definiáljuk pontosabban a ''zaj'' fogalmát.
+
  
 +
A zaj, azaz egy mennyiség várható érték körüli fluktuációja sok esetben lényeges többlet információt hordozhat a várható értékhez (pl. vezetőképességhez) képest<sup>[http://www.physicstoday.org/resource/1/phtoad/v56/i5/p37_s1 1]</sup>, amire a későbbiekben pár egyszerű példát mutatunk. Mindenek előtt azonban definiáljuk pontosabban a ''zaj'' fogalmát.
 
</wlatex>
 
</wlatex>
−
===A zaj definíciója===
+
==A zaj definíciója==
 
<wlatex>
 
<wlatex>
 +
Egy időben változó mennyiség (pl. $I(t)$ áram, lásd 2. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát, $\left<I(t)\right>$, illetve az átlagtól vett eltérést, $\Delta I=I(t)-\left<I(t)\right>$.
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Zaj_mint_jel_1.jpg|közép|400px|]]
+
| align="center"|[[Fájl:Zaj_mint_jel_1.jpg|közép|400px|]]
 
|-
 
|-
−
| align="center"|2. ábra
+
| align="center"|2. ábra. ''Az áram várható érték körüli szórása''
 
|}
 
|}
−
 
+
A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével, $\left<(\Delta I(t))^2\right>$, azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 3. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az $I(t)$ jelet egy $f_0$ középfrekvencia körüli $\Delta f$ szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző $\left<(\Delta I(t|f_0,\Delta f))^2\right>$ szórásnégyzetet mérünk.  
−
Egy időben változó mennyiség (pl. $I(t)$ áram, lásd 1. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát, $\left<I(t)\right>$, illetve az átlagtól vett eltérést, $\Delta I=I(t)-\left<I(t)\right>$. A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével, $\left<(\Delta I(t))^2\right>$, azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 2. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az $I(t)$ jelet egy $f_0$ középfrekvencia körüli $\Delta f$ szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző $\left<(\Delta I(t|f_0,\Delta f))^2\right>$ szórásnégyzetet mérünk.  
+
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Zaj_mint_jel_zajsuruseg.jpg|közép|400px|]]
+
| align="center"|[[Fájl:Zaj_mint_jel_zajsuruseg.jpg|közép|400px|]]
 
|-
 
|-
−
| align="center"|3. ábra
+
| align="center"|3. ábra. ''A zajsűrűség definíciója kísérleti megközelítésből''
 
|}
 
|}
 
Az így kapott szórásnégyzet kis $\Delta f$ esetén arányos a $\Delta f$ sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:
 
Az így kapott szórásnégyzet kis $\Delta f$ esetén arányos a $\Delta f$ sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:
44. sor: 42. sor:
 
Egy egyszerű ellenállás esetén $\Delta V=R\cdot \Delta I$, azaz $S_V=R^2\cdot S_I$.  
 
Egy egyszerű ellenállás esetén $\Delta V=R\cdot \Delta I$, azaz $S_V=R^2\cdot S_I$.  
  
−
Megmutatható, hogy az így definiált spektrális sűrűség egy kettes faktor erejéig megegyezik a $C(\tau)=<\Delta I(t)\cdot \Delta I(t+\tau)>$ áram-áram korrelációs függvény Fourier transzformáltjával,
+
Megmutatható, hogy az így definiált spektrális sűrűség egy kettes faktor erejéig megegyezik a $C(\tau)=\left< \Delta I(t)\cdot \Delta I(t+\tau)\right> $ áram-áram korrelációs függvény Fourier-transzformáltjával,
 
$$S(\omega )=2\cdot C(\omega).$$
 
$$S(\omega )=2\cdot C(\omega).$$
−
 
 
</wlatex>
 
</wlatex>
−
 
+
==''Puskalövések zaja''==
−
===''Puskalövések zaja''===
+
 
<wlatex>
 
<wlatex>
−
A zaj fogalma egy klasszikus példával is jól szemléltethető, nézzük meg hogy mi történik ha egy puskából véletlenszerűen lövöldözünk, úgy hogy a lövések időpontja egymástól teljesen független. Ha a szomszédos lövések között eltelt átlagos idő $\tau$ akkor $\Delta t$ idő alatt a lövések átlagos száma értelemszerűen $\left< N \right> =\Delta t/\tau$. A tényleges lövésszám azonban nyilvánvalóan fluktuálni fog az átlagérték körül. A szórásnégyzet meghatározásához érdemes kiszámolni a $P_N(\Delta t)$ valószínűséget, azaz annak a valószínűségét, hogy $\Delta t$ idő alatt $N$ lövés dördül. Ha $P_N(\Delta t)$ értékét ismerjük, akkor $P_N(\Delta t+dt)$ értéke a
+
A zaj fogalma egy klasszikus példával is jól szemléltethető, nézzük meg hogy mi történik ha egy puskából véletlenszerűen lövöldözünk, úgy hogy a lövések időpontja egymástól teljesen független. Ha a szomszédos lövések között eltelt átlagos idő $\tau$ akkor $\Delta t$ idő alatt a lövések átlagos száma értelemszerűen $\left< N \right> =\Delta t/\tau$. A tényleges lövésszám azonban fluktuálni fog az átlagérték körül. A szórásnégyzet meghatározásához érdemes kiszámolni a $P_N(\Delta t)$ valószínűséget, azaz annak a valószínűségét, hogy $\Delta t$ idő alatt $N$ lövés dördül. Ha $P_N(\Delta t)$ értékét ismerjük, akkor $P_N(\Delta t+dt)$ értéke a
 
$$P_N(\Delta t+dt)=P_{N-1}(\Delta t)\frac{dt}{\tau}+P_N(\Delta t)\left(1-\frac{dt}{\tau}\right)$$
 
$$P_N(\Delta t+dt)=P_{N-1}(\Delta t)\frac{dt}{\tau}+P_N(\Delta t)\left(1-\frac{dt}{\tau}\right)$$
 
egyenlettel írható fel, azaz a kezdeti $\Delta t$ és az utána következő $dt<<\tau$ idő alatt vagy $N-1$ ill. $1$ vagy $N$ ill. $0$ lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze.
 
egyenlettel írható fel, azaz a kezdeti $\Delta t$ és az utána következő $dt<<\tau$ idő alatt vagy $N-1$ ill. $1$ vagy $N$ ill. $0$ lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze.
58. sor: 54. sor:
 
differenciálegyenletet kapjuk. Megmutatható, hogy ezen feltételt a  
 
differenciálegyenletet kapjuk. Megmutatható, hogy ezen feltételt a  
 
$$P_N(\Delta t)=\frac{(\Delta t)^N}{\tau^N N!}e^{-\Delta t/\tau}$$
 
$$P_N(\Delta t)=\frac{(\Delta t)^N}{\tau^N N!}e^{-\Delta t/\tau}$$
−
Poisson eloszlás elégíti ki. A Poisson eloszlás speciális tulajdonsága, hogy a szórásnégyzet megegyezik a várható értékkel, azaz
+
Poisson-eloszlás elégíti ki. A Poisson-eloszlás speciális tulajdonsága, hogy a szórásnégyzet megegyezik a várható értékkel, azaz
 
$$\left< (\Delta N)^2 \right>=\left< N \right>=\frac{\Delta t}{\tau}.$$
 
$$\left< (\Delta N)^2 \right>=\left< N \right>=\frac{\Delta t}{\tau}.$$
 
</wlatex>
 
</wlatex>
−
===Elektronok sörétzaja===
+
==Elektronok sörétzaja==
 
<wlatex>
 
<wlatex>
−
A fenti gondolatmenetet vonatkoztathatjuk elektronokra is ha teljesül az, hogy az elektronok véletlenszerűen, egymástól függetlenül jutnak át az egyik elektródából a másikba. Tegyük fel, hogy mérőrendszerünkkel az elektromos áramot $\Delta t$ időbeli felbontással tudjuk mérni. Egy $\Delta t$ szélességű mintavételezési intervallum alatt $I=Ne/\Delta t$ áramot detektálunk ahol a $\Delta t$ idő alatt áthaladó eletronok $N$ számának eloszlását a fenti Poisson eloszlás adja meg. Így a mért áram várható értéke $\left< I \right>=\left< N \right>e/\Delta t$, míg az áram szórásnégyzete $\left< (\Delta I)^2 \right>=\left< (\Delta N)^2 \right>e^2/(\Delta t)^2=\left< N \right>e^2/(\Delta t)^2=\left< I \right>e/\Delta t$.  
+
A fenti gondolatmenetet vonatkoztathatjuk elektronokra is ha teljesül az, hogy az elektronok véletlenszerűen, egymástól függetlenül jutnak át az egyik elektródából a másikba. Tegyük fel, hogy mérőrendszerünkkel az elektromos áramot $\Delta t$ időbeli felbontással tudjuk mérni. Egy $\Delta t$ szélességű mintavételezési intervallum alatt $I=Ne/\Delta t$ áramot detektálunk ahol a $\Delta t$ idő alatt áthaladó elektronok $N$ számának eloszlását a fenti Poisson-eloszlás adja meg. Így a mért áram várható értéke $\left< I \right>=\left< N \right>e/\Delta t$, míg az áram szórásnégyzete $\left< (\Delta I)^2 \right>=\left< (\Delta N)^2 \right>e^2/(\Delta t)^2=\left< N \right>e^2/(\Delta t)^2=\left< I \right>e/\Delta t$.  
 
A [http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem Nyquist - Shannon mintavételezési törvény] szerint $\Delta t$ időfelbontás esetén a mért jelet $f_{\mathrm{max}}=1/2\Delta t$ maximális frekvenciáig tudjuk rekonstruálni. Ez alapján a mért áram szórásnégyzete:  
 
A [http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem Nyquist - Shannon mintavételezési törvény] szerint $\Delta t$ időfelbontás esetén a mért jelet $f_{\mathrm{max}}=1/2\Delta t$ maximális frekvenciáig tudjuk rekonstruálni. Ez alapján a mért áram szórásnégyzete:  
 
$$\left< I \right>e/\Delta t=\left< (\Delta I)^2 \right>=\int\limits_0^{1/2\Delta t}S_I(f)df.$$
 
$$\left< I \right>e/\Delta t=\left< (\Delta I)^2 \right>=\int\limits_0^{1/2\Delta t}S_I(f)df.$$
70. sor: 66. sor:
 
zajsűrűséggel.
 
zajsűrűséggel.
  
−
A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt ''sörétzajnak'' szokták nevezni. Fontos megemlíteni, hogy a fenti képlet alapján a sörétzaj fehér zaj, azaz a spektrális sűrűség frekvenciafüggetlen. Az előbbiekben levezetett zajformula a sörétzajnak is egyik speciális esetét írja le, az ún. Poisson zajt, mely egymástól független elektronok detektálására vonatkozik. A kvantummechanikából ismert Pauli elv szerint két elektron nem lehet ugyan abban az állapotban, azaz egy adott időpontban nem tudunk két teljesen egyforma állapotú elektront detektálni. Egy makroszkópikus vezetőben az elektronok nem egymástól függetlenül, hanem inkább ''sorban egymást követve'' érkeznek az árammérőhöz, így a fenti zajformula nem érvényes. Azonban a Poisson zaj feltételét megvalósíthatjuk akkor, ha az elektronok útjába egy olyan akadályt helyezünk, melyen véletlenszerűen az elektronoknak csak egy kis része tud keresztüljutni (3a. ábra).  
+
A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt ''sörétzajnak'' szokták nevezni. Az előbbiekben levezetett zajformula a sörétzajnak is egyik speciális esetét írja le, az ún. Poisson-zajt, mely egymástól független elektronok detektálására vonatkozik. A kvantummechanikából ismert Pauli-elv szerint két elektron nem lehet ugyanabban az állapotban, azaz egy adott időpontban nem tudunk két teljesen egyforma állapotú elektront detektálni. Egy makroszkopikus vezetőben az elektronok nem egymástól függetlenül, hanem inkább ''sorban egymást követve'' érkeznek az árammérőhöz, így a fenti zajformula nem érvényes. Azonban a Poisson-zaj feltételét megvalósíthatjuk akkor, ha az elektronok kis valószínűséggel emittálódnak egy forrásból.
  
−
Az első sörétzaj-mérést Walter Schottky végezte 1918-ban [2]: híres kísérletében egy vákuumdióda anódáramának zaját vizsgálta. A vákuumdióda felépítését a 3b. ábra szemlélteti. Egy fűtött katódból véletlenszerűen kilépő elektronok a katód és anód közé kapcsolt feszültség hatására eljutnak az anódba, ahol áramot detektálunk. A vákuumdióda ideális eszköz a sörétzaj tanulmányozásához, hiszen az elektronok valóban véletlenül, és egymástól függetlenül emittálódnak, így a mért zajsűrűség és az áram hányadosából az elektrontöltés a Poisson zaj formulája alapján meghatározható.
+
Az első sörétzaj-mérést Walter Schottky végezte 1918-ban:<sup>[http://onlinelibrary.wiley.com/doi/10.1002/andp.19183622304/abstract 2]</sup> híres kísérletében egy vákuumdióda anódáramának zaját vizsgálta. A vákuumdióda felépítését a 4. ábra szemlélteti. Egy fűtött katódból véletlenszerűen kilépő elektronok a katód és anód közé kapcsolt feszültség hatására eljutnak az anódba, ahol áramot detektálunk. A vákuumdióda ideális eszköz a sörétzaj tanulmányozásához, hiszen az elektronok valóban véletlenül, és egymástól függetlenül emittálódnak, így a mért zajsűrűség és az áram hányadosából az elektrontöltés a Poisson-zaj formulája alapján meghatározható.
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Zaj_mint_jel_barrier.jpg|közép|300px|]]
+
| align="center"|[[Fájl:Zaj_mint_jel_vakuumdioda.png|közép|550px|]]
−
| [[Fájl:Zaj_mint_jel_vakuumdioda.png|közép|400px|]]
+
 
|-
 
|-
−
| align="center"|3a. ábra
+
| align="center"|4. ábra. ''Vákuumdióda''
−
| align="center"|3b. ábra
+
 
|}
 
|}
  
−
Poisson zajt modern elektronikai eszközökben is tapasztalhatunk, például egy diódát alkotó félvezető p-n átmenet is biztosítja az elektronok véletlen és független emisszióját megfelelően kicsi áram esetén.  
+
Poisson-zajt modern elektronikai eszközökben is tapasztalhatunk, például egy diódát alkotó félvezető p-n átmenet is biztosítja az elektronok véletlen és független emisszióját megfelelően kicsi áram esetén. Ennek megfelelően az elektrontöltés értéke egy félvezető dióda zajának méréséből is meghatározható, amit a BME fizikus hallgatói [[a zaj mint jel]] című laborgyakorlat során ki is próbálhatnak.
−
</wlatex>
+
  
−
===Termikus zaj===
+
Poisson-zajt az 1. ábrán szemléltetett nanovezetékben is megvalósíthatunk ha a két kvantumvezetéket összekötő szórócentrum $\mathcal{T}\ll 1$ transzmissziós valószínűséggel rendelkezik. Ekkor [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Landauer-formula|az egycsatornás vezetékre vonatkozó Landauer formula alapján]] $I=2e^2\cdot \mathcal{T}\cdot V/h$, azaz a zajsűrűség:
 +
$$S_I=\frac{4e^2}{h}\cdot \mathcal{T} \cdot V.$$
 +
Láttuk, hogy tetszőleges $\mathcal{T}$ esetén a zaj $\mathcal{T}(1-\mathcal{T})$-vel skálázódik. Az ennek megfelelő a zajsűrűség
 +
$$S_I=\frac{4e^2}{h}\cdot \mathcal{T}(1-\mathcal{T}) \cdot V,$$
 +
mely $\mathcal{T}\ll 1$ esetben visszaadja a Poisson-zaj formuláját.
 +
[[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Landauer-formula|Több vezetési csatornával rendelkező nanovezeték esetén]] a zajformula általánosan
 +
$$S_I=\frac{4e^2}{h}\cdot V \sum_n \mathcal{T}_n(1-\mathcal{T}_n)$$
 +
képlettel adható meg, ahol $\mathcal{T}_n$ a ''sajátcsatornák'' transzmissziós együtthatói.
 +
</wlatex>
 +
==Termikus zaj==
 
<wlatex>
 
<wlatex>
−
Az előbbiekben bemutatott sörétzaj egy nemegyensúlyi zaj, melyet csak akkor tapasztalunk, ha a vizsgált áramköri elemen áramot folyatunk keresztül. Zajt azonban egyensúlyi állapotban is tapasztalhatunk pusztán az elektronok termikus fluktuációi miatt.  
+
Az előbbi képlet egy nanovezeték sörétzaját adta meg véges feszültség esetén. A formula alapján zérus zajsűrűséget kapunk $V=0$ feszültségnél, illetve akkor is ha minden nyitott vezetési csatornára $\mathcal{T}_n=1$, azaz ha a nanovezeték tökéletes (szórásmentes).  
 +
A fenti formula azonban nem vette figyelembe a hőmérsékleti fluktuációk hatását, hiszen véges hőmérsékleten zérus feszültség és tökéletes nanovezeték esetén is véges zajt várunk.
  
−
A termikus zaj jelenségét vizsgáljuk meg egy ideális kvantumvezetékben (lásd ?? fejezet), melyben az elektronállapotokat egydimenziós
+
Egyelőre a részletek ismerete nélkül vizsgáljunk egyetlen elektronállapotot. Az állapot tényleges betöltöttségét jelöljük $n_i$-vel, mely betöltött állapot esetén 1 betöltetlen állapot esetén 0 értéket vesz fel. Az állapot átlagos betöltöttségét termikus egyensúly esetén a Fermi-függvény írja le, azaz:
−
parabolikus diszperziós relációk írják le. Először vizsgáljuk a zajt egyetlen vezetési csatorna esetén. Egy adott hullámszámhoz tartozó elektronok árama:
+
$$\left< n_i \right>=f(\varepsilon_i)=\frac{1}{e^\frac{\varepsilon_i-\mu}{kT}+1}.$$
 +
Figyelembe véve hogy $n=1$ és $n=0$ esetén is $n^2=n$, így könnyen megadhatjuk a betöltési szám szórásnégyzetét is:
 +
$$\left< (n_i-\left< n_i \right> )^2 \right>=\left< n_i \right> - \left< n_i \right>^2 =f(\varepsilon_i)\left( 1-f(\varepsilon_i)\right) .$$
 +
Könnyen ellenőrizhető, hogy:
 +
$$f(\varepsilon_i)\left( 1-f(\varepsilon_i)\right)=-kT\frac{\mathrm{d}f(\varepsilon_i)}{\mathrm{d}\varepsilon},$$
 +
melyet energia szerint integrálva $kT$-t kapunk, azaz várakozásaink szerint a termikus fluktuációkból származó zaj a hőmérséklettel arányos.
 +
 
 +
Most vizsgáljuk meg egy konkrét rendszer, egy [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Landauer-formula|egycsatornás tökéletes nanovezeték]] ''termikus zaját''!
 +
A nanovezetékben az elektronállapotokat egydimenziós parabolikus diszperziós relációk írják le, a $k>0$ állapotok mind a bal oldali a $k<0$ állapotok pedig mind a jobb oldali elektródából származnak. Zérus feszültség esetén tetszőleges $k$-val rendelkező állapot betöltöttségét a Fermi-függvény írja le $\mu=\mu_L=\mu_R$ kémiai potenciállal.
 +
Egy adott hullámszámhoz tartozó elektronok árama:
 
$$I_k=\frac{2e}{L}\cdot v_k \cdot n_k,$$
 
$$I_k=\frac{2e}{L}\cdot v_k \cdot n_k,$$
−
ahol $n_k=1$ ha az állapot betöltött és $n_k=0$ ha az állapot betöltetlen. Az áram várható értéke:
+
ahol $n_k=1$ ha az állapot betöltött és $n_k=0$ ha az állapot betöltetlen.  
−
$$\left< I_k \right> =\frac{2e}{L}\cdot v_k \cdot f(\epsilon_k),$$
+
A betöltési szám fent kiszámolt szórásnégyzete alapján az áram szórásnégyzete:
−
ahol $f(\epsilon_k)=\left< n_k \right>$ a jobb és a bal oldali elektróda elektronállapotainak energia szerinti eloszlását adja meg véges hőmérsékleten, de zérus feszültség esetén.
+
$$\left< (\Delta I_k)^2 \right> =-kT\cdot \frac{4e^2}{L^2}\cdot v^2_k \cdot \frac{\mathrm{d}f(\varepsilon_k)}{\mathrm{d}\varepsilon_k}.$$
−
Az áram négyzetének várható értéke:
+
−
$$\left< I^2_k \right> =\frac{4e^2}{L^2}\cdot v^2_k \cdot \left< n^2_k \right>=\frac{4e^2}{L^2}\cdot v^2_k \cdot \left< n_k \right>=\frac{4e^2}{L^2}\cdot v^2_k \cdot f(\epsilon_k),$$
+
−
ahol kihasználtuk hogy $n_k$ akár 0 akár 1 értéket vesz fel $n^2_k=k_k$. Így az áram szórásnégyzete:
+
−
$$\left< (\Delta I_k)^2 \right> =\left< I_k^2 \right> -\left< I_k \right> ^2=\frac{4e^2}{L^2}\cdot v^2_k \cdot f(\epsilon_k)\cdot (1-f(\epsilon_k)).$$
+
 
Mivel a különböző $k$-hoz tartozó áramkomponensek egymástól függetlenek (nincs átszóródás) így szórásnégyzetük összeadódik, azaz a teljes áram szórásnégyzete:
 
Mivel a különböző $k$-hoz tartozó áramkomponensek egymástól függetlenek (nincs átszóródás) így szórásnégyzetük összeadódik, azaz a teljes áram szórásnégyzete:
−
$$\left< (\Delta I)^2 \right>=\frac{4e^2}{L^2} \sum_k v^2_k \cdot f(\epsilon_k)\cdot (1-f(\epsilon_k))=\frac{4e^2}{L^2}\frac{L}{2\pi } \int\limits_{-k_F}^{+k_F} \mathrm{d}k v^2_k \cdot f(\epsilon_k)\cdot (1-f(\epsilon_k))=2 \cdot \frac{4e^2}{L^2}\frac{L}{2\pi }  \int\limits_{0}^{+k_F} \mathrm{d}k v^2_k \cdot f(\epsilon_k)\cdot (1-f(\epsilon_k)).$$
+
$$\left< (\Delta I)^2 \right>=-kT\cdot \frac{4e^2}{L^2} \sum_k v^2_k \frac{\mathrm{d}f(\varepsilon_k)}{\mathrm{d}\varepsilon_k}=-kT\cdot \frac{4e^2}{L^2}\frac{L}{2\pi } \int\limits_{-\infty}^{+\infty} v^2_k \frac{\mathrm{d}f(\varepsilon_k)}{\mathrm{d}\varepsilon_k}\mathrm{d}k=-2kT \cdot \frac{4e^2}{L^2}\frac{L}{2\pi }  \int\limits_{0}^{+\infty} v^2_k \frac{\mathrm{d}f(\varepsilon_k)}{\mathrm{d}\varepsilon_k} \mathrm{d}k.$$
−
Kihasználva, hogy $\mathrm{d}k \cdot v_k=\mathrm{d}\epsilon /\hbar$, illetve hogy $f(\epsilon_k)\cdot (1-f(\epsilon_k))=-kT\mathrm{d}f(\epsilon_k)/\mathrm{d} \epsilon$ az áram szórásnégyzete:
+
Kihasználva, hogy $\mathrm{d}k \cdot v_k=\mathrm{d}\varepsilon /\hbar$ áttérhetünk energia szerinti integrálásra:
−
$$\left< (\Delta I)^2 \right>=-\frac{8e^2kT}{hL}\frac{L}{2\pi }\cdot  \int\limits_{\epsilon(k=0)}^{\epsilon_F} \mathrm{d}\epsilon v_k \cdot \frac{\mathrm{d}f}{\mathrm{d}\epsilon}\approx 4kT\cdot G_0 \cdot \frac{v_F}{L},$$
+
$$\left< (\Delta I)^2 \right>=-\frac{8e^2kT}{\hbar L}\frac{1}{2\pi }\cdot  \int\limits_{\varepsilon(k=0)}^{+\infty} v_k \frac{\mathrm{d}f}{\mathrm{d}\varepsilon}\mathrm{d}\varepsilon \approx 4kT\cdot G_0 \cdot \frac{v_F}{L}=\int\limits_{0}^{f_\mathrm{max}\approx \frac{v_F}{L}} S_I df,$$
−
ahol kihasználtuk, fogy a Fermi függvény deriváltja csak a Fermi energia körül véges, ahol a $v_k$ sebesség $v_F$-el közelíthető, illetve hogy az egycsatornás kvantumvezeték vezetőképessége $G_0=2e^2/h$.
+
ahol figyelembe vettük, fogy a Fermi-függvény deriváltja csak a Fermi-energia körül véges, ahol a $v_k$ sebesség $v_F$-el közelíthető, illetve hogy az egycsatornás kvantumvezeték vezetőképessége $G_0=2e^2/h$.
 +
 
 +
Az $L$ hosszúságú kvantumvezetéken $t=L/v_F$ idő alatt érnek át az elektronok, így ennél rövidebb időskálán nem látunk fluktuációt az áramban. Ennek megfelelően a termikus zaj jelentkezését $f_\mathrm{max}=v_F/L$ határfrekvenciáig várjuk. A határfrekvenciáig frekvenciafüggetlen zajsűrűséget feltételezve $S_I=4kT \cdot G_0$ zajsűrűséget kapunk. Több vezetési csatornát feltételezve (melyek ideális kvantumvezetékben egymástól függetlenek) a zajsűrűség $S_I=4kT \cdot MG_0=4kT \cdot G.$
  
−
Az $L$ hosszúságú kvantumvezetéken $t=L/v_F$ idő alatt érnek át az elektronok, így ennél rövidebb időskálán nem látunk fluktuációt az áramban. Ennek megfelelően a termikus zaj jelentkezését $f_\mathrm{max}=v_F/L$ határfrekvenciáig várjuk. A határfrekvenciáig frekvenciafüggetlen zajsűrűséget feltételezve a zajsűrűségre:
 
−
$$S_I=4kT \cdot G_0$$
 
−
zajsűrűséget kapunk. Több vezetési csatornát feltételezve (melyek ideális kvantumvezetékben egymástól függetlenek) a zajsűrűség:
 
−
$S_I=4kT \cdot MG_0=4kT \cdot G.$
 
 
Részletesebb számolások alapján megmutatható, hogy nemcsak  ideális kvantumvezeték esetén hanem tetszőleges vezetékre az áramzaj a vezetőképességgel illetve a hőmérséklettel arányosan skálázódik:
 
Részletesebb számolások alapján megmutatható, hogy nemcsak  ideális kvantumvezeték esetén hanem tetszőleges vezetékre az áramzaj a vezetőképességgel illetve a hőmérséklettel arányosan skálázódik:
 
$$S_I=4kT \cdot G,$$
 
$$S_I=4kT \cdot G,$$
 
és hasonlóképpen egy $R$ ellenállású áramköri elem feszültségzaja:
 
és hasonlóképpen egy $R$ ellenállású áramköri elem feszültségzaja:
−
$$S_V=4k_B T\cdot R.$$
+
$$S_V=4kT\cdot R$$
 +
attól függetlenül, hogy pontosan milyen fizikai rendszer adja az $R$ ellenállást. Ezt mondja ki a fluktuáció-disszipáció tétel is, mely egy fizikai rendszer egyensúlyi fluktuációja (jelen esetben zaj) és nemegyensúlyi lineáris válaszfüggvénye (jelen esetben ellenállás ill. vezetőképesség) között teremt kapcsolatot.
  
−
 
−
feszültségzaj-sűrűséget mérhetünk attól függetlenül, hogy pontosan milyen fizikai rendszer adja az $R$ ellenállást.
 
 
A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától.
 
A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától.
−
Ezen jelenség segítségével a $T$ hőmérséklet és az $R$ ellenállás ismeretében a feszültségzaj méréséből a Boltzmann-állandó meghatározható.
+
Ezen jelenség segítségével a $T$ hőmérséklet és az $R$ ellenállás ismeretében a feszültségzaj méréséből a Boltzmann-állandó meghatározható, melyre szintén lehetőség nyílik [[a zaj mint jel]] hallgatói mérés keretében.
 
</wlatex>
 
</wlatex>
  
−
===Egyéb zajforrások===
+
==Általános zajformula==
 +
<wlatex>
 +
Megmutatható, hogy egy nanovezeték áramzajának sűrűsége tetszőleges feszültségnél és hőmérsékleten:
 +
$$S_I=\frac{4e^2}{h}\left[ 2kT\sum_n \mathcal{T}_n^2+eV\coth{\left(\frac{eV}{2kT}\right)}\sum_n \mathcal{T}_n(1-\mathcal{T}_n)\right],$$
 +
Ahol a $\mathcal{T}_n$ transzmissziós együtthatók a [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Landauer-formula|sajátcsatornákhoz tartozó átmeneti valószínűségek]].
 +
 
 +
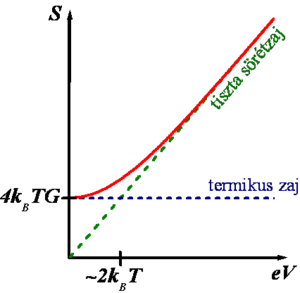
Az 5. ábra szemlélteti az átmenetet a zérus feszültségnél tapasztalható termikus zaj, illetve a magas ($eV\gg kT$) feszültségnél jelentkező, feszültséggel lineárisan változó sörétzaj között.
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| align="center"|[[Fájl:Zajformula.png|közép|300px|]]
 +
|-
 +
| align="center"|5. ábra. ''Zajsűrűség a feszültség függvényében: átmenet a termikus zaj és a tiszta sörétzaj között''
 +
|}
 +
Érdemes megjegyezni, hogy sörétzaj csak nanovezetékekben látszik, makroszkopikus áramköri elemeknél csak akkor tapasztalunk sörétzajt, ha az elektronok egy kis transzmissziós valószínűségű határátmeneten haladnak át (pl. félvezető dióda).
 +
 
 +
A sörétzaj értéke (azaz a 7. ábrán szemléltetett egyenes meredeksége) egy adott vezetőképességű nanovezetéknél akkor a legnagyobb, ha az összes csatorna transzmissziós együtthatója nagyon kicsi, $\mathcal{T}_n \ll 1$, azaz ha Poisson-zajt látunk. Ennek megfelelően a zajsűrűséget gyakran szokták az $F \le 1$ Fano-faktorral jellemezni, mely az adott vezetőképességű nanovezeték zajsűrűségének, és az ugyanolyan vezetőképességhez tartozó Poisson-zajnak az aránya.
 +
</wlatex>
 +
==Egyéb zajforrások==
 
<wlatex>
 
<wlatex>
 
A termikus zaj és a sörétzaj mellett érdemes megemlékezni az 1/f zajról, mely a zajsűrűség tipikus 1/f jellegű frekvenciafüggéséről kapta a nevét. Ezen zajtípus számos fizikai folyamatból származhat, például a szennyezők és rácshibák véletlen mozgásából adódó ellenállásfluktuációkból. Az 1/f zaj a sörétzajhoz hasonlóan nemegyensúlyi zaj, a spektrális sűrűség a feszültség növelésével nő. Az 1/f zaj tipikusan alacsonyfrekvenciás ($<100-1000 \mathrm{Hz}$) méréseknél dominál, míg magasabb frekvenciákon a termikus zaj illetve bizonyos eszközökben a sörétzaj a legfontosabb zajforrás.
 
A termikus zaj és a sörétzaj mellett érdemes megemlékezni az 1/f zajról, mely a zajsűrűség tipikus 1/f jellegű frekvenciafüggéséről kapta a nevét. Ezen zajtípus számos fizikai folyamatból származhat, például a szennyezők és rácshibák véletlen mozgásából adódó ellenállásfluktuációkból. Az 1/f zaj a sörétzajhoz hasonlóan nemegyensúlyi zaj, a spektrális sűrűség a feszültség növelésével nő. Az 1/f zaj tipikusan alacsonyfrekvenciás ($<100-1000 \mathrm{Hz}$) méréseknél dominál, míg magasabb frekvenciákon a termikus zaj illetve bizonyos eszközökben a sörétzaj a legfontosabb zajforrás.
130. sor: 152. sor:
 
==Kitekintés==
 
==Kitekintés==
 
<wlatex>
 
<wlatex>
−
Kutató laboratóriumokban azonban a zajmérést gyakran olyan területen alkalmazzák, ahol más mérési módszer csak korlátozottan, vagy egyáltalán nem áll rendelkezésre [1]. A következőkben ilyen mérésekből adunk rövid ízelítőt.
+
Kutató laboratóriumokban a zajmérést gyakran olyan területen alkalmazzák, ahol más mérési módszer csak korlátozottan, vagy egyáltalán nem áll rendelkezésre.<sup>[http://www.physicstoday.org/resource/1/phtoad/v56/i5/p37_s1 1]</sup> A következőkben ilyen mérésekből adunk rövid ízelítőt.
  
−
*A pontos hőmérsékletmérés - különösen extrém körülmények között - sokszor nehézséget jelent, hiszen számos fizikai folyamat (pl. fémek ellenállásváltozása, higanyszál megnyúlása) alkalmas a hőmérsékletváltozás detektálásra, azonban ezek a hőmérők az ''abszolút hőmérséklet'' mérésére csak pontos kalibráció után alkalmasak. Ezzel szemben a zajmérés segítségével közvetlenül az abszolút hőmérsékletet lehet meghatározni [3], így zajmérés megfelelő (a laborgyakorlat mérésénél lényegesn nagyobb) pontosság esetén akár hőmérsékletstandardként is használható.
+
*A pontos hőmérsékletmérés - különösen extrém körülmények között - sokszor nehézséget jelent, hiszen számos fizikai folyamat (pl. fémek ellenállásváltozása, higanyszál megnyúlása) alkalmas a hőmérsékletváltozás detektálásra, azonban ezek a hőmérők az ''abszolút hőmérséklet'' mérésére csak pontos kalibráció után alkalmasak. Ezzel szemben a zajmérés segítségével közvetlenül az abszolút hőmérsékletet lehet meghatározni,<sup>[http://www.sciencemag.org/content/300/5627/1929.short 3]</sup>, így zajmérés megfelelő pontosság esetén akár hőmérsékletstandardként is használható.
  
−
*Az elektron töltését jól ismerjük, azonban számos olyan rendszer ismert ahol a ''kvázirészecskék'' az elektrontöltés többszörösét vagy tört részét hordozzák. Ezen rendszereknél a zajmérés kiválóan alkalmas a kvázirészecske-töltés meghatározására [4,5].
+
*Az elektron töltését jól ismerjük, azonban számos olyan rendszer ismert ahol a ''kvázirészecskék'' az elektrontöltés többszörösét vagy tört részét hordozzák (pl. szupravezetés, tört számú kvantált Hall jelenség). Ezen rendszereknél a zajmérés kiválóan alkalmas a kvázirészecske-töltés meghatározására.<sup>[http://www.nature.com/nature/journal/v405/n6782/abs/405050a0.html 4],[http://www.nature.com/nature/journal/v389/n6647/abs/389162a0.html 5]</sup>
  
−
*Az elemi részecskék speciális statisztikákat követnek. Az elektronok például ''fermionként'' viselkednek, és a Pauli elv miatt két elektron nem lehet azonos kvantummechanikai állapotban, ezzel szemben a fotonok ''bosonként'' viselkednek, és szeretnek olyan állapotba szóródni amiben már több foton is található (lásd indukált emisszió a lézerekben). Ezen különbségek zajméréssel kiválóan kimutathatók, hiszen megfelelően megválasztott rendszerekben a fermionok a Poisson zajnál kisebb, míg a bosonok a Poisson zajnál nagyobb zajt mutatnak [6-8].
+
*Az elemi részecskék speciális statisztikákat követnek. Az elektronok például ''fermionként'' viselkednek, és a Pauli elv miatt két elektron nem lehet azonos kvantummechanikai állapotban, ezzel szemben a fotonok ''bozonként'' viselkednek, és szeretnek olyan állapotba szóródni amiben már több foton is található (lásd indukált emisszió a lézerekben). Ezen különbségek zajméréssel kiválóan kimutathatók, hiszen megfelelően megválasztott rendszerekben a fermionok a Poisson zajnál kisebb, míg a bozonok a Poisson zajnál nagyobb zajt mutatnak.<sup>[http://www.nature.com/nature/journal/v178/n4541/abs/1781046a0.html 6],[http://www.sciencemag.org/content/284/5412/299.abstract 7],[http://www.sciencemag.org/content/284/5412/296.abstract 8]</sup>
  
−
*A klasszikus és kvantumos kaotikus rendszerek jelentősen különböznek egymástól. A klasszikus káosz esetén ugyan a rendszer viselkedése érzékenyen függ a kezdeti feltételektől azonban mégis teljesen determinisztikus mozgást kapunk. Ezzel szemben kvantumkáosz esetén a részecskék viselkedése alapvetően véletlenszerű. A klasszikus és a kvantumkáosz közötti átmenet jól megmutatható zajmérésekkel, hiszen az előbbi esetben zérus, míg az utóbbiban véges sörétzajt várunk [9].
+
*A klasszikus és kvantumos kaotikus rendszerek jelentősen különböznek egymástól. A klasszikus káosz esetén ugyan a rendszer viselkedése érzékenyen függ a kezdeti feltételektől azonban mégis teljesen determinisztikus mozgást kapunk. Ezzel szemben kvantumkáosz esetén a részecskék viselkedése alapvetően véletlenszerű. A klasszikus és a kvantumkáosz közötti átmenet jól megmutatható zajmérésekkel, hiszen az előbbi esetben zérus, míg az utóbbiban véges sörétzajt várunk.<sup>[http://www.nature.com/nature/journal/v415/n6873/abs/415765a.html 9]</sup>
  
 
Zajmérésekkel részletesebben az [[Új kísérletek a nanofizikában]] tárgy keretében ismerkedhetünk meg.
 
Zajmérésekkel részletesebben az [[Új kísérletek a nanofizikában]] tárgy keretében ismerkedhetünk meg.
−
<wlatex>
+
</wlatex>
 
==Hivatkozások==
 
==Hivatkozások==
 +
 +
===Fent hivatkozott szakcikkek===
 
[1] [http://www.physicstoday.org/resource/1/phtoad/v56/i5/p37_s1 C. W. J. Beenakker, C. Schönenberger: ''Quantum shot noise'', '''Physics Today 56''', p37 (2003)]
 
[1] [http://www.physicstoday.org/resource/1/phtoad/v56/i5/p37_s1 C. W. J. Beenakker, C. Schönenberger: ''Quantum shot noise'', '''Physics Today 56''', p37 (2003)]
  
160. sor: 184. sor:
  
 
[9] [http://www.nature.com/nature/journal/v415/n6873/abs/415765a.html S. Oberholzer et al.: ''Crossover between classical and quantum shot noise in chaotic cavities'', '''Nature 415''', p765 (2002)]
 
[9] [http://www.nature.com/nature/journal/v415/n6873/abs/415765a.html S. Oberholzer et al.: ''Crossover between classical and quantum shot noise in chaotic cavities'', '''Nature 415''', p765 (2002)]
 +
 +
===Ajánlott könyvek és összefoglaló cikkek===
 +
*[http://dx.doi.org/10.1016/S0370-1573(99)00123-4 Ya. M. Blanter, M. Büttiker: ''Shot noise in mesoscopic conductors'' '''Physics Reports 336''' p1-166 (2000)]
 +
*[http://arxiv.org/abs/cond-mat/9611140 M. J. M. de Jong, C. W. J. Beenakker: ''Shot noise in mesoscopic systems'' (arXiv)]
 +
*[http://www.cambridge.org/us/academic/subjects/physics/condensed-matter-physics-nanoscience-and-mesoscopic-physics/electronic-noise-and-fluctuations-solids Sh. Kogan: ''Electronic noise and fluctuations in solids'' Cambridge University Press (1996)]
 +
 +
===Ajánlott kurzusok===
 +
*[[Új kísérletek a nanofizikában|''Új kísérletek a nanofizikában'', Halbritter András és Csonka Szabolcs, BME Fizika Tanszék]]
 +
*[http://www.phy.bme.hu/~zarand/mezoszkopia.html ''Mezoszkopikus rendszerek fizikája'', Zaránd Gergely, BME Elméleti Fizika Tanszék]

A lap jelenlegi, 2014. február 27., 22:54-kori változata

Tartalomjegyzék

Az áram időbeli fluktuációja


A korábbiakban láttuk, hogy egy egycsatornás kvantumvezeték vezetőképessége 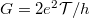\setbox0\hbox{$G=2e^2\mathcal{T}/h$}% \message{//depth:\the\dp0//}% \box0%, ahol \setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% a vezeték közepén elhelyezett szórócentrum transzmissziós valószínűsége. Ez a vezetőképesség abból adódik, hogy a bejövő elektronhullám parciálisan transzmittálódik illetve reflektálódik. A fotonokkal végzett kétrés kísérlethez hasonlóan ha megmérjük, hogy egy elektron áthaladt vagy visszaverődött a szórócentrumon, akkor csak azt kaphatjuk, hogy vagy az egész elektron áthaladt vagy az egész elektron visszaverődött, parciális töltés transzmisszióját nem mérhetjük. Így a mért áram (ill. 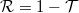vezetőképesség) abból adódik, hogy az elektronok \setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0%-ed része teljesen transzmittálódik, \setbox0\hbox{$\mathcal{R}=1-\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0%-ed része pedig reflektálódik (1. ábra). Innen már rögtön látszik, hogy a véletlenszerűen transzmittálódó töltéscsomagok árama a várható érték körül fluktuálni fog.

Zaj mint jel barrier.jpg
1. ábra. A bejövő elektronoknak csak egy része jut át a szórócentrumon, így az áramban zajt tapasztalunk


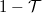Egy elektronra vonatkoztatva az áthaladt töltés \setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% valószínűséggel \setbox0\hbox{$e$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$1-\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% valószínűséggel pedig \setbox0\hbox{$0$}% \message{//depth:\the\dp0//}% \box0%, így várhatóértékben

\[\left< Q\right>=\mathcal{T}\cdot e+(1-\mathcal{T})\cdot 0=\mathcal{T}\cdot e,\]

azaz a Landauer-formulának megfelelően az áram \setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0%-vel arányos. Hasonlóan kiszámolhatjuk az áthaladt töltés szórásnégyzetét:

\[\left< (\Delta Q)^2\right>=\left< Q^2\right> -\left< Q\right> ^2=\mathcal{T}\cdot e^2 - (\mathcal{T}\cdot e)^2=\mathcal{T}(1-\mathcal{T})e^2,\]

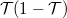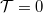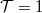azaz az áram szórásnégyzete \setbox0\hbox{$\mathcal{T}(1-\mathcal{T})$}% \message{//depth:\the\dp0//}% \box0%-vel arányos, ami \setbox0\hbox{$\mathcal{T}=0$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\mathcal{T}=1$}% \message{//depth:\the\dp0//}% \box0% kivételével mindig véges, azaz egy részlegesen transzmittáló nanovezeték mindig véges áramfluktuációt, véges zajt mutat.

A zaj, azaz egy mennyiség várható érték körüli fluktuációja sok esetben lényeges többlet információt hordozhat a várható értékhez (pl. vezetőképességhez) képest1, amire a későbbiekben pár egyszerű példát mutatunk. Mindenek előtt azonban definiáljuk pontosabban a zaj fogalmát.

A zaj definíciója


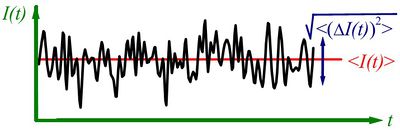
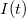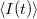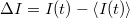Egy időben változó mennyiség (pl. \setbox0\hbox{$I(t)$}% \message{//depth:\the\dp0//}% \box0% áram, lásd 2. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát, \setbox0\hbox{$\left<I(t)\right>$}% \message{//depth:\the\dp0//}% \box0%, illetve az átlagtól vett eltérést, \setbox0\hbox{$\Delta I=I(t)-\left<I(t)\right>$}% \message{//depth:\the\dp0//}% \box0%.

Zaj mint jel 1.jpg
2. ábra. Az áram várható érték körüli szórása

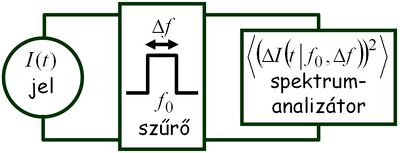
A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével, 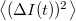\setbox0\hbox{$\left<(\Delta I(t))^2\right>$}% \message{//depth:\the\dp0//}% \box0%, azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 3. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az 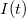\setbox0\hbox{$I(t)$}% \message{//depth:\the\dp0//}% \box0% jelet egy \setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0% középfrekvencia körüli \setbox0\hbox{$\Delta f$}% \message{//depth:\the\dp0//}% \box0% szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző 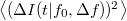\setbox0\hbox{$\left<(\Delta I(t|f_0,\Delta f))^2\right>$}% \message{//depth:\the\dp0//}% \box0% szórásnégyzetet mérünk.

Zaj mint jel zajsuruseg.jpg
3. ábra. A zajsűrűség definíciója kísérleti megközelítésből

Az így kapott szórásnégyzet kis \setbox0\hbox{$\Delta f$}% \message{//depth:\the\dp0//}% \box0% esetén arányos a \setbox0\hbox{$\Delta f$}% \message{//depth:\the\dp0//}% \box0% sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:

\[\left<(\Delta I(t|f_0,\Delta f))^2\right>=S_I(f_0)\Delta f.\]

Áramzaj esetén az 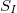\setbox0\hbox{$S_I$}% \message{//depth:\the\dp0//}% \box0% spektrális sűrűség mértékegysége 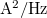\setbox0\hbox{$\mathrm{A}^2/\mathrm{Hz}$}% \message{//depth:\the\dp0//}% \box0%. A mérnöki gyakorlatban gyakran a spektrális sűrűség négyzetgyökével jellemzik egy eszköz zaját 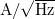\setbox0\hbox{$\mathrm{A}/\sqrt{\mathrm{Hz}}$}% \message{//depth:\the\dp0//}% \box0% mértékegységgel.

Az áramzajhoz hasonlóan definiálhatjuk a feszültségzajt is:
\[\left<(\Delta V(t|f_0,\Delta f))^2\right>=S_V(f_0)\Delta f.\]

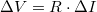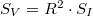Egy egyszerű ellenállás esetén \setbox0\hbox{$\Delta V=R\cdot \Delta I$}% \message{//depth:\the\dp0//}% \box0%, azaz \setbox0\hbox{$S_V=R^2\cdot S_I$}% \message{//depth:\the\dp0//}% \box0%.

Megmutatható, hogy az így definiált spektrális sűrűség egy kettes faktor erejéig megegyezik a 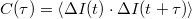\setbox0\hbox{$C(\tau)=\left< \Delta I(t)\cdot \Delta I(t+\tau)\right> $}% \message{//depth:\the\dp0//}% \box0% áram-áram korrelációs függvény Fourier-transzformáltjával,

\[S(\omega )=2\cdot C(\omega).\]

Puskalövések zaja


A zaj fogalma egy klasszikus példával is jól szemléltethető, nézzük meg hogy mi történik ha egy puskából véletlenszerűen lövöldözünk, úgy hogy a lövések időpontja egymástól teljesen független. 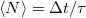Ha a szomszédos lövések között eltelt átlagos idő \setbox0\hbox{$\tau$}% \message{//depth:\the\dp0//}% \box0% akkor \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% idő alatt a lövések átlagos száma értelemszerűen \setbox0\hbox{$\left< N \right> =\Delta t/\tau$}% \message{//depth:\the\dp0//}% \box0%. A tényleges lövésszám azonban fluktuálni fog az átlagérték körül. A szórásnégyzet meghatározásához érdemes kiszámolni a 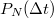\setbox0\hbox{$P_N(\Delta t)$}% \message{//depth:\the\dp0//}% \box0% valószínűséget, azaz annak a valószínűségét, hogy \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% idő alatt \setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0% lövés dördül. 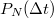Ha \setbox0\hbox{$P_N(\Delta t)$}% \message{//depth:\the\dp0//}% \box0% értékét ismerjük, akkor 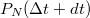\setbox0\hbox{$P_N(\Delta t+dt)$}% \message{//depth:\the\dp0//}% \box0% értéke a

\[P_N(\Delta t+dt)=P_{N-1}(\Delta t)\frac{dt}{\tau}+P_N(\Delta t)\left(1-\frac{dt}{\tau}\right)\]

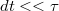egyenlettel írható fel, azaz a kezdeti \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% és az utána következő \setbox0\hbox{$dt<<\tau$}% \message{//depth:\the\dp0//}% \box0% idő alatt vagy 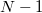\setbox0\hbox{$N-1$}% \message{//depth:\the\dp0//}% \box0% ill. \setbox0\hbox{$1$}% \message{//depth:\the\dp0//}% \box0% vagy \setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0% ill. \setbox0\hbox{$0$}% \message{//depth:\the\dp0//}% \box0% lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze. A fenti egyenlet átrendezésével a

\[\frac{dP_N(\Delta t)}{dt}=\frac{P_{N-1}(\Delta t)-P_N(\Delta t)}{\tau}\]

differenciálegyenletet kapjuk. Megmutatható, hogy ezen feltételt a

\[P_N(\Delta t)=\frac{(\Delta t)^N}{\tau^N N!}e^{-\Delta t/\tau}\]

Poisson-eloszlás elégíti ki. A Poisson-eloszlás speciális tulajdonsága, hogy a szórásnégyzet megegyezik a várható értékkel, azaz

\[\left< (\Delta N)^2 \right>=\left< N \right>=\frac{\Delta t}{\tau}.\]

Elektronok sörétzaja


A fenti gondolatmenetet vonatkoztathatjuk elektronokra is ha teljesül az, hogy az elektronok véletlenszerűen, egymástól függetlenül jutnak át az egyik elektródából a másikba. Tegyük fel, hogy mérőrendszerünkkel az elektromos áramot \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% időbeli felbontással tudjuk mérni. 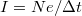Egy \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% szélességű mintavételezési intervallum alatt \setbox0\hbox{$I=Ne/\Delta t$}% \message{//depth:\the\dp0//}% \box0% áramot detektálunk ahol a \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% idő alatt áthaladó elektronok \setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0% számának eloszlását a fenti Poisson-eloszlás adja meg. 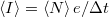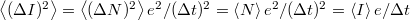Így a mért áram várható értéke \setbox0\hbox{$\left< I \right>=\left< N \right>e/\Delta t$}% \message{//depth:\the\dp0//}% \box0%, míg az áram szórásnégyzete \setbox0\hbox{$\left< (\Delta I)^2 \right>=\left< (\Delta N)^2 \right>e^2/(\Delta t)^2=\left< N \right>e^2/(\Delta t)^2=\left< I \right>e/\Delta t$}% \message{//depth:\the\dp0//}% \box0%. 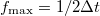A Nyquist - Shannon mintavételezési törvény szerint \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% időfelbontás esetén a mért jelet \setbox0\hbox{$f_{\mathrm{max}}=1/2\Delta t$}% \message{//depth:\the\dp0//}% \box0% maximális frekvenciáig tudjuk rekonstruálni. Ez alapján a mért áram szórásnégyzete:

\[\left< I \right>e/\Delta t=\left< (\Delta I)^2 \right>=\int\limits_0^{1/2\Delta t}S_I(f)df.\]

Ez akkor teljesülhet tetszőleges \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% esetén ha az áramzaj frekvenciafüggetlen (fehér zaj)

\[S_I=2e\left< I \right>\]

zajsűrűséggel.

A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt sörétzajnak szokták nevezni. Az előbbiekben levezetett zajformula a sörétzajnak is egyik speciális esetét írja le, az ún. Poisson-zajt, mely egymástól független elektronok detektálására vonatkozik. A kvantummechanikából ismert Pauli-elv szerint két elektron nem lehet ugyanabban az állapotban, azaz egy adott időpontban nem tudunk két teljesen egyforma állapotú elektront detektálni. Egy makroszkopikus vezetőben az elektronok nem egymástól függetlenül, hanem inkább sorban egymást követve érkeznek az árammérőhöz, így a fenti zajformula nem érvényes. Azonban a Poisson-zaj feltételét megvalósíthatjuk akkor, ha az elektronok kis valószínűséggel emittálódnak egy forrásból.

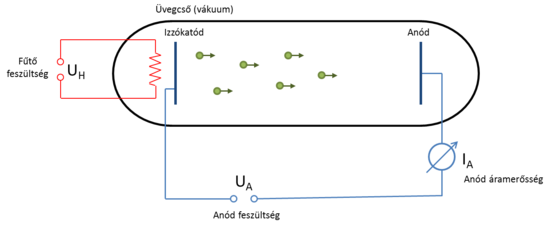
Az első sörétzaj-mérést Walter Schottky végezte 1918-ban:2 híres kísérletében egy vákuumdióda anódáramának zaját vizsgálta. A vákuumdióda felépítését a 4. ábra szemlélteti. Egy fűtött katódból véletlenszerűen kilépő elektronok a katód és anód közé kapcsolt feszültség hatására eljutnak az anódba, ahol áramot detektálunk. A vákuumdióda ideális eszköz a sörétzaj tanulmányozásához, hiszen az elektronok valóban véletlenül, és egymástól függetlenül emittálódnak, így a mért zajsűrűség és az áram hányadosából az elektrontöltés a Poisson-zaj formulája alapján meghatározható.

Zaj mint jel vakuumdioda.png
4. ábra. Vákuumdióda

Poisson-zajt modern elektronikai eszközökben is tapasztalhatunk, például egy diódát alkotó félvezető p-n átmenet is biztosítja az elektronok véletlen és független emisszióját megfelelően kicsi áram esetén. Ennek megfelelően az elektrontöltés értéke egy félvezető dióda zajának méréséből is meghatározható, amit a BME fizikus hallgatói a zaj mint jel című laborgyakorlat során ki is próbálhatnak.

Poisson-zajt az 1. ábrán szemléltetett nanovezetékben is megvalósíthatunk ha a két kvantumvezetéket összekötő szórócentrum 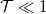\setbox0\hbox{$\mathcal{T}\ll 1$}% \message{//depth:\the\dp0//}% \box0% transzmissziós valószínűséggel rendelkezik. Ekkor az egycsatornás vezetékre vonatkozó Landauer formula alapján 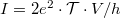\setbox0\hbox{$I=2e^2\cdot \mathcal{T}\cdot V/h$}% \message{//depth:\the\dp0//}% \box0%, azaz a zajsűrűség:

\[S_I=\frac{4e^2}{h}\cdot \mathcal{T} \cdot V.\]

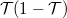Láttuk, hogy tetszőleges \setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% esetén a zaj \setbox0\hbox{$\mathcal{T}(1-\mathcal{T})$}% \message{//depth:\the\dp0//}% \box0%-vel skálázódik. Az ennek megfelelő a zajsűrűség

\[S_I=\frac{4e^2}{h}\cdot \mathcal{T}(1-\mathcal{T}) \cdot V,\]

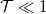mely \setbox0\hbox{$\mathcal{T}\ll 1$}% \message{//depth:\the\dp0//}% \box0% esetben visszaadja a Poisson-zaj formuláját. Több vezetési csatornával rendelkező nanovezeték esetén a zajformula általánosan

\[S_I=\frac{4e^2}{h}\cdot V \sum_n \mathcal{T}_n(1-\mathcal{T}_n)\]

képlettel adható meg, ahol 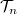\setbox0\hbox{$\mathcal{T}_n$}% \message{//depth:\the\dp0//}% \box0% a sajátcsatornák transzmissziós együtthatói.

Termikus zaj


Az előbbi képlet egy nanovezeték sörétzaját adta meg véges feszültség esetén. A formula alapján zérus zajsűrűséget kapunk 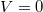\setbox0\hbox{$V=0$}% \message{//depth:\the\dp0//}% \box0% feszültségnél, illetve akkor is ha minden nyitott vezetési csatornára 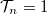\setbox0\hbox{$\mathcal{T}_n=1$}% \message{//depth:\the\dp0//}% \box0%, azaz ha a nanovezeték tökéletes (szórásmentes). A fenti formula azonban nem vette figyelembe a hőmérsékleti fluktuációk hatását, hiszen véges hőmérsékleten zérus feszültség és tökéletes nanovezeték esetén is véges zajt várunk.

Egyelőre a részletek ismerete nélkül vizsgáljunk egyetlen elektronállapotot. Az állapot tényleges betöltöttségét jelöljük 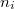\setbox0\hbox{$n_i$}% \message{//depth:\the\dp0//}% \box0%-vel, mely betöltött állapot esetén 1 betöltetlen állapot esetén 0 értéket vesz fel. Az állapot átlagos betöltöttségét termikus egyensúly esetén a Fermi-függvény írja le, azaz:

\[\left< n_i \right>=f(\varepsilon_i)=\frac{1}{e^\frac{\varepsilon_i-\mu}{kT}+1}.\]

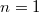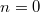Figyelembe véve hogy \setbox0\hbox{$n=1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$n=0$}% \message{//depth:\the\dp0//}% \box0% esetén is 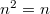\setbox0\hbox{$n^2=n$}% \message{//depth:\the\dp0//}% \box0%, így könnyen megadhatjuk a betöltési szám szórásnégyzetét is:

\[\left< (n_i-\left< n_i \right> )^2 \right>=\left< n_i \right> - \left< n_i \right>^2 =f(\varepsilon_i)\left( 1-f(\varepsilon_i)\right) .\]

Könnyen ellenőrizhető, hogy:

\[f(\varepsilon_i)\left( 1-f(\varepsilon_i)\right)=-kT\frac{\mathrm{d}f(\varepsilon_i)}{\mathrm{d}\varepsilon},\]

melyet energia szerint integrálva 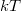\setbox0\hbox{$kT$}% \message{//depth:\the\dp0//}% \box0%-t kapunk, azaz várakozásaink szerint a termikus fluktuációkból származó zaj a hőmérséklettel arányos.

Most vizsgáljuk meg egy konkrét rendszer, egy egycsatornás tökéletes nanovezeték termikus zaját! A nanovezetékben az elektronállapotokat egydimenziós parabolikus diszperziós relációk írják le, a 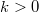\setbox0\hbox{$k>0$}% \message{//depth:\the\dp0//}% \box0% állapotok mind a bal oldali a 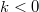\setbox0\hbox{$k<0$}% \message{//depth:\the\dp0//}% \box0% állapotok pedig mind a jobb oldali elektródából származnak. 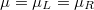Zérus feszültség esetén tetszőleges \setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0%-val rendelkező állapot betöltöttségét a Fermi-függvény írja le \setbox0\hbox{$\mu=\mu_L=\mu_R$}% \message{//depth:\the\dp0//}% \box0% kémiai potenciállal. Egy adott hullámszámhoz tartozó elektronok árama:

\[I_k=\frac{2e}{L}\cdot v_k \cdot n_k,\]

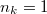ahol \setbox0\hbox{$n_k=1$}% \message{//depth:\the\dp0//}% \box0% ha az állapot betöltött és 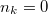\setbox0\hbox{$n_k=0$}% \message{//depth:\the\dp0//}% \box0% ha az állapot betöltetlen. A betöltési szám fent kiszámolt szórásnégyzete alapján az áram szórásnégyzete:

\[\left< (\Delta I_k)^2 \right> =-kT\cdot \frac{4e^2}{L^2}\cdot v^2_k \cdot \frac{\mathrm{d}f(\varepsilon_k)}{\mathrm{d}\varepsilon_k}.\]

Mivel a különböző \setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0%-hoz tartozó áramkomponensek egymástól függetlenek (nincs átszóródás) így szórásnégyzetük összeadódik, azaz a teljes áram szórásnégyzete:

\[\left< (\Delta I)^2 \right>=-kT\cdot \frac{4e^2}{L^2} \sum_k v^2_k \frac{\mathrm{d}f(\varepsilon_k)}{\mathrm{d}\varepsilon_k}=-kT\cdot \frac{4e^2}{L^2}\frac{L}{2\pi } \int\limits_{-\infty}^{+\infty} v^2_k \frac{\mathrm{d}f(\varepsilon_k)}{\mathrm{d}\varepsilon_k}\mathrm{d}k=-2kT \cdot \frac{4e^2}{L^2}\frac{L}{2\pi } \int\limits_{0}^{+\infty} v^2_k \frac{\mathrm{d}f(\varepsilon_k)}{\mathrm{d}\varepsilon_k} \mathrm{d}k.\]

Kihasználva, hogy 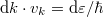\setbox0\hbox{$\mathrm{d}k \cdot v_k=\mathrm{d}\varepsilon /\hbar$}% \message{//depth:\the\dp0//}% \box0% áttérhetünk energia szerinti integrálásra:

\[\left< (\Delta I)^2 \right>=-\frac{8e^2kT}{\hbar L}\frac{1}{2\pi }\cdot \int\limits_{\varepsilon(k=0)}^{+\infty} v_k \frac{\mathrm{d}f}{\mathrm{d}\varepsilon}\mathrm{d}\varepsilon \approx 4kT\cdot G_0 \cdot \frac{v_F}{L}=\int\limits_{0}^{f_\mathrm{max}\approx \frac{v_F}{L}} S_I df,\]

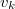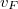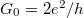ahol figyelembe vettük, fogy a Fermi-függvény deriváltja csak a Fermi-energia körül véges, ahol a \setbox0\hbox{$v_k$}% \message{//depth:\the\dp0//}% \box0% sebesség \setbox0\hbox{$v_F$}% \message{//depth:\the\dp0//}% \box0%-el közelíthető, illetve hogy az egycsatornás kvantumvezeték vezetőképessége \setbox0\hbox{$G_0=2e^2/h$}% \message{//depth:\the\dp0//}% \box0%.

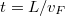Az \setbox0\hbox{$L$}% \message{//depth:\the\dp0//}% \box0% hosszúságú kvantumvezetéken \setbox0\hbox{$t=L/v_F$}% \message{//depth:\the\dp0//}% \box0% idő alatt érnek át az elektronok, így ennél rövidebb időskálán nem látunk fluktuációt az áramban. Ennek megfelelően a termikus zaj jelentkezését 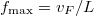\setbox0\hbox{$f_\mathrm{max}=v_F/L$}% \message{//depth:\the\dp0//}% \box0% határfrekvenciáig várjuk. A határfrekvenciáig frekvenciafüggetlen zajsűrűséget feltételezve 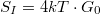\setbox0\hbox{$S_I=4kT \cdot G_0$}% \message{//depth:\the\dp0//}% \box0% zajsűrűséget kapunk. Több vezetési csatornát feltételezve (melyek ideális kvantumvezetékben egymástól függetlenek) a zajsűrűség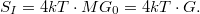 \setbox0\hbox{$S_I=4kT \cdot MG_0=4kT \cdot G.$}% \message{//depth:\the\dp0//}% \box0%

Részletesebb számolások alapján megmutatható, hogy nemcsak ideális kvantumvezeték esetén hanem tetszőleges vezetékre az áramzaj a vezetőképességgel illetve a hőmérséklettel arányosan skálázódik:

\[S_I=4kT \cdot G,\]

és hasonlóképpen egy \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0% ellenállású áramköri elem feszültségzaja:

\[S_V=4kT\cdot R\]

attól függetlenül, hogy pontosan milyen fizikai rendszer adja az \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0% ellenállást. Ezt mondja ki a fluktuáció-disszipáció tétel is, mely egy fizikai rendszer egyensúlyi fluktuációja (jelen esetben zaj) és nemegyensúlyi lineáris válaszfüggvénye (jelen esetben ellenállás ill. vezetőképesség) között teremt kapcsolatot.

A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától. Ezen jelenség segítségével a \setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0% hőmérséklet és az \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0% ellenállás ismeretében a feszültségzaj méréséből a Boltzmann-állandó meghatározható, melyre szintén lehetőség nyílik a zaj mint jel hallgatói mérés keretében.

Általános zajformula


Megmutatható, hogy egy nanovezeték áramzajának sűrűsége tetszőleges feszültségnél és hőmérsékleten:

\[S_I=\frac{4e^2}{h}\left[ 2kT\sum_n \mathcal{T}_n^2+eV\coth{\left(\frac{eV}{2kT}\right)}\sum_n \mathcal{T}_n(1-\mathcal{T}_n)\right],\]

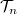Ahol a \setbox0\hbox{$\mathcal{T}_n$}% \message{//depth:\the\dp0//}% \box0% transzmissziós együtthatók a sajátcsatornákhoz tartozó átmeneti valószínűségek.

Az 5. ábra szemlélteti az átmenetet a zérus feszültségnél tapasztalható termikus zaj, illetve a magas (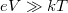\setbox0\hbox{$eV\gg kT$}% \message{//depth:\the\dp0//}% \box0%) feszültségnél jelentkező, feszültséggel lineárisan változó sörétzaj között.

Zajformula.png
5. ábra. Zajsűrűség a feszültség függvényében: átmenet a termikus zaj és a tiszta sörétzaj között

Érdemes megjegyezni, hogy sörétzaj csak nanovezetékekben látszik, makroszkopikus áramköri elemeknél csak akkor tapasztalunk sörétzajt, ha az elektronok egy kis transzmissziós valószínűségű határátmeneten haladnak át (pl. félvezető dióda).

A sörétzaj értéke (azaz a 7. ábrán szemléltetett egyenes meredeksége) egy adott vezetőképességű nanovezetéknél akkor a legnagyobb, ha az összes csatorna transzmissziós együtthatója nagyon kicsi, 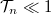\setbox0\hbox{$\mathcal{T}_n \ll 1$}% \message{//depth:\the\dp0//}% \box0%, azaz ha Poisson-zajt látunk. Ennek megfelelően a zajsűrűséget gyakran szokták az 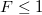\setbox0\hbox{$F \le 1$}% \message{//depth:\the\dp0//}% \box0% Fano-faktorral jellemezni, mely az adott vezetőképességű nanovezeték zajsűrűségének, és az ugyanolyan vezetőképességhez tartozó Poisson-zajnak az aránya.

Egyéb zajforrások


A termikus zaj és a sörétzaj mellett érdemes megemlékezni az 1/f zajról, mely a zajsűrűség tipikus 1/f jellegű frekvenciafüggéséről kapta a nevét. Ezen zajtípus számos fizikai folyamatból származhat, például a szennyezők és rácshibák véletlen mozgásából adódó ellenállásfluktuációkból. Az 1/f zaj a sörétzajhoz hasonlóan nemegyensúlyi zaj, a spektrális sűrűség a feszültség növelésével nő. Az 1/f zaj tipikusan alacsonyfrekvenciás (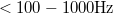\setbox0\hbox{$<100-1000 \mathrm{Hz}$}% \message{//depth:\the\dp0//}% \box0%) méréseknél dominál, míg magasabb frekvenciákon a termikus zaj illetve bizonyos eszközökben a sörétzaj a legfontosabb zajforrás.

Az eddigiekben csak a vizsgált rendszerünk belső zajáról beszéltünk, azonban zajmérésnél mindig fontos a külső forrásokból adódó elektromágneses zavarokra is gondolni. Egy áramkör kapacitív vagy induktív csatolással könnyen felvesz zajt a környezetből például az elektromos hálózat 50 Hz-es frekvenciájánál, monitorok képernyőjének frissítési frekvenciájánál, kapcsoló üzemű tápok működési frekvenciájánál, vagy akár rádióállomások, mobiltelefonok sugárzási frekvenciájánál. Ezen zavaró tényezők kiküszöbölésének alapvető módszere a vizsgált áramkör árnyékolása: alacsony jelszintű méréseknél mindig árnyékolt kábeleket, illetve fém dobozba zárt áramköröket érdemes használni.

Kitekintés


Kutató laboratóriumokban a zajmérést gyakran olyan területen alkalmazzák, ahol más mérési módszer csak korlátozottan, vagy egyáltalán nem áll rendelkezésre.1 A következőkben ilyen mérésekből adunk rövid ízelítőt.

  • A pontos hőmérsékletmérés - különösen extrém körülmények között - sokszor nehézséget jelent, hiszen számos fizikai folyamat (pl. fémek ellenállásváltozása, higanyszál megnyúlása) alkalmas a hőmérsékletváltozás detektálásra, azonban ezek a hőmérők az abszolút hőmérséklet mérésére csak pontos kalibráció után alkalmasak. Ezzel szemben a zajmérés segítségével közvetlenül az abszolút hőmérsékletet lehet meghatározni,3, így zajmérés megfelelő pontosság esetén akár hőmérsékletstandardként is használható.
  • Az elektron töltését jól ismerjük, azonban számos olyan rendszer ismert ahol a kvázirészecskék az elektrontöltés többszörösét vagy tört részét hordozzák (pl. szupravezetés, tört számú kvantált Hall jelenség). Ezen rendszereknél a zajmérés kiválóan alkalmas a kvázirészecske-töltés meghatározására.4,5
  • Az elemi részecskék speciális statisztikákat követnek. Az elektronok például fermionként viselkednek, és a Pauli elv miatt két elektron nem lehet azonos kvantummechanikai állapotban, ezzel szemben a fotonok bozonként viselkednek, és szeretnek olyan állapotba szóródni amiben már több foton is található (lásd indukált emisszió a lézerekben). Ezen különbségek zajméréssel kiválóan kimutathatók, hiszen megfelelően megválasztott rendszerekben a fermionok a Poisson zajnál kisebb, míg a bozonok a Poisson zajnál nagyobb zajt mutatnak.6,7,8
  • A klasszikus és kvantumos kaotikus rendszerek jelentősen különböznek egymástól. A klasszikus káosz esetén ugyan a rendszer viselkedése érzékenyen függ a kezdeti feltételektől azonban mégis teljesen determinisztikus mozgást kapunk. Ezzel szemben kvantumkáosz esetén a részecskék viselkedése alapvetően véletlenszerű. A klasszikus és a kvantumkáosz közötti átmenet jól megmutatható zajmérésekkel, hiszen az előbbi esetben zérus, míg az utóbbiban véges sörétzajt várunk.9

Zajmérésekkel részletesebben az Új kísérletek a nanofizikában tárgy keretében ismerkedhetünk meg.

Hivatkozások

Fent hivatkozott szakcikkek

[1] C. W. J. Beenakker, C. Schönenberger: Quantum shot noise, Physics Today 56, p37 (2003)

[2] W. Schottky: Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern, Annalen der Physik 57 p541–567 (1918)

[3] Lafe Spietz et al.: Primary Electronic Thermometry Using the Shot Noise of a Tunnel Junction, Science 300, p1929 (2003)

[4] Jehl et al.: Detection of doubled shot noise in short normal-metal/ superconductor junctions, Nature 405, p50 (2000)

[5] R. de-Picciotto et al.: Direct observation of a fractional charge, Nature 389, p162 (1997)

[6] R. Hanbury Brown and R. Q. Twiss: Correlation between Photons in two Coherent Beams of Light, Nature 177, p27 (1956).

[7] W.D. Oliver et al.: Hanbury Brown and Twiss-Type Experiment with Electrons, Science 284, p299 (1999)

[8] M. Henny et al.: The Fermionic Hanbury Brown and Twiss Experiment, Science 284, p296 (1999)

[9] S. Oberholzer et al.: Crossover between classical and quantum shot noise in chaotic cavities, Nature 415, p765 (2002)

Ajánlott könyvek és összefoglaló cikkek

Ajánlott kurzusok

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Zajjelenségek_nanoszerkezetekben&oldid=14297”