„Folyadékok felületi feszültségének mérése” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „Folyadékok felületi feszültségének mérése A mérés célja: - megismerkedni a folyadékok felületi feszültségének néhány mérési módszerével; - elmély…”)
 
 
(4 szerkesztő 22 közbeeső változata nincs mutatva)
1. sor: 1. sor:
−
Folyadékok felületi feszültségének mérése
+
<wlatex>
  
−
+
[[Kategória:Mechanika]]
−
A mérés célja:
+
<!--[[Kategória:Elektromosságtan]]-->
−
- megismerkedni a folyadékok felületi feszültségének néhány mérési módszerével;
+
[[Kategória:Hőtan]]
−
- elmélyíteni a felületi feszültséggel kapcsolatos ismere-teket.
+
<!--[[Kategória:Kvantummechanika]]-->
 +
<!--[[Kategória:Statisztikus fizika]]-->
 +
<!--[[Kategória:Nanofizika]]-->
 +
<!--[[Kategória:Optika]]-->
 +
<!--[[Kategória:Szilárdtestfizika]]-->
 +
<!--[[Kategória:Mag és részecskefizika]]-->     
 +
<!--[[Kategória:Informatika]]-->
 +
[[Kategória:Laborgyakorlat]]
 +
[[Kategória:Fizika laboratórium 1.]]
 +
<!--[[Kategória:Fizika laboratórium 2.]]-->
 +
<!--[[Kategória:Fizika laboratórium 3.]]-->
 +
<!--[[Kategória:Fizika laboratórium 4.]]-->
 +
[[Kategória:Szerkesztő:Vankó]]
  
−
Ennek érdekében:
+
''A mérés célja:''
−
- ismertetünk néhány a felületi feszültség mérésére al-kalmas módszert;
+
* megismerkedni a folyadékok felületi feszültségének néhány mérési módszerével,
−
- az ismertetett módszerek segítségével felületi feszült-séget mérünk;
+
* elmélyíteni a felületi feszültséggel kapcsolatos ismereteket.
−
- vizsgáljuk a folyadék felületi feszültségének a hőmér-séklettől és a folyadék összetételétől való függését.
+
  
−
1. Elméleti összefoglaló
+
''Ennek érdekében:''
 +
* ismertetünk néhány a felületi feszültség mérésére alkalmas módszert,
 +
* az ismertetett módszerek segítségével felületi feszültséget mérünk,
 +
* vizsgáljuk a folyadék felületi feszültségének a hőmérséklettől és a folyadék összetételétől való függését.
  
−
Tapasztalati tény, hogy a folyadékfelszín igyekszik a lehető legkisebbre összehúzódni. A folyadékfelszín visel-kedését egy olyan rugalmas hártya viselkedéséhez hason-líthatjuk, amelynek határvonalán erő hat. Ennek alapján a folyadék felszínét határoló görbe bármely l darabjára a felszín érintősíkjában a vonaldarabra merőlegesen
 
  
−
  (1)
+
__TOC__
  
−
nagyságú erő hat. Ugyanekkora erő hat a felszín bármely belső, elemien keskeny l hosszúságú ún. vonalelemének mindkét oldalára. Az (1) kifejezésben szereplő  arányos-sági tényezőt felületi feszültségnek nevezzük:
+
==Elméleti összefoglaló==
  
−
(2)
+
Tapasztalati tény, hogy a folyadékfelszín igyekszik a lehető legkisebbre összehúzódni. A folyadékfelszín viselkedését egy olyan rugalmas hártya viselkedéséhez hasonlíthatjuk, amelynek határvonalán erő hat. Ennek alapján a folyadék felszínét határoló görbe bármely $\Delta l$ darabjára a felszín érintősíkjában a vonaldarabra merőlegesen
  
−
A felületi feszültség az egységnyi vonalhosszúságra ható erő. Mértékegysége Nm-1. A felületi feszültség a folyadék-felszín növeléséhez szükséges munkával is kapcsolatba hozható. A folyadék felszínének A-val való megnövelé-séhez szükséges munka arányos a felület növekedésével és a   felületi szabadenergiával:
+
$$\Delta F = \alpha \Delta l$$
  
−
,   (3)
+
nagyságú erő hat. Ugyanekkora erő hat a felszín bármely belső, elemien keskeny $\Delta l$ hosszúságú ún. vonalelemének mindkét oldalára. A kifejezésben szereplő $\alpha$ arányossági tényezőt felületi feszültségnek nevezzük:
  
−
ahol a felületi szabadenergia mértékegysége Jm-2. Be-látható, hogy folyadékok esetében a felületi feszültség egyenlő a felületi szabadenergiával. Ezért a két mennyisé-get gyakran nem különböztetik meg. Az egyenlőség azon-ban kizárólag folyadékok esetén igaz, hiszen a szabad-energia mindig skalár, míg a felületi feszültség általában tenzor (pl. szilárdtestek esetén).
+
$$\alpha = \frac{\Delta F}{\Delta l}$$
−
+
−
Az, hogy a fenti két mennyiség folyadékok esetén va-lóban egyenlő, az 1. ábrán vázolt kísérlet elemzésével lát-ható be. Az (1) összefüggés szerint a hártya egyik oldalát alkotó l hosszúságú keretdarabra
+
  
−
          (4)
+
A felületi feszültség az egységnyi vonalhosszúságra ható erő. Mértékegysége Nm<sup>-1</sup>. A felületi feszültség a folyadékfelszín növeléséhez szükséges munkával is kapcsolatba hozható. A folyadék felszínének $\Delta A$-val való megnöveléséhez szükséges munka arányos a felület növekedésével és a $\gamma$ felületi szabadenergiával:
  
 +
$$\Delta W = \Delta E_f = \gamma \Delta A$$
 +
 +
ahol a felületi szabadenergia mértékegysége Jm<sup>-2</sup>. Belátható, hogy folyadékok esetében a felületi feszültség egyenlő a felületi szabadenergiával. Ezért a két mennyiséget gyakran nem különböztetik meg. Az egyenlőség azonban kizárólag folyadékok esetén igaz, hiszen a szabadenergia mindig skalár, míg a felületi feszültség általában tenzor (pl. szilárdtestek esetén).
 +
 +
[[Fájl:felfesz_1_abra.jpg|bélyegkép|200px|1.ábra]]
 +
Az, hogy a fenti két mennyiség folyadékok esetén valóban egyenlő, az 1. ábrán vázolt kísérlet elemzésével látható be. Az első összefüggés szerint a hártya egyik oldalát alkotó $l$ hosszúságú keretdarabra
 +
 +
$$F_f = 2 \alpha l$$
 
   
 
   
−
nagyságú erő hat. (A 2-es szorzó azt veszi figyelembe, hogy a hártya első és hátsó felszínén is fellép a felületi feszültség.) Ha a keret k-val jelölt, l hosszúságú darabját x-szel elmozdítjuk, és így a hártya felszínét 2lx = A-val megnöveljük, akkor a végzett munka:
+
nagyságú erő hat. (A 2-es szorzó azt veszi figyelembe, hogy a hártya első és hátsó felszínén is fellép a felületi feszültség.) Ha a keret k-val jelölt, $l$ hosszúságú darabját $\Delta x$-szel elmozdítjuk, és így a hártya felszínét $2 l \Delta x = \Delta A$-val megnöveljük, akkor a végzett munka:
  
−
      (5)
+
$$\Delta W = \Delta x F_h = \Delta x 2 \alpha l = \alpha \Delta A$$
  
−
melyet a (3) egyenlettel összevetve az = kapcsolat közvetlenül adódik. A felületi feszültség (első közelítésben) független a felszín alakjától, értéke a folya-dék minőségétől, állapotától valamint attól függ, hogy a szabad felszínnel milyen közeg érintkezik.
+
melyet az előző egyenlettel összevetve az $\alpha = \gamma$ kapcsolat közvetlenül adódik. A felületi feszültség (első közelítésben) független a felszín alakjától, értéke a folyadék minőségétől, állapotától valamint attól függ, hogy a szabad felszínnel milyen közeg érintkezik.
−
A táblázatokban található felületi feszültség értékek ál-talában a saját gőzével egyensúlyban lévő folyadékra vo-natkoznak. A felületi feszültség függ a hőmérséklettől, növekvő hőmérséklettel csökken és a kritikus ponton eltű-nik. Ez a viselkedés jól közelíthető az
+
A táblázatokban található felületi feszültség értékek általában a saját gőzével egyensúlyban lévő folyadékra vonatkoznak. A felületi feszültség függ a hőmérséklettől, növekvő hőmérséklettel csökken és a kritikus ponton eltűnik. Ez a viselkedés jól közelíthető az
  
−
  (6)
+
$$\alpha V^{2/3} = K \left( T_c-T \right)$$
  
−
Eötvös-formulával, ahol V a folyadék móltérfogata, K az Eötvös-állandó, míg Tc a kritikus hőmérséklet. Mivel a fe-lületi feszültség molekuláris erők következménye értékét erősen módosíthatja a határfelület szennyezettsége.
+
Eötvös-formulával, ahol $V$ a folyadék móltérfogata, $K$ az Eötvös-állandó, míg $T_c$ a kritikus hőmérséklet. Mivel a felületi feszültség molekuláris erők következménye értékét erősen módosíthatja a határfelület szennyezettsége.
  
−
2. Mérési módszerek
+
==Mérési módszerek==
  
−
2.1 Felületi feszültség mérése hajszálcső segítségével
+
===Felületi feszültség mérése hajszálcső segítségével===
  
−
Ha nagyobb szabad felületű folyadékba függőlegesen hajszálcsövet mártunk, akkor a cső belsejében a folyadék felszínének szintje a szabad felszín szintjéhez képest eltér. A csőben lévő folyadék szintje akkor magasabb, ha a fo-lyadék a cső falát nedvesíti, és akkor alacsonyabb, ha a fo-lyadék a cső falát nem nedvesíti. (2a ábra)
+
[[Fájl:felfesz_2_abra.jpg|bélyegkép|200px|2.ábra]]
−
A nedvesítő folyadékoknál a felületi feszültség hatásá-ra fellépő erő a felemelkedett folyadékoszlop súlyával tart egyensúlyt. Ebből levezethető, hogy:
+
[[Fájl:felfesz_3_abra.jpg|bélyegkép|200px|3.ábra]]
 +
Ha nagyobb szabad felületű folyadékba függőlegesen hajszálcsövet mártunk, akkor a cső belsejében a folyadék felszínének szintje a szabad felszín szintjéhez képest eltér. A csőben lévő folyadék szintje akkor magasabb, ha a folyadék a cső falát nedvesíti, és akkor alacsonyabb, ha a folyadék a cső falát nem nedvesíti. (2. ábra)
  
−
,   (7)
+
A nedvesítő folyadékoknál a felületi feszültség hatására fellépő erő a felemelkedett folyadékoszlop súlyával tart egyensúlyt. Ebből levezethető, hogy:
  
−
ahol h az emelkedés magassága,  a folyadék sűrűsége, g a nehézségi gyorsulás, r a cső sugara és  a nedvesítési szög. Ideálisan nedvesítő folyadék esetén ( = 0):
+
$$ \alpha = \frac{h \rho g r}{2 \cos \theta}$$
  
−
.   (8)
+
ahol $h$ az emelkedés magassága, $\rho$ a folyadék sűrűsége, $g$ a nehézségi gyorsulás, $r$ a cső sugara és $\theta$ a nedvesítési szög. Ideálisan nedvesítő folyadék esetén ($\theta = 0$):
  
−
A mérésnél a csőben lévő folyadékfelszín alsó pontjának magasságát mérjük meg (hm) és az emelkedés magasságát az alábbiak szerint számítjuk.(ld. 2b és 2c ábrák)
+
$$\alpha = h \rho g r / 2$$
  
−
.   (9)
+
A mérésnél a csőben lévő folyadékfelszín alsó pontjának magasságát mérjük meg ($h_m$) és az emelkedés magasságát az alábbiak szerint számítjuk (3. ábra).
  
−
A nedvesítési szög ismeretében tehát a felületi feszültség egy kapilláris, valamint a (7) és (9) kifejezések segítségé-vel határozható meg.
+
$$h = h_m + r/3$$
  
−
3.2 Felületi feszültség mérése csepegtetéssel
+
A nedvesítési szög ismeretében tehát a felületi feszültség egy kapilláris segítségével meghatározható.
  
−
+
===Felületi feszültség mérése csepegtetéssel===
−
Ezen mérési módszer alapgondolata az, hogy egy folyadékcsepp lecseppenése akkor következik be, amikor a csepp súlya meghaladja a leszakadási felületnél a felületi feszültségből származó erőt. Ha vastag falú, függőleges, alul síkra csiszolt kapilláris csőből lassan csepegtetjük ki a csövet jól nedvesítő folyadékot, akkor a csepp felszíne az r külső sugarú csővel 2r hosszú darabon érintkezik. Ekkor a felületi feszültségből származó erő legfeljebb G = 2r  súlyú cseppet tud megtartani. Valójában a leszakadó csepp súlya a 3. ábrán látható "befűződés" mi-att a fenti értéknél kisebb: G = kr, ahol a k állandó a fe-lületi fesztültségtől, a cső méretétől és a folyadék sűrűsé-gétől függő állandó, értéke 3,8 és 4,5 közötti.
+
−
Egy adott eszköz k értékét ismert felületi feszültségű anyagok segítségével határozhatjuk meg. Tájékozódó jel-legű összehasonlító méréseknél a k ismerete mellőzhető, mert ebben az esetben két folyadékra nézve
+
  
−
. (10)
+
[[Fájl:felfesz_4_abra.jpg|bélyegkép|80px|4. ábra]]
 +
[[Fájl:felfesz_5_abra.jpg|bélyegkép|200px|5.ábra]]
 +
Ezen mérési módszer alapgondolata az, hogy egy folyadékcsepp lecseppenése akkor következik be, amikor a csepp súlya meghaladja a leszakadási felületnél a felületi feszültségből származó erőt. Ha vastag falú, függőleges, alul síkra csiszolt kapilláris csőből lassan csepegtetjük ki a csövet jól nedvesítő folyadékot, akkor a csepp felszíne az $r$ külső sugarú csővel $2 r \pi$ hosszú darabon érintkezik. Ekkor a felületi feszültségből származó erő legfeljebb $G = 2 r \pi \alpha$ súlyú cseppet tud megtartani. Valójában a leszakadó csepp súlya a 3. ábrán látható "befűződés" miatt a fenti értéknél kisebb: $G = k r \alpha$, ahol a $k$ állandó a felületi feszültségtől, a cső méretétől és a folyadék sűrűségétől függő állandó, értéke 3,8 és 4,5 közötti.
 +
Egy adott eszköz $k$ értékét ismert felületi feszültségű anyagok segítségével határozhatjuk meg. Tájékozódó jellegű összehasonlító méréseknél a $k$ ismerete mellőzhető, mert ebben az esetben két folyadékra nézve
  
−
A csepegtetéssel működő felületi feszültség mérő eszkö-zöket sztalagmométereknek nevezzük.
+
$$\alpha_1 / \alpha_2 = G_1 / G_2$$
  
−
3.3 Felületi feszültség mérés szakításos módszerrel
+
A csepegtetéssel működő felületi feszültség mérő eszközöket sztalagmométereknek nevezzük.
  
 +
===Felületi feszültség mérés szakításos módszerrel===
 +
 +
Egy folyadékba mártott gyűrűt – amelynek anyagát a folyadék nedvesíti – lassan, függőlegesen kiemeljük a folyadékból, és közben folyamatosan mérjük az erőt (5. ábra). Az erő maximális értéke a gyűrű súlyával és a gyűrűhöz tapadó vékony folyadékhártya elszakításához szükséges erővel egyenlő.
 +
 +
Az 5/a ábrán látható elrendezés esetén:
 +
 +
$$F_{max} = G + 2 \pi \left( r_1 + r_2 \right) \alpha$$
 +
 +
az 5/b ábrán látható elrendezés esetén pedig:
 +
 +
$$F_{max} = G + 4 \pi r \alpha$$
 +
 +
A felületi feszültség hatására fellépő erő nagyon kicsi. A mérési gyakorlaton az erőt [[A_rugalmassági_együttható_meghatározása#Erő_mérése_induktív_mérőátalakítóval|induktív mérőátalakítóval]] mérjük, amely az erővel arányos feszültségjelet ad ki. A feszültségjelet az idő függvényében számítógépen lehet rögzíteni, és így az erő maximuma meghatározható.
 +
 +
==Erő mérése induktív mérőátalakítóval==
 +
 +
[[Fájl:rug_7_abra.jpg|bélyegkép|200px|6.ábra]]
 +
[[Fájl:rug_8_abra.jpg|bélyegkép|200px|7.ábra]]
 +
Az induktív mérőátalakító elmozdulás detektálására alkalmas, így felhasználható minden olyan mennyiség mérésére, melynek változása elmozdulást eredményez. Így például deformáció, és ezen keresztül erő mérésére is.
 
   
 
   
−
Egy folyadékba mártott gyűrűt – amelynek anyagát a folyadék nedvesíti – lassan, függőlegesen kiemeljük a fo-lyadékból, és közben folyamatosan mérjük az erőt. (4. áb-ra). Az erő maximális értéke a gyűrű súlyával és a gyűrű-höz tapadó vékony folyadékhártya elszakításához szüksé-ges erővel egyenlő.
+
Az induktív mérőátalakító a mérendő fizikai mennyiség változásának hatására induktivitásváltozást hoz létre. A mérendő fizikai mennyiség nagysága és a mérőátalakító induktivitása között egyértelmű kapcsolat van. Így induktivitás méréssel vagy az induktivitásváltozás egyéb módon való detektálásával a mérendő fizikai mennyiség nagysága meghatározható.
−
A 4a ábrán látható elrendezés esetén:
+
A legegyszerűbb, nyitott mágneses körű átalakító lényegében egy vasmagos tekercs. Vázlata a 6. ábrán látható. Ha a vasmag nélküli tekercs $L_0$ induktivitásából indulunk ki, könnyen belátható, hogy a vasmagnak a tekercsbe való bevitele az önindukciós együttható növekedését eredményezi. Az önindukciós együttható maximuma ott lesz, ahol a mágneses ellenállás a legkisebb, azaz ahol a vasmag teljes egészében a tekercsben helyezkedik el. A magot tovább mozgatva (a másik oldalon kihúzva a tekercsből) induktivitás az előzőekkel szimmetrikusan csökken.
  
−
, (11)
+
A nyitott mágneses körű mérőátalakító karakterisztikája a 7. ábrán látható. Önindukciós együtthatója a vasmag helyzetének függvénye, tehát az átalakító elmozdulás hatására induktivitás-változást hoz létre. A karakterisztika viszonylag hosszú lineáris szakasszal rendelkezik, ami nagy (néhány cm) elmozdulások mérésére teszi alkalmassá. A tekercs hossztengelye mentén a menetsűrűség megfelelő változtatásával a linearitási tartomány növelhető.
 +
A mérőátalakító induktivitása sokféleképp mérhető. Gyakran alkalmazzák az úgynevezett differenciál kialakítást. A differenciál kialakítású induktív adó két teljesen azonos induktív adó, úgy elhelyezve, hogy bemenőjel (vasmag elmozdulás) hatására az egyik átalakító induktivitása nő, a másiké csökken. A differenciál kialakítású induktív adó alkalmazása azzal az előnnyel jár, hogy a hídkapcsolás érzékenysége kétszerese lesz az egy adót tartalmazó híd érzékenységének, megnő a kapcsolás linearitási tartománya, míg a külső zavaró tényezők a híd két ágára egyszerre hatnak, így csökkentve fejtik ki hatásukat.
  
−
a 4b ábrán látható elrendezés esetén pedig
+
==Mérési feladatok==
  
−
. (12)
+
[[A méréshez rendelkezésre álló eszközök: Folyadékok felületi feszültségének mérése|A méréshez rendelkezésre álló eszközök]]
  
−
Mérési feladatok:
+
*''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
  
−
I. Víz-alkohol oldatok felületi feszültségének mérése csepegteté-ses módszerrel
+
'''1.''' Víz-alkohol oldatok felületi feszültségének mérése csepegtetéses módszerrel
  
−
1. Határozzuk meg a sztalagmométer k készülékállandóját desztillált víz segítségével!
+
{{figN|Felfesz2.jpg|figN:8|8. ábra: Sztalagmométer|200}}
−
A sztalagmométer egy csapos tölcsér. Ne érintsük kézzel a kapilláris zsírtalanított alsó peremét ill. a tölcsér belsejét! A sztalagmométert függőleges helyzetbe rögzítjük, majd a csap elzárása után a tölcsér feléig megtöltjük desztillált vízzel. A csepegtetés megkezdése előtt mérjünk le táramérleggel egy üres műanyag edényt, majd csepegtessünk a pohárba mini-málisan 100 cseppet. A csap óvatos nyitásával a folyadék-áramlást úgy szabályozzuk be, hogy a cseppek kényelmesen számolhatóak legyenek. Az edény visszamérése után 1 csepp átlagtömege, m számolható. Az egyensúly feltételéből gm = kr, ami alapján a desztillált víz felületi feszültségé-nek ismeretében a k készülékállandó meghatározható.
+
  
−
2. Ismételjük meg az 1. feladatot 10 és 20 %-os alkohol oldat-tal! Az oldatcseréhez engedjük le a tölcséres csepegtetőből a folyadékot, töltsük fel a következő oldattal, majd azt is fo-lyassuk ki. Egy újabb (második) feltöltés után az új oldat már mérhető. Az alkoholos oldatok maradékait kérjük a gyűjtőedénybe önteni.
+
'''a)''' Határozza meg a sztalagmométer $k$ készülékállandóját desztillált víz segítségével!
 +
A sztalagmométer egy csapos tölcsér. Ne érintse kézzel a kapilláris zsírtalanított alsó peremét ill. a tölcsér belsejét! A sztalagmométert függőleges helyzetbe rögzítse, majd a csap elzárása után a tölcsér feléig töltse meg desztillált vízzel. A csepegtetés megkezdése előtt mérjen le táramérleggel egy üres műanyag edényt, majd csepegtessen a pohárba minimálisan 100 cseppet. A csap óvatos nyitásával a folyadékáramlást úgy szabályozza be, hogy a cseppek kényelmesen számolhatóak legyenek. Az edény visszamérése után 1 csepp átlagtömege, $\Delta m$ számolható. Az egyensúly feltételéből $g \Delta m = k r \alpha $, ami alapján a desztillált víz felületi feszültségének ismeretében a $k$ készülékállandó meghatározható.
  
−
II. Szakításos felületi feszültség mérő beállítása és kalibrálása
+
'''b)''' Ismételje meg az a) feladatot 10 és 20 %-os alkohol oldattal! Az oldatcseréhez engedje le a tölcséres csepegtetőből a folyadékot, töltse fel a következő oldattal, majd azt is folyassa ki. Egy újabb (második) feltöltés után az új oldat már mérhető.
 +
* ''Az alkoholos oldatok maradékait kérjük a megfelelő gyűjtőedénybe önteni!''
  
−
3. Állítsuk össze a szakításos felületi feszültség mérőt! Az in-duktív erőmérő elektronikája az erőhatással arányos -10 és +10 V közötti feszültségjelet generál, melynek a nulla szintje potméterrel szabályozható. Ezt a feszültségjelet kös-sük a HAMEG digitális multiméterre. A mért feszültséget számítógépes interfészen keresztül, a felfesz_meres.exe program segítségével rögzítjük. Ellenőrizzük a program működését, és állítsuk be az induktív erőmérő nullszintjét  -6 V és -3 V közötti értékre. Figyelem! A mérőkeretet elő-zetesen zsírtalanítottuk, ezért azt kézzel érinteni tilos!
+
'''2.''' Szakításos felületi feszültség mérő beállítása és kalibrálása
  
−
4. Kalibráljuk az induktív erőmérőt! Akasszunk növekvő számban felfüggeszthető súlyokat az erőmérőre, és a súlyok számának függvényében vegyük fel az erőmérő kimenő fe-szültségét, illesszünk egyenest a mért pontokra. (Megj.: a súlyokat ne a mérőkeretre, hanem a mérőkeret feletti mű-anyag lapon található lyukakba akasszuk. Ügyeljünk a keret egyenletes terhelésére, ha a súlyok egy oldalra húzzák a ke-retet, megnő az induktív erőmérőben a súrlódás, ami növeli a mérési hibát. A súlyok átlagos tömege: 0,47 g)
+
{{figN|Felfesz1.png|figN:9|9. ábra|300}}
  
−
5. Vízszintezzük a mérőkeretet! Ehhez helyezzünk a keret alá egy állítható lábú plexi asztalkát. Az asztalra helyezett víz-szintmérő segítségével vízszintezzük az aszalt olyan ma-gasságban, hogy a mérőkeret éppen ne érjen hozzá. Ezután a mérőkeret feletti műanyag tárcsán található piros csava-rok segítségével állítsuk be a mérőkeretet az asztal síkjával párhuzamosan. A mérőkeret vízszintességét a mérés során többször is ellenőrizzük, és szükség esetén korrigáljuk.  
+
'''a)''' Állítsa össze a szakításos felületi feszültség mérőt! Az induktív erőmérő elektronikája az erőhatással arányos -10 és +10 V közötti feszültségjelet generál, melynek a nulla szintje potméterrel szabályozható. Ezt a feszültségjelet kösse a HAMEG digitális multiméterre. A mért feszültséget számítógépes interfészen keresztül, a ''felfesz_meres.exe'' program segítségével rögzíti. Ellenőrizze a program működését, és állítsa be az induktív erőmérő nullszintjét -6 V és -3 V közötti értékre.
 +
* ''Figyelem! A mérőkeretet előzetesen zsírtalanítottuk, ezért azt kézzel érinteni tilos!''
  
 +
'''b)''' Kalibrálja az induktív erőmérőt! Akasszon növekvő számban felfüggeszthető súlyokat az erőmérőre, és a súlyok számának függvényében vegye fel az erőmérő kimenő feszültségét, illesszen egyenest a mért pontokra.
 +
* ''A súlyokat ne a mérőkeretre, hanem a mérőkeret feletti műanyag lapon található lyukakba akassza. Ügyeljen a keret egyenletes terhelésére, ha a súlyok egy oldalra húzzák a keretet, megnő az induktív erőmérőben a súrlódás, ami növeli a mérési hibát. A súlyok átlagos tömege: 0,47 g.''
 +
 +
'''c)''' Vízszintezze a mérőkeretet! Ehhez helyezze a keret alá egy állítható lábú plexi asztalkát. Az asztalra helyezett vízszintmérő segítségével vízszintezze az aszalt olyan magasságban, hogy a mérőkeret éppen ne érjen hozzá. Ezután a mérőkeret feletti műanyag tárcsán található piros csavarok segítségével állítsa be a mérőkeretet az asztal síkjával párhuzamosan.
 +
* ''A mérőkeret vízszintességét a mérés során többször is ellenőrizze, és szükség esetén korrigálja.''
 
   
 
   
−
III. Víz-alkohol oldatok felületi feszültségének mérése szakítá-sos módszerrel
+
'''3.''' Víz-alkohol oldatok felületi feszültségének mérése szakításos módszerrel
 +
* ''Becsülje meg, és állítsa be az erőmérés számítógépes rögzítésének optimális mintavételezési frekvenciáját!''
 +
 
 +
'''a)''' Helyezze a ''deszt. víz'' feliratú, leeresztő csappal ellátott edényt a mérőkeret alá. Töltse fel az edényt desztillált vízzel addig, hogy a vízszint pár mm magasan legyen a keret alsó éle felett. Gyors csepegtetéssel eressze le az edényből a vizet a ''deszt. víz'' feliratú gyűjtőedénybe, közben vegye fel az erő változását a gyűrű szakadásáig. Ekkor a csapot elzárva a pohárból töltse vissza a vizet a keret közepébe (nem a keretre!) és a szakítási kísérletet ismételje meg legalább kétszer!
 +
* ''Az erőt mindig az elszakadás előtti és a szakadás utáni feszültségszint különbségéből állapítsa meg!''
 +
* ''A mérőkeret átmérője a szakítási élnél 91 mm.''
 +
 
 +
'''b)''' Az a) mérést ismételje meg 10 %-os és 20 %-os alkohololdattal.
 +
* ''Figyelem! Az oldatokat mindig a koncentrációnak megfelelő feliratú edénybe töltse, majd a mérés végén ne öntse ki, hanem töltse vissza a megfelelő tároló edénybe. Ügyeljen rá, hogy az oldatok ne keveredjenek.''
 +
* ''Hasonlítsa össze az egyes oldatok csepegtetéses és szakításos módszerrel meghatározott felületi feszültség értékeit egymással, valamint a rendelkezésre álló irodalmi adatokkal!''
 +
''
 +
 
 +
'''4.''' Desztillált víz felületi feszültségének hőmérséklet függése, Eötvös-féle szabály igazolása
  
−
6. Helyezzük a deszt. víz feliratú, leeresztő csappal ellátott edényt a mérőkeret alá. Töltsük fel az edényt desztillált víz-zel addig, hogy a vízszint pár mm magasan legyen a keret alsó éle felett. Gyors csepegtetéssel eresszük le az edényből a vizet a deszt. víz feliratú gyűjtőedénybe, közben vegyük fel az erő változását a gyűrű szakadásáig. Ekkor a csapot elzárva a pohárból töltsük vissza a vizet a keret közepébe (nem a keretre!) és a szakítási kísérletet ismételjük meg legalább kétszer! (Megj.: az erőt mindig az elszakadás előtti és a szakadás utáni feszültségszint különbségéből állapítsuk meg. A mérőkeret átmérője a szakítási élnél: 91 mm)
+
A 4/a mérést ismételje meg desztillált vízzel 40 és 60 °C-os hőmérsékleten. A hőmérséklet méréséhez rögzítse a higanyszálas hőmérőt a bunsen állványhoz. A víz melegítése közben használjon mágneses keverőt, de az erőmérés előtt kapcsolja ki a keverőt, és várja meg, míg a vízfelszín megnyugszik.
 +
Ábrázolja a felületi feszültséget a hőmérséklet függvényében, és illesszen egyenest a mérési pontokra! Az egyenes paramétereiből határozza meg az Eötvös-állandót és a kritikus hőmérsékletet.
  
−
7. A 6. mérést ismételjük meg 10 %-os és 20 %-os alkoholol-dattal. Figyelem! Az oldatokat mindig a koncentrációnak megfelelő feliratú edénybe töltsük, majd a mérés végén ne öntsük ki, hanem töltsük vissza a megfelelő tároló edénybe. Ügyeljünk rá, hogy az oldatok ne keveredjenek.
 
  
−
IV. Desztillált víz felületi feszültségének hőmérséklet függése, Eötvös-féle szabály igazolása
+
[[Fizika laboratórium 1.|Vissza a Fizika laboratórium 1. tárgyoldalára.]]
  
−
8. A 6. mérést ismételjük meg desztillált vízzel 40 és 60 °C-os hőmérsékleten. Hőmérséklet méréséhez rögzítsük a higany-szálas hőmérőt a bunsen állványhoz. A víz melegítése köz-ben használjunk mágneses keverőt, de az erőmérés előtt kapcsoljuk ki a keverőt, és várjuk meg, míg a vízfelszín megnyugszik.
+
</wlatex>
−
Ábrázoljuk a felületi feszültséget a hőmérséklet függvényé-ben, és illesszünk egyenest a mérési pontokra! Az egyenes paramétereiből határozzuk meg az Eötvös-állandót és a kri-tikus hőmérsékletet.
+

A lap jelenlegi, 2015. február 24., 21:40-kori változata


A mérés célja:

  • megismerkedni a folyadékok felületi feszültségének néhány mérési módszerével,
  • elmélyíteni a felületi feszültséggel kapcsolatos ismereteket.

Ennek érdekében:

  • ismertetünk néhány a felületi feszültség mérésére alkalmas módszert,
  • az ismertetett módszerek segítségével felületi feszültséget mérünk,
  • vizsgáljuk a folyadék felületi feszültségének a hőmérséklettől és a folyadék összetételétől való függését.


Tartalomjegyzék


Elméleti összefoglaló

Tapasztalati tény, hogy a folyadékfelszín igyekszik a lehető legkisebbre összehúzódni. A folyadékfelszín viselkedését egy olyan rugalmas hártya viselkedéséhez hasonlíthatjuk, amelynek határvonalán erő hat. Ennek alapján a folyadék felszínét határoló görbe bármely 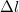\setbox0\hbox{$\Delta l$}% \message{//depth:\the\dp0//}% \box0% darabjára a felszín érintősíkjában a vonaldarabra merőlegesen

\[\Delta F = \alpha \Delta l\]

nagyságú erő hat. Ugyanekkora erő hat a felszín bármely belső, elemien keskeny 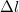\setbox0\hbox{$\Delta l$}% \message{//depth:\the\dp0//}% \box0% hosszúságú ún. vonalelemének mindkét oldalára. A kifejezésben szereplő \setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0% arányossági tényezőt felületi feszültségnek nevezzük:

\[\alpha = \frac{\Delta F}{\Delta l}\]

A felületi feszültség az egységnyi vonalhosszúságra ható erő. Mértékegysége Nm-1. A felületi feszültség a folyadékfelszín növeléséhez szükséges munkával is kapcsolatba hozható. A folyadék felszínének 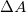\setbox0\hbox{$\Delta A$}% \message{//depth:\the\dp0//}% \box0%-val való megnöveléséhez szükséges munka arányos a felület növekedésével és a \setbox0\hbox{$\gamma$}% \message{//depth:\the\dp0//}% \box0% felületi szabadenergiával:

\[\Delta W = \Delta E_f = \gamma \Delta A\]

ahol a felületi szabadenergia mértékegysége Jm-2. Belátható, hogy folyadékok esetében a felületi feszültség egyenlő a felületi szabadenergiával. Ezért a két mennyiséget gyakran nem különböztetik meg. Az egyenlőség azonban kizárólag folyadékok esetén igaz, hiszen a szabadenergia mindig skalár, míg a felületi feszültség általában tenzor (pl. szilárdtestek esetén).

1.ábra

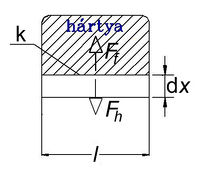
Az, hogy a fenti két mennyiség folyadékok esetén valóban egyenlő, az 1. ábrán vázolt kísérlet elemzésével látható be. Az első összefüggés szerint a hártya egyik oldalát alkotó \setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0% hosszúságú keretdarabra

\[F_f = 2 \alpha l\]

nagyságú erő hat. (A 2-es szorzó azt veszi figyelembe, hogy a hártya első és hátsó felszínén is fellép a felületi feszültség.) Ha a keret k-val jelölt, \setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0% hosszúságú darabját 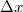\setbox0\hbox{$\Delta x$}% \message{//depth:\the\dp0//}% \box0%-szel elmozdítjuk, és így a hártya felszínét 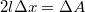\setbox0\hbox{$2 l \Delta x = \Delta A$}% \message{//depth:\the\dp0//}% \box0%-val megnöveljük, akkor a végzett munka:

\[\Delta W = \Delta x F_h = \Delta x 2 \alpha l = \alpha \Delta A\]

melyet az előző egyenlettel összevetve az 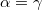\setbox0\hbox{$\alpha = \gamma$}% \message{//depth:\the\dp0//}% \box0% kapcsolat közvetlenül adódik. A felületi feszültség (első közelítésben) független a felszín alakjától, értéke a folyadék minőségétől, állapotától valamint attól függ, hogy a szabad felszínnel milyen közeg érintkezik. A táblázatokban található felületi feszültség értékek általában a saját gőzével egyensúlyban lévő folyadékra vonatkoznak. A felületi feszültség függ a hőmérséklettől, növekvő hőmérséklettel csökken és a kritikus ponton eltűnik. Ez a viselkedés jól közelíthető az

\[\alpha V^{2/3} = K \left( T_c-T \right)\]

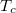Eötvös-formulával, ahol \setbox0\hbox{$V$}% \message{//depth:\the\dp0//}% \box0% a folyadék móltérfogata, \setbox0\hbox{$K$}% \message{//depth:\the\dp0//}% \box0% az Eötvös-állandó, míg \setbox0\hbox{$T_c$}% \message{//depth:\the\dp0//}% \box0% a kritikus hőmérséklet. Mivel a felületi feszültség molekuláris erők következménye értékét erősen módosíthatja a határfelület szennyezettsége.

Mérési módszerek

Felületi feszültség mérése hajszálcső segítségével

2.ábra
3.ábra

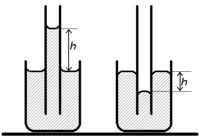
Ha nagyobb szabad felületű folyadékba függőlegesen hajszálcsövet mártunk, akkor a cső belsejében a folyadék felszínének szintje a szabad felszín szintjéhez képest eltér. A csőben lévő folyadék szintje akkor magasabb, ha a folyadék a cső falát nedvesíti, és akkor alacsonyabb, ha a folyadék a cső falát nem nedvesíti. (2. ábra)

A nedvesítő folyadékoknál a felületi feszültség hatására fellépő erő a felemelkedett folyadékoszlop súlyával tart egyensúlyt. Ebből levezethető, hogy:

\[ \alpha = \frac{h \rho g r}{2 \cos \theta}\]

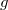ahol \setbox0\hbox{$h$}% \message{//depth:\the\dp0//}% \box0% az emelkedés magassága, \setbox0\hbox{$\rho$}% \message{//depth:\the\dp0//}% \box0% a folyadék sűrűsége, \setbox0\hbox{$g$}% \message{//depth:\the\dp0//}% \box0% a nehézségi gyorsulás, \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0% a cső sugara és \setbox0\hbox{$\theta$}% \message{//depth:\the\dp0//}% \box0% a nedvesítési szög. 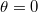Ideálisan nedvesítő folyadék esetén (\setbox0\hbox{$\theta = 0$}% \message{//depth:\the\dp0//}% \box0%):

\[\alpha = h \rho g r / 2\]

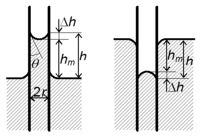
A mérésnél a csőben lévő folyadékfelszín alsó pontjának magasságát mérjük meg (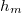\setbox0\hbox{$h_m$}% \message{//depth:\the\dp0//}% \box0%) és az emelkedés magasságát az alábbiak szerint számítjuk (3. ábra).

\[h = h_m + r/3\]

A nedvesítési szög ismeretében tehát a felületi feszültség egy kapilláris segítségével meghatározható.

Felületi feszültség mérése csepegtetéssel

4. ábra
5.ábra

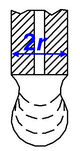
Ezen mérési módszer alapgondolata az, hogy egy folyadékcsepp lecseppenése akkor következik be, amikor a csepp súlya meghaladja a leszakadási felületnél a felületi feszültségből származó erőt. 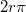Ha vastag falú, függőleges, alul síkra csiszolt kapilláris csőből lassan csepegtetjük ki a csövet jól nedvesítő folyadékot, akkor a csepp felszíne az \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0% külső sugarú csővel \setbox0\hbox{$2 r \pi$}% \message{//depth:\the\dp0//}% \box0% hosszú darabon érintkezik. Ekkor a felületi feszültségből származó erő legfeljebb 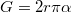\setbox0\hbox{$G = 2 r \pi \alpha$}% \message{//depth:\the\dp0//}% \box0% súlyú cseppet tud megtartani. Valójában a leszakadó csepp súlya a 3. 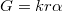ábrán látható "befűződés" miatt a fenti értéknél kisebb: \setbox0\hbox{$G = k r \alpha$}% \message{//depth:\the\dp0//}% \box0%, ahol a \setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0% állandó a felületi feszültségtől, a cső méretétől és a folyadék sűrűségétől függő állandó, értéke 3,8 és 4,5 közötti. Egy adott eszköz \setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0% értékét ismert felületi feszültségű anyagok segítségével határozhatjuk meg. Tájékozódó jellegű összehasonlító méréseknél a \setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0% ismerete mellőzhető, mert ebben az esetben két folyadékra nézve

\[\alpha_1 / \alpha_2 = G_1 / G_2\]

A csepegtetéssel működő felületi feszültség mérő eszközöket sztalagmométereknek nevezzük.

Felületi feszültség mérés szakításos módszerrel

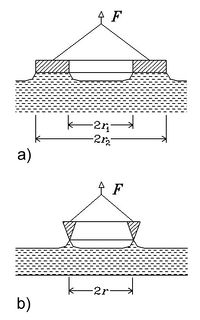
Egy folyadékba mártott gyűrűt – amelynek anyagát a folyadék nedvesíti – lassan, függőlegesen kiemeljük a folyadékból, és közben folyamatosan mérjük az erőt (5. ábra). Az erő maximális értéke a gyűrű súlyával és a gyűrűhöz tapadó vékony folyadékhártya elszakításához szükséges erővel egyenlő.

Az 5/a ábrán látható elrendezés esetén:

\[F_{max} = G + 2 \pi \left( r_1 + r_2 \right) \alpha\]

az 5/b ábrán látható elrendezés esetén pedig:

\[F_{max} = G + 4 \pi r \alpha\]

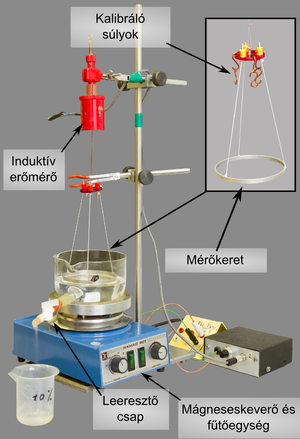
A felületi feszültség hatására fellépő erő nagyon kicsi. A mérési gyakorlaton az erőt induktív mérőátalakítóval mérjük, amely az erővel arányos feszültségjelet ad ki. A feszültségjelet az idő függvényében számítógépen lehet rögzíteni, és így az erő maximuma meghatározható.

Erő mérése induktív mérőátalakítóval

6.ábra
7.ábra

Az induktív mérőátalakító elmozdulás detektálására alkalmas, így felhasználható minden olyan mennyiség mérésére, melynek változása elmozdulást eredményez. Így például deformáció, és ezen keresztül erő mérésére is.

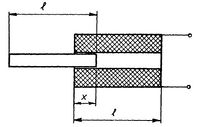
Az induktív mérőátalakító a mérendő fizikai mennyiség változásának hatására induktivitásváltozást hoz létre. A mérendő fizikai mennyiség nagysága és a mérőátalakító induktivitása között egyértelmű kapcsolat van. Így induktivitás méréssel vagy az induktivitásváltozás egyéb módon való detektálásával a mérendő fizikai mennyiség nagysága meghatározható. A legegyszerűbb, nyitott mágneses körű átalakító lényegében egy vasmagos tekercs. Vázlata a 6. ábrán látható. Ha a vasmag nélküli tekercs 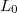\setbox0\hbox{$L_0$}% \message{//depth:\the\dp0//}% \box0% induktivitásából indulunk ki, könnyen belátható, hogy a vasmagnak a tekercsbe való bevitele az önindukciós együttható növekedését eredményezi. Az önindukciós együttható maximuma ott lesz, ahol a mágneses ellenállás a legkisebb, azaz ahol a vasmag teljes egészében a tekercsben helyezkedik el. A magot tovább mozgatva (a másik oldalon kihúzva a tekercsből) induktivitás az előzőekkel szimmetrikusan csökken.

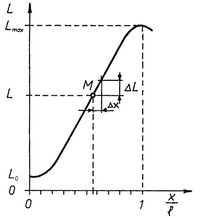
A nyitott mágneses körű mérőátalakító karakterisztikája a 7. ábrán látható. Önindukciós együtthatója a vasmag helyzetének függvénye, tehát az átalakító elmozdulás hatására induktivitás-változást hoz létre. A karakterisztika viszonylag hosszú lineáris szakasszal rendelkezik, ami nagy (néhány cm) elmozdulások mérésére teszi alkalmassá. A tekercs hossztengelye mentén a menetsűrűség megfelelő változtatásával a linearitási tartomány növelhető. A mérőátalakító induktivitása sokféleképp mérhető. Gyakran alkalmazzák az úgynevezett differenciál kialakítást. A differenciál kialakítású induktív adó két teljesen azonos induktív adó, úgy elhelyezve, hogy bemenőjel (vasmag elmozdulás) hatására az egyik átalakító induktivitása nő, a másiké csökken. A differenciál kialakítású induktív adó alkalmazása azzal az előnnyel jár, hogy a hídkapcsolás érzékenysége kétszerese lesz az egy adót tartalmazó híd érzékenységének, megnő a kapcsolás linearitási tartománya, míg a külső zavaró tényezők a híd két ágára egyszerre hatnak, így csökkentve fejtik ki hatásukat.

Mérési feladatok

A méréshez rendelkezésre álló eszközök

  • A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.

1. Víz-alkohol oldatok felületi feszültségének mérése csepegtetéses módszerrel

8. ábra: Sztalagmométer

a) Határozza meg a sztalagmométer \setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0% készülékállandóját desztillált víz segítségével! A sztalagmométer egy csapos tölcsér. Ne érintse kézzel a kapilláris zsírtalanított alsó peremét ill. a tölcsér belsejét! A sztalagmométert függőleges helyzetbe rögzítse, majd a csap elzárása után a tölcsér feléig töltse meg desztillált vízzel. A csepegtetés megkezdése előtt mérjen le táramérleggel egy üres műanyag edényt, majd csepegtessen a pohárba minimálisan 100 cseppet. A csap óvatos nyitásával a folyadékáramlást úgy szabályozza be, hogy a cseppek kényelmesen számolhatóak legyenek. Az edény visszamérése után 1 csepp átlagtömege, 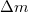\setbox0\hbox{$\Delta m$}% \message{//depth:\the\dp0//}% \box0% számolható. Az egyensúly feltételéből 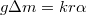\setbox0\hbox{$g \Delta m = k r \alpha $}% \message{//depth:\the\dp0//}% \box0%, ami alapján a desztillált víz felületi feszültségének ismeretében a \setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0% készülékállandó meghatározható.

b) Ismételje meg az a) feladatot 10 és 20 %-os alkohol oldattal! Az oldatcseréhez engedje le a tölcséres csepegtetőből a folyadékot, töltse fel a következő oldattal, majd azt is folyassa ki. Egy újabb (második) feltöltés után az új oldat már mérhető.

  • Az alkoholos oldatok maradékait kérjük a megfelelő gyűjtőedénybe önteni!

2. Szakításos felületi feszültség mérő beállítása és kalibrálása

9. ábra

a) Állítsa össze a szakításos felületi feszültség mérőt! Az induktív erőmérő elektronikája az erőhatással arányos -10 és +10 V közötti feszültségjelet generál, melynek a nulla szintje potméterrel szabályozható. Ezt a feszültségjelet kösse a HAMEG digitális multiméterre. A mért feszültséget számítógépes interfészen keresztül, a felfesz_meres.exe program segítségével rögzíti. Ellenőrizze a program működését, és állítsa be az induktív erőmérő nullszintjét -6 V és -3 V közötti értékre.

  • Figyelem! A mérőkeretet előzetesen zsírtalanítottuk, ezért azt kézzel érinteni tilos!

b) Kalibrálja az induktív erőmérőt! Akasszon növekvő számban felfüggeszthető súlyokat az erőmérőre, és a súlyok számának függvényében vegye fel az erőmérő kimenő feszültségét, illesszen egyenest a mért pontokra.

  • A súlyokat ne a mérőkeretre, hanem a mérőkeret feletti műanyag lapon található lyukakba akassza. Ügyeljen a keret egyenletes terhelésére, ha a súlyok egy oldalra húzzák a keretet, megnő az induktív erőmérőben a súrlódás, ami növeli a mérési hibát. A súlyok átlagos tömege: 0,47 g.

c) Vízszintezze a mérőkeretet! Ehhez helyezze a keret alá egy állítható lábú plexi asztalkát. Az asztalra helyezett vízszintmérő segítségével vízszintezze az aszalt olyan magasságban, hogy a mérőkeret éppen ne érjen hozzá. Ezután a mérőkeret feletti műanyag tárcsán található piros csavarok segítségével állítsa be a mérőkeretet az asztal síkjával párhuzamosan.

  • A mérőkeret vízszintességét a mérés során többször is ellenőrizze, és szükség esetén korrigálja.

3. Víz-alkohol oldatok felületi feszültségének mérése szakításos módszerrel

  • Becsülje meg, és állítsa be az erőmérés számítógépes rögzítésének optimális mintavételezési frekvenciáját!

a) Helyezze a deszt. víz feliratú, leeresztő csappal ellátott edényt a mérőkeret alá. Töltse fel az edényt desztillált vízzel addig, hogy a vízszint pár mm magasan legyen a keret alsó éle felett. Gyors csepegtetéssel eressze le az edényből a vizet a deszt. víz feliratú gyűjtőedénybe, közben vegye fel az erő változását a gyűrű szakadásáig. Ekkor a csapot elzárva a pohárból töltse vissza a vizet a keret közepébe (nem a keretre!) és a szakítási kísérletet ismételje meg legalább kétszer!

  • Az erőt mindig az elszakadás előtti és a szakadás utáni feszültségszint különbségéből állapítsa meg!
  • A mérőkeret átmérője a szakítási élnél 91 mm.

b) Az a) mérést ismételje meg 10 %-os és 20 %-os alkohololdattal.

  • Figyelem! Az oldatokat mindig a koncentrációnak megfelelő feliratú edénybe töltse, majd a mérés végén ne öntse ki, hanem töltse vissza a megfelelő tároló edénybe. Ügyeljen rá, hogy az oldatok ne keveredjenek.
  • Hasonlítsa össze az egyes oldatok csepegtetéses és szakításos módszerrel meghatározott felületi feszültség értékeit egymással, valamint a rendelkezésre álló irodalmi adatokkal!

4. Desztillált víz felületi feszültségének hőmérséklet függése, Eötvös-féle szabály igazolása

A 4/a mérést ismételje meg desztillált vízzel 40 és 60 °C-os hőmérsékleten. A hőmérséklet méréséhez rögzítse a higanyszálas hőmérőt a bunsen állványhoz. A víz melegítése közben használjon mágneses keverőt, de az erőmérés előtt kapcsolja ki a keverőt, és várja meg, míg a vízfelszín megnyugszik. Ábrázolja a felületi feszültséget a hőmérséklet függvényében, és illesszen egyenest a mérési pontokra! Az egyenes paramétereiből határozza meg az Eötvös-állandót és a kritikus hőmérsékletet.


Vissza a Fizika laboratórium 1. tárgyoldalára.


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Folyadékok_felületi_feszültségének_mérése&oldid=16219”