„Ellenőrző kérdések, példák (Fizika I.)” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<wlatex> '''1. Tér és idő''' Igaz/Hamis állítások: : A másodperc (szekundum) SI-alapegység. :: IGEN. A másodperc az [http://en.wikipedia.org/wiki/International_…”) |
|||
| 24. sor: | 24. sor: | ||
: A sebesség olyan vektormennyiség, amely megadja a mozgás irányát is. | : A sebesség olyan vektormennyiség, amely megadja a mozgás irányát is. | ||
:: IGEN. A a sebességet az elmozdulásvektor segítségével vektoriális mennyiségként definiáljuk: $\vec{v}=\frac{{\rm d}\vec{r}}{{\rm d}t}$ | :: IGEN. A a sebességet az elmozdulásvektor segítségével vektoriális mennyiségként definiáljuk: $\vec{v}=\frac{{\rm d}\vec{r}}{{\rm d}t}$ | ||
| + | |||
Feladatok: | Feladatok: | ||
| − | : Egy | + | : Egy futó a 100 m-es vágtaszámot 10,3 s- os eredménnyel nyerte meg. Egy másik futó 10,8-as idővel futott be. Feltéve, hogy az atléták a teljes távon egyenletesen futottak, határozzuk meg, hogy milyen távol volt a második futó a céltól, amikor a győztes átszakította a célszalagot! |
| + | ::: Megoldás: 4,63 m-re van a második futó a céltól abban a pillanatban, mikor az első célba ér. | ||
| + | : Egy követ 50 m mély kútba ejtettünk. Határozzuk meg, hogy mennyi idő múlva halljuk a kő csobbanását! (A hang terjedési sebessége 330 m/s.) | ||
| + | ::: Megoldás: 3,19 s + 0,15 s = 3,34 s. | ||
| + | : . Egy csapból egyenletesen csöpög a víz a 30 cm-rel lejjebb elhelyezett mosogatóba. A csepegés üteme olyan, hogy amikor egy csepp becsapódik, akkor a következő már a levegőben van és a harmadik éppen leszakad a csapról. Határozzuk meg, hogy hány csepp esik le percenként! | ||
| + | ::: Megoldás: 486 csepp. | ||
'''2. Mozgás és megjelenítése''' | '''2. Mozgás és megjelenítése''' | ||
| + | Igaz/Hamis állítások: | ||
: Egy test mindig a rá ható erők eredőjének irányába mozog. | : Egy test mindig a rá ható erők eredőjének irányába mozog. | ||
| + | :: NEM A testre ható erők eredője csak a gyorsulás irányát adja meg. A mozgás iránya (a sebességvektor iránya) ettől eltérő lehet. Gondoljunk az egyenletes körmozgásra, vagy a ferde hajításra. | ||
: Testek egymásra hatásakor fellépő erő, ellenerő kioltja egymást. | : Testek egymásra hatásakor fellépő erő, ellenerő kioltja egymást. | ||
| + | :: NEM A két erő nem ugyanarra a testre hat nincs értelme összegezni őket. | ||
: Körpályán mozgó test gyorsulása lehet zérus. | : Körpályán mozgó test gyorsulása lehet zérus. | ||
| + | :: NEM Ha a test körpályán mozog akkor gyorsulásvektorának kell lenni centripetális komponensének. | ||
: A testre ható súrlódási erő növelheti a test sebességét. | : A testre ható súrlódási erő növelheti a test sebességét. | ||
| + | :: IGEN Ezt tapasztalhatjuk például járás közben, vagy amikor kirántjuk az abroszt a tányér alól. | ||
: Körpályán mozgó test gyorsulása mindig a középpont felé mutat. | : Körpályán mozgó test gyorsulása mindig a középpont felé mutat. | ||
| + | :: NEM Csak ha egyenletes a körmozgás. Gyorsuló körmozgás esetén van a gyorsulásvektornak érintő irányú komponense is. | ||
: Fonálinga lengésekor a legnagyobb erő a fonálban a szélső helyzetekben ébred. | : Fonálinga lengésekor a legnagyobb erő a fonálban a szélső helyzetekben ébred. | ||
| + | :: NEM A legnagyobb erő a fonálban akkor ébred, ha a test a függőleges helyzeten halad át. Ebben a pillanatban a fonálerőnek biztosítani kell a körpályán mozgáshoz szükséges centripetális erőt és ellensúlyozni kell a testre ható nehézségi erőt is. | ||
: Az alátámasztásra kifejtett erő (nyomóerő) csak a súlyerőtől függ. | : Az alátámasztásra kifejtett erő (nyomóerő) csak a súlyerőtől függ. | ||
| − | : Két kiskocsit vizsgálunk. Az egyikre kötött, csigán átvetett fonalat $\rm 20 N $ erővel húzzuk, a másikra $\rm 2 kg $ tömegű testet akasztottunk. A kocsik tömege egyenlő (1kg), $\rm g =10 m/s^{2}$. | + | :: NEM Az alátámasztásra kifejtett erő függ a test mozgásállapotától is. Például lefelé gyorsuló liftben a test súlya csökken (a súlyerő természetesen nem változik). Ha a lift szabadon esik, akkor a nyomóerő megszűnik, a tárgy súlytalan lesz, pedig ekkor is hat a súlyerő. |
| + | : Két kiskocsit vizsgálunk. Az egyikre kötött, csigán átvetett fonalat $\rm 20 N $ erővel húzzuk, a másikra $\rm 2 kg $ tömegű testet akasztottunk. A kocsik tömege egyenlő (1kg), $\rm g =10 m/s^{2}$. Az első kocsi gyorsulása nagyobb. | ||
| + | :: IGEN Az első kocsinál a húzóerő csak a kocsit gyorsítja. A második kocsinál a húzóerőt a kötél végére rögzített testre ható nehézségi erő szolgáltatja aminek két tömeget kell gyorsítani. | ||
| + | : Van olyan mozgás, amelyben a test gyorsul, de sebessége se nem nő se nem csökken. | ||
| + | :: IGEN Az egyenletes körmozgás. | ||
| + | |||
| + | |||
| + | Feladatok: | ||
| + | : Egy testet $\rm 5 N$ állandó erővel tudunk egyenletesen felfelé húzni egy $\rm \alpha =30^0$ hajlásszögű lejtőn. Ugyanezen a lejtőn lefelé szabadon csúszva a test $\rm 5 m/s$ sebességről $\rm5 m $ hosszú úton áll meg. Mekkora a súrlódási együttható? | ||
| + | ::: Megoldás: $\rm \mu = 0,81$. | ||
| + | : . Egy $\rm 800 N $ súlyú testet nyugalmi helyzetéből indítva állandó gyorsulással, kötéllel húzunk függőlegesen felfelé. A test ily módon $\rm5s$ alatt $\rm25m$ magasra jut. Mekkora munkát végzett az emelő erő? | ||
| + | ::: Megoldás: W=24000 J. | ||
| + | |||
'''3. Megmaradási törvények a mechanikában''' | '''3. Megmaradási törvények a mechanikában''' | ||
| + | Igaz/Hamis állítások: | ||
: A gravitációs erő munkája független a kezdő – és végpont közötti útvonaltól. | : A gravitációs erő munkája független a kezdő – és végpont közötti útvonaltól. | ||
| + | :: IGEN A gravitációs erőtér konzervatív. | ||
: Egy test potenciális energiája lehet negatív. | : Egy test potenciális energiája lehet negatív. | ||
| + | :: IGEN Attól függően, hogy hol vesszük fel a helyzeti (potenciális) energia null szintjét a helyzeti energia lehet negatív. | ||
| + | : Ha egy testre disszipatív erők is hatnak, akkor a munkatétel nem érvényes. | ||
| + | :: NEM A munkatétel ekkor is érvényes. (A mechanikai energia megmaradásának tétele azonban nem!)Ha ismerjük a testre ható erőket, akkor munkájukat kiszámítva meghatározhatjuk a test mozgási energiájának megváltozását. | ||
| + | |||
| + | |||
| + | Feladatok: | ||
| + | : Egy $\rm v_o=400m/s $ kezdősebességű és $\rm \alpha=30^o $ alatt fellőtt lövedék pályájának tetőpontjában egy m és egy 2m tömegű részre robban szét. Mindkét rész egyszerre éri a talajt, és az m tömegű rész a kilövés helyén csapódik be. Hol csapódik be a 2m tömegű rész? | ||
| + | ::: Megoldás: A 2m tömegű rész a kilövés helyétől kb. 20km-re esik le. | ||
| + | : . Felfüggesztett, $\rm 100 kg $ tömegű homokzsák (ballisztikus inga) egy $\rm 200 g $ tömegű lövedék becsapódása után $\rm 10^0-kal $ kilendül. Mennyi volt a lövedék sebessége, ha az inga hossza $\rm 2 m $ ? | ||
| + | ::: Megoldás: 310 m/s. | ||
| + | : . Az $\rm r_1=0.1m $ sugarú tárcsa és az $\rm r_2=0.15m $ sugarú henger egymással párhuzamos forgási szimmetriatengelyei surlódásmentesen csapágyazott forgási tengelyek. A henger tehetetlenségi nyomatéka $\rm \theta =5kg.m^2 $. A tárcsa és a henger a kerületükön összeérnek és $\rm F=500N $ erő szorítja őket egymáshoz, miközben a két felület között a csúszási súrlódási tényező $\rm \mu=0.5 $. Kezdetben a tárcsa és a henger nyugalmi helyzetben van, majd a tárcsa $\rm n_1=5s^{-1} $ állandó fordulatszámmal forogni kezd. | ||
| + | :: a.) Mennyi idő elteltével szűnik meg a tárcsa és a henger érintkező felületeinek a csúszása? | ||
| + | :: b.) Hogyan aránylik a henger mozgási energiája az előbbi időpontban a tárcsa által addig végzett munkához? | ||
| + | ::: Megoldás: t=2,8 s; a henger mozgási energiája és a tárcsa által addig végzett munkája aránya: 0,5. | ||
| + | |||
'''4. Rezgések''' | '''4. Rezgések''' | ||
| + | |||
| + | Igaz/Hamis állítások: | ||
: Fonálinga lengésideje kis kitérések esetén függ a tömegtől. | : Fonálinga lengésideje kis kitérések esetén függ a tömegtől. | ||
:: NEM Fonálinga lengésideje kis kitérések esetén csak az inga hosszától (és a nehézségi gyorsulástól) függ. | :: NEM Fonálinga lengésideje kis kitérések esetén csak az inga hosszától (és a nehézségi gyorsulástól) függ. | ||
| 55. sor: | 99. sor: | ||
: Csillapított rezgőmozgást végző test sebessége és gyorsulása között a fáziskülönbség 90°. | : Csillapított rezgőmozgást végző test sebessége és gyorsulása között a fáziskülönbség 90°. | ||
:: NEM Gondoljunk a különböző csillapítású (pl. túlcsillapított) rezgésekre. | :: NEM Gondoljunk a különböző csillapítású (pl. túlcsillapított) rezgésekre. | ||
| − | |||
| − | + | Feladatok: | |
| + | : Pontszerűnek tekinthető $\rm 1 kg $ tömegű testre $\rm F=-Dx $ alakú rugalmas erő hat. A rugóállandó $\rm D=0.25 N/cm$. A $\rm t=0$ pillanatban a kitérés $\rm 20 cm$, a sebesség $\rm 2.83 m/s$. Mekkora a rezgés frekvenciája, amplitúdója és a kezdőfázisa? Írja fel a kitérés - idő függvényt! | ||
| + | ::: Megoldás: f=0.8 Hz; A=0.6 m; $\rm \alpha=-70^o; x=0.6 cos(5t-70^0)$. | ||
| + | : Egy $\rm 5 N/m $ rugóállandójú rugóhoz kapcsolt $\rm 0.2 kg $ tömegű test csillapodó rezgéseket végez. Energiája $\rm 50 s $ alatt exponenciálisan az e-ed részére csökken. Mekkora a rezgés frekvenciája és 10 rezgés alatt az amplitúdó hány százalékkal csökken? | ||
| + | ::: Megoldás: f=0.8 Hz. Az eddigiek alapján 10 rezgés alatt az amplitúdó 12%-al csökken. | ||
| + | : Két rezgés frekvenciája és amplitúdója azonos, rezgésirányuk egymásra merőleges, fáziskülönbségük $\rm \pi/3$. Milyen eredő rezgés keletkezik? | ||
| + | ::: Megoldás: $\rm x^2+y^2-xy=3/4. Ez egy origó középpontú ellipszis egyenlete, melynek tengelyei nem esnek egybe az x és y tengelyekkel. | ||
| − | |||
| − | |||
| − | + | '''5. Rend és rendetlenség''' | |
| − | + | ||
| − | + | ||
| − | + | Igaz/Hamis állítások: | |
| − | + | : Az intenzív állapotjelzők (pl. hőmérséklet, nyomás) a rendszer méretétől függetlenek, két rendszer egyesítésekor átlagolódnak. | |
| − | + | :: IGEN Az említett állapotjelzők (és például még: sűrűség, kémiai potenciál) intenzív állapotjelzők, amelyekre igaz, hogy a rendszer méretétől függetlenek és két rendszer egyesítésekor átlagolódnak. Az extenzív állapotjelzők a rendszer méretével együtt nőnek, két rendszer egyesítésekor összeadódnak: ilyen pl. a térfogat, a tömeg, a mólszám, a belső energia és az entrópia. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | b.) Mekkora az előbbi állapotban az entrópia? | + | Feladatok: |
| + | : $\rm10^{-3}m^{3}$ térfogatú tartályban a gáz nyomása 200 kPa, a molekulák átlagos kinetikus energiája $\rm10^{-21}J$. Mennyi a molekulák száma és hány mól ez az anyag? | ||
| + | ::: Megoldás: N=$\rm 3.10^{22}$db. A mólok száma: 0,05. | ||
| + | : Egy $10^{-3} \, {\rm m^{3}}$ térfogatú edényben N számú hidrogénmolekula tartózkodik szobahőmérsékleten. Állapítsuk meg annak az állapotnak a p valószínűségét, amelyben az összes molekula az edény egyik felében tartózkodik! | ||
| + | ::: Megoldás: p=$\rm\frac{1}{2^N}$. | ||
| + | : Az oxigénmolekulák termikus sebessége $\rm 0 ^{o}C$-on $\rm 425 m/s$, tömegük $\rm 5,3\cdot 10^{-26} kg$. Hány oxigénmolekulának kell $\rm1 s$ alatt a gáztartály $\rm1 cm^{2}$ felületű részének ütközni, hogy a normál légköri nyomás alakuljon ki? | ||
| + | ::: Megoldás: N=$\rm 1,33.10^{24}$db. | ||
| + | : Televízió képcsövében alkalmazott elektronnyalábban az elektronok $\rm8\cdot10^{7}m/s $ sebességgel mozognak. A képernyő $\rm 1 mm^{2}$ nagyságú felületére $\rm5\cdot10^{14}$ elektron érkezik másodpercenként. Határozzuk meg az általuk kifejtett nyomást, ha feltételezzük, hogy az elektronok nem pattannak vissza a képernyő felületéről! (Az elektronok tömege: $\rm9,1\cdot10^{-31}kg.$) | ||
| + | ::: Megoldás: p=$\rm 0,036$ Pa. | ||
| + | : A világűrben a hőmérséklet átlagosan 3 K. Határozzuk meg itt a protonok legvalószínűbb sebességét! ($\rm m_p=1,67\cdot10^{-27}kg$) | ||
| + | ::: Megoldás: $\rm v_0 = 223 m/s$ | ||
| + | : Egy 1 literes edény $\rm10^{24}$ db, egyenként $\rm5,3\cdot10^{-26}kg$ tömegű gázmolekulát tartalmaz, 273 K-on. Mennyi a gázrészecskék termikus sebessége és mennyi az ideálisnak tekintett gáz nyomása? | ||
| + | ::: Megoldás: $\rm v_T = 462$ m/s. p=3,8 MPa. | ||
| + | : Számítsuk ki, hogy mekkora a relatív valószínűsége annak, hogy $\rm10^{-7}J$ energia $\rm14^{o}C$ hőmérsékletű testről egy $\rm15^{o}C$ hőmérsékletű testre önként átmenjen. | ||
| + | ::: Megoldás: $\rm {e^{-10}}^{11}$. | ||
| + | : Ideális gáz N molekuláját tartalmazó edény $\rm V_1$ és $\rm V_2$ térfogatú részre különül el. Mekkora a valószínűsége, hogy a $\rm V_1$ térfogatú részben $\rm N_1$ és a $\rm V_2$ térfogatban $\rm N_2$ részecske van? | ||
| + | ::: Megoldás: $\rm p=\frac{N!}{N_1!.N_2!}.p_1^{N_1}.p_2^{N_2}$, ahol $\rm p_1=\frac{V_1}{V_1 + V_2}$ és $\rm p_2=1-p_1$. | ||
| + | : Egy részecskerendszer 10 klasszikusan tárgyalható részecskéből áll, és 6 lehetséges energiaállapottal rendelkezik. | ||
| + | ::a.) Mekkora a termodinamikai valószínűsége annak a makroállapotnak, amelynél a fáziscellák betöltési számai: 0 2 1 0 4 3? | ||
| + | ::b.) Mekkora az előbbi állapotban az entrópia? ($\rm k_B = 1,38\cdot10^{-23}J/K$) | ||
| + | ::: Megoldás: W=$\rm12600$. S=$\rm 1,3.10^{-22} J/K$. | ||
| + | : Mekkora egy $\rm H_2$ molekula legvalószínűbb sebessége $\rm 27^{o}C$ hőmérsékleten? Hány fokra kell növelni a hőmérsékletet ahhoz, hogy megkétszereződjön a legvalószínűbb sebesség? | ||
| + | ::: Megoldás: $\rm v_0 = 1576$ m/s. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''6. Hideg-meleg''' | '''6. Hideg-meleg''' | ||
| + | Igaz/Hamis állítások: | ||
| + | : Adott mennyiségű normálállapotú gáz hőmérsékletét kétféleképpen változtatjuk meg: izobár, ill. izochor módon. Mindkét esetben azonos ideig melegítjük ugyanazzal az elektromos fűtőszállal. Az izochor folyamatban nagyobb a hőmérséklet változás. | ||
| + | :: IGEN Izobár állapotváltozás esetén a gázzal közölt hőmennyiség munkavégzésre és a belső energia növelésére fordítódik. Izochor állapotváltozás esetén a közölt hő csak a belső energiát növeli. | ||
| + | : Ideális gáz izotermikus állapotváltozásakor a gáz belső energiája nem változik. | ||
| + | :: IGEN Izotermikus állapotváltozáskor a gáz hőmérséklete állandó. Ez pedig azt jelenti, hogy a belső energia nem változik. | ||
| + | : Súrlódáskor hő keletkezik. | ||
| + | :: NEM Súrlódáskor a testek belső energiája nő meg. Ez a hőmérséklet emelkedésében jelentkezik legnyilvánvalóbban. A hő nem energia! | ||
| + | |||
| + | |||
'''7. Töltések''' | '''7. Töltések''' | ||
| + | |||
| + | Igaz/Hamis állítások: | ||
: Az elektroszkóp töltések előállítására szolgál. | : Az elektroszkóp töltések előállítására szolgál. | ||
:: NEM Az [http://en.wikipedia.org/wiki/Electroscope elektroszkóp] töltések kimutatására (esetleg töltésmennyiség mérésére) szolgál. Töltések előállítására (pontosabban: szétválasztására) használhatjuk például a [http://en.wikipedia.org/wiki/Van_de_Graaff_generator Van de Graaff generátort]. | :: NEM Az [http://en.wikipedia.org/wiki/Electroscope elektroszkóp] töltések kimutatására (esetleg töltésmennyiség mérésére) szolgál. Töltések előállítására (pontosabban: szétválasztására) használhatjuk például a [http://en.wikipedia.org/wiki/Van_de_Graaff_generator Van de Graaff generátort]. | ||
| 130. sor: | 179. sor: | ||
| − | + | Feladatok: | |
| − | + | : Egymástól 5 cm távolságban lévő nagy kiterjedésű párhuzamos síkok felületi töltéssűrűsége $\rm 8.10^{-8} \frac{C}{m^2}$ illetve $\rm 9.10^{-8} \frac{C}{m^2}$. Határozzuk meg a térerősségeket az elrendezés terében! | |
| + | ::: Megoldás: A rétegek között: $\rm E=E_2-E_1=0.6.10^3 V/m$, Kívül: $\rm E=E_2+E_1=9.5.10^3 V/m$. | ||
'''8. Vezetők és szigetelők''' | '''8. Vezetők és szigetelők''' | ||
| + | |||
| + | Igaz/Hamis állítások: | ||
: Ugyanolyan mértékben feltöltött két vezető esetén ugyanolyan távolságnál nagyobb az erőhatás, ha ellentétesen töltöttük fel a vezetőket. | : Ugyanolyan mértékben feltöltött két vezető esetén ugyanolyan távolságnál nagyobb az erőhatás, ha ellentétesen töltöttük fel a vezetőket. | ||
:: IGEN Ha ellentétesen töltöttük fel a vezetőket, a fém felületen elmozdulni tudó töltések az egy máshoz közelebbi felületrészekre gyűlnek, míg azonos előjelű töltés esetén a távolabbi felületrészeken lesznek a töltések. A Coulomb erő pedig a távolság négyzetével fordítottan arányos. | :: IGEN Ha ellentétesen töltöttük fel a vezetőket, a fém felületen elmozdulni tudó töltések az egy máshoz közelebbi felületrészekre gyűlnek, míg azonos előjelű töltés esetén a távolabbi felületrészeken lesznek a töltések. A Coulomb erő pedig a távolság négyzetével fordítottan arányos. | ||
| 145. sor: | 197. sor: | ||
: Ha felfújt léggömbre töltéseket viszünk, akkor a léggömb mérete kissé megnő. | : Ha felfújt léggömbre töltéseket viszünk, akkor a léggömb mérete kissé megnő. | ||
:: IGEN Azonos előjelű töltések taszítják egymást, így ez az erőhatás okozhatja a léggömb anyagának kismértékű megnyúlását. | :: IGEN Azonos előjelű töltések taszítják egymást, így ez az erőhatás okozhatja a léggömb anyagának kismértékű megnyúlását. | ||
| + | |||
'''9. Az elektromos potenciál és energia''' | '''9. Az elektromos potenciál és energia''' | ||
| + | |||
| + | Igaz/Hamis állítások: | ||
: Egy töltött tömör fémgömb belsejében a potenciál zérus. | : Egy töltött tömör fémgömb belsejében a potenciál zérus. | ||
:: IGEN Ha a potenciál zérustól különböző lenne akkor a töltések valamilyen úton elmozdulhatnának és végső soron sérülne az energiamegmaradás törvénye. | :: IGEN Ha a potenciál zérustól különböző lenne akkor a töltések valamilyen úton elmozdulhatnának és végső soron sérülne az energiamegmaradás törvénye. | ||
| 169. sor: | 224. sor: | ||
: Az elektromos potenciális energia különbsége és az elektromos potenciálkülönbség azonos. | : Az elektromos potenciális energia különbsége és az elektromos potenciálkülönbség azonos. | ||
:: NEM Nem azonos típusú mennyiségek. Az elektromos potenciális energia egy töltött részecske potenciális energiájának megváltozása (vagy értéke egy adott pontban egy referencia ponthoz képest). Mértékegysége: Joul. Az elektromos potenciálkülönbség az elektromos térre jellemző mennyiség. Segítségével kiszámíthatjuk adott töltés esetén mekkora munkavégzés történik, ha a töltést az egyik pontból a másikba visszük. Mértékegysége: Volt=Joul/Coulomb. | :: NEM Nem azonos típusú mennyiségek. Az elektromos potenciális energia egy töltött részecske potenciális energiájának megváltozása (vagy értéke egy adott pontban egy referencia ponthoz képest). Mértékegysége: Joul. Az elektromos potenciálkülönbség az elektromos térre jellemző mennyiség. Segítségével kiszámíthatjuk adott töltés esetén mekkora munkavégzés történik, ha a töltést az egyik pontból a másikba visszük. Mértékegysége: Volt=Joul/Coulomb. | ||
| − | + | ||
| + | |||
| + | Feladatok: | ||
| + | : Mekkora a potenciál a 8 cm sugarú gömb középpontjából 70cm távolságban, ha a gömbön $\rm 10^{-8} \frac{C}{cm^2}$ töltéssűrűség és a térben $\rm \epsilon_r=5$ dielektromos állandójú közeg van? | ||
| + | ::: Megoldás: U= $\rm 2.10^4 V$. | ||
| + | : Egy $\rm 6 \mu F$-os és egy $\rm 8 \mu F$-os kapacitású kondenzátort sorba kötünk. Az igy kapott rendszer sarkaira 16 V feszültséget kapcsolunk. Mekkora a kondenzátorok töltése? | ||
| + | ::: Megoldás: $\rm Q_1=Q_2=5.43.10^{-5} [C] $ | ||
'''10. Az elektromos mező energiája''' | '''10. Az elektromos mező energiája''' | ||
| + | |||
| + | Igaz/Hamis állítások: | ||
: Ha elektromos térben töltést mozgatunk, akkor minden esetben változik a elektromos tér energiája. | : Ha elektromos térben töltést mozgatunk, akkor minden esetben változik a elektromos tér energiája. | ||
:: NEM Az elektromos tér energiája csak akkor változik, ha a töltés mozgatásakor munkavégzés történt. (Ha a mozgatáskor munkát végzünk, azzal növeljük a tér energiáját.) Ha a töltést az erővonalakra merőlegesen mozgatjuk, nem történik munkavégzés, a tér energiája nem változik. | :: NEM Az elektromos tér energiája csak akkor változik, ha a töltés mozgatásakor munkavégzés történt. (Ha a mozgatáskor munkát végzünk, azzal növeljük a tér energiáját.) Ha a töltést az erővonalakra merőlegesen mozgatjuk, nem történik munkavégzés, a tér energiája nem változik. | ||
| 190. sor: | 253. sor: | ||
: A dielektrikumra - annak sérülése nélkül – jóval nagyobb elektromos tér kapcsolható, mintha a kondenzátor lemezei között légüres tér vagy levegő lenne. | : A dielektrikumra - annak sérülése nélkül – jóval nagyobb elektromos tér kapcsolható, mintha a kondenzátor lemezei között légüres tér vagy levegő lenne. | ||
:: IGEN A polárossá váló dielektrikum csökkenti a tér erősségét egy a dielektrikumra jellemző határig ([http://en.wikipedia.org/wiki/Dielectric_strength átütési szilárdság]). | :: IGEN A polárossá váló dielektrikum csökkenti a tér erősségét egy a dielektrikumra jellemző határig ([http://en.wikipedia.org/wiki/Dielectric_strength átütési szilárdság]). | ||
| + | |||
| + | |||
</wlatex> | </wlatex> | ||
A lap jelenlegi, 2011. július 1., 14:24-kori változata
1. Tér és idő
Igaz/Hamis állítások:
- A másodperc (szekundum) SI-alapegység.
- IGEN. A másodperc az SI rendszerben a hét alapegység egyike.
- A fényév az idő mértékegysége.
- NEM. A fényév a távolság csillagászatban használatos mértékegysége. Egy fényév
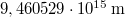 .
.
- NEM. A fényév a távolság csillagászatban használatos mértékegysége. Egy fényév
- A csillagászati egység SI egysége a távolságnak.
- NEM. A csillagászati egység SI-n kívüli távolságegység. A Nap és a Föld átlagos távolsága, azaz
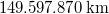 .
.
- NEM. A csillagászati egység SI-n kívüli távolságegység. A Nap és a Föld átlagos távolsága, azaz
- A kinematika (mozgástan) a mechanika azon részterülete, amelynek feladata a mozgások leírása.
- IGEN. A kinematika segítségével tetszőleges időpontban meghatározhatjuk egy test helyét, illetve helyzetét egy másik testhez képest.
- Egy tömegpont mozgását csak akkor írjuk le egyértelműen, ha megadjuk a helyét sebességét és gyorsulását az idő függvényében.
- NEM. Egy tömegpont mozgásának egyértelmű megadásához elegendő a helyét megadnunk az idő függvényében.
- A tömegpont modellel leírhatjuk a test forgó mozgását is.
- NEM. A tömegpont modell csak a test haladó mozgásának vizsgálatára alkalmas.
- Az elmozdulás skalármennyiség és a megtett úttal egyezik meg.
- NEM. Az elmozdulás vektormennyiség és a helyvektor megváltozásával egyezik meg.
- Az út skalármennyiség.
- IGEN. A test által a vizsgált idő alatt befutott pályaszakasz hossza.
- Az átlagsebesség vektormennyiség.
- NEM. Az átlagsebesség az összes megtett út és a mozgáshoz szükséges teljes idő hányadosával kapható meg.
- A sebesség olyan vektormennyiség, amely megadja a mozgás irányát is.
- IGEN. A a sebességet az elmozdulásvektor segítségével vektoriális mennyiségként definiáljuk:
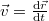
- IGEN. A a sebességet az elmozdulásvektor segítségével vektoriális mennyiségként definiáljuk:
Feladatok:
- Egy futó a 100 m-es vágtaszámot 10,3 s- os eredménnyel nyerte meg. Egy másik futó 10,8-as idővel futott be. Feltéve, hogy az atléták a teljes távon egyenletesen futottak, határozzuk meg, hogy milyen távol volt a második futó a céltól, amikor a győztes átszakította a célszalagot!
- Megoldás: 4,63 m-re van a második futó a céltól abban a pillanatban, mikor az első célba ér.
- Egy követ 50 m mély kútba ejtettünk. Határozzuk meg, hogy mennyi idő múlva halljuk a kő csobbanását! (A hang terjedési sebessége 330 m/s.)
- Megoldás: 3,19 s + 0,15 s = 3,34 s.
- . Egy csapból egyenletesen csöpög a víz a 30 cm-rel lejjebb elhelyezett mosogatóba. A csepegés üteme olyan, hogy amikor egy csepp becsapódik, akkor a következő már a levegőben van és a harmadik éppen leszakad a csapról. Határozzuk meg, hogy hány csepp esik le percenként!
- Megoldás: 486 csepp.
2. Mozgás és megjelenítése
Igaz/Hamis állítások:
- Egy test mindig a rá ható erők eredőjének irányába mozog.
- NEM A testre ható erők eredője csak a gyorsulás irányát adja meg. A mozgás iránya (a sebességvektor iránya) ettől eltérő lehet. Gondoljunk az egyenletes körmozgásra, vagy a ferde hajításra.
- Testek egymásra hatásakor fellépő erő, ellenerő kioltja egymást.
- NEM A két erő nem ugyanarra a testre hat nincs értelme összegezni őket.
- Körpályán mozgó test gyorsulása lehet zérus.
- NEM Ha a test körpályán mozog akkor gyorsulásvektorának kell lenni centripetális komponensének.
- A testre ható súrlódási erő növelheti a test sebességét.
- IGEN Ezt tapasztalhatjuk például járás közben, vagy amikor kirántjuk az abroszt a tányér alól.
- Körpályán mozgó test gyorsulása mindig a középpont felé mutat.
- NEM Csak ha egyenletes a körmozgás. Gyorsuló körmozgás esetén van a gyorsulásvektornak érintő irányú komponense is.
- Fonálinga lengésekor a legnagyobb erő a fonálban a szélső helyzetekben ébred.
- NEM A legnagyobb erő a fonálban akkor ébred, ha a test a függőleges helyzeten halad át. Ebben a pillanatban a fonálerőnek biztosítani kell a körpályán mozgáshoz szükséges centripetális erőt és ellensúlyozni kell a testre ható nehézségi erőt is.
- Az alátámasztásra kifejtett erő (nyomóerő) csak a súlyerőtől függ.
- NEM Az alátámasztásra kifejtett erő függ a test mozgásállapotától is. Például lefelé gyorsuló liftben a test súlya csökken (a súlyerő természetesen nem változik). Ha a lift szabadon esik, akkor a nyomóerő megszűnik, a tárgy súlytalan lesz, pedig ekkor is hat a súlyerő.
- Két kiskocsit vizsgálunk. Az egyikre kötött, csigán átvetett fonalat
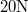 erővel húzzuk, a másikra
erővel húzzuk, a másikra 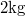 tömegű testet akasztottunk. A kocsik tömege egyenlő (1kg),
tömegű testet akasztottunk. A kocsik tömege egyenlő (1kg), 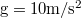 . Az első kocsi gyorsulása nagyobb.
. Az első kocsi gyorsulása nagyobb.
- IGEN Az első kocsinál a húzóerő csak a kocsit gyorsítja. A második kocsinál a húzóerőt a kötél végére rögzített testre ható nehézségi erő szolgáltatja aminek két tömeget kell gyorsítani.
- Van olyan mozgás, amelyben a test gyorsul, de sebessége se nem nő se nem csökken.
- IGEN Az egyenletes körmozgás.
Feladatok:
- Egy testet
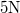 állandó erővel tudunk egyenletesen felfelé húzni egy
állandó erővel tudunk egyenletesen felfelé húzni egy 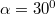 hajlásszögű lejtőn. Ugyanezen a lejtőn lefelé szabadon csúszva a test
hajlásszögű lejtőn. Ugyanezen a lejtőn lefelé szabadon csúszva a test 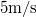 sebességről
sebességről 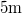 hosszú úton áll meg. Mekkora a súrlódási együttható?
hosszú úton áll meg. Mekkora a súrlódási együttható?
- Megoldás:
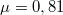 .
.
- Megoldás:
- . Egy
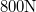 súlyú testet nyugalmi helyzetéből indítva állandó gyorsulással, kötéllel húzunk függőlegesen felfelé. A test ily módon
súlyú testet nyugalmi helyzetéből indítva állandó gyorsulással, kötéllel húzunk függőlegesen felfelé. A test ily módon 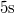 alatt
alatt 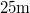 magasra jut. Mekkora munkát végzett az emelő erő?
magasra jut. Mekkora munkát végzett az emelő erő?
- Megoldás: W=24000 J.
3. Megmaradási törvények a mechanikában
Igaz/Hamis állítások:
- A gravitációs erő munkája független a kezdő – és végpont közötti útvonaltól.
- IGEN A gravitációs erőtér konzervatív.
- Egy test potenciális energiája lehet negatív.
- IGEN Attól függően, hogy hol vesszük fel a helyzeti (potenciális) energia null szintjét a helyzeti energia lehet negatív.
- Ha egy testre disszipatív erők is hatnak, akkor a munkatétel nem érvényes.
- NEM A munkatétel ekkor is érvényes. (A mechanikai energia megmaradásának tétele azonban nem!)Ha ismerjük a testre ható erőket, akkor munkájukat kiszámítva meghatározhatjuk a test mozgási energiájának megváltozását.
Feladatok:
- Egy
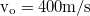 kezdősebességű és
kezdősebességű és 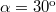 alatt fellőtt lövedék pályájának tetőpontjában egy m és egy 2m tömegű részre robban szét. Mindkét rész egyszerre éri a talajt, és az m tömegű rész a kilövés helyén csapódik be. Hol csapódik be a 2m tömegű rész?
alatt fellőtt lövedék pályájának tetőpontjában egy m és egy 2m tömegű részre robban szét. Mindkét rész egyszerre éri a talajt, és az m tömegű rész a kilövés helyén csapódik be. Hol csapódik be a 2m tömegű rész?
- Megoldás: A 2m tömegű rész a kilövés helyétől kb. 20km-re esik le.
- . Felfüggesztett,
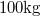 tömegű homokzsák (ballisztikus inga) egy
tömegű homokzsák (ballisztikus inga) egy 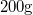 tömegű lövedék becsapódása után
tömegű lövedék becsapódása után 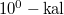 kilendül. Mennyi volt a lövedék sebessége, ha az inga hossza
kilendül. Mennyi volt a lövedék sebessége, ha az inga hossza 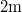 ?
?
- Megoldás: 310 m/s.
- . Az
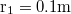 sugarú tárcsa és az
sugarú tárcsa és az 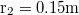 sugarú henger egymással párhuzamos forgási szimmetriatengelyei surlódásmentesen csapágyazott forgási tengelyek. A henger tehetetlenségi nyomatéka
sugarú henger egymással párhuzamos forgási szimmetriatengelyei surlódásmentesen csapágyazott forgási tengelyek. A henger tehetetlenségi nyomatéka 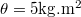 . A tárcsa és a henger a kerületükön összeérnek és
. A tárcsa és a henger a kerületükön összeérnek és 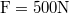 erő szorítja őket egymáshoz, miközben a két felület között a csúszási súrlódási tényező
erő szorítja őket egymáshoz, miközben a két felület között a csúszási súrlódási tényező 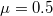 . Kezdetben a tárcsa és a henger nyugalmi helyzetben van, majd a tárcsa
. Kezdetben a tárcsa és a henger nyugalmi helyzetben van, majd a tárcsa 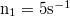 állandó fordulatszámmal forogni kezd.
állandó fordulatszámmal forogni kezd.
- a.) Mennyi idő elteltével szűnik meg a tárcsa és a henger érintkező felületeinek a csúszása?
- b.) Hogyan aránylik a henger mozgási energiája az előbbi időpontban a tárcsa által addig végzett munkához?
- Megoldás: t=2,8 s; a henger mozgási energiája és a tárcsa által addig végzett munkája aránya: 0,5.
4. Rezgések
Igaz/Hamis állítások:
- Fonálinga lengésideje kis kitérések esetén függ a tömegtől.
- NEM Fonálinga lengésideje kis kitérések esetén csak az inga hosszától (és a nehézségi gyorsulástól) függ.
- A liftbe ingaórát helyezünk. Ha a lift felfelé gyorsul, az óra sietni fog.
- IGEN Fonálinga lengésideje kis kitérések esetén függ a nehézségi gyorsulástól. Gyorsuló koordináta rendszerben hat a tehetetlenségi erő is, így a "tapasztalt" g értéke nagyobb. Ebből következik, hogy a lengés periódusideje kisebb, tehét az óra gyorsabban jár.
- Harmonikus rezgőmozgásnál a rezgés körfrekvenciája független az amplitúdótól.
- IGEN A rezgés korfrekvenciája a rugóállandótól és a tömegtől függ.
- Csillapított rezgőmozgást végző test sebessége és gyorsulása között a fáziskülönbség 90°.
- NEM Gondoljunk a különböző csillapítású (pl. túlcsillapított) rezgésekre.
Feladatok:
- Pontszerűnek tekinthető
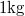 tömegű testre
tömegű testre 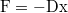 alakú rugalmas erő hat. A rugóállandó
alakú rugalmas erő hat. A rugóállandó 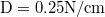 . A
. A 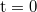 pillanatban a kitérés
pillanatban a kitérés 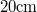 , a sebesség
, a sebesség 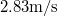 . Mekkora a rezgés frekvenciája, amplitúdója és a kezdőfázisa? Írja fel a kitérés - idő függvényt!
. Mekkora a rezgés frekvenciája, amplitúdója és a kezdőfázisa? Írja fel a kitérés - idő függvényt!
- Megoldás: f=0.8 Hz; A=0.6 m;
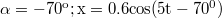 .
.
- Megoldás: f=0.8 Hz; A=0.6 m;
- Egy
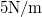 rugóállandójú rugóhoz kapcsolt
rugóállandójú rugóhoz kapcsolt 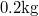 tömegű test csillapodó rezgéseket végez. Energiája
tömegű test csillapodó rezgéseket végez. Energiája 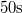 alatt exponenciálisan az e-ed részére csökken. Mekkora a rezgés frekvenciája és 10 rezgés alatt az amplitúdó hány százalékkal csökken?
alatt exponenciálisan az e-ed részére csökken. Mekkora a rezgés frekvenciája és 10 rezgés alatt az amplitúdó hány százalékkal csökken?
- Megoldás: f=0.8 Hz. Az eddigiek alapján 10 rezgés alatt az amplitúdó 12%-al csökken.
- Két rezgés frekvenciája és amplitúdója azonos, rezgésirányuk egymásra merőleges, fáziskülönbségük
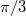 . Milyen eredő rezgés keletkezik?
. Milyen eredő rezgés keletkezik?
- Megoldás: $\rm x^2+y^2-xy=3/4. Ez egy origó középpontú ellipszis egyenlete, melynek tengelyei nem esnek egybe az x és y tengelyekkel.
5. Rend és rendetlenség
Igaz/Hamis állítások:
- Az intenzív állapotjelzők (pl. hőmérséklet, nyomás) a rendszer méretétől függetlenek, két rendszer egyesítésekor átlagolódnak.
- IGEN Az említett állapotjelzők (és például még: sűrűség, kémiai potenciál) intenzív állapotjelzők, amelyekre igaz, hogy a rendszer méretétől függetlenek és két rendszer egyesítésekor átlagolódnak. Az extenzív állapotjelzők a rendszer méretével együtt nőnek, két rendszer egyesítésekor összeadódnak: ilyen pl. a térfogat, a tömeg, a mólszám, a belső energia és az entrópia.
Feladatok:
-
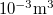 térfogatú tartályban a gáz nyomása 200 kPa, a molekulák átlagos kinetikus energiája
térfogatú tartályban a gáz nyomása 200 kPa, a molekulák átlagos kinetikus energiája 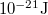 . Mennyi a molekulák száma és hány mól ez az anyag?
. Mennyi a molekulák száma és hány mól ez az anyag?
- Megoldás: N=
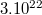 db. A mólok száma: 0,05.
db. A mólok száma: 0,05.
- Megoldás: N=
- Egy
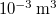 térfogatú edényben N számú hidrogénmolekula tartózkodik szobahőmérsékleten. Állapítsuk meg annak az állapotnak a p valószínűségét, amelyben az összes molekula az edény egyik felében tartózkodik!
térfogatú edényben N számú hidrogénmolekula tartózkodik szobahőmérsékleten. Állapítsuk meg annak az állapotnak a p valószínűségét, amelyben az összes molekula az edény egyik felében tartózkodik!
- Megoldás: p=
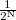 .
.
- Megoldás: p=
- Az oxigénmolekulák termikus sebessége
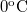 -on
-on 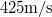 , tömegük
, tömegük 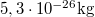 . Hány oxigénmolekulának kell
. Hány oxigénmolekulának kell 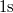 alatt a gáztartály
alatt a gáztartály 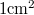 felületű részének ütközni, hogy a normál légköri nyomás alakuljon ki?
felületű részének ütközni, hogy a normál légköri nyomás alakuljon ki?
- Megoldás: N=
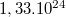 db.
db.
- Megoldás: N=
- Televízió képcsövében alkalmazott elektronnyalábban az elektronok
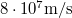 sebességgel mozognak. A képernyő
sebességgel mozognak. A képernyő 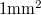 nagyságú felületére
nagyságú felületére 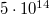 elektron érkezik másodpercenként. Határozzuk meg az általuk kifejtett nyomást, ha feltételezzük, hogy az elektronok nem pattannak vissza a képernyő felületéről! (Az elektronok tömege:
elektron érkezik másodpercenként. Határozzuk meg az általuk kifejtett nyomást, ha feltételezzük, hogy az elektronok nem pattannak vissza a képernyő felületéről! (Az elektronok tömege: 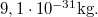 )
)
- Megoldás: p=
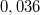 Pa.
Pa.
- Megoldás: p=
- A világűrben a hőmérséklet átlagosan 3 K. Határozzuk meg itt a protonok legvalószínűbb sebességét! (
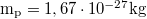 )
)
- Megoldás:
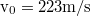
- Megoldás:
- Egy 1 literes edény
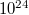 db, egyenként
db, egyenként 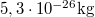 tömegű gázmolekulát tartalmaz, 273 K-on. Mennyi a gázrészecskék termikus sebessége és mennyi az ideálisnak tekintett gáz nyomása?
tömegű gázmolekulát tartalmaz, 273 K-on. Mennyi a gázrészecskék termikus sebessége és mennyi az ideálisnak tekintett gáz nyomása?
- Megoldás:
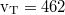 m/s. p=3,8 MPa.
m/s. p=3,8 MPa.
- Megoldás:
- Számítsuk ki, hogy mekkora a relatív valószínűsége annak, hogy
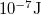 energia
energia 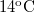 hőmérsékletű testről egy
hőmérsékletű testről egy 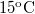 hőmérsékletű testre önként átmenjen.
hőmérsékletű testre önként átmenjen.
- Megoldás:
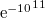 .
.
- Megoldás:
- Ideális gáz N molekuláját tartalmazó edény
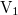 és
és 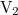 térfogatú részre különül el. Mekkora a valószínűsége, hogy a
térfogatú részre különül el. Mekkora a valószínűsége, hogy a 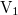 térfogatú részben
térfogatú részben 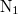 és a
és a 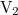 térfogatban
térfogatban 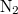 részecske van?
részecske van?
- Megoldás:
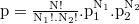 , ahol
, ahol 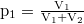 és
és 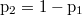 .
.
- Megoldás:
- Egy részecskerendszer 10 klasszikusan tárgyalható részecskéből áll, és 6 lehetséges energiaállapottal rendelkezik.
- a.) Mekkora a termodinamikai valószínűsége annak a makroállapotnak, amelynél a fáziscellák betöltési számai: 0 2 1 0 4 3?
- b.) Mekkora az előbbi állapotban az entrópia? (
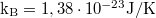 )
)
- Megoldás: W=
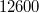 . S=
. S=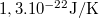 .
.
- Megoldás: W=
- Mekkora egy
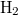 molekula legvalószínűbb sebessége
molekula legvalószínűbb sebessége 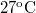 hőmérsékleten? Hány fokra kell növelni a hőmérsékletet ahhoz, hogy megkétszereződjön a legvalószínűbb sebesség?
hőmérsékleten? Hány fokra kell növelni a hőmérsékletet ahhoz, hogy megkétszereződjön a legvalószínűbb sebesség?
- Megoldás:
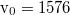 m/s.
m/s.
- Megoldás:
6. Hideg-meleg
Igaz/Hamis állítások:
- Adott mennyiségű normálállapotú gáz hőmérsékletét kétféleképpen változtatjuk meg: izobár, ill. izochor módon. Mindkét esetben azonos ideig melegítjük ugyanazzal az elektromos fűtőszállal. Az izochor folyamatban nagyobb a hőmérséklet változás.
- IGEN Izobár állapotváltozás esetén a gázzal közölt hőmennyiség munkavégzésre és a belső energia növelésére fordítódik. Izochor állapotváltozás esetén a közölt hő csak a belső energiát növeli.
- Ideális gáz izotermikus állapotváltozásakor a gáz belső energiája nem változik.
- IGEN Izotermikus állapotváltozáskor a gáz hőmérséklete állandó. Ez pedig azt jelenti, hogy a belső energia nem változik.
- Súrlódáskor hő keletkezik.
- NEM Súrlódáskor a testek belső energiája nő meg. Ez a hőmérséklet emelkedésében jelentkezik legnyilvánvalóbban. A hő nem energia!
7. Töltések
Igaz/Hamis állítások:
- Az elektroszkóp töltések előállítására szolgál.
- NEM Az elektroszkóp töltések kimutatására (esetleg töltésmennyiség mérésére) szolgál. Töltések előállítására (pontosabban: szétválasztására) használhatjuk például a Van de Graaff generátort.
- Az elektromos térerősség vektormennyiség.
- IGEN Az egységnyi pozitív töltésre ható erő adja meg irányát, mérőszámát. Mértékegysége Newton/Coulomb, vagy Volt/méter.
- Egy test töltésének nagysága (mérőszáma) tetszőleges szám lehet.
- NEM A töltés legkisebb egysége (szabad részecskére) az elemi töltés, vagyis a proton töltése. Az összes szabad részecske töltése ennek egész számú többszöröse.
- Az elektrosztatikus mező erővonalai önmagukban záródó görbék.
- NEM Az elektrosztatikus tér forrásos tér, vagyis az erővonalak pozitív töltésekről indulnak és negatív töltésen végződnek. Ha lennének önmagukba záródó erővonalak, akkor az ellentmondana az energiamegmaradás törvényének.
- Az elektromos töltés megmaradó mennyiség.
- IGEN Bármilyen fizikai folyamat során a folyamatban részt vevő anyag össztöltése nem változhat.
- Inhomogén erőtérbe helyezett dipólusra csak forgatónyomaték hat.
- NEM Inhomogén erőtérben a dipólus töltéseire ható erők nem egyenlőek ezért a dipólus a nagyobb térerősség felé mozdul el.
- Az elektromos erővonalak keresztezhetik egymást.
- NEM Az erővonalak olyan képzeletbeli vonalak, amelyekkel az elektromos erőtér szerkezetét, tulajdonságait szemléltetjük. Az erővonalak megadják többek között az adott pontban ható elektrosztatikus erő hatásvonalát. Többek között ezért sem keresztezhetik egymást.
- Az elektromos dipólusmomentum vektormennyiség.
- IGEN A dipólusmomentum, melynek egysége a coulomb-méter (Cm), vektormennyiség, amelynek iránya definíció szerint a dipólus tengelye mentén a negatív töltéstől a pozitív felé mutat.
- Van két töltésünk. Ha a töltések terét ábrázoljuk, akkor az elsőből hat erővonalat kell berajzolnunk, míg a másodikba négy erővonal végződik. A két töltés ellenkező előjelű és töltésük nagyságának arányára fennáll:
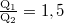 .
.
- IGEN Az erővonalak a pozitív töltésből indulnak és a negatív töltésen végződnek. Az erővonalak sűrűsége a tér erősségével arányos.
- Ha egy kisméretű pozitív töltés és egy nagyméretű fémgömb vonzza egymást, akkor az azt jelenti, hogy a fémgömbnek negatív töltése van.
- NEM A pozitív töltés és a fémgömb között akkor is lehet vonzóerő, ha a fémgömb eredetileg nem rendelkezett többlettöltéssel. Ekkor ugyanis a pozitív töltés hatására a fémgömb felületén megosztás révén töltések jelennek meg. Negatív töltések lesznek a pozitív töltéshez közelebbi oldalon, míg pozitív töltések a távolabbi oldalra gyűlnek. Eredőben tehát vonzóerőt tapasztalhatunk.
Feladatok:
- Egymástól 5 cm távolságban lévő nagy kiterjedésű párhuzamos síkok felületi töltéssűrűsége
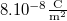 illetve
illetve 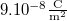 . Határozzuk meg a térerősségeket az elrendezés terében!
. Határozzuk meg a térerősségeket az elrendezés terében!
- Megoldás: A rétegek között:
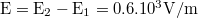 , Kívül:
, Kívül: 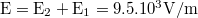 .
.
- Megoldás: A rétegek között:
8. Vezetők és szigetelők
Igaz/Hamis állítások:
- Ugyanolyan mértékben feltöltött két vezető esetén ugyanolyan távolságnál nagyobb az erőhatás, ha ellentétesen töltöttük fel a vezetőket.
- IGEN Ha ellentétesen töltöttük fel a vezetőket, a fém felületen elmozdulni tudó töltések az egy máshoz közelebbi felületrészekre gyűlnek, míg azonos előjelű töltés esetén a távolabbi felületrészeken lesznek a töltések. A Coulomb erő pedig a távolság négyzetével fordítottan arányos.
- Az elektromos megosztásnál töltéseket viszünk a vezető felületére.
- NEM Megosztásnál a vezető össztöltése zérus, csak az elmozdulni képes szabad elektronok miatt a felült egyik része pozitív töltést mutat, míg a másik fele negatív töltésűnek mutatkozik.
- Feltöltött fémgömbben egyenletesen oszlanak el a töltések.
- NEM A fémben a töltések elmozdulhatnak. Mivel azonos nemű töltések taszítják egymást ezért a töltések igyekeznek a legmesszebb távolodni, így vezető esetén a töltések csak a vezető felületén találhatók.
- Fémes vezetőkben a pozitív töltéshordozók is mozoghatnak.
- NEM A pozitív töltéshordozó ionok (azaz az atommagok és a vezetésben nem résztvevő elektronok) nem mozognak. A pozitív és negatív töltések mozgása mögött a szabad elektronok mozgása van.
- Fémes vezető anyagban nem haladnak erővonalak (a térerősség zérus)
- IGEN Fémes vezető anyagban nincsenek töltések így erővonalak sem. (Természetesen egy fémből készült gömbhéj belsejében lévő szigetelőben, például levegőben már lehetnek erővonalak, ha ott töltés is van)
- Ha felfújt léggömbre töltéseket viszünk, akkor a léggömb mérete kissé megnő.
- IGEN Azonos előjelű töltések taszítják egymást, így ez az erőhatás okozhatja a léggömb anyagának kismértékű megnyúlását.
9. Az elektromos potenciál és energia
Igaz/Hamis állítások:
- Egy töltött tömör fémgömb belsejében a potenciál zérus.
- IGEN Ha a potenciál zérustól különböző lenne akkor a töltések valamilyen úton elmozdulhatnának és végső soron sérülne az energiamegmaradás törvénye.
- Az elektromos potenciál skalármennyiség.
- IGEN Hasonlóan a mechanikához itt is az egységnyi próbatöltésen végzett munkával definiáljuk a potenciált.
- Az elektrosztatikus tér konzervatív, így jellemezhetjük az elektromos potenciállal.
- IGEN Minden konzervatív erőtér jellemezhető a potenciális energiával és potenciállal.
- Az elektronvolt csak elektromos eredetű energiák jellemzésére használható energiaegység.
- NEM Az elektronvolt természetesen használható nem eredetű energiák nagyságának jellemzésére is. Például, szokás úgy megadni a levegő molekuláinak energiáját, hogy szobahőmérsékleten kb. 1/40 eV átlagos energiája van egy molekulának.
- Az elektromos térerősséget számíthatjuk az elektromos potenciálból.
- IGEN Az elektromos térerősség a potenciáltér negatív gradiense.
- Ekvipotenciális felületen mozgatva a töltést nincs munkavégzés.
- IGEN Ekvipotenciális felületen mozgatva a töltést a töltésre ható coulomb erő mindig merőleges az elmozdulásra, így a munkavégzés zérus. (Ha a töltött részecskének figyelembe kell venni a tömegét is, akkor már modellünk megengedi a gyorsítást, így ekvipotenciális felületen mozgatva a töltéssel rendelkező tömeget már végezhetünk munkát, amely a test mozgási energiájának növelésére fordítódik.)
- Fém esetén az elektromos erővonalak merőlegesen lépnek ki a felületből.
- IGEN A fém felülete ekvipotenciális felület. Ebből következik, hogy az erővonalak minden pontban merőlegesek a fém felületére.
- Pontszerű töltés köré vezető gömbhéjat helyezünk el. Az elektromos erőtér mindig gömbszimmetrikus marad, akárhova is helyezzük az üreg belsejében a pontszerű töltést.
- IGEN Bár a fém gömbhéj belső felületén változik a töltéselrendezés, a külső felületen a töltések nem mozdulnak, mivel a fém felületén az erővonalak mindig merőlegesek, vagyis nincs erőkomponens, ami a töltéseket mozgatná.
- Egy vezető belsejében lévő, töltést nem tartalmazó zárt üregben a térerősség zérus, függetlenül attól, hogy a vezető felületén vannak-e töltések vagy sem.
- IGEN Ha nem így lenne, akkor találhatnánk olyan zárt görbét, amelyen mozgatva a töltést folyamatos munkavégzéshez jutnánk. Ez pedig sérti az energiamegmaradás törvényét.
- Az elektromos potenciális energia különbsége és az elektromos potenciálkülönbség azonos.
- NEM Nem azonos típusú mennyiségek. Az elektromos potenciális energia egy töltött részecske potenciális energiájának megváltozása (vagy értéke egy adott pontban egy referencia ponthoz képest). Mértékegysége: Joul. Az elektromos potenciálkülönbség az elektromos térre jellemző mennyiség. Segítségével kiszámíthatjuk adott töltés esetén mekkora munkavégzés történik, ha a töltést az egyik pontból a másikba visszük. Mértékegysége: Volt=Joul/Coulomb.
Feladatok:
- Mekkora a potenciál a 8 cm sugarú gömb középpontjából 70cm távolságban, ha a gömbön
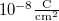 töltéssűrűség és a térben
töltéssűrűség és a térben 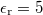 dielektromos állandójú közeg van?
dielektromos állandójú közeg van?
- Megoldás: U=
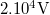 .
.
- Megoldás: U=
- Egy
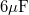 -os és egy
-os és egy 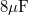 -os kapacitású kondenzátort sorba kötünk. Az igy kapott rendszer sarkaira 16 V feszültséget kapcsolunk. Mekkora a kondenzátorok töltése?
-os kapacitású kondenzátort sorba kötünk. Az igy kapott rendszer sarkaira 16 V feszültséget kapcsolunk. Mekkora a kondenzátorok töltése?
- Megoldás:
![\setbox0\hbox{$\rm Q_1=Q_2=5.43.10^{-5} [C] $}% \message{//depth:\the\dp0//}% \box0%](/images/math/8/e/a/8eae4343ef19517e93b0e89eae92fc63.png)
- Megoldás:
10. Az elektromos mező energiája
Igaz/Hamis állítások:
- Ha elektromos térben töltést mozgatunk, akkor minden esetben változik a elektromos tér energiája.
- NEM Az elektromos tér energiája csak akkor változik, ha a töltés mozgatásakor munkavégzés történt. (Ha a mozgatáskor munkát végzünk, azzal növeljük a tér energiáját.) Ha a töltést az erővonalakra merőlegesen mozgatjuk, nem történik munkavégzés, a tér energiája nem változik.
- Síkkondenzátor homogén elektrosztatikus terében töltést mozgatunk két pont között különböző utakon. Akkor végzünk legkevesebb munkát, ha a töltést a két pontot összekötő egyenes mentén mozgatjuk.
- NEM Az elektrosztatikus térben a munkavégzés független a megtett úttól, csak a kezdő és a végpont helyzetétől függ. Az elektrosztatikus tér konzervatív.
- Ha kétszeresére növeljük a síkkondenzátor fegyverzeteinek felületét, akkor a kapacitás is kétszeresére nő.
- IGEN Síkkondenzátor kapacitása kifejezhető geometriai jellemzőivel.
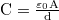
- IGEN Síkkondenzátor kapacitása kifejezhető geometriai jellemzőivel.
- Ha a síkkondenzátor fegyverzetei között lévő csillámlapot eltávolítjuk a kondenzátor energiája csökken.
- IGEN A csillámlap kihúzásakor munkát kell végeznünk, ugyanis a kondenzátor lemezein lévő töltések a csillám felületén indukált töltésekre vonzóerőt gyakorolnak. A munkavégzés nagysága a csillámmal kitöltött, illetve az üres kondenzátorok potenciális energiájának különbsége.
- A feltöltött síkkondenzátor kapacitása nem változik, ha a lemezek közé, velük párhuzamosan vékony fémfóliát helyezünk.
- IGEN A feltöltött síkkondenzátor lemezei közötti elektromos erőtér szerkezete változatlan marad. A homogén erőtér nem változik, ha az erővonalakra merőlegesen behelyezzük a vékony fémfóliát.
- Lehetséges, hogy a kondenzátor lemezein különböző nagyságú töltések vannak.
- NEM A kondenzátor töltésekor minden esetben azonos nagyságú pozitív és negatív töltés kerül a lemezekre.
- Kondenzátorok soros kapcsolásából feszültségosztót hozhatunk létre.
- IGEN Kapacitások soros kapcsolásánál a két kapacitáson azonos a töltések mennyisége. A kapacitás definíciójából következik, hogy az egyes kapacitásokon mérhető feszültség különböző lesz.
- Ha kondenzátor lemezei közé dielektrikumot (pl. csillámlap) helyezünk, akkor a kondenzátor kapacitása megnő, mert töltéseket juttatunk a rendszerbe.
- NEM A rendszerbe nem viszünk be töltést. A behelyezett dielektrikum ugyanannyi pozitív és negatív töltéssel bír. A kondenzátor kapacitása azért nő meg, mert a polárossá váló dielektrikum csökkenti a tér erősségét és ezáltal az adott töltésű kondenzátor feszültségét.
- A dielektrikumra - annak sérülése nélkül – jóval nagyobb elektromos tér kapcsolható, mintha a kondenzátor lemezei között légüres tér vagy levegő lenne.
- IGEN A polárossá váló dielektrikum csökkenti a tér erősségét egy a dielektrikumra jellemző határig (átütési szilárdság).