„Fajhő mérése” változatai közötti eltérés

A Fizipedia wikiből
 
(5 szerkesztő 35 közbeeső változata nincs mutatva)
1. sor: 1. sor:
 
<wlatex>
 
<wlatex>
−
 
 
<!--[[Kategória:Mechanika]]-->  
 
<!--[[Kategória:Mechanika]]-->  
 
<!--[[Kategória:Elektromosságtan]]-->
 
<!--[[Kategória:Elektromosságtan]]-->
12. sor: 11. sor:
 
<!--[[Kategória:Informatika]]-->  
 
<!--[[Kategória:Informatika]]-->  
 
[[Kategória:Laborgyakorlat]]
 
[[Kategória:Laborgyakorlat]]
−
<!--[[Kategória:Fizika laboratórium 1.]]-->
+
[[Kategória:Fizika laboratórium 1.]]
−
[[Kategória:Fizika laboratórium 2.]]
+
<!--[[Kategória:Fizika laboratórium 2.]]-->
 
<!--[[Kategória:Fizika laboratórium 3.]]-->
 
<!--[[Kategória:Fizika laboratórium 3.]]-->
 
<!--[[Kategória:Fizika laboratórium 4.]]-->
 
<!--[[Kategória:Fizika laboratórium 4.]]-->
 
[[Kategória:Szerkesztő:Vankó]]
 
[[Kategória:Szerkesztő:Vankó]]
−
 
−
Szerkesztés alatt!
 
−
 
 
''A mérés célja:''
 
''A mérés célja:''
 
* elmélyíteni a hallgatók fajhővel kapcsolatos ismereteit,
 
* elmélyíteni a hallgatók fajhővel kapcsolatos ismereteit,
36. sor: 32. sor:
 
$$ \Delta U = \Delta Q + \Delta W $$
 
$$ \Delta U = \Delta Q + \Delta W $$
  
−
ahol $\Delta U$ a belső energia megváltozása, $\Delta W$ a testen végzett makroszkopikus munka, $\Delta Q$ pedig a molekuláris mechanizmussal a testnek átadott energia, amit \textit{hőnek} (hőmennyiségnek) nevezünk. Ha egy testtel hőt közlünk (pl. elektromos fűtőtesttel melegítjük), akkor belső energiája és ezzel együtt hőmérséklete is megváltozik. A tapasztalat szerint nem túl nagy hőmennyiség közlése esetén a bekövetkező hőmérséklet-változás ($\Delta t$) egyenesen arányos a közölt hővel ($Q$), fordítottan arányos a vizsgált anyag tömegével ($m$) és függ a vizsgált anyag minőségétől is:
+
ahol $\Delta U$ a belső energia megváltozása, $\Delta W$ a testen végzett makroszkopikus munka, $\Delta Q$ pedig a molekuláris mechanizmussal a testnek átadott energia, amit ''hőnek'' (hőmennyiségnek) nevezünk. Ha egy testtel hőt közlünk (pl. elektromos fűtőtesttel melegítjük), akkor belső energiája és ezzel együtt hőmérséklete is megváltozik. A tapasztalat szerint nem túl nagy hőmennyiség közlése esetén a bekövetkező hőmérséklet-változás ($\Delta t$) egyenesen arányos a közölt hővel ($Q$), fordítottan arányos a vizsgált anyag tömegével ($m$) és függ a vizsgált anyag minőségétől is:
  
 
$$ \Delta t = \frac{Q}{cm} $$
 
$$ \Delta t = \frac{Q}{cm} $$
  
 
ahol az anyagra jellemző $c$ állandót fajhőnek nevezzük. Számértéke megadja, hogy egységnyi tömegű anyaggal mennyi hőt kell közölnünk ahhoz, hogy hőmérsékletét 1 K-nel megváltoztassuk. Mértékegysége $Jkg^{-1}K^{-1}$.
 
ahol az anyagra jellemző $c$ állandót fajhőnek nevezzük. Számértéke megadja, hogy egységnyi tömegű anyaggal mennyi hőt kell közölnünk ahhoz, hogy hőmérsékletét 1 K-nel megváltoztassuk. Mértékegysége $Jkg^{-1}K^{-1}$.
 +
 
A testtel közölt hő azonban nemcsak a belső energia megváltoztatására, hanem munkavégzésre is fordítódhat:
 
A testtel közölt hő azonban nemcsak a belső energia megváltoztatására, hanem munkavégzésre is fordítódhat:
  
50. sor: 47. sor:
  
 
Mivel a munkavégzés függ a folyamat körülményeitől, a fajhő csak akkor határozható meg egyértelműen, ha a hőközlés folyamatát pontosan rögzítjük. Ennek megfelelően, elvileg igen sokféle fajhő definiálható, a gyakorlatban ezek közül kettőt használnak, az állandó térfogaton ($c_V$) és az állandó nyomáson ($c_p$) mért fajhőt. Gázok esetében e kétféle fajhő számottevően különböző, szilárd és folyékony anyagoknál közel azonos értékű.
 
Mivel a munkavégzés függ a folyamat körülményeitől, a fajhő csak akkor határozható meg egyértelműen, ha a hőközlés folyamatát pontosan rögzítjük. Ennek megfelelően, elvileg igen sokféle fajhő definiálható, a gyakorlatban ezek közül kettőt használnak, az állandó térfogaton ($c_V$) és az állandó nyomáson ($c_p$) mért fajhőt. Gázok esetében e kétféle fajhő számottevően különböző, szilárd és folyékony anyagoknál közel azonos értékű.
 +
 
A fajhő – különösen alacsony hőmérsékleten – a hőmérséklettől is függ. A mérés során szilárd anyagokat vizsgálunk amelyeknek fajhője a vizsgált hőmérsékleteken állandónak tekinthető és amelyeknél a $c_p$ és $c_V$ eltérése is elhanyagolható. Ezért a továbbiakban egyszerűen "fajhő"-ről beszélünk és az index nélküli $c$ jelölést használunk. (Szigorúan véve $c_p$-t mérjük.)
 
A fajhő – különösen alacsony hőmérsékleten – a hőmérséklettől is függ. A mérés során szilárd anyagokat vizsgálunk amelyeknek fajhője a vizsgált hőmérsékleteken állandónak tekinthető és amelyeknél a $c_p$ és $c_V$ eltérése is elhanyagolható. Ezért a továbbiakban egyszerűen "fajhő"-ről beszélünk és az index nélküli $c$ jelölést használunk. (Szigorúan véve $c_p$-t mérjük.)
 +
 
A mérnöki gyakorlatban a hűtő- és fűtő berendezések és határoló szerkezetek hőtani viselkedésének egyik meghatározója az alkalmazott anyagok fajhője. Az anyagtudományban a fajhő mérésével bizonyos anyagszerkezeti változásokat – fázisátalakulásokat – követhetünk nyomon. A fajhő meghatározása a $c=\frac{Q}{m\Delta t}$ képlet alapján lehetséges. Megmérve a vizsgált anyag tömegét, az anyaggal közölt ill. a tőle elvont hő mennyiségét és a bekövetkezett hőmérsékletváltozást, a fajhő kiszámítható.
 
A mérnöki gyakorlatban a hűtő- és fűtő berendezések és határoló szerkezetek hőtani viselkedésének egyik meghatározója az alkalmazott anyagok fajhője. Az anyagtudományban a fajhő mérésével bizonyos anyagszerkezeti változásokat – fázisátalakulásokat – követhetünk nyomon. A fajhő meghatározása a $c=\frac{Q}{m\Delta t}$ képlet alapján lehetséges. Megmérve a vizsgált anyag tömegét, az anyaggal közölt ill. a tőle elvont hő mennyiségét és a bekövetkezett hőmérsékletváltozást, a fajhő kiszámítható.
 +
 
A gyakorlatban sok esetben közvetlenül a testtel közölt hő és a hőmérsékletváltozás összefüggésére van szükség, így a fajhő helyett az adott testre jellemző $C=mc$ mennyiséget használják, amelyet hőkapacitásnak neveznek. A $c=\frac{Q}{m\Delta t}$ összefüggés így a  $C=\frac{Q}{\Delta t} $ alakot ölti.
 
A gyakorlatban sok esetben közvetlenül a testtel közölt hő és a hőmérsékletváltozás összefüggésére van szükség, így a fajhő helyett az adott testre jellemző $C=mc$ mennyiséget használják, amelyet hőkapacitásnak neveznek. A $c=\frac{Q}{m\Delta t}$ összefüggés így a  $C=\frac{Q}{\Delta t} $ alakot ölti.
 +
 
A vizsgált anyaggal történő hőközlés két módszere terjedt el, a különböző hőmérsékletű anyagok összekeverésével ill. az elektromos fűtőtesttel történő hőközlés. Az alábbiakban ezen két módszer alapgondolatát ismertetjük.
 
A vizsgált anyaggal történő hőközlés két módszere terjedt el, a különböző hőmérsékletű anyagok összekeverésével ill. az elektromos fűtőtesttel történő hőközlés. Az alábbiakban ezen két módszer alapgondolatát ismertetjük.
  
62. sor: 63. sor:
  
 
ami alapján az ismeretlen $c$ fajhő meghatározható.
 
ami alapján az ismeretlen $c$ fajhő meghatározható.
 +
 
Ez a módszer elsősorban szilárd testek és folyadékok fajhőjének meghatározására alkalmas, de segítségével gázok állandó nyomáson mért fajhője is megmérhető. Ebben az esetben a vizsgált gázt cső-spirálon áramoltatják a folyadékon át. A gáz tömegének, hőmérsékletváltozásának valamint a mérő folyadék adatainak ismeretében a gáz állandó nyomáson mért fajhője ($c_p$) meghatározható. Az állandó nyomáson mért fajhő ismeretében az állandó térfogaton mért fajhő, ($c_V$) szintén meghatározható (pl. [http://www.kfki.hu/fszemle/archivum/fsz0910/holics0910.html hangsebesség-méréssel]).
 
Ez a módszer elsősorban szilárd testek és folyadékok fajhőjének meghatározására alkalmas, de segítségével gázok állandó nyomáson mért fajhője is megmérhető. Ebben az esetben a vizsgált gázt cső-spirálon áramoltatják a folyadékon át. A gáz tömegének, hőmérsékletváltozásának valamint a mérő folyadék adatainak ismeretében a gáz állandó nyomáson mért fajhője ($c_p$) meghatározható. Az állandó nyomáson mért fajhő ismeretében az állandó térfogaton mért fajhő, ($c_V$) szintén meghatározható (pl. [http://www.kfki.hu/fszemle/archivum/fsz0910/holics0910.html hangsebesség-méréssel]).
  
71. sor: 73. sor:
  
 
amiből az UI fűtőteljesítmény, a $\tau$ melegítési idő, a vizsgált anyag $m$ tömege és a $\Delta t$ hőmérsékletváltozás ismeretében a $c$ fajhő meghatározható.
 
amiből az UI fűtőteljesítmény, a $\tau$ melegítési idő, a vizsgált anyag $m$ tömege és a $\Delta t$ hőmérsékletváltozás ismeretében a $c$ fajhő meghatározható.
 +
 
A módszer elsősorban folyadékok fajhőjének meghatározására alkalmas. Használható azonban szilárd anyagok esetén is, ha azokat folyadékba helyezve a folyadékkal együtt melegítjük.
 
A módszer elsősorban folyadékok fajhőjének meghatározására alkalmas. Használható azonban szilárd anyagok esetén is, ha azokat folyadékba helyezve a folyadékkal együtt melegítjük.
  
 
===A kaloriméter hőkapacitása és a hőmérsékleti korrekció===
 
===A kaloriméter hőkapacitása és a hőmérsékleti korrekció===
  
−
A keveréssel és az elektromos melegítéssel történő fajhőmérés esetén eddig feltételeztük, hogy a folyamat a környezettől hőtanilag jól elszigetelve, hőveszteség nélkül játszódik le. Ennek a feltételnek a teljesítése érdekében a hőközlés a környezettől jó hőszigetelő anyagokkal elválasztott edényben, kaloriméterben történik. (Egy keverési és egy elektromos kaloriméter vázlatát az 1. ábra mutatja.)
+
A keveréssel és az elektromos melegítéssel történő fajhőmérés esetén eddig feltételeztük, hogy a folyamat a környezettől hőtanilag jól elszigetelve, hőveszteség nélkül játszódik le. Ennek a feltételnek a teljesítése érdekében a hőközlés a környezettől jó hőszigetelő anyagokkal elválasztott edényben, kaloriméterben történik. (Egy keverési és egy elektromos kaloriméter vázlatát az [[#fig:1|1. ábra]] mutatja.)
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="right"
 +
|-
 +
|{{fig1|Kalorimeter.JPG|fig:1|1. ábra|}}
 +
|-
 +
|}
 +
 
 
Ennek ellenére a hőveszteség nélküli mérés mégsem valósítható meg, elsősorban az alábbi két ok miatt: az egyik az, hogy az edény hőmérséklete is változik a mérés közben és ez is energiát igényel, a másik pedig, hogy bármilyen jó hőszigetelést is alkalmazunk a környezet felé mindig történik energiaátadás. Ez a két ok (hiba) a kaloriméter hőkapacitásának figyelembevételével illetve a hőveszteségek becslésével csökkenthető.
 
Ennek ellenére a hőveszteség nélküli mérés mégsem valósítható meg, elsősorban az alábbi két ok miatt: az egyik az, hogy az edény hőmérséklete is változik a mérés közben és ez is energiát igényel, a másik pedig, hogy bármilyen jó hőszigetelést is alkalmazunk a környezet felé mindig történik energiaátadás. Ez a két ok (hiba) a kaloriméter hőkapacitásának figyelembevételével illetve a hőveszteségek becslésével csökkenthető.
  
 
==== A kaloriméter hőkapacitása ====  
 
==== A kaloriméter hőkapacitása ====  
 +
 +
Ha tudnánk azt, hogy a kaloriméter egyes részei milyen tömegűek, mekkora a fajhőjük és milyen mértékben melegszenek fel, akkor meg tudnánk határozni a kísérlet közben a kaloriméter egyes részeinek melegítéséhez szükséges energiát. Ez az eljárás gyakorlatilag megvalósíthatatlan. Ehelyett mérés segítségével meghatározzuk a kaloriméter $C$ hőkapacitását. Ha a kaloriméter hőkapacitását is figyelembe vesszük, akkor a hőcserét leíró egyenleteink az alábbiak szerint módosulnak:
 +
 +
$$ c m ( t - t_k ) = c_i m_i ( t_k - t_i ) + C ( t_k - t_i )$$
 +
 +
$$ U I \tau = c m \Delta t  + C \Delta t. $$
 +
 +
A kaloriméter hőkapacitásának meghatározásához ismert fajhőjű ($c_i$ , $c$) anyagok alkalmazásával a fenti egyenletek valamelyikével történik. Ismert fajhőjű anyagként rendszerint vizet alkalmazunk.
 +
 +
==== A hőmérsékleti korrekció ====
 +
 +
A kaloriméter belseje és a környezet között energiaátadást a belső tér ($t_b$) és a környezet ($t_0$) hőmérséklete közötti eltérés eredményezi. Az ezen hőmérsékletkülönbség okozta energiaátadást jó hőszigeteléssel valamint egymáshoz közeli $t_b$ és $t_0$ választással csökkentjük. A kaloriméter belseje és a külső tér között mindezek ellenére fellépő energiacsere "hőmérsékleti korrekcióval" vehető figyelembe. Az alábbiakban a hőmérsékleti korrekció grafikus végrehajtását mutatjuk be.
 +
 +
{|  cellpadding="5" cellspacing="0" align="right"
 +
|-
 +
|{{fig1|Fajho_korrekcio.jpg|fig:2|2. ábra|}}
 +
|-
 +
|}
 +
 +
A [[#fig:2|2. ábra]] a kaloriméteres mérés során a kaloriméter hőmérsékletének változását mutatja be az idő függvényében. A görbe három jól elkülöníthető szakaszra osztható, az egyes szakaszokon lejátszódó folyamatokat áttekintjük:
 +
 +
* ''Előperiódus'': A kaloriméterbe helyezett folyadék (víz, olaj stb.) és a kaloriméter, valamint a folyadék és a környezet közötti hőmérsékleti egyensúly kialakulásának folyamata. A kaloriméter és a mérő folyadék hőmérsékletétől függően ebben a szakaszban a belső tér hőmérséklete csökken ha $t_{b0} > t_0$ vagy növekszik ha $t_{b0} < t_0$ ($t_{b0}$ a belső tér hőmérséklete kísérlet indításakor). Ebben a szakaszban a kis hőmérsékletkülönbségek miatt a hőmérséklet - idő kapcsolat jó közelítéssel lineárisnak tekinthető.
 +
 +
* ''Főperiódus'': Az előperiódus a fő energiaátadási folyamattal folytatódik (főperiódus), amely az anyagok összekeveredésével illetve a fűtőtest bekapcsolásával kezdődik. A főperiódusban a belső tér hőmérséklete ($t_b$) emelkedik. Ebben a szakaszban megy végbe az energiacsere az összekevert különböző hőmérsékletű anyagok között, vagy a kaloriméterben levő anyagok és a fűtőtest között. A kaloriméter belsejének hőmérséklete a környezeti hőmérséklet fölé emelkedik $t_{b} > t_0$ és ezért energialeadás történik a környezet felé. A hőveszteség  miatt a belső tér hőmérséklete nem érheti el a tökéletes hőszigetelés esetén várható $t_k$ egyensúlyi hőmérsékletet. A főperiódust követő szakasz (az utóperiódus) hőmérséklet-idő grafikonjából azonban következtetni tudunk erre az értékre.
 +
 +
* ''Utóperiódus'': Ebben a szakaszban $t_{b} > t_0$ és a nem tökéletes hőszigetelés miatt lassan csökken a kaloriméter belsejében a hőmérséklet. A hőmérsékletcsökkenést most is lineárisnak tekintjük.
 +
 +
Látható, hogy a folyamat a nem tökéletes hőszigetelésből adódó hibák miatt az ideálistól eltérően alakul. A hőmérséklet - idő görbe felvétele azonban lehetőséget ad a hibák korrigálására. A hőmérsékleti korrekció gyakorlati végrehajtása a következőképpen történik ([[#fig:2|2. ábra]]).  Felvesszük a kaloriméter hőmérsékletének időfüggvényét. Az elő- és utóperiódus szakaszára egyenest illesztünk. Tegyük fel, hogy az előperiódusra illesztett egyenes utolsó érintési pontjának koordinátái $\tau_1, t_1$. Az utóperiódusra illesztett egyenes első érintkezési pontjának koordinátái $\tau_2, t_2$. Ezek megállapítása után megrajzoljuk a $t=(t_1+t_2)/2$ időtengellyel párhuzamos egyenest. Ennek az egyenesnek és a főperiódus görbéjének metszéspontján keresztül párhuzamost húzunk a hőmérséklettengellyel. Ez utóbbi egyenesnek és az időperiódusra illesztett egyenesnek a metszéspontját tekintjük a kaloriméter + mérőfolyadék rendszer kezdeti hőmérsékletének ($t_1$), az utóperiódusra illesztett egyenessel való metszéspontját fogadjuk el közös hőmérsékletnek ($t_k$).
 +
 +
A korrekció fenti módon történő végrehajtása az alábbiakon alapul: A környezettel való energiacsere miatt a kaloriméterben állandóan változik a hőmérséklet, egyensúlyi hőmérséklet sem alakulhat ki, így sem a kiindulási, sem a véghőmérsékletet nem tudjuk megmérni. Az előperiódusra fektetett egyenes mutatja, hogy hogyan változna a kaloriméter belsejében a hőmérséklet, ha nem indulna meg az energiacsere a főperiódusban. Ebből lehet a valódi kezdeti hőmérsékletre következtetni.
 +
 +
Az utóperiódusra fektetett egyenes segítségével arra lehet következtetni, hogy milyen hőmérséklet értéket vehetett volna fel a kaloriméter belseje ideális hőszigetelés mellett.
 +
 +
A jó minőségű kaloriméter hőkapacitása kicsi és hőszigetelése jó, azaz kicsi a környezettel való energiacsere. Ekkor a hőmérséklet közel állandó az elő- és utóperiódus során.
 +
 +
== A mérőeszköz ==
 +
 +
{|  cellpadding="5" cellspacing="0" align="right"
 +
|-
 +
|{{fig2|Fajho.png|fig:3|3. ábra|}}
 +
|-
 +
|}
 +
 +
A méréshez használt eszközök:
 +
 +
* 2 db 0,75 l űrtartalmú duplafalú rozsdamentes termosz platina vékonyréteg ellenálláshőmérőkkel
 +
 +
* elektromos vízforraló
 +
 +
* 1,2 $\Omega$-os, 50 W maximális teljesítményű fűtőellenállás
 +
 +
* Hameg multiméter számítógépes kezelőprogrammal
 +
 +
* tápegység a fűtőellenállás meghajtásához
 +
 +
* mérőhelyenként 1 db alumínium és 1 db sárgaréz próbatest, a próbatestek tömegei:
 +
** ''A'' jelű alumínium tömb 594,5 g (± 0,2 g)
 +
** ''B'' jelű alumínium tömb 533,2 g (± 0,2 g)
 +
** ''C'' jelű sárgaréz tömb 1605 g (± 5 g)
 +
** ''D'' jelű sárgaréz tömb 1600 g (± 5 g)
 +
:: ''Ellenőrizzük, hogy melyik próbatesten végezzük a mérést!''
 +
 +
* jég
 +
 +
* mérőhenger
 +
 +
* 1 db kalibrált higanyszálas hőmérő
 +
 +
*      mágneses keverő
 +
 +
*      digitális mérleg
 +
 +
*      tartó állvány a termoszokhoz
 +
 +
== Mérési feladatok ==
 +
 +
[[A méréshez rendelkezésre álló eszközök: Fajhő mérése|A méréshez rendelkezésre álló eszközök]]
 +
 +
*''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
 +
 +
*'''Figyelem! A forró víz komoly égési sérüléseket okozhat, így a mérési gyakorlaton különös figyelmet és óvatosságot várunk el! Figyeljünk arra, hogy a forró víz ne ömöljön ki, ill. hogy a forró fém próbatesteket kézzel ne érintsük! A forróvizes termoszt mindig rögzítsük az erre szolgáló állvány segítségével, hogy véletlenül se tudjon kiborulni! '''
 +
 +
*'''A műanyag mérőhengerekbe sose töltsünk forró vizet, mert az a hengerek károsodásához vezet!'''
 +
 +
*''A méréseknél használt vízmennyiségek pontosabb meghatározásához segítséget nyújtanak a rendelkezésre álló digitális mérlegek! Célszerű a mérés elején az üres termoszok tömegét meghatározni.''
 +
 +
*''A pontos fajhőmérés alapvető feltétele a termikus egyensúly kialakulása, melyet mágneses keverő segítségével jelentősen felgyorsíthatunk!''
 +
 +
*''A mágneses keverő közvetlen közelében elhelyezkedő hőmérővezetékekben a keverő jelentős zajt indukál, így a vezetékeket a keverőtől minél távolabb rögzítsük!''
 +
 +
*''A mérések közben értékeljük ki az eredményeket! Lehetőség szerint a 4-8. méréseket ismételjük meg. Ha jelentős eltérést tapasztalunk mérések között, illetve ha a mért értékek jelentősen eltérnek az irodalmi adatoktól, próbáljuk megtalálni, és kiküszöbölni a mérési hiba okát!''
 +
 +
'''1.''' A hőmérők kalibrálása
 +
 +
A méréshez Pt 100-as szabvány vékonyréteg ellenálláshőmérőket használunk, melyek ellenállása 0 °C-on 100 $\Omega$, és melegítés hatására lineárisan, 0,39 $\Omega/$°C meredekséggel nő. A számítógépes mérőprogram ez alapján az összefüggés alapján számolja a hőmérsékletet. A hőmérőhöz vezető drótok, a banándugók és a forrasztás véges ellenállása miatt viszont megjelenik egy konstans (hőmérsékletfüggetlen) soros ellenállás, ami miatt a mért hőmérsékletérték korrekcióra szorul.
 +
 +
*''Ebből milyen irányú hőmérsékleti korrekciót várunk?''
 +
 +
Mindkét termosz hőmérőjét hitelesítsük hideg csapvízben higanyszálas hőmérő segítségével! Határozzuk meg a soros ellenállás értékét és az ebből adódó hőmérsékletkorrekciót!
 +
 +
*''Melyik mérési feladatnál okozná a legnagyobb problémát, ha a hőmérők nullponteltolódását nem vennénk figyelembe?''
 +
 +
'''2.''' A termosz hőveszteségének becslése
 +
 +
Töltsünk a termoszba forró vizet, várjuk meg amíg a rendszer termalizálódik. Ezután a rendszer a nem teljesen tökéletes szigetelés miatt kismértékben hőt ad le a környezetének, és emiatt lassan csökken a hőmérséklete. Becsüljük meg a hőleadás sebességét!
 +
 +
*''A hőleadást legalább 5 percen keresztül mérjük!''
 +
*''Adjunk számszerű becslést arra, hogy a termosz hőveszteségének elhanyagolása illetve a fent részletezett hőmérsékleti korrekció elhagyása milyen nagyságrendű hibát okozna az alábbi méréseknél!''
 +
 +
'''3.''' A termosz hőkapacitásának becslése
 +
 +
Mérjük meg a rozsdamentes termosz tömegét! A rozsdamentes acél fajhője 500 J/kg°C, termosz külső és belső falának vastagsága megegyezik. Becsüljük meg a termosz saját hőkapacitását!
 +
 +
'''4.''' A víz fajhőjének mérése fűtéses módszerrel
 +
 +
Töltsünk az egyik termoszba 0,6 l hideg csapvizet. Helyezzük a fűtőellenállást az edénybe, és $P\approx$ 50 W fűtőteljesítmény mellett mérjük a víz melegedését 10 percen keresztül.
 +
 +
*''Az 50 W fűtőteljesítményt csak a már vízbe helyezett fűtőellenállásra alkalmazzuk, levegőben ez a fűtőteljesítmény az ellenállás károsodásához vezethet!''
 +
*''A pontos fűtőteljesítmény meghatározásához digitális multiméterrel mérjük meg az áram és a feszültség pontos értékét.''
 +
 +
A leadott hőmennyiség és a mért hőmérsékletváltozás alapján határozzuk meg a víz fajhőjét!
 +
 +
*''Az edény hőkapacitását a 3. feladatban becsült értékkel vegyük figyelembe.''
 +
 +
'''5.''' A termosz hőkapacitásának mérése keveréses módszerrel
 +
 +
Forraljunk fel 0,35 l vizet, majd a forró vizet töltsük az egyik termoszba. A másik termoszba töltsünk 0,35 l hideg csapvizet. Várjuk meg az egyensúlyi hőmérsékletek beálltát. Ezután a hideg vizet töltsük át a forró vizes termoszba, és keverés mellett várjuk meg az egyensúlyi hőmérséklet kialakulását. A mért hőmérsékletváltozások ill. a hideg és a forró víz tömege alapján határozzuk meg a termosz saját hőkapacitását! A mért értéket hasonlítsuk össze a ''3. feladatban'' becsült hőkapacitással!
 +
 +
* ''A mérésekhez csak egy mágneses keverő áll rendelkezésre, ezzel mindig a melegvizes termoszt keverjük!''
 +
 +
'''6.''' Fém minta fajhőjének mérése
 +
 +
Forraljunk fel 0,5 l vizet, majd a forró vizet töltsük az egyik termoszba. A másik termoszba töltsünk 0,5 l hideg csapvizet. A hideg vízbe helyezzük bele a fém tömböt, várjuk meg amíg mindkét edényben kialakul az egyensúlyi hőmérséklet. A fém tömböt helyezzük át a forró vízbe, és várjuk meg a közös hőmérséklet kialakulását. A hőmérsékletváltozások alapján határozzuk meg az adott fém fajhőjét!
 +
 +
'''7.''' A jég olvadáshőjének mérése
 +
 +
''Fakultatív feladat! (Ennek a feladatnak a megoldása nem kötelező, csak akkor foglalkozzon vele, ha marad elég idő rá.)''
 +
 +
Forraljunk fel 0,45 l vizet, majd a forró vizet töltsük az egyik termoszba. Várjuk meg az egyensúlyi hőmérséklet kialakulását. Töltsük fel a termoszt olvadásban lévő jéggel, majd várjuk meg míg elolvad a jég, és kialakul az egyensúlyi hőmérséklet. Mérjük le a termoszban lévő víz térfogatát (vagy tömegét), ebből határozzuk meg, hogy mennyi jeget tettünk a termoszba! Határozzuk meg a jég olvadáshőjét!
 +
 +
<!--'''8.''' Sárgaréz fajhőjének mérése
 +
 +
A ''7. feladatot'' ismételjük meg sárgarézzel!-->
  
 
</wlatex>
 
</wlatex>

A lap jelenlegi, 2016. március 4., 10:58-kori változata

A mérés célja:

  • elmélyíteni a hallgatók fajhővel kapcsolatos ismereteit,
  • megismertetni a hallgatókat a fajhőmérés két módszerével.

Ennek érdekében:

  • összefoglaljuk a fajhő mérésével kapcsolatos ismereteket, ismertetjük a keverési kaloriméterrel ill. az elektromos fűtésű kaloriméterrel történő fajhőmérést,
  • a gyakorlat során megmérjük néhány anyag fajhőjét.

Tartalomjegyzék


Elméleti összefoglaló

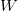Egy anyag belső energiája (\setbox0\hbox{$U$}% \message{//depth:\the\dp0//}% \box0%) a rajta végzett makroszkopikus munka (\setbox0\hbox{$W$}% \message{//depth:\the\dp0//}% \box0%), vagy egy másik testtel létrejött kontaktus során molekuláris szinten lezajló energia átadás (\setbox0\hbox{$Q$}% \message{//depth:\the\dp0//}% \box0%) útján változtatható meg. Ezt a tapasztalatot rögzíti a hőtan I. főtétele:

\[ \Delta U = \Delta Q + \Delta W \]

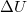ahol \setbox0\hbox{$\Delta U$}% \message{//depth:\the\dp0//}% \box0% a belső energia megváltozása, 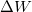\setbox0\hbox{$\Delta W$}% \message{//depth:\the\dp0//}% \box0% a testen végzett makroszkopikus munka, 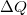\setbox0\hbox{$\Delta Q$}% \message{//depth:\the\dp0//}% \box0% pedig a molekuláris mechanizmussal a testnek átadott energia, amit hőnek (hőmennyiségnek) nevezünk. Ha egy testtel hőt közlünk (pl. elektromos fűtőtesttel melegítjük), akkor belső energiája és ezzel együtt hőmérséklete is megváltozik. A tapasztalat szerint nem túl nagy hőmennyiség közlése esetén a bekövetkező hőmérséklet-változás (\setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0%) egyenesen arányos a közölt hővel (\setbox0\hbox{$Q$}% \message{//depth:\the\dp0//}% \box0%), fordítottan arányos a vizsgált anyag tömegével (\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%) és függ a vizsgált anyag minőségétől is:

\[ \Delta t = \frac{Q}{cm} \]

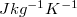ahol az anyagra jellemző \setbox0\hbox{$c$}% \message{//depth:\the\dp0//}% \box0% állandót fajhőnek nevezzük. Számértéke megadja, hogy egységnyi tömegű anyaggal mennyi hőt kell közölnünk ahhoz, hogy hőmérsékletét 1 K-nel megváltoztassuk. Mértékegysége \setbox0\hbox{$Jkg^{-1}K^{-1}$}% \message{//depth:\the\dp0//}% \box0%.

A testtel közölt hő azonban nemcsak a belső energia megváltoztatására, hanem munkavégzésre is fordítódhat:

\[ \Delta Q = \Delta U - \Delta W \]

Ennek megfelelően a fajhő:

\[ c = \frac{1}{m} \frac{\Delta Q}{\Delta t} = \frac{1}{m} \frac{\Delta U}{\Delta t} - \frac{1}{m} \frac{\Delta W}{\Delta t} \]

Mivel a munkavégzés függ a folyamat körülményeitől, a fajhő csak akkor határozható meg egyértelműen, ha a hőközlés folyamatát pontosan rögzítjük. Ennek megfelelően, elvileg igen sokféle fajhő definiálható, a gyakorlatban ezek közül kettőt használnak, az állandó térfogaton (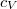\setbox0\hbox{$c_V$}% \message{//depth:\the\dp0//}% \box0%) és az állandó nyomáson (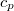\setbox0\hbox{$c_p$}% \message{//depth:\the\dp0//}% \box0%) mért fajhőt. Gázok esetében e kétféle fajhő számottevően különböző, szilárd és folyékony anyagoknál közel azonos értékű.

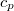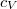A fajhő – különösen alacsony hőmérsékleten – a hőmérséklettől is függ. A mérés során szilárd anyagokat vizsgálunk amelyeknek fajhője a vizsgált hőmérsékleteken állandónak tekinthető és amelyeknél a \setbox0\hbox{$c_p$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$c_V$}% \message{//depth:\the\dp0//}% \box0% eltérése is elhanyagolható. Ezért a továbbiakban egyszerűen "fajhő"-ről beszélünk és az index nélküli \setbox0\hbox{$c$}% \message{//depth:\the\dp0//}% \box0% jelölést használunk. 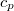(Szigorúan véve \setbox0\hbox{$c_p$}% \message{//depth:\the\dp0//}% \box0%-t mérjük.)

A mérnöki gyakorlatban a hűtő- és fűtő berendezések és határoló szerkezetek hőtani viselkedésének egyik meghatározója az alkalmazott anyagok fajhője. Az anyagtudományban a fajhő mérésével bizonyos anyagszerkezeti változásokat – fázisátalakulásokat – követhetünk nyomon. A fajhő meghatározása a 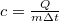\setbox0\hbox{$c=\frac{Q}{m\Delta t}$}% \message{//depth:\the\dp0//}% \box0% képlet alapján lehetséges. Megmérve a vizsgált anyag tömegét, az anyaggal közölt ill. a tőle elvont hő mennyiségét és a bekövetkezett hőmérsékletváltozást, a fajhő kiszámítható.

A gyakorlatban sok esetben közvetlenül a testtel közölt hő és a hőmérsékletváltozás összefüggésére van szükség, így a fajhő helyett az adott testre jellemző 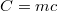\setbox0\hbox{$C=mc$}% \message{//depth:\the\dp0//}% \box0% mennyiséget használják, amelyet hőkapacitásnak neveznek. A 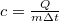\setbox0\hbox{$c=\frac{Q}{m\Delta t}$}% \message{//depth:\the\dp0//}% \box0% összefüggés így a 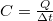\setbox0\hbox{$C=\frac{Q}{\Delta t} $}% \message{//depth:\the\dp0//}% \box0% alakot ölti.

A vizsgált anyaggal történő hőközlés két módszere terjedt el, a különböző hőmérsékletű anyagok összekeverésével ill. az elektromos fűtőtesttel történő hőközlés. Az alábbiakban ezen két módszer alapgondolatát ismertetjük.

Fajhőmérés keveréssel

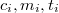A mérendő \setbox0\hbox{$c$}% \message{//depth:\the\dp0//}% \box0% fajhőjű, \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0% tömegű, \setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0% hőmérsékletű anyagot ismert paraméterekkel (\setbox0\hbox{$c_i, m_i, t_i$}% \message{//depth:\the\dp0//}% \box0%) rendelkező anyaggal – általában olyan folyadékkal, amely nem lép kémiai reakcióba a mérendő anyaggal – összekeverjük, majd megmérjük a beálló közös hőmérsékletet (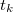\setbox0\hbox{$t_k$}% \message{//depth:\the\dp0//}% \box0%). Feltéve, hogy a keverés során a két anyag között kizárólag hőátadás történik, a vizsgálandó anyag által felvett (vagy leadott) hő egyenlő az ismert anyag által felvett (vagy leadott) hővel, ezért

\[ c m ( t - t_k ) = c_i m_i ( t_k - t_i ) \]

ami alapján az ismeretlen \setbox0\hbox{$c$}% \message{//depth:\the\dp0//}% \box0% fajhő meghatározható.

Ez a módszer elsősorban szilárd testek és folyadékok fajhőjének meghatározására alkalmas, de segítségével gázok állandó nyomáson mért fajhője is megmérhető. Ebben az esetben a vizsgált gázt cső-spirálon áramoltatják a folyadékon át. A gáz tömegének, hőmérsékletváltozásának valamint a mérő folyadék adatainak ismeretében a gáz állandó nyomáson mért fajhője (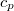\setbox0\hbox{$c_p$}% \message{//depth:\the\dp0//}% \box0%) meghatározható. Az állandó nyomáson mért fajhő ismeretében az állandó térfogaton mért fajhő, (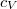\setbox0\hbox{$c_V$}% \message{//depth:\the\dp0//}% \box0%) szintén meghatározható (pl. hangsebesség-méréssel).

Fajhőmérés elektromos energiaközléssel

Ennél a módszernél a vizsgált anyag (fajhője \setbox0\hbox{$c$}% \message{//depth:\the\dp0//}% \box0%, tömege \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%) hőmérsékletét elektromos fűtőtest segítségével \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% értékkel megnöveljük. Feltéve, hogy a fűtőtest által leadott energia teljes egészében a vizsgált anyag belső energiáját növeli:

\[ U I \tau = c m \Delta t \]

amiből az UI fűtőteljesítmény, a \setbox0\hbox{$\tau$}% \message{//depth:\the\dp0//}% \box0% melegítési idő, a vizsgált anyag \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0% tömege és a \setbox0\hbox{$\Delta t$}% \message{//depth:\the\dp0//}% \box0% hőmérsékletváltozás ismeretében a \setbox0\hbox{$c$}% \message{//depth:\the\dp0//}% \box0% fajhő meghatározható.

A módszer elsősorban folyadékok fajhőjének meghatározására alkalmas. Használható azonban szilárd anyagok esetén is, ha azokat folyadékba helyezve a folyadékkal együtt melegítjük.

A kaloriméter hőkapacitása és a hőmérsékleti korrekció

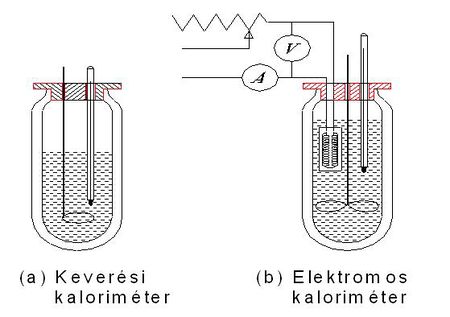
A keveréssel és az elektromos melegítéssel történő fajhőmérés esetén eddig feltételeztük, hogy a folyamat a környezettől hőtanilag jól elszigetelve, hőveszteség nélkül játszódik le. Ennek a feltételnek a teljesítése érdekében a hőközlés a környezettől jó hőszigetelő anyagokkal elválasztott edényben, kaloriméterben történik. (Egy keverési és egy elektromos kaloriméter vázlatát az 1. ábra mutatja.)

1. ábra

Ennek ellenére a hőveszteség nélküli mérés mégsem valósítható meg, elsősorban az alábbi két ok miatt: az egyik az, hogy az edény hőmérséklete is változik a mérés közben és ez is energiát igényel, a másik pedig, hogy bármilyen jó hőszigetelést is alkalmazunk a környezet felé mindig történik energiaátadás. Ez a két ok (hiba) a kaloriméter hőkapacitásának figyelembevételével illetve a hőveszteségek becslésével csökkenthető.

A kaloriméter hőkapacitása

Ha tudnánk azt, hogy a kaloriméter egyes részei milyen tömegűek, mekkora a fajhőjük és milyen mértékben melegszenek fel, akkor meg tudnánk határozni a kísérlet közben a kaloriméter egyes részeinek melegítéséhez szükséges energiát. Ez az eljárás gyakorlatilag megvalósíthatatlan. Ehelyett mérés segítségével meghatározzuk a kaloriméter \setbox0\hbox{$C$}% \message{//depth:\the\dp0//}% \box0% hőkapacitását. Ha a kaloriméter hőkapacitását is figyelembe vesszük, akkor a hőcserét leíró egyenleteink az alábbiak szerint módosulnak:

\[ c m ( t - t_k ) = c_i m_i ( t_k - t_i ) + C ( t_k - t_i )\]
\[ U I \tau = c m \Delta t + C \Delta t. \]

A kaloriméter hőkapacitásának meghatározásához ismert fajhőjű (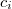\setbox0\hbox{$c_i$}% \message{//depth:\the\dp0//}% \box0% , \setbox0\hbox{$c$}% \message{//depth:\the\dp0//}% \box0%) anyagok alkalmazásával a fenti egyenletek valamelyikével történik. Ismert fajhőjű anyagként rendszerint vizet alkalmazunk.

A hőmérsékleti korrekció

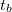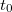A kaloriméter belseje és a környezet között energiaátadást a belső tér (\setbox0\hbox{$t_b$}% \message{//depth:\the\dp0//}% \box0%) és a környezet (\setbox0\hbox{$t_0$}% \message{//depth:\the\dp0//}% \box0%) hőmérséklete közötti eltérés eredményezi. 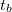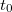Az ezen hőmérsékletkülönbség okozta energiaátadást jó hőszigeteléssel valamint egymáshoz közeli \setbox0\hbox{$t_b$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$t_0$}% \message{//depth:\the\dp0//}% \box0% választással csökkentjük. A kaloriméter belseje és a külső tér között mindezek ellenére fellépő energiacsere "hőmérsékleti korrekcióval" vehető figyelembe. Az alábbiakban a hőmérsékleti korrekció grafikus végrehajtását mutatjuk be.

2. ábra

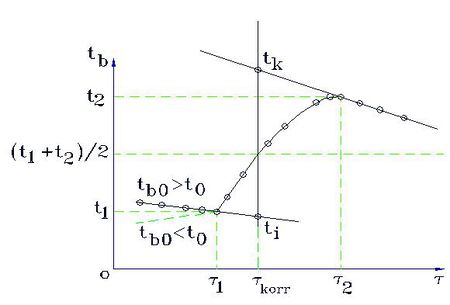
A 2. ábra a kaloriméteres mérés során a kaloriméter hőmérsékletének változását mutatja be az idő függvényében. A görbe három jól elkülöníthető szakaszra osztható, az egyes szakaszokon lejátszódó folyamatokat áttekintjük:

  • Előperiódus: A kaloriméterbe helyezett folyadék (víz, olaj stb.) és a kaloriméter, valamint a folyadék és a környezet közötti hőmérsékleti egyensúly kialakulásának folyamata. A kaloriméter és a mérő folyadék hőmérsékletétől függően ebben a szakaszban a belső tér hőmérséklete csökken ha 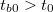\setbox0\hbox{$t_{b0} > t_0$}% \message{//depth:\the\dp0//}% \box0% vagy növekszik ha 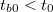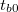\setbox0\hbox{$t_{b0} < t_0$}% \message{//depth:\the\dp0//}% \box0% (\setbox0\hbox{$t_{b0}$}% \message{//depth:\the\dp0//}% \box0% a belső tér hőmérséklete kísérlet indításakor). Ebben a szakaszban a kis hőmérsékletkülönbségek miatt a hőmérséklet - idő kapcsolat jó közelítéssel lineárisnak tekinthető.
  • Főperiódus: Az előperiódus a fő energiaátadási folyamattal folytatódik (főperiódus), amely az anyagok összekeveredésével illetve a fűtőtest bekapcsolásával kezdődik. A főperiódusban a belső tér hőmérséklete (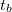\setbox0\hbox{$t_b$}% \message{//depth:\the\dp0//}% \box0%) emelkedik. Ebben a szakaszban megy végbe az energiacsere az összekevert különböző hőmérsékletű anyagok között, vagy a kaloriméterben levő anyagok és a fűtőtest között. A kaloriméter belsejének hőmérséklete a környezeti hőmérséklet fölé emelkedik 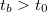\setbox0\hbox{$t_{b} > t_0$}% \message{//depth:\the\dp0//}% \box0% és ezért energialeadás történik a környezet felé. A hőveszteség miatt a belső tér hőmérséklete nem érheti el a tökéletes hőszigetelés esetén várható 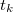\setbox0\hbox{$t_k$}% \message{//depth:\the\dp0//}% \box0% egyensúlyi hőmérsékletet. A főperiódust követő szakasz (az utóperiódus) hőmérséklet-idő grafikonjából azonban következtetni tudunk erre az értékre.
  • Utóperiódus: Ebben a szakaszban 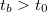\setbox0\hbox{$t_{b} > t_0$}% \message{//depth:\the\dp0//}% \box0% és a nem tökéletes hőszigetelés miatt lassan csökken a kaloriméter belsejében a hőmérséklet. A hőmérsékletcsökkenést most is lineárisnak tekintjük.

Látható, hogy a folyamat a nem tökéletes hőszigetelésből adódó hibák miatt az ideálistól eltérően alakul. A hőmérséklet - idő görbe felvétele azonban lehetőséget ad a hibák korrigálására. A hőmérsékleti korrekció gyakorlati végrehajtása a következőképpen történik (2. ábra). Felvesszük a kaloriméter hőmérsékletének időfüggvényét. Az elő- és utóperiódus szakaszára egyenest illesztünk. Tegyük fel, hogy az előperiódusra illesztett egyenes utolsó érintési pontjának koordinátái 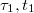\setbox0\hbox{$\tau_1, t_1$}% \message{//depth:\the\dp0//}% \box0%. Az utóperiódusra illesztett egyenes első érintkezési pontjának koordinátái 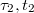\setbox0\hbox{$\tau_2, t_2$}% \message{//depth:\the\dp0//}% \box0%. Ezek megállapítása után megrajzoljuk a 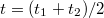\setbox0\hbox{$t=(t_1+t_2)/2$}% \message{//depth:\the\dp0//}% \box0% időtengellyel párhuzamos egyenest. Ennek az egyenesnek és a főperiódus görbéjének metszéspontján keresztül párhuzamost húzunk a hőmérséklettengellyel. 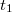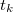Ez utóbbi egyenesnek és az időperiódusra illesztett egyenesnek a metszéspontját tekintjük a kaloriméter + mérőfolyadék rendszer kezdeti hőmérsékletének (\setbox0\hbox{$t_1$}% \message{//depth:\the\dp0//}% \box0%), az utóperiódusra illesztett egyenessel való metszéspontját fogadjuk el közös hőmérsékletnek (\setbox0\hbox{$t_k$}% \message{//depth:\the\dp0//}% \box0%).

A korrekció fenti módon történő végrehajtása az alábbiakon alapul: A környezettel való energiacsere miatt a kaloriméterben állandóan változik a hőmérséklet, egyensúlyi hőmérséklet sem alakulhat ki, így sem a kiindulási, sem a véghőmérsékletet nem tudjuk megmérni. Az előperiódusra fektetett egyenes mutatja, hogy hogyan változna a kaloriméter belsejében a hőmérséklet, ha nem indulna meg az energiacsere a főperiódusban. Ebből lehet a valódi kezdeti hőmérsékletre következtetni.

Az utóperiódusra fektetett egyenes segítségével arra lehet következtetni, hogy milyen hőmérséklet értéket vehetett volna fel a kaloriméter belseje ideális hőszigetelés mellett.

A jó minőségű kaloriméter hőkapacitása kicsi és hőszigetelése jó, azaz kicsi a környezettel való energiacsere. Ekkor a hőmérséklet közel állandó az elő- és utóperiódus során.

A mérőeszköz

3. ábra

A méréshez használt eszközök:

  • 2 db 0,75 l űrtartalmú duplafalú rozsdamentes termosz platina vékonyréteg ellenálláshőmérőkkel
  • elektromos vízforraló
  • 1,2 \setbox0\hbox{$\Omega$}% \message{//depth:\the\dp0//}% \box0%-os, 50 W maximális teljesítményű fűtőellenállás
  • Hameg multiméter számítógépes kezelőprogrammal
  • tápegység a fűtőellenállás meghajtásához
  • mérőhelyenként 1 db alumínium és 1 db sárgaréz próbatest, a próbatestek tömegei:
    • A jelű alumínium tömb 594,5 g (± 0,2 g)
    • B jelű alumínium tömb 533,2 g (± 0,2 g)
    • C jelű sárgaréz tömb 1605 g (± 5 g)
    • D jelű sárgaréz tömb 1600 g (± 5 g)
Ellenőrizzük, hogy melyik próbatesten végezzük a mérést!
  • jég
  • mérőhenger
  • 1 db kalibrált higanyszálas hőmérő
  • mágneses keverő
  • digitális mérleg
  • tartó állvány a termoszokhoz

Mérési feladatok

A méréshez rendelkezésre álló eszközök

  • A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
  • Figyelem! A forró víz komoly égési sérüléseket okozhat, így a mérési gyakorlaton különös figyelmet és óvatosságot várunk el! Figyeljünk arra, hogy a forró víz ne ömöljön ki, ill. hogy a forró fém próbatesteket kézzel ne érintsük! A forróvizes termoszt mindig rögzítsük az erre szolgáló állvány segítségével, hogy véletlenül se tudjon kiborulni!
  • A műanyag mérőhengerekbe sose töltsünk forró vizet, mert az a hengerek károsodásához vezet!
  • A méréseknél használt vízmennyiségek pontosabb meghatározásához segítséget nyújtanak a rendelkezésre álló digitális mérlegek! Célszerű a mérés elején az üres termoszok tömegét meghatározni.
  • A pontos fajhőmérés alapvető feltétele a termikus egyensúly kialakulása, melyet mágneses keverő segítségével jelentősen felgyorsíthatunk!
  • A mágneses keverő közvetlen közelében elhelyezkedő hőmérővezetékekben a keverő jelentős zajt indukál, így a vezetékeket a keverőtől minél távolabb rögzítsük!
  • A mérések közben értékeljük ki az eredményeket! Lehetőség szerint a 4-8. méréseket ismételjük meg. Ha jelentős eltérést tapasztalunk mérések között, illetve ha a mért értékek jelentősen eltérnek az irodalmi adatoktól, próbáljuk megtalálni, és kiküszöbölni a mérési hiba okát!

1. A hőmérők kalibrálása

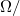A méréshez Pt 100-as szabvány vékonyréteg ellenálláshőmérőket használunk, melyek ellenállása 0 °C-on 100 \setbox0\hbox{$\Omega$}% \message{//depth:\the\dp0//}% \box0%, és melegítés hatására lineárisan, 0,39 \setbox0\hbox{$\Omega/$}% \message{//depth:\the\dp0//}% \box0%°C meredekséggel nő. A számítógépes mérőprogram ez alapján az összefüggés alapján számolja a hőmérsékletet. A hőmérőhöz vezető drótok, a banándugók és a forrasztás véges ellenállása miatt viszont megjelenik egy konstans (hőmérsékletfüggetlen) soros ellenállás, ami miatt a mért hőmérsékletérték korrekcióra szorul.

  • Ebből milyen irányú hőmérsékleti korrekciót várunk?

Mindkét termosz hőmérőjét hitelesítsük hideg csapvízben higanyszálas hőmérő segítségével! Határozzuk meg a soros ellenállás értékét és az ebből adódó hőmérsékletkorrekciót!

  • Melyik mérési feladatnál okozná a legnagyobb problémát, ha a hőmérők nullponteltolódását nem vennénk figyelembe?

2. A termosz hőveszteségének becslése

Töltsünk a termoszba forró vizet, várjuk meg amíg a rendszer termalizálódik. Ezután a rendszer a nem teljesen tökéletes szigetelés miatt kismértékben hőt ad le a környezetének, és emiatt lassan csökken a hőmérséklete. Becsüljük meg a hőleadás sebességét!

  • A hőleadást legalább 5 percen keresztül mérjük!
  • Adjunk számszerű becslést arra, hogy a termosz hőveszteségének elhanyagolása illetve a fent részletezett hőmérsékleti korrekció elhagyása milyen nagyságrendű hibát okozna az alábbi méréseknél!

3. A termosz hőkapacitásának becslése

Mérjük meg a rozsdamentes termosz tömegét! A rozsdamentes acél fajhője 500 J/kg°C, termosz külső és belső falának vastagsága megegyezik. Becsüljük meg a termosz saját hőkapacitását!

4. A víz fajhőjének mérése fűtéses módszerrel

Töltsünk az egyik termoszba 0,6 l hideg csapvizet. Helyezzük a fűtőellenállást az edénybe, és 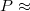\setbox0\hbox{$P\approx$}% \message{//depth:\the\dp0//}% \box0% 50 W fűtőteljesítmény mellett mérjük a víz melegedését 10 percen keresztül.

  • Az 50 W fűtőteljesítményt csak a már vízbe helyezett fűtőellenállásra alkalmazzuk, levegőben ez a fűtőteljesítmény az ellenállás károsodásához vezethet!
  • A pontos fűtőteljesítmény meghatározásához digitális multiméterrel mérjük meg az áram és a feszültség pontos értékét.

A leadott hőmennyiség és a mért hőmérsékletváltozás alapján határozzuk meg a víz fajhőjét!

  • Az edény hőkapacitását a 3. feladatban becsült értékkel vegyük figyelembe.

5. A termosz hőkapacitásának mérése keveréses módszerrel

Forraljunk fel 0,35 l vizet, majd a forró vizet töltsük az egyik termoszba. A másik termoszba töltsünk 0,35 l hideg csapvizet. Várjuk meg az egyensúlyi hőmérsékletek beálltát. Ezután a hideg vizet töltsük át a forró vizes termoszba, és keverés mellett várjuk meg az egyensúlyi hőmérséklet kialakulását. A mért hőmérsékletváltozások ill. a hideg és a forró víz tömege alapján határozzuk meg a termosz saját hőkapacitását! A mért értéket hasonlítsuk össze a 3. feladatban becsült hőkapacitással!

  • A mérésekhez csak egy mágneses keverő áll rendelkezésre, ezzel mindig a melegvizes termoszt keverjük!

6. Fém minta fajhőjének mérése

Forraljunk fel 0,5 l vizet, majd a forró vizet töltsük az egyik termoszba. A másik termoszba töltsünk 0,5 l hideg csapvizet. A hideg vízbe helyezzük bele a fém tömböt, várjuk meg amíg mindkét edényben kialakul az egyensúlyi hőmérséklet. A fém tömböt helyezzük át a forró vízbe, és várjuk meg a közös hőmérséklet kialakulását. A hőmérsékletváltozások alapján határozzuk meg az adott fém fajhőjét!

7. A jég olvadáshőjének mérése

Fakultatív feladat! (Ennek a feladatnak a megoldása nem kötelező, csak akkor foglalkozzon vele, ha marad elég idő rá.)

Forraljunk fel 0,45 l vizet, majd a forró vizet töltsük az egyik termoszba. Várjuk meg az egyensúlyi hőmérséklet kialakulását. Töltsük fel a termoszt olvadásban lévő jéggel, majd várjuk meg míg elolvad a jég, és kialakul az egyensúlyi hőmérséklet. Mérjük le a termoszban lévő víz térfogatát (vagy tömegét), ebből határozzuk meg, hogy mennyi jeget tettünk a termoszba! Határozzuk meg a jég olvadáshőjét!


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Fajhő_mérése&oldid=18374”