„Elektromos töltések mozgása statikus mágneses térben” változatai közötti eltérés
Papp (vitalap | szerkesztései) |
Papp (vitalap | szerkesztései) |
||
| 354. sor: | 354. sor: | ||
|- | |- | ||
| [[Fájl:Rúdmágnes_4.jpg |közép|350px|]] | | [[Fájl:Rúdmágnes_4.jpg |közép|350px|]] | ||
| − | | [[Fájl:Rúdmágnes_5.jpg |közép| | + | | [[Fájl:Rúdmágnes_5.jpg |közép|400px|]] |
|- | |- | ||
| align="center"|10.2 a ábra | | align="center"|10.2 a ábra | ||
A lap 2011. szeptember 11., 17:06-kori változata
Mágneses tér
Ebben a fejezetben betekintést nyerhetünk olyan fizikai folyamatokba, amelyek alapját képezik olyan berendezéseknek, melyek a részecskefizikai kutatásokban (részecskegyorsító berendezés)vagy az anyagvizsgálatban (tömeg-spektrográf) játszanak kitüntetett szerepet. Látjuk majd azt is, hogy a Föld mágnese tere hogyan védi meg akár az internetet (az elektromos információs hálózatokat), a műholdak egy részét és hogy miért is alakul ki az északi fény. A mágneses jelenségek tárgyalása után érthetővé válik a mágneses szondák működési elve is, és hogy a tengeri térképeken hogyan jelölik az északi (mágneses) irányt. Van néhány – mindenki által ismert effektus – melynek segítségével megmondhatjuk, hogy egy térrészben van-e mágneses tér, vagy nincs. Az egyik ilyen – már több ezer éve ismert (Kína, iránytű) – jelenség a mágneses térnek a mágnesre gyakorolt hatása. Az inhomogén mágneses térben egyrészt erő hat a mágnesre, másrészt pedig helyzetéből függően többnyire forgatónyomaték is; erről általában már gyermekkorában szerez az ember tapasztalatot. A mágneses tér jelenlétéről árulkodik még egy másik - talán kevésbé közismert - jelenség; nevezetesen, hogy a mágneses térben mozgó töltött részecskére erő hat. Minthogy az elektrosztatikában is azt a szemléletet követtük, hogy a tér, pontosabban az elektromos erőtér mérését az erő mérésére lehet visszavezetni, most is ezt a módszert követjük.
A mágneses indukciós tér jelölése: 
. Mértékegysége a 
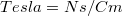, jele: 
. Az 1 T erősségű mágneses indukciós tér igen erős, azaz ez az egység ”igen nagy”; a Föld mágneses terének indukciója az egyenlítő környékén kb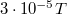 
.
A indukciójú mágneses térben a 
töltéssel rendelkező (pontszerűnek tekintett) részecskére ható mágneses Lorentz-erő:
![\[\vec F = q \vec v \times \vec B \]](/images/math/b/d/4/bd4473b591a8a58e18ae4b41b88ad71f.png) |
(1.1) |
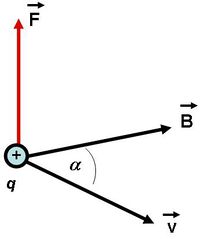
A Lorentz-erő merőleges a részecske sebességére, valamint a mágneses indukciós térre, nagysága:
![\[F = q v B sin \alpha \]](/images/math/7/1/6/7160a5a79e3301a222dc4f4159fde5f9.png) |
(1.2) |
Ahol 
a részecske sebességvektora és a tér vektora közötti szög (1.1 ábra).
 |
| 1.1 ábra |
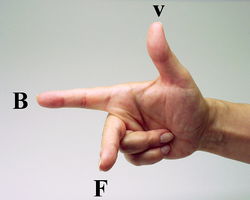
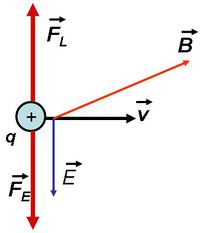
A Lorentz-erő merőleges a részecske sebességére, tehát infinitezimális elmozdulására is, azaz a homogén indukciós tér nem végez munkát a töltött részecskén, vagyis a részecske sebességének nagyságát nem, csak az irányát képes megváltoztatni. A csak mágneses indukciós térben haladó pozitív töltéssel rendelkező részecskére ható erő irányát könnyű meghatározni (és emlékezni a módszerre) a jobbkéz-szabály alapján (természetesen egy negatív töltésre ellenkező irányú erő hat):
 |
| 1.2 ábra |
Amennyiben elektromos tér is hat a részecskére és az 1.1 formulát kiegészítjük az elektrosztatikus erővel, akkor kapjuk a Lorentz-erő általános alakját:
![\[\vec F = q (\vec E + \vec v \times \vec B) \]](/images/math/9/4/5/945a92000e1af1a935a7ab8b927857b0.png) |
(1.3) |
Fontos megjegyezni, hogy az előzőek alapján már most jól látszik, hogy a töltött részecskére ható elektromos és a mágneses erő "más szerkezetű" és ez a különbség az 
és a között még szembetűnőbb lesz az elektromos és mágneses terek egységes tárgyalását lehetővé tevő Maxwell-egyenletekben. Ez a természet sok jelenségének leírásában fontos szerephez jut, tehát akár azt is mondhatnánk, hogy ez is az oka annak, hogy olyan a világ körülöttünk, amilyennek ismerjük.
Elektromos töltések mozgása statikus elektromos és mágneses térben
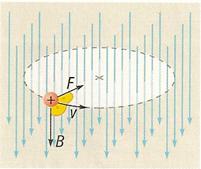
Ezután tekintsünk néhány egyszerű berendezést az indukciós tér alkalmazására. Ennek a bemutatásához először vizsgáljuk meg, hogy hogyan is mozog egy töltött részecske homogén indukciós térben. Ehhez tekintsük a 2.1 ábrát
 |
| 2.1 ábra |
Homogén indukciós térben a Lorentz-erő nagysága állandó és iránya merőleges a sebesség irányára; ez pedig éppen a centripetális erő (minthogy kielégíti az egyenletes körmozgás dinamikai feltételét), így:
![\[qvB = m \frac{v^2}{R} \]](/images/math/3/2/0/320c9091f3c5177aaea68ceaae946a27.png) |
(2.1) |
ahol is 
a részecske tömege és 
a körpálya sugara, ez az 2.1 – ből átrendezéssel kifejezhető:
![\[R = \frac{mv}{qB} \]](/images/math/e/9/6/e9664aa737fe96e60d050987e8bf0b67.png) |
(2.2) |
Most már könnyen kiszámítható a periódusidő is, azaz, hogy mennyi idő alatt futja be a töltött részecske az sugarú kört:
![\[T = \frac{2R\pi}{v} \qquad {\rm azaz} \qquad T = \frac{2\pi m}{qB}\]](/images/math/5/9/4/594e1a5357f096d699b592ce13a8c732.png) |
(2.3) |
Érdekes és fontos (megjegyzendő!) következmény, hogy a periódusidő nem függ a részecske sebességétől.
A sebességszűrő
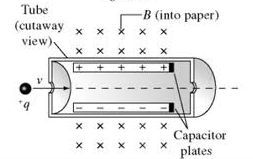
A legtöbb – a későbbiekben bemutatásra kerülő – berendezés (valamint az elektrosztatikában már tárgyalt CRT monitor) is olyan részecskenyalábbal működik, amelyben a részecskék sebességének nagysága és iránya állandó, azaz a részecskenyalábot preparálni, szűrni kell. Az erre szolgáló eszköz a sebességszűrő. Ahhoz, hogy működését megértsük, lássuk a következő ábrát:
 |
| 3.1 ábra |
Az egymásra – és a sebesség vektorára is – merőleges és tér által a töltött részecskére ható két erő egymással ellentétes irányú:
 |
| 3.2 ábra |
A Lorentz-erő és az elektrosztatikus erő abban az esetben ejti ki egymást, ha
![\[qE = qvB \]](/images/math/c/8/5/c85ad852cf2902c699e51257e6cfb290.png) |
(3.1) |
tehát azok a részecskék jutnak át a sebességszűrőn, vagyis azoknak nem változik a pályája, amelyeknek a sebessége:
![\[v = \frac {E}{B} \]](/images/math/9/0/9/909448a7e1777472f71e797fa22bbead.png) |
(3.2) |
A tömegspektrométer
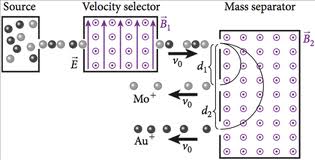
Az 3.2 formula alapján nyilvánvaló, hogy a sebességszűrőn átjutott töltött részecskék, vagy ionizált atomok mindegyikének sebessége ugyanaz, viszont ez a formula nem tartalmazza a tömeget, így tehát az atomok tömege különböző lehet (pl. izotópok). A sebességszűrővel preparált részecskenyaláb ezután bejut egy olyan térrészbe, ahol a különböző tömegű izotópok vagy atomok - az 2.2 következményeként – a homogén indukciós térben, arra merőleges síkban más-más sugarú köríven mozognak, így szeparálásuk egyszerűen megoldható, mint az az 4.1 ábrán is látható.
 |
| 4.1 ábra |
A kimenethez általában egy számítógéphez csatlakoztatott detektorsort illesztenek, így a minta anyagi összetétele a monitoron láthatóvá tehető.
A ciklotron
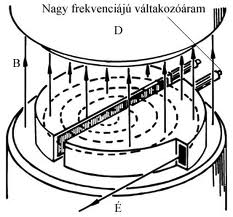
A részecskék gyorsítására szolgáló berendezés, amelyet bemutatunk, a ciklotron. Láttuk, hogy az állandó mágneses térre merőlegesen belőtt töltött részecskék körpályán mozoghatnak és a keringési idő nem függ (nemrelativisztikus esetben, azaz ha v << c) a sebességtől (2.3), ellenben a körpálya sugara arányos azzal (2.2). Ennek a két ténynek a felhasználásával készítik a ciklotronokat. Vizsgálatához tekintsük a 5.1 a. és b. ábrán látható berendezést!
 |
 |
| 5.1 a ábra | 5.2 b ábra |
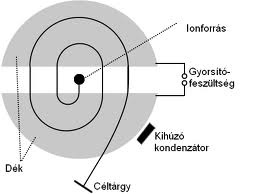
Az ionforrásból kilépő gyorsítandó ionok (vagy töltött részecskék) a sebességükre merőleges mágneses térben köríven mozognak a félhenger alakú szegmenseken belül. Az elektrosztatika fejezetben láttuk, hogy egy üreges vezető belsejében az elektromos potenciál állandó, tehát az elektromos tér a szegmensek belsejében csaknem zérus. A félhengerek közötti térrészben viszont a részecskék gyorsíthatók, ha gyorsítófeszültséget kapcsolnak a szegmensekre, melyet azonban minden félperiódusban ellenkező előjelűre kell átkapcsolni. Ez azt jelenti, hogy (2.3) formula által meghatározott időtartamnak megfelelő ciklotronfrekvencia (5.1) kétszeresével szükséges a feszültség előjelét ellenkezőjére megváltoztatni.
![\[f_{cikl.} = \frac {qB}{2\pi m} \]](/images/math/c/1/1/c11037562662faf755f73424f95edfec.png) |
(5.1) |
Félperiódusonként növekszik tehát a töltött részecske sebessége és így körívének sugara, ezért – mint ahogy az ábrákon látható – gyakorlatilag egy "spirálpályán" mozogva gyorsul kifelé. A megfelelő sebességre felgyorsított részecskéket aztán egy kihúzó kondenzátor segítségével a kilépő ablakon kivezetik.
Az elektronmikroszkóp
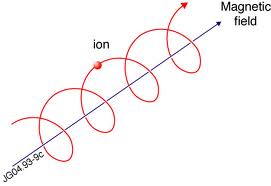
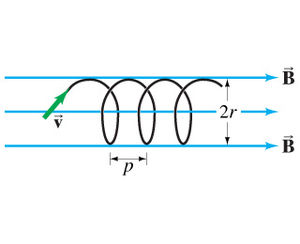
Végül az utolsó berendezés, melynek működési elvét csak vázlatosan mutatjuk be, az elektronmikroszkóp. Az optikai mikroszkóp felbontásának fizikai korlátai vannak; gyakorlatilag fél hullámhossznál nagyobb felbontás nem érhető el, azaz a 200 nm-nél kisebb részletek általában nem láthatók. Nagy sebességű elektronok De Broglie hullámhossza ennél nagyságrendekkel kisebb lehet, tehát elektronhullámokkal sokkal nagyobb felbontás érhető el. Amennyiben egy elektron nem az indukciós tér vektorára merőleges síkban mozog, hanem sebessége 90°-nál kisebb szöget zár be az indukciós térrel, akkor a 6.1 a és b ábrán látható módon helikális pályán (csavarvonalon) halad, azaz a térre merőlegesen körmozgást végez, miközben a térrel párhuzamosan állandó sebességgel halad.
 |
 |
| 6.1 a ábra | 6.1 b ábra |
A csavarvonal menetemelkedése (a jobboldali ábrán 
-vel jelöltük) egyszerűen kiszámítható.
Bontsuk fel az elektron sebességvektorát a -re merőleges 
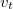és azzal párhuzamos 
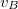komponensekre. A periódusidő és 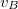szorzata adja -t, a menetemelkedést:
![\[p = v_B T = v cos(\theta)\frac{2 \pi m}{qB} \]](/images/math/6/8/8/688a647a2e1edeb41eef8f270d74f959.png) |
(6.1) |
ahol 
a sebességvektor és az indukciós tér vektora által bezárt szög.
Amennyiben a szög elég kicsi ( < 5° ), akkor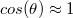 
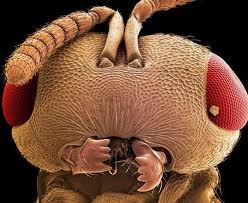
, így nem függ a szögtől. Emiatt az egy pontból különböző szögben induló részecskék – különböző pályákon mozogva – mind (a kiindulási ponttól mért) ugyanakkora távolságban találkoznak, tehát lefókuszálódnak. Ez tehát azt jelenti, hogy a mágneses tér leképezi az egy pontból kiinduló elektronokat, vagyis kielégülnek a képalkotás feltételei; ez adja az elektronmikroszkóp működésének fizikai alapját. Az elektronmikroszkóp felbontása a látható fény hullámhosszának akár század vagy ezredrésze is lehet. Jó példa erre a következő két felvétel, amelyeken jól látszik, hogy fél mikronnál (látható fény hullámhossza) kisebb részletek is megfigyelhetők.
 |
 |
| 6.2 a ábra | 6.2 b ábra |
Áramra ható erő mágneses térben
Láttuk, hogy egy mozgó töltött részecskére erő hat az indukciós térben, a Lorentz-erő. Ezután kézenfekvőnek tűnik a kérdés, hogy hat-e erő a mágneses térbe helyezett áramjárta huzalra. A válasz az, hogy igen, és a Lorentz-erőt megadó formula ügyes átalakításával annak matematikai alakját is könnyedén meghatározhatjuk:
![\[\vec F = q \vec v \times \vec B \qquad \Rightarrow \qquad \vec F = dq \vec v \times \vec B = dq \frac {d \vec s}{dt} \times \vec B = \frac {dq}{dt} d\vec s \times \vec B \]](/images/math/0/b/9/0b9de642f48176360c1f8a317be0a4f5.png) |
(7.1) |
Egy véges, áramjárta vezetékdarabra ható erő 7.1 alapján:
![\[\vec F = I \int_s d\vec s \times \vec B \]](/images/math/8/0/8/808aea5e3820ba98e46774a51c0c80be.png) |
(7.2) |
Ennek egyszerűbb alakját kapjuk abban az esetben, amikor egy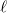 
hosszúságú, áramjárta vezetékdarab homogén mágneses indukciós térben van:
![\[\vec F = I \vec {\ell} \times \vec B \]](/images/math/8/d/1/8d1fed6a3ee5da437329b8c4e30f17d5.png) |
(7.3) |
Áramhurokra ható forgatónyomaték mágneses térben
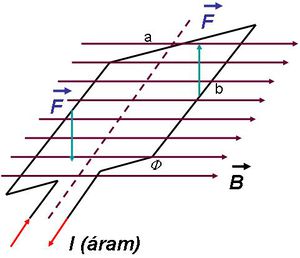
Most nézzük meg, hogy mi is történik egy téglalap alakú vezető hurokkal, amiben áram folyik, és amely egy olyan térrészben van, ahol az indukciós tér homogén. Ehhez tekintsük a következő ábrát:
 |
| 8.1 ábra |
A (6.3) formula alapján érthető, hogy a tekercsre egy erőpár, azaz forgatónyomaték hat. Az említett formula segítségével megadhatjuk a jelölt oldalakra ható erő nagyságát is: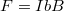 
. (A másik két oldalra is hat erő, de ezek összege zérus, és nem fejtenek ki forgatónyomatékot.) A tekercsre ható forgatónyomaték nagysága ezután az ábra jelöléseit használva könnyen felírható:
![\[M = 2 \frac{a}{2} F cos (\phi)=IabB cos (\phi) \qquad \Rightarrow \qquad M= IABcos (\phi) \]](/images/math/5/9/6/59685a093e226062d05fc1bc1ee73353.png) |
(8.1) |
ahol 
az áramhurok területe és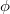 
a tekercs síkja és az indukciós tér által bezárt szög. A forgatónyomaték vektoriális alakját a 8.1 általánosításával kapjuk:
![\[\vec M = I \vec A \times \vec B \]](/images/math/e/6/6/e663641234f83aa9d6e0541bd78423a7.png) |
(8.2) |
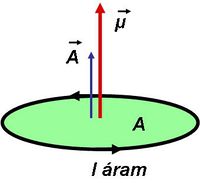
Az általánosításban még tovább léphetünk, ha bevezetjük a tekercs mágneses dipólmomentumát: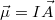 
(az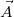 
merőleges a tekercs síkjára - 8.2 ábra - és irányát az áram iránya valamint a jobbkéz-szabály határozza meg), így:
![\[\vec M = \vec {\mu} \times \vec B \]](/images/math/2/1/1/2113fa207ea533b9a992b039a9768b2b.png) |
(8.3) |
 |
| 8.2 ábra |
Most már tudjuk tehát, hogy ha a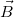 
és a 
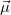közötti szög 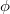, akkor a mágneses dipólmomentumra 
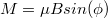nagyságú forgatónyomaték hat. Ennek a formulának a felhasználásával azt is ki tudjuk számítani, hogy mekkora a mágneses dipólus potenciális energiája:
![\[E_p = \int\limits_0^\theta M(\phi)d\phi = \int\limits_0^\theta \mu B sin(\phi)d\phi = \mu B [1 - cos(\phi)]_0^\theta = \mu B - \mu B cos(\theta) \]](/images/math/7/f/5/7f5a42160834be1d09cd2a05f01d03cc.png) |
(8.4) |
A potenciális energia zéruspontját - mint azt a mechanikában és az elektrosztatikában tanultuk - tetszőlegesen választhatjuk meg, így:
![\[E_p = - \vec {\mu} \cdot \vec B \]](/images/math/b/4/d/b4dc245be847d32d69a5a3c4e723875d.png) |
(8.5) |
A most bemutatott jelenségek lehetőséget adnak arra, hogy megmérjük a mágneses indukciós tér nagyságát és irányát. Nem kell mást tennünk, mindössze egy áramjárta vezetőhurkon meg kell mérni az arra ható forgatónyomatékot. Régebben használtak is ilyen szondákat.
A Hall-effektus
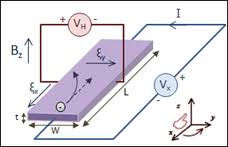
Az indukciós tér mérésére újabban inkább a Hall effektuson alapuló Hall szondát használnak. A jelenség vizsgálatához tekintsük a következő ábrán lévő elrendezést:
 |
| 9.1 ábra |
A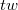 
keresztmetszetű és 
hosszúságú vezetőn 
áram folyik és az indukciós tér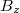 
komponense merőleges rá, mint az 9.1 ábrán látható. A vezetőben a 
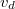drift-sebességgel mozgó elektronokra hat a Lorentz-erő: 
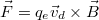. Ez az erő merőleges az áram irányára. Ennek hatására töltések mozdulnak el oldalirányban mindaddig, amíg annyi töltés nem ül ki a vezető oldalára, hogy az általuk létrehozott ellentér már megakadályozza újabb töltések oldalirányú áramlását. A 
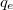töltésre ható Lorentz-erőt tehát a vezető szélén összegyűlt töltések által létrehozott ellentérben fellépő 
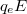elektrosztatikus erő oltja ki. Az így létrejött 
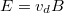nagyságú elektromos erőtér jelenléte miatt viszont a lemez két széle között 
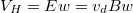feszültség alakul ki, amelyet műszerrel mérni lehet, és Hall-feszültségnek hívják. Eredetileg ezt a mérést az elektromos vezetés tanulmányozására építették. Ez érthető, hiszen ha az egyenáram fejezet 1.5 formulájából kifejezzük a 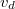sebességet és behelyettesítjük a Hall-feszültséget megadó formulába, akkor kapjuk a
![\[U_H = \frac {BI}{nq_e t} \]](/images/math/8/0/7/8073cbcad9f411de9a05ec0fad356ffb.png) |
(9.1) |
Hall-feszültséget, amely segítségünkre lehet például az 
töltéssűrűség meghatározására. Az 9.1 ábrán látható berendezés a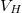 
mérésével azonban a mágneses indukciós tér nagyságának meghatározására is alkalmas, így működik a Hall-szonda.
A rúdmágnes és a Föld mágneses tere
Idáig arra láttunk példákat, hogy miként is mozoghatnak töltött részecskék mágneses indukciós térben. A következő megválaszolandó kérdés pedig az, hogy mi lehet a mágneses tér forrása?
Idáig arra láttunk példákat, hogy miként is mozoghatnak töltött részecskék mágneses indukciós térben. A következő megválaszolandó kérdés pedig az, hogy mi lehet a mágneses tér forrása? A bevezetőben már említettük, hogy "Az inhomogén mágneses térben egyrészt erő hat a mágnesre, másrészt pedig helyzetéből függően többnyire forgatónyomaték is…" Egy iránytű gyakorlatilag egy kis rúdmágnes, amelynek két mágneses pólusa – északi (N) és déli (S) – van. A 10.1 ábrán két – boltban is kapható – megfelelő színkóddal ellátott rúdmágnes látható. Az azonos pólusok (N-N és S-S) taszítják egymást, azonban az ellentétes pólusok között vonzó kölcsönhatás van.
 |
| 10.1 ábra |
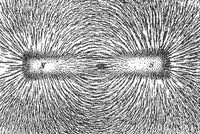
A mágneses indukciós térbe helyezett vasreszelék darabkái felmágneseződhetnek, kis mágnesként viselkedhetnek, így láthatóvá tehetik az indukciós erővonalakat (10.2 a. és b. ábra). Ez hasonló ahhoz, ahogyan az elektromos erőtérvonalak is szemléltethetővé tehetők olyan anyaggal, amely polarizálható és kis darabkái elektromos dipólként viselkednek.
 |
 |
| 10.2 a ábra | 10.2 b ábra |
A rúdmágnes indukciós tere igen nagy hasonlatosságot mutat az elektromos dipól elektromos terének szerkezetével:
10.3 ábra
Az erőtérvonalak ábráit szemlélve úgy tűnik, hogy az analógia teljes, azaz a két töltésközépponttal rendelkező elektromos dipólushoz hasonlóan, a mágneses dipólusnak is van két pólusa. Az erővonalak az északi pólusból indulnak a déli pólus felé. Legalább is a mágnes anyagán kívül! A hasonlóság abban az értelemben is jól működik, hogy az elektromos dipólok közötti kölcsönhatás hasonló a rúdmágnesek között fellépő erőkhöz, valamint hogy az elektromos dipól elektromos térben hasonlóan viselkedik, mint egy rúdmágnes (vagy iránytű) az indukciós térben. Egy lényeges különbség azonban mégiscsak van; amennyiben széttörjük két darabra a mágnesünket, akkor két kisebb rúdmágnest kapunk, azaz nem tudom szétválasztani az északi és a déli pólust. Ez egy fontos természeti törvény: mágneses monopólus nem létezik. Ennek következménye a mágneses Gauss törvény:
![\[ \oint\limits_A \vec B d \vec A = 0 \]](/images/math/1/3/0/1304a9ebeed7f0db910011d7bc7ef73b.png) |
(10.1) |
Ez azt jelenti, hogy a mágneses indukciós erőtér vonalai nem kezdődnek ill. nem végződnek (pl. egy mágneses monopóluson), hanem zárt hurkot alkotnak, azaz önmagukba záródnak, mint a saját farkába harapó kígyó.
Még mindig nem adtunk kimerítő választ az eredeti kérdésre, vagyis, hogy mi is a mágneses tér forrása. A körülöttünk tapasztalható, csaknem mindenhol mérhető indukciós tér forrása a Föld mágneses tere.
10.4. a. és b. ábra
Az előző két ábra mutatja a Föld mágneses indukciós térerősség vonalait. A térerősség vonalak irányának mérése történhet egy iránytűvel is, amelynek északi pólusa többé-kevésbé a Föld földrajzi északi pólusa felé mutat. A térerősség-vonalak szerkezete azt mutatja, mintha a Föld belsejében egy hatalmas rúdmágnes, pontosabban egy mágneses dipólus lenne. Mivel az iránytű északi pólusa mutat észak felé megállapodás szerint, ezért megállapíthatjuk, hogy a földi mágneses dipól déli pólusa van valahol a geográfiai északi pólus közelében. A pontosabb mérések alapján a Föld forgástengelye és a mágneses dipól tengelye kb. 11.3° – ot zárnak be. Ráadásul a mágneses pólusok – úgy tűnik egymástól függetlenül – vándorolnak is; egy év alatt akár 15 km-t is elmozdulhatnak (10.5 ábra).
10.5 ábra
A pontosabb navigáció érdekében a pólusok mozgását a tengeri térképeken is jelölik. Egy ilyen jelölés például így néz ki: 3°23'E 2006 (7'E). Ez azt jelenti, hogy a 2006-ban mért adatok alapján a térkép adott helyéről nézve a mágneses északi sark a geográfiai északi sarkhoz képest keletre látszik 3°23' szögben (ezt nevezik variációnak) és az éves változás 7' (ezt deviációnak hívják és előjelesen adják meg); így az eltérés pl. 2011-ben: 3°58' keletre. Sokan azt gondolhatnák, hogy ilyen számításokra már nincs szükség, hiszen a GPS segítségével könnyű navigálni. Néha azonban nem használható a GPS (hadgyakorlat, háború vagy biztonsági intézkedések miatt), ilyenkor a térkép és az iránytű segítségével lehet az útvonalat megtervezni vagy a pozíciót meghatározni.
A Föld mágneses terének igen fontos szerepe van a földi élet védelmezésében is. A világűrből érkező vagy a légkör felső rétegeiben a kozmikus sugárzás hatására keletkező ionok ill. egyéb töltött részecskék felfűződnek a Föld mágneses indukciós erővonalaira, azok mentén helikális pályán mozognak a pólusok között oda-vissza. A mágneses erőtér vonalai által "becsapdázott" részecskék sokasága egy Van Allen övnek nevezett védőernyőt képez (10.6 a. ábra) bolygónk körül, amely megszűri a világűrből érkező UV ill. kozmikus sugárzást. Ez a védőernyő azonban nem csak a bioszférát védi, hanem műszereinket, számítógépeinket és műholdjainkat is. E nélkül a védelem nélkül a kozmikus sugárzás tönkretenné a processzorokat, az elektromágneses viharok pedig, amelyeket pl. a napszél okozna, használhatatlanná tenné az elektronikus távközlést (pl. mobiltelefon, vezetékes hálózatok, GPS, stb.) A nagysebességű töltött részecskékből álló napszél természetesen módosítja bolygónk mágneses terének szerkezetét is; ezt mutatja a 10.6 b. ábra (fantáziakép).
