„Mozgó töltések és áramok által keltett tér” változatai közötti eltérés
Papp (vitalap | szerkesztései) |
Papp (vitalap | szerkesztései) |
||
| 25. sor: | 25. sor: | ||
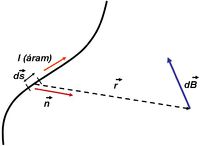
A jelenség vizsgálatához tekintsük az elképzelhető legegyszerűbb modellt, vagyis vizsgáljuk meg egy igen kisméretű, áramjárta vezetékdarab által keltett mágneses indukciós teret (1.2 ábra) és adjuk meg ennek matematikai alakját! | A jelenség vizsgálatához tekintsük az elképzelhető legegyszerűbb modellt, vagyis vizsgáljuk meg egy igen kisméretű, áramjárta vezetékdarab által keltett mágneses indukciós teret (1.2 ábra) és adjuk meg ennek matematikai alakját! | ||
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| − | + | |- | |
| − | + | | [[Fájl:Biot_Savart_1.JPG|közép|200px|1.1 ábra]] | |
| + | |- | ||
| + | | align="center"|1.1.2 ábra | ||
| + | |} | ||
A mérések azt mutatják, hogy a $d\vec s$ áramjárta kis vezetékdarab indukciós terét az $\vec r$ helyvektorral megadott pontban a '''Biot-Savart törvény''' segítségével adhatjuk meg: | A mérések azt mutatják, hogy a $d\vec s$ áramjárta kis vezetékdarab indukciós terét az $\vec r$ helyvektorral megadott pontban a '''Biot-Savart törvény''' segítségével adhatjuk meg: | ||
A lap 2011. szeptember 15., 10:17-kori változata
Tartalomjegyzék[elrejtés] |
Az elektromos áram mágneses tere
A Biot-Savart törvény
A válasszal, hogy mi is az indukciós tér forrása, még adósak vagyunk. Néhány egyszerű kísérlettel könnyű bemutatni, hogy az elektromos áram mágneses teret kelt maga körül. Egy kis vasreszelék vagy egy iránytű alkalmazásával szemléletesen láthatóvá lehet tenni egy áramjárta vezető mágneses terét.
| 1.1.1 a ábra | 1.1.1 b ábra | 1.1.1 c ábra |
A jelenség vizsgálatához tekintsük az elképzelhető legegyszerűbb modellt, vagyis vizsgáljuk meg egy igen kisméretű, áramjárta vezetékdarab által keltett mágneses indukciós teret (1.2 ábra) és adjuk meg ennek matematikai alakját!
| 1.1.2 ábra |
A mérések azt mutatják, hogy a 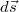 áramjárta kis vezetékdarab indukciós terét az
áramjárta kis vezetékdarab indukciós terét az 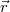 helyvektorral megadott pontban a Biot-Savart törvény segítségével adhatjuk meg:
helyvektorral megadott pontban a Biot-Savart törvény segítségével adhatjuk meg:
![\[d\vec B = \frac {\mu_o}{4\pi} I \frac{d\vec s \times \vec n}{r^2} \]](/images/math/8/9/e/89ef1468568844f12b21b181312740c3.png) |
(1.1.1) |
ahol is 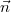 az
az 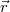 -el párhuzamos egységvektor és
-el párhuzamos egységvektor és 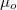 a vákuum mágneses permeabilitása, melynek értéke:
a vákuum mágneses permeabilitása, melynek értéke: 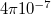 Tm/A.
Tm/A.
Jó példa a Biot-Savart törvény egyszerű alkalmazására a körvezető terének meghatározása a szimmetriatengelyen. (Természetesen jó példa a végtelen hosszú, áramjárta vezető is, de ezt a problémát majd az előadáson vagy a gyakorlaton oldjuk meg.) Ehhez tekintsük az ábrán látható a sugarú körvezetőt, melynek indukciós terét a szimmetriatengelyen a kör középpontjától x távolságban szeretnénk meghatározni.
1.1.3 ábra
A körvezető egy kis, az  pontot is tartalmazó,
pontot is tartalmazó, 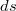 darabkáján átfolyó áram hatásaként kialakul a – felfelé mutató –
darabkáján átfolyó áram hatásaként kialakul a – felfelé mutató – 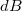 tér, mint ez az 1.3 ábrán is látszik, és amelynek nagysága a Biot-Savart törvény alapján:
tér, mint ez az 1.3 ábrán is látszik, és amelynek nagysága a Biot-Savart törvény alapján:
![\[dB = \frac {\mu_o}{4\pi} I \frac{ds}{r^2}= \frac {\mu_o}{4\pi} I \frac{ds}{a^2+x^2} \]](/images/math/6/3/7/6374a089e889774a7a573e978fd3f738.png) |
(1.1.2) |
mivel a  pontba mutató
pontba mutató  vektor merőleges a vezető síkjára, így a
vektor merőleges a vezető síkjára, így a 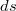 vezető darabra is. Jól látszik az ábrán az is, hogy az átellenes, azaz a
vezető darabra is. Jól látszik az ábrán az is, hogy az átellenes, azaz a  pontot is tartalmazó, ugyanolyan hosszú
pontot is tartalmazó, ugyanolyan hosszú 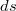 szakasz által keltett
szakasz által keltett 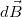 tér a tengelyre szimmetrikusan helyezkedik el az
tér a tengelyre szimmetrikusan helyezkedik el az  pontot magába foglaló szakasz
pontot magába foglaló szakasz 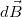 teréhez képest. A két
teréhez képest. A két 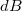 vektor tengelyre merőleges komponense összeadásnál kiejti egymást. Ez azt jelenti, hogy mindössze a tengely-menti komponensekkel kell számolnunk, azaz:
vektor tengelyre merőleges komponense összeadásnál kiejti egymást. Ez azt jelenti, hogy mindössze a tengely-menti komponensekkel kell számolnunk, azaz:
![\[dB = \frac {\mu_o}{4\pi} I \frac{ds}{a^2+x^2}sin(\phi)= \frac {\mu_o}{4\pi} I \frac{ds}{a^2+x^2} \frac {a}{\sqrt {a^2+x^2}}= \frac {\mu_o}{4\pi} I \frac {ds} {\left[a^2+x^2 \right]^{\frac32}}a \]](/images/math/7/3/d/73d9d1ac59e7b4b1bceaeaccd34a3797.png) |
(1.1.3) |
A P pontban megkapjuk az indukciós tér nagyságát, ha kiintegrálunk az egész körre, azaz 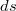 helyett
helyett 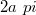 – t helyettesítünk be:
– t helyettesítünk be:
![\[B = \frac {\mu_o}{2} \frac {Ia^2} {\left[a^2+x^2 \right]^{\frac32}} \qquad {\rm illetve} \qquad \vec B = \frac {\mu_o}{2\pi} \frac {\vec {\mu}} {\left[a^2+x^2 \right]^{\frac32}} \]](/images/math/0/7/0/0705f2dcb4cc3cf726c7f4fba34656d6.png) |
(1.1.4) |
ahol kihasználtuk, hogy a körvezető mágneses momentuma 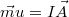 . Ebből az eredményből például következik, hogy a körvezető középpontjában az indukciós tér nagysága:
. Ebből az eredményből például következik, hogy a körvezető középpontjában az indukciós tér nagysága:
![\[B = \frac {\mu_o}{2} \frac {I} {a} \]](/images/math/a/7/f/a7f76e566d0d05910f53de3917db9299.png) |
(1.1.5) |
Az 1.1.3 második formulájából pedig következik, hogy távoltérben 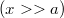 a
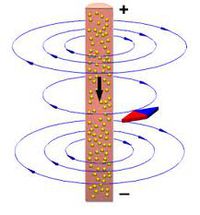
a 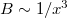 – nel. Ez igen érdekes eredmény, hiszen az elektrosztatikában láttuk, hogy egy elektromos dipólus elektromos terének nagysága távoltéri közelítésben szintén a távolság köbével fordítottan arányos. Ez azt jelenti, hogy egy körvezető tere hasonló egy északi és egy déli pólussal rendelkező rúdmágnes teréhez, lásd a 1.1.4 és 1.1.5 ábrát.
– nel. Ez igen érdekes eredmény, hiszen az elektrosztatikában láttuk, hogy egy elektromos dipólus elektromos terének nagysága távoltéri közelítésben szintén a távolság köbével fordítottan arányos. Ez azt jelenti, hogy egy körvezető tere hasonló egy északi és egy déli pólussal rendelkező rúdmágnes teréhez, lásd a 1.1.4 és 1.1.5 ábrát.
1.1.4 és 1.1.5 ábra
Foglaljuk most össze ezt az igen fontos eredményt: egy köráram bizonyos szempontból úgy viselkedik, mint egy rúdmágnes, azaz a mágneses tere (távoltérben) hasonló szerkezetű. Azt is láttuk , hogy a mágneses térbe helyezett köráramra ható forgatónyomaték is hasonlóan írható fel (Elektromos töltések mozgása statikus mágneses térben 8.3), mint egy dipólus (mágneses) esetében. (Ez - az elektrosztatikai analógiát felhasználva - abból következik, ahogyan az elektromos dipólus kölcsönhat az elektromos térrel, azaz 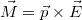 ; könnyű észrevenni a hasonlóságot a
; könnyű észrevenni a hasonlóságot a 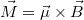 formulával.)
formulával.)
Az Ampèr törvény
Bár a Biot-Savart törvény alkalmazása áramjárta vezetők mágneses indukciós terének meghatározására a magnetosztatikában egy jól használható általános módszer, azonban néhány, valamilyen szimmetriával rendelkező elrendezés esetében egy másik módszer segítségével könnyebben, azaz egyszerűbb számolással juthatunk ugyanarra az eredményre. Lássuk ezt a másik módszert! Ehhez tekintsük a következő ábrát!
1.2.1 ábra
Az áramokat körülvevő - akár fiktív – zárt hurok mentén kiintegrált indukciós tér arányos a hurkon átmenő teljes árammal; ez az Ampère törvény:
![\[ \oint\limits_s \vec B d\vec s = {\mu_o}\sum_{j=1}^N I_j \]](/images/math/0/a/d/0ad9a6482cbb040e55937f16010636d6.png) |
(1.2.1) |
(ahol a 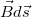 skalárszorzatot jelent)
Azt, hogy az áramokat milyen előjellel vegyük figyelembe a jobbkéz-szabály alapján határozhatjuk meg:
skalárszorzatot jelent)
Azt, hogy az áramokat milyen előjellel vegyük figyelembe a jobbkéz-szabály alapján határozhatjuk meg:
1.2.2 a és b ábra
A 1.2.1 ábrán látható elrendezést tekintve tehát: 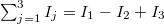 .
.
Az Ampère-törvény használhatóságára lássunk két példát! Az első az áramjárta 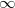 hosszú, egyenes vezető tere. A 1.1.1 a ábra jól mutatja, hogy a mágneses indukciós tér szerkezete – az elrendezés hengerszimmetriájából adódóan – olyan, hogy nagysága csak a vezetőtől mért távolságtól függ; irányának megállapításához pedig a jobbkéz-szabály vagy a Biot Savart alkalmazására van szükség. A törvény alkalmazása most már igen egyszerű (az 1.2.2 b ábra alapján):
hosszú, egyenes vezető tere. A 1.1.1 a ábra jól mutatja, hogy a mágneses indukciós tér szerkezete – az elrendezés hengerszimmetriájából adódóan – olyan, hogy nagysága csak a vezetőtől mért távolságtól függ; irányának megállapításához pedig a jobbkéz-szabály vagy a Biot Savart alkalmazására van szükség. A törvény alkalmazása most már igen egyszerű (az 1.2.2 b ábra alapján):
![\[ \oint\limits_s \vec B d\vec s = 2r\pi B \qquad {\rm illetve} \qquad {\mu_o}\sum_{j=1}^N I_j = {\mu_o}I \]](/images/math/f/8/d/f8d46f7caeb22bf6fbe912df291d5438.png) |
(1.2.2) |
tehát:
![\[ 2r\pi B = {\mu_o}I \qquad {\rm azaz} \qquad B = \frac {{\mu_o}I}{2r\pi} \]](/images/math/8/f/5/8f5969acd97319c494ff27a154247b5f.png) |
(1.2.3) |
A másik – viszonylag egyszerű, de igen fontos – elrendezés a szolenoid vagy hosszú, egyenes tekercs, amelynek hossza általában jóval nagyobb, mint az átmérője; lásd a 1.2.3 a és b ábrát:
1.2.3 a és b ábra
A 1.2.3 b ábra, mely a szolenoid mágneses terét mutatja vasreszelékkel, jól szemlélteti azt a tapasztalati tényt (ezt egyébként a Biot-Savart törvény segítségével ki is lehet számítani, de csak a bátrabbak próbálkozzanak vele; a számításokból egyébként az is kijön, hogy az indukciós tér a tekercs végénél fele akkora, mint belül), miszerint az indukciós tér a tekercsen belül homogén, míg a szolenoidon kívül közvetlenül mellette csaknem zérus. Kihasználjuk még azt is, hogy az indukciós tér vektora a tekercs szélénél csaknem párhuzamos a tekercs tengelyével. Tekintsük most az 1.2.4 ábrán látható  menetű,
menetű, 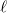 hosszúságú szolenoidot:
hosszúságú szolenoidot:
1.2.4 ábra
Ezután próbáljuk meg alkalmazni az Ampère-törvényt! Az 1.2.1 bal oldalán szereplő körintegrált a kék vonallal jelölt hurokra kell kiszámítani. Az előzőekben felsorolt tapasztalati tények alapján (melyeket a 1.2.3 b ábra szemléltet) a körintegrál egyszerűsödik a 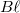 szorzatra, míg az összáram:
szorzatra, míg az összáram: 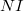 (hiszen az
(hiszen az  áram
áram  -szer megy át a hurok által határolt területen). Ezeket a tagokat behelyettesítve az 1.2.1-be némi átrendezés után kapjuk a szolenoid belsejében kialakult indukciós tér nagyságát:
-szer megy át a hurok által határolt területen). Ezeket a tagokat behelyettesítve az 1.2.1-be némi átrendezés után kapjuk a szolenoid belsejében kialakult indukciós tér nagyságát:
![\[ B = \frac {{\mu_o}NI}{\ell} \]](/images/math/5/b/f/5bf5b2eef48e5c9d288a026f37c40d38.png) |
(1.2.4) |
A toroid (1.2.5 a ába) esetében hasonlóan járunk el a mágneses indukciós tér nagyságának meghatározásánál.
1.2.5 a és b ábra
Első közelítésben úgy tekinthetünk egy – az ábrán is látható – toroidot, mint egy körbe hajlított szolenoidot, amelynek hossza helyett most a toroid középkörének 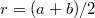 kerületét helyettesítjük. Ezek szerint tehát a szaggatott vonal mentén B értéke:
kerületét helyettesítjük. Ezek szerint tehát a szaggatott vonal mentén B értéke:
![\[ B = \frac {{\mu_o}NI}{2r\pi} \]](/images/math/3/9/4/3946c8f0297e1118e9e7e5bcadede1aa.png) |
(1.2.5) |
Azonban nem ez az igazán lényeges különbség a szolenoid és a toroid között. A szolenoid mágneses erővonalai kijutnak a tekercs belsejéből és "kívül záródnak", míg a toroid indukciós erővonalai (koncentrikus köröket alkotva; lásd az 1.2.5 b ábra) belül záródnak és kívül az indukciós tér csaknem zérus.