„Holography” változatai közötti eltérés
(→Theoretical background) |
(→Theoretical background) |
||
| 35. sor: | 35. sor: | ||
<wlatex> | <wlatex> | ||
For the case of amplitude holograms, this is how we can demonstrate that during reconstruction it is indeed the original object wave that is diffracted on the holographic grating. Consider the amplitude of the light wave in the immediate vicinity of the holographic plate. Let the complex amplitude of the two interfering waves during recording be $\mathbf{r}(x,y)=R(x,y)e^{i\varphi_r(x,y)}$ for the reference wave and $\mathbf{t}(x,y)=T(x,y)e^{i\varphi_t(x,y)}$ for the object wave, where R and T are the amplitudes (as real numbers). The amplitude of the reference wave along the plane of the holographic plate, R(x,y), is only slowly changing, so R can be taken to be constant. The intensity distribution along the plate, i.e. the interference pattern that is recorded on the plate can be written as | For the case of amplitude holograms, this is how we can demonstrate that during reconstruction it is indeed the original object wave that is diffracted on the holographic grating. Consider the amplitude of the light wave in the immediate vicinity of the holographic plate. Let the complex amplitude of the two interfering waves during recording be $\mathbf{r}(x,y)=R(x,y)e^{i\varphi_r(x,y)}$ for the reference wave and $\mathbf{t}(x,y)=T(x,y)e^{i\varphi_t(x,y)}$ for the object wave, where R and T are the amplitudes (as real numbers). The amplitude of the reference wave along the plane of the holographic plate, R(x,y), is only slowly changing, so R can be taken to be constant. The intensity distribution along the plate, i.e. the interference pattern that is recorded on the plate can be written as | ||
| − | $$I_{\rm{exp}}=|\mathbf{r}+\mathbf{t}|^2 = R^2+T^2+\mathbf{rt^*+r^*t}\quad\rm{(1)}$$ | + | $$I_{\rm{exp}}=|\mathbf{r}+\mathbf{t}|^2 = R^2+T^2+\mathbf{rt^*+r^*t}\quad\rm{(1)}$$ |
| − | where $*$ denotes complex conjugate. For an ideal holographic plate with a linear response, the opacity of the final hologram | + | where $*$ denotes complex conjugate. For an ideal holographic plate with a linear response, the opacity of the final hologram is linearly proportional to this intensity distribution, so the transmittance $\tau$ of the plate can be written as $$\tau=1–\alpha I_{\rm{exp}}\quad\rm{(2)}$$ where $\alpha$ is the product of a material constant and the time of exposure. When the holographic plate is illuminated with the original reference wave during reconstruction, the complex amplitude just behind the plate is $$\mathbf{a} = \mathbf{r}\tau=\mathbf{r}(1–\alpha R^2–\alpha T^2)–\alpha\mathbf{r}^2\mathbf{t}^*–\alpha R^2\mathbf{t}\quad\rm{(3)}$$. Ennek első tagja a referenciahullám áthaladó hányada, második $\mathbf{t}^*$-al arányos tagja egy fókuszálódó (ez $\mathbf{r}^2$ miatt lehet) konjugált kép, harmadik t-vel arányos tagja pedig az eredeti tárgyhullám mása (vegyük észre, hogy az arányossági tényezők mind valós állandók!). Ez virtuális képet ad, mivel közvetlenül a hologramlemez mögötti síkdarabon így ugyanolyan hullámtér áll elő (fázisát is tekintve, hisz t komplex), mint az eredeti tárgyról érkező fény esetén. A (3) összefüggést épp ezért a holográfia alapegyenletének is nevezik. Off-axis hologram esetén ez a három elhajlási rend ($0$ és $\pm 1$) irányban szétválik, ellenkező esetben viszont nem. (Megjegyzés: ha a lemez viselkedése nem teljesen lineáris, megjelenhetnek magasabb diffrakciós rendek is) |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | $$\mathbf{a} = \mathbf{r}\tau=\mathbf{r}(1–\alpha R^2–\alpha T^2)–\alpha\mathbf{r}^2\mathbf{t}^*–\alpha R^2\mathbf{t}\quad\rm{(3)}$$ | + | |
| − | + | ||
</wlatex> | </wlatex> | ||
A lap 2017. szeptember 29., 14:56-kori változata
Tartalomjegyzék[elrejtés] |
Introduction
Humans have the ability to observe their surroundings in three dimensions. A large part of this is due to the fact that we have two eyes, and hence stereoscopic vision. The detector in the human eye - the retina - is a two-dimensional surface that detects the intensity of the light that hits it. Similarly, in conventional photography, the object is imaged by an optical system onto a two-dimensional photosensitive surface, i.e. the photographic plate. Any point, or "pixel", of the photographic plate is sensitive only to the intensity of the light that hits it, not to the entire complex amplitude (magnitude and phase) of the light wave at the given point.
Holography - invented by Dennis Gabor (1947), who received the Nobel Prize in Physics in 1971 - is different from conventional photography in that it enables us to record the phase of the light wave, despite the fact that we still use the same kind of intensity-sensitive photographic material as in conventional photography. The "trick" by which holography achieves this is to encode phase information as intensity information, and thus to make it detectable for the photographic material. Encoding is done using interference: the intensity of interference fringes between two waves depends on the phase difference between the two phase. Thus, in order to encode phase information as intensity information, we need, in addition to the light wave scattered from the object, another wave too. To make these two light waves - the "object wave" and the "reference wave" - capable of interference we need a coherent light source (a laser). Also, the detector (the photographic material) has to have a high enough resolution to be able to resolve and record the fine interference pattern created by the two waves. Once the interference pattern is recorded and the photographic plate is developed, the resulting hologram is illuminated with an appropriately chosen light beam, as described in detail below. This illuminating beam is then diffracted on the fine interference pattern that was recorded on the hologram, and the diffracted wave carries the phase as well as the amplitude information of the wave that was originally scattered from the object: we can thus observe a realistic three-dimensional image of the object. A hologram is not only a beautiful and spectacular three-dimensional image, but can also be used in many areas of optical metrology.
Theory
Recording and reconstructing a transmission hologram
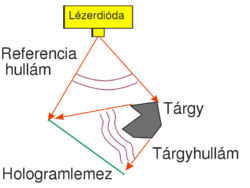
One possible holographic is shown in Fig. 1/a. This setup can be used to record a so-called off-axis transmission hologram. The source is a highly coherent laser diode that is able to produce a high-contrast interference pattern. All other light sources must be eliminated during the recording. The laser diode does not have a beam-shaping lens in front of it, and thus emits a diverging wavefront with an ellipsoidal shape. The reference wave is the part of this diverging wave that directly hits the holographic plate, and the object wave is the part of the diverging wave that hits the object first and is then scattered by the object onto the holographic plate. The reference wave and the object wave hit the holographic plate simultaneously and create an interference pattern on the plate.
The holographic plate is usually a glass plate with thin, high-resolution optically sensitive layer. The spatial resolution of holographic plates in higher by 1-2 orders of magnitude than that of photographic films used in conventional cameras. Our aim is to make the interference pattern, i.e. the so-called "holographic grating", consist of high-contrast fringes. To achieve this, the intensity ratio of the object wave and the reference wave, their total intensity, and the exposure time must all be controlled carefully. Since the exposure time can be as long as several minutes, we also have to make sure that the interference pattern does not move or vibrate relative to the holographic plate during the exposure. To avoid vibrations, the entire setup is placed on a special rigid, vibration-free optical table. Air-currents and strong background lights must also be eliminated. Note that, unlike in conventional photography or in human vision, in the setup of Fig. 1/a there is no imaging lens between the object and the photosensitive material. This also means that a given point on the object scatters light toward the entire holographic plate, i.e. there is no 1-to-1 correspondence (no "imaging") between object points and points on the photosensitive plate. This is in contrast with how conventional photography works. The setup of Fig. 1/a is called off-acis, because there is a large angle between the directions of propagation of the object wave and the reference wave.
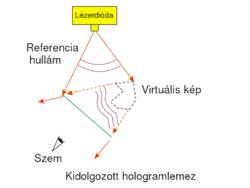
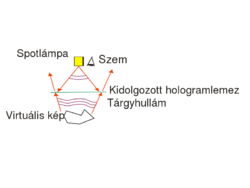
The exposed holographic plate is then chemically developed. (Note that if the holographic plate uses photopolymers then no such chemical process is needed.) Under conventional illumination with a lamp or under sunlight, the exposed holographic plate with the recorded interference pattern on it does not seem to contain any information about the object in any recognizable form. In order to "decode" the information stored in the interference pattern, i.e. in order to reconstruct the image of the object from the hologram, we need to use the setup shown in Fig. 1/b. The object itself is no longer in the setup, and the hologram is illuminated with the reference beam alone. The reference beam is then diffracted on the holographic grating. (Depending on the process used the holographic grating consists of series of dark and transparent lines ("amplitude hologram") or of a series of lines with alternating higher and lower indices of refraction ("phase hologram").) The diffracted wave is a diverging wavefront that is identical to the wavefront that was originally emitted by the object during recording. This is the so-called virtual image of the object. The virtual image appears at the location where the object was originally placed, and is of the same size and orientation as the object was during recording. In order to see the virtual image, the hologram must be viewed from the side opposite to where the reconstructing reference wave comes from. The virtual image contains the full 3D information about the object, so by moving your head sideways or up-and-down, you can see the appearance of the object from different viewpoints. This is in contrast with 3D cinema where only two distinct viewpoints (a stereo pair) is available from the scene. Another difference between holography and 3D cinema is that on a hologram you can choose different parts on the object located at different depths, and focus your eyes on those parts separately. Note, however, that both to record and to reconstruct a hologram, we need a monochromatic laser source (there is no such limitation in 3D cinema), and thus the holographic image is intrinsically monochromatic.
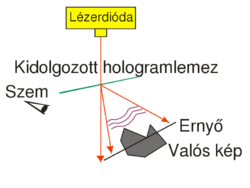
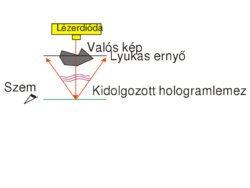
This type of hologram is called transmission hologram, because during reconstruction (Fig. 1/b) the laser source and our eye are at two opposite sides of the hologram, so light has to pass through the hologram in order to each our eye. Besides the virtual image, there is another reconstructed wave (not shown in Fig. 1/b) that is converging and can thus be observed on a screen as the real image of the object. For an off-axis setup the reconstructing waves that create the virtual and the real image, respectively, propagate in two different directions in space. In order to view the real image in a convenient way it is best to use the setup shown in Fig. 1/c. Here a sharp laser beam illuminates a small region of the entire hologram, and the geometry of this sharp reconstructing beam is chosen such that it travels in the opposite direction from what the propagation direction of the reference beam was during recording.
Theoretical background
For the case of amplitude holograms, this is how we can demonstrate that during reconstruction it is indeed the original object wave that is diffracted on the holographic grating. Consider the amplitude of the light wave in the immediate vicinity of the holographic plate. Let the complex amplitude of the two interfering waves during recording be 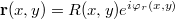 for the reference wave and
for the reference wave and 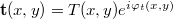 for the object wave, where R and T are the amplitudes (as real numbers). The amplitude of the reference wave along the plane of the holographic plate, R(x,y), is only slowly changing, so R can be taken to be constant. The intensity distribution along the plate, i.e. the interference pattern that is recorded on the plate can be written as
for the object wave, where R and T are the amplitudes (as real numbers). The amplitude of the reference wave along the plane of the holographic plate, R(x,y), is only slowly changing, so R can be taken to be constant. The intensity distribution along the plate, i.e. the interference pattern that is recorded on the plate can be written as
![\[I_{\rm{exp}}=|\mathbf{r}+\mathbf{t}|^2 = R^2+T^2+\mathbf{rt^*+r^*t}\quad\rm{(1)}\]](/images/math/0/e/5/0e5e499a307e206fcbd6654adb0bd680.png)
 denotes complex conjugate. For an ideal holographic plate with a linear response, the opacity of the final hologram is linearly proportional to this intensity distribution, so the transmittance
denotes complex conjugate. For an ideal holographic plate with a linear response, the opacity of the final hologram is linearly proportional to this intensity distribution, so the transmittance  of the plate can be written as
of the plate can be written as ![\[\tau=1–\alpha I_{\rm{exp}}\quad\rm{(2)}\]](/images/math/4/3/1/4316070b90b4e57f9bcdaba597113d90.png)
 is the product of a material constant and the time of exposure. When the holographic plate is illuminated with the original reference wave during reconstruction, the complex amplitude just behind the plate is
is the product of a material constant and the time of exposure. When the holographic plate is illuminated with the original reference wave during reconstruction, the complex amplitude just behind the plate is ![\[\mathbf{a} = \mathbf{r}\tau=\mathbf{r}(1–\alpha R^2–\alpha T^2)–\alpha\mathbf{r}^2\mathbf{t}^*–\alpha R^2\mathbf{t}\quad\rm{(3)}\]](/images/math/d/3/8/d386e74bb76234220d62f5895d592352.png)
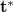 -al arányos tagja egy fókuszálódó (ez
-al arányos tagja egy fókuszálódó (ez 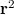 miatt lehet) konjugált kép, harmadik t-vel arányos tagja pedig az eredeti tárgyhullám mása (vegyük észre, hogy az arányossági tényezők mind valós állandók!). Ez virtuális képet ad, mivel közvetlenül a hologramlemez mögötti síkdarabon így ugyanolyan hullámtér áll elő (fázisát is tekintve, hisz t komplex), mint az eredeti tárgyról érkező fény esetén. A (3) összefüggést épp ezért a holográfia alapegyenletének is nevezik. Off-axis hologram esetén ez a három elhajlási rend (
miatt lehet) konjugált kép, harmadik t-vel arányos tagja pedig az eredeti tárgyhullám mása (vegyük észre, hogy az arányossági tényezők mind valós állandók!). Ez virtuális képet ad, mivel közvetlenül a hologramlemez mögötti síkdarabon így ugyanolyan hullámtér áll elő (fázisát is tekintve, hisz t komplex), mint az eredeti tárgyról érkező fény esetén. A (3) összefüggést épp ezért a holográfia alapegyenletének is nevezik. Off-axis hologram esetén ez a három elhajlási rend ( és
és 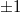 ) irányban szétválik, ellenkező esetben viszont nem. (Megjegyzés: ha a lemez viselkedése nem teljesen lineáris, megjelenhetnek magasabb diffrakciós rendek is)
) irányban szétválik, ellenkező esetben viszont nem. (Megjegyzés: ha a lemez viselkedése nem teljesen lineáris, megjelenhetnek magasabb diffrakciós rendek is)
Reflexiós hologram készítése és rekonstrukciója
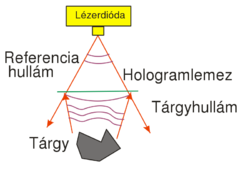
A fejezet elején említett fehérfényű látványhologramok az eddig tárgyalt típustól abban térnek el, hogy in-line elrendezésűek, azaz a nyalábok a lemez normálisával nulla vagy kis szöget zárnak be, valamint reflexiós elrendezésűek: a referencia és a tárgynyaláb a lemez átellenes oldaláról érkezik, rekonstrukciókor pedig a megvilágítás és a megfigyelés van azonos oldalon. A reflexiós hologramok rögzítésének elrendezését a 2/a. ábra mutatja. Ilyen hologramok esetén is megfigyelhető valós és virtuális rekonstruált kép, az ezekhez tartozó elrendezés a 2/b. és 2/c. ábrán látható.
Fehér fényben ezek a hologramok azért tekinthetők meg, mert kb. 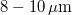 vagy még vastagabb fényérzékeny réteget tartalmazó lemezre készülnek, így már ún. vastag hologramnak tekinthetők a hullámhosszhoz képest. A vastag diffrakciós rácsok ún. Bragg-effektust mutatnak: a fehér fényt alkotó hullámokból csak a rögzítésnél használthoz közeli hullámhosszakon diffraktálnak jelentősen, így „szelektálnak” a színek között, továbbá érzékenyek a rekonstrukciónál alkalmazott megvilágítás irányára is, amelynek nagyjából azonosnak kell lennie a felvételkori referencia nyaláb irányával, ez pedig egy irányszelektivitást jelent. Ez utóbbi tulajdonságnak köszönhetően vastag hologramlemezbe többet is lehet exponálni úgy, hogy a rögzített képek közül lényegében mindig csak egy rekonstruálódik a megvilágítás irányától függően. (Minél vastagabb, „térfogatibb” egy hologram, annál szelektívebb, így szélsőséges esetben rengeteg hologram - vagyis kép, azaz akár bináris adat - rögzíthető a fényérzékeny anyag egyazon térfogatába. Ez az alapja a holografikus adattárolásnak.)
vagy még vastagabb fényérzékeny réteget tartalmazó lemezre készülnek, így már ún. vastag hologramnak tekinthetők a hullámhosszhoz képest. A vastag diffrakciós rácsok ún. Bragg-effektust mutatnak: a fehér fényt alkotó hullámokból csak a rögzítésnél használthoz közeli hullámhosszakon diffraktálnak jelentősen, így „szelektálnak” a színek között, továbbá érzékenyek a rekonstrukciónál alkalmazott megvilágítás irányára is, amelynek nagyjából azonosnak kell lennie a felvételkori referencia nyaláb irányával, ez pedig egy irányszelektivitást jelent. Ez utóbbi tulajdonságnak köszönhetően vastag hologramlemezbe többet is lehet exponálni úgy, hogy a rögzített képek közül lényegében mindig csak egy rekonstruálódik a megvilágítás irányától függően. (Minél vastagabb, „térfogatibb” egy hologram, annál szelektívebb, így szélsőséges esetben rengeteg hologram - vagyis kép, azaz akár bináris adat - rögzíthető a fényérzékeny anyag egyazon térfogatába. Ez az alapja a holografikus adattárolásnak.)
Holografikus interferometria
Mivel a rekonstruált tárgyhullám komplex amplitúdóját maga az eredeti tárgy határozza meg, pl. annak alakja, felületi minősége, így a hologram ezekről is tárol valamennyi információt. Ha egyetlen tárgyról annak két különböző állapotában készítünk egy-egy hologramot ugyanarra a lemezre egymás után azonos referenciával, az így kapott lemezt kétexpozíciós hologramnak hívjuk:
![\[I_{12}=|\mathbf r+\mathbf t_1|^2+|\mathbf r+\mathbf t_2|^2=R^2+T^2+\mathbf r\mathbf t_1^*+\mathbf r^*\mathbf t_1+R^2+T^2+\mathbf r\mathbf t_2^*+\mathbf r^*\mathbf t_2=2R^2+2T^2+(\mathbf r\mathbf t_1^*+\mathbf r\mathbf t_2^*)+(\mathbf r^*\mathbf t_1+\mathbf r^*\mathbf t_2)\]](/images/math/0/0/7/0078c0b66dacd94102d005e54b295c25.png)
(Itt feltételeztük, hogy a tárgynyalábnak csak a fázisa változott meg érdemben, T valós amplitúdója nem, továbbá az indexek az állapotokat jelölik.) Rekonstrukciókor a két állapot egyidejűleg jelenik meg:
![\[\mathbf a_{12}=\mathbf r\tau=\mathbf r(1-\alpha I_{12})=\mathbf r(1-2\alpha R^2-2\alpha T^2)-\alpha \mathbf r^2(\mathbf t_1^*+\mathbf t_2^*)+\alpha R^2(\mathbf t_1+\mathbf t_2)\]](/images/math/8/7/d/87ddc9647964e179953751d45f3d011d.png)
azaz az 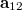 hullámtérben egy
hullámtérben egy 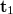 -el és egy
-el és egy 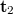 -vel arányos tag is szerepel mindkét első elhajlási rendben, amelyek a képeket adják. Ha a virtuális képet szemléljük, ott csak az utolsó
-vel arányos tag is szerepel mindkét első elhajlási rendben, amelyek a képeket adják. Ha a virtuális képet szemléljük, ott csak az utolsó 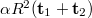 tagoknak van járuléka, hisz a többi rend „máshová” terjed, így az
tagoknak van járuléka, hisz a többi rend „máshová” terjed, így az 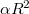 arányossági tényezőktől eltekintve a megfigyelhető intenzitás ebben a diffrakciós rendben az alábbi:
arányossági tényezőktől eltekintve a megfigyelhető intenzitás ebben a diffrakciós rendben az alábbi:
![\[I_{12,\text{virt}}=|\mathbf a_{12,\text{virt}}|^2=|\mathbf t_1+\mathbf t_2|^2=2T^2+(\mathbf t_1^* \mathbf t_2+\mathbf t_1 \mathbf t_2^*)=2T^2+(\mathbf t_1^* \mathbf t_2+c.c.)\]](/images/math/9/4/f/94f5caf469c66f3743dd11c3b159cc5f.png)
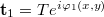 és
és 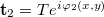 , így
, így ![\[\mathbf t_1^*\mathbf t_2=T^2e^{i[\varphi_2(x,y)-\varphi_1(x,y)]},\]](/images/math/1/d/a/1da9f8fae36674a1795aeb6b666ca89a.png)
![\[2T^2\cos[\varphi_2(x,y)-\varphi_1(x,y)]\]](/images/math/c/5/2/c524dd642789e50faaf392bad825e5de.png)
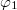 ill.
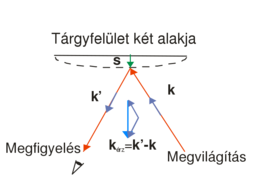
ill. 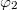 fázisokat a 3. ábra alapján felírva belátható, hogy a különbségüket a
fázisokat a 3. ábra alapján felírva belátható, hogy a különbségüket a ![\[\Delta\varphi=\varphi_2-\varphi_1=\vec s\cdot(\vec k'-\vec k)=\vec s\cdot\vec k_\text{érz}\quad\rm{(9)}\]](/images/math/8/9/1/891425874558cd6d11faaed2cf22109b.png)
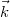 a tárgyat megvilágító síkhullám hullámvektora,
a tárgyat megvilágító síkhullám hullámvektora, 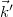 pedig a tárgyról a megfigyelés irányába kiinduló nyaláb hullámvektora (
pedig a tárgyról a megfigyelés irányába kiinduló nyaláb hullámvektora (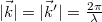 ), valamint
), valamint 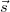 az elmozdulásvektor és
az elmozdulásvektor és 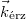 az úgynevezett érzékenységi vektor. Az ábrán a piros nyilak önkényesen kiragadott sugarak a kiterjedt nyalábból. Mivel általános esetben az elmozdulásvektor a felület különböző részein nem állandó, a fáziskülönbség is helyfüggő lesz. A skaláris szorzásból látható, hogy az
az úgynevezett érzékenységi vektor. Az ábrán a piros nyilak önkényesen kiragadott sugarak a kiterjedt nyalábból. Mivel általános esetben az elmozdulásvektor a felület különböző részein nem állandó, a fáziskülönbség is helyfüggő lesz. A skaláris szorzásból látható, hogy az 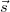 vektornak csak az érzékenységi vektor irányú komponense számít, azaz csak az mérhető. Az érzékenységi vektor iránya és hossza is változtatható, ha a megvilágítás illetve a megfigyelés (szemlélés) irányát változtatjuk, így pl. ha mozgunk egy kétexpozíciós hologram előtt, a csíkrendszer is mozog, változik, mivel a fáziskülönbség is változni fog.
vektornak csak az érzékenységi vektor irányú komponense számít, azaz csak az mérhető. Az érzékenységi vektor iránya és hossza is változtatható, ha a megvilágítás illetve a megfigyelés (szemlélés) irányát változtatjuk, így pl. ha mozgunk egy kétexpozíciós hologram előtt, a csíkrendszer is mozog, változik, mivel a fáziskülönbség is változni fog.
A fentiekhez hasonló, a tárgy megváltozását kontúrozó interferenciacsíkokat lehet látni akkor is, ha csak egyet exponálunk a tárgyról, a kidolgozott hologramlemezt tized-mikrométeres pontossággal (!) visszahelyezzük az erre alkalmas tartóba, majd a tárgyat továbbra is az eredeti nyalábokkal megvilágítva deformáljuk. Ekkor az eredeti állapot képe interferál a megváltozott állapot élő képével, így ahogy változik a deformáció, úgy változnak az interferenciacsíkok is. Ennek az igen látványos módszerenek a neve real-time holografikus interferometria, és mutatja, hogy megfelelő technológia mellett a fázishelyes fényhullám rekonstrukciót mennyire komolyan lehet venni.
Holografikus optikai elemek
Ha a tárgyhullám és a referenciahullám egyaránt síkhullám, amelyek valamilyen szöget zárnak be, a hologramon rögzülő interferenciakép egyszerű, ekvidisztáns egyenes csíkokból álló rács lesz. Az ilyen diffrakciós rácsot tekinthetjük a legegyszerűbb példának a holografikus optikai elemekre (HOE-kre). A holografikus úton létrehozott rács előnye, hogy egyszerűen előállítható, nagyon jó hatásfokú diszperzív elemet szolgáltat spektroszkópiai alkalmazásokhoz. Természetesen a rácsállandó a két síkhullám hullámhosszának és bezárt szögének függvényében pontosan beállítható. Komplexebb feladatokat ellátó (pl. helyfüggő rácsállandójú vagy fókuszáló) diffrakciós rácsokat is egyszerűen előállíthatunk holografikus úton: mindössze a két interferáló síkhullám egyikét kell kicserélnünk alkalmasan megtervezett hullámfrontú nyalábra.
Mivel a hologram által rekonstruált kép olyan, mintha a tárgy teljes valójában „ott lenne“, várható, hogy ha a tárgy szerepét valamilyen optikai eszköz, pl. egy lencse vagy egy tükör tölti be, akkor a hologram bizonyos korlátok között valóban úgy fog működni, mint az adott optikai eszköz, amelyről készült (tehát pl. az adott módon fókuszálni vagy reflektálni fogja a fényt). Az ilyen egyszerű holografikus lencsék vagy tükrök is a HOE-k csoportjába tartoznak.
Az alábbiakban egy konkrét példaként megnézzük, hogyan lehet két egyszerű gömbhullám interferenciájának rögzítésével holografikus lencsét előállítani. Feltételezzük, hogy mindkét gömbhullám a hologram síkjára merőleges optikai tengelyről indul ki (ezt ún. on-axis elrendezésnek nevezzük). Az egyik (nevezzük ezt a referenciahullámnak) 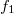 , a másik (nevezzük ezt a tárgyhullámnak)
, a másik (nevezzük ezt a tárgyhullámnak) 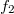 távolságra a hologramtól. Ekkor – a gömbhullámok jólismert parabolikus/paraxiális közelítését alkalmazva, és mindkét hullámnál konstans egységnyi amplitudót feltételezve – a referenciahullám és a tárgyhullám (1) egyenletben szereplő
távolságra a hologramtól. Ekkor – a gömbhullámok jólismert parabolikus/paraxiális közelítését alkalmazva, és mindkét hullámnál konstans egységnyi amplitudót feltételezve – a referenciahullám és a tárgyhullám (1) egyenletben szereplő  ill.
ill. 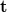 komplex amplitudója az alábbi alakban írható a hologram síkjának (x,y) pontjában:
komplex amplitudója az alábbi alakban írható a hologram síkjának (x,y) pontjában:
![\[\mathbf r=e^{i\frac{2\pi}{\lambda}\left(\frac{x^2+y^2}{2f_1}\right)},\,\mathbf t=e^{i\frac{2\pi}{\lambda}\left(\frac{x^2+y^2}{2f_2}\right)}\quad\rm{(10)}\]](/images/math/1/7/0/1706a6214a80fea2bb97548d644aa4c3.png)
A hologramon rögzülő interferenciakép ekkor így alakul:
![\[I=2+e^{i\frac{2\pi}{\lambda}\left(\frac{x^2+y^2}2\left( \frac 1{f_2}-\frac 1{f_1}\right)\right)}+e^{-i\frac{2\pi}{\lambda}\left(\frac{x^2+y^2}2\left( \frac 1{f_2}-\frac 1{f_1}\right)\right)}\quad\rm{(11)}\]](/images/math/3/b/8/3b841288512c58c73b684f4ad7b370b6.png)
a hologram  áteresztőképessége pedig ismét a (2) egyenlettel írható fel, tehát lineáris függvénye
áteresztőképessége pedig ismét a (2) egyenlettel írható fel, tehát lineáris függvénye  -nek. Rekonstruáljuk most a hologramot az
-nek. Rekonstruáljuk most a hologramot az  referenciahullám helyett egy merőleges beesésű síkhullámmal (amelynek tehát a komplex amplitudója a hologram síkjában
referenciahullám helyett egy merőleges beesésű síkhullámmal (amelynek tehát a komplex amplitudója a hologram síkjában  , egy valós konstans). Ekkor a (3) egyenlet
, egy valós konstans). Ekkor a (3) egyenlet 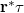 kifejezése helyett
kifejezése helyett 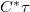 szerepel, azaz egy konstans faktortól eltekintve maga a
szerepel, azaz egy konstans faktortól eltekintve maga a  áteresztőképesség-függvény adja meg az átvilágított lemez mögött előálló fényhullám komplex amplitudóját. Ebből és a (2) és (11) egyenletekből látható, hogy a hologramból rekonstruálódó három elhajlási rend a következő lesz:
áteresztőképesség-függvény adja meg az átvilágított lemez mögött előálló fényhullám komplex amplitudóját. Ebből és a (2) és (11) egyenletekből látható, hogy a hologramból rekonstruálódó három elhajlási rend a következő lesz:
- egy konstans komplex amplitudójú merőleges síkhullám (nulladrend, a megvilágító nyaláb elhajlás nélkül továbbhaladó része),
- egy
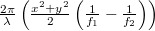 fázissal leírható hullám (+1-rend),
fázissal leírható hullám (+1-rend),
- egy
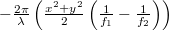 fázissal leírható hullám (-1-rend).
fázissal leírható hullám (-1-rend).
A 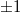 -rendű tagok fázisának matematikai alakjából látható (emlékeztetők: a (10) képletek), hogy ezek voltaképpen olyan (paraxiális) gömbhullámok, amelyek
-rendű tagok fázisának matematikai alakjából látható (emlékeztetők: a (10) képletek), hogy ezek voltaképpen olyan (paraxiális) gömbhullámok, amelyek 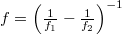 , ill.
, ill. 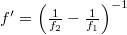 távolságra fókuszálódnak a hologram síkjától. Természetesen
távolságra fókuszálódnak a hologram síkjától. Természetesen  és
és 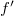 közül az egyik pozitív, a másik negatív, tehát a
közül az egyik pozitív, a másik negatív, tehát a 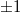 -rendek közül az egyik konvergens, a másik divergens gömbhullám, mindkettő
-rendek közül az egyik konvergens, a másik divergens gömbhullám, mindkettő 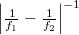 fókusztávolsággal. Összefoglalva: a két on-axis gömbhullám interferenciáját rögzítő hologrammal olyan HOE-t kaptunk, amely gyűjtő- és szórólencseként is funkcionálhat, attól függően hogy egy adott alkalmazáskor melyik rekonstruált elhajlási rendet használjuk fel.
fókusztávolsággal. Összefoglalva: a két on-axis gömbhullám interferenciáját rögzítő hologrammal olyan HOE-t kaptunk, amely gyűjtő- és szórólencseként is funkcionálhat, attól függően hogy egy adott alkalmazáskor melyik rekonstruált elhajlási rendet használjuk fel.
A HOE-k legfontosabb alkalmazási területeit azok az esetek jelentik, amikor bonyolult, összetett optikai manipulációkat végrehajtó elrendezések (pl. az optikai távközlésben demultiplexelésre használt sokfókuszú lencsék) helyettesítését szeretnénk megoldani egyetlen egyszerű és kompakt hologrammal. Ilyenkor a legfőbb előny a holográfia alkalmazásával elérhető méret- és költségcsökkenés.
Digitális holográfia
A lézeres hagyományos holográfiával szinte egyidős az a szándék (és az első kezdetleges megvalósítás is), hogy a referencia és a tárgyhullám interferenciájának eredőjét, a holografikus rácsot elektronikus vagy digitális jel formájában kezeljék. Ez egyrészt jelentheti a létező hullámfrontok által generált interferencia mező digitális megörökítését, másrészt jelentheti a digitálisan kiszámolt hologram valós rekonstrukcióját. Az elektronikus eszközök használatának további előnye még a körülményes kémiai eljárások mellőzhetősége is.
A digitális holográfia fejlődését sokáig hátráltatta három eszköz fejletlen volta:
- Megfelelő képbeviteli eszköz nélkül a tárgyhullám és a referenciahullám finom struktúráját nem lehet megörökíteni. Ez nem csak nagy (kb. 100 vonal/mm) felbontást jelent, hanem a szükséges jel/zaj viszonyt és stabil képbevitelt is.
- A hatalmas adatmennyiség kezelése nagy számítási kapacitást igényel.
- A hullámfrontok rekonstrukciója nagyfelbontású megjelenítő eszközt kívánna.
A hagyományos fotográfiai eljárások fejlettsége (mint amelyeket a nyomtatott áramkörök készítésénél alkalmaznak) először a digitálisan kiszámolt hologramok valós rekonstrukciójának vizsgálatát tette lehetővé. Ezt a szűkebb kutatási területet manapság számítógépes holográfiának nevezik. A nagyteljesítményű számítógépek megjelenése, rohamos fejlődése, valamint a nagy felbontású CCD és CMOS kamerák kifejlesztése idővel lehetővé tette a létező hullámfrontok által generált interferencia mező digitális megörökítését is. Az elmúlt évtizedben megjelent új eszközcsalád - a térbeli fénymodulátorok (SLM) - pedig a digitális hologramok valós idejű megjelenítését teszik lehetővé. Mindezeknek köszönhetően a digitális holográfia teljesítőképessége elérte azt a szintet, hogy méréstechnikai alkalmazásai is léteznek.
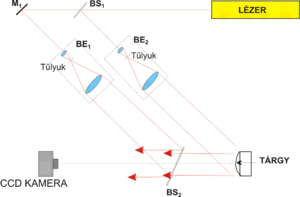
Röviden érdemes megjegyezni, hogy az analóg, kémiai, kétdimenziós képérzékelő és fénymoduláló hologramlemez cseréje szintén kétdimenziós digitális eszközökre nem érinti a holográfia lényegét/elvét, a fázisinformáció intenzitásba kódolását, ezért is működhetnek a digitális változatok.Digitális hologram felvételére lényegében egy a hagyományos holográfiában is alkalmazott optikai elrendezést kell megépíteni, melynek vázlata a 4. ábrán látható. Az elrendezés Mach-Zehnder típusú interferométer, melyben a BS1 nyalábosztó tükrön áthaladó fény kitágítás és párhuzamosítás/kollimálás után (kollimátoros nyalábtágító, BE1) alkotja a sík referenciahullámot. Az osztón tükröződő fény kitágítás és kollimálás után (BE2) megvilágítja a tárgyat, a tárgyról szóródott fényhullám pedig a BS2 nyalábosztón egyesül a referencia hullámmal, és együtt jutnak a CCD kamerára. (Az analóg holográfiához hasonlóan az elrendezésben legtöbbször nem található lencse, bár létezik ilyen megvalósítás is.)
A legfontosabb eltérés a digitális holográfiában alkalmazható elrendezések kiválasztásánál a digitális kamerák és a hologramlemezek felbontása közötti különbségből adódik. Míg egy hologramlemez elemi érzékelőinek (anyagszemcsék) mérete/távolsága a látható fény hullámhosszával összemérhető, a digitális kamerák képpontjainak mérete jellemzően egy nagyságrenddel nagyobb, átlagosan 4-10 µm. A mintavételezési tétel csak akkor teljesül, ha a holografikus rács állandója nagyobb, mint két képpont (kamera pixel). Ez akkor valósul meg, ha a tárgy látószöge a kamera egy pontjából nézve elég kicsi, és ha a referenciahullám a tárgyhullámmal kis szöget zár be. (Megjegyezzük, hogy mivel a kamerák mintavételezése integráló jellegű, és nem pontszerű, a mintavételezési tétel megszegése csak folytonos kontrasztcsökkenést okoz a rögzített képeken, tehát kis mértékben még megszeghető a feltétel.) E felbontásbeli különbség miatt a hagyományos holográfia megengedi a tárgy és a referencia nyaláb 1/a. ábrán látható nagyszögű találkozását, a digitális holográfia a technológia jelenlegi állása mellett azonban nem, így csak kvázi – de nem teljesen - in-line elrendezés használható. A digitális kamerák érzékenysége és dinamika tartománya (jelszintek, szürkeségi szintek száma) szintén eltér a hologramlemezekétől, így az exponálás feltételei is mások lesznek.
Mint ismeretes, két síkhullám interferenciája során a keletkezett interferencia csíkrendszer legkisebb térközöltsége: 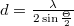 , ahol
, ahol 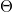 a terjedési irányok közötti szög. Ezt az összefüggést felhasználva, és figyelembe véve a mintavételi tételt egy adott képpontméretű (
a terjedési irányok közötti szög. Ezt az összefüggést felhasználva, és figyelembe véve a mintavételi tételt egy adott képpontméretű (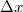 ) kamerára megadható az a maximális szög, amelyet a tárgyhullám és a referenciahullám bezárhat:
) kamerára megadható az a maximális szög, amelyet a tárgyhullám és a referenciahullám bezárhat: 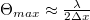 . Ez a szög a digitális kamerák pixelméretei mellett és látható fény esetén tipikusan
. Ez a szög a digitális kamerák pixelméretei mellett és látható fény esetén tipikusan 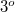 körül van, ez indokolja a 4. ábrán látható elrendezés használatát.
körül van, ez indokolja a 4. ábrán látható elrendezés használatát.
Szemléltetésképp az alábbi ábra digitális hologramokra mutat példát: az a)-c) ábrák szimulált hologramokat, a d) ábra egy a fenti elrendezésben rögzített valós tárgy digitális hologramját mutatja.
A digitális hologramok numerikus rekonstrukciójához (digitális rekonstrukció) az analóg amplitúdó hologramok optikai rekonstrukcióját szimuláljuk a számítógépen. Ha a hologramlemezt mint amplitúdó moduláló eszközt (transzparenciát) a referenciahullámmal átvilágítjuk, akkor sík referenciahullám esetén ennek az az egyszerű modell felel meg, hogy tekintsük a digitális hologramot a hullámfront amplitúdójának, melynek fázisa egyébként állandó. Ez megfelel a valóságban a közvetlenül a hologramlemez mögött észlelhető hullámnak. Ha a referenciahullám gömbhullám volt, akkor a digitális hologramhoz állandó fázis helyett gömbhullám fázisát kell rendelni, így ekkor már komplex amplitúdójú hullámot kapunk.
Ismert tehát a hullám közvetlenül a virtuális hologramlemez mögött, a következő lépés a hullám terjedésének szimulációja. Mivel a valós tárgy és a CCD kamera távolsága véges volt, a terjedést is ebben a véges távolságban kell kiszámolni. Lencse nem szerepelt az optikai elrendezésben, tehát szabad hullámterjedéssel van dolgunk, azaz diffrakciós integrált kell numerikusan kiszámolni. A CCD kamera korlátozott felbontásából és a kis térszögű hullámok alkalmazásából rögtön következik, hogy alkalmazható a Fresnel-féle parabolikus/paraxiális közelítés, ami nagy könnyebbséget jelent a számolás szempontjából, mivel így az visszavezethető egy Fourier-transzformációra. A diffrakció Fresnel-közelítésben esetünkben az alábbi módon írható fel:![\[A(u,v)=\frac{i}{\lambda D}e^{\frac{-i\pi}{\lambda D}(u^2+v^2)}\int_{\infty}^{\infty}\int_{\infty}^{\infty}R(x,y)h(x,y) e^{\frac{-i\pi}{\lambda D}(x^2+y^2)}e^{i2\pi(xu+yv)}\textup{d}x\textup{d}y,\]](/images/math/a/f/4/af45dae0275f89c2b7b88949029ea181.png)
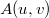 az eredmény (rekonstruált kép) komplex amplitúdó eloszlása, tehát fázisinformáció is van (!),
az eredmény (rekonstruált kép) komplex amplitúdó eloszlása, tehát fázisinformáció is van (!), 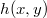 a digitális hologram,
a digitális hologram, 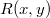 a referencia hullám komplex amplitúdója,
a referencia hullám komplex amplitúdója,  a rekonstrukció/tárgy/kép sík távolsága a hologramtól (CCD kamerától),
a rekonstrukció/tárgy/kép sík távolsága a hologramtól (CCD kamerától),  pedig a fény hullámhossza. A fenti összefüggést a Fourier-transzformáció segítségével tovább írhatjuk, valamint áttérve diszkrét numerikus koordinátákra:
pedig a fény hullámhossza. A fenti összefüggést a Fourier-transzformáció segítségével tovább írhatjuk, valamint áttérve diszkrét numerikus koordinátákra: ![\[A(u',v')=\frac{i}{\lambda D}e^{\frac{-i\pi}{\lambda D}\left((u'\Delta x')^2+(v'\Delta y')^2\right)}\mathcal F^{-1} \left[R(x,y)h(x,y) e^{\frac{-i\pi}{\lambda D}\left((k\Delta x)^2+(l\Delta y)^2\right)}\right],\]](/images/math/4/b/5/4b50a83f1598f3e0c4d8a9de93e5f26a.png)
Látható, hogy a numerikus rekonstrukció paraméterei a D rekonstrukciós távolság kivételével tulajdonképpen adottak, mivel mind a hologram képpontméretei, mind a fényhullámhossz már a hologram felvételekor meghatározottak. A D távolságot azonban viszonylag szabadon lehet - és mélységben tagolt tárgy esetén kell is - változtatni, méghozzá a valós tárgy-kamera távolság környékén, így az A(u,v)-ból képzett intezitás-eloszlásban a tárgy éles képe lesz látható. Ez ahhoz hasonlít, mint mikor fókuszálunk a fényképezésnél, amikor is kell találnunk egy olyan tárgytávolságot, amelynél a tárgy minden része elfogadhatóan éles. Az előző összefüggéssel kapcsolatban még meg kell jegyezni, hogy a Fourier-transzformáció megköti az (u,v) képsíkbeli Δx′, Δy′ képpontméretet az alábbiak szerint: 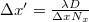 ahol
ahol 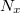 a gyors-Fourier-algoritmusban alkalmazott (lineáris) mátrixméret
a gyors-Fourier-algoritmusban alkalmazott (lineáris) mátrixméret  irányban. A fenti összefüggés szerint tehát a képsíkbeli képpontméret változik, méghozzá egyenesen arányos a D rekonstrukciós távolsággal. Ezt a rekonstruált képen látható méretek helyes értelmezéséhez figyelembe kell venni!
irányban. A fenti összefüggés szerint tehát a képsíkbeli képpontméret változik, méghozzá egyenesen arányos a D rekonstrukciós távolsággal. Ezt a rekonstruált képen látható méretek helyes értelmezéséhez figyelembe kell venni!
Mivel egy digitális hologramból a teljes komplex hullám kinyerhető, valamint a különböző elhajlási rendek térben szétválnak (azaz a rekonstruált kép különböző helyein jelennek meg), a tárgy éles képének területén a többi rend járuléka gyakorlatilag nulla: ezen a területen tisztán a tárgyhullám jelenik meg, amplitúdója és fázisa egyaránt ismert. Elvi akadálya tehát nincs, hogy interferometrikus elvű holografikus méréseket digitális változatban is megvalósítsunk. Ha rögzítünk egy digitális hologramot a tárgy alapállapotában, terheljük, majd rögzítünk egy másik hologramot ebben az állapotában is, a továbbiakban csak számítógépes feldolgozásra van szükség.
Az analóg holográfiában kétexpozíciós hologramnál a két állapothoz tartozó két hullám összege, azaz interferenciájuk jelenítené meg az elmozdulásmező kontúrvonalait, így most ezt kell szimulálni. Számoljuk ki a két digitális hologram numerikus rekonstrukcióját a megfelelő távolságban, mindkét hologramnál ugyanott, majd adjuk össze őket. Mivel a két tárgy hullámterét komplex mátrixok reprezentálják a számolásban, az összeadás is természetesen komplex, és mivel az összeadás pontművelet, nem keveri össze a már szétvált elhajlási rendeket. Az így kapott eredő komplex amplitúdóból képezzük pl. az intenzitást, amelyen interferenciacsíkok jelennek meg, vagy tekinthetjük közvetlenül a fázist is, hisz az egyaránt rendelkezésre áll. Ha összeadás helyett a két hullámot kivonjuk egymásból (összeadás ellenfázisban), akkor a fényes nulladrendű folt középen eltűnik. A csíkos interferenciaképet tulajdonképpen a hely szerint változó fáziseltérés (lásd a 9-es összefüggést) okozza a két hullám között, és a digitális holográfia lehetőségeinek köszönhetően ez meg is jeleníthető.
Szemcsekép interferometria, vagy TV holográfia
Ha a referenciaágba a kamerától épp tárgytávolságnyira egy mattüveg diffúzort helyezünk, az így rögzített digitális hologram lényegében már nem rekonstruálható, mert nem igazán ismert a diffúz nyaláb fázisa a kamera síkjában, tehát az R(x,y) komplex függvény. Ellenben ha ilyenkor a kamerára objektívet is csavarunk, és élesre állítjuk a tárgy képét, a rekonstrukciós lépésre nincs is szükség. Ilyenkor a tárgyfelület és a diffúzor mint referenciafelület képének interferenciáját rögzítjük. Mivel mindkét kép önmagában egy szemcsés kép lenne, az interferenciájuk is egy szemcsés kép, és innen származik az eljárás egyik neve. A másik neve onnan ered, hogy az így rögzített kép közvetlenül élőben nézhető egy monitoron, régebben TV képernyőn. Önmagában egyetlen szemcsekép interferogram semmi látványosat nem mutat, azonban ha a kétexpozíciós holográfiához hasonlóan egy tárgy két állapotában is rögzítünk ilyen szemcseképet, akkor ezekből már kinyerhető az okozott fázisváltozás információja. Ehhez ebben az esetben elég a két szemcsekép interferogram különbségének aboszlút értékét venni.
Mérési feladatok
Reflexiós (látvány-) hologram készítése
A mérési gyakorlat első részében egy kb. 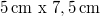 -es hologramlemezre egy hasonló méretű erősen reflektáló, lehetőleg csillogó tárgyról készítünk fehérfényű hologramot. A fényforrás egy
-es hologramlemezre egy hasonló méretű erősen reflektáló, lehetőleg csillogó tárgyról készítünk fehérfényű hologramot. A fényforrás egy 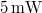 névleges teljesítményű,
névleges teljesítményű, 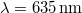 hullámhosszúságú vörös fényű diódalézer, mely
hullámhosszúságú vörös fényű diódalézer, mely 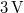 táplálás mellett kb.
táplálás mellett kb. 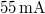 áramot vesz fel, és fix befogóval rendelkezik. Ez a lézerdióda „csupasz”, így nyalábja eleve tágul. A hologramlemezek LITIHOLO RRT20 típusú, ~500-660 nm hullámhossztartományra érzékeny, ún. instant filmmel (amely fotopolimer emulziót tartalmaz) bevont üveglemezek. Az RRT20 film megfelelő expozíciójához
áramot vesz fel, és fix befogóval rendelkezik. Ez a lézerdióda „csupasz”, így nyalábja eleve tágul. A hologramlemezek LITIHOLO RRT20 típusú, ~500-660 nm hullámhossztartományra érzékeny, ún. instant filmmel (amely fotopolimer emulziót tartalmaz) bevont üveglemezek. Az RRT20 film megfelelő expozíciójához 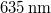 -en minimálisan
-en minimálisan 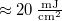 (átlagos) energiasűrűség szükséges, felső korlátja ennek a mennyiségnek nincs, de az emulzió rendelkezik egy alsó (és a véges sebességű monomerdiffúzió miatt felső) átlagintezitás-küszöbbel is, így a laborban gyenge szórt fény is jelen lehet. A fényérzékeny réteg
(átlagos) energiasűrűség szükséges, felső korlátja ennek a mennyiségnek nincs, de az emulzió rendelkezik egy alsó (és a véges sebességű monomerdiffúzió miatt felső) átlagintezitás-küszöbbel is, így a laborban gyenge szórt fény is jelen lehet. A fényérzékeny réteg 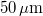 -es vastagsága jóval nagyobb a megvilágító hullámhossznál, ami a 2. pontban leírtak szerint azt jelenti, hogy a használt hologramlemezek alkalmasak vastag hologramok rögzítésére. Exponáláskor az instant filmben a megvilágítás intenzitásától függő törésmutató-változás rögzül. Az interferenciakép tehát törésmutató-moduláció formájában valós időben kódolódik a film anyagában. Ennek az anyagnak az egyik fő előnye, hogy exponálás után semmilyen, a hagyományos holografikus emulziók esetén használatos kémiai eljárást (előhívás, halványítás, rögzítés), vagy más fotopolimereknél szükséges UV illetve hőkezelést nem igényel, mivel a holografikus rács a beírás folyamán végleges formájában rögzül az anyagban. A hologramlemezek fényzáró dobozban találhatók, melyet csak gyenge háttérfény esetén, közvetlenül az exponálás előtt szabad kinyitni, majd egy lemezt kiemelve rögtön visszazárni.
-es vastagsága jóval nagyobb a megvilágító hullámhossznál, ami a 2. pontban leírtak szerint azt jelenti, hogy a használt hologramlemezek alkalmasak vastag hologramok rögzítésére. Exponáláskor az instant filmben a megvilágítás intenzitásától függő törésmutató-változás rögzül. Az interferenciakép tehát törésmutató-moduláció formájában valós időben kódolódik a film anyagában. Ennek az anyagnak az egyik fő előnye, hogy exponálás után semmilyen, a hagyományos holografikus emulziók esetén használatos kémiai eljárást (előhívás, halványítás, rögzítés), vagy más fotopolimereknél szükséges UV illetve hőkezelést nem igényel, mivel a holografikus rács a beírás folyamán végleges formájában rögzül az anyagban. A hologramlemezek fényzáró dobozban találhatók, melyet csak gyenge háttérfény esetén, közvetlenül az exponálás előtt szabad kinyitni, majd egy lemezt kiemelve rögtön visszazárni.
Állítsa össze a 2/a. ábra elrendezését az optikai asztalon látható felnyitható tetejű fadoboz belsejében, és dokumentálja a ténylegesen használt elrendezést lehetőleg digitális fénykép készítésével, vagy megfelelő eszköz hiányában méretarányos rajzzal, mely nagyságrendileg szöghelyes és rajta a jellemző távolságok is fel vannak tüntetve. Az elemek egy része mágneses talpakon található, melyeket forgatógombbal lehet lazítani illetve rögzíteni. A többi állítási lehetőséget a szárnyas anyát használó befogások jelentik. Használja a mérőhelyen található próbalemezt és azonos méretű papírt a beállításhoz, a nyaláb követéséhez. Helyezze a tárgyat egy hasábra a megfelelő magasság eléréséhez. A lemezt speciális tartóba lehet helyezni, mely csavarokkal szorítja a lemezt a helyére. Ellenőrizze, hogy a lemez majdnem teljes felülete és a tárgy megfelelő oldala is elegendően nagy felületen árnyékmentesen meg van világítva. Helyezze a tárgyat és a lemezt a lehető legközelebb egymáshoz. Segíti a későbbi rekonstrukciót, ha a megvilágítás valamennyire ferdén felülről érkezik a függőleges helyzetű lemezre. A lemez egyik oldalán található a fényérzékeny fólia, ennek célszerű a tárgy felőli oldalra kerülnie. Ellenőrizze, hogy a rögzítések megfelelőek, nincs-e „nyitva” hagyott mágneses talp, vagy laza szárnyas anya.
Exponálás előtt mutassa meg az elrendezést a mérésvezetőnek. Jóváhagyás után megkezdődhet az exponálás. Ehhez kapcsolja le a szoba mennyezeti fénycsöveit, eressze le majdnem teljesen a sötétítőket, kapcsolja le a lézert (tápegységen output off), majd vegyen ki egy lemezt a tartódobozból, és azt zárja vissza. Fogja be a lemezt a tartóba, majd fél perces várakozást követően kapcsolja vissza a lézert. Az exponálás időtartamára az anyag viselkedése miatt szintén minimumfeltétel vonatkozik, ez kb. 5 perc. Exponálás közben a lemez átlátszósága megnövekszik, mivel a kiépülő hologram rekonstruált képe egyre több fényt juttat a tárgyra, így az exponálás folyamata élőben is "követhető", illetve megállapítható a vége. Ha bizonytalan az időt illetően, inkább exponáljon tovább 2 perccel. A hologram készítése közben kerülni kell a zavaró fényeket, mozgást és rezgést, így a többi mérőcsoport figyelmét is fel kell hívni a megfelelő viselkedésre.
Exponálás után vegye ki a helyéről a tárgyat, és a lézer fényében figyelje meg a rekonstruált virtuális képet. Ezután vegye ki a tartóból a hologramot, és a laborban található színes és fehér nagyteljesítményű LED-ek fényében is rekonstruálja a virtuális képet. Milyen színben látható fehér LED esetén a tárgy virtuális képe? És ha nagyon ferdén nézzük és világítjuk meg? Mi látható, ha a lemezt az oldalán átfordítva nézzük? Jegyezze fel tapasztalatait, és lehetőleg dokumentálja a látottakat (akár utólag otthon) digitális fényképpel is!
Megjegyzés: Az előbbi feladathoz saját tárgyakat is lehet hozni, de rendelkezünk jól bevált tárgykészlettel. Alkalmas tárgyak: érmék, kulcsok, fém dísztárgyak (méretkorláttal), és arany vagy ezüst festékkel csillogóra festett egyéb tárgyak, macskaszem prizma. Korlátozottan alkalmasak fehér, sima felületű tárgyak, kis plüssfigurák (rövid szőrrel), fehér LEGO elemek.
Elmozdulásmező vizsgálata real-time holografikus interferometriával reflexiós elrendezésben
Az előző mérési feladattal lényegében megegyező elrendezést kell itt is használni, mindössze a tárgyat kell kicserélni a laborban található középen megnyomható membránra, és annak felületére merőleges megvilágításra van szükség. A merőlegességet a (9) képlet alkalmazásánál fogjuk felhasználni. A membrán közepét egy mikrométerorsó nyomja, mely 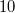 mikronos osztású, és
mikronos osztású, és 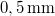 egy fordulata. Ezt az orsót egy hozzá rögzített karon keresztül forgatjuk, melynek végét egy ugyanilyen orsó mozgatja. Mérje meg, hogy milyen hosszú a „külső“ orsó karja, azaz hol érinti azt a „belső“ orsó tengelyétől számítva, és határozza meg, hogy a külső orsó egy fordulata mennyivel nyomja meg a membrán közepét. A kar általában úgy van ráerősítve a "belső" mikrométer orsóra, hogy a kar mozgatásakor az már felütközik a membrán belső felületén. Hogy ez tényleg így van, vagy valamilyen hallgatói beavatkozás miatt mégsem, arról úgy lehet megyőződni, hogy a membrán felüleltén lézeres megvilágítás esetén látható úgynevezett lézerszemcsék a kar mozgatásakor radiális mozgást végeznek-e vagy sem.
egy fordulata. Ezt az orsót egy hozzá rögzített karon keresztül forgatjuk, melynek végét egy ugyanilyen orsó mozgatja. Mérje meg, hogy milyen hosszú a „külső“ orsó karja, azaz hol érinti azt a „belső“ orsó tengelyétől számítva, és határozza meg, hogy a külső orsó egy fordulata mennyivel nyomja meg a membrán közepét. A kar általában úgy van ráerősítve a "belső" mikrométer orsóra, hogy a kar mozgatásakor az már felütközik a membrán belső felületén. Hogy ez tényleg így van, vagy valamilyen hallgatói beavatkozás miatt mégsem, arról úgy lehet megyőződni, hogy a membrán felüleltén lézeres megvilágítás esetén látható úgynevezett lézerszemcsék a kar mozgatásakor radiális mozgást végeznek-e vagy sem.
A real-time interferogram készítéséhez a membránról reflexiós hologramot kell készíteni az előző mérési feladattal megegyező módon. Ezután nem szabad semmit el- vagy megmozdítani a külső orsó kivételével! Mivel a holografikus rács már ilyenkor is diffraktál, a membránt részben a referencia és részben a tárgyhullám világítja meg (azaz a saját virtuális képe). Továbbra is sötétben lassan tekerjen a külső orsón néhány egész fordulatot, és közben figyelje a membrán felületét a hologramlemezen keresztül. A növekvő deformációval egyre sűrűbb csíkrendszer áll elő, amely a membrán alap és deformált állapota közötti interferencia eredményeképp jön létre. Ez a real-time interferogram. Két-három különböző mértékben benyomott állapotban rögzítse az orsó tekeréseinek számát, és számlálja le a hozzá tartozó csíkszámot a membrán felületén 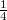 csík pontossággal, majd a mérés kontúrtávolságával (lásd korábbi interferométeres mérések) szorozva állapítsa meg a membrán közepén fellépő legnagyobb elmozdulás névleges(mikrométerről leolvastható) és mért (interferogramról leolvasható) értékeit. Ha a leolvasások végeztével kicsit elmozdítja akár a tárgyat, akár a hologramlemezt, mit tapasztal? Mit árul el a csíkok alakja az elmozdulásmezőről? Értelmezze a látottakat. (Megj.: Ha a feladat végeztével az edereti tárgy nélküli rekonstrukciókor látható valamilyen kétexpozíciós csíkrendszer a virtuális tárgyfelületen, arról a látványról is érdemes fényképet készíteni a jegyzőkönyv számára.)
csík pontossággal, majd a mérés kontúrtávolságával (lásd korábbi interferométeres mérések) szorozva állapítsa meg a membrán közepén fellépő legnagyobb elmozdulás névleges(mikrométerről leolvastható) és mért (interferogramról leolvasható) értékeit. Ha a leolvasások végeztével kicsit elmozdítja akár a tárgyat, akár a hologramlemezt, mit tapasztal? Mit árul el a csíkok alakja az elmozdulásmezőről? Értelmezze a látottakat. (Megj.: Ha a feladat végeztével az edereti tárgy nélküli rekonstrukciókor látható valamilyen kétexpozíciós csíkrendszer a virtuális tárgyfelületen, arról a látványról is érdemes fényképet készíteni a jegyzőkönyv számára.)
Holografikus optikai elem készítése
Ismételje meg az első feladatot tárgyként a mérőhelyen található domború tükröt használva. Vizsgálja meg a kész holografikus tükör működését, és jegyezze fel tapasztalatait. Hogyan jelenik meg a domború tükörnek megfelelő tükörkép? Hogyan viselkedik az optikai elemünk, ha a másik oldalát használjuk? Mi változik, ha a beeső fénysugarak és a megfigyelés is ferdék? Lehetséges valós, vetített képet készíteni az elemmel? Használja a mérőhelyen található piros és fehér LED fényforrásokat, vagy egy mobiltelefon vakuzó LED-jét folytonos üzemben. Lehetőség szerint dokumentálja is a látottakat digitális fényképekkel.
Transzmissziós hologram készítése
Állítson össze transzmissziós hologram elrendezést az 1/a. ábra szerint, és dokumentálja azt az első feladathoz hasonlóan. Ellenőrizze, hogy a lemez helyéről mi látszik a tárgyból, illetve hogy szóródik-e róla fény a lemez felé. Törekedjen arra, hogy a referencia és a tárgynyaláb egymással bezért szöge 30-45 fok körül legyen, valamint az úthosszak különbsége se legyen 10 centinél sokkal nagyobb. A lemezt úgy kell a tartóba helyezni, hogy a fóliázott rész a beérkező nyalábok felé nézzen. Az exponálást az első feladatban leírtaknak megfelelően kell végezni. A kész hologram csak lézerfényben tekinthető meg. Nézze meg az eredményt az 1/b. és az 1/c. ábrák elrendezésében is, utóbbihoz egy másik, nem táguló nyalábú lézer szükséges. Hogyan jelenik meg a holografikus kép térbelisége? Működhet-e a rekonstrukció más színű lézerrel? Lehetőség szerint készítsen digitális fényképet a rekonstrukciókor látottakról.
Elmozdulásmező vizsgálata digitális holográfiával
A mérési gyakorlat második részében megmérjük egy membrán közepén a síkra merőleges elmozdulás legnagyobb értékét. A méréshez a 4. ábrán látható elrendezést használjuk, de a valóságos kitágított nyalábjaink nem tökéletes síkhullámok. A fényforrás egy 35 mW teljesítményű 632,8 nm-es vörös fényű léghűtéses He-Ne gázlézer. A képeket egy Baumer Optronics MX13 típusú 1280x1024 képpont felbontású monokróm CCD kamerával rögzítjük, melynek képpontmérete 6,7 μm x 6,7 μm, és saját kezelőprogrammal rendelkezik. Ebben a kamera élőképe is megtekinthető (jobb oldalon a kék film gomb, a szürke azonnali lefagyást okoz!), valamint kézzel állíthatók az exponálás (záridő, erősítés) paraméterei a távcső ikonnal ellátott gomb alatti gombbal. Az erősítés optimális értéke 100-120 körüli az állító csúszka középső tartományában. A rögzített 8 bites színmélységű kép hisztogramja (különböző szürkeségi szintű pixelek számának eloszlása) egy másik programmal tekinthető meg. Ebben a Hisztogram gombra kattintva a mintavevő ablak a címsorát egérrel elhúzva a megfelelő képterületre helyezhető, majd dupla kattintással rögzül. Ezután a Timer gombbal ki/be kapcsolható a hisztogram élő követése. A hisztogram ábra és a felette található limitszámlálók értéke alapján állapítható meg pontosan, hogy a kép esetleg alul- vagy túlexponált. (A hisztogram funkció számos digitális fényképezőgépben is megtalálható már.) Az elrendezésben található BS1 nyalábosztó forgatható, ezáltal az intenzitás osztásaránya változtatható a tárgy- és a referenciaág között, de a referenciaágban található még egy forgatható nyalábosztó, amelyet további gyengítésre használunk. A digitális hologramokat egy HoloVision 2.2 nevű szabadon felhasználható programmal rekonstruáljuk (projekt honlap).
A tényleges mérés előtt ellenőrizzük az elrendezést és annak beállításait. Mérje meg a kamera és a tárgy távolságát. Az elrendezésben a megfigyelés merőleges a membrán felületére, a megvilágítás azonban nem. Mérje meg ennek szögét távolságokból, és az adatok alapján a (9) összefüggés alkalmazásával határozza meg azt a síkra merőleges elmozdulásértéket, amelynél az okozott fázisváltozás 2π. (Ehhez vegyen fel egy derékszögű koordinátarendszert a membránhoz igazodva.) Ez lesz a mérés ún. kontúrtávolsága, azaz lényegében alapvető nagyságrendje.
Ellenőrizze a rögzíthető képek exponáltságát kitakart referencia és tárgynyaláb esetén, valamint kitakarás nélkül. Szükség esetén állítson az expozíció paraméterein és a forgatható nyalábosztókon: se a tárgynyaláb, se a referencianyaláb ne legyen önmagában túl sötét, az interferenciaképük viszont ne legyen túl világos. Figyelje meg, mi látható a kamera élőképén, ha a BS2 osztótükröt finoman rezgetjük? Hogyan néz ki a kép hisztogramja megfelelő beállítások esetén?
Ha az exponálás már megfelelő, vegyen fel egy képet, és rekonstruálja azt a HoloVisionnel (Image/Reconstruct menüparancs). A digitális hologram hisztogramját és az expozíció paramétereit vegye bele a jegyzőkönyvbe. Értékelje a rekonstrukció intenzitásképének élességét a rögzítőkeret membránra vetett árnyéka alapján. Vizsgálja meg az élesség változását 5-10 centivel kisebb illetve nagyobb rekonstrukciós távolságok esetén. Hol a legélesebb a kép? Eltér ez a távolság a ténylegesen mérttől, ha igen vajon miért? Mekkora a képpontméret ebben a távolságban? Mennyire egyezik a képről leolvasható tárgyméret a valóságossal?
Vegyen fel egy hologramot a membránról, majd deformálja azt 5 μm-nél kisebb mértékben a hátulján található csavarmikrométerhez csatlakoztatott szerkezet segítségével (lásd a mérés első részében használt áttételezést) . Vegyen fel még egy képet. Adja össze a két hologramot (Image/Calculations menüparancs), majd rekonstruálja az összeget. Mi látható az intenzitásképen? Az eredményt mellékelje a jegyzőkönyvbe is. Most az összeg helyett rekonstruálja a különbséget. Miben tér el az intenzitáskép az előzőtől? A csíkrendszer kvalitatíve mit árul el az elmozdulásmezőről? Értelmezze a látottakat. Számlálja le a csíkokat a membrán szélétől a közepéig 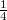 csík pontossággal, majd a mérés kontúrtávolságával szorozva állapítsa meg a legnagyobb elmozdulást (megnyomást). Vesse össze a mikrométerről „névlegesen” leolvasható értékkel.
csík pontossággal, majd a mérés kontúrtávolságával szorozva állapítsa meg a legnagyobb elmozdulást (megnyomást). Vesse össze a mikrométerről „névlegesen” leolvasható értékkel.
Ha megfelelő interferogramokat kapott, térjen át a következő feladatra, szemcsekép interferogram készítésére. Csavarja rá a kamerára az ott található foto-objektívet, majd helyezze el a diffúzort a referencia nyaláb útjába úgy, hogy a kamera azonos távolságban érzékelje, mint a tárgyat. Állítsa élesre a tárgyon a keret önárnyékának képét kis rekeszérték (f/2.8) és így kis mélységélesség mellett. A rekeszállító gyűrű lépcsőzetes működésű. Ha a kép kellően éles, akkor nagy, f/16-os rekeszérték mellett a tárgy deformációjakor a rajta látható lézerszemcsék nem mozognak, csak a fényességük változik. Ha ez sikerült, végül állítsa f/16-os értékre a rekeszt. Az osztótükör és a referencia ágban található gyengítő forgatásával érje el, hogy a tárgyfelület és a diffúzor képe azonos fényességűnek látszódjon. Rögzítsen egy-egy szemcseképet a tárgy kétféle terhelési állapotában, majd képezze ezek különbségét a Holovisionnel, és jelenítse meg ennek "Modulus"-át, azaz abszolút értékét. Mit lát a képen? Hogyan értelmezhetők a látottak? Vajon miért nem ad hasonló eredményt a szemcseképek összegzése is, mint digitális holográfia esetén?
Egyéb információk
A jegyzőkönyvben: elméleti bevezető nem szükséges, de saját igény esetén se legyen több egy oldalnál. Foglalja össze a mérés során tapasztaltakat! Mellékelje a ténylegesen használt elrendezések rajzát vagy fényképét, és ha készültek digitális fényképek a rekonstrukciókról, azokat is. Térjen ki a mérési feladatokban megfogalmazott kérdésekre is!
Biztonsági tudnivalók: A direkt lézerfénybe ne nézzünk bele, különösen a digitális holográfia résznél használtba! A nem kitágított vagy nem szórt lézerfénnyel megvilágított pontokat lehetőleg ne nézzük hosszabb ideig, a szórt lézerfénybe pedig csak a szükséges ideig nézzünk! A csillogó ékszereket vagy karórákat vegyük le, az optikai asztalok magasságába ne hajoljunk le! Mozogjunk körültekintően a laborban: vigyázzunk az asztal széléhez közel lévő beállított elemekre, illetve a nyalábtágítókig található elemekre!
Linkek: