„Nagyfrekvenciás jelek terjedésének fizikai alapjai” változatai közötti eltérés
(Új oldal, tartalma: „__TOC__ ==Bevezetés== <wlatex> A laborgyakorlat célja, hogy a nagyfrekvenciás ($f>1-10$ MHz) méréstechika és jelátvitel területén felmerülő alapfogalmakat …”) |
|||
| 10. sor: | 10. sor: | ||
A hullámjelenségek figyelembevétele a modern kommunikációs eszközöknél még fontosabb, mivel pl. 9 GHz-es vivőfrekvenciára (ami egy elterjedt kommunikációs sáv) a hullámhossz mindössze 3 cm. Egy másik gyakorlati példánk a számítógépek, melyek tipikusan 2-3 GHz-es jelekkel dolgoznak ($\lambda \approx 10~\textrm{cm}$), melyeket 10-20 cm távolságra juttatnak el, így itt nyilvánvalóan szükséges a hullámjelenségek figyelembevétele az áramkörök tervezésekor. A későbbi tanulmányaink során hasonló jelenségekkel találkozhatunk az ''Önálló labor'' tárgy NMR (magmágneses-rezonancia) és ESR (elektronspin-rezonancia) laborgyakorlatain.</wlatex> | A hullámjelenségek figyelembevétele a modern kommunikációs eszközöknél még fontosabb, mivel pl. 9 GHz-es vivőfrekvenciára (ami egy elterjedt kommunikációs sáv) a hullámhossz mindössze 3 cm. Egy másik gyakorlati példánk a számítógépek, melyek tipikusan 2-3 GHz-es jelekkel dolgoznak ($\lambda \approx 10~\textrm{cm}$), melyeket 10-20 cm távolságra juttatnak el, így itt nyilvánvalóan szükséges a hullámjelenségek figyelembevétele az áramkörök tervezésekor. A későbbi tanulmányaink során hasonló jelenségekkel találkozhatunk az ''Önálló labor'' tárgy NMR (magmágneses-rezonancia) és ESR (elektronspin-rezonancia) laborgyakorlatain.</wlatex> | ||
| + | |||
| + | ==Elméleti háttér== | ||
| + | |||
| + | ===A távíróegyenletek=== | ||
| + | <wlatex> | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:vezetek_sema.jpg|közép|300px|]] | ||
| + | |- | ||
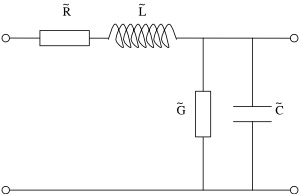
| + | | align="center"|1. ábra: A jelterjedésben vizsgált vezeték egy darabjának áramköri modellje. | ||
| + | |} | ||
| + | Tekintsük a jelet továbbító vezeték egy infinitezimálisan kicsi darabját, ami \aref{vezetek_sema} ábrán látható. Ezt legáltalánosabban egy soros ún. \textit{elosztott ellenállás}, $\widetilde{R}$ (egysége Ohm per méter), \textit{elosztott induktivitás}, $\widetilde{L}$ (egysége Henry per méter), \textit{elosztott kapacitás}, $\widetilde{C}$ (egysége Farád per méter), és a két drót közti \textit{elosztott vezetés}, $\widetilde{G}$ (egysége Siemens per méter) jellemzi. | ||
| + | A soros ellenállás oka a vezetékdarabokban lévő veszteség, az induktivitás oka pedig az, hogy az egyes drótdarabokat mágneses tér veszi körbe, ezért lesz egyetlen drótszálnak is önindukciója. A $\widetilde{G}$ írja le a két vezetékdarab közti elektromos vezetést, ami akkor is jelen van, ha nagyon jó dielektrikum választja el a két vezetőt egymástól. Mivel a két drót nincs azonos ponteciálon, ezért lesz köztük a $\widetilde{C}$ kapacitás. | ||
| + | </wlatex> | ||
A lap 2018. február 21., 22:47-kori változata
Tartalomjegyzék |
Bevezetés
A laborgyakorlat célja, hogy a nagyfrekvenciás (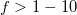
MHz) méréstechika és jelátvitel területén felmerülő alapfogalmakat és jelenségeket bemutassa. A legfontosabb amit érdemes megjegyezni az, hogy az alacsony frekvenciás hálózatok vizsgálatakor megszokott leírásmódok nagyobb frekvenciákon érvényüket vesztik, és a hagyományos áramköri jelenségeken túlmutató, szokatlan jelenségek lépnek fel, mint pl. a jelek reflexiója. A fizika szempontjából itt a Maxwell-egyenletek nagyfrekvenciás, azaz hullámjelenségeket is figyelembe vevő alkalmazásáról van szó kábelek esetére.
A XIX. század közepén felmerült az igény a nagy távolságokra történő adattovábbításra, akár kontinensnyi távolságokban, pl. tenger alatti kábelek segítségével. (Az első transzatlanti kábelt 1858-ban helyezték üzembe.) Hamar kiderült, hogy a vezetékben történő jeltovábbításánál lényeges a hullámjelenségek figyelembevétele. Ez a technológiai fejlődés és igény az elméleti leírásra időben közel volt a Maxwell-egyenletek (1861) megszületéséhez. A vezetékben terjedő hullámjelenségek leírását ma mint az ún. távíróegyenleteket ismerjük. Ez a Maxwell-egyenletek által megjósolt elektromágneses hullámjelenségek egyik gyakorlati alkalmazása, és e leírás gyakorlati sikere is inspirálóan hatott az elektromágneses sugárzás későbbi felfedezésére (Hertz, 1886).
A fizikus tanulmányok során eddigiekben felmerült egyenáramú (DC) és alacsony frekvenciás váltóáramú (AC) hálózatok vizsgálatakor nem törődtünk azzal, hogy a jel terjedési sebessége véges. Feltételeztük, hogy adott ponton feszültséget kapcsolva egy áramkörre az pillanatszerűen megjelenik minden azonos potenciálú helyen. Mindez nyilvánalóan érvényét veszíti, amikor a jel számára szükséges terjedési idő,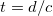 
(itt 
a kábel hossza, 
a közegben érvényes fénysebesség), összemérhető a jel periódusidejével: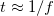 
(a gyakorlatban inkább a 
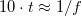feltétel a használatos). Például a transzatlanti kábel esetére az így kapott frekvencia 
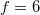Hz. Ez az eredmény azt jelenti, hogy a hullámjelenségek figyelembe vétele nélkül a transzatlanti kommunikáció csak ennél lényegesen alacsonyabb frekvencián, mai szóhasználattal kb. 
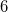Hz sávszélességen (azaz 6 bit/sec) mehetne csak végbe.
A hullámjelenségek figyelembevétele a modern kommunikációs eszközöknél még fontosabb, mivel pl. 9 GHz-es vivőfrekvenciára (ami egy elterjedt kommunikációs sáv) a hullámhossz mindössze 3 cm. Egy másik gyakorlati példánk a számítógépek, melyek tipikusan 2-3 GHz-es jelekkel dolgoznak (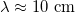
), melyeket 10-20 cm távolságra juttatnak el, így itt nyilvánvalóan szükséges a hullámjelenségek figyelembevétele az áramkörök tervezésekor. A későbbi tanulmányaink során hasonló jelenségekkel találkozhatunk az Önálló labor tárgy NMR (magmágneses-rezonancia) és ESR (elektronspin-rezonancia) laborgyakorlatain.
Elméleti háttér
A távíróegyenletek
 |
| 1. ábra: A jelterjedésben vizsgált vezeték egy darabjának áramköri modellje. |
Tekintsük a jelet továbbító vezeték egy infinitezimálisan kicsi darabját, ami \aref{vezetek_sema} ábrán látható. Ezt legáltalánosabban egy soros ún. \textit{elosztott ellenállás},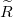 
(egysége Ohm per méter), \textit{elosztott induktivitás}, 
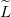(egysége Henry per méter), \textit{elosztott kapacitás}, 
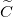(egysége Farád per méter), és a két drót közti \textit{elosztott vezetés}, 
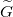(egysége Siemens per méter) jellemzi.
A soros ellenállás oka a vezetékdarabokban lévő veszteség, az induktivitás oka pedig az, hogy az egyes drótdarabokat mágneses tér veszi körbe, ezért lesz egyetlen drótszálnak is önindukciója. A 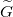írja le a két vezetékdarab közti elektromos vezetést, ami akkor is jelen van, ha nagyon jó dielektrikum választja el a két vezetőt egymástól. Mivel a két drót nincs azonos ponteciálon, ezért lesz köztük a 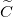kapacitás.
