„Spektrumanalízis szerkesztőlap” változatai közötti eltérés
(→Spektrumanalízis) |
(→Spektrumanalízis) |
||
| 1. sor: | 1. sor: | ||
===Spektrumanalízis=== | ===Spektrumanalízis=== | ||
| + | ==Fourier-transzformáció== | ||
<wlatex> | <wlatex> | ||
Egy időben változó jel spektrumát a Fourier-transzformáció segítségével ismerhetjük meg. | Egy időben változó jel spektrumát a Fourier-transzformáció segítségével ismerhetjük meg. | ||
| 14. sor: | 15. sor: | ||
azaz a spektrum $\omega$ frekvenciájához az ablakfüggvény bekever jelet az $\omega'$ frekvenciából is. Ezt a jelenséget spektrális szivárgásnak nevezzük. | azaz a spektrum $\omega$ frekvenciájához az ablakfüggvény bekever jelet az $\omega'$ frekvenciából is. Ezt a jelenséget spektrális szivárgásnak nevezzük. | ||
| − | + | </wlatex> | |
| + | ==DFT, FFT== | ||
| + | <wlatex> | ||
A gyakorlati spektrumanalizáláshoz nem csak a véges időintervallumban végzett mérést kell figyelembe venni, hanem azt is, hogy a mért jelet nem folytonosan, hanem diszkrét pontokon mintavételezzük. | A gyakorlati spektrumanalizáláshoz nem csak a véges időintervallumban végzett mérést kell figyelembe venni, hanem azt is, hogy a mért jelet nem folytonosan, hanem diszkrét pontokon mintavételezzük. | ||
Az ablakfüggvénnyel szorzott jel integrálját ennek megfelelően egy diszkrét összeggel közelítjük: | Az ablakfüggvénnyel szorzott jel integrálját ennek megfelelően egy diszkrét összeggel közelítjük: | ||
$$f_W(\omega)=\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t,$$ | $$f_W(\omega)=\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t,$$ | ||
| − | ahol $\Delta t$ a két diszkrét mintavételezés között eltelt idő (a mérési idő $T=N\Delta t$). | + | ahol $\Delta t$ a két diszkrét mintavételezés között eltelt idő (a mérési idő $T=N\Delta t$). A diszkrét Fourier-transzformáció (DFT) tehát a diszkrét pontokon felvett függvény spektrumát adja meg.A Nyquist-Shannon mintavételezési törvény értelmében $\Delta t$ mintavételezési idővel legfeljebb $\omega_{max}=\frac{2\pi}{2\Delta t}$ maximális frekvenciáig lehetséges a jel rekonstrukciója. |
| − | A diszkrét Fourier-transzformáció (DFT) tehát a diszkrét pontokon felvett függvény spektrumát adja meg. | + | |
| + | A fenti mennyiség abszolútérték négyzete pedig nem más, mint a mért jel teljesítményspektruma (''Power Spectrum''): | ||
| + | $$PS\abs{\sum_{n=0}^{N-1}W(n\Delta t) V(N\Delta t)e^{-i\omega n\Delta t}\Delta t}^2,$$ | ||
| − | |||
Nem csak a mintavételezés történik diszkrét időnként, hanem a DFT kiszámítása is diszkrét $\omega_k$ értéken valósul meg. A diszkrét Fourier-transzformáció műveletigénye egyszerű "brute force" eljárással N frekvencia pont esetén $\mathcal{O}(N^2)$ műveletet igényel. Ez rendkívül időigényes, ezért egy más számítási algoritmust használnak a szoftverek a jel feldolgozásához. Ez a gyors Fourier-transzformáció (FFT), amelynek működési alapelve, hogy a mintát kettéválasztja páros és páratlan pontokra, így az N pontos DFT két N/2 pontos DFT-re bomlik. Ezt követően ezeket tovább felezi, és azokat is tovább, stb. Ehhez természetesen szükséges, hogy a mérési pontok száma kettő hatványa legyen. Könnyen belátható, hogy ennek az algoritmusnak a műveletigénye $\mathcal{O}(NlogN)$ nagyságrendű. Az FFT algoritmus az $N=2^n$ adatpontból álló jel Fourier-spektrumát $\omega_k=\frac{2\pi k}{N\Delta t}, k=0,1,..N/2$ diszkrét körfrekvenciapontokon adja meg. | Nem csak a mintavételezés történik diszkrét időnként, hanem a DFT kiszámítása is diszkrét $\omega_k$ értéken valósul meg. A diszkrét Fourier-transzformáció műveletigénye egyszerű "brute force" eljárással N frekvencia pont esetén $\mathcal{O}(N^2)$ műveletet igényel. Ez rendkívül időigényes, ezért egy más számítási algoritmust használnak a szoftverek a jel feldolgozásához. Ez a gyors Fourier-transzformáció (FFT), amelynek működési alapelve, hogy a mintát kettéválasztja páros és páratlan pontokra, így az N pontos DFT két N/2 pontos DFT-re bomlik. Ezt követően ezeket tovább felezi, és azokat is tovább, stb. Ehhez természetesen szükséges, hogy a mérési pontok száma kettő hatványa legyen. Könnyen belátható, hogy ennek az algoritmusnak a műveletigénye $\mathcal{O}(NlogN)$ nagyságrendű. Az FFT algoritmus az $N=2^n$ adatpontból álló jel Fourier-spektrumát $\omega_k=\frac{2\pi k}{N\Delta t}, k=0,1,..N/2$ diszkrét körfrekvenciapontokon adja meg. | ||
Most a DFT definiálását követően megvizsgálhatjuk az ablakfüggvények különböző tulajdonságát. Tételezzük fel, hogy egy egykomponensű $\omega_0$ jelet vizsgálunk. Könnyen belátható, hogy ha $\omega_0=\omega_k$ $k$ bármelyik értékére, akkor a spektrális szivárgás nulla lesz. Ez pontosan annak felel meg, amikor a jelünk a T időablakban periodikus. Azonban az esetek többségében értelemszerűen ez nem teljesül. Ekkor a spektrális szivárgáson kívül romlik a jel frekvenciafelbontása és amplitúdópontossága is. Ez előbbi a centrális csúcs keskenységével jellemezhető, míg az utóbbinál éppen ellenkezőleg arra van szükség, hogy megfelelően lapos legyen az $f_W(\omega)$ jelünk $\omega_0$ környékén. | Most a DFT definiálását követően megvizsgálhatjuk az ablakfüggvények különböző tulajdonságát. Tételezzük fel, hogy egy egykomponensű $\omega_0$ jelet vizsgálunk. Könnyen belátható, hogy ha $\omega_0=\omega_k$ $k$ bármelyik értékére, akkor a spektrális szivárgás nulla lesz. Ez pontosan annak felel meg, amikor a jelünk a T időablakban periodikus. Azonban az esetek többségében értelemszerűen ez nem teljesül. Ekkor a spektrális szivárgáson kívül romlik a jel frekvenciafelbontása és amplitúdópontossága is. Ez előbbi a centrális csúcs keskenységével jellemezhető, míg az utóbbinál éppen ellenkezőleg arra van szükség, hogy megfelelően lapos legyen az $f_W(\omega)$ jelünk $\omega_0$ környékén. | ||
| + | </wlatex> | ||
| + | ==A zaj definíciója== | ||
| + | |||
| + | Egy $V(t)$ időben fluktuáló zaj jellegű (azaz széles frekvenciaspektrumú) jelet egy $f_0$ középfrekvencia körüli $\Delta f$ szélességű sávszűrűn keresztül vizsgálva azt találjuk, hogy a szűrt jel szórásnégyzete arányos a frekvenciatartomány $\Delta f$ szélességével, az arányossági tényező a feszültségzaj spektrális sűrűsége (spectral density of noise), azaz a teljesítmény spektrális sűrűsége (Power Spectrum Density - PSD): | ||
| + | |||
| + | $$\left\langle (\Delta V(t|f_0,\Delta f))^2 \right\rangle=s_V(f_0)\Delta f.$$ | ||
| + | |||
| + | Ez a zaj kísérleti definíciója. A feszültség szórásnégyzete a zajsűrűség teljes frekvenciatartományra vett integráljával egyenlő. | ||
| + | |||
| + | $$\langle(\Delta V(t))^2 \rangle=\int_{0}^{\infty} df s_V(f).$$ | ||
| + | |||
| + | Ez a képlet közvetlenül is használható a zajspektrum kísérleti meghatározásához, azonban emellett jó kiindulópontként szolgál más fizikai mennyiségekkel való kapcsolatának vizsgálatára is. Érdemes megvizsgálni a zajsűrűség és a feszültség korrelációs függvény kapcsolatát. Ez utóbbi a következőképpen definiálható: | ||
| + | |||
| + | $$C(\Delta t)=\langle\Delta V(t)\cdotp\Delta V(t+\Delta t) \rangle=\lim\limits_{T\rightarrow\infty}\frac{1}{T}\int_{0}^{T}dt\Delta V(t)\cdotp\Delta V(t+\Delta t).$$ | ||
| + | |||
| + | Könnyen belátható, hogy a korrelációs függvény $\Delta t=0$-ban megegyezik a feszültség szórásnégyzetével. | ||
| + | |||
| + | $$C(0)=\langle(\Delta V(t))^2 \rangle.$$ | ||
| + | Most fejezzük ki a korrelációs függvényt a Fourier-transzformáltja segítségével: | ||
| + | $$\C(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega e^{i\omega t}c(\omega).$$ | ||
| + | |||
| + | Ez alapján a feszültség szórásnégyzete: | ||
| + | |||
| + | $$\langle(\Delta V(t))^2 \rangle=C(0)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega c(\omega)=\frac{1}{\pi}\int_{0}^{\infty}d\omega c(\omega),$$ | ||
| + | |||
| + | mivel $c(\omega)=c(-\omega)$. | ||
| + | Másrészt a (\ref{eq:zajdef2})-as egyenletből következik: | ||
| + | |||
| + | $$\langle(\Delta V(t))^2 \rangle=\frac{1}{2\pi} \int_{0}^{\infty} d\omega s_V(\omega).$$ | ||
| + | |||
| + | Az utóbbi két egyenletből látható, hogy a zaj teljesítménysűrűsége a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese. | ||
| + | |||
| + | Sikerült kapcsolatot teremteni a zajsűrűség és a feszültség korrelációs függvény között. Most vizsgáljuk meg a feszültség korrelációs függvény és a feszültség mint mérhető fizikai mennyiségek kapcsolatát. A feszültség átlagtól való eltérésének ($\Delta V(t)=V(t)-\langle V(t)\rangle $) a Fourier-transzformáltja szerint: | ||
| + | |||
| + | $$\Delta v(\omega)= \int_{-\infty}^{\infty} dt \Delta V(t)e^{-i\omega t}.$$ | ||
| + | |||
| + | Vizsgáljuk ezen Fourier-transzformált abszolút érték négyzetének várható értékét: | ||
| + | |||
| + | $$\langle|(\Delta v(\omega))|^2 \rangle= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} dt' dt \langle\Delta V(t)\Delta V(t') \rangle e^{-i\omega t} e^{i\omega t'}.$$ | ||
| + | |||
| + | Az egyenlet jobb oldalán látható korrelációs függvény kifejezhető a következőképpen: | ||
| + | |||
| + | $$ \langle\Delta V(t)\Delta V(t')\rangle=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega'c(\omega')e^{i\omega'(t-t')}.$$ | ||
| + | |||
| + | Továbbá az exponenciális tagokat átcsoportosítva a következő tag integrálja egy Dirac-deltát ad: | ||
| + | |||
| + | $$\int_{-\infty}^{\infty}dt'\frac{e^{i(\omega+\omega')t'}}{2\pi}=\delta(\omega+\omega').$$ | ||
| + | |||
| + | Így a feszültség Fourier-transzformált abszolút érték négyzetének várható értéke könnyen belátható, hogy arányos a korrelációs függvény Fourier-transzformáltjával, illetve az időablak szélességével: | ||
| + | |||
| + | $$\langle|(\Delta v(\omega))|^2 \rangle= c(\omega) \int_{-\infty}^{\infty} dt.$$ | ||
| + | |||
| + | |||
| + | Innen könnyen kifejezhető a zaj teljesítménysűrűsége, felhasználva, hogy az a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese. | ||
| + | |||
| + | $$s_V(\omega)=\lim\limits_{T->\infty} \frac{2}{T}\left\langle \abs{\int_{-T/2}^{T/2} dt \Delta V(t)e^{-i\omega t}}^2\right\rangle.$$ | ||
| + | |||
| + | A mérésünk során diszkrét pontokon történik a mintavételezés, így ugyanez a számolás DFT segítségével a következő módon fejezhető ki: | ||
| + | |||
| + | $$s_V(\omega)\approx\frac{2}{N\Delta t}\abs{\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}\Delta t}^2=\frac{2\Delta t}{N}\abs{\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}}^2.$$ | ||
| + | |||
| + | A fentiekben sikerült megállapítanunk, hogy a vizsgált $\Delta V(t)$ jel Fourier-transzformáltjából hogyan számolható a zaj spektrális sűrűsége. Azonban ennél a számolásnál nem vettünk figyelembe ablakfüggvényt, vagy fogalmazhatunk úgy is, hogy téglalap ablakkal számoltunk. | ||
| + | |||
| + | Nézzük meg, hogy egy tetszőleges ablakfüggvény esetén hogyan származtatható a zajsűrűség. Sajnos tetszőleges spektrumú zajra és tetszőleges ablakfüggvényre általános összefüggés nem adható, viszont ha $\Delta V(t)$ fehér zaj, akkor tetszőleges ablakfüggvényre egyszerűen számolható a konverziós faktor. | ||
| + | |||
| + | Az ablakfüggvénnyel szorzott jel Fourier-transzformáltja: | ||
| + | |||
| + | $$\Delta v_W(\omega)=\int_{-\infty}^{\infty}dt\Delta V(t)W(t)e^{-i\omega t}.$$ | ||
| + | |||
| + | Vizsgáljuk meg ezen Fourier-transzformált abszolút érték négyzetének várható értékét, ekkor a következőt kapjuk: | ||
| + | |||
| + | $$\langle|\Delta v(\omega)|^2\rangle=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}dtdt'W(t)W(t')\langle\Delta V(t)\Delta V(t')\rangle e^{-i\omega t}e^{-i\omega t'}.$$ | ||
| + | |||
| + | A fehér zaj jellegéből következik, hogy: | ||
| + | |||
| + | $$\langle\Delta V(t)\Delta V(t')\rangle=C(t-t')=\frac{s_0}{2}\delta(t-t').$$ | ||
| + | |||
| + | Így a Fourier-transzformált abszolút érték négyzetének várható értéke a következőképpen egyszerűsödik: | ||
| + | |||
| + | $$\langle|\Delta v_W(\omega)|^2\rangle=\frac{s_0}{2}\int_{-\infty}^{\infty}W^2(t)dt.$$ | ||
| + | |||
| + | Azaz a spektrális sűrűség számolása: | ||
| + | |||
| + | $$s_0=\frac{2\langle|v_W(\omega)|^2\rangle}{\int_{-\infty}^{\infty}W^2(t)dt}.$$ | ||
| + | |||
| + | A feszültségzaj spektrális sűrűsége egy normálási faktor erejéig egyenlő a mért feszültségpontok diszkrét Fourier-transzformáltjának abszolútérték-négyzetének kétszeresével. A normálási faktor az ablakfüggvény négyzetének a mérési időablakra vett integrálja. Láttuk, hogy ez téglalap ablakkal számolva $T$. Most vizsgáljuk meg a zajméréshez leggyakrabban használt Hanning-ablakot, melynek ablakfüggvénye: | ||
| + | |||
| + | $$W(t)=2\sin^2\left(\frac{t\pi}{T}\right).$$ | ||
| + | |||
| + | A zajsűrűség Hanning-ablakot használva: | ||
| + | |||
| + | $$s_0=\frac{3\langle|v_W(\omega)|^2\rangle}{4T}.$$ | ||
| + | |||
| + | Diszkrét mérési pontok esetén a következőképpen módosul a kifejezés: | ||
| + | |||
| + | $$s_0\approx\dfrac{2}{\sum_{n=0}^{N-1}W^2(n\Delta t)\Delta t}\abs{\sum_{n=0}^{N-1}W(n\Delta t) V(N\Delta t)e^{-i\omega n\Delta t}\Delta t}^2.$$ | ||
| + | |||
| + | Hanning-ablakkal számolva: | ||
| + | |||
| + | $$s_0\approx\frac{3\Delta t}{4N}\abs{\sum_{n=0}^{N-1}W(n\Delta t)\Delta V(n\Delta t)e^{-i\omega n\Delta t}}^2.$$ | ||
| + | |||
| + | Így frekvenciafüggetlen zajsűrűségek esetén sikerült meghatározni, hogy a mérési pontokból miképpen számolható ki a zaj spektrális sűrűsége. | ||
A lap 2018. május 16., 20:22-kori változata
Tartalomjegyzék[elrejtés] |
Spektrumanalízis
Fourier-transzformáció
Egy időben változó jel spektrumát a Fourier-transzformáció segítségével ismerhetjük meg.
![\[f(\omega)=\int_{-\infty}^{\infty}F(t)e^{-i\omega t}dt.\]](/images/math/8/5/e/85ef324eb4aa203303778f249b1a850f.png)
Azonban mivel a mérést véges időintervallumban végezzük a spektrum felbontása nem tökéletes. A véges ideig mért jel spektrumára gyakorlatilag úgy tekinthetünk, mintha az a T ideig mért jel periodikus kiterjesztésének a spektruma lenne. Ha a mért jelünk a T időablakban nem periodikus, akkor a periodikusan kiterjesztett jel az időablak határain ugrásokat mutathat, melyek miatt fals nagyfrekvenciás komponensek jelennek meg a spektrumban. Ezen probléma kiküszöbölésére olyan ablakfüggvények használatára van szükség, amelyek a mérési intervallum szélén eltűnnek. A Fourier-transzformációt tehát a vizsgált jel és az ablakfüggvény szorzatán végezzük
![\[f_W(\omega)=\int_{-\infty}^{\infty}W(t)F(t)e^{-i\omega t}dt,\]](/images/math/3/5/8/358e08414d5fd63a56b0bd3f383c0404.png)
ahol 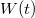 súlyfüggvény egy T időablakon kívül zérus.
súlyfüggvény egy T időablakon kívül zérus.
Két függvény szorzata a Fourier-térben a függvények Fourier-transzfor-máltjának konvolúciójával egyezik meg:
![\[f_W(\omega)=\int_{-\infty}^{\infty}f(\omega')w(\omega-\omega')\frac{d\omega'}{2\pi},\]](/images/math/3/b/b/3bbabc3324c3fcc7a2837a36d2369ce3.png)
azaz a spektrum  frekvenciájához az ablakfüggvény bekever jelet az
frekvenciájához az ablakfüggvény bekever jelet az 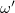 frekvenciából is. Ezt a jelenséget spektrális szivárgásnak nevezzük.
frekvenciából is. Ezt a jelenséget spektrális szivárgásnak nevezzük.
DFT, FFT
A gyakorlati spektrumanalizáláshoz nem csak a véges időintervallumban végzett mérést kell figyelembe venni, hanem azt is, hogy a mért jelet nem folytonosan, hanem diszkrét pontokon mintavételezzük.
Az ablakfüggvénnyel szorzott jel integrálját ennek megfelelően egy diszkrét összeggel közelítjük:
![\[f_W(\omega)=\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t,\]](/images/math/8/1/e/81e072541760e95c8c13a9926ef052ec.png)
ahol  a két diszkrét mintavételezés között eltelt idő (a mérési idő
a két diszkrét mintavételezés között eltelt idő (a mérési idő 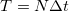 ). A diszkrét Fourier-transzformáció (DFT) tehát a diszkrét pontokon felvett függvény spektrumát adja meg.A Nyquist-Shannon mintavételezési törvény értelmében
). A diszkrét Fourier-transzformáció (DFT) tehát a diszkrét pontokon felvett függvény spektrumát adja meg.A Nyquist-Shannon mintavételezési törvény értelmében  mintavételezési idővel legfeljebb
mintavételezési idővel legfeljebb 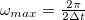 maximális frekvenciáig lehetséges a jel rekonstrukciója.
maximális frekvenciáig lehetséges a jel rekonstrukciója.
A fenti mennyiség abszolútérték négyzete pedig nem más, mint a mért jel teljesítményspektruma (Power Spectrum):
\[PS\abs{\sum_{n=0}^{N-1}W(n\Delta t) V(N\Delta t)e^{-i\omega n\Delta t}\Delta t}^2,\]
Nem csak a mintavételezés történik diszkrét időnként, hanem a DFT kiszámítása is diszkrét 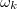 értéken valósul meg. A diszkrét Fourier-transzformáció műveletigénye egyszerű "brute force" eljárással N frekvencia pont esetén
értéken valósul meg. A diszkrét Fourier-transzformáció műveletigénye egyszerű "brute force" eljárással N frekvencia pont esetén 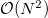 műveletet igényel. Ez rendkívül időigényes, ezért egy más számítási algoritmust használnak a szoftverek a jel feldolgozásához. Ez a gyors Fourier-transzformáció (FFT), amelynek működési alapelve, hogy a mintát kettéválasztja páros és páratlan pontokra, így az N pontos DFT két N/2 pontos DFT-re bomlik. Ezt követően ezeket tovább felezi, és azokat is tovább, stb. Ehhez természetesen szükséges, hogy a mérési pontok száma kettő hatványa legyen. Könnyen belátható, hogy ennek az algoritmusnak a műveletigénye
műveletet igényel. Ez rendkívül időigényes, ezért egy más számítási algoritmust használnak a szoftverek a jel feldolgozásához. Ez a gyors Fourier-transzformáció (FFT), amelynek működési alapelve, hogy a mintát kettéválasztja páros és páratlan pontokra, így az N pontos DFT két N/2 pontos DFT-re bomlik. Ezt követően ezeket tovább felezi, és azokat is tovább, stb. Ehhez természetesen szükséges, hogy a mérési pontok száma kettő hatványa legyen. Könnyen belátható, hogy ennek az algoritmusnak a műveletigénye 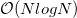 nagyságrendű. Az FFT algoritmus az
nagyságrendű. Az FFT algoritmus az 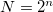 adatpontból álló jel Fourier-spektrumát
adatpontból álló jel Fourier-spektrumát 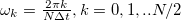 diszkrét körfrekvenciapontokon adja meg.
diszkrét körfrekvenciapontokon adja meg.
Most a DFT definiálását követően megvizsgálhatjuk az ablakfüggvények különböző tulajdonságát. Tételezzük fel, hogy egy egykomponensű  jelet vizsgálunk. Könnyen belátható, hogy ha
jelet vizsgálunk. Könnyen belátható, hogy ha 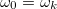
 bármelyik értékére, akkor a spektrális szivárgás nulla lesz. Ez pontosan annak felel meg, amikor a jelünk a T időablakban periodikus. Azonban az esetek többségében értelemszerűen ez nem teljesül. Ekkor a spektrális szivárgáson kívül romlik a jel frekvenciafelbontása és amplitúdópontossága is. Ez előbbi a centrális csúcs keskenységével jellemezhető, míg az utóbbinál éppen ellenkezőleg arra van szükség, hogy megfelelően lapos legyen az
bármelyik értékére, akkor a spektrális szivárgás nulla lesz. Ez pontosan annak felel meg, amikor a jelünk a T időablakban periodikus. Azonban az esetek többségében értelemszerűen ez nem teljesül. Ekkor a spektrális szivárgáson kívül romlik a jel frekvenciafelbontása és amplitúdópontossága is. Ez előbbi a centrális csúcs keskenységével jellemezhető, míg az utóbbinál éppen ellenkezőleg arra van szükség, hogy megfelelően lapos legyen az 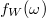 jelünk
jelünk  környékén.
környékén.
A zaj definíciója
Egy $V(t)$ időben fluktuáló zaj jellegű (azaz széles frekvenciaspektrumú) jelet egy $f_0$ középfrekvencia körüli $\Delta f$ szélességű sávszűrűn keresztül vizsgálva azt találjuk, hogy a szűrt jel szórásnégyzete arányos a frekvenciatartomány $\Delta f$ szélességével, az arányossági tényező a feszültségzaj spektrális sűrűsége (spectral density of noise), azaz a teljesítmény spektrális sűrűsége (Power Spectrum Density - PSD):
$$\left\langle (\Delta V(t|f_0,\Delta f))^2 \right\rangle=s_V(f_0)\Delta f.$$
Ez a zaj kísérleti definíciója. A feszültség szórásnégyzete a zajsűrűség teljes frekvenciatartományra vett integráljával egyenlő.
$$\langle(\Delta V(t))^2 \rangle=\int_{0}^{\infty} df s_V(f).$$
Ez a képlet közvetlenül is használható a zajspektrum kísérleti meghatározásához, azonban emellett jó kiindulópontként szolgál más fizikai mennyiségekkel való kapcsolatának vizsgálatára is. Érdemes megvizsgálni a zajsűrűség és a feszültség korrelációs függvény kapcsolatát. Ez utóbbi a következőképpen definiálható:
$$C(\Delta t)=\langle\Delta V(t)\cdotp\Delta V(t+\Delta t) \rangle=\lim\limits_{T\rightarrow\infty}\frac{1}{T}\int_{0}^{T}dt\Delta V(t)\cdotp\Delta V(t+\Delta t).$$
Könnyen belátható, hogy a korrelációs függvény $\Delta t=0$-ban megegyezik a feszültség szórásnégyzetével.
$$C(0)=\langle(\Delta V(t))^2 \rangle.$$ Most fejezzük ki a korrelációs függvényt a Fourier-transzformáltja segítségével: $$\C(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega e^{i\omega t}c(\omega).$$
Ez alapján a feszültség szórásnégyzete:
$$\langle(\Delta V(t))^2 \rangle=C(0)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega c(\omega)=\frac{1}{\pi}\int_{0}^{\infty}d\omega c(\omega),$$
mivel $c(\omega)=c(-\omega)$. Másrészt a (\ref{eq:zajdef2})-as egyenletből következik:
$$\langle(\Delta V(t))^2 \rangle=\frac{1}{2\pi} \int_{0}^{\infty} d\omega s_V(\omega).$$
Az utóbbi két egyenletből látható, hogy a zaj teljesítménysűrűsége a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese.
Sikerült kapcsolatot teremteni a zajsűrűség és a feszültség korrelációs függvény között. Most vizsgáljuk meg a feszültség korrelációs függvény és a feszültség mint mérhető fizikai mennyiségek kapcsolatát. A feszültség átlagtól való eltérésének ($\Delta V(t)=V(t)-\langle V(t)\rangle $) a Fourier-transzformáltja szerint:
$$\Delta v(\omega)= \int_{-\infty}^{\infty} dt \Delta V(t)e^{-i\omega t}.$$
Vizsgáljuk ezen Fourier-transzformált abszolút érték négyzetének várható értékét:
$$\langle|(\Delta v(\omega))|^2 \rangle= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} dt' dt \langle\Delta V(t)\Delta V(t') \rangle e^{-i\omega t} e^{i\omega t'}.$$
Az egyenlet jobb oldalán látható korrelációs függvény kifejezhető a következőképpen:
$$ \langle\Delta V(t)\Delta V(t')\rangle=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega'c(\omega')e^{i\omega'(t-t')}.$$
Továbbá az exponenciális tagokat átcsoportosítva a következő tag integrálja egy Dirac-deltát ad:
$$\int_{-\infty}^{\infty}dt'\frac{e^{i(\omega+\omega')t'}}{2\pi}=\delta(\omega+\omega').$$
Így a feszültség Fourier-transzformált abszolút érték négyzetének várható értéke könnyen belátható, hogy arányos a korrelációs függvény Fourier-transzformáltjával, illetve az időablak szélességével:
$$\langle|(\Delta v(\omega))|^2 \rangle= c(\omega) \int_{-\infty}^{\infty} dt.$$
Innen könnyen kifejezhető a zaj teljesítménysűrűsége, felhasználva, hogy az a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese.
$$s_V(\omega)=\lim\limits_{T->\infty} \frac{2}{T}\left\langle \abs{\int_{-T/2}^{T/2} dt \Delta V(t)e^{-i\omega t}}^2\right\rangle.$$
A mérésünk során diszkrét pontokon történik a mintavételezés, így ugyanez a számolás DFT segítségével a következő módon fejezhető ki:
$$s_V(\omega)\approx\frac{2}{N\Delta t}\abs{\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}\Delta t}^2=\frac{2\Delta t}{N}\abs{\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}}^2.$$
A fentiekben sikerült megállapítanunk, hogy a vizsgált $\Delta V(t)$ jel Fourier-transzformáltjából hogyan számolható a zaj spektrális sűrűsége. Azonban ennél a számolásnál nem vettünk figyelembe ablakfüggvényt, vagy fogalmazhatunk úgy is, hogy téglalap ablakkal számoltunk.
Nézzük meg, hogy egy tetszőleges ablakfüggvény esetén hogyan származtatható a zajsűrűség. Sajnos tetszőleges spektrumú zajra és tetszőleges ablakfüggvényre általános összefüggés nem adható, viszont ha $\Delta V(t)$ fehér zaj, akkor tetszőleges ablakfüggvényre egyszerűen számolható a konverziós faktor.
Az ablakfüggvénnyel szorzott jel Fourier-transzformáltja:
$$\Delta v_W(\omega)=\int_{-\infty}^{\infty}dt\Delta V(t)W(t)e^{-i\omega t}.$$
Vizsgáljuk meg ezen Fourier-transzformált abszolút érték négyzetének várható értékét, ekkor a következőt kapjuk:
$$\langle|\Delta v(\omega)|^2\rangle=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}dtdt'W(t)W(t')\langle\Delta V(t)\Delta V(t')\rangle e^{-i\omega t}e^{-i\omega t'}.$$
A fehér zaj jellegéből következik, hogy:
$$\langle\Delta V(t)\Delta V(t')\rangle=C(t-t')=\frac{s_0}{2}\delta(t-t').$$
Így a Fourier-transzformált abszolút érték négyzetének várható értéke a következőképpen egyszerűsödik:
$$\langle|\Delta v_W(\omega)|^2\rangle=\frac{s_0}{2}\int_{-\infty}^{\infty}W^2(t)dt.$$
Azaz a spektrális sűrűség számolása:
$$s_0=\frac{2\langle|v_W(\omega)|^2\rangle}{\int_{-\infty}^{\infty}W^2(t)dt}.$$
A feszültségzaj spektrális sűrűsége egy normálási faktor erejéig egyenlő a mért feszültségpontok diszkrét Fourier-transzformáltjának abszolútérték-négyzetének kétszeresével. A normálási faktor az ablakfüggvény négyzetének a mérési időablakra vett integrálja. Láttuk, hogy ez téglalap ablakkal számolva $T$. Most vizsgáljuk meg a zajméréshez leggyakrabban használt Hanning-ablakot, melynek ablakfüggvénye:
$$W(t)=2\sin^2\left(\frac{t\pi}{T}\right).$$
A zajsűrűség Hanning-ablakot használva:
$$s_0=\frac{3\langle|v_W(\omega)|^2\rangle}{4T}.$$
Diszkrét mérési pontok esetén a következőképpen módosul a kifejezés:
$$s_0\approx\dfrac{2}{\sum_{n=0}^{N-1}W^2(n\Delta t)\Delta t}\abs{\sum_{n=0}^{N-1}W(n\Delta t) V(N\Delta t)e^{-i\omega n\Delta t}\Delta t}^2.$$
Hanning-ablakkal számolva:
$$s_0\approx\frac{3\Delta t}{4N}\abs{\sum_{n=0}^{N-1}W(n\Delta t)\Delta V(n\Delta t)e^{-i\omega n\Delta t}}^2.$$
Így frekvenciafüggetlen zajsűrűségek esetén sikerült meghatározni, hogy a mérési pontokból miképpen számolható ki a zaj spektrális sűrűsége.