„Poisson zaj szerkesztőlap” változatai közötti eltérés
(Új oldal, tartalma: „===Poisson zaj=== A Poisson-zaj az elektronok diszkrét töltéséből fakadó áramzajnak, azaz a sörétzaj egy speciális fajtája. A Poisson-zaj specialitását az …”) |
(→Poisson zaj) |
||
| 1. sor: | 1. sor: | ||
===Poisson zaj=== | ===Poisson zaj=== | ||
| + | <wlatex> | ||
A Poisson-zaj az elektronok diszkrét töltéséből fakadó áramzajnak, azaz a sörétzaj egy speciális fajtája. A Poisson-zaj specialitását az egymástól független elektronok detektálása jelenti. Az elnevezése is innen származik, hiszen ahogyan a klasszikus példában a véletlen időközönként elsütött puskagolyók, úgy az egymástól függetlenül kilépő elektronok száma is Poisson-eloszlást mutat. A Poisson-eloszlás sörétzaj szempontjából fontos tulajdonsága, hogy a várható értéke megegyezik a szórásnégyzetével: | A Poisson-zaj az elektronok diszkrét töltéséből fakadó áramzajnak, azaz a sörétzaj egy speciális fajtája. A Poisson-zaj specialitását az egymástól független elektronok detektálása jelenti. Az elnevezése is innen származik, hiszen ahogyan a klasszikus példában a véletlen időközönként elsütött puskagolyók, úgy az egymástól függetlenül kilépő elektronok száma is Poisson-eloszlást mutat. A Poisson-eloszlás sörétzaj szempontjából fontos tulajdonsága, hogy a várható értéke megegyezik a szórásnégyzetével: | ||
| 47. sor: | 48. sor: | ||
$$s_I(f)=2e\langle I\rangle.$$ | $$s_I(f)=2e\langle I\rangle.$$ | ||
| + | </wlatex> | ||
A lap jelenlegi, 2018. május 16., 20:18-kori változata
Poisson zaj
A Poisson-zaj az elektronok diszkrét töltéséből fakadó áramzajnak, azaz a sörétzaj egy speciális fajtája. A Poisson-zaj specialitását az egymástól független elektronok detektálása jelenti. Az elnevezése is innen származik, hiszen ahogyan a klasszikus példában a véletlen időközönként elsütött puskagolyók, úgy az egymástól függetlenül kilépő elektronok száma is Poisson-eloszlást mutat. A Poisson-eloszlás sörétzaj szempontjából fontos tulajdonsága, hogy a várható értéke megegyezik a szórásnégyzetével:
![\[\langle N\rangle=\langle (\Delta N)^2\rangle.\]](/images/math/0/c/b/0cbf76e8a53c85f26d6b4cbeaafb2b77.png)
Tegyük fel, hogy 
idő alatt átlagosan N elektron lép ki az egyik elektródából. Ekkor az áram várható értéke a következőképpen definiálható:
![\[\langle I\rangle=\langle N\rangle\frac{e}{\Delta t}.\]](/images/math/4/3/1/43134253ea237625df6026d88d1889a6.png)
Az áram szórásnégyzete pedig felhasználva a várható érték és szórásnégyzet közötti egyenlőséget:
![\[\langle (\Delta I)^2\rangle=\langle (\Delta N)^2\rangle\left(\dfrac{e}{\Delta t}\right)^2=\langle I\rangle\frac{e}{\Delta t}.\]](/images/math/9/e/5/9e543806163d27007b6da7d9ad38faa8.png)
Ebben az esetben azonban a nem a fentebb definiált két diszkrét mintavételezés között eltelt időt jelenti, hanem azt az időintervallumot, amelyen belül az áram várható értéke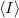 
, illetve szórásnégyzete 
.
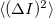Határozzuk meg ebben az időintervallumban az átlagos áramot. Ehhez a jelünket konvolváljuk össze egy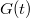 
függvénnyel, amely egyenlő 
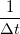-vel, ha 
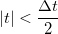, egyébként nulla.
![\[I_{out}(t)=\int_{-\infty}^{\infty}dt'I_{in}(t')G(t-t')=\frac{1}{\Delta t}\int_{t-\frac{\Delta t}{2}}^{t+\frac{\Delta t}{2}}dt'I_{in}(t').\]](/images/math/f/d/d/fdda2738e77acc0eb16abe5aa0d08a3d.png)
A konvolúció Fourier-transzformáltja a Fourier-transzformáltak szorzatával egyenlő:
![\[i_{out}(\omega)=i_{in}(\omega)g(\omega).\]](/images/math/8/2/9/829367a8b41b6331e7bc923cc438ff6e.png)
Ez az összefüggés azt sejteti, hogy a konvolváló függvény szűrőként viselkedik. Mivel a zaj az áram Fourier-transzformáltjának négyzetével arányos az áramzajok aránya a szűrő karakterisztika Fourier-transzformáltjának négyzete lesz:
![\[s_{out}(\omega)=s_{in}(\omega)g^2(\omega).\]](/images/math/7/5/9/759ca2234c0102cf091504ed2482f1c8.png)
Vizsgáljuk meg a szűrő karakterisztikáját:
![\[g(\omega)=\int_{-\infty}^{\infty}dtg(t)e^{-i\omega t}=\frac{1}{\Delta t}\int_{-\frac{\Delta t}{2}}^{+\frac{\Delta t}{2}}dte^{-i\omega t}=\frac{2}{\omega \Delta t}sin\left(\frac{\omega \Delta t}{2}\right).\]](/images/math/2/6/9/269f158eea7317a97e5628f40d665bef.png)
A továbbiakhoz bevezetjük az ekvivalens zaj sávszélesség (Equivalent Noise Bandwidth, ENBW) fogalmát. Az ENBW az a sávszélesség, amelyen fehér zajt feltételezve ugyanakkorának adódik az áram szórásnégyzete, mint a szűrőnkön mérve.
![\[\langle (\Delta I)^2\rangle=\frac{1}{2\pi}\int_{0}^{\infty}d\omega s_{out}(\omega)=\frac{s_0}{\pi \Delta t}\int_{0}^{\infty}\frac{sin^2(x)}{x^2}=\frac{s_0}{2\Delta t}=s_0f_{max}.\]](/images/math/c/a/2/ca22cb4ebe7355290d5225c1e22fd173.png)
Azaz az ekvivalens zaj sávszélesség:
![\[ENBW=\frac{1}{2\Delta t}.\]](/images/math/7/c/e/7ce1c947eb5c347f8259226055c573ec.png)
Ez az összefüggés érezhetően összecseng a Nquist-Shannon mintavételezési törvénnyel. Ha egy időablakra átlagolunk egy jelet, az a konvolúció egy olyan szűrőként viselkedik a frekvenciatérben, melyen keresztül fehér zajt mérve az áram szórásnégyzet egyenlő lesz egy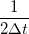 
tökéletes sávszűrőn mért szórásnégyzettel.
Most vizsgáljuk az áram szórásnégyzetét:
![\[\langle (\Delta I)^2\rangle=\langle I\rangle\dfrac{e}{\Delta t}=\int_{0}^{\infty}s_I(f)g(f)df=\int_{0}^{\frac{1}{2\Delta t}}s_I(f)df.\]](/images/math/c/2/0/c20ebbde3fd6c7b498184f399cf0c8ab.png)
Ez bármely szélességű átlagolási időre csak akkor teljesülhet, ha a zajsűrűség független a frekvenciától, értéke pedig:
![\[s_I(f)=2e\langle I\rangle.\]](/images/math/0/b/7/0b7c201ad4cc0af42ed36530052db89f.png)
