„Termoelektromos jelenségek” változatai közötti eltérés

A Fizipedia wikiből
(→‎Kapcsolat a makroszkopikus skálán tapasztalható termoelektromos jelenségekkel)
 
(egy szerkesztő 39 közbeeső változata nincs mutatva)
1. sor: 1. sor:
 +
__TOC__
 
<wlatex>
 
<wlatex>
 +
A [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás|Landauer-formula]] tárgyalásakor láttuk, hogy egy elektródából egy egycsatornás nanovezetékbe folyó áram az elektróda Fermi-függvényének energia szerinti integrálja szerint származtatható:
 +
$$\frac{2}{L} \sum (-e) \cdot v_k \cdot f(\varepsilon_k) =  -\frac{2}{h}\int e\cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I.$$
 +
Ha egy $\mathcal{T}$ transzmissziós valószínűségű szórócentrumot tartalmazó egycsatornás nanovezeték elektródái közé $V$ feszültséget kapcsolunk, a nanovezetékben
 +
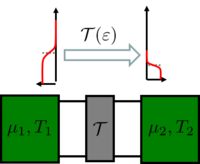
$$I=\frac{2 e}{h} \cdot \int \mathcal{T}\cdot [f_1(\varepsilon)-f_2(\varepsilon)]\mathrm{d}\varepsilon$$ áram folyik, mely alapján $G=(2e^2/h)\cdot\mathcal{T}$ vezetőképességet kapunk. A következőkben azt vizsgáljuk meg, hogy mi történik, ha elektródáknak nem csak a kémiai potenciálja tér el, hanem a hőmérsékletük is különböző lehet (1. ábra).
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| align="center"|[[Fájl:Termoelectric1.png|közép|200px]]
 +
|-
 +
| align="center"|1. ábra. ''Különböző kémiai potenciálú és hőmérsékletű elektródák közötti $\mathcal{T}$ átmeneti valószínűségű szórócentrummal rendelkező egycsatornás nanovezeték elektromos és hőtranszport tulajdonságaira vagyunk kíváncsiak.''
 +
|}
 +
Az elektromos áram továbbra is a fenti képlettel számítható figyelembe véve, hogy az elektródák Fermi-függvényeiben nem csak a kémiai potenciál, hanem a hőmérséklet is eltérő:
 +
$$I=\frac{2 e}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon.$$
 +
A termodinamikából ismert $dQ=dE-\mu dN$ összefüggés alapján hasonlóan származtatható az elektródából a nanovezetékbe folyó $I_Q$ hőáram is:
 +
$$\frac{2}{L} \sum (\varepsilon_k-\mu) \cdot v_k \cdot f(\varepsilon_k) =  \frac{2}{h}\int (\varepsilon-\mu) \cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I_Q,$$
 +
illetve ennek megfelelően a két elektróda között folyó hőáram $\mathcal{T}$ transzmissziós valószínűség esetén: 
 +
$$I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon.$$
 +
Itt fontos megjegyezni, hogy ha az első elektródából/elektródába folyó hőáramot számítjuk, akkor a fenti képletben $(\varepsilon-\mu_1)$ szerepel. Ugyanígy számíthatnánk a 2. elektródából/elektródába folyó hőáramot, ekkor az energia szerinti integrálban $(\varepsilon-\mu_2)$ szorzófaktor szerepelne. Mivel ez a két számolás ugyanakkora hőáramot kell hogy adjon, így a kétféle számolás szükségszerűen ugyanarra az eredményre vezet.
  
 +
A fentiek alapján az elektromos vezetőképesség számolását (Landauer-formula) kiegészítve kiszámolhatjuk az 1. ábrán látható rendszer hővezetőképsségét, illettve Seebeck- és Peltier-együtthatóját is. 
 +
</wlatex>
 +
==Termofeszültség számolása (Seebeck-effektus)==
 +
<wlatex>
 +
Számoljuk ki az 1. ábrán szereplő rendszerre az elektromos áramot a két elektróda eltérő hőmérséklete esetén! Ehhez hívjuk segítségül [[a szilárdtestfizika alapjai]] tárgyban már megismert Sommerfeld-sorfejtést, melynek segítségével egy tetszőleges energiafüggő mennyiség Fermi-fügvénnyel vett szorzatának integrálja közelíthető:
 +
$$\int_{-\infty}^\infty H(\varepsilon)\cdot f(\varepsilon,\mu,T)\,\mathrm{d}\varepsilon = \int_{-\infty}^\mu H(\varepsilon)\,\mathrm{d}\varepsilon + \frac{\pi^2}{6}(kT)^2 H^\prime(\mu) + \mathrm{O} \left(\frac{kT}{\mu}\right)^4.$$
 +
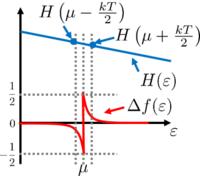
Ezen Sommerfeld-sorfejtés alapját az képezi, hogy az $f(\varepsilon,\mu,T)$ függvényt $f(\varepsilon,\mu,T=0)+\Delta f$ alakban közelítjük, ahol a $\Delta f=f(\varepsilon,\mu,T)-f(\varepsilon,\mu,T=0)$ függvényt a 2. ábra szemlélteti. A Sommerfeld-sorfejtés első tagja a zérus hőmérsékletű Fermi-függvénnyel, azaz $\varepsilon=\mu$-nél zérussá váló lépcsőfügvénnyel vett integrál. A második tag  $(\int H(\varepsilon)\Delta f)$ energiafüggetlen $H$ esetén értelemszerűen zérust ad (lásd 2. ábra), így ezen integrál első rendben $H'(\mu)$-vel arányos. A 2. ábra alpján a $(kT)^2$ függés is indokolható.   
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| align="center"|[[Fájl:Termoelektromos1.jpg|közép|300px]]
+
| align="center"|[[Fájl:Termoelektromos2.png|közép|200px]]
 
|-
 
|-
−
| align="center"|1. ábra. ''Különböző kémiai potenciálú és hőmérsékletű elektródák közötti $\mathcal{T}$ átmeneti valószínűségű szórócentrummal rendelkező egycsatornás nanovezeték elektromos és hőtranszport tulajdonságaira vagyunk kíváncsiak''
+
| align="center"|2. ábra. ''A Sommerfeld-sorfejtés szemléltetése. A $\Delta f$ függvényen látható negatív és pozitív csúcs alatti (egyenlő) terület $kT$ nagyságrendbe esik, így $\int H(\varepsilon)\Delta f\mathrm{d}\varepsilon \sim kT\cdot H(\mu+kT/2) - kT\cdot H(\mu-kT/2)\approx (kT)^2\cdot H'(\mu)$.''
 
|}
 
|}
  
−
$$I=\frac{2 e}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon$$
+
A Sommerfeld-sorfejtés alapján:
−
 
+
$$I=\frac{2 e}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon\approx\frac{2 e}{h} \cdot \int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)\,\mathrm{d}\varepsilon +\frac{2 e}{h}\frac{\pi^2}{6}(kT_1)^2 \mathcal{T}^\prime(\mu_1)-\frac{2 e}{h}\frac{\pi^2}{6}(kT_2)^2 \mathcal{T}^\prime(\mu_2).$$
−
$$\int_{-\infty}^\infty H(\varepsilon)\cdot f(\varepsilon,\mu,T)\,\mathrm{d}\varepsilon = \int_{-\infty}^\mu H(\varepsilon)\,\mathrm{d}\varepsilon + \frac{\pi^2}{6}(kT)^2 H^\prime(\mu) + \mathrm{O} \left(\frac{kT}{\mu}\right)^4$$
+
Ha $\mathcal{T}$ energiafüggését csak lineáris rendben tekintjük, $\mathcal{T}^\prime(\mu_2)=\mathcal{T}^\prime(\mu_1)$, így
−
 
+
$$I\approx \frac{2 e}{h} \cdot eV \cdot\bar{\mathcal{T}}(\varepsilon)+\frac{2 e}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot\mathcal{T}^\prime(\mu),$$
−
$$I\approx\frac{2 e}{h} \cdot \int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)\,\mathrm{d}\varepsilon +\frac{2 e}{h}\frac{\pi^2}{6}(kT_1)^2 \mathcal{T}^\prime(\mu_1)-\frac{2 e}{h}\frac{\pi^2}{6}(kT_2)^2 \mathcal{T}^\prime(\mu_2)\approx \frac{2 e}{h} \cdot eV \cdot\bar{\mathcal{T}}(\varepsilon)+\frac{2 e}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot\mathcal{T}^\prime(\mu)$$
+
ahol $\Delta T=T_1-T_2$, $\ \ T=(T_1+T_2)/2$, $\ \ \mu=(\mu_1+\mu_2)/2$,$\ \ \bar{\mathcal{T}}$ pedig a transzmissziós valószínűség átlaga $\mu_1$ és $\mu_2$ között. Tegyük fel, hogy csak egy végtelen belső ellenállású feszültségmérőt kapcsolunk a két elektróda közé. Ekkor a nanovezetéken értelemszerűen zérus áram folyik. Ha a két elektróda hőmérséklete megegyezik, akkor a Landauer-formulává egyszerűsödő fenti képlet szerint zérus áramnál zérus feszültséget mérünk. Ha viszont a két elektróda hőmérséklete eltér, akkor zérus áram mellett 
−
 
+
−
$$\Delta T=T_1-T_2;\ \ \  T=\frac{T_1+T_2}{2};\ \ \ \mu=\frac{\mu_1+\mu_2}{2}$$
+
−
 
+
 
$$V \big|_{I=0}=\underbrace{-\frac{\pi^2 k^2 T}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon )}{\partial \varepsilon} \bigg|_{\mu}}_{S} \cdot \Delta T$$
 
$$V \big|_{I=0}=\underbrace{-\frac{\pi^2 k^2 T}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon )}{\partial \varepsilon} \bigg|_{\mu}}_{S} \cdot \Delta T$$
 +
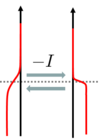
termofeszültség jelentkezik, ahol $S$ a nanovezeték Seebeck-együtthatója. Látszik, hogy nagy termofeszültséget erősen energifaüggő transzmisszió esetén kapunk. Ezt szemléletesen is megérthetjük a 3. ábra segítségével. Először tételezzük fel, hogy a két elektróda kémiai potenciálja még megegyezik. Ekkor a közös kémiai potenciál fölött a melegebb oldalon több betöltött elektronállapot található, így onnan elektronok indulnak el a hidegebb oldal felé. A közös kémiai potenciál alatt viszont a hidegebb oldalon található több betöltött, míg a melegebb oldalon több betöltetlen állapot, így itt a melegebb elektróda felé indulnak meg elektronok. Ha a transzmisszió energiafüggetlen, akkor a kémiai potenciál fölötti és alatti energiáknál elinduló ellentétes előjelű áramkomponensek kiegyenlítik egymást, így összességében nem történik töltésátrendeződés. Ha viszont a transzmisszió erősen energiafüggő, akkor ezen két áramkomponens eltér, és így töltések rendeződnek át az egyik elektródáról a másikra. Ennek köszönhetően felépül egy véges (termo)feszültség a két elektróda között, melynél a nanovezetéken folyó áram zérussá válik.   
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| align="center"|[[Fájl:Termoelektromos3.png|közép|100px]]
 +
|-
 +
| align="center"|3. ábra. ''Seebeck-effektus fizikai alapjának szemléltetése.''
 +
|}
  
−
$$\frac{2}{L} \sum (-e) \cdot v_k \cdot f(\varepsilon_k) =  -\frac{2}{h}\int e\cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I$$
+
</wlatex>
  
 +
==Hővezetőképesség, Wiedemann-Franz törvény==
 +
<wlatex>
 +
Következő lépésként számoljuk ki a két elektróda között folyó hőáramot zérus feszültségkülönbség ($\mu_1=\mu_2=\mu$) és véges hőmérsékletkülönbség $T_1\neq T_2$ esetén. A hőáramra korábban felírt képletre egyszerűen alkalmazható a Sommerfeld-sorfejtés, hiszen a nulladrendű tag a megegyező kémiai potenciálok miatt kiesik: 
 +
$$I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu)\cdot \left[f_1(\varepsilon,\mu,T_1)-f_2(\varepsilon,\mu,T_2)\right]\mathrm{d}\varepsilon\approx\frac{2}{h}\frac{\pi^2}{6}(kT_1)^2\cdot\left[\mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu)\right]'_\mu -\frac{2}{h}\frac{\pi^2}{6}(kT_2)^2\cdot \left[\mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu)\right]'_\mu =\frac{2}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot \mathcal{T}(\mu).$$
 +
A hővezetőképességet $$G_Q=I_Q/ \Delta T$$
 +
képlettel definiálva
 +
$$G_Q=\frac{2}{h}\frac{\pi^2 k^2}{3}\cdot T \cdot \mathcal{T}(\mu)$$
 +
adódik. Ezt összehasonlítva a Landauer-formulából adódó $G=(2e^2/h)\cdot\mathcal{T}$ elektromos vezetőképsséggel
 +
$$\frac{G_Q}{G}=\mathcal{L}\cdot T;\ \ \ \mathcal{L}=\frac{\pi^2k^2}{3e^2}=2.44\times 10^{-8}\,\mathrm{W\,\Omega\,K^{-2}}$$,
 +
ahol $\mathcal{L}$ a csupán természeti állandókat tartalmazó, ún. Lorentz-szám. Azaz látjuk, hogy az elektromos vezetőképesség arányos az elektronok által közvetített hővezetőképességgel, ezt nevezzük Wiedemann-Franz törvénynek. Fontos azonban megjegyezni, hogy hővezetést a fononok is megvalósíthatnak, amit a fentiekben nem vettünk figyelembe.
 +
</wlatex>
  
−
$$\frac{2}{L} \sum \varepsilon_k \cdot v_k \cdot f(\varepsilon_k) = \frac{2}{h}\int \varepsilon \cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I_\varepsilon$$
+
==Peltier-effektus==
−
 
+
<wlatex>
−
$$\frac{2}{L} \sum (\varepsilon_k-\mu) \cdot v_k \cdot f(\varepsilon_k) = \frac{2}{h}\int (\varepsilon-\mu) \cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I_Q$$
+
Végezetül vizsgáljuk meg az inverz Seebeck-effektust, azaz a Peltier effektust, melynél a nanovezetéken keresztül folyatott elektromos áram hatására hőáram indul el zérus hőmérsékletkülönbségnél ($T_1=T_2=T$). Az utóbbi azért fontos, mert véges hőmérsékletkülönbségnél a Peltier-effektusból adódó hőáram mellett a hővezetésből adódó hőáram is megjelenik. A hőáramot ismét a fentiekben megismert formula Sommerfeld-sorfejtésével számoljuk:
−
 
+
$$I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T)-f_2(\varepsilon,\mu_2,T)\right]\mathrm{d}\varepsilon\approx\frac{2}{h} \cdot \underbrace{\int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\,\mathrm{d}\varepsilon}_{\sim (eV)^2} +\frac{2}{h}\frac{\pi^2}{6}(kT)^2\left[\overbrace{\underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime |_{\mu_1}}_{\mathcal{T}(\mu_1)}- \underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime|_{\mu_2}}_{\mathcal{T}^\prime (\mu_2)(\mu_2-\mu_1)+\mathcal{T}(\mu_2)}}^{2\mathcal{T}^\prime (\mu)\cdot eV}\right].$$
−
$$I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon$$
+
A Sommerfeld-sorfejtés első tagja a feszültségben másodrendű járulékot ad, így ezt elhanyaguljuk. A fennmaradó tagok további átrendezésével
−
 
+
−
$$I_Q\approx\frac{2}{h}\frac{\pi^2}{6}(kT_1)^2\cdot\mathcal{T}(\mu) -\frac{2}{h}\frac{\pi^2}{6}(kT_2)^2\cdot \mathcal{T}(\mu) =\frac{2}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot \mathcal{T}(\mu)$$
+
−
 
+
−
$$I=G\cdot V;\ \ \ I_Q=G_Q \cdot \Delta T$$
+
−
 
+
−
$$\frac{G_Q}{G}=\mathcal{L}\cdot T;\ \ \ \mathcal{L}=\frac{\pi^2k^2}{3e^2}=2.44\times 10^{-8}\,\mathrm{W\,\Omega\,K^{-2}}$$
+
−
 
+
−
$$\frac{\kappa}{\sigma}=\mathcal{L}\cdot T$$
+
−
 
+
−
 
+
−
$$I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T)-f_2(\varepsilon,\mu_2,T)\right]\mathrm{d}\varepsilon$$
+
−
 
+
−
 
+
−
$$I_Q\approx\frac{2}{h} \cdot \underbrace{\int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\,\mathrm{d}\varepsilon}_{\sim (eV)^2} +\frac{2}{h}\frac{\pi^2}{6}(kT)^2\left[\overbrace{\underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime |_{\mu_1}}_{\mathcal{T}(\mu_1)}- \underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime|_{\mu_2}}_{\mathcal{T}^\prime (\mu_2)(\mu_2-\mu_1)+\mathcal{T}(\mu_2)}}^{2\mathcal{T}^\prime (\mu)\cdot eV}\right]$$
+
−
 
+
 
$$I_Q\approx \frac{2e}{h}\frac{\pi^2 k^2 T^2}{3}\cdot \frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu \cdot V$$
 
$$I_Q\approx \frac{2e}{h}\frac{\pi^2 k^2 T^2}{3}\cdot \frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu \cdot V$$
−
 
+
adódik. A Peltier-együtthatót a hőáram és az $I= -(2e^2/h)\cdot\mathcal{T}\cdot V$ elektromos áram hányadosaként definiáljuk:
−
$$I= -\frac{2e^2}{h}\mathcal{T}\cdot V$$
+
$$\frac{I_Q}{I}\bigg|_{T_1=T_2}\approx -\frac{\pi^2 k^2 T^2}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu =\Pi=T\cdot S.$$
−
 
+
Ezt az eredményt a Seebeck-együtthatóval összehasonlítva $\Pi=T\cdot S$ adódik, amit Kelvin-féle összefüggésnek nevezünk.
−
$$\frac{I_Q}{I}\bigg|_{T_1=T_2}\approx -\frac{\pi^2 k^2 T^2}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu =\Pi=T\cdot S$$
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
−
 
+
 
</wlatex>
 
</wlatex>

A lap jelenlegi, 2018. május 18., 12:58-kori változata

Tartalomjegyzék


A Landauer-formula tárgyalásakor láttuk, hogy egy elektródából egy egycsatornás nanovezetékbe folyó áram az elektróda Fermi-függvényének energia szerinti integrálja szerint származtatható:

\[\frac{2}{L} \sum (-e) \cdot v_k \cdot f(\varepsilon_k) = -\frac{2}{h}\int e\cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I.\]

Ha egy \setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% transzmissziós valószínűségű szórócentrumot tartalmazó egycsatornás nanovezeték elektródái közé \setbox0\hbox{$V$}% \message{//depth:\the\dp0//}% \box0% feszültséget kapcsolunk, a nanovezetékben

\[I=\frac{2 e}{h} \cdot \int \mathcal{T}\cdot [f_1(\varepsilon)-f_2(\varepsilon)]\mathrm{d}\varepsilon\]
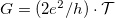áram folyik, mely alapján \setbox0\hbox{$G=(2e^2/h)\cdot\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% vezetőképességet kapunk. A következőkben azt vizsgáljuk meg, hogy mi történik, ha elektródáknak nem csak a kémiai potenciálja tér el, hanem a hőmérsékletük is különböző lehet (1. ábra).
Termoelectric1.png
1. ábra. Különböző kémiai potenciálú és hőmérsékletű elektródák közötti \setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% átmeneti valószínűségű szórócentrummal rendelkező egycsatornás nanovezeték elektromos és hőtranszport tulajdonságaira vagyunk kíváncsiak.

Az elektromos áram továbbra is a fenti képlettel számítható figyelembe véve, hogy az elektródák Fermi-függvényeiben nem csak a kémiai potenciál, hanem a hőmérséklet is eltérő:

\[I=\frac{2 e}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon.\]

A termodinamikából ismert 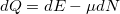\setbox0\hbox{$dQ=dE-\mu dN$}% \message{//depth:\the\dp0//}% \box0% összefüggés alapján hasonlóan származtatható az elektródából a nanovezetékbe folyó 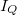\setbox0\hbox{$I_Q$}% \message{//depth:\the\dp0//}% \box0% hőáram is:

\[\frac{2}{L} \sum (\varepsilon_k-\mu) \cdot v_k \cdot f(\varepsilon_k) = \frac{2}{h}\int (\varepsilon-\mu) \cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I_Q,\]

illetve ennek megfelelően a két elektróda között folyó hőáram \setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% transzmissziós valószínűség esetén:

\[I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon.\]

Itt fontos megjegyezni, hogy ha az első elektródából/elektródába folyó hőáramot számítjuk, akkor a fenti képletben 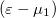\setbox0\hbox{$(\varepsilon-\mu_1)$}% \message{//depth:\the\dp0//}% \box0% szerepel. Ugyanígy számíthatnánk a 2. elektródából/elektródába folyó hőáramot, ekkor az energia szerinti integrálban 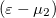\setbox0\hbox{$(\varepsilon-\mu_2)$}% \message{//depth:\the\dp0//}% \box0% szorzófaktor szerepelne. Mivel ez a két számolás ugyanakkora hőáramot kell hogy adjon, így a kétféle számolás szükségszerűen ugyanarra az eredményre vezet.

A fentiek alapján az elektromos vezetőképesség számolását (Landauer-formula) kiegészítve kiszámolhatjuk az 1. ábrán látható rendszer hővezetőképsségét, illettve Seebeck- és Peltier-együtthatóját is.

Termofeszültség számolása (Seebeck-effektus)


Számoljuk ki az 1. ábrán szereplő rendszerre az elektromos áramot a két elektróda eltérő hőmérséklete esetén! Ehhez hívjuk segítségül a szilárdtestfizika alapjai tárgyban már megismert Sommerfeld-sorfejtést, melynek segítségével egy tetszőleges energiafüggő mennyiség Fermi-fügvénnyel vett szorzatának integrálja közelíthető:

\[\int_{-\infty}^\infty H(\varepsilon)\cdot f(\varepsilon,\mu,T)\,\mathrm{d}\varepsilon = \int_{-\infty}^\mu H(\varepsilon)\,\mathrm{d}\varepsilon + \frac{\pi^2}{6}(kT)^2 H^\prime(\mu) + \mathrm{O} \left(\frac{kT}{\mu}\right)^4.\]

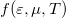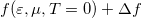Ezen Sommerfeld-sorfejtés alapját az képezi, hogy az \setbox0\hbox{$f(\varepsilon,\mu,T)$}% \message{//depth:\the\dp0//}% \box0% függvényt \setbox0\hbox{$f(\varepsilon,\mu,T=0)+\Delta f$}% \message{//depth:\the\dp0//}% \box0% alakban közelítjük, ahol a 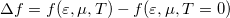\setbox0\hbox{$\Delta f=f(\varepsilon,\mu,T)-f(\varepsilon,\mu,T=0)$}% \message{//depth:\the\dp0//}% \box0% függvényt a 2. ábra szemlélteti. A Sommerfeld-sorfejtés első tagja a zérus hőmérsékletű Fermi-függvénnyel, azaz 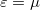\setbox0\hbox{$\varepsilon=\mu$}% \message{//depth:\the\dp0//}% \box0%-nél zérussá váló lépcsőfügvénnyel vett integrál. 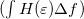A második tag \setbox0\hbox{$(\int H(\varepsilon)\Delta f)$}% \message{//depth:\the\dp0//}% \box0% energiafüggetlen \setbox0\hbox{$H$}% \message{//depth:\the\dp0//}% \box0% esetén értelemszerűen zérust ad (lásd 2. 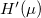ábra), így ezen integrál első rendben \setbox0\hbox{$H'(\mu)$}% \message{//depth:\the\dp0//}% \box0%-vel arányos. A 2. ábra alpján a 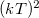\setbox0\hbox{$(kT)^2$}% \message{//depth:\the\dp0//}% \box0% függés is indokolható.

Termoelektromos2.png
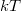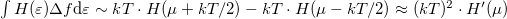2. ábra. A Sommerfeld-sorfejtés szemléltetése. A \setbox0\hbox{$\Delta f$}% \message{//depth:\the\dp0//}% \box0% függvényen látható negatív és pozitív csúcs alatti (egyenlő) terület \setbox0\hbox{$kT$}% \message{//depth:\the\dp0//}% \box0% nagyságrendbe esik, így \setbox0\hbox{$\int H(\varepsilon)\Delta f\mathrm{d}\varepsilon \sim kT\cdot H(\mu+kT/2) - kT\cdot H(\mu-kT/2)\approx (kT)^2\cdot H'(\mu)$}% \message{//depth:\the\dp0//}% \box0%.

A Sommerfeld-sorfejtés alapján:

\[I=\frac{2 e}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon\approx\frac{2 e}{h} \cdot \int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)\,\mathrm{d}\varepsilon +\frac{2 e}{h}\frac{\pi^2}{6}(kT_1)^2 \mathcal{T}^\prime(\mu_1)-\frac{2 e}{h}\frac{\pi^2}{6}(kT_2)^2 \mathcal{T}^\prime(\mu_2).\]

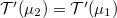Ha \setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% energiafüggését csak lineáris rendben tekintjük, \setbox0\hbox{$\mathcal{T}^\prime(\mu_2)=\mathcal{T}^\prime(\mu_1)$}% \message{//depth:\the\dp0//}% \box0%, így

\[I\approx \frac{2 e}{h} \cdot eV \cdot\bar{\mathcal{T}}(\varepsilon)+\frac{2 e}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot\mathcal{T}^\prime(\mu),\]

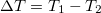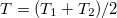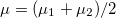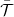ahol \setbox0\hbox{$\Delta T=T_1-T_2$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$\ \ T=(T_1+T_2)/2$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$\ \ \mu=(\mu_1+\mu_2)/2$}% \message{//depth:\the\dp0//}% \box0%,\setbox0\hbox{$\ \ \bar{\mathcal{T}}$}% \message{//depth:\the\dp0//}% \box0% pedig a transzmissziós valószínűség átlaga 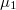\setbox0\hbox{$\mu_1$}% \message{//depth:\the\dp0//}% \box0% és \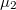setbox0\hbox{$\mu_2$}% \message{//depth:\the\dp0//}% \box0% között. Tegyük fel, hogy csak egy végtelen belső ellenállású feszültségmérőt kapcsolunk a két elektróda közé. Ekkor a nanovezetéken értelemszerűen zérus áram folyik. Ha a két elektróda hőmérséklete megegyezik, akkor a Landauer-formulává egyszerűsödő fenti képlet szerint zérus áramnál zérus feszültséget mérünk. Ha viszont a két elektróda hőmérséklete eltér, akkor zérus áram mellett

\[V \big|_{I=0}=\underbrace{-\frac{\pi^2 k^2 T}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon )}{\partial \varepsilon} \bigg|_{\mu}}_{S} \cdot \Delta T\]

termofeszültség jelentkezik, ahol \setbox0\hbox{$S$}% \message{//depth:\the\dp0//}% \box0% a nanovezeték Seebeck-együtthatója. Látszik, hogy nagy termofeszültséget erősen energifaüggő transzmisszió esetén kapunk. Ezt szemléletesen is megérthetjük a 3. ábra segítségével. Először tételezzük fel, hogy a két elektróda kémiai potenciálja még megegyezik. Ekkor a közös kémiai potenciál fölött a melegebb oldalon több betöltött elektronállapot található, így onnan elektronok indulnak el a hidegebb oldal felé. A közös kémiai potenciál alatt viszont a hidegebb oldalon található több betöltött, míg a melegebb oldalon több betöltetlen állapot, így itt a melegebb elektróda felé indulnak meg elektronok. Ha a transzmisszió energiafüggetlen, akkor a kémiai potenciál fölötti és alatti energiáknál elinduló ellentétes előjelű áramkomponensek kiegyenlítik egymást, így összességében nem történik töltésátrendeződés. Ha viszont a transzmisszió erősen energiafüggő, akkor ezen két áramkomponens eltér, és így töltések rendeződnek át az egyik elektródáról a másikra. Ennek köszönhetően felépül egy véges (termo)feszültség a két elektróda között, melynél a nanovezetéken folyó áram zérussá válik.

Termoelektromos3.png
3. ábra. Seebeck-effektus fizikai alapjának szemléltetése.


Hővezetőképesség, Wiedemann-Franz törvény


Következő lépésként számoljuk ki a két elektróda között folyó hőáramot zérus feszültségkülönbség (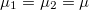\setbox0\hbox{$\mu_1=\mu_2=\mu$}% \message{//depth:\the\dp0//}% \box0%) és véges hőmérsékletkülönbség 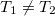\setbox0\hbox{$T_1\neq T_2$}% \message{//depth:\the\dp0//}% \box0% esetén. A hőáramra korábban felírt képletre egyszerűen alkalmazható a Sommerfeld-sorfejtés, hiszen a nulladrendű tag a megegyező kémiai potenciálok miatt kiesik:

\[I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu)\cdot \left[f_1(\varepsilon,\mu,T_1)-f_2(\varepsilon,\mu,T_2)\right]\mathrm{d}\varepsilon\approx\frac{2}{h}\frac{\pi^2}{6}(kT_1)^2\cdot\left[\mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu)\right]'_\mu -\frac{2}{h}\frac{\pi^2}{6}(kT_2)^2\cdot \left[\mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu)\right]'_\mu =\frac{2}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot \mathcal{T}(\mu).\]
A hővezetőképességet
\[G_Q=I_Q/ \Delta T\]

képlettel definiálva

\[G_Q=\frac{2}{h}\frac{\pi^2 k^2}{3}\cdot T \cdot \mathcal{T}(\mu)\]

adódik. Ezt összehasonlítva a Landauer-formulából adódó 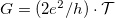\setbox0\hbox{$G=(2e^2/h)\cdot\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0% elektromos vezetőképsséggel

\[\frac{G_Q}{G}=\mathcal{L}\cdot T;\ \ \ \mathcal{L}=\frac{\pi^2k^2}{3e^2}=2.44\times 10^{-8}\,\mathrm{W\,\Omega\,K^{-2}}\]
,

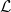ahol \setbox0\hbox{$\mathcal{L}$}% \message{//depth:\the\dp0//}% \box0% a csupán természeti állandókat tartalmazó, ún. Lorentz-szám. Azaz látjuk, hogy az elektromos vezetőképesség arányos az elektronok által közvetített hővezetőképességgel, ezt nevezzük Wiedemann-Franz törvénynek. Fontos azonban megjegyezni, hogy hővezetést a fononok is megvalósíthatnak, amit a fentiekben nem vettünk figyelembe.

Peltier-effektus


Végezetül vizsgáljuk meg az inverz Seebeck-effektust, azaz a Peltier effektust, melynél a nanovezetéken keresztül folyatott elektromos áram hatására hőáram indul el zérus hőmérsékletkülönbségnél (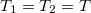\setbox0\hbox{$T_1=T_2=T$}% \message{//depth:\the\dp0//}% \box0%). Az utóbbi azért fontos, mert véges hőmérsékletkülönbségnél a Peltier-effektusból adódó hőáram mellett a hővezetésből adódó hőáram is megjelenik. A hőáramot ismét a fentiekben megismert formula Sommerfeld-sorfejtésével számoljuk:

\[I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T)-f_2(\varepsilon,\mu_2,T)\right]\mathrm{d}\varepsilon\approx\frac{2}{h} \cdot \underbrace{\int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\,\mathrm{d}\varepsilon}_{\sim (eV)^2} +\frac{2}{h}\frac{\pi^2}{6}(kT)^2\left[\overbrace{\underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime |_{\mu_1}}_{\mathcal{T}(\mu_1)}- \underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime|_{\mu_2}}_{\mathcal{T}^\prime (\mu_2)(\mu_2-\mu_1)+\mathcal{T}(\mu_2)}}^{2\mathcal{T}^\prime (\mu)\cdot eV}\right].\]

A Sommerfeld-sorfejtés első tagja a feszültségben másodrendű járulékot ad, így ezt elhanyaguljuk. A fennmaradó tagok további átrendezésével

\[I_Q\approx \frac{2e}{h}\frac{\pi^2 k^2 T^2}{3}\cdot \frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu \cdot V\]

adódik. A Peltier-együtthatót a hőáram és az 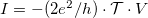\setbox0\hbox{$I= -(2e^2/h)\cdot\mathcal{T}\cdot V$}% \message{//depth:\the\dp0//}% \box0% elektromos áram hányadosaként definiáljuk:

\[\frac{I_Q}{I}\bigg|_{T_1=T_2}\approx -\frac{\pi^2 k^2 T^2}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu =\Pi=T\cdot S.\]

Ezt az eredményt a Seebeck-együtthatóval összehasonlítva 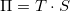\setbox0\hbox{$\Pi=T\cdot S$}% \message{//depth:\the\dp0//}% \box0% adódik, amit Kelvin-féle összefüggésnek nevezünk.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termoelektromos_jelenségek&oldid=22644”