„TLS noise” változatai közötti eltérés
| 1. sor: | 1. sor: | ||
<wlatex> | <wlatex> | ||
Next, we model the temporal fluctuations of the conductance based on the scattering on two level systems in a point contact geometry following the theoretical models summarized in [Fredicikk]. First we emphasize, that a point-contact, i.e. a small, nanometer-scale junction between macroscopic electrodes always acts as a magnifier, i.e. all the scattering processes happening in the vicinity of the junction have highly enhanced influance on the conductance, and therefore it is even possible to observe the temporal conductance fluctuations due to a single two level system [Ralph, Caro, Kaijsers]. On the other hand the processes happening far away from the junction have highly suppressed contribution to the conductance. For the sake of simplicity we model an orifice like point contact, i.e. an orifice with diameter d in an infinite isolating plane between two conducting electrodes (see Figure). Without any scattering in the junction region, this orifice like \emph{ballistic} point contact has a conductance of [Fredicikk] | Next, we model the temporal fluctuations of the conductance based on the scattering on two level systems in a point contact geometry following the theoretical models summarized in [Fredicikk]. First we emphasize, that a point-contact, i.e. a small, nanometer-scale junction between macroscopic electrodes always acts as a magnifier, i.e. all the scattering processes happening in the vicinity of the junction have highly enhanced influance on the conductance, and therefore it is even possible to observe the temporal conductance fluctuations due to a single two level system [Ralph, Caro, Kaijsers]. On the other hand the processes happening far away from the junction have highly suppressed contribution to the conductance. For the sake of simplicity we model an orifice like point contact, i.e. an orifice with diameter d in an infinite isolating plane between two conducting electrodes (see Figure). Without any scattering in the junction region, this orifice like \emph{ballistic} point contact has a conductance of [Fredicikk] | ||
| − | $$G_\textrm{ballistic}=\frac{2e^2}{h}M,\ M=\left(\frac{k_\textrm{F}a}{2}\right)^2$$ | + | $$G_\textrm{ballistic}=\frac{2e^2}{h}M,\ M=\left(\frac{k_\textrm{F}a}{2}\right)^2,$$ |
| − | + | where M is the number of open conductance channels in the contact, $a$ is the radius of the contact and $k_\textrm{F}$ is the Fermi wavenumber. | |
[[file:Ballistic_diffusive.png|500px]] | [[file:Ballistic_diffusive.png|500px]] | ||
</wlatex> | </wlatex> | ||
A lap 2018. november 12., 09:49-kori változata
Next, we model the temporal fluctuations of the conductance based on the scattering on two level systems in a point contact geometry following the theoretical models summarized in [Fredicikk]. First we emphasize, that a point-contact, i.e. a small, nanometer-scale junction between macroscopic electrodes always acts as a magnifier, i.e. all the scattering processes happening in the vicinity of the junction have highly enhanced influance on the conductance, and therefore it is even possible to observe the temporal conductance fluctuations due to a single two level system [Ralph, Caro, Kaijsers]. On the other hand the processes happening far away from the junction have highly suppressed contribution to the conductance. For the sake of simplicity we model an orifice like point contact, i.e. an orifice with diameter d in an infinite isolating plane between two conducting electrodes (see Figure). Without any scattering in the junction region, this orifice like \emph{ballistic} point contact has a conductance of [Fredicikk]
![\[G_\textrm{ballistic}=\frac{2e^2}{h}M,\ M=\left(\frac{k_\textrm{F}a}{2}\right)^2,\]](/images/math/c/9/a/c9a2f7766c9f70a9691b01f14c11e40f.png)
where M is the number of open conductance channels in the contact, 
is the radius of the contact and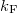 
is the Fermi wavenumber.
