„A zaj mint jel” változatai közötti eltérés
| (5 szerkesztő 39 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | |||
| − | + | [[Kategória:Laborgyakorlat]] | |
| + | [[Kategória:Fizika laboratórium 4.]] | ||
| + | [[Kategória:Szerkesztő:Halbritt]] | ||
| + | |||
| + | Ez a leírás a korábbi egyalkalmas Zaj mint jel című hallgató laborhoz tartozik. Az aktuális, kétalkalmas változat itt érhető el: [[Zaj mint jel]]. | ||
==A mérés célja== | ==A mérés célja== | ||
| − | Különböző mennyiségek mérésénél általában a vizsgált mennyiség várható értékére vagyunk kíváncsiak, és a várható érték körüli fluktuációt zavaró tényezőnek tekintjük. Sok esetben viszont egy fizikai mennyiség | + | Különböző mennyiségek mérésénél általában a vizsgált mennyiség várható értékére vagyunk kíváncsiak, és a várható érték körüli fluktuációt zavaró tényezőnek tekintjük. Sok esetben viszont egy fizikai mennyiség “zaja” több információt hordoz a rendszerről, mint maga a várható érték [1]. A mérési gyakorlaton különböző zajjelenségeket vizsgálunk egy spektrumanalizátor segítségével. Először ellenállások termikus zajának mérése alapján meghatározzuk a Boltzmann-állandó értékét. Ezután egy félvezető dióda zajának méréséből az elektrontöltés értékét határozzuk meg. |
| − | + | __TOC__ | |
==Elméleti összefoglalás== | ==Elméleti összefoglalás== | ||
===A zaj definíciója=== | ===A zaj definíciója=== | ||
| − | + | <wlatex> | |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| 32. sor: | 35. sor: | ||
A fenti definíciók megismerése után érdemes megnézni a mérésnél használt Stanford Research Systems 770 típusú spektrumanalizátor [http://www.thinksrs.com/downloads/PDFs/Catalog/SR760770c.pdf specificációit], melyek szerint a műszer bemeneti zaja a legkisebb méréshatárban $5\mathrm{nV}/\sqrt{\mathrm{Hz}}$. Ez azt jelenti, hogy a műszer bemenetét rövidre zárva a várt zérus feszültség helyett a bemeneti erősítő feszültségzaját látjuk, melynek a szórása $5\mathrm{nV}$ $1\mathrm{Hz}$-es sávszélességű mérés esetén. | A fenti definíciók megismerése után érdemes megnézni a mérésnél használt Stanford Research Systems 770 típusú spektrumanalizátor [http://www.thinksrs.com/downloads/PDFs/Catalog/SR760770c.pdf specificációit], melyek szerint a műszer bemeneti zaja a legkisebb méréshatárban $5\mathrm{nV}/\sqrt{\mathrm{Hz}}$. Ez azt jelenti, hogy a műszer bemenetét rövidre zárva a várt zérus feszültség helyett a bemeneti erősítő feszültségzaját látjuk, melynek a szórása $5\mathrm{nV}$ $1\mathrm{Hz}$-es sávszélességű mérés esetén. | ||
| + | </wlatex> | ||
===''Puskalövések zaja''=== | ===''Puskalövések zaja''=== | ||
| − | + | <wlatex> | |
| − | A zaj fogalma egy klasszikus példával is jól szemléltethető | + | A zaj fogalma egy klasszikus példával is jól szemléltethető. Nézzük meg, hogy mi történik, ha egy puskából véletlenszerűen lövöldözünk úgy, hogy a lövések időpontja egymástól teljesen független. Ha a szomszédos lövések között eltelt átlagos idő $\tau$, akkor $\Delta t$ idő alatt a lövések átlagos száma értelemszerűen $\left< N \right> =\Delta t/\tau$. A tényleges lövésszám azonban nyilvánvalóan fluktuálni fog az átlagérték körül. A szórásnégyzet meghatározásához érdemes kiszámolni a $P_N(\Delta t)$ valószínűséget, azaz annak a valószínűségét, hogy $\Delta t$ idő alatt $N$ lövés dördül. Ha $P_N(\Delta t)$ értékét ismerjük, akkor $P_N(\Delta t+dt)$ értéke a |
$$P_N(\Delta t+dt)=P_{N-1}(\Delta t)\frac{dt}{\tau}+P_N(\Delta t)\left(1-\frac{dt}{\tau}\right)$$ | $$P_N(\Delta t+dt)=P_{N-1}(\Delta t)\frac{dt}{\tau}+P_N(\Delta t)\left(1-\frac{dt}{\tau}\right)$$ | ||
| − | egyenlettel írható fel, azaz a kezdeti $\Delta t$ és az utána következő $dt<<\tau$ idő alatt vagy $N-1$ ill. $1$ vagy $N$ ill. $0$ lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze. | + | egyenlettel írható fel, azaz a kezdeti $\Delta t$ és az utána következő $dt<<\tau$ idő alatt vagy $N-1$, ill. $1$ vagy $N$, ill. $0$ lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze. |
A fenti egyenlet átrendezésével a | A fenti egyenlet átrendezésével a | ||
$$\frac{dP_N(\Delta t)}{dt}=\frac{P_{N-1}(\Delta t)-P_N(\Delta t)}{\tau}$$ | $$\frac{dP_N(\Delta t)}{dt}=\frac{P_{N-1}(\Delta t)-P_N(\Delta t)}{\tau}$$ | ||
differenciálegyenletet kapjuk. Megmutatható, hogy ezen feltételt a | differenciálegyenletet kapjuk. Megmutatható, hogy ezen feltételt a | ||
$$P_N(\Delta t)=\frac{(\Delta t)^N}{\tau^N N!}e^{-\Delta t/\tau}$$ | $$P_N(\Delta t)=\frac{(\Delta t)^N}{\tau^N N!}e^{-\Delta t/\tau}$$ | ||
| − | Poisson eloszlás elégíti ki. A Poisson eloszlás speciális tulajdonsága, hogy a szórásnégyzet megegyezik a várható értékkel, azaz | + | Poisson-eloszlás elégíti ki. A Poisson-eloszlás speciális tulajdonsága, hogy a szórásnégyzet megegyezik a várható értékkel, azaz |
$$\left< (\Delta N)^2 \right>=\left< N \right>=\frac{\Delta t}{\tau}.$$ | $$\left< (\Delta N)^2 \right>=\left< N \right>=\frac{\Delta t}{\tau}.$$ | ||
| + | </wlatex> | ||
===Elektronok sörétzaja=== | ===Elektronok sörétzaja=== | ||
| − | A fenti gondolatmenetet vonatkoztathatjuk elektronokra is ha teljesül az, hogy az elektronok véletlenszerűen, egymástól függetlenül jutnak át az egyik elektródából a másikba. Tegyük fel, hogy mérőrendszerünkkel az elektromos áramot $\Delta t$ időbeli felbontással tudjuk mérni. Egy $\Delta t$ szélességű mintavételezési intervallum alatt $I=Ne/\Delta t$ áramot detektálunk ahol a $\Delta t$ idő alatt áthaladó | + | <wlatex> |
| − | A [http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem | + | A fenti gondolatmenetet vonatkoztathatjuk elektronokra is, ha teljesül az, hogy az elektronok véletlenszerűen, egymástól függetlenül jutnak át az egyik elektródából a másikba. Tegyük fel, hogy mérőrendszerünkkel az elektromos áramot $\Delta t$ időbeli felbontással tudjuk mérni. Egy $\Delta t$ szélességű mintavételezési intervallum alatt $I=Ne/\Delta t$ áramot detektálunk, ahol a $\Delta t$ idő alatt áthaladó elektronok $N$ számának eloszlását a fenti Poisson-eloszlás adja meg. Így a mért áram várható értéke $\left< I \right>=\left< N \right>e/\Delta t$, míg az áram szórásnégyzete $\left< (\Delta I)^2 \right>=\left< (\Delta N)^2 \right>e^2/(\Delta t)^2=\left< N \right>e^2/(\Delta t)^2=\left< I \right>e/\Delta t$. |
| − | $$ | + | A [http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem Nyquist–Shannon mintavételezési törvény] szerint $\Delta t$ időfelbontás esetén a mért jelet $f_{\mathrm{max}}=1/2\Delta t$ maximális frekvenciáig tudjuk rekonstruálni. Ez alapján az áram szórásnégyzete: |
| + | $$\left< (\Delta I)^2 \right>=\int_0^{f_\mathrm{max}}S_I(f)df=2e\left< I \right>\cdot f_\mathrm{max},$$ | ||
| + | azaz: | ||
| + | $$S_I=2e\left< I \right>.$$ | ||
| − | A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt ''sörétzajnak'' szokták nevezni. Fontos megemlíteni, hogy a sörétzaj fehér zaj, azaz a spektrális sűrűség frekvenciafüggetlen. Az előbbiekben levezetett zajformula a sörétzajnak is egyik speciális esetét írja le, az ún. Poisson zajt, mely egymástól független elektronok detektálására vonatkozik. A kvantummechanikából ismert Pauli elv szerint két elektron nem lehet ugyan abban az állapotban, azaz egy adott időpontban nem tudunk két teljesen egyforma állapotú elektront detektálni. Egy | + | A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt ''sörétzajnak'' szokták nevezni. Fontos megemlíteni, hogy a fenti képlet alapján a sörétzaj fehér zaj, azaz a spektrális sűrűség frekvenciafüggetlen. Az előbbiekben levezetett zajformula a sörétzajnak is egyik speciális esetét írja le, az ún. Poisson-zajt, mely egymástól független elektronok detektálására vonatkozik. A kvantummechanikából ismert Pauli-elv szerint két elektron nem lehet ugyan abban az állapotban, azaz egy adott időpontban nem tudunk két teljesen egyforma állapotú elektront detektálni. Egy makroszkopikus vezetőben az elektronok nem egymástól függetlenül, hanem inkább ''sorban egymást követve'' érkeznek az árammérőhöz, így a fenti zajformula nem érvényes. Azonban a Poisson-zaj feltételét megvalósíthatjuk akkor, ha az elektronok útjába egy olyan akadályt helyezünk, melyen véletlenszerűen az elektronoknak csak egy kis része tud keresztüljutni (3a. ábra). |
| − | Az első | + | Az első sörétzajmérést Walter Schottky végezte 1918-ban [2]: híres kísérletében egy vákuumdióda anódáramának zaját vizsgálta. A vákuumdióda felépítését a 3b. ábra szemlélteti. Egy fűtött katódból véletlenszerűen kilépő elektronok a katód és anód közé kapcsolt feszültség hatására eljutnak az anódba, ahol áramot detektálunk. A vákuumdióda ideális eszköz a sörétzaj tanulmányozásához, hiszen az elektronok valóban véletlenül, és egymástól függetlenül emittálódnak, így a mért zajsűrűség és az áram hányadosából az elektrontöltés a Poisson-zaj formulája alapján meghatározható. |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 63. sor: | 71. sor: | ||
|} | |} | ||
| − | Poisson zajt modern elektronikai eszközökben is tapasztalhatunk, például egy diódát alkotó félvezető p-n átmenet is biztosítja az elektronok véletlen és független emisszióját megfelelően kicsi áram esetén. | + | Poisson-zajt modern elektronikai eszközökben is tapasztalhatunk, például egy diódát alkotó félvezető p-n átmenet is biztosítja az elektronok véletlen és független emisszióját megfelelően kicsi áram esetén. |
| − | + | </wlatex> | |
===Termikus zaj=== | ===Termikus zaj=== | ||
| − | + | <wlatex> | |
Az előbbiekben bemutatott sörétzaj egy nemegyensúlyi zaj, melyet csak akkor tapasztalunk, ha a vizsgált áramköri elemen áramot folyatunk keresztül. Zajt azonban egyensúlyi állapotban is tapasztalhatunk pusztán az elektronok termikus fluktuációi miatt. A ''termikus zaj'' megértése komolyabb elméleti hátteret igényel, azonban maga a jelenség egy nagyon egyszerű formulával leírható: egy $R$ elektromos ellenállással rendelkező áramköri elemen | Az előbbiekben bemutatott sörétzaj egy nemegyensúlyi zaj, melyet csak akkor tapasztalunk, ha a vizsgált áramköri elemen áramot folyatunk keresztül. Zajt azonban egyensúlyi állapotban is tapasztalhatunk pusztán az elektronok termikus fluktuációi miatt. A ''termikus zaj'' megértése komolyabb elméleti hátteret igényel, azonban maga a jelenség egy nagyon egyszerű formulával leírható: egy $R$ elektromos ellenállással rendelkező áramköri elemen | ||
$$S_V=4k_B T\cdot R$$ | $$S_V=4k_B T\cdot R$$ | ||
| 72. sor: | 80. sor: | ||
A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától. | A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától. | ||
Ezen jelenség segítségével a $T$ hőmérséklet és az $R$ ellenállás ismeretében a feszültségzaj méréséből a Boltzmann-állandó meghatározható. | Ezen jelenség segítségével a $T$ hőmérséklet és az $R$ ellenállás ismeretében a feszültségzaj méréséből a Boltzmann-állandó meghatározható. | ||
| + | </wlatex> | ||
===Egyéb zajforrások=== | ===Egyéb zajforrások=== | ||
| + | <wlatex> | ||
| + | A termikus zaj és a sörétzaj mellett érdemes megemlékezni az 1/f zajról, mely a zajsűrűség tipikus 1/f-jellegű frekvenciafüggéséről kapta a nevét. Ezen zajtípus számos fizikai folyamatból származhat, például a szennyezők és rácshibák véletlen mozgásából adódó ellenállásfluktuációkból. Az 1/f zaj a sörétzajhoz hasonlóan nemegyensúlyi zaj, a spektrális sűrűség a feszültség növelésével nő. Az 1/f zaj tipikusan alacsony frekvenciás ($<100-1000 \mathrm{Hz}$) méréseknél dominál, míg magasabb frekvenciákon a termikus zaj, illetve bizonyos eszközökben a sörétzaj a legfontosabb zajforrás. | ||
| − | + | Az eddigiekben csak a vizsgált rendszerünk ''belső'' zajáról beszéltünk, azonban zajmérésnél mindig fontos a külső forrásokból adódó elektromágneses zavarokra is gondolni. Egy áramkör kapacitív vagy induktív csatolással könnyen felvesz zajt a környezetből, például az elektromos hálózat 50 Hz-es frekvenciájánál, monitorok képernyőjének frissítési frekvenciájánál, kapcsoló üzemű tápok működési frekvenciájánál, vagy akár rádióállomások, mobiltelefonok sugárzási frekvenciájánál. Ezen zavaró tényezők kiküszöbölésének alapvető módszere a vizsgált áramkör árnyékolása: alacsony jelszintű méréseknél mindig árnyékolt kábeleket, illetve fém dobozba zárt áramköröket érdemes használni. | |
| − | + | </wlatex> | |
| − | Az eddigiekben csak a vizsgált rendszerünk ''belső'' zajáról beszéltünk, azonban zajmérésnél mindig fontos a külső forrásokból adódó elektromágneses zavarokra is gondolni. Egy áramkör kapacitív vagy induktív csatolással könnyen felvesz zajt a környezetből például az elektromos hálózat 50 Hz-es frekvenciájánál, monitorok képernyőjének frissítési frekvenciájánál, kapcsoló üzemű tápok működési frekvenciájánál, vagy akár rádióállomások, mobiltelefonok sugárzási frekvenciájánál. Ezen zavaró tényezők kiküszöbölésének alapvető módszere a vizsgált áramkör árnyékolása: alacsony jelszintű méréseknél mindig árnyékolt kábeleket, illetve fém dobozba zárt áramköröket érdemes használni. | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==Mérési elrendezés== | ==Mérési elrendezés== | ||
===A méréshez használt eszközök=== | ===A méréshez használt eszközök=== | ||
| + | <wlatex> | ||
| + | A méréshez egy Stanford Reserch Systems 770 típusú spektrumanalizátort használunk. A későbbiekben csak a műszer legfontosabb funkcióit ismertetjük, részletes specifikációk és leírás a műszer [http://www.thinksrs.com/downloads/PDFs/Catalog/SR760770c.pdf adatlapjában] és [http://www.thinksrs.com/downloads/PDFs/Manuals/SR770m.pdf használati utasításában] érhető el. A műszer előlapjának fényképe és a kezelőfelülete szintén az említett adatlapban tekinthetők meg. | ||
| − | + | A spektrumanalizátor jele egy saját fejlesztésű szoftverrel (SRS770_beolvasas.exe) számítógépbe beolvasható, illetve fájlba kimenthető. | |
| − | + | ||
| − | A spektrumanalizátor jele egy saját fejlesztésű szoftverrel (SRS770_beolvasas.exe) számítógépbe beolvasható illetve fájlba kimenthető. | + | |
| − | A termikus és a sörétzaj méréséhez egy lezárható | + | A termikus és a sörétzaj méréséhez egy lezárható alumíniumdobozba helyezett panel áll rendelkezésre. A panelen levő csatlakozókba lehet bekötni a termikus zaj méréséhez használt R ellenállásokat és a sörétzaj méréséhez szükséges R1 és R2 ellenállásokat. (4. ábra). A dobozon három BNC csatlakozó és a tápfeszültség bekapcsolására szolgáló kapcsoló található. |
| − | A méréshez különböző áramköri elemek állnak rendelkezésre: ellenállások, | + | A méréshez különböző áramköri elemek állnak rendelkezésre: ellenállások, jumper, kondenzátorok, BNC-BNC toldó, BNC csatlakozós koax kábel. |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | [[Fájl: | + | | [[Fájl:IMG_3432_annot.jpg|közép|300px|]] |
|- | |- | ||
| align="center"|4. ábra | | align="center"|4. ábra | ||
|} | |} | ||
| + | </wlatex> | ||
===A termikus zaj mérésének elve=== | ===A termikus zaj mérésének elve=== | ||
| − | + | <wlatex> | |
| − | A termikus zaj mérésénél a doboz egyik BNC csatlakozójának belső pontja és földpontja közé egy ellenállást kötünk, a BNC csatlakozót pedig egy BNC-BNC toldó segítségével (lásd 4. ábra felső csatlakozó) közvetlenül a spektrumanalizátor ''Signal In (A)'' bemenetére kötjük és ebben az elrendezésben mérjük az ellenállás feszültségzaját. Mivel a mért termikus zaj összemérhető a műszer bemeneti zajával ($\approx 5\mathrm{nV}/\sqrt{\mathrm{Hz}}$) ezért a mért zaj a termikus zaj és a műszer bemeneti zajának összege lesz: | + | A termikus zaj mérésénél a doboz egyik BNC csatlakozójának belső pontja és földpontja közé egy ellenállást kötünk, a BNC csatlakozót pedig egy BNC-BNC toldó segítségével (lásd 4. ábra felső csatlakozó) közvetlenül a spektrumanalizátor ''Signal In (A)'' bemenetére kötjük és ebben az elrendezésben mérjük az ellenállás feszültségzaját. Mivel a mért termikus zaj összemérhető a műszer bemeneti zajával ($\approx 5\mathrm{nV}/\sqrt{\mathrm{Hz}}$), ezért a mért zaj a termikus zaj és a műszer bemeneti zajának összege lesz: |
$$S_V=4k_B T\cdot R + S_0.$$ | $$S_V=4k_B T\cdot R + S_0.$$ | ||
Ha a mérést több ellenálláson is megismételjük akkor az $S_V(R)$ függvény meredekségéből a szobahőmérséklet ismeretében megkapjuk a Boltzmann-állandó értékét. | Ha a mérést több ellenálláson is megismételjük akkor az $S_V(R)$ függvény meredekségéből a szobahőmérséklet ismeretében megkapjuk a Boltzmann-állandó értékét. | ||
| + | </wlatex> | ||
===A sörétzaj mérésének elve=== | ===A sörétzaj mérésének elve=== | ||
| − | + | <wlatex> | |
| − | A sörétzaj mérésekor az 5. ábrán bemutatott kapcsolást érdemes alkalmazni. Tápegységként használjunk egy | + | A sörétzaj mérésekor az 5. ábrán bemutatott kapcsolást érdemes alkalmazni. Tápegységként használjunk egy 9 V-os elemet, így a meghajtó feszültségünk zaja kisebb lesz, mint ha bármilyen elektromos hálózatra kötött tápegységet használnánk. A teleppel kössünk sorba egy nagy ellenállást ($R_1$) és egy félvezető diódát. Diódaként érdemes egy alacsony zajszintű tranzisztort használni úgy, hogy azt az 5. ábra szerint nyitó irányban a bázis és emitter kontaktusokon keresztül kötjük az áramkörbe és a kollektor elektródát nem használjuk. |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 125. sor: | 133. sor: | ||
ahol $R_d$ a dióda differenciális ellenállása a beállított munkapontban, $S_0$ pedig a műszer bemeneti zaja. | ahol $R_d$ a dióda differenciális ellenállása a beállított munkapontban, $S_0$ pedig a műszer bemeneti zaja. | ||
| − | A következő lépés a dióda differenciális ellenállásának a meghatározása. Ehhez a spektrumanalizátor ''Source Out'' kimenetéről egy $R_2$ ellenálláson és egy $C$ kondenzátoron keresztül váltóáramot keverünk a telepből jövő egyenáramhoz, és a spektrumanalizátorral megmérjük a | + | A következő lépés a dióda differenciális ellenállásának (lásd alább) a meghatározása. Ehhez a spektrumanalizátor ''Source Out'' kimenetéről egy $R_2$ ellenálláson és egy $C$ kondenzátoron keresztül váltóáramot keverünk a telepből jövő egyenáramhoz, és a spektrumanalizátorral megmérjük a váltóáramú feszültségesést a meghajtó jellel azonos frekvencián. A spektrumanalizátor kimeneti feszültségszintjét és az $R_2$ ellenállást úgy kell megválasztani, hogy a diódán folyó váltóáram az egyenáramnál lényegesen kisebb legyen. A $C$ kapacitás azt a célt szolgálja, hogy a telepből jövő egyenáramból semennyi ne tudjon a spektrumanalizátor kimenete felé elfolyni. Célszerű $C$ értékét úgy megválasztani, hogy a meghajtó frekvencián vett impedancia lényegesen kisebb legyen $R_2$-nél. Így a differenciális ellenállást |
$R_d=\Delta U_{\mathrm{rms}}/\Delta I_{\mathrm{rms}}$ | $R_d=\Delta U_{\mathrm{rms}}/\Delta I_{\mathrm{rms}}$ | ||
képlet szerint számoljuk, ahol $\Delta I_{\mathrm{rms}}$ a ''Source Out'' kimeneten kiadott váltófeszültség rms értékének (szórásának) és $R_2$ ellenállásnak a hányadosa, $\Delta U_{\mathrm{rms}}$ pedig a diódán mért váltóáramú feszültség rms értéke. | képlet szerint számoljuk, ahol $\Delta I_{\mathrm{rms}}$ a ''Source Out'' kimeneten kiadott váltófeszültség rms értékének (szórásának) és $R_2$ ellenállásnak a hányadosa, $\Delta U_{\mathrm{rms}}$ pedig a diódán mért váltóáramú feszültség rms értéke. | ||
| − | Ha különböző $R_1$ ellenállásokkal megmérjük $S_V$, $\left< I \right>$ és $R_d$ értékét akkor az $S_V(\left< I \right> \cdot R_d^2)$ függvényre egyenest illesztve megkapjuk az elektron töltésének értékét. | + | Ha különböző $R_1$ ellenállásokkal megmérjük $S_V$, $\left< I \right>$ és $R_d$ értékét, akkor az $S_V(\left< I \right> \cdot R_d^2)$ függvényre egyenest illesztve megkapjuk az elektron töltésének értékét. |
| + | </wlatex> | ||
| − | |||
| − | + | ''Differenciális ellenállás:'' A diódára kapcsolt egyenfeszültség egy állandó átfolyó áramot határoz meg, vagyis meghatározza a karakterisztika egy pontját, ezt nevezzük munkapontnak. A munkapontban tudjuk definiálni a dióda egyenáramú ellenállását, ami a rákapcsolt egyenfeszültség és az átfolyó áram hányadosa. A feszültség kis változtatásának (modulálás) hatása az áramra attól függ, hogy hol van a munkapont, hiszen a karakterisztika nemlineáris. A dióda differenciális (dinamikus) ellenállásának az adott munkaponti feszültség kis változását és a kialakuló áramváltozás hányadosát nevezzük. | |
==Az SRS770 spektrumanalizátor használata és beállítása== | ==Az SRS770 spektrumanalizátor használata és beállítása== | ||
| + | <wlatex> | ||
| + | Az SRS770 spektrumanalizátor egy egycsatornás 100 kHz sávszélességű 16 bit felbontású műszer, mely a bemenetén mért jel Fourier-spektrumát határozza meg. A műszer legfontosabb funkciói a MENU gombcsoport segítségével állíthatók. | ||
| − | + | *A '''FREQ''' gomb segítségével lehet a vizsgált frekvenciatartományt beállítani. A ''FREQ'' gomb megnyomása után a képernyő jobb szélén jelennek meg a beállítási lehetőségek, melyeket a képernyő melletti gombokkal érünk el. Számértékeket a forgató gombbal, illetve az ''ENTRY'' gombcsoporttal állíthatunk be. A legfontosabb beállítás a ''Span'', mellyel a vizsgált frekvenciatartomány szélességét állíthatjuk be. A frekvenciatartomány kezdeti vagy középfrekvenciáját a ''Start freq'' vagy ''Center freq'' menüben állíthatjuk. Fontos megjegyezni, hogy ''Span''-ben beállított frekvenciasávot a műszer mindig 400 mérési pontra osztja, így a legnagyobb 100 kHz-es sávszélességnél 100 kHz/400 azaz 250 Hz felbontással tudjuk felvenni a spektrumot. | |
| − | *A ''' | + | *A '''MEAS''' gomb segítségével állítható be, hogy pontosan mit akarunk mérni. Ezen belül a ''Measure'' menüben választhatjuk ki, hogy a jel komplex Fourier transzformáltját (''Spectrum'') vagy a zajsűrűséget (''PSD'', [http://en.wikipedia.org/wiki/Power_spectral_density power spectral density]) akarjuk mérni. Belátható hogy a ''PSD'' a Fourier-transzformált abszolútérték-négyzete megfelelő normálással. A ''Display'' menüben ''Log Mag'' funkciót állítsunk be, a ''Units'' menüben pedig ''Volts RMS'' mértékegységet válasszunk ki. A ''Window'' menüben választható ki az FFT-nél alkalmazott [http://en.wikipedia.org/wiki/Window_function ablakfüggvény], ezt PSD mérésekor ''Hanning'' ablakra állítsuk. |
| − | *A ''' | + | *A '''DISPLAY''' gomb segítségével állíthatjuk be a képernyőn megjelenő ''Marker''-eket. A ''CONTROL/MARKER'' gomb megnyomása után a forgatógombbal állíthatjuk be a ''Marker'' pozícióját. A képernyő tetején leolvasható a ''Marker'' pozíciója és az adott pozíciónál mért érték. ''Marker width=Spot'' beállításnál egy konkrét pontnál olvashatjuk le a spektrumot, míg ''Marker width=Norm/Wide'' és ''Marker Seeks=Mean'' beállításnál pedig az adott ''Marker'' pozíció körüli szélesebb tartományban vett átlagos spektrumot kapjuk meg. |
| − | + | *Az '''INPUT''' gomb megnyomása után ''Input Source=A'', ''Grounding=Ground'', ''Coupling=AC'' beállításokat alkalmazzunk. Az ''Input range'' menüben állíthatjuk be a mérés érzékenységét, ezt mindig az adott mérésnél alkalmazható legérzékenyebb értékre állítsuk. Zajspektrum mérésekor lehetőleg a legérzékenyebb, -60 dBV méréshatárt válasszuk, mely 1 mV-os méréshatárnak felel meg. A képernyő alsó részén mindig láthatjuk az aktuális méréshatár értékét. Ha ez alatt az ''OVERLOAD'' felirat villog, akkor a bemenetet túlvezéreltük, így a mért adatok nem használhatók. | |
| − | + | ||
| − | *Az '''INPUT''' gomb megnyomása után ''Input Source=A'', ''Grounding=Ground'', ''Coupling=AC'' beállításokat alkalmazzunk. Az ''Input range'' menüben állíthatjuk be a mérés érzékenységét, ezt mindig az adott mérésnél alkalmazható legérzékenyebb értékre állítsuk. Zajspektrum mérésekor lehetőleg a legérzékenyebb, - | + | |
*A '''SCALE''' gomb megnyomásával változtathatjuk az ábrázolt adatok skáláját. Az ''X-axis''-t állítsuk ''log'' skálára. Az ''Y/Div'' menü segítségével nagyíthatjuk ki a számunkra érdekes görbeszakaszt y irányban. Automatikus skálát az ''ENTRY/AUTOSCALE'' gombbal állíthatunk be. | *A '''SCALE''' gomb megnyomásával változtathatjuk az ábrázolt adatok skáláját. Az ''X-axis''-t állítsuk ''log'' skálára. Az ''Y/Div'' menü segítségével nagyíthatjuk ki a számunkra érdekes görbeszakaszt y irányban. Automatikus skálát az ''ENTRY/AUTOSCALE'' gombbal állíthatunk be. | ||
| 151. sor: | 159. sor: | ||
*Az '''ANALYZE''' gomb megnyomása után ''None'' beállítást alkalmazzunk. | *Az '''ANALYZE''' gomb megnyomása után ''None'' beállítást alkalmazzunk. | ||
| − | *Az '''AVERAGE''' gomb megnyomása után állíthatjuk be az átlagolás értékét, | + | *Az '''AVERAGE''' gomb megnyomása után állíthatjuk be az átlagolás értékét, célszerű 1000-2000 görbére átlagolni. |
| − | *A '''SOURCE''' gombbal állíthatjuk be a ''Source Out'' kimenetet. Ha nincs szükség meghajtó jelre akkor mindig kapcsoljuk ki a kimenetet. Kimenő jel alkalmazása esetén a ''Configure'' menüben állíthatjuk be a kimenő jel frekvenciáját és | + | *A '''SOURCE''' gombbal állíthatjuk be a ''Source Out'' kimenetet. Ha nincs szükség meghajtó jelre akkor mindig kapcsoljuk ki a kimenetet. Kimenő jel alkalmazása esetén a ''Configure'' menüben állíthatjuk be a kimenő jel frekvenciáját és amplitúdóját. |
| − | *A '''SYSTEM''' menü ''Setup commun'' almenüjében ''Output to= | + | *A '''SYSTEM''' menü ''Setup commun'' almenüjében ''Output to=GPIB''-t válasszunk. Ezen beállítások mellett tudjuk a mért értékeket a számítógép soros portján keresztül beolvasni. |
*A mintavételezést a '''CONTROL/START''' gombbal indíthatjuk. | *A mintavételezést a '''CONTROL/START''' gombbal indíthatjuk. | ||
| + | </wlatex> | ||
==Mérési feladatok== | ==Mérési feladatok== | ||
| − | ===A | + | ===0. A Spektrumanalizátor használatának begyakorlása=== |
| + | Nulladik feladatként ismerkedjünk meg a spektrumanalizátor kezelésével! Az Input A bemenetre csatlakoztassuk Vegyük sorra az előző pontban ismertetett ''Menu'' funkciókat. Nézzük meg, hogy az egyes funkciókon belül milyen paramétereket, mérési, számítási, megjelenítési, skálázási módokat lehet állítani. Ha szükséges, nézzük meg az egyes beállítások definícióját, értelmezését a műszer gépkönyvében. Egy funkció áttekintése végén olyan értékeket, beállításokat hagyjunk, amelyek a termikus zaj méréséhez szükségesek. A készüléknek hagyományos, katódsugárcsöves monitora van. Ezen a kijelzőn rendkívül sok információ jelenik meg: leolvashatók a mérési adatok és a lényeges mérési paraméterek beállított értékei. Próbáljuk ki az adatok beolvasását a számítógépbe és a mentést excel fájlba. | ||
| + | ===1. Külső zajok azonosítása=== | ||
| + | Azonosítsuk a spektrumban jelentkező nagyobb csúcsok forrását! Ehhez az áramkört körülvevő fémdobozt levett tetővel egy hosszabb koax kábelen keresztül csatlakoztassuk a spektrumanalizátorhoz, és a doboz mozgatása közben figyeljük meg, hogy hol nő, illetve csökken a spektrumban megjelenő csúcsok amplitúdója. | ||
| + | A 0-100 kHz-es frekvenciatartományban egy mérési pont 250 Hz szélességű tartománynak felel meg. Ilyen felbontású mérésnél bizonyos csúcsok beleolvadhatnak a fehérzajháttérbe, pl. az 50 Hz-es hálózati frekvenciát és annak felharmonikusait nyilvánvalóan nem látjuk ilyen felbontásnál. Emiatt érdemes a spektrum különböző szűkebb tartományait lényegesen jobb frekvenciafelbontással is felvenni. Keressünk jellemző zaj-frekvenciákat a katódsugárcső előtt, a számítógép tápegységénél és a monitora körül, a multiméter közelében és értelmezzük azokat! | ||
| + | |||
| + | ===2. A Boltzmann-állandó meghatározása=== | ||
| + | <wlatex> | ||
Mérjük meg különböző ellenállások feszültségzaját, és határozzuk meg a Boltzmann-állandó értékét! | Mérjük meg különböző ellenállások feszültségzaját, és határozzuk meg a Boltzmann-állandó értékét! | ||
| − | A méréshez használjunk | + | A méréshez használjunk 0Ω-os ellenállást (rövidzár), illetve $1~k\Omega$-os, $3,3~k\Omega$-os, $6,8~k\Omega$-os és $10~k\Omega$-os ellenállásokat. A spektrumanalizátort ''PSD'' mérésre állítsuk, célszerű a mértékegységet Vrms-nek beállítani. A spektrumanalizátort állítsuk a lehető legkisebb méréshatárba (-60 dBV), és figyeljünk arra hogy a mérés közben soha ne villogjon az ''Overload'' jelzés. A ''PSD'' számolásához állítsunk be ''Hanning'' ablakot. |
| − | A spektrumot vegyük fel a műszer teljes frekvenciatartományában (0- | + | A spektrumot vegyük fel a műszer teljes frekvenciatartományában (0-100 kHz), és számoljunk egy átlagos spektrális sűrűséget egy szélesebb frekvenciatartományra. A mért spektrumból csak azokat a tartományokat vegyük figyelembe, ahol egyértelműen termikus zajra utaló fehérzajt látunk. Alacsony frekvencián ettől eltérést okozhat az 1/f zaj, magas frekvencián pedig az ellenállásból és a műszer kapacitásából adódó levágási frekvencia. A spektrumban a környezetben elhelyezett műszerekre jellemző frekvenciáknál csúcsok jelennek meg, ezeket ki kell hagyni az átlagos zajsűrűség számolásánál. A mérés során érdemes kiszámolni az adott ellenállásra várt zajsűrűség értékét, hiszen így rögtön észrevesszük, ha például egy érintkezési hiba miatt téves értékeket mérünk. |
| + | </wlatex> | ||
| − | A | + | ===4. Az elektron töltésének mérése=== |
| + | <wlatex> | ||
| + | Állítsuk össze az 5. ábrán szemléltetett kapcsolást, és mérjük meg a BD139 tranzisztor feszültségzaját különböző $R_1$ ellenállásoknál úgy, hogy a diódán keresztül kb. 1, 3 és 10 $\mu\mathrm{A}$ áram folyjon. (''PSD'' mérés, ''Hanning'' ablak, -60 dBV méréshatár.) Az áram értékét mindig pontosan határozzuk meg az $R_1$ ellenálláson eső feszültség mérése alapján. A spektrumot 0-100 kHz frekvenciatartományban mérjük, az ''SCALE - Y/div'' menü segítségével nagyítsuk ki úgy a jelet, hogy ne a kiugró csúcsok, hanem a számunkra érdekes háttér dominálja a képernyőt. Válasszuk ki azt a frekvenciatartományt, ahol már lecseng az alacsony frekvenciás 1/f zaj, de még nem kezd el levágni a zajsűrűség az RC időállandók miatt. A spektrumot ''log'' x skála mellett vizsgáljuk. | ||
| − | + | Minden $R_1$ ellenállás-értéknél mérjük meg a dióda differenciális ellenállását. Ehhez a ''Source Out'' kimeneten keresztül keverjünk ~1 kHz-es váltóáramot a 9 V-os elemből jövő egyenáramhoz. A csatoló kondenzátor értéke 100 nF, számítással igazoljuk, hogy az ellenállása elhanyagolható a kör összes ellenállása mellett. Az áramkör összeállítása előtt érdemes a ''Source Out'' kimenetet közvetlenül a ''Signal In (A)'' bemenetre kötni, és megmérni a kimeneti feszültséget. Ehhez 1 kHz középfrekvencia körüli keskeny (~300 Hz) frekvenciasávot használjunk, a műszerrel ''PSD'' helyett ''Spectrum''-ot mérjünk ''Flattop'' ablakkal. Állítsuk be a legkisebb méréshatárt, melynél még nem tapasztalunk ''Overload''-ot. Érdemes arra figyelni, hogy a kimeneti jel beállításánál amplitúdót állítunk be, míg a Fourier-spektrumban rms értéket mérünk. | |
| + | Ha ezen tesztméréssel meggyőződtünk a műszer helyes beállításáról, akkor csatlakoztassuk az 5. ábrán pirossal jelölt áramköri részt és mérjük meg a differenciális ellenállások értékét. Figyeljünk arra, hogy a váltóáram kicsi maradjon az egyenáramhoz képest, érdemes a tranzisztoron jelentkező váltóáramú feszültséget 5 mVrms alatt tartani. | ||
| − | + | A különböző $R_1$ értékeknél mért $S_V$, $\left< I \right>$ és $R_d$ értékek alapján határozzuk meg az elektron töltését. | |
| + | </wlatex> | ||
| − | + | ==Kitekintés== | |
| + | <wlatex> | ||
| + | A mérési gyakorlat keretében két - más mérésből jól ismert - fizikai állandó értékét mérjük meg zajmérés segítségével. Kutató laboratóriumokban azonban a zajmérést gyakran olyan területen alkalmazzák, ahol más mérési módszer csak korlátozottan, vagy egyáltalán nem áll rendelkezésre [1]. A következőkben ilyen mérésekből adunk rövid ízelítőt. | ||
| − | + | *A pontos hőmérsékletmérés - különösen extrém körülmények között - sokszor nehézséget jelent, hiszen számos fizikai folyamat (pl. fémek ellenállás-változása, higanyszál megnyúlása) alkalmas a hőmérsékletváltozás detektálásra, azonban ezek a hőmérők az ''abszolút hőmérséklet'' mérésére csak pontos kalibráció után alkalmasak. Ezzel szemben a zajmérés segítségével közvetlenül az abszolút hőmérsékletet lehet meghatározni [3], így zajmérés megfelelő (a laborgyakorlat mérésénél lényegesen nagyobb) pontosság esetén akár hőmérsékletsztenderdként is használható. | |
| − | + | ||
| − | + | *Az elektron töltését jól ismerjük, azonban számos olyan rendszer ismert, ahol a ''kvázirészecskék'' az elektrontöltés többszörösét vagy tört részét hordozzák. Ezen rendszereknél a zajmérés kiválóan alkalmas a kvázirészecske-töltés meghatározására [4,5]. | |
| − | + | *Az elemi részecskék speciális statisztikákat követnek. Az elektronok például ''fermionként'' viselkednek, és a Pauli-elv miatt két elektron nem lehet azonos kvantummechanikai állapotban, ezzel szemben a fotonok ''bozonként'' viselkednek, és szeretnek olyan állapotba szóródni, amiben már több foton is található (lásd indukált emisszió a lézerekben). Ezen különbségek zajméréssel kiválóan kimutathatók, hiszen megfelelően megválasztott rendszerekben a fermionok a Poisson-zajnál kisebb, míg a bozonok a Poisson-zajnál nagyobb zajt mutatnak [6-8]. | |
| − | + | *A klasszikus és kvantumos kaotikus rendszerek jelentősen különböznek egymástól. A klasszikus káosz esetén ugyan a rendszer viselkedése érzékenyen függ a kezdeti feltételektől azonban mégis teljesen determinisztikus mozgást kapunk. Ezzel szemben kvantumkáosz esetén a részecskék viselkedése alapvetően véletlenszerű. A klasszikus és a kvantumkáosz közötti átmenet jól megmutatható zajmérésekkel, hiszen az előbbi esetben zérus, míg az utóbbiban véges sörétzajt várunk [9]. | |
| − | == | + | Zajmérésekkel részletesebben az [[Új kísérletek a nanofizikában]] tárgy keretében ismerkedhetünk meg. |
| + | <wlatex> | ||
| + | ==Hivatkozások== | ||
| + | [1] [http://www.physicstoday.org/resource/1/phtoad/v56/i5/p37_s1 C. W. J. Beenakker, C. Schönenberger: ''Quantum shot noise'', '''Physics Today 56''', p37 (2003)] | ||
| − | + | [2] [http://onlinelibrary.wiley.com/doi/10.1002/andp.19183622304/abstract W. Schottky: ''Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern'', '''Annalen der Physik 57''' p541–567 (1918)] | |
| − | + | [3] [http://www.sciencemag.org/content/300/5627/1929.short Lafe Spietz et al.: ''Primary Electronic Thermometry Using the Shot Noise of a Tunnel Junction'', '''Science 300''', p1929 (2003)] | |
| − | + | [4] [http://www.nature.com/nature/journal/v405/n6782/abs/405050a0.html Jehl et al.: ''Detection of doubled shot noise in short normal-metal/ superconductor junctions'', '''Nature 405''', p50 (2000)] | |
| − | + | [5] [http://www.nature.com/nature/journal/v389/n6647/abs/389162a0.html R. de-Picciotto et al.: ''Direct observation of a fractional charge'', '''Nature 389''', p162 (1997)] | |
| − | + | [6] [http://www.nature.com/nature/journal/v178/n4541/abs/1781046a0.html R. Hanbury Brown and R. Q. Twiss: ''Correlation between Photons in two Coherent Beams of Light'', '''Nature 177''', p27 (1956).] | |
| − | + | [7] [http://www.sciencemag.org/content/284/5412/299.abstract W.D. Oliver et al.: ''Hanbury Brown and Twiss-Type Experiment with Electrons'', '''Science 284''', p299 (1999)] | |
| − | + | ||
| − | + | ||
| − | [ | + | |
| − | + | [8] [http://www.sciencemag.org/content/284/5412/296.abstract M. Henny et al.: ''The Fermionic Hanbury Brown and Twiss Experiment'', '''Science 284''', p296 (1999)] | |
| + | |||
| + | [9] [http://www.nature.com/nature/journal/v415/n6873/abs/415765a.html S. Oberholzer et al.: ''Crossover between classical and quantum shot noise in chaotic cavities'', '''Nature 415''', p765 (2002)] | ||
A lap jelenlegi, 2019. május 17., 09:23-kori változata
Ez a leírás a korábbi egyalkalmas Zaj mint jel című hallgató laborhoz tartozik. Az aktuális, kétalkalmas változat itt érhető el: Zaj mint jel.
A mérés célja
Különböző mennyiségek mérésénél általában a vizsgált mennyiség várható értékére vagyunk kíváncsiak, és a várható érték körüli fluktuációt zavaró tényezőnek tekintjük. Sok esetben viszont egy fizikai mennyiség “zaja” több információt hordoz a rendszerről, mint maga a várható érték [1]. A mérési gyakorlaton különböző zajjelenségeket vizsgálunk egy spektrumanalizátor segítségével. Először ellenállások termikus zajának mérése alapján meghatározzuk a Boltzmann-állandó értékét. Ezután egy félvezető dióda zajának méréséből az elektrontöltés értékét határozzuk meg.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglalás
A zaj definíciója
| 1. ábra |
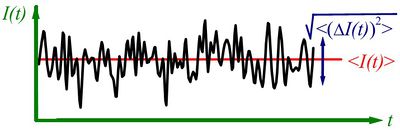
Egy időben változó mennyiség (pl. 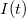 áram, lásd 1. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát,
áram, lásd 1. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát, 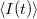 , illetve az átlagtól vett eltérést,
, illetve az átlagtól vett eltérést, 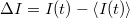 . A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével,
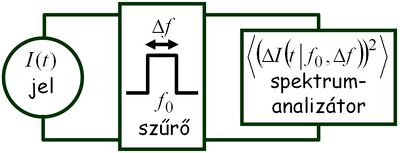
. A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével, 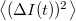 , azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 2. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az
, azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 2. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az 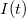 jelet egy
jelet egy  középfrekvencia körüli
középfrekvencia körüli  szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző
szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző 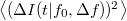 szórásnégyzetet mérünk.
szórásnégyzetet mérünk.
| 2. ábra |
Az így kapott szórásnégyzet kis  esetén arányos a
esetén arányos a  sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:
sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:
![\[\left<(\Delta I(t|f_0,\Delta f))^2\right>=S_I(f_0)\Delta f.\]](/images/math/3/3/f/33ff88a562de7a830d972009efd5d850.png)
Áramzaj esetén az 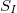 spektrális sűrűség mértékegysége
spektrális sűrűség mértékegysége 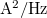 . A mérnöki gyakorlatban gyakran a spektrális sűrűség négyzetgyökével jellemzik egy eszköz zaját
. A mérnöki gyakorlatban gyakran a spektrális sűrűség négyzetgyökével jellemzik egy eszköz zaját 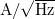 mértékegységgel.
mértékegységgel.
![\[\left<(\Delta V(t|f_0,\Delta f))^2\right>=S_V(f_0)\Delta f.\]](/images/math/8/9/a/89add176c6c234d68ca1a7b6097619e0.png)
Egy egyszerű ellenállás esetén 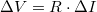 , azaz
, azaz 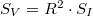 . Egy nemlineáris eszköznél, pl. egy diódánál
. Egy nemlineáris eszköznél, pl. egy diódánál 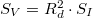 , ahol
, ahol 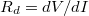 az eszköz differenciális ellenállása a mérésnél alkalmazott munkapontban.
az eszköz differenciális ellenállása a mérésnél alkalmazott munkapontban.
A fenti definíciók megismerése után érdemes megnézni a mérésnél használt Stanford Research Systems 770 típusú spektrumanalizátor specificációit, melyek szerint a műszer bemeneti zaja a legkisebb méréshatárban 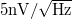 . Ez azt jelenti, hogy a műszer bemenetét rövidre zárva a várt zérus feszültség helyett a bemeneti erősítő feszültségzaját látjuk, melynek a szórása
. Ez azt jelenti, hogy a műszer bemenetét rövidre zárva a várt zérus feszültség helyett a bemeneti erősítő feszültségzaját látjuk, melynek a szórása 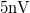
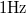 -es sávszélességű mérés esetén.
-es sávszélességű mérés esetén.
Puskalövések zaja
A zaj fogalma egy klasszikus példával is jól szemléltethető. Nézzük meg, hogy mi történik, ha egy puskából véletlenszerűen lövöldözünk úgy, hogy a lövések időpontja egymástól teljesen független. Ha a szomszédos lövések között eltelt átlagos idő  , akkor
, akkor  idő alatt a lövések átlagos száma értelemszerűen
idő alatt a lövések átlagos száma értelemszerűen 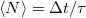 . A tényleges lövésszám azonban nyilvánvalóan fluktuálni fog az átlagérték körül. A szórásnégyzet meghatározásához érdemes kiszámolni a
. A tényleges lövésszám azonban nyilvánvalóan fluktuálni fog az átlagérték körül. A szórásnégyzet meghatározásához érdemes kiszámolni a 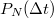 valószínűséget, azaz annak a valószínűségét, hogy
valószínűséget, azaz annak a valószínűségét, hogy  idő alatt
idő alatt  lövés dördül. Ha
lövés dördül. Ha 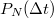 értékét ismerjük, akkor
értékét ismerjük, akkor 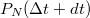 értéke a
értéke a
![\[P_N(\Delta t+dt)=P_{N-1}(\Delta t)\frac{dt}{\tau}+P_N(\Delta t)\left(1-\frac{dt}{\tau}\right)\]](/images/math/3/f/4/3f4062d58cc637d85054d98f2b6b3f49.png)
egyenlettel írható fel, azaz a kezdeti  és az utána következő
és az utána következő 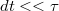 idő alatt vagy
idő alatt vagy 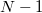 , ill.
, ill.  vagy
vagy  , ill.
, ill.  lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze.
A fenti egyenlet átrendezésével a
lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze.
A fenti egyenlet átrendezésével a
![\[\frac{dP_N(\Delta t)}{dt}=\frac{P_{N-1}(\Delta t)-P_N(\Delta t)}{\tau}\]](/images/math/b/6/4/b64ef404ea69d3816419cfebef01952b.png)
differenciálegyenletet kapjuk. Megmutatható, hogy ezen feltételt a
![\[P_N(\Delta t)=\frac{(\Delta t)^N}{\tau^N N!}e^{-\Delta t/\tau}\]](/images/math/f/b/b/fbb852541ecee469bb9e8e91c30241fe.png)
Poisson-eloszlás elégíti ki. A Poisson-eloszlás speciális tulajdonsága, hogy a szórásnégyzet megegyezik a várható értékkel, azaz
![\[\left< (\Delta N)^2 \right>=\left< N \right>=\frac{\Delta t}{\tau}.\]](/images/math/c/9/2/c925d13d542008c08786e26fc2259b03.png)
Elektronok sörétzaja
A fenti gondolatmenetet vonatkoztathatjuk elektronokra is, ha teljesül az, hogy az elektronok véletlenszerűen, egymástól függetlenül jutnak át az egyik elektródából a másikba. Tegyük fel, hogy mérőrendszerünkkel az elektromos áramot  időbeli felbontással tudjuk mérni. Egy
időbeli felbontással tudjuk mérni. Egy  szélességű mintavételezési intervallum alatt
szélességű mintavételezési intervallum alatt 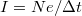 áramot detektálunk, ahol a
áramot detektálunk, ahol a  idő alatt áthaladó elektronok
idő alatt áthaladó elektronok  számának eloszlását a fenti Poisson-eloszlás adja meg. Így a mért áram várható értéke
számának eloszlását a fenti Poisson-eloszlás adja meg. Így a mért áram várható értéke 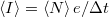 , míg az áram szórásnégyzete
, míg az áram szórásnégyzete 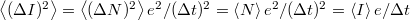 .
A Nyquist–Shannon mintavételezési törvény szerint
.
A Nyquist–Shannon mintavételezési törvény szerint  időfelbontás esetén a mért jelet
időfelbontás esetén a mért jelet 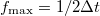 maximális frekvenciáig tudjuk rekonstruálni. Ez alapján az áram szórásnégyzete:
maximális frekvenciáig tudjuk rekonstruálni. Ez alapján az áram szórásnégyzete:
![\[\left< (\Delta I)^2 \right>=\int_0^{f_\mathrm{max}}S_I(f)df=2e\left< I \right>\cdot f_\mathrm{max},\]](/images/math/0/2/d/02d4546bad22d8b92bbfec96ba35ed53.png)
azaz:
![\[S_I=2e\left< I \right>.\]](/images/math/1/a/c/1ac0f27491897d7a5c456a1b44bb8271.png)
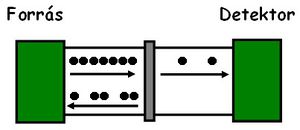
A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt sörétzajnak szokták nevezni. Fontos megemlíteni, hogy a fenti képlet alapján a sörétzaj fehér zaj, azaz a spektrális sűrűség frekvenciafüggetlen. Az előbbiekben levezetett zajformula a sörétzajnak is egyik speciális esetét írja le, az ún. Poisson-zajt, mely egymástól független elektronok detektálására vonatkozik. A kvantummechanikából ismert Pauli-elv szerint két elektron nem lehet ugyan abban az állapotban, azaz egy adott időpontban nem tudunk két teljesen egyforma állapotú elektront detektálni. Egy makroszkopikus vezetőben az elektronok nem egymástól függetlenül, hanem inkább sorban egymást követve érkeznek az árammérőhöz, így a fenti zajformula nem érvényes. Azonban a Poisson-zaj feltételét megvalósíthatjuk akkor, ha az elektronok útjába egy olyan akadályt helyezünk, melyen véletlenszerűen az elektronoknak csak egy kis része tud keresztüljutni (3a. ábra).
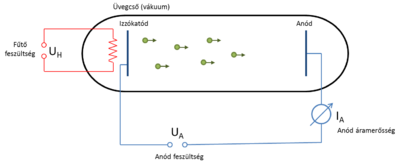
Az első sörétzajmérést Walter Schottky végezte 1918-ban [2]: híres kísérletében egy vákuumdióda anódáramának zaját vizsgálta. A vákuumdióda felépítését a 3b. ábra szemlélteti. Egy fűtött katódból véletlenszerűen kilépő elektronok a katód és anód közé kapcsolt feszültség hatására eljutnak az anódba, ahol áramot detektálunk. A vákuumdióda ideális eszköz a sörétzaj tanulmányozásához, hiszen az elektronok valóban véletlenül, és egymástól függetlenül emittálódnak, így a mért zajsűrűség és az áram hányadosából az elektrontöltés a Poisson-zaj formulája alapján meghatározható.
| 3a. ábra | 3b. ábra |
Poisson-zajt modern elektronikai eszközökben is tapasztalhatunk, például egy diódát alkotó félvezető p-n átmenet is biztosítja az elektronok véletlen és független emisszióját megfelelően kicsi áram esetén.
Termikus zaj
Az előbbiekben bemutatott sörétzaj egy nemegyensúlyi zaj, melyet csak akkor tapasztalunk, ha a vizsgált áramköri elemen áramot folyatunk keresztül. Zajt azonban egyensúlyi állapotban is tapasztalhatunk pusztán az elektronok termikus fluktuációi miatt. A termikus zaj megértése komolyabb elméleti hátteret igényel, azonban maga a jelenség egy nagyon egyszerű formulával leírható: egy  elektromos ellenállással rendelkező áramköri elemen
elektromos ellenállással rendelkező áramköri elemen
![\[S_V=4k_B T\cdot R\]](/images/math/8/5/0/8500771d360277ebaf7f4f7c0a6fef77.png)
feszültségzaj-sűrűséget mérhetünk attól függetlenül, hogy pontosan milyen fizikai rendszer adja az  ellenállást.
A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától.
Ezen jelenség segítségével a
ellenállást.
A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától.
Ezen jelenség segítségével a  hőmérséklet és az
hőmérséklet és az  ellenállás ismeretében a feszültségzaj méréséből a Boltzmann-állandó meghatározható.
ellenállás ismeretében a feszültségzaj méréséből a Boltzmann-állandó meghatározható.
Egyéb zajforrások
A termikus zaj és a sörétzaj mellett érdemes megemlékezni az 1/f zajról, mely a zajsűrűség tipikus 1/f-jellegű frekvenciafüggéséről kapta a nevét. Ezen zajtípus számos fizikai folyamatból származhat, például a szennyezők és rácshibák véletlen mozgásából adódó ellenállásfluktuációkból. Az 1/f zaj a sörétzajhoz hasonlóan nemegyensúlyi zaj, a spektrális sűrűség a feszültség növelésével nő. Az 1/f zaj tipikusan alacsony frekvenciás (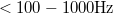 ) méréseknél dominál, míg magasabb frekvenciákon a termikus zaj, illetve bizonyos eszközökben a sörétzaj a legfontosabb zajforrás.
) méréseknél dominál, míg magasabb frekvenciákon a termikus zaj, illetve bizonyos eszközökben a sörétzaj a legfontosabb zajforrás.
Az eddigiekben csak a vizsgált rendszerünk belső zajáról beszéltünk, azonban zajmérésnél mindig fontos a külső forrásokból adódó elektromágneses zavarokra is gondolni. Egy áramkör kapacitív vagy induktív csatolással könnyen felvesz zajt a környezetből, például az elektromos hálózat 50 Hz-es frekvenciájánál, monitorok képernyőjének frissítési frekvenciájánál, kapcsoló üzemű tápok működési frekvenciájánál, vagy akár rádióállomások, mobiltelefonok sugárzási frekvenciájánál. Ezen zavaró tényezők kiküszöbölésének alapvető módszere a vizsgált áramkör árnyékolása: alacsony jelszintű méréseknél mindig árnyékolt kábeleket, illetve fém dobozba zárt áramköröket érdemes használni.
Mérési elrendezés
A méréshez használt eszközök
A méréshez egy Stanford Reserch Systems 770 típusú spektrumanalizátort használunk. A későbbiekben csak a műszer legfontosabb funkcióit ismertetjük, részletes specifikációk és leírás a műszer adatlapjában és használati utasításában érhető el. A műszer előlapjának fényképe és a kezelőfelülete szintén az említett adatlapban tekinthetők meg.
A spektrumanalizátor jele egy saját fejlesztésű szoftverrel (SRS770_beolvasas.exe) számítógépbe beolvasható, illetve fájlba kimenthető.
A termikus és a sörétzaj méréséhez egy lezárható alumíniumdobozba helyezett panel áll rendelkezésre. A panelen levő csatlakozókba lehet bekötni a termikus zaj méréséhez használt R ellenállásokat és a sörétzaj méréséhez szükséges R1 és R2 ellenállásokat. (4. ábra). A dobozon három BNC csatlakozó és a tápfeszültség bekapcsolására szolgáló kapcsoló található. A méréshez különböző áramköri elemek állnak rendelkezésre: ellenállások, jumper, kondenzátorok, BNC-BNC toldó, BNC csatlakozós koax kábel.
| 4. ábra |
A termikus zaj mérésének elve
A termikus zaj mérésénél a doboz egyik BNC csatlakozójának belső pontja és földpontja közé egy ellenállást kötünk, a BNC csatlakozót pedig egy BNC-BNC toldó segítségével (lásd 4. ábra felső csatlakozó) közvetlenül a spektrumanalizátor Signal In (A) bemenetére kötjük és ebben az elrendezésben mérjük az ellenállás feszültségzaját. Mivel a mért termikus zaj összemérhető a műszer bemeneti zajával (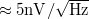 ), ezért a mért zaj a termikus zaj és a műszer bemeneti zajának összege lesz:
), ezért a mért zaj a termikus zaj és a műszer bemeneti zajának összege lesz:
![\[S_V=4k_B T\cdot R + S_0.\]](/images/math/a/b/d/abd2e7c79dbc44dd178c08da8a388ecc.png)
Ha a mérést több ellenálláson is megismételjük akkor az 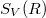 függvény meredekségéből a szobahőmérséklet ismeretében megkapjuk a Boltzmann-állandó értékét.
függvény meredekségéből a szobahőmérséklet ismeretében megkapjuk a Boltzmann-állandó értékét.
A sörétzaj mérésének elve
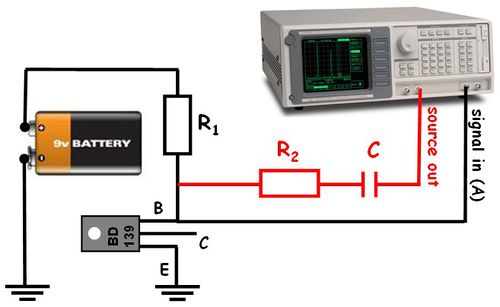
A sörétzaj mérésekor az 5. ábrán bemutatott kapcsolást érdemes alkalmazni. Tápegységként használjunk egy 9 V-os elemet, így a meghajtó feszültségünk zaja kisebb lesz, mint ha bármilyen elektromos hálózatra kötött tápegységet használnánk. A teleppel kössünk sorba egy nagy ellenállást ( ) és egy félvezető diódát. Diódaként érdemes egy alacsony zajszintű tranzisztort használni úgy, hogy azt az 5. ábra szerint nyitó irányban a bázis és emitter kontaktusokon keresztül kötjük az áramkörbe és a kollektor elektródát nem használjuk.
) és egy félvezető diódát. Diódaként érdemes egy alacsony zajszintű tranzisztort használni úgy, hogy azt az 5. ábra szerint nyitó irányban a bázis és emitter kontaktusokon keresztül kötjük az áramkörbe és a kollektor elektródát nem használjuk.
| 5. ábra |
A körben folyó egyenáramot könnyen meghatározhatjuk az  ellenálláson eső feszültség mérése alapján (a biztonság kedvéért érdemes az
ellenálláson eső feszültség mérése alapján (a biztonság kedvéért érdemes az  ellenállás értékét is pontosan megmérni, és ezzel számolni a névleges érték helyett). A feszültség- és ellenállás-méréshez használjunk 4.5 digites Goodwill digitális multimétert.
ellenállás értékét is pontosan megmérni, és ezzel számolni a névleges érték helyett). A feszültség- és ellenállás-méréshez használjunk 4.5 digites Goodwill digitális multimétert.
Az áram meghatározása után mérjük meg a spektrumanalizátorral a diódán jelentkező feszültségzajt. (Ennél a mérésnél az ábrán pirossal jelölt  ellenállást és
ellenállást és  kondenzátort ne kössük az áramkörbe!) Az így mért feszültségzaj
kondenzátort ne kössük az áramkörbe!) Az így mért feszültségzaj
![\[S_V=2e\left< I \right> \cdot R_d^2 +S_0,\]](/images/math/c/b/b/cbb0b32f6c711a3163b5c6a7e91a8bc6.png)
ahol 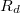 a dióda differenciális ellenállása a beállított munkapontban,
a dióda differenciális ellenállása a beállított munkapontban, 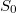 pedig a műszer bemeneti zaja.
pedig a műszer bemeneti zaja.
A következő lépés a dióda differenciális ellenállásának (lásd alább) a meghatározása. Ehhez a spektrumanalizátor Source Out kimenetéről egy  ellenálláson és egy
ellenálláson és egy  kondenzátoron keresztül váltóáramot keverünk a telepből jövő egyenáramhoz, és a spektrumanalizátorral megmérjük a váltóáramú feszültségesést a meghajtó jellel azonos frekvencián. A spektrumanalizátor kimeneti feszültségszintjét és az
kondenzátoron keresztül váltóáramot keverünk a telepből jövő egyenáramhoz, és a spektrumanalizátorral megmérjük a váltóáramú feszültségesést a meghajtó jellel azonos frekvencián. A spektrumanalizátor kimeneti feszültségszintjét és az  ellenállást úgy kell megválasztani, hogy a diódán folyó váltóáram az egyenáramnál lényegesen kisebb legyen. A
ellenállást úgy kell megválasztani, hogy a diódán folyó váltóáram az egyenáramnál lényegesen kisebb legyen. A  kapacitás azt a célt szolgálja, hogy a telepből jövő egyenáramból semennyi ne tudjon a spektrumanalizátor kimenete felé elfolyni. Célszerű
kapacitás azt a célt szolgálja, hogy a telepből jövő egyenáramból semennyi ne tudjon a spektrumanalizátor kimenete felé elfolyni. Célszerű  értékét úgy megválasztani, hogy a meghajtó frekvencián vett impedancia lényegesen kisebb legyen
értékét úgy megválasztani, hogy a meghajtó frekvencián vett impedancia lényegesen kisebb legyen  -nél. Így a differenciális ellenállást
-nél. Így a differenciális ellenállást
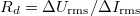 képlet szerint számoljuk, ahol
képlet szerint számoljuk, ahol 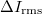 a Source Out kimeneten kiadott váltófeszültség rms értékének (szórásának) és
a Source Out kimeneten kiadott váltófeszültség rms értékének (szórásának) és  ellenállásnak a hányadosa,
ellenállásnak a hányadosa, 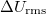 pedig a diódán mért váltóáramú feszültség rms értéke.
pedig a diódán mért váltóáramú feszültség rms értéke.
Ha különböző  ellenállásokkal megmérjük
ellenállásokkal megmérjük 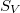 ,
, 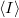 és
és 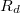 értékét, akkor az
értékét, akkor az 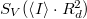 függvényre egyenest illesztve megkapjuk az elektron töltésének értékét.
függvényre egyenest illesztve megkapjuk az elektron töltésének értékét.
Differenciális ellenállás: A diódára kapcsolt egyenfeszültség egy állandó átfolyó áramot határoz meg, vagyis meghatározza a karakterisztika egy pontját, ezt nevezzük munkapontnak. A munkapontban tudjuk definiálni a dióda egyenáramú ellenállását, ami a rákapcsolt egyenfeszültség és az átfolyó áram hányadosa. A feszültség kis változtatásának (modulálás) hatása az áramra attól függ, hogy hol van a munkapont, hiszen a karakterisztika nemlineáris. A dióda differenciális (dinamikus) ellenállásának az adott munkaponti feszültség kis változását és a kialakuló áramváltozás hányadosát nevezzük.
Az SRS770 spektrumanalizátor használata és beállítása
Az SRS770 spektrumanalizátor egy egycsatornás 100 kHz sávszélességű 16 bit felbontású műszer, mely a bemenetén mért jel Fourier-spektrumát határozza meg. A műszer legfontosabb funkciói a MENU gombcsoport segítségével állíthatók.
- A FREQ gomb segítségével lehet a vizsgált frekvenciatartományt beállítani. A FREQ gomb megnyomása után a képernyő jobb szélén jelennek meg a beállítási lehetőségek, melyeket a képernyő melletti gombokkal érünk el. Számértékeket a forgató gombbal, illetve az ENTRY gombcsoporttal állíthatunk be. A legfontosabb beállítás a Span, mellyel a vizsgált frekvenciatartomány szélességét állíthatjuk be. A frekvenciatartomány kezdeti vagy középfrekvenciáját a Start freq vagy Center freq menüben állíthatjuk. Fontos megjegyezni, hogy Span-ben beállított frekvenciasávot a műszer mindig 400 mérési pontra osztja, így a legnagyobb 100 kHz-es sávszélességnél 100 kHz/400 azaz 250 Hz felbontással tudjuk felvenni a spektrumot.
- A MEAS gomb segítségével állítható be, hogy pontosan mit akarunk mérni. Ezen belül a Measure menüben választhatjuk ki, hogy a jel komplex Fourier transzformáltját (Spectrum) vagy a zajsűrűséget (PSD, power spectral density) akarjuk mérni. Belátható hogy a PSD a Fourier-transzformált abszolútérték-négyzete megfelelő normálással. A Display menüben Log Mag funkciót állítsunk be, a Units menüben pedig Volts RMS mértékegységet válasszunk ki. A Window menüben választható ki az FFT-nél alkalmazott ablakfüggvény, ezt PSD mérésekor Hanning ablakra állítsuk.
- A DISPLAY gomb segítségével állíthatjuk be a képernyőn megjelenő Marker-eket. A CONTROL/MARKER gomb megnyomása után a forgatógombbal állíthatjuk be a Marker pozícióját. A képernyő tetején leolvasható a Marker pozíciója és az adott pozíciónál mért érték. Marker width=Spot beállításnál egy konkrét pontnál olvashatjuk le a spektrumot, míg Marker width=Norm/Wide és Marker Seeks=Mean beállításnál pedig az adott Marker pozíció körüli szélesebb tartományban vett átlagos spektrumot kapjuk meg.
- Az INPUT gomb megnyomása után Input Source=A, Grounding=Ground, Coupling=AC beállításokat alkalmazzunk. Az Input range menüben állíthatjuk be a mérés érzékenységét, ezt mindig az adott mérésnél alkalmazható legérzékenyebb értékre állítsuk. Zajspektrum mérésekor lehetőleg a legérzékenyebb, -60 dBV méréshatárt válasszuk, mely 1 mV-os méréshatárnak felel meg. A képernyő alsó részén mindig láthatjuk az aktuális méréshatár értékét. Ha ez alatt az OVERLOAD felirat villog, akkor a bemenetet túlvezéreltük, így a mért adatok nem használhatók.
- A SCALE gomb megnyomásával változtathatjuk az ábrázolt adatok skáláját. Az X-axis-t állítsuk log skálára. Az Y/Div menü segítségével nagyíthatjuk ki a számunkra érdekes görbeszakaszt y irányban. Automatikus skálát az ENTRY/AUTOSCALE gombbal állíthatunk be.
- Az ANALYZE gomb megnyomása után None beállítást alkalmazzunk.
- Az AVERAGE gomb megnyomása után állíthatjuk be az átlagolás értékét, célszerű 1000-2000 görbére átlagolni.
- A SOURCE gombbal állíthatjuk be a Source Out kimenetet. Ha nincs szükség meghajtó jelre akkor mindig kapcsoljuk ki a kimenetet. Kimenő jel alkalmazása esetén a Configure menüben állíthatjuk be a kimenő jel frekvenciáját és amplitúdóját.
- A SYSTEM menü Setup commun almenüjében Output to=GPIB-t válasszunk. Ezen beállítások mellett tudjuk a mért értékeket a számítógép soros portján keresztül beolvasni.
- A mintavételezést a CONTROL/START gombbal indíthatjuk.
Mérési feladatok
0. A Spektrumanalizátor használatának begyakorlása
Nulladik feladatként ismerkedjünk meg a spektrumanalizátor kezelésével! Az Input A bemenetre csatlakoztassuk Vegyük sorra az előző pontban ismertetett Menu funkciókat. Nézzük meg, hogy az egyes funkciókon belül milyen paramétereket, mérési, számítási, megjelenítési, skálázási módokat lehet állítani. Ha szükséges, nézzük meg az egyes beállítások definícióját, értelmezését a műszer gépkönyvében. Egy funkció áttekintése végén olyan értékeket, beállításokat hagyjunk, amelyek a termikus zaj méréséhez szükségesek. A készüléknek hagyományos, katódsugárcsöves monitora van. Ezen a kijelzőn rendkívül sok információ jelenik meg: leolvashatók a mérési adatok és a lényeges mérési paraméterek beállított értékei. Próbáljuk ki az adatok beolvasását a számítógépbe és a mentést excel fájlba.
1. Külső zajok azonosítása
Azonosítsuk a spektrumban jelentkező nagyobb csúcsok forrását! Ehhez az áramkört körülvevő fémdobozt levett tetővel egy hosszabb koax kábelen keresztül csatlakoztassuk a spektrumanalizátorhoz, és a doboz mozgatása közben figyeljük meg, hogy hol nő, illetve csökken a spektrumban megjelenő csúcsok amplitúdója. A 0-100 kHz-es frekvenciatartományban egy mérési pont 250 Hz szélességű tartománynak felel meg. Ilyen felbontású mérésnél bizonyos csúcsok beleolvadhatnak a fehérzajháttérbe, pl. az 50 Hz-es hálózati frekvenciát és annak felharmonikusait nyilvánvalóan nem látjuk ilyen felbontásnál. Emiatt érdemes a spektrum különböző szűkebb tartományait lényegesen jobb frekvenciafelbontással is felvenni. Keressünk jellemző zaj-frekvenciákat a katódsugárcső előtt, a számítógép tápegységénél és a monitora körül, a multiméter közelében és értelmezzük azokat!
2. A Boltzmann-állandó meghatározása
Mérjük meg különböző ellenállások feszültségzaját, és határozzuk meg a Boltzmann-állandó értékét!
A méréshez használjunk 0Ω-os ellenállást (rövidzár), illetve 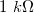 -os,
-os, 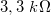 -os,
-os, 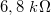 -os és
-os és 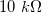 -os ellenállásokat. A spektrumanalizátort PSD mérésre állítsuk, célszerű a mértékegységet Vrms-nek beállítani. A spektrumanalizátort állítsuk a lehető legkisebb méréshatárba (-60 dBV), és figyeljünk arra hogy a mérés közben soha ne villogjon az Overload jelzés. A PSD számolásához állítsunk be Hanning ablakot.
-os ellenállásokat. A spektrumanalizátort PSD mérésre állítsuk, célszerű a mértékegységet Vrms-nek beállítani. A spektrumanalizátort állítsuk a lehető legkisebb méréshatárba (-60 dBV), és figyeljünk arra hogy a mérés közben soha ne villogjon az Overload jelzés. A PSD számolásához állítsunk be Hanning ablakot.
A spektrumot vegyük fel a műszer teljes frekvenciatartományában (0-100 kHz), és számoljunk egy átlagos spektrális sűrűséget egy szélesebb frekvenciatartományra. A mért spektrumból csak azokat a tartományokat vegyük figyelembe, ahol egyértelműen termikus zajra utaló fehérzajt látunk. Alacsony frekvencián ettől eltérést okozhat az 1/f zaj, magas frekvencián pedig az ellenállásból és a műszer kapacitásából adódó levágási frekvencia. A spektrumban a környezetben elhelyezett műszerekre jellemző frekvenciáknál csúcsok jelennek meg, ezeket ki kell hagyni az átlagos zajsűrűség számolásánál. A mérés során érdemes kiszámolni az adott ellenállásra várt zajsűrűség értékét, hiszen így rögtön észrevesszük, ha például egy érintkezési hiba miatt téves értékeket mérünk.
4. Az elektron töltésének mérése
Állítsuk össze az 5. ábrán szemléltetett kapcsolást, és mérjük meg a BD139 tranzisztor feszültségzaját különböző  ellenállásoknál úgy, hogy a diódán keresztül kb. 1, 3 és 10
ellenállásoknál úgy, hogy a diódán keresztül kb. 1, 3 és 10 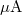 áram folyjon. (PSD mérés, Hanning ablak, -60 dBV méréshatár.) Az áram értékét mindig pontosan határozzuk meg az
áram folyjon. (PSD mérés, Hanning ablak, -60 dBV méréshatár.) Az áram értékét mindig pontosan határozzuk meg az  ellenálláson eső feszültség mérése alapján. A spektrumot 0-100 kHz frekvenciatartományban mérjük, az SCALE - Y/div menü segítségével nagyítsuk ki úgy a jelet, hogy ne a kiugró csúcsok, hanem a számunkra érdekes háttér dominálja a képernyőt. Válasszuk ki azt a frekvenciatartományt, ahol már lecseng az alacsony frekvenciás 1/f zaj, de még nem kezd el levágni a zajsűrűség az RC időállandók miatt. A spektrumot log x skála mellett vizsgáljuk.
ellenálláson eső feszültség mérése alapján. A spektrumot 0-100 kHz frekvenciatartományban mérjük, az SCALE - Y/div menü segítségével nagyítsuk ki úgy a jelet, hogy ne a kiugró csúcsok, hanem a számunkra érdekes háttér dominálja a képernyőt. Válasszuk ki azt a frekvenciatartományt, ahol már lecseng az alacsony frekvenciás 1/f zaj, de még nem kezd el levágni a zajsűrűség az RC időállandók miatt. A spektrumot log x skála mellett vizsgáljuk.
Minden  ellenállás-értéknél mérjük meg a dióda differenciális ellenállását. Ehhez a Source Out kimeneten keresztül keverjünk ~1 kHz-es váltóáramot a 9 V-os elemből jövő egyenáramhoz. A csatoló kondenzátor értéke 100 nF, számítással igazoljuk, hogy az ellenállása elhanyagolható a kör összes ellenállása mellett. Az áramkör összeállítása előtt érdemes a Source Out kimenetet közvetlenül a Signal In (A) bemenetre kötni, és megmérni a kimeneti feszültséget. Ehhez 1 kHz középfrekvencia körüli keskeny (~300 Hz) frekvenciasávot használjunk, a műszerrel PSD helyett Spectrum-ot mérjünk Flattop ablakkal. Állítsuk be a legkisebb méréshatárt, melynél még nem tapasztalunk Overload-ot. Érdemes arra figyelni, hogy a kimeneti jel beállításánál amplitúdót állítunk be, míg a Fourier-spektrumban rms értéket mérünk.
Ha ezen tesztméréssel meggyőződtünk a műszer helyes beállításáról, akkor csatlakoztassuk az 5. ábrán pirossal jelölt áramköri részt és mérjük meg a differenciális ellenállások értékét. Figyeljünk arra, hogy a váltóáram kicsi maradjon az egyenáramhoz képest, érdemes a tranzisztoron jelentkező váltóáramú feszültséget 5 mVrms alatt tartani.
ellenállás-értéknél mérjük meg a dióda differenciális ellenállását. Ehhez a Source Out kimeneten keresztül keverjünk ~1 kHz-es váltóáramot a 9 V-os elemből jövő egyenáramhoz. A csatoló kondenzátor értéke 100 nF, számítással igazoljuk, hogy az ellenállása elhanyagolható a kör összes ellenállása mellett. Az áramkör összeállítása előtt érdemes a Source Out kimenetet közvetlenül a Signal In (A) bemenetre kötni, és megmérni a kimeneti feszültséget. Ehhez 1 kHz középfrekvencia körüli keskeny (~300 Hz) frekvenciasávot használjunk, a műszerrel PSD helyett Spectrum-ot mérjünk Flattop ablakkal. Állítsuk be a legkisebb méréshatárt, melynél még nem tapasztalunk Overload-ot. Érdemes arra figyelni, hogy a kimeneti jel beállításánál amplitúdót állítunk be, míg a Fourier-spektrumban rms értéket mérünk.
Ha ezen tesztméréssel meggyőződtünk a műszer helyes beállításáról, akkor csatlakoztassuk az 5. ábrán pirossal jelölt áramköri részt és mérjük meg a differenciális ellenállások értékét. Figyeljünk arra, hogy a váltóáram kicsi maradjon az egyenáramhoz képest, érdemes a tranzisztoron jelentkező váltóáramú feszültséget 5 mVrms alatt tartani.
A különböző  értékeknél mért
értékeknél mért 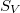 ,
, 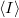 és
és 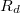 értékek alapján határozzuk meg az elektron töltését.
értékek alapján határozzuk meg az elektron töltését.
Kitekintés
A mérési gyakorlat keretében két - más mérésből jól ismert - fizikai állandó értékét mérjük meg zajmérés segítségével. Kutató laboratóriumokban azonban a zajmérést gyakran olyan területen alkalmazzák, ahol más mérési módszer csak korlátozottan, vagy egyáltalán nem áll rendelkezésre [1]. A következőkben ilyen mérésekből adunk rövid ízelítőt.
- A pontos hőmérsékletmérés - különösen extrém körülmények között - sokszor nehézséget jelent, hiszen számos fizikai folyamat (pl. fémek ellenállás-változása, higanyszál megnyúlása) alkalmas a hőmérsékletváltozás detektálásra, azonban ezek a hőmérők az abszolút hőmérséklet mérésére csak pontos kalibráció után alkalmasak. Ezzel szemben a zajmérés segítségével közvetlenül az abszolút hőmérsékletet lehet meghatározni [3], így zajmérés megfelelő (a laborgyakorlat mérésénél lényegesen nagyobb) pontosság esetén akár hőmérsékletsztenderdként is használható.
- Az elektron töltését jól ismerjük, azonban számos olyan rendszer ismert, ahol a kvázirészecskék az elektrontöltés többszörösét vagy tört részét hordozzák. Ezen rendszereknél a zajmérés kiválóan alkalmas a kvázirészecske-töltés meghatározására [4,5].
- Az elemi részecskék speciális statisztikákat követnek. Az elektronok például fermionként viselkednek, és a Pauli-elv miatt két elektron nem lehet azonos kvantummechanikai állapotban, ezzel szemben a fotonok bozonként viselkednek, és szeretnek olyan állapotba szóródni, amiben már több foton is található (lásd indukált emisszió a lézerekben). Ezen különbségek zajméréssel kiválóan kimutathatók, hiszen megfelelően megválasztott rendszerekben a fermionok a Poisson-zajnál kisebb, míg a bozonok a Poisson-zajnál nagyobb zajt mutatnak [6-8].
- A klasszikus és kvantumos kaotikus rendszerek jelentősen különböznek egymástól. A klasszikus káosz esetén ugyan a rendszer viselkedése érzékenyen függ a kezdeti feltételektől azonban mégis teljesen determinisztikus mozgást kapunk. Ezzel szemben kvantumkáosz esetén a részecskék viselkedése alapvetően véletlenszerű. A klasszikus és a kvantumkáosz közötti átmenet jól megmutatható zajmérésekkel, hiszen az előbbi esetben zérus, míg az utóbbiban véges sörétzajt várunk [9].
Zajmérésekkel részletesebben az Új kísérletek a nanofizikában tárgy keretében ismerkedhetünk meg.
Hivatkozások
[1] C. W. J. Beenakker, C. Schönenberger: Quantum shot noise, Physics Today 56, p37 (2003)
[5] R. de-Picciotto et al.: Direct observation of a fractional charge, Nature 389, p162 (1997)
[7] W.D. Oliver et al.: Hanbury Brown and Twiss-Type Experiment with Electrons, Science 284, p299 (1999)
[8] M. Henny et al.: The Fermionic Hanbury Brown and Twiss Experiment, Science 284, p296 (1999)