„Elektromos egyenáramú alapmérések” változatai közötti eltérés
| 49. sor: | 49. sor: | ||
ahol $Q$ egy adott felületen átáramló töltést és $t$ az időt jelenti. Az áramerősség egysége az amper (A). Az egyenáram irányát – megállapodás alapján – a pozitív töltéshordozók mozgásának iránya adja meg. Egyenáramról beszélünk, ha az áram erőssége időben állandó. | ahol $Q$ egy adott felületen átáramló töltést és $t$ az időt jelenti. Az áramerősség egysége az amper (A). Az egyenáram irányát – megállapodás alapján – a pozitív töltéshordozók mozgásának iránya adja meg. Egyenáramról beszélünk, ha az áram erőssége időben állandó. | ||
| − | Egy vezető két pontja között levő $U$ potenciálkülönbség ( | + | Egy vezető két pontja között levő $U$ potenciálkülönbség (feszültség) áram kialakulásához vezet. A vezetőre kapcsolt feszültség és a benne folyó áram között sok esteben (pl. fémes vezetőkben) az |
$$U=RI$$ | $$U=RI$$ | ||
| 57. sor: | 57. sor: | ||
$$R=\rho\frac{l}{A}$$ | $$R=\rho\frac{l}{A}$$ | ||
| − | A fajlagos ellenállás – sok más anyagi jellemzőhöz hasonlóan – hőmérsékletfüggő | + | A fajlagos ellenállás – sok más anyagi jellemzőhöz hasonlóan – hőmérsékletfüggő: |
$$\rho=\rho_0\left[1+\alpha(t-t_0)+\beta(t-t_0)^2+...\right]$$ | $$\rho=\rho_0\left[1+\alpha(t-t_0)+\beta(t-t_0)^2+...\right]$$ | ||
| 66. sor: | 66. sor: | ||
A töltésmegmaradás törvényének kifejezése az úgynevezett csomóponti törvény: egy csomópontba összefutó áramok előjeles összege nulla. Ha a ki- és befolyó áramokat ellentétes előjelűnek tekintjük: | A töltésmegmaradás törvényének kifejezése az úgynevezett csomóponti törvény: egy csomópontba összefutó áramok előjeles összege nulla. Ha a ki- és befolyó áramokat ellentétes előjelűnek tekintjük: | ||
| − | $$\sum_{ | + | $$\sum_{i=1}^n I_i=0$$ |
| − | Az | + | Az energiamegmaradás törvényének következménye a huroktörvény, mely szerint egy zárt vezetőhurok feszültségeinek előjeles összege zérus: |
| − | + | ||
| + | $$\sum_{i=1}^n U_i=0$$ | ||
A Kirchhoff-törvények alkalmazásának egy lehetséges módja az alábbi: | A Kirchhoff-törvények alkalmazásának egy lehetséges módja az alábbi: | ||
* Felrajzoljuk az áramkört és bejelöljük a telepek polaritását. | * Felrajzoljuk az áramkört és bejelöljük a telepek polaritását. | ||
* Tetszőlegesen felvesszük az ág áramokat és bejelöljük az irányukat. | * Tetszőlegesen felvesszük az ág áramokat és bejelöljük az irányukat. | ||
| − | * Bejelöljük a hurkokban | + | * Bejelöljük a hurkokban tetszőleges körüljárási irányokat. |
* Felírjuk a csomóponti egyenleteket. (Például a csomópontba befolyó áramokat tekintjük pozitívnak, a kifolyókat pedig negatívnak.) | * Felírjuk a csomóponti egyenleteket. (Például a csomópontba befolyó áramokat tekintjük pozitívnak, a kifolyókat pedig negatívnak.) | ||
| − | * Felírjuk a hurokegyenleteket. Ilyenkor úgy | + | * Felírjuk a hurokegyenleteket. Ilyenkor pl. úgy járhatunk el, hogy a telepeken a pozitív pólustól a negatív pólus felé haladva a telep $U_0$ üresjárati feszültségét pozitív előjellel vesszük figyelembe (fordított esetben pedig negatívval), az ellenállásokon eső feszültséget ($U=RI$) pedig akkor vesszük pozitív előjellel számításba, ha a körüljárási irány és a bejelölt ág áram iránya megegyezik (ellenkező esetben pedig negatívval). |
* Megoldjuk az egyenletrendszert. Azok az áramok, amelyek pozitívnak adódnak ténylegesen az előzete-sen felvett irányban folynak. Ha a számítások alapján az áramra negatív érték jön ki, a tényleges áramirány a felvettel éppen ellenkező. | * Megoldjuk az egyenletrendszert. Azok az áramok, amelyek pozitívnak adódnak ténylegesen az előzete-sen felvett irányban folynak. Ha a számítások alapján az áramra negatív érték jön ki, a tényleges áramirány a felvettel éppen ellenkező. | ||
| − | + | Megmutatható, hogy egy áramkör esetében annyi egymástól független egyenlet írható fel, amennyi az ágak – vagyis az áramok – száma. | |
A Kirchhoff-törvények alkalmazásával könnyen megkapható, hogy $n$ darab sorba kapcsolt ellenállás eredője | A Kirchhoff-törvények alkalmazásával könnyen megkapható, hogy $n$ darab sorba kapcsolt ellenállás eredője | ||
| − | + | $$R_s=\sum_{k=i}^n R_i$$ | |
illetve a párhuzamosan kapcsolt ellenállások esetében az eredő reciproka: | illetve a párhuzamosan kapcsolt ellenállások esetében az eredő reciproka: | ||
| − | + | $$\frac{1}{R_p}=\sum_{i=1}^n \frac{1}{R_i}$$ | |
| − | Az áramkörbe be nem kötött, ún. nyitott telep sarkai között fellépő feszültség az | + | Az áramkörbe be nem kötött, ún. nyitott telep sarkai között fellépő feszültség az üresjárati feszültség ($U_0$), melynek nagysága megegyezik a telep elektromotoros erejével. Az áramkörbe bekötött (árammal átjárt) telep sarkai között fennálló feszültség a kapocsfeszültség ($U_k$). Ennek értéke és előjele a telepen átfolyó áram irányától és nagyságától függően az üresjárási feszültségétől igen különböző lehet. Az eltérés az $R_b$ belső ellenálláson eső feszültségből adódik: |
| − | + | ||
| + | $$U_k=U_0-R_bI$$ | ||
===Áram és feszültség mérése=== | ===Áram és feszültség mérése=== | ||
A lap 2012. február 2., 21:33-kori változata
Tartalomjegyzék[elrejtés] |
A mérés célja:
- megismerkedni a legfontosabb elektromos jellemzők (az áram, a feszültség és az ellenállás) mérésének néhány egyszerű módszerével.
Ennek érdekében:
- áttekintjük az egyenáramú áramkörök törvényszerűségeit,
- ismertetjük a gyakorlat során alkalmazott mérési módszereket,
- egyszerű felépítésű áramkörök jellemzőit vizsgáljuk.
Elméleti összefoglaló
Az egyenáramú körökkel kapcsolatos alapfogalmak és törvények rövid összefoglalása
A töltéshordozók áramlásának intenzitását jellemző mennyiség az áramerősség
![\[I=\frac{{\rm d}Q}{{\rm d}t}\]](/images/math/c/1/d/c1dc84d50abe61ab7ea9c23f7be10f5b.png)
ahol 
egy adott felületen átáramló töltést és 
az időt jelenti. Az áramerősség egysége az amper (A). Az egyenáram irányát – megállapodás alapján – a pozitív töltéshordozók mozgásának iránya adja meg. Egyenáramról beszélünk, ha az áram erőssége időben állandó.
Egy vezető két pontja között levő 
potenciálkülönbség (feszültség) áram kialakulásához vezet. A vezetőre kapcsolt feszültség és a benne folyó áram között sok esteben (pl. fémes vezetőkben) az
![\[U=RI\]](/images/math/d/a/7/da7dfc4aaac334c33bcb08664604f794.png)
összefüggés – az Ohm törvény – áll fenn. Itt 
a vezető ellenállása, amely a geometriai adatoktól (
hosszúság és 
keresztmetszet) valamint a vezető anyagától (
fajlagos ellenállás ) az alábbi módon függ:
![\[R=\rho\frac{l}{A}\]](/images/math/9/7/6/976cfd771443eee081282dffb56840c6.png)
A fajlagos ellenállás – sok más anyagi jellemzőhöz hasonlóan – hőmérsékletfüggő:
![\[\rho=\rho_0\left[1+\alpha(t-t_0)+\beta(t-t_0)^2+...\right]\]](/images/math/7/4/0/740ec02430313e290154d4d285124a6a.png)
ahol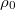 
a fajlagos ellenállás 
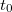hőmérsékleten, 
, 
, ... stb. anyagi állandók és a fajlagos ellenállás hőmérsékleten felvett értéke. A vizsgált hőmérsékleti tartomány nagysága és a kívánt pontosság meghatározza, hogy konkrét esetben a fajlagos ellenállás hőmérsékletfüggésének leírásánál milyen közelítést alkalmazunk, azaz a kifejezésben hányadrendű tagig megyünk el.
Egyenáramú áramkörökkel kapcsolatos számításokat a Kirchhoff-törvények segítségével végezhetünk. A töltésmegmaradás törvényének kifejezése az úgynevezett csomóponti törvény: egy csomópontba összefutó áramok előjeles összege nulla. Ha a ki- és befolyó áramokat ellentétes előjelűnek tekintjük:
![\[\sum_{i=1}^n I_i=0\]](/images/math/e/d/0/ed0ab427e26431a3a1a2d79e07330421.png)
Az energiamegmaradás törvényének következménye a huroktörvény, mely szerint egy zárt vezetőhurok feszültségeinek előjeles összege zérus:
![\[\sum_{i=1}^n U_i=0\]](/images/math/0/8/5/0851e4174ef34b149e0a18de582eb0fc.png)
A Kirchhoff-törvények alkalmazásának egy lehetséges módja az alábbi:
- Felrajzoljuk az áramkört és bejelöljük a telepek polaritását.
- Tetszőlegesen felvesszük az ág áramokat és bejelöljük az irányukat.
- Bejelöljük a hurkokban tetszőleges körüljárási irányokat.
- Felírjuk a csomóponti egyenleteket. (Például a csomópontba befolyó áramokat tekintjük pozitívnak, a kifolyókat pedig negatívnak.)
- Felírjuk a hurokegyenleteket. Ilyenkor pl. úgy járhatunk el, hogy a telepeken a pozitív pólustól a negatív pólus felé haladva a telep
üresjárati feszültségét pozitív előjellel vesszük figyelembe (fordított esetben pedig negatívval), az ellenállásokon eső feszültséget (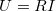
) pedig akkor vesszük pozitív előjellel számításba, ha a körüljárási irány és a bejelölt ág áram iránya megegyezik (ellenkező esetben pedig negatívval).
- Megoldjuk az egyenletrendszert. Azok az áramok, amelyek pozitívnak adódnak ténylegesen az előzete-sen felvett irányban folynak. Ha a számítások alapján az áramra negatív érték jön ki, a tényleges áramirány a felvettel éppen ellenkező.
Megmutatható, hogy egy áramkör esetében annyi egymástól független egyenlet írható fel, amennyi az ágak – vagyis az áramok – száma.
A Kirchhoff-törvények alkalmazásával könnyen megkapható, hogy 
darab sorba kapcsolt ellenállás eredője
![\[R_s=\sum_{k=i}^n R_i\]](/images/math/1/b/2/1b2531feef0ae8bd4cbee70c5ebb1371.png)
illetve a párhuzamosan kapcsolt ellenállások esetében az eredő reciproka:
![\[\frac{1}{R_p}=\sum_{i=1}^n \frac{1}{R_i}\]](/images/math/c/c/8/cc8c9f16cafd86b5d9071a4c8ed1dd4f.png)
Az áramkörbe be nem kötött, ún. nyitott telep sarkai között fellépő feszültség az üresjárati feszültség (), melynek nagysága megegyezik a telep elektromotoros erejével. Az áramkörbe bekötött (árammal átjárt) telep sarkai között fennálló feszültség a kapocsfeszültség (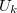
). Ennek értéke és előjele a telepen átfolyó áram irányától és nagyságától függően az üresjárási feszültségétől igen különböző lehet. Az eltérés az 
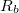belső ellenálláson eső feszültségből adódik:
![\[U_k=U_0-R_bI\]](/images/math/2/3/d/23d30fd9a10e698b33003e9eaca922de.png)
