„2. Mérés: Nemlineáris eszköz vizsgálata, oszcilloszkóp használata” változatai közötti eltérés
A Fizipedia wikiből
| 18. sor: | 18. sor: | ||
$$ I=\frac{1}{R}U, $$ | $$ I=\frac{1}{R}U, $$ | ||
| − | ahol $I$ az $R$ ellenálláson folyó áram, $U$ pedig a rajta eső feszültség. | + | ahol $I$ az $R$ ellenálláson folyó áram, $U$ pedig a rajta eső feszültség. A vezetőképességet, $G$ az ellenállás inverzeként szokás definiálni, mértékegysége $S$ (1 Siemens = 1 $\Omega^{-1}$). |
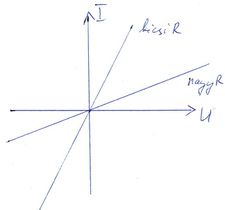
| [[File:IV_R.jpg|225px|thumb|right|Kis és nagy ohmikus ellenállás áram-feszültség karakterisztikája]] | | [[File:IV_R.jpg|225px|thumb|right|Kis és nagy ohmikus ellenállás áram-feszültség karakterisztikája]] | ||
|} | |} | ||
A lap 2019. október 31., 16:17-kori változata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Áram-feszültség karakterisztika
Ohmikus ellenállások áram-feszültség összefüggését Ohm törvénye adja meg:
![\[ I=\frac{1}{R}U, \]](/images/math/9/2/1/9211784a68cb1d6b23c5005cdbe41776.png) ahol |
Egyenirányító dióda
Mérési feladatok
1. Feladat
 az
az  ellenálláson folyó áram,
ellenálláson folyó áram,  pedig a rajta eső feszültség. A vezetőképességet,
pedig a rajta eső feszültség. A vezetőképességet, 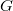 az ellenállás inverzeként szokás definiálni, mértékegysége
az ellenállás inverzeként szokás definiálni, mértékegysége  (1 Siemens = 1
(1 Siemens = 1 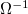 ).
).