„2. Mérés: Nemlineáris eszköz vizsgálata, oszcilloszkóp használata” változatai közötti eltérés
A Fizipedia wikiből
| 18. sor: | 18. sor: | ||
$$ I=\frac{1}{R}U, $$ | $$ I=\frac{1}{R}U, $$ | ||
| − | ahol $I$ az $R$ ellenálláson folyó áram, $U$ pedig a rajta eső feszültség. A vezetőképességet, $G$ az ellenállás inverzeként szokás definiálni, mértékegysége $S$ | + | ahol $I$ az $R$ ellenálláson folyó áram, $U$ pedig a rajta eső feszültség. A vezetőképességet, $G$ az ellenállás inverzeként szokás definiálni, mértékegysége ''Siemens'' (1 $S$ = 1 $\Omega^{-1}$). Általános esetben azonban az $I(U)$ görbe nemlineáris, melyre példa az egyenirányító dióda alább tárgyalt esete. |
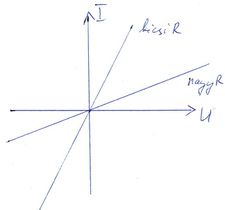
| [[File:IV_R.jpg|225px|thumb|right|Kis és nagy ohmikus ellenállás áram-feszültség karakterisztikája]] | | [[File:IV_R.jpg|225px|thumb|right|Kis és nagy ohmikus ellenállás áram-feszültség karakterisztikája]] | ||
|} | |} | ||
===Egyenirányító dióda=== | ===Egyenirányító dióda=== | ||
| + | {| | ||
| + | |- | ||
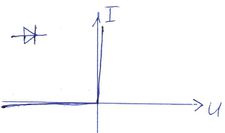
| + | | Az egyenirányító dióda idealizált áram-feszültség összefüggése pozitív feszültségekre egy végtelen nagy míg negatív feszültségekre egy nulla vezetőképességű ellenállással közelíthető. Pozitív feszültségek esetén nyitó- míg negatív feszültségek esetén záróirányról szokás beszélni. | ||
| + | | [[File:IV_D_ideal.jpg|225px|thumb|right|Az egyenirányító dióda idealizált áram-feszültség karakterisztikája]] | ||
| + | |} | ||
| + | {| | ||
| + | |- | ||
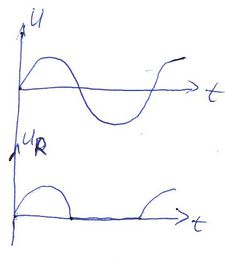
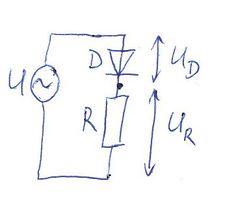
| + | | Ha megvizsgálunk egy szinuszos váltófeszültséggel táplált áramkört, melyben egy ilyen diódát egy $R$ fogyasztóval sorba kapcsolunk, az $R$ ellenálláson csak az egyik félperiodusban mérhetünk véges feszültséget. | ||
| + | | [[File:RD_circuit.jpg|225px|thumb|right|$D$ ideális diódából és $R$ ohmikus ellenállásból álló áramkör.]] | ||
| + | | [[File:Ut.jpg|225px|thumb|right|Tápfeszültés és az $R$ ellenálláson eső feszültségek időfüggése]] | ||
| + | |} | ||
==Mérési feladatok== | ==Mérési feladatok== | ||
A lap 2019. október 31., 16:31-kori változata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Áram-feszültség karakterisztika
Ohmikus ellenállások áram-feszültség összefüggését Ohm törvénye adja meg:
![\[ I=\frac{1}{R}U, \]](/images/math/9/2/1/9211784a68cb1d6b23c5005cdbe41776.png) ahol |
Egyenirányító dióda
| Az egyenirányító dióda idealizált áram-feszültség összefüggése pozitív feszültségekre egy végtelen nagy míg negatív feszültségekre egy nulla vezetőképességű ellenállással közelíthető. Pozitív feszültségek esetén nyitó- míg negatív feszültségek esetén záróirányról szokás beszélni. |
Ha megvizsgálunk egy szinuszos váltófeszültséggel táplált áramkört, melyben egy ilyen diódát egy  fogyasztóval sorba kapcsolunk, az fogyasztóval sorba kapcsolunk, az  ellenálláson csak az egyik félperiodusban mérhetünk véges feszültséget. ellenálláson csak az egyik félperiodusban mérhetünk véges feszültséget.
|
Mérési feladatok
1. Feladat
 az
az  pedig a rajta eső feszültség. A vezetőképességet,
pedig a rajta eső feszültség. A vezetőképességet, 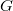 az ellenállás inverzeként szokás definiálni, mértékegysége Siemens (1
az ellenállás inverzeként szokás definiálni, mértékegysége Siemens (1  = 1
= 1 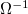 ). Általános esetben azonban az
). Általános esetben azonban az 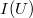 görbe nemlineáris, melyre példa az egyenirányító dióda alább tárgyalt esete.
görbe nemlineáris, melyre példa az egyenirányító dióda alább tárgyalt esete.
 ideális diódából és
ideális diódából és