„2. Mérés: Nemlineáris eszköz vizsgálata, oszcilloszkóp használata” változatai közötti eltérés
| 46. sor: | 46. sor: | ||
| [[File:IV_D_graphical.jpg|250px|thumb|right|Az egyenirányító dióda idealizált áram-feszültség karakterisztikája]] | | [[File:IV_D_graphical.jpg|250px|thumb|right|Az egyenirányító dióda idealizált áram-feszültség karakterisztikája]] | ||
|} | |} | ||
| + | |||
| + | ==Mérésben használt műszerek== | ||
| + | |||
| + | A mérésben a '''National Instruments myDAQ digitalizálókártya''' által szintetizált váltakozó feszültség jelet illetve a mérőkártya által megvalósítótt oszcilloszkópot fogjuk használni. Egy analóg oszcilloszkóp működését az alábbi leírás taglalja: [[https://fizipedia.bme.hu/index.php/Vizsg%C3%A1lat_oszcilloszk%C3%B3ppal]]. A mérőkártya hasonló oszcilloszkópot valósít meg digitálisan. | ||
| + | |||
==Mérési feladatok== | ==Mérési feladatok== | ||
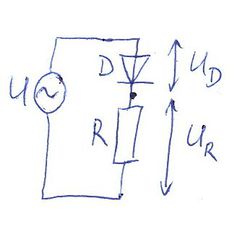
| − | '''1. Feladat''' | + | '''1. Feladat''' A próbapanelen állítsuk össze a fenti diódából és ellenállásból álló kapcsolást! Az $R$ ellenállás legyen 1\,k$\Omega$, a $D$ pedig egy (Schottky) dióda. Az ellenálláson és a diódán eső feszültségeket kapcsoljuk a mérőkártya AI 0+, AI 0- illetve AI 1+, AI 1- csatlakozói közé. U meghajtófeszültséget a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenete szolgáltatja. A függvénygenerátor program segítségével állítsunk elő $f$=200\,Hz frekvenciájú, $V_{pp}$=1.6\,V-os háromszög jelet. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást, valamint a triggert a felfutó élre. Honnan látható a dióda egyenirányító hatása? |
| + | |||
| + | '''2. Feladat''' Rögzítsük mindkét csatornán a feszültség időfüggését, majd az IGOR segítségével olvassuk be a jeleket. Az ellenálláson eső feszültségből számítsuk ki a körben folyó áramot és ábrázoljuk a dióda áram-feszültség karakterisztikáját. Adjunk becslést a nyitófeszültségre! Az ideális dióda I-V görbéjét az alábbi formula adja meg: | ||
| + | $$ I=I_0(exp^\frac{eV}{kT}-1) $$ | ||
| + | ahol $I_0$ a ''szaturációs áram'', $e$ az elektron töltése, $k$ a Boltzmann állandó és $T$ az abszolút hőmérséklet. A mért görbére illesszük a fenti formulát, majd a terem hőmérsékletének ismeretében határozzuk meg az elemi töltés és a Boltzmann állandó hányadosát, és hasonlítsuk össze azt az irodalomból ismert adattal! | ||
</wlatex> | </wlatex> | ||
A lap 2019. október 31., 16:55-kori változata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Áram-feszültség karakterisztika
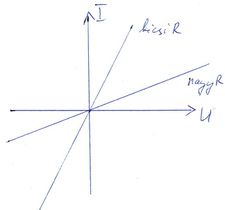
Ohmikus ellenállások áram-feszültség összefüggését Ohm törvénye adja meg:
![\[ I=\frac{1}{R}U, \]](/images/math/9/2/1/9211784a68cb1d6b23c5005cdbe41776.png) ahol |
Egyenirányító dióda
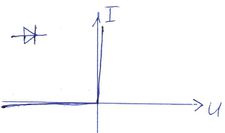
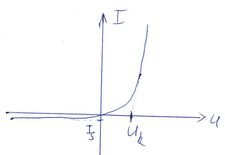
| Az egyenirányító dióda idealizált áram-feszültség összefüggése pozitív feszültségekre egy végtelen nagy míg negatív feszültségekre egy nulla vezetőképességű ellenállással közelíthető. Pozitív feszültségek esetén nyitó- míg negatív feszültségek esetén záróirányról szokás beszélni. |
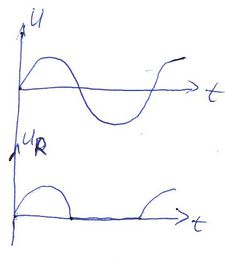
Ha megvizsgálunk egy szinuszos váltófeszültséggel táplált áramkört, melyben egy ilyen diódát egy  fogyasztóval sorba kapcsolunk, az fogyasztóval sorba kapcsolunk, az  ellenálláson csak az egyik félperiodusban mérhetünk véges feszültséget. A pozitív félperiodusban a dióda ellenállása elhanyagolható, így a teljes feszültség az ellenálláson esik. A negatív félperiodusban a dióda ellenállása dominálja az eredő ellenállást, hozzáképest az ellenálláson csak az egyik félperiodusban mérhetünk véges feszültséget. A pozitív félperiodusban a dióda ellenállása elhanyagolható, így a teljes feszültség az ellenálláson esik. A negatív félperiodusban a dióda ellenállása dominálja az eredő ellenállást, hozzáképest az  ellenállás elhanyagolható. ellenállás elhanyagolható.
|
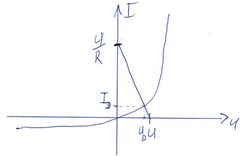
Valódi egyenirányító dióda áram görbéje összefüggése erősen aszimetrikus függvénye a feszültségnek. Pozitív feszültségek esetén egy kritikus, nyitófeszültség felett az áram gyorsan növekszik. Félvezető Ge és Si dióda esetén 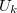 = 0,3..0,4 V illetve 0,6..0,7 V. Valós diódára kapcsolt negatív feszültség estén véges, ún. záróirányú áram folyik, mely tipikusan = 0,3..0,4 V illetve 0,6..0,7 V. Valós diódára kapcsolt negatív feszültség estén véges, ún. záróirányú áram folyik, mely tipikusan  A nagyságú. Egy általános A nagyságú. Egy általános 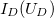 áram-feszültség karakterisztikával rendelkező diódával sorba kapcsolt áram-feszültség karakterisztikával rendelkező diódával sorba kapcsolt  ellenállás a körben folyó áramot illetve a diódán és az ellenálláson eső feszültségeket grafikusan tudjuk meghatározni. A körben azonos ellenállás a körben folyó áramot illetve a diódán és az ellenálláson eső feszültségeket grafikusan tudjuk meghatározni. A körben azonos 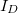 áram halad át a diódán és az ellenálláson is, a körben eső feszültségekre pedig teljesül: áram halad át a diódán és az ellenálláson is, a körben eső feszültségekre pedig teljesül:
![\[U=U_D+RI_D\]](/images/math/7/c/5/7c509f3a40fdd4eb0c5a06be2270f866.png) összefüggést, melyet átrendezve kapjuk a grafikus megoldáshoz szükséges alakot: ![\[\frac{U-U_D}{R}=I_D(U_D).\]](/images/math/3/8/5/3850a7c2a1377ccc88737e83970d9a6d.png) Az egyenlet bal oldala egy egyenest ír le, míg a jobboldalon a dióda áram-feszültség karakterisztikája látható. |
Mérésben használt műszerek
A mérésben a National Instruments myDAQ digitalizálókártya által szintetizált váltakozó feszültség jelet illetve a mérőkártya által megvalósítótt oszcilloszkópot fogjuk használni. Egy analóg oszcilloszkóp működését az alábbi leírás taglalja: [[1]]. A mérőkártya hasonló oszcilloszkópot valósít meg digitálisan.
Mérési feladatok
1. Feladat A próbapanelen állítsuk össze a fenti diódából és ellenállásból álló kapcsolást! Az  ellenállás legyen 1\,k
ellenállás legyen 1\,k , a
, a  pedig egy (Schottky) dióda. Az ellenálláson és a diódán eső feszültségeket kapcsoljuk a mérőkártya AI 0+, AI 0- illetve AI 1+, AI 1- csatlakozói közé. U meghajtófeszültséget a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenete szolgáltatja. A függvénygenerátor program segítségével állítsunk elő
pedig egy (Schottky) dióda. Az ellenálláson és a diódán eső feszültségeket kapcsoljuk a mérőkártya AI 0+, AI 0- illetve AI 1+, AI 1- csatlakozói közé. U meghajtófeszültséget a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenete szolgáltatja. A függvénygenerátor program segítségével állítsunk elő  =200\,Hz frekvenciájú,
=200\,Hz frekvenciájú, 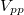 =1.6\,V-os háromszög jelet. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást, valamint a triggert a felfutó élre. Honnan látható a dióda egyenirányító hatása?
=1.6\,V-os háromszög jelet. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást, valamint a triggert a felfutó élre. Honnan látható a dióda egyenirányító hatása?
2. Feladat Rögzítsük mindkét csatornán a feszültség időfüggését, majd az IGOR segítségével olvassuk be a jeleket. Az ellenálláson eső feszültségből számítsuk ki a körben folyó áramot és ábrázoljuk a dióda áram-feszültség karakterisztikáját. Adjunk becslést a nyitófeszültségre! Az ideális dióda I-V görbéjét az alábbi formula adja meg:
![\[ I=I_0(exp^\frac{eV}{kT}-1) \]](/images/math/5/3/6/5365ec46a77b39f0491c7ca9ab440706.png)
ahol 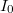 a szaturációs áram,
a szaturációs áram,  az elektron töltése,
az elektron töltése,  a Boltzmann állandó és
a Boltzmann állandó és  az abszolút hőmérséklet. A mért görbére illesszük a fenti formulát, majd a terem hőmérsékletének ismeretében határozzuk meg az elemi töltés és a Boltzmann állandó hányadosát, és hasonlítsuk össze azt az irodalomból ismert adattal!
az abszolút hőmérséklet. A mért görbére illesszük a fenti formulát, majd a terem hőmérsékletének ismeretében határozzuk meg az elemi töltés és a Boltzmann állandó hányadosát, és hasonlítsuk össze azt az irodalomból ismert adattal!
 az
az  pedig a rajta eső feszültség. A vezetőképességet,
pedig a rajta eső feszültség. A vezetőképességet, 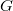 az ellenállás inverzeként szokás definiálni, mértékegysége Siemens (1
az ellenállás inverzeként szokás definiálni, mértékegysége Siemens (1  = 1
= 1 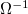 ). Általános esetben azonban az
). Általános esetben azonban az 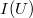 görbe nemlineáris, melyre példa az egyenirányító dióda alább tárgyalt esete.
görbe nemlineáris, melyre példa az egyenirányító dióda alább tárgyalt esete.