„Fotoeffektus vizsgálata” változatai közötti eltérés
| (3 szerkesztő 8 közbeeső változata nincs mutatva) | |||
| 10. sor: | 10. sor: | ||
*Megmérjük egy tranzisztor p-n átmenetének karakterisztikáját | *Megmérjük egy tranzisztor p-n átmenetének karakterisztikáját | ||
*Meghatározzuk különböző színű fénykibocsátó diódák hullámhosszát egy mobiltelefon és egy CD darab segítségével | *Meghatározzuk különböző színű fénykibocsátó diódák hullámhosszát egy mobiltelefon és egy CD darab segítségével | ||
| − | *Megmérjük a | + | *Megmérjük a fénykibocsátó diódák áram-feszültség karakterisztikáját |
*Megmérjük egy vákuumfotodióda lezárási feszültségét különböző intenzitású fénynél és különböző hullámhosszú fénynél | *Megmérjük egy vákuumfotodióda lezárási feszültségét különböző intenzitású fénynél és különböző hullámhosszú fénynél | ||
| 55. sor: | 55. sor: | ||
===Fénykibocsátó dióda (LED)=== | ===Fénykibocsátó dióda (LED)=== | ||
| − | A fotoeffektus tulajdonságaiból adódik, hogy a fenti méréshez olyan fényt kell juttatni a fotocellára, mely monokromatikus. Ez a fénykibocsátó diódákra, azaz a LED-ekre jó közelítéssel teljesül. A LED-ek, ahogy a nevük is mutatja olyan félvezető p-n átmenetek (diódák), melyek fotonokat képesek | + | A fotoeffektus tulajdonságaiból adódik, hogy a fenti méréshez olyan fényt kell juttatni a fotocellára, mely monokromatikus. Ez a fénykibocsátó diódákra, azaz a LED-ekre jó közelítéssel teljesül. A LED-ek, ahogy a nevük is mutatja olyan félvezető p-n átmenetek (diódák), melyek fotonokat képesek kibocsátani, tehát egy, a fotoeffektussal ellentétes folyamat megy bennük végre, amiben a p-n átmeneten áthaladó, majd rekombinálódó elektronok energiát adnak le egy foton kibocsátása formájában. |
====Félvezető p-n átmenet tulajdonságai - e/k állandó meghatározása==== | ====Félvezető p-n átmenet tulajdonságai - e/k állandó meghatározása==== | ||
| 82. sor: | 82. sor: | ||
<span id="fig:1">[[Fájl:Tranzisztor kapcsolása.bmp|közép|bélyegkép|300px|1.ábra: a dióda karakterisztikájának a meghatározásához használt áramkör]]</span>--> | <span id="fig:1">[[Fájl:Tranzisztor kapcsolása.bmp|közép|bélyegkép|300px|1.ábra: a dióda karakterisztikájának a meghatározásához használt áramkör]]</span>--> | ||
| − | Így a [[#eq:5|(5)]] alakú karakterisztikából az $e/k$ hányados elvileg meghatározható, de az összefüggés egyszerűsítésével a feladat is egyszerűsíthető. Mivel méréseinket szobahőmérséklethez közeli hőmérsékleteken végezzük, érvényes, hogy $e^{\frac{eU}{kT} }\gg 1$, így az egyenletben az exponenciális tag mellett az „1” elhanyagolható, mivel a félvezetők jellemző tiltott sávszélessége $ | + | Így a [[#eq:5|(5)]] alakú karakterisztikából az $e/k$ hányados elvileg meghatározható, de az összefüggés egyszerűsítésével a feladat is egyszerűsíthető. Mivel méréseinket szobahőmérséklethez közeli hőmérsékleteken végezzük, érvényes, hogy $e^{\frac{eU}{kT} }\gg 1$, így az egyenletben az exponenciális tag mellett az „1” elhanyagolható, mivel a félvezetők jellemző tiltott sávszélessége $100$ meV nagyságrendű. Ezért jó közelítéssel érvényes, hogy |
{{eq| I{{=}}I_se^{\frac{eU}{kT} }. |eq:6| (6) }} | {{eq| I{{=}}I_se^{\frac{eU}{kT} }. |eq:6| (6) }} | ||
Ha az egyenlet mindkét oldalának a természetes alapú logaritmusát vesszük, akkor az $I–U$ összefüggés linearizálható, hiszen | Ha az egyenlet mindkét oldalának a természetes alapú logaritmusát vesszük, akkor az $I–U$ összefüggés linearizálható, hiszen | ||
| − | {{eq|ln I {{=}}ln I_s+\frac{e}{kT}U. |eq:7| (7)}} | + | {{eq|\ln I {{=}}\ln I_s+\frac{e}{kT}U. |eq:7| (7)}} |
Ez azt jelenti, hogy ha a hőmérsékletet állandó értéken tartva megmérjük az áram-feszültség karakterisztikát, majd az áramértékek természetes logaritmusát ábrázoljuk a feszültség függvényében, akkor a pontok egy egyenest adnak. Jelölje a mérési pontokhoz illesztett egyenes meredekségét $M_U$. | Ez azt jelenti, hogy ha a hőmérsékletet állandó értéken tartva megmérjük az áram-feszültség karakterisztikát, majd az áramértékek természetes logaritmusát ábrázoljuk a feszültség függvényében, akkor a pontok egy egyenest adnak. Jelölje a mérési pontokhoz illesztett egyenes meredekségét $M_U$. | ||
{{eq| M_U{{=}}\frac{e}{kT} |eq:8| (8)}} | {{eq| M_U{{=}}\frac{e}{kT} |eq:8| (8)}} | ||
összefüggés, amiből az $e/k$ hányadosra azt kapjuk, hogy | összefüggés, amiből az $e/k$ hányadosra azt kapjuk, hogy | ||
| − | {{eq| \frac{e}{k} {{=}}M_UT |eq:9| (9)}} | + | {{eq| \frac{e}{k} {{=}}M_UT. |eq:9| (9)}} |
Ezzel a hőmérséklet ismeretében meghatározható az $e/k$ arány. | Ezzel a hőmérséklet ismeretében meghatározható az $e/k$ arány. | ||
| − | ====Planck-állandó és | + | ====A Planck-állandó és az elektrontöltés arányának meghatározása LED-ekkel==== |
| − | Ahogy már említettük, a LED-ek gyakorlatilag p-n átmenetek, melyek kontaktpotenciálja az $1-3V$-os tartományba esik. Ha a LED-re „nyitóirányban” feszültséget kapcsolunk, az a kialakult kontaktpotenciált csökkenti és egy diódára jellemző értéknél (ún. nyitófeszültség) kiegyenlíti, ekkor az elektronok/lyukak áramlása jelentősen megnő, ezáltal a diódán áram folyik. Ennek következtében a p-n átmenet határára folyamatosan töltéshordozók érkeznek és ott rekombinálódnak, mely során a félvezető tiltott sávnak megfelelő | + | Ahogy már említettük, a LED-ek gyakorlatilag p-n átmenetek, melyek kontaktpotenciálja az $1-3V$-os tartományba esik. Ha a LED-re „nyitóirányban” feszültséget kapcsolunk, az a kialakult kontaktpotenciált csökkenti és egy diódára jellemző értéknél (ún. nyitófeszültség) kiegyenlíti, ekkor az elektronok/lyukak áramlása jelentősen megnő, ezáltal a diódán áram folyik. Ennek következtében a p-n átmenet határára folyamatosan töltéshordozók érkeznek és ott rekombinálódnak, mely során a félvezető tiltott sávnak megfelelő energiát adnak le fotonok formájában, így a LED fényt bocsát ki. Ezzel gyakorlatilag a fotoeffektus ellentétes folyamata játszódik le és mivel a LED nyitófeszültsége jó közelítéssel (idealizált esetben) arányos a tiltott sáv szélességével, különböző színű LED-ek nyitófeszültségének és a kibocsátott fényük frekvenciájának vizsgálatával szintén meghatározható a $h/e$ arány. |
<!-- | <!-- | ||
Tekintsünk vissza a [[#eq:7|7]]. képletre, melyben szerepel az $I_s$ telítési áram logaritmusa, ami a [[#eq:3|3]]. képlet alapján arányos az $U_D$ kontaktpotenciállal, azaz: | Tekintsünk vissza a [[#eq:7|7]]. képletre, melyben szerepel az $I_s$ telítési áram logaritmusa, ami a [[#eq:3|3]]. képlet alapján arányos az $U_D$ kontaktpotenciállal, azaz: | ||
| 101. sor: | 101. sor: | ||
Ezt az összefüggést helyettesítsük vissza a [[#eq:7|7]]. képletbe: | Ezt az összefüggést helyettesítsük vissza a [[#eq:7|7]]. képletbe: | ||
{{eq|ln I {{=}}\frac{e}{kT}U -\frac{e}{kT} U_{D} + ln C, |eq:11| (11)}} | {{eq|ln I {{=}}\frac{e}{kT}U -\frac{e}{kT} U_{D} + ln C, |eq:11| (11)}} | ||
| − | aminek eredményeként egy $U$ - $ln I$ grafikonon egyenest adó kifejezést kapunk, és az illesztett egyenes meredeksége ($A$) megadja az $e/kT$ arányt, míg a tengelymetszet ($B$) az $-eU_{D}/kT+ln C$ étékét, ebből az $U_D$ | + | aminek eredményeként egy $U$ - $ln I$ grafikonon egyenest adó kifejezést kapunk, és az illesztett egyenes meredeksége ($A$) megadja az $e/kT$ arányt, míg a tengelymetszet ($B$) az $-eU_{D}/kT+ln C$ étékét, ebből az $U_D$ feszültség kifejezhető az alábbi formulával: |
{{eq|U_{D} {{=}}- \frac{B}{A} - \frac{kT}{e} ln C, |eq:12| (12)}}. | {{eq|U_{D} {{=}}- \frac{B}{A} - \frac{kT}{e} ln C, |eq:12| (12)}}. | ||
Ezt átrendezve és a $-B/A=U_{s}$ jelölést bevezetve a [[#eq:5|5]]. egyenlethez hasonló összefüggést kapunk: | Ezt átrendezve és a $-B/A=U_{s}$ jelölést bevezetve a [[#eq:5|5]]. egyenlethez hasonló összefüggést kapunk: | ||
| 108. sor: | 108. sor: | ||
===Hullámhossz meghatározása diffrakció segítségével=== | ===Hullámhossz meghatározása diffrakció segítségével=== | ||
| − | A tapasztalat szerint egy akadály mellett elhaladó fénysugár az akadályoknál részben elhajlik, behatol az árnyéktérbe is. Ez a diffrakció (fényelhajlás) jelensége. A jelenséget a "Huygens-Fresnel-elv" segítségével lehet | + | A tapasztalat szerint egy akadály mellett elhaladó fénysugár az akadályoknál részben elhajlik, behatol az árnyéktérbe is. Ez a diffrakció (fényelhajlás) jelensége. A jelenséget a "Huygens--Fresnel-elv" segítségével lehet megmagyarázni: a Huygens--Fresnel-elv alapján a hullámfelület minden pontja elemi hullámforrásnak tekintendő, és ezeknek az egymással koherens elemi gömbhullámoknak az interferenciája szabja meg a tér egy pontjában a fényhatást. |
{{fig2|Opt_2_kep_3.JPG|fig:2|2. ábra}} | {{fig2|Opt_2_kep_3.JPG|fig:2|2. ábra}} | ||
| 227. sor: | 227. sor: | ||
* '''FIGYELEM!''' A lámpa doboza hűtőbordaként funkcionál és működés közben felmelegszik, ezért mindig óvatosan érintse meg! | * '''FIGYELEM!''' A lámpa doboza hűtőbordaként funkcionál és működés közben felmelegszik, ezért mindig óvatosan érintse meg! | ||
'''b)''' Amíg a lámpa bemelegszik állítsa össze a mérési elrendezést! | '''b)''' Amíg a lámpa bemelegszik állítsa össze a mérési elrendezést! | ||
| − | * '' | + | * '' Ragasszon a mobiltelefon kamerája elé egy CD darabot! |
| − | + | ||
* '' Helyezze be a telefont a tartóba és irányítsa rá a higanygőzlámpára. A telefonnal vizsgálja meg a lámpa spektrumát. Ahogy a lámpa melegszik, egyre jobban kivehetők a spektrum jellegzetes komponensei. Érdemes néhány fotót is készíteni! | * '' Helyezze be a telefont a tartóba és irányítsa rá a higanygőzlámpára. A telefonnal vizsgálja meg a lámpa spektrumát. Ahogy a lámpa melegszik, egyre jobban kivehetők a spektrum jellegzetes komponensei. Érdemes néhány fotót is készíteni! | ||
'''c)''' Helyezze a milliméterpapírral ellátott lapot a higanygőzlámpa elé a lehető legszorosabban! Vegye figyelembe, hogy a kalibráció után sem a mobiltelefon, sem a lap nem szabad, hogy elmozduljon! | '''c)''' Helyezze a milliméterpapírral ellátott lapot a higanygőzlámpa elé a lehető legszorosabban! Vegye figyelembe, hogy a kalibráció után sem a mobiltelefon, sem a lap nem szabad, hogy elmozduljon! | ||
| 250. sor: | 249. sor: | ||
* '' A LED hosszabbik lába az anód, ezt kell a pozitív aljzathoz csatlakoztatni (kivéve fekete bevonatos LD271 infra LED-et)! Mindig ügyeljen a megfelelő polaritásra! | * '' A LED hosszabbik lába az anód, ezt kell a pozitív aljzathoz csatlakoztatni (kivéve fekete bevonatos LD271 infra LED-et)! Mindig ügyeljen a megfelelő polaritásra! | ||
| − | '''c)''' Kapcsolja fel a kapcsolót, ha mindent megfelelően csinált, akkor a LED világítani fog! Olvassa le a mellékmaximum | + | '''c)''' Kapcsolja fel a kapcsolót, ha mindent megfelelően csinált, akkor a LED világítani fog! Olvassa le a mellékmaximum pozicióját, valamint készítsen fotókat a mérésről! |
* '' A mérést sötétben/félhomályban végezze! A fényviszonyoktól függően elképzelhető, hogy nehéz úgy beállítani a telefon expozícióját, hogy a milliméterpapír beosztásai és a fényfoltok is jól látszódjanak a képen. Ekkor használjon egy plusz fényforrást (pl. egy másik telefon vakuját) és azzal világítsa meg az elrendezést! | * '' A mérést sötétben/félhomályban végezze! A fényviszonyoktól függően elképzelhető, hogy nehéz úgy beállítani a telefon expozícióját, hogy a milliméterpapír beosztásai és a fényfoltok is jól látszódjanak a képen. Ekkor használjon egy plusz fényforrást (pl. egy másik telefon vakuját) és azzal világítsa meg az elrendezést! | ||
* '' A milliméterpapírt semmiképpen se firkálja össze! | * '' A milliméterpapírt semmiképpen se firkálja össze! | ||
| 281. sor: | 280. sor: | ||
'''c)''' Ábrázolja az $I_{C}(V_{BE})$ görbét lineáris skálájú (lin-lin) grafikonon és logaritmikus y skálájú (lin-log) grafikonon is! Utóbbi grafikon alapján határozza meg a zajszintet, illetve vizsgálja meg, hogy a nagyobb $V_{BE}$ értékeknél is teljesül-e az exponenciális függés (azaz lin-log skálán egyenes jelleg). | '''c)''' Ábrázolja az $I_{C}(V_{BE})$ görbét lineáris skálájú (lin-lin) grafikonon és logaritmikus y skálájú (lin-log) grafikonon is! Utóbbi grafikon alapján határozza meg a zajszintet, illetve vizsgálja meg, hogy a nagyobb $V_{BE}$ értékeknél is teljesül-e az exponenciális függés (azaz lin-log skálán egyenes jelleg). | ||
| − | '''d)''' Készítsen egy olyan | + | '''d)''' Készítsen egy olyan függvényt Matlabban, ami levágja az adatokat a megadott minimum (pl. zajszint) és maximum (pl. exponenciális viselkedés határa) alatt és felett, és a megtartott adatokra egyenest illeszt! Az illesztett egyenes meredekségéből határozza meg az $e/k$ arányt és vesse össze az irodalmi értékkel! |
*'' Az $e/k$ arány meghatározásához ismernie kell a hőmérsékletet. Ezt egy higanyos hőmérővel mérheti meg, melyet a mérésvezetőtől kérhet el. | *'' Az $e/k$ arány meghatározásához ismernie kell a hőmérsékletet. Ezt egy higanyos hőmérővel mérheti meg, melyet a mérésvezetőtől kérhet el. | ||
*'' Ha időhiányban szenved, akkor a gyakorlaton elvégezheti a feladatot függvénykészítés nélkül, azonban otthon érdemes megcsinálnia a függvényt, mert a LED-ek I(V) karakterisztikájának mérésekor visszatérő feladat lesz az adatok levágása és az illesztés elvégzése! | *'' Ha időhiányban szenved, akkor a gyakorlaton elvégezheti a feladatot függvénykészítés nélkül, azonban otthon érdemes megcsinálnia a függvényt, mert a LED-ek I(V) karakterisztikájának mérésekor visszatérő feladat lesz az adatok levágása és az illesztés elvégzése! | ||
| 298. sor: | 297. sor: | ||
===5. $h/e$ arány meghatározása LED-ek nyitófeszültsége alapján=== | ===5. $h/e$ arány meghatározása LED-ek nyitófeszültsége alapján=== | ||
| − | '''a)''' Készítse el az $ | + | '''a)''' Készítse el az $f - U_{nyito}$ grafikont! |
*''Számolja ki a különböző LED-ekhez tartozó frekvenciát a hullámhosszakból! Elméleti megfontolások alapján az ideális viselkedéstől való eltérést (pl. nem monokromatikus spektrum, nem megfelelő I(V) karakterisztika) hibaként vegye figyelembe! Ezt jelölje a grafikonon is! | *''Számolja ki a különböző LED-ekhez tartozó frekvenciát a hullámhosszakból! Elméleti megfontolások alapján az ideális viselkedéstől való eltérést (pl. nem monokromatikus spektrum, nem megfelelő I(V) karakterisztika) hibaként vegye figyelembe! Ezt jelölje a grafikonon is! | ||
| 320. sor: | 319. sor: | ||
===7. $h/e$ arány meghatározása fotocellával=== | ===7. $h/e$ arány meghatározása fotocellával=== | ||
| − | '''a)''' Készítse el az $ | + | '''a)''' Készítse el az $f - U_{foto}$ grafikont! |
*''Számolja ki a különböző LED-ekhez tartozó frekvenciát a hullámhosszakból! Elméleti megfontolások alapján az ideális viselkedéstől való eltérést (pl. nem monokromatikus spektrum, nem megfelelő I(V) karakterisztika) hibaként vegye figyelembe! Ezt jelölje a grafikonon is! | *''Számolja ki a különböző LED-ekhez tartozó frekvenciát a hullámhosszakból! Elméleti megfontolások alapján az ideális viselkedéstől való eltérést (pl. nem monokromatikus spektrum, nem megfelelő I(V) karakterisztika) hibaként vegye figyelembe! Ezt jelölje a grafikonon is! | ||
A lap jelenlegi, 2024. október 2., 13:02-kori változata
A mérés célja:
- Megismerkedni a fényelektromos jelenségekkel, a fénykibocsátó diódákkal és egyéb félvezető átmenetekkel, valamint a diffrakció jelenségével,
- megismerkedni a myDAQ adatgyűjtő kártyával és gyakorlatot szerezni a Matlabbal történő mérésvezérlésben.
- Igazolni, hogy a fotoelektronok kinetikus energiája, illetőleg a vele arányos lezáró feszültség független a fény intenzitásától,
- továbbá az
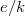és a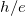 
arány meghatározása méréssel.
Ennek érdekében:
- Megmérjük egy tranzisztor p-n átmenetének karakterisztikáját
- Meghatározzuk különböző színű fénykibocsátó diódák hullámhosszát egy mobiltelefon és egy CD darab segítségével
- Megmérjük a fénykibocsátó diódák áram-feszültség karakterisztikáját
- Megmérjük egy vákuumfotodióda lezárási feszültségét különböző intenzitású fénynél és különböző hullámhosszú fénynél
Elméleti összefoglaló
A fotoeffektus
A külső fényelektromos hatás alapjelensége: ha egy fémlemezre fény esik, a lemezből elektronok lépnek ki. E jelenség vizsgálata néhány olyan eredményre vezetett, melyeket a fény folytonos hullámelméletével nem lehet megmagyarázni. Ezek a következők:
- Az elektronok csak akkor lépnek ki, ha a fény frekvenciája nagyobb egy, az illető fémre jellemző határfrekvenciánál. A klasszikus szemlélet szerint azonban a
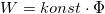feltételnek megfelelő sugárzási intenzitás minden frekvencián biztosítható.
- Megfelelő fényfrekvencia esetén az elektronok kilépése akármilyen gyenge fény hatására azonnal (10-9 s-on belül) bekövetkezik. (A kísérletek során használt fémeknél a kilépési munka 10-19 J nagyságrendű, az elektron által „lefedett” terület, ahonnan energiát gyűjthet ~
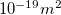, egy átlagos megvilágítást feltételezve, ami 
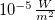, a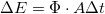 
alapján 
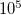s , ~ 28 óra lenne a folyamathoz szükséges idő.)
- A kilépő elektronok száma arányos a megvilágítás erősségével, de energiaeloszlásuk független attól. A maximális mozgási energia a fény frekvenciájának lineáris függvénye, a klasszikus számítások szerint ez nem lineáris.
E kvalitatív tapasztalatok kvantitatív magyarázatát Albert Einstein adta meg azzal, hogy Planck kvantumhipotézisét a fényjelenségekre is kiterjesztette. Feltételezte, hogy a Planck-féle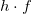 
energiacsomag nem csak a sugárzó oszcillátor diszkrét energiaváltozásait adja meg, hanem a sugárzási térben is 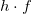adagokban van jelen az energia. A fényenergia diszkrét energiaadagokban terjed. Ezek a fotonok.
Tehát egy foton energiája:
![\[E = h \cdot f \]](/images/math/5/c/0/5c07bee9bace405835bbce9a8dd08e00.png)
ahol 
a Planck-féle állandó, 
pedig a sugárzás– esetünkben a fény – frekvenciája. Az elektronok kilépése csak akkor indulhat meg, ha a beeső fotonok energiája legalább az elektronok kötési energiájával egyenlő. A kilépés feltétele tehát:
![\[ h \cdot f \geq W = h \cdot f_{0} \]](/images/math/1/a/4/1a46565ae3f9a2d869c6e6f813b4772b.png)
ahol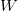 
az elektron kötési energiája, az úgynevezett kilépési munka, 
pedig a fémre jellemző küszöbfrekvencia. Általános esetben:
![\[ h \cdot f = W + \frac{1}{2} m v^2 \]](/images/math/3/4/b/34b779e4ab9bda9585f2c8e861050c97.png)
vagyis a foton energiatöbblete a kilépő elektron kinetikus energiájaként jelenik meg. Nagyobb fényintenzitás több fotont, tehát több kilépő elektront jelent. Ilyen módon magyarázatot nyert a külső fényelektromos jelenség valamennyi felsorolt sajátsága.
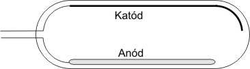
A fényelektromos jelenség egyik legelterjedtebb gyakorlati alkalmazása a fotocella, ami egy légritkított üvegcső, mely egyik oldalán a belső felületére felvitt fémréteg képezi a katódot, a vele szemben elhelyezett dróthurok pedig az anód (1.ábra). Mint a (3) egyenletből látható, a határfrekvencia esetétől eltekintve a kilépő elektronok kinetikus energiával is rendelkeznek, ami feszültségmentes tér esetén elegendő ahhoz, hogy az anódig repüljenek, ezért 0 anódfeszültség esetén is mérhető bizonyos – igen kicsi – áram.
Ahhoz, hogy a fotocella tetszőleges megvilágítás ellenére teljesen árammentes legyen, akkora ellenteret kell az anód és a katód között létesíteni, mely a legnagyobb energiájú elektronokat is meggátolja az anód elérésében. Az árammentesség feltétele tehát:
![\[ e U_{0} = \frac{1}{2} m v^2_{max} \]](/images/math/b/1/6/b167bd4a9a4b50f7679105d3418c2382.png)
ahol 
az elektron töltése, 
pedig a lezáró feszültség. A fotocella anódja és a katódja tekinthető egy kapacitásnak, mely a fotoáram hatására elektromosan feltöltődik (ha a kimenetei "lebegnek", azaz nem zárjuk rövidre egy véges ellenállással) mindaddig, amíg potenciálja el nem éri az lezáró feszültséget. Erre az feszültségre a (3) és (4) egyenletekbe a következő kifejezést kapjuk:
![\[ U_{0} = \frac{h}{e} f - \frac{W}{e} \]](/images/math/f/c/7/fc712ba7b78513272126457b561a81b9.png)
A fotocellát különböző, jól meghatározott frekvenciájú fénnyel megvilágítva a - 
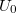grafikonon egy egyenest kapunk, melynek meredeksége a Planck-állandó () és az elektron töltésének () hányadosa.
Fénykibocsátó dióda (LED)
A fotoeffektus tulajdonságaiból adódik, hogy a fenti méréshez olyan fényt kell juttatni a fotocellára, mely monokromatikus. Ez a fénykibocsátó diódákra, azaz a LED-ekre jó közelítéssel teljesül. A LED-ek, ahogy a nevük is mutatja olyan félvezető p-n átmenetek (diódák), melyek fotonokat képesek kibocsátani, tehát egy, a fotoeffektussal ellentétes folyamat megy bennük végre, amiben a p-n átmeneten áthaladó, majd rekombinálódó elektronok energiát adnak le egy foton kibocsátása formájában.
Félvezető p-n átmenet tulajdonságai - e/k állandó meghatározása
Félvezetőkben az elektromos áramot elektronok és lyukak (elektronhiányok) mozgása eredményezi. Bizonyos adalék anyagok (foszfor, arzén) hatására a félvezetőkben az elektronok annyira túlsúlyba kerülnek a lyukakhoz képest, hogy gyakorlatilag csak elektronvezetés alakul ki: az ilyen félvezetőt n típusúnak nevezik. Más adalékok (bór, gallium, alumínium) viszont a félvezetőben lyukvezetést hoznak létre: az ilyen félvezetők a p típusú félvezetők.
Ha egy p típusú és egy n típusú félvezetőt érintkezésbe hozunk (ez az ún. p–n átmenet), akkor az érintkezési helyen kontaktpotenciál jön létre, mert energetikai okok miatt az n típusú részből elektronok mennek át a p típusú részbe (így az negatív többlettöltésre tesz szert), a p típusú részből viszont lyukak mennek át az n típusú részbe (így abban pozitív többlettöltés jön létre). A kontaktus létrejöttének pillanatában tehát egy, a p rétegből az n rétegbe irányuló kezdeti áram folyik. Az áram hatására a potenciálkülönbség nő, ami egyre jobban akadályozza a további töltésátmenetet, ezért egy bizonyos feszültség elérése után a p→n irányú áram megszűnik, és kialakul egy állandósult kontaktpotenciál. Ezzel egyidejűleg a kontaktus két oldalán létrejön egy olyan tartomány, amelyben nincsenek mozgásképes töltéshordozók. A töltéshordozók áthaladását (a p→n irányú áramot) ezen a kiürített tartományon át a létrejött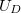 
magasságú potenciálgát akadályozza, ezért külső feszültség nélkül a töltéshordozók csak a termikus mozgás segítségével, véletlenszerűen jutnak át.
Eléggé általánosan igaz, hogy a termikusan aktivált folyamat gyakorisága az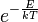 
faktorral arányos, ahol 
a továbbhaladáshoz szükséges energia, 
a Boltzmann-állandó, 
pedig az abszolút hőmérséklet. Ennek megfelelően annak gyakorisága, hogy egy lyuk p→n irányban vagy egy elektron n→p irányban az 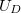magasságú potenciálgáton átugrik, az 
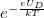faktorral arányos ( az elektron töltésének nagysága). Ez egyben azt is jelenti, hogy a termikus aktiváció segítségével a potenciálgáton át egy p→n irányú, ún. injektált áram folyik:
![\[ I_I = C e^{-\frac{e U_D}{kT} } \]](/images/math/d/5/e/d5ef6635b7ee6ed2836b080edd6ef241.png)
A kiürített tartományon át ugyanakkor létrjön egy ellenkező irányú áram is, ami annak következménye, hogy a termikus mozgás (termikus aktiváció) révén, ha kis számban is, de mindig keletkeznek töltéshordozók, így – többek között – a kiürített réteg n oldalán lyukak, p oldalán pedig elektronok jelennek meg. Mivel a kontaktpotenciál ezeknek a mozgását a kontaktuson át éppen elősegíti, ily módon egy n→p irányú, ún. telítési (szaturációs) áram,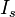 
jön létre. Ez az áram nem függ a kontaktuson kialakult feszültségtől, csak a termikusan keltett töltéshordozók mennyiségétől. Külső feszültség nélküli (egyensúlyi) állapotban a két áram egymást kiegyenlíti, vagyis ekkor 
.
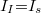Ha a p–n átmenetre 
külső feszültséget kapcsolunk, akkor ez módosítja a potenciálgát magasságát, ezért megváltoztatja az injektált áramot, amely most
![\[ I_I = C e^{-\frac{e\left( U_D - U \right)}{kT} } \]](/images/math/8/d/5/8d52f071d230da35dd0220e54f80dabc.png)
Itt 
állandó, az feszültség pedig negatív, ha a feszültség a kontaktpotenciállal egyirányú, és pozitív, ha azzal ellentétes. Mivel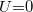 
esetén 
,
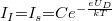![\[ C=I_se^{\frac{eU_D}{kT} }, \]](/images/math/1/3/4/1348ca7c3a4c1bbff6ab1dbb2f69fa94.png)
amivel az injektált áramra azt kapjuk, hogy
![\[ I_I=I_se^{\frac{eU}{kT} }. \]](/images/math/8/2/5/825146574af2ec40b07a5921788d49ac.png)
A kontaktuson átfolyó 
eredő áram a feszültségfüggő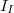 
injektált áram és a feszültségtől független 
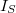telítési áram különbsége:
![\[ I=I_s\left(e^{\frac{eU}{kT} }-1 \right). \]](/images/math/d/c/f/dcf37ff96daa7fc6c936dfd244f50db0.png)
Ez az összefüggés azt az ismert tapasztalatot tükrözi, hogy egy ilyen kontaktus különböző irányban előfeszítve különböző nagyságú áramot bocsát át, más szóval egyenirányít. Az ilyen egyenirányító p–n átmenetet félvezető diódának nevezik.
Ha megvizsgáljuk az (5) egyenlettel leírható áram-feszültség összefüggést (ún. áram–feszültség karakterisztikát), látható, hogy az exponensben megjelenik az elektron töltésének () és a Boltzmann-állandónak () a hányadosa.
Így a (5) alakú karakterisztikából az 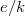hányados elvileg meghatározható, de az összefüggés egyszerűsítésével a feladat is egyszerűsíthető. Mivel méréseinket szobahőmérséklethez közeli hőmérsékleteken végezzük, érvényes, hogy 
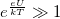, így az egyenletben az exponenciális tag mellett az „1” elhanyagolható, mivel a félvezetők jellemző tiltott sávszélessége 
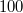meV nagyságrendű. Ezért jó közelítéssel érvényes, hogy
![\[ I=I_se^{\frac{eU}{kT} }. \]](/images/math/f/b/8/fb885b29064cfb53dcb289a9fddeb3e9.png)
Ha az egyenlet mindkét oldalának a természetes alapú logaritmusát vesszük, akkor az 
összefüggés linearizálható, hiszen
![\[\ln I =\ln I_s+\frac{e}{kT}U. \]](/images/math/6/7/c/67caf63f1c4db73137c975bbf3b327b9.png)
Ez azt jelenti, hogy ha a hőmérsékletet állandó értéken tartva megmérjük az áram-feszültség karakterisztikát, majd az áramértékek természetes logaritmusát ábrázoljuk a feszültség függvényében, akkor a pontok egy egyenest adnak. Jelölje a mérési pontokhoz illesztett egyenes meredekségét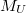 
.
![\[ M_U=\frac{e}{kT} \]](/images/math/d/b/e/dbe303f83138bf5e451e17680d13b539.png)
összefüggés, amiből az 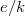hányadosra azt kapjuk, hogy
![\[ \frac{e}{k} =M_UT. \]](/images/math/1/3/a/13a0184c59e2f89e86078103b4f6a05c.png)
Ezzel a hőmérséklet ismeretében meghatározható az 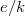arány.
A Planck-állandó és az elektrontöltés arányának meghatározása LED-ekkel
Ahogy már említettük, a LED-ek gyakorlatilag p-n átmenetek, melyek kontaktpotenciálja az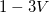 
-os tartományba esik. Ha a LED-re „nyitóirányban” feszültséget kapcsolunk, az a kialakult kontaktpotenciált csökkenti és egy diódára jellemző értéknél (ún. nyitófeszültség) kiegyenlíti, ekkor az elektronok/lyukak áramlása jelentősen megnő, ezáltal a diódán áram folyik. Ennek következtében a p-n átmenet határára folyamatosan töltéshordozók érkeznek és ott rekombinálódnak, mely során a félvezető tiltott sávnak megfelelő energiát adnak le fotonok formájában, így a LED fényt bocsát ki. Ezzel gyakorlatilag a fotoeffektus ellentétes folyamata játszódik le és mivel a LED nyitófeszültsége jó közelítéssel (idealizált esetben) arányos a tiltott sáv szélességével, különböző színű LED-ek nyitófeszültségének és a kibocsátott fényük frekvenciájának vizsgálatával szintén meghatározható a 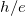arány.
Hullámhossz meghatározása diffrakció segítségével
A tapasztalat szerint egy akadály mellett elhaladó fénysugár az akadályoknál részben elhajlik, behatol az árnyéktérbe is. Ez a diffrakció (fényelhajlás) jelensége. A jelenséget a "Huygens--Fresnel-elv" segítségével lehet megmagyarázni: a Huygens--Fresnel-elv alapján a hullámfelület minden pontja elemi hullámforrásnak tekintendő, és ezeknek az egymással koherens elemi gömbhullámoknak az interferenciája szabja meg a tér egy pontjában a fényhatást.
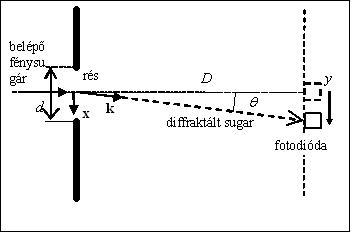
Egyszerű példaképp vizsgáljuk meg az optikai rés esetét. A rés egy átlátszatlan felületen kialakított keskeny, a fény hullámhosszával összemérhető szélességű, hosszú nyílás. Világítsuk meg a rést egy koherens, párhuzamos fénynyalábbal (legegyszerűbben egy lézer fényével). A fény a résen áthaladva elhajlik. A réstől távol elhelyezett ernyőn a résből kiinduló elemi hullámok interferenciája alakítja ki a diffrakciós képet. A diffrakciós képet – az intenzitást a hely függvényében - egy fotodióda mozgatásával könnyen meg lehet mérni (2. ábra).
A k hullámszámvektor irányában a relatív intenzitást a Fourier-integrál segítségével lehet kiszámítani. Az intenzitás arányos az integrál abszolút értékének négyzetével:
![\[ I(\pmb{k}) = \left \lvert \int_{-\infty}^{\infty} e^{\pmb{kx}i}f(\pmb{x})d\pmb{x} \right \rvert^2. \]](/images/math/9/6/6/9663788744b887e93547c4b60e644842.png)
A kifejezésben
![\[|\pmb{k}| = k = \frac{2\pi}{\lambda},\]](/images/math/e/e/d/eede5e35ac948ed5edd2f2c0e0f933f8.png)
![\[\pmb{kx} = kx \sin \theta \approx kx\theta \; (\theta\ll1), \]](/images/math/1/6/3/16352f870f8061cacbb3124b500b23b9.png)
![\[ f(x) = \begin{cases} \frac{1}{d} \; \mathrm{ha} \; x \in \left[-\frac{d}{2};\frac{d}{2}\right] \\ 0\; \mathrm{ha} \; x \notin \left[-\frac{d}{2};\frac{d}{2}\right]. \end{cases} \]](/images/math/8/0/f/80fc88f0461a627382a9bb9ce5f935cc.png)
Felhasználva, hogy
![\[ y = D \mathrm{tg} \theta \approx D\theta \; (\theta<<1), \]](/images/math/f/2/2/f22288c877cdce402826e2269aca0b3b.png)
és elvégezve az integrálást
![\[ I(y) = \left( \frac{\lambda D}{\pi yd} \right)^2\sin^2\left( \frac{\pi yd}{\lambda D} \right).\]](/images/math/0/a/6/0a6a92de54041fb3e92b33500738749a.png)
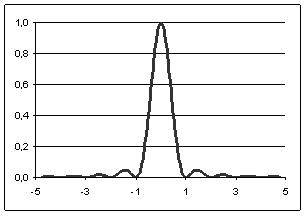
A diffrakciós kép az 3. ábrán látható. A vízszintes tengely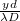 
egységekben van skálázva. Az intenzitás az 
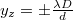helyen válik először zérussá. Az két zérushely közti távolság (
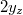) és a 
távolság mérésével a 
hullámhossz ismeretében a 
résszélesség, ismeretében pedig a hullámhossz meghatározható.
Bonyolultabb optikai struktúrák (például egy optikai rács) esetén a diffrakciós kép hasonlóan kiszámítható, csak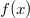 
kifejezését kell ennek megfelelően módosítani. A részletes számítást elvégezve megállapítható, hogy egy optikai rács esetén a maximumok távolsága szintén arányos a hullámhosszal, illetve a geometriai paraméterekkel. Így egy ismert hullámhosszú fényforrás diffrakciós képe alapján egy fixált geometriájú elrendezés kalibrálható és segítségével meghatározható ismeretlen fényforrások hullámhossza.
Méréshez használt eszközök
Pasco fotoeffektus mérőberendezés (4.ábra)
A laborgyakorlat során az egyes feladatokban a 4.ábrán látható Pasco fotoeffektus készletet fogja használni. A készlet elemei:
- Mérőegység (a fotodiódát és az elektronikát tartalmazó doboz)(5.ábra és 6.ábra)
- Higanygőzlámpa, hűtő- és védőburában
- Lépcsős szürke fényszűrő, áteresztőképessége:100, 80, 60 40, 20%
- Sárga és zöld színszűrők
- Optikai rács és lencse együttese, a továbbiakban együtt: rács-lencse
A higanygőzlámpa fénye nem monokromatikus, azonban az optikai rács használatával monokromatikus spektrumvonalakra bontható. Mind az első, mind a második rendben jól megfigyelhetők az alábbi spektrumvonalak:
| szín | hullámhossz |
| sárga | 578 nm |
| zöld | 546 nm |
| kék | 436 nm |
| ibolya1 | 405 nm |
| ibolya2 | 365 nm |
 |
 |
 |
A készlet önállóan alkalmas a fotoeffektus vizsgálatára, a fotodiódát tartalmazó detektorra irányítva a különböző hullámhosszú fény által kialakított fotofeszültség mérhető és ezzel vizsgálható a 5. egyenlet teljesülése és meghatározható a (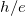) arány. A gyakorlat során viszont nem az eredeti elrendezést, hanem az egyes komponenseket külön-külön használjuk fel. A higanygőzlámpa ismert spektrumával kalibráljuk a CD lemezből és mobiltelefonból kialakított mérőrendszerünket, a fotodetektor segítségével pedig a LED-ek fotofeszültségét határozzuk meg.
National Instruments myDAQ adatgyűjtő kártya
A félvezető eszközök I(V) karakterisztikájának vizsgálatához egy National Instruments myDAQ adatgyűjtőkártyát fog használni, melyet a Matlabbal vezérel. A myDAQ kártya rendelkezik 2-2 db +-10V-os analóg, 1-1db audió, 8db digitális ki- és bemenettel, valamint 5V-os és +-15V-os tápfeszültség kimenettel és digitális multiméter funkcióval. Jelen méréshez a fenti funkciók közül egy analóg kimenetetés két analóg bemenetet használunk.
A mérőkártya programozásával későbbi tanulmányai során fog megismerkedni, jelen labor keretében az alábbi előre elkészített függvényekkel fog dolgozni, melyek elvégzik a mérőkártya konfigurálását és a jelek kiadását/adatgyűjtés:
- A myDAQ_init nevű függvénnyel tudja elvégezni a mérőkártya inicializálását a mérés elején, azaz konfigurálja az "AO0" kimeneti, valamint az "AI0" és "AI1" bemeneti csatornákat, illetve beállítja a 200kHz-es mintavételezési frekvenciát. Ezt a függvényt csak egyszer szükséges meghívni (kivéve, ha újraindítja a Matlab-ot).
- A myDAQ_arb_rw függévénnyel egy tetszőleges pontonként definiált jelet tud a kártya "AO0" csatornáján kiadni, miközben az "AI0" és "AI1" csatornákon mintavételez. A szinkronizálásból adódó problémák elkerülése érdekében a tényleges kiadott jel egy 100ms-os előszakasz és egy szintén 100ms-os utószakaszt is tartalmaz, amik alatt a felhasználó által definiált jel első, illetve utolsó feszültségértékét adja ki a mérőkártya. A függvény egyetlen paramétert vár, magát a kiadandó jelet, mely sor- vagy oszlopvektor formátumú kell legyen és a pontonkénti feszültséget tartalmazza Volt egységben. A maximális engedélyezett amplitúdó +-10V. A függvény kimenetként visszaadja (a felsorolás sorrendjében) az időalapot, a kimenetre küldött programozott jelet és a két bemeneti csatornán mért adatokat.
- A myDAQ_sin_rw függvénnyel egy 0.1Hz-50kHz frekvenciájú és 0.01-5V amplitúdójú megadott számú periódusból álló szinuszjelet tud a kártya "AO0" csatornáján kiadni, miközben az "AI0" és "AI1" csatornákon mintavétele. A függvény egy szoftveres triggerelést valósít meg (felmenő éra), melyhez egy 100ms-os előszakasz és egy szintén 100ms-os utószakasszal egészíti ki a felhasználó által definiált jelet. A függvény első bemeneti paramétere a szinuszjel frekvenciája Hz egységekben, második paramétere a periódusok száma, míg harmadik (opcionális) paramétere az amplitúdó (alapértelmezett értéke 1V). A függvény kimenetként visszaadja (a felsorolás sorrendjében) az időalapot, a kimenetre küldött programozott jelet és a két bemeneti csatornán mért adatokat.
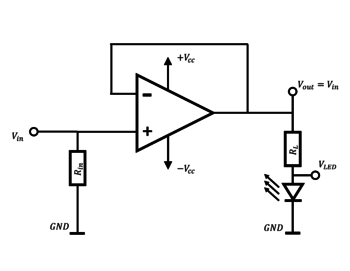
Egyszerű követőerősítő
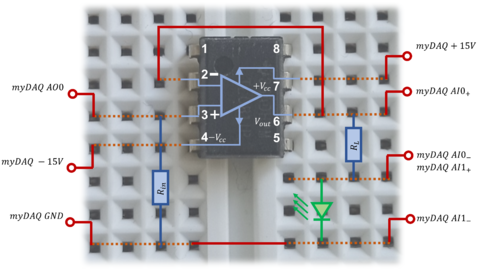
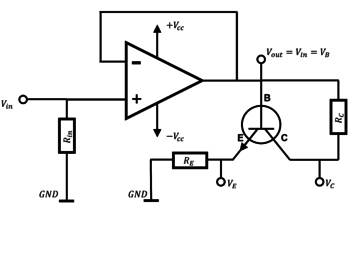
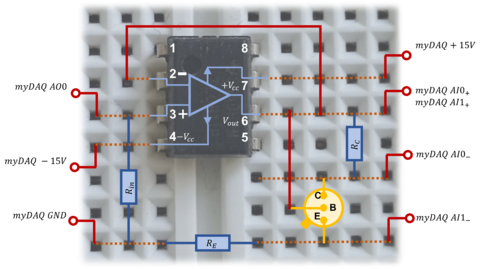
Mivel a myDAQ kártya kimenetének maximális terhelhetősége csak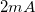 
, a LED-eket viszont 
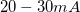-rel szeretnénk meghajtani, ezért egy erősítő áramkört kell alkalmaznunk, melynek kapcsolási rajza és fotója látható a 7. és 8. ábrákon.
 |
 |
Mérési feladatok
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
A fealdatokat nem osztjuk fel első/második alkalom alapján, a méréssel folytonosan lehet haladni. Optimális esetben az első alkalmon legalább a 3. feladatot be kell fejezni.
1. Hullámhossz mérésére alkalmazott elrendezés kalibrálása higanygőzlámpával
a) Kapcsolja be a higanygőzlámpát. Hagyja legalább 10 percig bemelegedni.
- FIGYELEM! Ahogy a fenti táblázatból is látszik, a higanygőzlámpa spektruma UV komponenseket is tartalmaz. Biztonsági okokból ne nézzen bele közvetlenük a lámpa fényébe!
- FIGYELEM! A lámpa doboza hűtőbordaként funkcionál és működés közben felmelegszik, ezért mindig óvatosan érintse meg!
b) Amíg a lámpa bemelegszik állítsa össze a mérési elrendezést!
- Ragasszon a mobiltelefon kamerája elé egy CD darabot!
- Helyezze be a telefont a tartóba és irányítsa rá a higanygőzlámpára. A telefonnal vizsgálja meg a lámpa spektrumát. Ahogy a lámpa melegszik, egyre jobban kivehetők a spektrum jellegzetes komponensei. Érdemes néhány fotót is készíteni!
c) Helyezze a milliméterpapírral ellátott lapot a higanygőzlámpa elé a lehető legszorosabban! Vegye figyelembe, hogy a kalibráció után sem a mobiltelefon, sem a lap nem szabad, hogy elmozduljon!
- Az esetleges rövidzárlat elkerülése érdekében a dugasztáp csatlakozóját mindenképpen húzza ki a lapon található foglalatból!
- A telefont mozgassa úgy, hogy a főmaximumot és a mellékmaximumokat összekötő vonal a milliméterpapír vonalaival párhuzamos legyen! Ez megkönnyíti majd a pozíciók leolvasását.
- A kalibráció befejeztével a higanygőzlámpát el kell mozdítani (félre kell tenni), de a mobiltelefont és a lapot nem szabad megmozdítani. Ügyeljen arra, hogy az elrendezést úgy állítsa össze, hogy a higanygőzlámpa eltávolítása után a lap hátulja jól hozzáférhető legyen, mert a következő feladatban ide kell csatlakoztatni a különböző LED-eket.
d) Olvassa le a higanygőzlámpa spektrumának különböző komponenseihez tartozó pozíciókat a milliméterpapírról és készítsen kalibrációs egyenest! Mindenképpen készítsen fotót is a mérésről!
- A spektrumból általában a sárga és zöld, illetve a kék (enyhén lilába hajló színnel) komponens látszik jól kivehetően, de beállítástól függően megjelenhet a többi komponens is.
- A mérést sötétben/félhomályban végezze! A fényviszonyoktól függően elképzelhető, hogy nehéz úgy beállítani a telefon expozícióját, hogy a milliméterpapír beosztásai és a fényfoltok is jól látszódjanak a képen. Ekkor használjon egy plusz fényforrást (pl. egy másik telefon vakuját) és azzal világítsa meg az elrendezést!
- Ha a higanygőzlámpa fénye túl erős, akkor egy papírdarabbal takarja ki a nyílás egy részét, így élesebb vonalakat kaphat a maximumok helyén.
- A milliméterpapírt semmiképpen se firkálja össze!
- FIGYELEM! Ha befejezte a mérést, kapcsolja ki a higanygőzlámpát és húzza ki a hálózati aljzatból, majd tegye félre úgy, hogy a későbbi feladatokban ne zavarja!
2. LED-ek hullámhosszának meghatározása
a) Csatlakoztassa a dugasztápot a milliméterpapírral ellátott laphoz és állítsa a kapcsolót kikapcsolt állapotba!
- A táp csatlakoztatásakor stabilan fogja meg a lapot, hogy ne tudjon elmozdulni! Amennyiben a lap a feladat során elmozdul, a korábbi kalibrációt és az addigi méréseket meg kell ismételni!
b) Óvatosan helyezzen egy LED-et a lap hátulján lévő sorkapocsba, majd rögzítse a csavarokkal! Ha megtörtént, akkor óvatosan hajtsa meg a LED lábait úgy, hogy a LED csúcspontja a lapon található lyukhoz essen!
- Most is nagyon figyeljen arra, hogy a lap ne mozduljon el!
- A LED hosszabbik lába az anód, ezt kell a pozitív aljzathoz csatlakoztatni (kivéve fekete bevonatos LD271 infra LED-et)! Mindig ügyeljen a megfelelő polaritásra!
c) Kapcsolja fel a kapcsolót, ha mindent megfelelően csinált, akkor a LED világítani fog! Olvassa le a mellékmaximum pozicióját, valamint készítsen fotókat a mérésről!
- A mérést sötétben/félhomályban végezze! A fényviszonyoktól függően elképzelhető, hogy nehéz úgy beállítani a telefon expozícióját, hogy a milliméterpapír beosztásai és a fényfoltok is jól látszódjanak a képen. Ekkor használjon egy plusz fényforrást (pl. egy másik telefon vakuját) és azzal világítsa meg az elrendezést!
- A milliméterpapírt semmiképpen se firkálja össze!
- Érdemes több fotót készítenie, hogy a PC-n megtekintve a kiértékelés során ki tudja választani a legjobbat.
d) Ismételje meg a b-c) lépéseket a többi LED-del is! Mérjen meg minél több LED-et és elemezze a "spektrumukat"! Mit tapasztal?
- Az LD271 típusú infra LED (fekete bevonatos LED) maximumát nem biztos, hogy látni fogja a telefonnal, ebben az esetben használja a LED itt elérhető adatlapját a hullámhossz meghatározására!
- A megmért LED-eket mind az első, mint a második alkalom további feladataiban használni fogja, ezért fontos, hogy tegye őket el úgy, hogy később azonosítani tudja!
e) Határozza meg az egyes LED-ek hullámhosszát! Készítsen egy fotomontázst a mérés fotóiból, melyen egyszerre látszanak a különböző színű LED-ek mellékmaximumai!
- Ha nincs ideje, akkor a hullámhosszak meghatározásához a gyakorlat alatt használhatja a leolvasott pozíciókat is, de otthon készítse el az összevágott fotókból a fotomontázst!
- A fotók összevágásához javasolt a Power Point használata, de természetesen egyéb megoldásokat is használhat!
- Ha az elrendezés stabil volt a mérése alatt, akkor a különböző fotók megfelelő részei teljesen passzolnak egymáshoz! A milliméterpapír beosztásainak alapos szemrevételezésével meg tudja állapítani, hogy elmozdult-e az elrendezés. Amennyiben túlzott elmozdulást tapasztal, a mérést a második alkalom során ismételje meg!
3. Félvezető p-n átmenet I(V) karakterisztikájának vizsgálata - e/k állandó meghatározása
a) Állítson össze egy 9. és 10. ábráknak megfelelő kapcsolást a próbapanelen! Bemeneti ellenállásnak (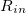
) használjon egy 
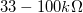-os ellenállást, emitter ellenállásként (
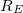) egy 
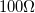-os ellenállást, kollektor ellenállásként (
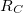) pedig egy 
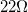-os ellenállást!
- Az ellenállás színkód alapján történő meghatározásához itt talál információt.
- Ha összeállította a kapcsolást, jelezze a mérésvezetőnek!
 |
 |
b) Vegye fel a tranzisztor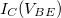 
görbéjét 
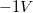és 
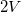között oda-vissza irányban!
- A myDAQ kártya vezérléséhez használja a myDAQ_arb_rw függvényt, illetve a feszültségjel definiálásához a Matlab beépített linspace() függvényét!
- A fenti elrendezésben a kollektoráramot (
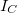) a myDAQ kártyan AI0 kimenetén mért feszültség és a kollektor ellenállás (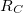) hányadosaként kapja meg, míg a bázis-emitter feszültsége a kártya AI1 bemenete méri.
c) Ábrázolja az 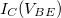görbét lineáris skálájú (lin-lin) grafikonon és logaritmikus y skálájú (lin-log) grafikonon is! Utóbbi grafikon alapján határozza meg a zajszintet, illetve vizsgálja meg, hogy a nagyobb 
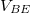értékeknél is teljesül-e az exponenciális függés (azaz lin-log skálán egyenes jelleg).
d) Készítsen egy olyan függvényt Matlabban, ami levágja az adatokat a megadott minimum (pl. zajszint) és maximum (pl. exponenciális viselkedés határa) alatt és felett, és a megtartott adatokra egyenest illeszt! Az illesztett egyenes meredekségéből határozza meg az 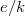arányt és vesse össze az irodalmi értékkel!
- Az 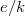arány meghatározásához ismernie kell a hőmérsékletet. Ezt egy higanyos hőmérővel mérheti meg, melyet a mérésvezetőtől kérhet el.
- Ha időhiányban szenved, akkor a gyakorlaton elvégezheti a feladatot függvénykészítés nélkül, azonban otthon érdemes megcsinálnia a függvényt, mert a LED-ek I(V) karakterisztikájának mérésekor visszatérő feladat lesz az adatok levágása és az illesztés elvégzése!
- Az adatok levágásához célszerű a Matlab beépített find() függvényét használni, de használhat for ciklust és if parancsot is.
4. Különböző hullámhosszú LED-ek I(V) karakterisztikájának vizsgálata és nyitófeszültségek meghatározása
a) Állítson össze egy 7. és 8. ábráknak megfelelő kapcsolást a próbapanelen! Bemeneti ellenállásnak (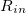) használjon egy 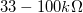-os ellenállást, áramkorlátozó ellenállásként (
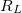) pedig egy 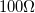-os ellenállást!
b) Az előző feladathoz hasonlóan vegye fel a különböző LED-ek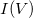 
karakterisztikáit 
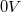és 
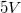között oda-vissza irányban! Készítse el a lin-lin és a lin-log I(V) grafikonokat és a megfelelő tartományra végezzen egyenesillesztést!
- Az ábrázoláshoz, az adatok levágásához és az illesztéshez használja az előző feladatban készített függvényt!
- Vesse össze a különböző LED-ek karakterisztikáját egymással és a tranzisztor p-n átmenetének karakterisztikájával! Mit tapasztal? Visszakapja az 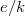arányt?
c) Határozza meg a LED-ek nyitófeszültségét!
5. 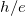arány meghatározása LED-ek nyitófeszültsége alapján
a) Készítse el az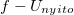 
grafikont!
- Számolja ki a különböző LED-ekhez tartozó frekvenciát a hullámhosszakból! Elméleti megfontolások alapján az ideális viselkedéstől való eltérést (pl. nem monokromatikus spektrum, nem megfelelő I(V) karakterisztika) hibaként vegye figyelembe! Ezt jelölje a grafikonon is!
b) Végezzen egyenesillesztést és határozza meg a 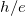értékét!
- A kapott értéket vesse össze az irodalmi adattal!
6. Különböző hullámhosszú LED-ek fotofeszültségének vizsgálata
a) Készítse elő az elrendezést!
- A méréshez az 5. és 6.ábrán látható fotodiódát és elektronikát tartalmazó mérőegységet használja!
- Kapcsolja be a mérő egységet, és az erre szolgáló (kék) csatlakozókon feszültségmérővel ellerőrizze a tápfeszültséget adó telepek feszültségét. (Legalább
6 V szükséges a helyes működéshez. A készülék azért elemes (akkumulátoros) táplálású, mert ez biztosítja a leginkább zajmentes tápellátást.
- Helyezze el úgy a LED-ek hullámhosszának méréséhez használt milliméterpapírral ellátott lemezt, hogy a rajt található lyuk a mérőegység nyílásához essen! Figyelem, a lemezt óvatosan mozgassa, nehogy eltörje!
- Célszerű a lemezt a lehető legszorosabban a nyíláshoz elhelyezni, így elkerülhető a háttérfény bejutása.
b) Mérje meg a különböző LED-ekkel történő megvilágítás hatására kialakuló feszültséget a fotocellán!
- Helyezzen egy LED-et a foglalatba, majd adjon rá feszültséget a kapcsoló felkapcsolásával! Forgassa el a mérőegységen lévő fényárnyékoló hengert, hogy láthatóvá váljék a doboz belsejében a fotodióda előtt lévő maszk és rajta az ablak. Erre az ablakra irányítsa a LED fényét! Ezután fordítsa a helyére a fényárnyékoló hengert!
- Minden mérés előtt nyomja be a mérőegységen levő piros nullázó gombot! Ezzel kisüti az elektronikai rendszerben keletkezett feltöltődést; így biztosíthatjuk azt, hogy csak a kiválasztott spektrumvonal által keltett fotóáram következtében létrejött potenciált mérjük.
- Várja meg, míg a feszültség stabilizálódik és jegyezze le az értékét! Ha további enyhe növekedést/csökkenést vagy esetleg ingadozást tapasztal, akkor azt hibaként vegye figyelembe!
7. 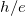arány meghatározása fotocellával
a) Készítse el az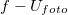 
grafikont!
- Számolja ki a különböző LED-ekhez tartozó frekvenciát a hullámhosszakból! Elméleti megfontolások alapján az ideális viselkedéstől való eltérést (pl. nem monokromatikus spektrum, nem megfelelő I(V) karakterisztika) hibaként vegye figyelembe! Ezt jelölje a grafikonon is!
b) Végezzen egyenesillesztést és határozza meg a 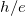értékét!
- A kapott értéket vesse össze az 5. feladat eredményével és az irodalmi adattal!
8. Fotoeffektus intenzitásfüggésének vizsgálata
Végezze el a 6-7. feladatokat úgy, hogy a nyílás elé helyezi az intenzitásszűrő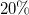 
-os részét!
- Ügyeljen arra, hogy a kisebb intenzitás miatt hosszabb ideig tarthat a feszültség beállása, ezért a következőképpen járjon el: előbb hagyja 1-2 percig állandósulni az értéket, majd nullázzon, és az imént elért értéknél 2mV-al kisebb feszültség eléréséig mérje a beállási időt.
