„A zaj mint jel” változatai közötti eltérés
| 51. sor: | 51. sor: | ||
A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt ''sörétzajnak'' szokták nevezni. Fontos megemlíteni, hogy a sörétzaj fehérzaj, azaz a spektrális sűrűség frekvenciafüggetlen. | A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt ''sörétzajnak'' szokták nevezni. Fontos megemlíteni, hogy a sörétzaj fehérzaj, azaz a spektrális sűrűség frekvenciafüggetlen. | ||
| − | A sörétzajra kapott képlet alapján az elektronttöltés egyszerűen meghatározható az áram zajának és várható értékének mérése alapján. Ezzel a lehetőséggel élt [[Walter Schottky]] 1918-ban, mikor korszakalkotó kísérletében az | + | A sörétzajra kapott képlet alapján az elektronttöltés egyszerűen meghatározható az áram zajának és várható értékének mérése alapján. Ezzel a lehetőséggel élt [[Walter Schottky]] 1918-ban, mikor korszakalkotó kísérletében az vákuumdiódában fellépő sörétzajt vizsgálta [1]. A vákuumdióda felépítését a 3. ábra szemlélteti. Egy fűtött katódból véletlenszerűen kilépő elektronok a katód és anód közé kapcsolt feszültség hatására eljutnak az anódba, ahol áramot detektálunk. |
| − | + | A vákuumdióda ideális eszköz a sörétzaj tanulmányozásához, hiszen az elektronok valóban véletlenül, és egymástól függetlenül emittálódnak. Fontos azonban megemlíteni, hogy az elektronok függetlensége nem nyílvánvaló, hiszen a kvantummechanikában megfogalmazott Pauli elve szerint két elektron nem lehet ugyan abban az állapotban, így | |
| − | + | ||
| − | + | ||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
A lap 2012. szeptember 9., 06:47-kori változata
SZERKESZTÉS ALATT!
A mérés célja
Különböző mennyiségek mérésénél általában a vizsgált mennyiség várható értékére vagyunk kíváncsiak, és a várható érték körüli fluktuációt zavaró tényezőnek tekintjük. Sok esetben viszont egy fizikai mennyiség "zaja" több információt hordoz a rendszerről mint maga a várható érték. A mérési gyakorlaton különböző zajjelenségeket vizsgálunk egy spektrumanalizátor segítségével. Először ellenállások termikus zajának mérése alapján meghatározzuk a Boltzmann állandó értékét. Ezután egy félvezető dióda zajának méréséből az elektrontöltés értékét határozzuk meg. Végül a Barkhausen zaj jelenségét tanulmányozzuk.
A zaj definíciója
| 1. ábra |
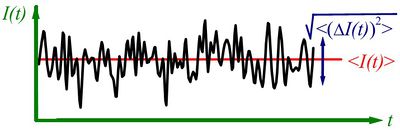
Előszöris definiáljuk zaj fogalmát. Egy időben változó mennyiség (pl. 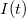 áram, lásd 1. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát,
áram, lásd 1. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát, 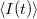 , illetve az átlagtól vett eltérést,
, illetve az átlagtól vett eltérést, 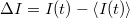 . A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével,
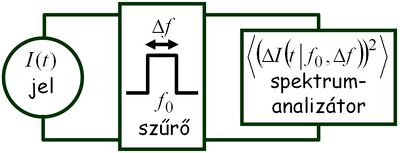
. A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével, 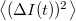 , azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 2. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az
, azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 2. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az 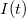 jelet egy
jelet egy  középfrekvencia körüli
középfrekvencia körüli  szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző
szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző 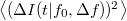 szórásnégyzetet mérünk.
szórásnégyzetet mérünk.
| 2. ábra |
Az így kapott szórásnégyzet kis  esetén arányos a
esetén arányos a  sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:
sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:
![\[\left<(\Delta I(t|f_0,\Delta f))^2\right>=S_I(f_0)\Delta f.\]](/images/math/3/3/f/33ff88a562de7a830d972009efd5d850.png)
Áramzaj esetén az 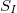 spektrális sűrűség mértékegysége
spektrális sűrűség mértékegysége 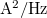 . A mérnöki gyakorlatban gyakran a spektrális sűrűség négyzetgyökével jellemzik egy eszköz zaját
. A mérnöki gyakorlatban gyakran a spektrális sűrűség négyzetgyökével jellemzik egy eszköz zaját 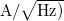 mértékegységgel.
mértékegységgel.
![\[\left<(\Delta V(t|f_0,\Delta f))^2\right>=S_V(f_0)\Delta f.\]](/images/math/8/9/a/89add176c6c234d68ca1a7b6097619e0.png)
Egy egyszerű ellenállás esetén 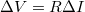 , azaz
, azaz 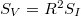 . Egy nemlineáris eszköznél, pl. egy diódánál
. Egy nemlineáris eszköznél, pl. egy diódánál 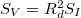 , ahol
, ahol 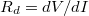 az eszköz differenciális ellenállása a mérésnél alkalmazott munkapontban.
az eszköz differenciális ellenállása a mérésnél alkalmazott munkapontban.
A fenti definíciók megismerése után érdemes megnézni a mérésnél használt Stanford research Systems 770 típusú spektrumanalizátor specificációit, melyek szerint a műszer bemeneti zaja a legkisebb méréshatárban 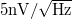 . Ez azt jelenti, hogy a műszer bemenetét rövidre zárva a várt zérus feszültség helyett a bemeneti erősítő feszültségzaját látjuk, melynek a szórása
. Ez azt jelenti, hogy a műszer bemenetét rövidre zárva a várt zérus feszültség helyett a bemeneti erősítő feszültségzaját látjuk, melynek a szórása 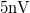
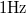 -es sávszélességű mérés esetén.
-es sávszélességű mérés esetén.
A kvantált elektromos töltésből adódó "sörétzaj"
Puskagolyók zaja
A sörétzaj fogalma egy klasszikus példával is jól szemléltethető, nézzük meg hogy mi történik ha egy puskából véletlenszerűen lövöldözünk, úgy hogy a lövések időpontja egymástól teljesen független. Ha a szomszédos lövések között eltelt átlagos idő  akkor
akkor  idő alatt a lövések átlagos száma értelemszerűen
idő alatt a lövések átlagos száma értelemszerűen 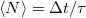 . Az átlag körüli szórás meghatározásához érdemes kiszámolni a
. Az átlag körüli szórás meghatározásához érdemes kiszámolni a 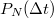 valószínűséget, azaz annak a valószínűségét, hogy
valószínűséget, azaz annak a valószínűségét, hogy  idő alatt
idő alatt  lövés dördül. Ha
lövés dördül. Ha 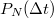 értékét ismerjük, akkor
értékét ismerjük, akkor 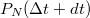 értéke a
értéke a
![\[P_N(\Delta t+dt)=P_{N-1}(\Delta t)\frac{dt}{\tau}+P_N(\Delta t)\left(1-\frac{dt}{\tau}\right)\]](/images/math/3/f/4/3f4062d58cc637d85054d98f2b6b3f49.png)
egyenlettel írható fel, azaz a kezdeti  és az utána következő
és az utána következő 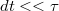 idő alatt vagy
idő alatt vagy 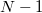 ill.
ill.  vagy
vagy  ill.
ill.  lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze.
A fenti egyenlet átrendezésével a
lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze.
A fenti egyenlet átrendezésével a
![\[\frac{dP_N(\Delta t)}{dt}=\frac{P_{N-1}(\Delta t)-P_N(\Delta t)}{\tau}\]](/images/math/b/6/4/b64ef404ea69d3816419cfebef01952b.png)
differenciálegyenletet kapjuk. Megmutatható, hogy ezen feltételt a
![\[P_N(\Delta t)=\frac{(\Delta t)^N}{\tau^N N!}e^{-\Delta t/\tau}\]](/images/math/f/b/b/fbb852541ecee469bb9e8e91c30241fe.png)
Poisson eloszlás elégíti ki. A Poisson eloszlás speciális tulajdonsága, hogy a szórásnégyzet megegyezik a várható értékkel, azaz
![\[\left< (\Delta N)^2 \right>=\left< N \right>=\frac{\Delta t}{\tau}.\]](/images/math/c/9/2/c925d13d542008c08786e26fc2259b03.png)
Elektronok sörétzaja
A fenti gondolatmenetet vonatkoztathatjuk elektronokra is ha teljesül az, hogy az elektronok véletlenszerűen, egymástól függetlenül jutnak át az egyik elektródából a másikba. Tegyük fel, hogy mérőrendszerünkkel az elektromos áramot  időbeli felbontással tudjuk mérni. Egy
időbeli felbontással tudjuk mérni. Egy  szélességű mintavételezési intervallum alatt
szélességű mintavételezési intervallum alatt 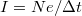 áramot detektálunk ahol a
áramot detektálunk ahol a  idő alatt áthaladó eletronok
idő alatt áthaladó eletronok  számának eloszlását a fenti Poisson eloszlás adja meg. Így a mért áram várható értéke
számának eloszlását a fenti Poisson eloszlás adja meg. Így a mért áram várható értéke 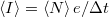 , míg az áram szórásnégyzete
, míg az áram szórásnégyzete 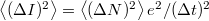 . A Nyquist - Shannon mintavételezési törvény szerint
. A Nyquist - Shannon mintavételezési törvény szerint  időfelbontás esetén a mért jelet
időfelbontás esetén a mért jelet 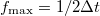 maximális frekvenciáig tudjuk rekonstruálni. Ez alapján a mért áramzaj spektrális sűrűsége:
maximális frekvenciáig tudjuk rekonstruálni. Ez alapján a mért áramzaj spektrális sűrűsége:
![\[S_I=\frac{\left< (\Delta I)^2 \right>}{f_{\mathrm{max}}}=2e\left< I \right>.\]](/images/math/b/8/9/b897997349b4a8f111d035c2c475d355.png)
A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt sörétzajnak szokták nevezni. Fontos megemlíteni, hogy a sörétzaj fehérzaj, azaz a spektrális sűrűség frekvenciafüggetlen.
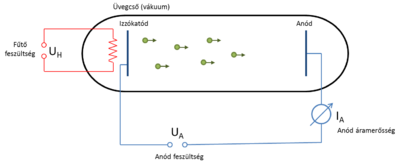
A sörétzajra kapott képlet alapján az elektronttöltés egyszerűen meghatározható az áram zajának és várható értékének mérése alapján. Ezzel a lehetőséggel élt Walter Schottky 1918-ban, mikor korszakalkotó kísérletében az vákuumdiódában fellépő sörétzajt vizsgálta [1]. A vákuumdióda felépítését a 3. ábra szemlélteti. Egy fűtött katódból véletlenszerűen kilépő elektronok a katód és anód közé kapcsolt feszültség hatására eljutnak az anódba, ahol áramot detektálunk.
A vákuumdióda ideális eszköz a sörétzaj tanulmányozásához, hiszen az elektronok valóban véletlenül, és egymástól függetlenül emittálódnak. Fontos azonban megemlíteni, hogy az elektronok függetlensége nem nyílvánvaló, hiszen a kvantummechanikában megfogalmazott Pauli elve szerint két elektron nem lehet ugyan abban az állapotban, így
| 2. ábra |
Termikus zaj
A termikus zaj véges hőmérsékleten jelentkezik a különböző állapotok betöltésének termikus fluktuációi miatt. Egy fermionikus rendszerben egy állapot betöltési száma n=0,1 lehet. A betöltési szám várható értéke a Fermi függvény,
.
A betöltési szám szórás négyzete:
,
ahol kihasználtuk, hogy fermionokra n2=n. A kifejezést energia szerint kiintegrálva ( ) rögtön látszik, hogy a termikus zaj arányos a hőmérséklettel.
A termikus zaj spektrális sűrűségét a fluktuáció-disszipáció tétel alapján adhatjuk meg, mely egy rendszer egyensúlyi fluktuációi és az egyensúlyból kitérített rendszer lineáris válaszfüggvénye között teremt összefüggést. Elektromos áram esetén az ez egyensúlyi fluktuáció nem más mint az áramzaj, a lineáris válaszfüggvény pedig a külső feszültségre adott válasz, vagyis a vezetőképesség. Így egy rendszer áramzaja:
.
Így alacsony frekvencián ( ) az áramfluktuációk termikus zaja:
.
Hasonlóképpen a feszültségzaj:
Látjuk, hogy a termikus zaj segítségével "csupán" feszültségmérés alapján meghatározhatjuk egy rendszer abszolút hőmérsékletét. Persze a precíz zajmérések komoly méréstechnikai kihívást jelentenek, hiszen nanovoltos vagy még kisebb feszültségek fluktuációját kell pontosan mérni. Ennek ellenére a termikus zaj mérésének komoly metrológiai jelentősége van, hiszen számos módszerrel mérhetünk precízen hőmérsékletváltozást, de az abszolút hőmérsékletet nem könnyű meghatározni. A jelenleg érvényes hőmérsékletstandardok mind ún. másodlagos hőmérők, melyek nem alapvető fizikai törvény hanem megfelelő kalibráció alapján mérik az abszolút hőmérékletet. (A szobahőmérséklet körüli széles tartományban pl. platina vékonyréteg ellenálláshőmérőt használnak standardként.) A termikus zaj mérése alapvető fizikai állandók (Boltzmann állandó + elektron töltés) alapján vezeti vissza a hőmérsékletmérést feszültségmérésre, így a hőmérsékletstandardok kalibrálásának egyik alapvető módszere.
==1/f zaj
A termikus zaj és a sörétzaj mellett még két fontos zajtípusról érdemes megemlékezni. A szennyezők és rácshibák véletlen mozgásából adódó ún. 1/f zaj, mely alacsony frekvenciákon dominál, és a nevét is a zajsűrűség tipikus frekvenciafüggéséről kapta.
Hivatkozások
[1] Schottky, W. Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern, Annalen der Physik 57 p541–567 (1918).