„Mérések Michelson-interferométerrel” változatai közötti eltérés
A Fizipedia wikiből
| 19. sor: | 19. sor: | ||
Szerkesztés alatt! | Szerkesztés alatt! | ||
| + | |||
| + | ''A mérés célja:'' | ||
| + | * koherens optikai jelenségek tanulmányozása. | ||
| + | |||
| + | ''Ennek érdekében:'' | ||
| + | * áttekintjük a diffrakció és az interferencia elméletét, | ||
| + | * megmérjük a lézerfény koherenciahosszát, | ||
| + | * méréseket végzünk interferométerrel, | ||
| + | * diffrakciós méréseket végzünk. | ||
| + | |||
| + | ==Elméleti összefoglaló== | ||
| + | |||
| + | ===Koherencia fogalma=== | ||
| + | |||
| + | A koherencia fogalmát a következő egyszerű képen keresztül definiálhatjuk. Tételezzük fel, hogy egy hullám egy $A$ kiindulási pontból két úton keresztül juthat el a $B$ pontba. Az 1. és 2. úton a $B$ pontba érkező nyalábokat $A_1e^{i\phi_1}$ és $A_2e^{i\phi_2}$ komplex számokkal jellemezhetjük, ahol $A_1$ és $A_2$ a nyalábok amplitúdóit, $\phi_1$ és $\phi_2$ pedig a fázisukat adják meg. ''B'' pontban a két nyaláb a szuperpozíció elve alapján összeadódik, így az eredő komplex amplitúdó $A_1e^{i\phi_1}+A_2e^{i\phi_2}$ lesz. Detektoraink viszont nem a komplex amplitúdót, hanem annak az abszolút érték négyzetét, az intenzitást érzékelik, mely egyszerű számolás alapján: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
</wlatex> | </wlatex> | ||
A lap 2012. október 2., 12:13-kori változata
Szerkesztés alatt!
A mérés célja:
- koherens optikai jelenségek tanulmányozása.
Ennek érdekében:
- áttekintjük a diffrakció és az interferencia elméletét,
- megmérjük a lézerfény koherenciahosszát,
- méréseket végzünk interferométerrel,
- diffrakciós méréseket végzünk.
Elméleti összefoglaló
Koherencia fogalma
A koherencia fogalmát a következő egyszerű képen keresztül definiálhatjuk. Tételezzük fel, hogy egy hullám egy 
kiindulási pontból két úton keresztül juthat el a 
pontba. Az 1. és 2. úton a pontba érkező nyalábokat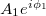 
és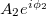 
komplex számokkal jellemezhetjük, ahol 
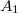és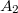 
a nyalábok amplitúdóit, 
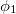és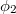 
pedig a fázisukat adják meg. B pontban a két nyaláb a szuperpozíció elve alapján összeadódik, így az eredő komplex amplitúdó 
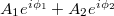lesz. Detektoraink viszont nem a komplex amplitúdót, hanem annak az abszolút érték négyzetét, az intenzitást érzékelik, mely egyszerű számolás alapján:
