„Lencsehibák vizsgálata sugárkövetés módszerével” változatai közötti eltérés
Lenk (vitalap | szerkesztései) |
Lenk (vitalap | szerkesztései) |
||
| 86. sor: | 86. sor: | ||
Kifejezve ${\cos ^2}\beta $-t az alábbi egyenlet adódik: | Kifejezve ${\cos ^2}\beta $-t az alábbi egyenlet adódik: | ||
| − | + | {{eq|{\cos ^2}\beta {{=}} 1 + ( {\cos ^2}\alpha - 1 )\cdot \frac{n_0^2}{n_1^2}|eq:6|(11.6)}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | {{eq|{\cos ^2}\beta {{=}} 1 + ( {\cos ^2}\alpha - 1 \cdot \frac{n_0^2}{n_1^2}|eq:6|(11.6)}} | + | |
Kihasználjuk továbbá azt a tényt, hogy a beeső nyaláb, a megtört nyaláb és a beesési merőleges egy síkban fekszik, így a megtört nyaláb irányába mutató egységvektor felírható a beeső nyaláb <u>s</u><sub>0</sub>, és a beesési merőleges <u>s</u><sub>2</sub> egységvektorok lineáris kombinációjaként (lásd 11.3. ábra). | Kihasználjuk továbbá azt a tényt, hogy a beeső nyaláb, a megtört nyaláb és a beesési merőleges egy síkban fekszik, így a megtört nyaláb irányába mutató egységvektor felírható a beeső nyaláb <u>s</u><sub>0</sub>, és a beesési merőleges <u>s</u><sub>2</sub> egységvektorok lineáris kombinációjaként (lásd 11.3. ábra). | ||
A lap 2012. november 9., 07:43-kori változata
Tartalomjegyzék |
Szerkesztés alatt!
Elméleti összefoglaló
Bevezetés
A személyi számítógépek tömeges elterjedése sok más klasszikus tudományterület mellett a fizika, ezen belül a geometriai optika módszereit is gyökeresen megváltoztatta. A zárt formulák és képletek helyett széles körben elterjedtek a numerikus módszerek. Számítógépek alkalmazásával kiküszöbölhető a geometriai optikával együtt járó algebrai számítások nagy része, és a számítási eredmények szemléletesen meg is jeleníthetők a képernyőn. Interaktív programok alkalmazásával lehetőség van számítógépes kísérleteket végzni és összetett lencserendszereket tervezni, optimalizálni.
Jelen mérés is egy ilyen grafikus, interaktív, számítógépes kísérletezésre alkalmas programra mutat példát, amely az áthaladó fénysugarak valós (nem csak az elsőrendben közelített, ú.n. paraxiális) menetét határozza meg. A mérésben használt program egy lencsetervező rendszer, amely alkalmas az optikai rendszerek részletes analízisére, és optimalizálására. A mérés során a program nyújtotta szolgáltatások közül csak a sugárátvezetést és a grafikus megjelenítést használjuk ki. Az optikai rendszerek részletes analízise, és az optimalizálás messze meghaladja egy alap fizika laboratórium kereteit (ezt az Optikai rendszerek tervezése c. választható tárgy keretei között sajátíthatják el).
A geometriai optika középiskolából ismert egyszerű közelítő eljárásai (ld. pl. lencsetörvény) csak az optikai tengelyhez közeli tárgy-kép pontokra, és a tengellyel kis szöget bezáró paraxiálisnak nevezett sugarakra érvényesek (lásd pl. Budó-Mátrai: Kísérleti Fizika III. 35-76. oldal). A paraxiális közelítés hatalmas előnye abban rejlik, hogy keretei között teljesülnek az ideális képalkotást feltételei (többek között éles, torzításmentes az így kapott kép). A tengelytől távol haladó, valamint a tengellyel nagy szöget bezáró sugarak különböző képalkotási hibákat okoznak, mint pl. nyíláshiba (vagy gömbi eltérés), asztigmatizmus, kóma, képmezőhajlás. A lencsék anyagaként használt üvegek törésmutatójának hullámhossz függése (diszperziója) miatt fellép továbbá színi hiba (kromatikus aberráció) is. A felsorolt hibák pontos tárgyalása bonyolult és hosszadalmas. Jelen mérés célja ezen hibák kísérleti bemutatása a számítógép adta lehetőségek felhasználásával. (A hibák leírását lásd Budó-Mátrai: Kísérleti Fizika III. 65-69 oldal).
A sugárkövetés fizikai alapjai
A sugárkövetés során a törési törvény sorozatos alkalmazására kerül sor. A számításokat a 11.1. ábra koordináta rendszerében végezzük. Gömbsüveg alakú lencsék, tükrök esetén az egyes törő-/ tükröző felületeket négy adattal jellemezzük:
- - görbületi sugár (görbület ≡ 1 / görbületi sugár),
- - a törőfelületet követő anyag törésmutatója,
- - a törőfelületet követő felület távolsága,
- - a törőfelület apertúrájának (nyílásának) sugara
(Ezt a számításnál általában nem használja a program, csak a rajz elkészítésénél).
11.1. ábra. A felületen a fénytörést a felülethez rendelt lokális koordinátarendszerben vizsgáljuk (ld. az ábrán az első felületnél x1, y1), amelynek origója a felület és az optikai tengely metszéspontja. A szokásos konvenciónak megfelelően az ábrán feltüntetett első felület görbületi sugara (R1) pozitív, a másodiké (R2) negatív.
Az abszolút koordináta-rendszer origója a tárgy és az optikai tengely metszéspontjában van. A z-tengely egybeesik az optikai tengellyel. Az első törőfelület előtt a program automatikusan levegőt (n0=1 törésmutatót) tételez fel. Az utolsó törőfelület után - a felhasználó által megadott távolságban - a program automatikusan egy zérus görbületű felületet (sík ernyőt) tételez fel (képsík).
Egy fénysugarat a tér adott pontjában általános esetben hat adat ír le:
- X0 : x koordináta,
- Y0 : y koordináta,
- Z0 : z koordináta,
- K : az x tengellyel bezárt szög koszinusza,
- L : az y tengellyel bezárt szög koszinusza,
- M : a z tengellyel bezárt szög koszinusza.
Az (X0, V0, Z0), a sugár kiinduló pontját, vagy egy törőfelülettel alkotott metszéspontját jelenti. (K, L, M) jelöli az iránykoszinuszokat (azaz a fénysugár irányú egységvektor koordinátáit), amelyek közül csak kettő független. A számítások során a program meghatározza a sugár metszéspontját a következő törőfelülettel, és a törési törvény alapján kiszámítja a sugár új irányát/iránykoszinuszait a következő közegben. A metszéspont meghatározása a (11.1) egyenletrendszer megoldását jelenti:
![\[x = {{\rm{X}}_{\rm{0}}} + {\rm{K}}t\]](/images/math/4/5/e/45ece3cbd11a9e89dd02e8148658dd24.png)
![\[y = {{\rm{Y}}_{\rm{0}}} + {\rm{L}}t\]](/images/math/5/b/b/5bb3d96169c5569d5cc7ed90275b8716.png)
![\[z = {{\rm{Z}}_{\rm{0}}} + {\rm{M}}t\]](/images/math/b/c/1/bc14fe8287fd819bc8bf1ec6162a7ecf.png)
![\[{{R^2} = {x^2} + {y^2} + {(z - R)^2}}\]](/images/math/9/6/0/960de4162c3fc61eeea705653eb8af10.png)
A program a számításokat mindig egy lokális, az adott törőfelület és a z-tengely metszéspontjához rögzített koordináta-rendszerben végzi. Így a z koordináta értékeket ahol szükséges, át kell számolni abszolút koordinátákra. Az új közegben érvényes iránykoszinuszokat a 11.2. ábra alapján határozhatjuk meg. A számítások során a (11.2.), (11.3) egyenletekből indulunk ki.
11.2. ábra. Az új közegben érvényes iránykoszinuszok meghatározása
A beesési szög koszinusza a beeső nyaláb és a beesési pontba húzott felületi normális skaláris szorzatából számolható:
![\[C_xK + C_yL + C_zM = cos\alpha \]](/images/math/0/7/5/075f68ea98cdc048178f17187af2ccbe.png)
Itt (Cx, Cy, Cz) a beesési pontba húzott felületnormális vektor iránykoszinuszait jelentik (lásd a 11.2. ábrát). Az (Cx, Cy, Cz) iránykoszinuszok a beesési pont meghatározása után számolhatók. A törési szög a Snellius-Descartes-törvényből számolható:
![\[\frac{\sin \alpha }{\sin \beta }=\frac{n_1}{n_0}=\sqrt {\frac{{1 - {\cos ^2}\alpha }}{{1 - {\cos ^2}\beta }}}\]](/images/math/b/c/0/bc0439efa14b0f05d39a8abd109dbf3d.png)
Ebből az iránykoszinuszokra az alábbi egyenletet kapjuk:
![\[\frac{{1 - {\cos ^2}\alpha }}{{1 - {\cos ^2}\beta }} =\frac{n_1^2}{n_0^2}\]](/images/math/f/d/0/fd091cd2cfa3343b7987064cf266b2c1.png)
![\[{(1 - {\cos ^2}\alpha )}\cdot \frac{n_0^2}{n_1^2} = 1 - {\cos ^2}\beta \]](/images/math/0/9/7/097ba67763248d6863df256720f4a1ae.png)
Kifejezve 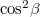 -t az alábbi egyenlet adódik:
-t az alábbi egyenlet adódik:
![\[{\cos ^2}\beta = 1 + ( {\cos ^2}\alpha - 1 )\cdot \frac{n_0^2}{n_1^2}\]](/images/math/e/3/d/e3d513c560263495fd7fe162441332a7.png)
Kihasználjuk továbbá azt a tényt, hogy a beeső nyaláb, a megtört nyaláb és a beesési merőleges egy síkban fekszik, így a megtört nyaláb irányába mutató egységvektor felírható a beeső nyaláb s0, és a beesési merőleges s2 egységvektorok lineáris kombinációjaként (lásd 11.3. ábra).
![\[{\underline {\rm{s}} _1} = k{\underline {\rm{s}} _0} + u{\underline {\rm{s}}_2}\]](/images/math/f/b/f/fbf85a91e43a212f7d36d6fe9208a38f.png)
(11.7.)
A (11.7.) egyenletet s0 -al, illetve s2 -vel beszorozva az alábbi két egyenletet nyerjük:
![\[{\underline s _0}{\underline s _1} = \cos \left( {\alpha - \beta } \right) = k + u\cos \alpha\]](/images/math/5/0/6/506f8be532797260bae381336d18ab07.png)
(11.8.)
![\[{\underline s _2}{\underline s _1} = \cos \beta = k\cos \alpha + u\]](/images/math/b/1/b/b1b350293b743db6b95eb6c40e2288c0.png)
(11.9.)
11.3. ábra. A törési törvény felírásánál használt koordinátarendszer
A 11.8 és 11.9 egyenletekből a „k” és „u” ismeretlen paraméterek meghatározhatók:
![\[k=\frac{\sin \beta }{\sin \alpha }=\frac{n_0}{n_1}\]](/images/math/e/a/c/eacead7a6fc144489b07b55453b1d2d1.png)
![\[{{u = \cos \beta - k \cdot \cos \alpha = \cos \beta \frac{{{{\rm{n}}_0}}}{{{{\rm{n}}_1}}} \cdot \cos \alpha}}\]](/images/math/7/b/9/7b9d66b166dc95213f0fa2161d5a2f80.png)
Ezek alapján a keresett egységvektor a következő egyenlet szerint írható le:
![\[{\underline {\rm{s}} _1} = k \cdot {\underline {\rm{s}} _0} + u \cdot {\underline {\rm{s}} _2} = \frac{{{{\rm{n}}_0}}}{{{{\rm{n}}_1}}}{\underline {\rm{s}} _0} + \frac{{\rm{1}}}{{{{\rm{n}}_{\rm{1}}}}}\left( {{{\rm{n}}_1} \cdot \cos \beta - {{\rm{n}}_0} \cdot \cos \alpha } \right){\underline {\rm{s}} _2}\]](/images/math/6/9/a/69a01b626f7a340d7da3c19866d97416.png)
(11.12)
A (11.12.) vektoregyenlet három skalár egyenlet megoldását jelenti. Ezek megadják a megtört sugár iránykoszinuszait.
![\[{\underline s _1} = \left[ {\begin{array}{*{20}{c}} {K'}\\ {L'}\\ {M'} \end{array}} \right]\]](/images/math/6/8/a/68a04787495db1efa5632dc7fdcb9b7c.png)
(11.13)
Ezek alapján a sugármenet számítására alkalmas program az alábbi számításokat végzi:
- - A belépő sugár (X0, Y0, Z0) kiinduló koordinátái és (K, L, M) iránykoszinuszai alapján a (11.1) egyenletrendszer megoldásával meghatározza a sugár és a felület (x, y, z) metszéspontját.
- - A (11.10), (11.11), (11.12 ) és (11.13) egyenletek alapján pedig kiszámítja a megtört sugár új iránykoszinuszait.
A program a fenti két számítási lépést végzi el az összes belépő sugárra és az összes törőfelületre. Az eredmények numerikusan listázhatók, vagy különböző grafikus formákban megjeleníthetők.
Néhány szokásos elnevezés, definíció
- Paraxiális sugarak: az optikai tengellyel kis szöget bezáró (kb. 5° vagy kisebb, amelyekre teljesül sin
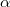
 [rad]), és a tengelyhez közel haladó sugarak (x, y << R).
[rad]), és a tengelyhez közel haladó sugarak (x, y << R).
- Paraxiális fókuszpont: az optikai rendszer fókuszpontja végtelen távoli tárgypontból érkező paraxiális sugarak esetén.
- Fősík: paraxiális közelítésben az a két sík, amelyek m = +1-es nagyítású képei egymásnak. Ezek vékony lencse esetén egy síkká fajulnak, ami megegyezik a lencse síkjával. Tetszőlegesen bonyolult leképező rendszernél is meghatározható, és mindig csak kettő van belőle (első és hátsó).
- Effektív fókusztávolság: a paraxiális fókuszpont és a hátsó fősík „f” távolsága. Ha a „t” tárgytávolságot az első, a „k” képtávolságot pedig a hátsó fősíktól mérjük, akkor minden leképező rendszernél igaz a jól ismert lencsetörvény: 1/k = 1/f + 1/t.
- Apertúra: magyarul nyílás. Ez lehet a lencse külső pereme, a lencsét tartó foglalat pereme, vagy egy külön erre a célra odahelyezett blende nyílása.
- Tárgyszög: a tárgytér szélén lévő tárgypontból az optikai rendszerhez érkező fénynyaláb központi fénysugarának az optikai tengellyel bezárt szöge.
- Alaktényező:
![\[S = \frac{{{R_1} + {R_2}}}{{{R_1} - {R_2}}}\]](/images/math/c/2/a/c2a0a28b850613e0b5cb1cc3a5311d08.png)
(11.14)
„S” egy-egy lencsetag jellemzője. Az összefüggés jól használható a különböző geometriai adatokkal rendelkező, de közel azonos fókusztávolságú lencsék szimmetriájának ill. aszimmetriájának jellemzésére. „S” értéke a leképezési hibákat (aberrációkat) befolyásolja.
- Szóródási folt: Ha a lencsére nagy átmérőjű, az optikai tengellyel párhuzamos fénynyalábot ejtünk, akkor az a paraxiális közelítéstől eltérően nem egy pontban egyesül. Egy, az optikai tengelyre merőleges sík (általában a képsík) és a rendszeren átvezetett fénysugarak metszéspontjainak halmazát szóródási foltnak nevezzük. Elég sok sugarat átvezetve a képsíkon a szóródási folt jól modellezi a fényintenzitás eloszlást. Ahol nagy a metszéspontok sűrűsége, ott az intenzitás is nagy. Kevés metszéspont kisebb intenzitást jelent.
- Aberráció: tágabb értelemben minden képalkotási hiba. Szűkebb értelemben a leképezés elmélet harmadrendű közelítésében megkülönböztethető leképezési hibák fajtái. Néhány fontosabb aberráció jellemző képfoltját mutatja a 11.4 ábra.
- Diffrakciókorlátos rendszer: A közel ideális, geometriai optikai hibáktól mentes rendszerek képfoltja sem matematikai értelemben vett pont, hanem egy kis tartomány. Ilyen esetekben a képfolt méretét a diffrakció (fényelhajlás) határozza meg (felülről korlátozza). Kör alakú lencsét feltételezve a képfolt sugarát paraxiális esetben (f >> A) a (11.15.) összefüggés adja meg (lásd a 11.5. ábrát).
![\[\Delta r = \frac{{1.22\lambda f}}{A}\]](/images/math/d/c/4/dc4a473a2f0c9bb670d3ee6b6ba0da8e.png)
(11.15)
, ahol
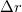 a diffrakciós folt első nullahelyének sugara, „f” a lencse fókusztávolsága, „A” a fénynyaláb átmérője a lencsén,
a diffrakciós folt első nullahelyének sugara, „f” a lencse fókusztávolsága, „A” a fénynyaláb átmérője a lencsén, 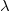 a hullámhossz az adott közegben. Az optikai rendszert diffrakció korlátosnak hívjuk, ha a geometriai optikai úton számolt szóródási folt méret kisebb, mint a diffrakciós folt.
a hullámhossz az adott közegben. Az optikai rendszert diffrakció korlátosnak hívjuk, ha a geometriai optikai úton számolt szóródási folt méret kisebb, mint a diffrakciós folt.
- Numerikus apertúra (NA): Egy hengerszimmetrikus nyaláb konvergenciáját leíró számadat, amelynek értéke definíció szerint:
![\[NA = n \cdot \sin \Theta\]](/images/math/3/a/d/3ad672a0c530cd4285001c191945589d.png)
„n” a közeg törésmutatója, 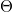 pedig a nyaláb fél-kúpszöge (lásd a 11.5. ábrát). Az NA-t lencsék vagy objektívek felbontóképességének jellemzésére szokták használni (NA nagy → felbontóképesség nagy), mivel nagyobb kúpszögek esetén a 11.15 összefüggés helyett a diffrakciós folt mérete az alábbi képlettel számolható ki:
pedig a nyaláb fél-kúpszöge (lásd a 11.5. ábrát). Az NA-t lencsék vagy objektívek felbontóképességének jellemzésére szokták használni (NA nagy → felbontóképesség nagy), mivel nagyobb kúpszögek esetén a 11.15 összefüggés helyett a diffrakciós folt mérete az alábbi képlettel számolható ki:
![\[\Delta r = \frac{{1.22{\lambda _0}}}{{2 \cdot NA}}\]](/images/math/8/d/f/8dff30ee4b604b0405c3d39f840a02b2.png)
,ahol 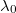 a levegőben mért hullámhossz.
a levegőben mért hullámhossz.
11.4. ábra. Néhány fontosabb aberráció jellemző képfoltja geometriai optikai közelítésben.
11.5. ábra. Lencsék diffrakciós foltjának meghatározásánál alkalmazott jelölések. A /b és /c ábrán a lencse fókuszpont környéki intenzitás eloszlása látható (Airy-folt), ideális leképezés esetén.
Vastag lencsékre és paraxiális sugarakra vonatkozó közelítő összefüggések
"szerkesztés alatt!"
Az alkalmazott optikai tervező program leírása
"szerkesztés alatt!"
Mérési feladatok
"szerkesztés alatt!"
PDF formátum
