„Gammasugárzás abszorpciója, folyadékszint- és sűrűségmérés” változatai közötti eltérés

A Fizipedia wikiből
a
a
76. sor: 76. sor:
 
Ha az I vastagságú vizsgált mintát párhuzamos A<sub>0</sub> intenzitású sugárnyalábbal sugározzuk be, akkor annak intenzitása az anyagon áthaladva a
 
Ha az I vastagságú vizsgált mintát párhuzamos A<sub>0</sub> intenzitású sugárnyalábbal sugározzuk be, akkor annak intenzitása az anyagon áthaladva a
 
{{eq|A{{=}} A_0\cdot e^{-\mu \cdot I} {{=}} A_0\cdot e^{-\mu'\cdot \rho\cdot I}|eq:6|(6)}}
 
{{eq|A{{=}} A_0\cdot e^{-\mu \cdot I} {{=}} A_0\cdot e^{-\mu'\cdot \rho\cdot I}|eq:6|(6)}}
−
törvény szerint változik, ahol μ az ún. lineáris, abszorpciós együttható, $\mu' {{=}} \frac{\mu}{\rho}\left[\frac{cm^2}{g}\right]$ a tömegabszorpciós együttható. Mivel μ a sűrűséggel közelítőleg lineáris kapcsolatban van, a tömegabszorpciós együttható sűrűségfüggését első közelítésben elhanyagolhatjuk, csak a mért anyag minőségétől, a használt sugárzás energiájától függ. Ez utóbbiakat, valamint a mért anyagvastagságot, I-t állandónak tartva a dózisintenzitás ΔA megváltozása a Δρ sűrűségváltozástól függ. ([[#fig:6|6.]])-t differenciálva
+
törvény szerint változik, ahol μ az ún. lineáris, abszorpciós együttható, $\mu' {{=}} \frac{\mu}{\rho}\left[\frac{cm^2}{g}\right]$ a tömegabszorpciós együttható. Mivel μ a sűrűséggel közelítőleg lineáris kapcsolatban van, a tömegabszorpciós együttható sűrűségfüggését első közelítésben elhanyagolhatjuk, csak a mért anyag minőségétől, a használt sugárzás energiájától függ. Ez utóbbiakat, valamint a mért anyagvastagságot, I-t állandónak tartva a dózisintenzitás ΔA megváltozása a Δρ sűrűségváltozástól függ. ([[#eq:6|6.]])-t differenciálva
 
{{eq|\Delta A{{=}} \frac {\partial A}{\partial \rho} \cdot \Delta \rho{{=}} \frac{\partial}{\partial \rho} \left(A_0 \cdot e^{-\mu' \cdot\rho \cdot I}\right)\cdot \Delta\rho {{=}}\mu'\cdot I\cdot A \cdot \Delta \rho|eq:7|(7)}}
 
{{eq|\Delta A{{=}} \frac {\partial A}{\partial \rho} \cdot \Delta \rho{{=}} \frac{\partial}{\partial \rho} \left(A_0 \cdot e^{-\mu' \cdot\rho \cdot I}\right)\cdot \Delta\rho {{=}}\mu'\cdot I\cdot A \cdot \Delta \rho|eq:7|(7)}}
 +
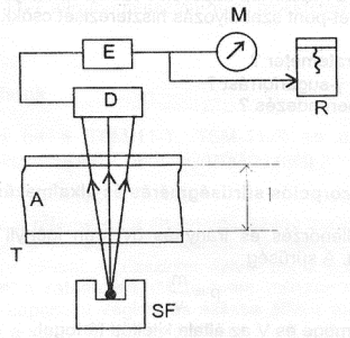
A ([[#eq:7|7]].) egyenletből látható, hogy a mérés érzékenysége nagy, ha jól abszorbeálódó sugárzást emittáló sugárforrást használunk (μ’ nagy), illetve ha a mérési úthossz (I) és a forrás aktivitása (A<sub>0</sub>) megfelelően nagy. A sűrűségmérő elvi elrendezése a [[#fig:11|11. ábrán]] látható.
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{fig|Gamma_11.png|fig:11|11. ábra γ-sugár abszorpciós sűrűségmérés. SF sugárforrás, T tartály, A mérendő anyag, D detektor, E elektronikus jelfeldolgozó, M kijelző, R regisztráló}}
 +
|}
 +
 +
===Szemcseméret-eloszlás mérése sugárabszorpciós módszerrel===
 +
A gyakorlatban számos esetben előfordul, hogy szuszpenziókban, azaz folyadékokban lebegő - ülepedő szilárd szemcsézettel rendelkező anyagokban az átlagos szemcseméretet, a szemcseméret eloszlását kell meghatározni. Gyors és pontos módszer erre az ülepedés mérése sugárabszorpciós módszerrel. A mérés elvi elrendezése a [[#fig:12|12. ábrán]] látható.
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
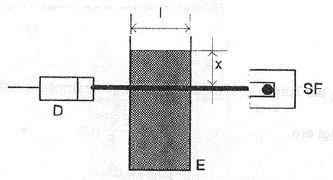
| {{fig|Gamma_12.png|fig:12|12. ábra Szemcseméretűeloszlás mérése. SF sugárforrás, E ülepítő edény, D detektor}}
 +
|}
 +
Az ülepítő közegben egyenletesen elkevert szemcsés anyag az I átmérőjű edényben van. A felszíntől x távolságra levő SF sugárforrásból kilépő, a folyadékfelszínnel közel párhuzamos sugárnyaláb intenzitását a D detektor méri.
 +
 +
Az abszorpció a tiszta ülepítő közegben
  
−
===Szemcseméret-eloszlás mérése sugárabszorpciósmódszerrel===
 
 
===A sűrűségmérő berendezés===
 
===A sűrűségmérő berendezés===
 
===Mérési feladatok===
 
===Mérési feladatok===

A lap 2013. február 1., 13:28-kori változata


Tartalomjegyzék


Szerkesztés alatt!

Elméleti összefoglaló

Izotópos mérésekről általában

Izotópos mérések összehasonlítása

A TSM-11 univerzális ipari sugárzásmérő

A berendezés felépítése

A TSM-11 univerzális sugárzásmérő alkalmazása

Az izotópos szintjelzés elve

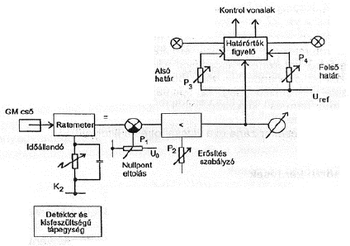
Ratemeter

A mérőberendezés leírása

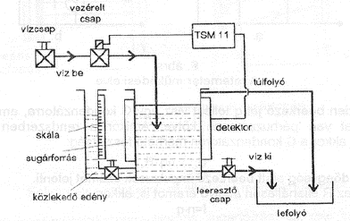
A mérőberendezés egy hengeres acéledényből, egy, az acélhengeren kívül elhelyezkedő pontforrásokból kialakított "vonalforrásból", és ezzel szemben az acélcső másik oldalán elhelyezkedő lineáris detektorból (G.M.- cső) áll. A detektor egy TSM-11-T típusú ratemeterhez csatlakozik. Az acéledényekhez egy átlátszó közlekedő edény csatlakozik hitelesítési célra (8. ábra).

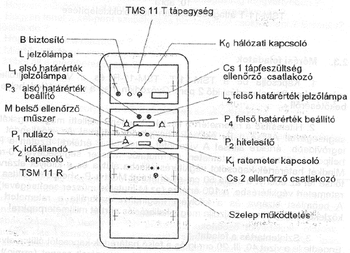
8. ábra Laboratóriumi folyadékszint mérő berendezés

A 9. és 10. ábrákon az Izotóp Intézet által megvalósított és forgalmazott TSM-11-T elnevezésű átlagbeütésszámmérő kezelő szervei és blokkfelépítése látható. A készülék legfőbb elemét az integrátort a jelformáló egy digitális osztón keresztül hajtja meg. Az integrátor időállandója a K2 fokozatkapcsolóval változtatható. Ez a kezelőszerv a műszeren kívül is hozzáférhető, ahogyan a 9. ábrán látható. Az integrátort a kijelzést szolgáló egységek követik, a "0" pont eltolást és a hitelesítést vagy skálanyújtást biztosító szervek. Ezeket egy-egy helipot segítségével (P1 és P2) lehet beállítani, amelyek szintén kívülről kezelhetők, a 9. ábrán látható P3 és P4 potméterek előre megadott határértékek beállítására szolgálnak. A beállított értékek elérésekor az alsó, illetve L2 felső határértéket jelző lámpák jeleznek a műszer (M) állásának megfelelően. A lámpák jelzéseivel egy időben a készülékben lévő relék egy-egy kapcsoló állapotát megváltoztatják, amelyek valamely más készülék vezérlésére, indítására használhatunk. Az egyéb kezelőszervek a készülék áramellátását, illetve az áramellátás jelzését szolgálják. Az egyéb kezelőszervek megnevezése a 9. ábráról leolvasható.

9. ábra TMS-11-T berendezés kezelőszervei

A ratemeter házában két rekesz csak speciális kivitelnél van kihasználva, ezért a mi méréseinkben ez lehetőséget adott arra, hogy az adott méréshez szükséges elektronika ezekbe a szabadon hagyott rekeszekbe kerüljön. Ezek kezelése az adott mérési feladatoknál megtalálható.

10. ábra TSM-11-T átlagbeütésszám-mérő blokkfelépítése

Mérési feladatok

  1. Kapcsolja be a TSM-11-T, TSM-11-R és a Valve Controller műszereket! Bemelegedési idő 2 perc. Győződjön meg a vízvezetékek helyes bekötéséről!
  2. Hitelesítse a ratemetert a közlekedő edény melletti magasságskála segítségével! Állítsa a P1 és a P2 helipotot 0 állásba! Az időállandót a legrövidebb értékre állítsa! A vízszintet állítsa be 0 értékre! Ezután a P1 helipottal állítsa be a ratametert (M mutatós műszer segítségével) 0-ra! Mindkét határérték-kapcsolót végkitérés állásba állítva és a kifolyót elzárva töltse fel az edényt a skála 50 cm-es értékéig! Most a P2 helipottal állítsa a ratemetert végkitérésbe, a 100 értékre (az M mutatós műszer segítségével)! A beömlést elzárva és a kifolyást megindítva kalibrálja a ratemetert a közlekedő edényben! Rajzolja meg a kalibrációs görbét!
  3. Szintentartás a feladat. Engedje le a vizet 40, ill. 20 cm-ig és a felső határérték kapcsolót állítsa olyan állásba, hogy a beállított értéknél nyissa-zárja a vezérelt csapot (x=min)! A vízcsap és a kifolyó együttes megnyitása után a magára hagyott rendszer a beállított érték körül ingadozik. Vizsgálja meg az ingadozás mértékét az alsó határérték-kapcsoló, valamint az időállandó beállításának függvényében! Írja le megfigyeléseit! Állítsa be a lehető legkisebb hiszterézist! Ügyeljen arra, hogy a víz befolyási sebessége körülbelül egyezzen meg a kifolyási sebességgel! (A vízbevezető csapot csak kicsit szabad megnyitni!)
  4. Kapcsolási hiszterézis vizsgálata. A feladat a víz 27 cm-en való tartása. Állítsa be a vízszintet 25 cm-re! A helipottal állítsa a ratemetert 0-ra! Állítsa be a P2 helipottal a maximális értéket a ratemeteren (maximális erősítés!). A be- és kifolyás fenntartása mellett a felső határérték-kapcsolóval álljon be 27 cm-re! Vizsgálja meg a hiszterézist az időállandó függvényében és hasonlítsa össze a 3. feladatban tapasztalattal! Keresse meg az optimális alsó határérték állást, ahol a rendszer már nem esik ki a vezérlésből! Írja le tapasztalatait!

A mérés befejezésekor zárja el a vízcsapot és a kifolyót!

Ellenőrző kérdések

  • Mi a pontszerű és mi a lineáris sugárforrás?
  • Állandó folyadék-szint mellett, hogyan változik az átlag beütésszám? Mi a szerepe az időállandónak?
  • Hogyan változik a kifolyás sebessége a vízmagasság függvényében?
  • Hogyan működik a határérték-kapcsolós szelepszabályozás?
  • Hogyan lehet a két-pont szabályozás hiszterézisét csökkenteni? Erősítés? Időállandó?
  • Hogy működik a ratemeter?
  • Miért használunk γ-sugárforrást?
  • Miből áll a mérőberendezés?

Gamma-sugárzás abszorpciós sűrűségmérés és alkalmazása

A folyamatellenőrzés és irányítás gyakran igényli az anyagsűrűség folyamatos mérését. A sűrűség

 
\[\rho= \frac{m}{V}\]
(5)

ahol m az anyag tömege és V az általa kitöltött térfogat.

Az iparban a sűrűségmérést számos területen alkalmazzák, ilyen pl. a bányászat, vegyipar, kőolajipar, textilipar, stb., elsősorban különböző transzport vagy egyéb technológiai folyamatok ellenőrzésére, szabályozására. A leggyakoribb probléma különböző folyadékok, oldatok, emulziók és szuszpenziók (zagyok) sűrűségének mérése. Az ipari alkalmazások szempontjából érdekes sűrűségtartomány a 500-2500 kg/m3. A radioaktív izotópos méréstechnikán alapuló sűrűségmérés elsősorban érintkezésmentes jellege miatt a legtöbb esetben jelentős előnyt kínál a többi sűrűségmérő módszerrel szemben (úszós, hidrosztatikus, mérleges, pneumatikus), sőt nemegyszer ez az egyetlen üzembiztos megoldás.

A Gamma-sugár abszorpciós sűrűségmérés elve

Ha az I vastagságú vizsgált mintát párhuzamos A0 intenzitású sugárnyalábbal sugározzuk be, akkor annak intenzitása az anyagon áthaladva a

 
\[A= A_0\cdot e^{-\mu \cdot I} = A_0\cdot e^{-\mu'\cdot \rho\cdot I}\]
(6)

törvény szerint változik, ahol μ az ún. lineáris, abszorpciós együttható, \setbox0\hbox{$\mu' {{=}} \frac{\mu}{\rho}\left[\frac{cm^2}{g}\right]$}% \message{//depth:\the\dp0//}% \box0% a tömegabszorpciós együttható. Mivel μ a sűrűséggel közelítőleg lineáris kapcsolatban van, a tömegabszorpciós együttható sűrűségfüggését első közelítésben elhanyagolhatjuk, csak a mért anyag minőségétől, a használt sugárzás energiájától függ. Ez utóbbiakat, valamint a mért anyagvastagságot, I-t állandónak tartva a dózisintenzitás ΔA megváltozása a Δρ sűrűségváltozástól függ. (6.)-t differenciálva

 
\[\Delta A= \frac {\partial A}{\partial \rho} \cdot \Delta \rho= \frac{\partial}{\partial \rho} \left(A_0 \cdot e^{-\mu' \cdot\rho \cdot I}\right)\cdot \Delta\rho =\mu'\cdot I\cdot A \cdot \Delta \rho\]
(7)

A (7.) egyenletből látható, hogy a mérés érzékenysége nagy, ha jól abszorbeálódó sugárzást emittáló sugárforrást használunk (μ’ nagy), illetve ha a mérési úthossz (I) és a forrás aktivitása (A0) megfelelően nagy. A sűrűségmérő elvi elrendezése a 11. ábrán látható.

11. ábra γ-sugár abszorpciós sűrűségmérés. SF sugárforrás, T tartály, A mérendő anyag, D detektor, E elektronikus jelfeldolgozó, M kijelző, R regisztráló

Szemcseméret-eloszlás mérése sugárabszorpciós módszerrel

A gyakorlatban számos esetben előfordul, hogy szuszpenziókban, azaz folyadékokban lebegő - ülepedő szilárd szemcsézettel rendelkező anyagokban az átlagos szemcseméretet, a szemcseméret eloszlását kell meghatározni. Gyors és pontos módszer erre az ülepedés mérése sugárabszorpciós módszerrel. A mérés elvi elrendezése a 12. ábrán látható.

12. ábra Szemcseméretűeloszlás mérése. SF sugárforrás, E ülepítő edény, D detektor

Az ülepítő közegben egyenletesen elkevert szemcsés anyag az I átmérőjű edényben van. A felszíntől x távolságra levő SF sugárforrásból kilépő, a folyadékfelszínnel közel párhuzamos sugárnyaláb intenzitását a D detektor méri.

Az abszorpció a tiszta ülepítő közegben

A sűrűségmérő berendezés

Mérési feladatok

Ellenőrző kérdések

Mérési feladatok

PDF formátum


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Gammasugárzás_abszorpciója,_folyadékszint-_és_sűrűségmérés&oldid=7288”