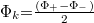„Magneto-optikai Kerr-szög mérése” változatai közötti eltérés
Lenk (vitalap | szerkesztései) a |
Lenk (vitalap | szerkesztései) |
||
| 51. sor: | 51. sor: | ||
\end{array}} \right \} \qquad \Leftrightarrow \qquad \mathbf{D} = \mathbf{\underline{\underline{\epsilon} } } \cdot \mathbf{E}$$ | \end{array}} \right \} \qquad \Leftrightarrow \qquad \mathbf{D} = \mathbf{\underline{\underline{\epsilon} } } \cdot \mathbf{E}$$ | ||
{{eq||eq:3|(3)}} | {{eq||eq:3|(3)}} | ||
| − | ahol $\mathbf{\underline{\underline{\epsilon}}}$ az ún. dielektromos tenzor, melynek elemei általános esetben ''komplex értékű''ek. A legtöbb közegben található egy olyan x-y-z koordináta rendszer (ld. kristálytani tengelyek), ahol ε diagonálisra redukálódik. Általános esetben azonban a dielektromos tenzor nem diagonális és nem is konstans, elemei függnek az elektromos/mágneses térerősségektől és ezek deriváltjaitól. Ezen anyagok tárgyalásával a nemlineáris optika foglalkozik. A nem-lineáris közegek egy csoportjában az elektromos térerősség hely szerinti deriváltjától függő komponenseket is tartalmaz | + | ahol $\mathbf{\underline{\underline{\epsilon}}}$ az ún. dielektromos tenzor, melynek elemei általános esetben ''komplex értékű''ek. A legtöbb közegben található egy olyan x-y-z koordináta rendszer (ld. kristálytani tengelyek), ahol ε diagonálisra redukálódik. Általános esetben azonban a dielektromos tenzor nem diagonális és nem is konstans, elemei függnek az elektromos/mágneses térerősségektől és ezek deriváltjaitól. Ezen anyagok tárgyalásával a nemlineáris optika foglalkozik. A nem-lineáris közegek egy csoportjában az elektromos térerősség hely szerinti deriváltjától függő komponenseket is tartalmaz $\mathbf{\underline{\underline{\epsilon} } }$, amelyről belátható, hogy síkhullám terjedés, valamint egytengelyű anizotrópia esetén a következő alakú lesz (a tenzorelemek általános esetben komplex értékűek!): |
$${\mathbf{\underline{\underline{\epsilon} } } } = \epsilon_0 \cdot \left[ {\begin{array}{ccc} | $${\mathbf{\underline{\underline{\epsilon} } } } = \epsilon_0 \cdot \left[ {\begin{array}{ccc} | ||
{\epsilon_{xx}} & {\epsilon_{xy}} & {0} \\ | {\epsilon_{xx}} & {\epsilon_{xy}} & {0} \\ | ||
| 122. sor: | 122. sor: | ||
ahol feltételeztük, hogy a külső közeg törésmutatója egységnyi. A visszavert fény polarizációs állapotának megváltozását magneto-optikai Kerr-effektusnak (MOKE) nevezik (megkülönböztetendő az elektro-optikai Kerr-effektustól!). A visszavert fény polarizációjának ellipticitása a reflexiós tényezők ρ<sub>±</sub> abszolút értékétől, a polarizációs ellipszis elfordulása pedig a relatív fázisuktól függ (ld. [[#fig:3|3. ábra]]): | ahol feltételeztük, hogy a külső közeg törésmutatója egységnyi. A visszavert fény polarizációs állapotának megváltozását magneto-optikai Kerr-effektusnak (MOKE) nevezik (megkülönböztetendő az elektro-optikai Kerr-effektustól!). A visszavert fény polarizációjának ellipticitása a reflexiós tényezők ρ<sub>±</sub> abszolút értékétől, a polarizációs ellipszis elfordulása pedig a relatív fázisuktól függ (ld. [[#fig:3|3. ábra]]): | ||
{{eq|\Theta_k {{=}} \frac{\Theta_+ - \Theta_-}{2} {{=}} \frac{1}{2}\cdot arg\left( \frac{r_+}{r_-}\right) \approx Im\left ( \frac{n_- - n_+}{1 - n_+ n_-} \right ) \approx Im\left\{ \frac{i\chi \cdot B}{(\epsilon_{xx} - 1)\cdot \sqrt{\epsilon_{xx} } } \right \} \qquad \left[ rad \right]|eq:15|(15)}} | {{eq|\Theta_k {{=}} \frac{\Theta_+ - \Theta_-}{2} {{=}} \frac{1}{2}\cdot arg\left( \frac{r_+}{r_-}\right) \approx Im\left ( \frac{n_- - n_+}{1 - n_+ n_-} \right ) \approx Im\left\{ \frac{i\chi \cdot B}{(\epsilon_{xx} - 1)\cdot \sqrt{\epsilon_{xx} } } \right \} \qquad \left[ rad \right]|eq:15|(15)}} | ||
| − | ahol θ<sub>k</sub> (Kerr-szög) jelöli a polarizációs ellipszis elfordulását a beesési polarizációs irányhoz képest. A ([[#eq:15|15]]) képlet kis, kb. 15°-nál kisebb szögekre érvényes közelítés, amit a formulák első rendű Taylor-sorba fejtéséből kaptunk, felhasználva, hogy 1 >> | | + | ahol θ<sub>k</sub> (Kerr-szög) jelöli a polarizációs ellipszis elfordulását a beesési polarizációs irányhoz képest. A ([[#eq:15|15]]) képlet ''kis, kb. 15°-nál kisebb szögekre érvényes közelítés'', amit a formulák első rendű Taylor-sorba fejtéséből kaptunk, felhasználva, hogy 1 >> |n<sub>−</sub>−n<sub>+</sub>| és |ε| >> |χB| : |
{{eq|\frac{r_+}{r_-} {{=}} \frac{1 + (n_- - n_+) - n_+ n_-}{1 - (n_- - n_+) - n_+ n_-}\approx 1 + \frac{2(n_- -n_+)}{1 - n_+ n_-}\qquad \acute{e}s\qquad \frac{n_- - n_+}{1 - n_+ n_-}\approx \frac{i \chi \cdot B}{(\epsilon_{xx} - 1)\cdot \sqrt{\epsilon_{xx} } }|eq:16|(16)}} | {{eq|\frac{r_+}{r_-} {{=}} \frac{1 + (n_- - n_+) - n_+ n_-}{1 - (n_- - n_+) - n_+ n_-}\approx 1 + \frac{2(n_- -n_+)}{1 - n_+ n_-}\qquad \acute{e}s\qquad \frac{n_- - n_+}{1 - n_+ n_-}\approx \frac{i \chi \cdot B}{(\epsilon_{xx} - 1)\cdot \sqrt{\epsilon_{xx} } }|eq:16|(16)}} | ||
([[#eq:15|15]])-ből látható, hogy a mágneses indukció irányának megfordítása felcseréli n<sub>+</sub> és n<sub>−</sub> értékeit, azaz θ<sub>k</sub> előjelet vált „B” előjelváltása esetén. Mivel abszorpciómentes közegben ε tisztán valós és χ tisztán képzetes, ([[#eq:15|15]])-ből az is következik, hogy a reflektált fény polarizációs iránya csak abban az esetben fordul el, ha az anyag fényelnyelő (abszorbens). | ([[#eq:15|15]])-ből látható, hogy a mágneses indukció irányának megfordítása felcseréli n<sub>+</sub> és n<sub>−</sub> értékeit, azaz θ<sub>k</sub> előjelet vált „B” előjelváltása esetén. Mivel abszorpciómentes közegben ε tisztán valós és χ tisztán képzetes, ([[#eq:15|15]])-ből az is következik, hogy a reflektált fény polarizációs iránya csak abban az esetben fordul el, ha az anyag fényelnyelő (abszorbens). | ||
A lap 2013. február 7., 08:31-kori változata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Bevezetés
A számítástechnika fejlődése napjainkban egyre nagyobb kapacitású adattároló eszközöket igényel. A nagytömegű adattárolás egyik jellemző eszközcsaládja az optikai adattárolók. Bennük az információ kiolvasása optikai úton, fény segítségével történik. Az információs egység legkisebb méretét ily módon a fény hullámhossza és az optikai leképező rendszer minősége (elsősorban az alkalmazott fókuszáló lencse numerikus apertúrája) határozza meg.
Az optikai adattárolás napjainkban elterjedt eszközei a compact disc (CD), és a digital versatile disc (DVD), melyek újraírható, törölhető optikai lemezt használnak, egyesítve a winchester típusú merev mágneslemezes eszközök nagy kapacitását a floppy lemezek cserélhetőségével. A fentiekhez hasonló tárolókapacitással és hozzáférési sebességekkel jellemezhető rendszer a magneto-optikai (MO) tároló (a cserélhető, CD-méretű MO lemezek kapacitása kb. 5,2 Gbyte), melyben az információ tárolása mágneses úton, kiolvasása pedig optikailag történik. MO adathordozókkal és meghajtókkal Európában kevésbé találkozhatunk, alkalmazásuk a távol-keleten, elsősorban Japánban elterjedt. A MO lemez kiolvasása a magneto-optikai Kerr-effektus segítségével történik.
Elméleti alapok
A mérés során vizsgált jelenség, a magneto-optikai Kerr-effektus (MOKE), a fény polarizációs természetével van kapcsolatban, ezért most röviden összefoglaljuk az ide tartozó optikai alapismereteket. A fény transzverzális elektromágneses hullám, melyben az energiaterjedés iránya (Poynting-vektor), az elektromos térerősség vektor (E) és a mágneses térerősség vektor (H) kölcsönösen merőlegesek egymásra. Természetes (polarizálatlan) fényben nincs kitüntetett rezgési irány, az ilyen sugárzás végtelen sok, független, különböző irányú E vektorral jellemezhető rezgés összegeként írható le. Polarizált fényben az elektromos térerősség vektor végpontja szabályos görbét ír le a fényterjedés iránya körül. E görbének a terjedés irányára merőleges síkra vett vetülete általános esetben ellipszis, amely speciális esetben egyenessé (lineárisan polarizált fény), vagy körré (cirkulárisan polarizált fény) fajulhat. Mivel minden elektromágneses hullám felbontható kölönböző frekvenciájú és irányú síkhullámok összegére (ld. szögspektrumra bontás vagy 2D Fourier-transzformáció), az egyszerűség kedvéért most csak egy, a z-irányba terjedő, ω körfekvenciájú monokromatikus síkhullámot, E(z, t)-t vizsgálunk. A komplex formalizmus alkalmazásával a terjedési irányra merőleges x-y síkban a térerősség vektorkomponensei a következő alakban írhatók fel:
![\[\mathbf{E_x}\left (z,t \right ) {{=}} \mathbf{E}_{x0} \cdot e^{i(\omega t - kz + \phi_x)}\]](/images/math/a/5/6/a56d307a1136200340ac56387da645cf.png)
![\[\mathbf{E_y}\left (z,t \right ) = \mathbf{E}_{y0} \cdot e^{i(\omega t - kz + \phi_{y})}\]](/images/math/f/8/0/f802582c388baaf9692ecabfaa64c3c5.png)
ahol „k” a hullámszám vektor abszolút értéke, 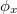 és
és 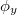 az x és y irányú vektorkomponensek kezdőfázisai,
az x és y irányú vektorkomponensek kezdőfázisai, 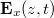 és
és 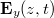 komplex,
komplex, 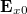 és
és 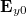 pedig valós vektorok. (Emlékeztetőül: a valódi térerősségvektor komponensek értékét a komplex vektorkomponensek valós részei képezik.) Általános esetben tehát
pedig valós vektorok. (Emlékeztetőül: a valódi térerősségvektor komponensek értékét a komplex vektorkomponensek valós részei képezik.) Általános esetben tehát 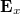 és
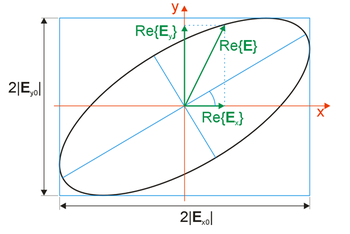
és 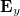 valós eredője ellipszist ír le (1. ábra), melyet a kis- és nagytengelyek hossza, a nagytengely és az x tengely által bezárt szög és térerősségvektor forgási iránya jellemez. Speciálisan, ha
valós eredője ellipszist ír le (1. ábra), melyet a kis- és nagytengelyek hossza, a nagytengely és az x tengely által bezárt szög és térerősségvektor forgási iránya jellemez. Speciálisan, ha 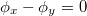 vagy 180°, az E mindig egy egyenesbe esik, így a fény lineárisan poláros. Ha az x és y komponensek
vagy 180°, az E mindig egy egyenesbe esik, így a fény lineárisan poláros. Ha az x és y komponensek 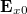 ,
, 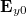 amplitúdóinak abszolút értékei megegyeznek, és közöttük 90° vagy 270° a fáziskülönbség, az elektromos térerősségvektor végpontja egy kör mentén fog az első esetben jobbra, a második esetben balra forogni. A fény ekkor jobbra vagy balra cirkulárisan poláros.
amplitúdóinak abszolút értékei megegyeznek, és közöttük 90° vagy 270° a fáziskülönbség, az elektromos térerősségvektor végpontja egy kör mentén fog az első esetben jobbra, a második esetben balra forogni. A fény ekkor jobbra vagy balra cirkulárisan poláros.
Mivel vizsgálatainkat monokromatikus sugárzásra korlátozzuk, a térerősségek időfüggését (azaz az ωt-s tagot) a továbbiakban elhagyjuk. Ráadásul az elektromágneses teret csak egyetlen síkhullámra, a tér egyetlen pontjában akarjuk meghatározni, így a helyfüggés (k∙z) is elhagyható, azaz elegendő számításainkat csupán a térerősség komplex amplitudóin végezni:
![\[\mathbf{E_x} {{=}} \mathbf{E}_{x0} \cdot e^{i\phi_x}\]](/images/math/4/2/d/42df04c2f57faac12be2d8f7009f822a.png)
![\[\mathbf{E_y} = \mathbf{E}_{y0} \cdot e^{i\phi_y}\]](/images/math/0/7/7/077fbf784fdca481108a288ef291f88c.png)
Optikai aktivitás
A magneto-optikai Kerr-effektus (MOKE) egyes anyagok speciális anizotrópiájának a következménye: olyan közegekben lép fel, amelyek ún. optikai aktivitást mutatnak. A MOKE megértéséhez tehát meg kell ismerkednünk az optikai aktivitás jelenségével. Léteznek olyan anyagok, amelyeken ha lineárisan polarizált síkhullám halad át, a kilépő fény polarizációs síkja az anyagvastagságtól függő mértékben elfordul – az ilyen effektust kiváltó anyagokat nevezik optikailag aktív közegeknek. Mivel ez a jelenség általános formában csak igen bonyolult módon írható le, jelen mérési leírásban megelégszünk az optikai aktivitás jelentősen leegyszerűsített tárgyalásával.
Az anizotrópia tejredési irány és polarizáció függő fényterjedést jelent. Anizotróp közegekben az E elektromos térerősség vektor és a D dielektromos eltolás vektor közötti kapcsolat a következő egyenletrendszerrel írható le:
![\[ \left. {\begin{array}{c} {D_x = \epsilon_{xx}E_x + \epsilon_{xy}E_y + \epsilon_{xz}E_z }\\ {D_y = \epsilon_{yx}E_x + \epsilon_{yy}E_y + \epsilon_{yz}E_z }\\ {D_z = \epsilon_{zx}E_x + \epsilon_{zy}E_y + \epsilon_{zz}E_z }\\ \end{array}} \right \} \qquad \Leftrightarrow \qquad \mathbf{D} = \mathbf{\underline{\underline{\epsilon} } } \cdot \mathbf{E}\]](/images/math/8/8/1/8815c506ee5a7a3a00eb484b55073c57.png)
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
ahol  az ún. dielektromos tenzor, melynek elemei általános esetben komplex értékűek. A legtöbb közegben található egy olyan x-y-z koordináta rendszer (ld. kristálytani tengelyek), ahol ε diagonálisra redukálódik. Általános esetben azonban a dielektromos tenzor nem diagonális és nem is konstans, elemei függnek az elektromos/mágneses térerősségektől és ezek deriváltjaitól. Ezen anyagok tárgyalásával a nemlineáris optika foglalkozik. A nem-lineáris közegek egy csoportjában az elektromos térerősség hely szerinti deriváltjától függő komponenseket is tartalmaz
az ún. dielektromos tenzor, melynek elemei általános esetben komplex értékűek. A legtöbb közegben található egy olyan x-y-z koordináta rendszer (ld. kristálytani tengelyek), ahol ε diagonálisra redukálódik. Általános esetben azonban a dielektromos tenzor nem diagonális és nem is konstans, elemei függnek az elektromos/mágneses térerősségektől és ezek deriváltjaitól. Ezen anyagok tárgyalásával a nemlineáris optika foglalkozik. A nem-lineáris közegek egy csoportjában az elektromos térerősség hely szerinti deriváltjától függő komponenseket is tartalmaz  , amelyről belátható, hogy síkhullám terjedés, valamint egytengelyű anizotrópia esetén a következő alakú lesz (a tenzorelemek általános esetben komplex értékűek!):
, amelyről belátható, hogy síkhullám terjedés, valamint egytengelyű anizotrópia esetén a következő alakú lesz (a tenzorelemek általános esetben komplex értékűek!):
![\[{\mathbf{\underline{\underline{\epsilon} } } } = \epsilon_0 \cdot \left[ {\begin{array}{ccc} {\epsilon_{xx}} & {\epsilon_{xy}} & {0} \\ {- \epsilon_{xy}} & {\epsilon_{xx}} & {0}\\ {0} & {0} & {\epsilon_{zz}} \end{array}} \right]\]](/images/math/8/5/d/85d387d846780de4418696f293ff8112.png)
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
Ezek az ún. optikai aktivitást mutató anyagok. A fenti képletből következik, hogy ilyen közegekben a z-irány kitüntetett szereppel bír: ez az anyag szimmetria tengelye (optikai tengelynek is nevezik). Ilyenek egyes kristályok pl. a kvarc (SiO2) vagy a tellúrdioxid (TeO2). (Optikailag lehetnek aktívak izotróp közegek is, pl. higanyszulfid (HgS) vagy a közönséges cukoroldat; ekkor εxx = εzz.) A továbbiakban feltételezzük, hogy az optikai tengely egybeesik a fény terjedési irányával, azaz a z-tengellyel, tehát (4)-et behelyettesítve (3)-ból a következő másodrendű egyenletrendszer marad:
![\[ \left [ {\begin{array}{c} {D_x} \\ {D_y} \\ \end{array}} \right ] = \left [ {\begin{array}{cc} {\epsilon_{xx}} & {\epsilon_{xy}} \\ {- \epsilon_{yx}} & {\epsilon_{xx}} \\ \end{array}} \right ] \cdot \left [ {\begin{array}{c} {E_x} \\ {E_y} \\ \end{array}} \right ]\]](/images/math/2/1/2/2123fa6e1277d227d702d363056e15ae.png)
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
Az ilyen anyagokban (z-irányú fényterjedés esetén) létezik két olyan E+ és E− vektor, amelyekből a hozzájuk tartozó D± vektorok skalárral való szorzással kaphatók meg:
![\[ \mathbf{D}_{\pm} = \epsilon_0\cdot n_{\pm}^2\cdot \mathbf{E}_{\pm}\]](/images/math/8/7/5/8751e76e7d56b0ccbf974ee68580c6a2.png)
ahol n± a két speciális térerősség vektorhoz rendelhető komplex törésmutató. A dielektromos eltolás vektort (3)-ból ide behelyettesítve kapjuk a következő sajátérték egyenletet:
![\[\mathbf{\underline{\underline{\epsilon} } } \cdot \mathbf{E}_{\pm} = \epsilon_0 \cdot n_{\pm}^2 \cdot \mathbf{E}_{\pm}\]](/images/math/2/f/8/2f82e37a343ca79ac12471c96c1b0df3.png)
A (4) dielektromos tenzorral jellemezhető anyagokban az E± sajátvektorok komplex amplitudói a következőek (a z-től és t-től való függés az egyenletekből kiesik):
![\[\mathbf{E}_+ = \frac{E_0}{\sqrt{2} } \cdot \left [ {\begin{array}{c} {1} \\ {i} \\ \end{array}} \right ]\qquad ; \qquad \mathbf{E}_- = \frac{E_0}{\sqrt{2} } \cdot \left [ {\begin{array}{c} {1} \\ {-i} \\ \end{array}} \right ] \]](/images/math/4/2/e/42e1f79a9c7b44dadcda30d0ddf4b58d.png)
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
ahol E0 a térerősség vektor abszolút értéke. Ez (5)-nek valóban megoldása. Behelyettesítve:
![\[ \left [ {\begin{array}{cc} {\epsilon_{xx}} & {\epsilon_{xy}} \\ {- \epsilon_{xy}} & {\epsilon_{xx}} \\ \end{array}} \right ] \cdot \left [ {\begin{array}{c} {1} \\ {\pm i} \\ \end{array}} \right ] = n_{\pm}^2\cdot \left [ {\begin{array}{c} {1} \\ {\pm i} \\ \end{array}} \right ] \]](/images/math/b/1/5/b154c61205bb01a4f962f0ccbbcfb9d4.png)
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
ahol a megoldásként kapott n±2 sajátértékekből kifejezett (komplex) törésmutatók értéke:
![\[n_+ = \sqrt{\epsilon_{xx} + i \epsilon_{xy} } \qquad \acute{e}s \qquad n_- = \sqrt{\epsilon_{xx} - i \epsilon_{xy} }\]](/images/math/f/5/f/f5f88608d33bc2941efbd8843f310958.png)
A (8) egyenletből látható, hogy a térerősség sajátvektorok olyan komplex amplitudójú vektorkomponensekkel rendelkeznek, amelyek kielégítik az elméleti alapoknál bemutatott cirkuláris polarizációs állapotot (azonos vektorkomponens amplitudók, 90° fáziskülönbség). A sajátvektorok y-komponenseiben szereplő ellenkező előjel a térerősségvektorok ellentétes forgásirányára vonatkozik. Összefoglalva: a (4) tenzorral jellemezhető közegekben a jobbra és balra forgó cirkulárisan polarizált nyalábok polarizációs állapot változás nélkül terjednek, azaz a közegbe való belépés után megmarad a cirkularitásuk, az eltérő törésmutatók miatt csupán a terjedési sebességük lesz különböző.
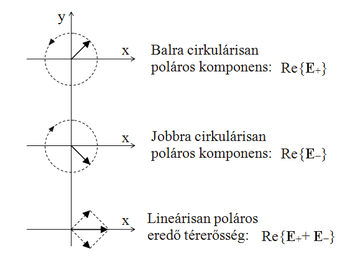
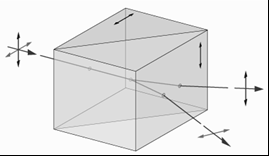
A fent bemutatott közegen áthaladó lineárisan polarizált nyaláb polarizációs síkja elfordul, mégpedig a terjedés irányától függetlenül mindig ugyanabba az irányba. Ezt az effektust nevezik optikai aktivitásnak, ami könnyen megérthető, ha a bejövő lineárisan polarizált nyalábot két azonos amplitudójú, ellentétesen forgó cirkulárisan polarizált nyalábra bontjuk fel (ld. 2. ábra). A két cirkuláris nyaláb komplex amplitudója az optikailag aktív közeg dielektromos tenzorának sajátvektora, tehát terjedés közben a polarizációs állapotuk nem változik meg. A különböző terjedési sebességek miatt viszont eltérő fázisban érik el az optikailag aktív közeg kilépő felületét, ami elfordítja a két nyaláb eredőjeként kapott lineárisan polarizált nyaláb polarizációs síkját.
A magneto-optikai Kerr-effektus
Az optikai aktivitás nem feltétlenül egy anyag természetes tulajdonsága, kiváltható pl. erős mágneses térrel is. Alkalmazzunk egy (4) dielektromos tenzorral jellemzett anyagra z-irányú konstans B mágneses indukciójú mágneses teret. Ha εxy arányos B abszolút értékével, ún. mágnesesen indukált optikai aktivitást tapasztalunk:
![\[\epsilon_{xy} = \chi \cdot B\]](/images/math/e/9/6/e969ae5973a29b715f00eea15edbd84b.png)
ahol χ általános esetben komplex szám. Ezt az effektust Faraday-effektusnak is nevezik. A (10) összefüggés alapján a törésmutató sajátértékek a következők lesznek:
![\[n_{\pm} = \sqrt{\epsilon_{xx} \pm i\chi\cdot B}\]](/images/math/2/8/d/28d6c7902ee5a56230d0de64d7df9746.png)
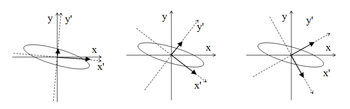
Az ilyen anyagok felületére ejtett lineárisan polarizált fény (Ebe) reflexió után (Erefl) elliptikusan polarizálttá válik. Ennek oka az Ebe,± jobbra-balra forgó cirkuláris sajátvektorok eltérő törésmutatója, ami eltérő r+ és r− reflexiós tényezőket eredményez (ld. 3. ábra):
![\[\mathbf{E}_{refl,\pm} = r_{\pm} \cdot \mathbf{E}_{be,\pm}\]](/images/math/f/b/a/fba02ba20314b4ff92d4b5964f856458.png)
ahol a felületre merőleges beesés esetén a reflexiós tényező:
![\[r_{\pm} = \frac{1 - n_{\pm} }{1 + n_{\pm} } = \rho_{\pm} \cdot e^{i\Phi_{\pm} }\]](/images/math/0/7/3/0733659b66f2989d32d24f774587aaea.png)
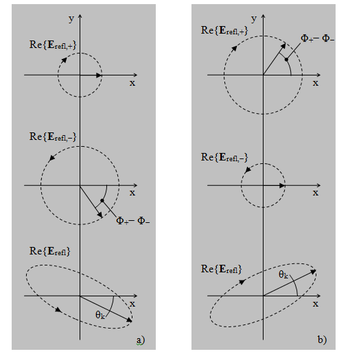
ahol feltételeztük, hogy a külső közeg törésmutatója egységnyi. A visszavert fény polarizációs állapotának megváltozását magneto-optikai Kerr-effektusnak (MOKE) nevezik (megkülönböztetendő az elektro-optikai Kerr-effektustól!). A visszavert fény polarizációjának ellipticitása a reflexiós tényezők ρ± abszolút értékétől, a polarizációs ellipszis elfordulása pedig a relatív fázisuktól függ (ld. 3. ábra):
![\[\Theta_k = \frac{\Theta_+ - \Theta_-}{2} = \frac{1}{2}\cdot arg\left( \frac{r_+}{r_-}\right) \approx Im\left ( \frac{n_- - n_+}{1 - n_+ n_-} \right ) \approx Im\left\{ \frac{i\chi \cdot B}{(\epsilon_{xx} - 1)\cdot \sqrt{\epsilon_{xx} } } \right \} \qquad \left[ rad \right]\]](/images/math/c/0/f/c0faf8ce4505bb1e45425cd7f0b309cd.png)
ahol θk (Kerr-szög) jelöli a polarizációs ellipszis elfordulását a beesési polarizációs irányhoz képest. A (15) képlet kis, kb. 15°-nál kisebb szögekre érvényes közelítés, amit a formulák első rendű Taylor-sorba fejtéséből kaptunk, felhasználva, hogy 1 >> |n−−n+| és |ε| >> |χB| :
![\[\frac{r_+}{r_-} = \frac{1 + (n_- - n_+) - n_+ n_-}{1 - (n_- - n_+) - n_+ n_-}\approx 1 + \frac{2(n_- -n_+)}{1 - n_+ n_-}\qquad \acute{e}s\qquad \frac{n_- - n_+}{1 - n_+ n_-}\approx \frac{i \chi \cdot B}{(\epsilon_{xx} - 1)\cdot \sqrt{\epsilon_{xx} } }\]](/images/math/0/a/0/0a05c9b2c5dcd262e8aa72c33858436c.png)
(15)-ből látható, hogy a mágneses indukció irányának megfordítása felcseréli n+ és n− értékeit, azaz θk előjelet vált „B” előjelváltása esetén. Mivel abszorpciómentes közegben ε tisztán valós és χ tisztán képzetes, (15)-ből az is következik, hogy a reflektált fény polarizációs iránya csak abban az esetben fordul el, ha az anyag fényelnyelő (abszorbens).
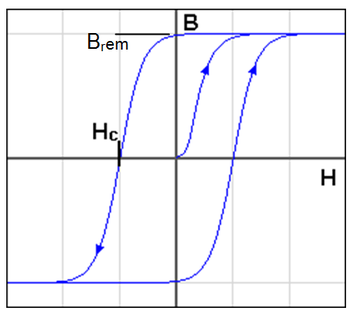
A magneto-optikai adattárolásban olyan ferromágneses ritkaföldfém anyagokat használnak adathordozó közegként, amelyekben a remanens mágneses indukció (Brem) értéke nagy, hogy az indukált optikai aktivitást a külső mágneses tér kikapcsolásakor is fenntartsa. Ily módon kétféle irányú mágneses indukció tárolható a közegben, amely a hozzájuk tartozó eltérő előjelű Kerr-szögek révén detektálható. E két állapot egy bit 0 és 1 értékének feleltethető meg. Az anyaggal szemben támasztott másik követelmény, hogy kisebb, zavaró mágneses terek ne fordítsák át a mágnesezettséget, ami nagy koercitív erejű (Hc) anyagokra jellemző.
A Kerr-szögmérés elve
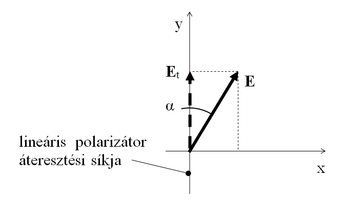
A fény polarizációs állapotát polarizátorokkal lehet vizsgálni. A lineáris polarizátor olyan eszköz, amely a fényt attól függően engedi át, hogy a térerősségvektor milyen szöget zár be a polarizátor áteresztési síkjával. A lineáris polarizátor csak azt a térerősség vektor komponenst engedi át, amelynek polarizációs síkja megegyezik a polarizátor áteresztési síkjával.
A 4. ábra szerint a fény az ábra síkjára merőlegesen terjed és lineárisan polarizált. Az E valós elektromos térerősség vektora α szöget zár be a polarizátor áteresztési síkjával. A polarizátor E-nek csak Et vetületét engedi át, azaz az áteresztett térerősségvektor nagysága 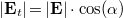 . A polarizátor után mérhető fényintenzitás arányos a térerősség négyzetével, vagyis az E és a polarizátor áteresztési síkja közötti szög koszinuszának négyzetével (Malus-törvény). Ha a térerősségvektor a MO-rétegről reflektálódva θk szöggel elfordul az analizátor áteresztési síkja irányába, vagy a tér átfordításakor az ellenkező irányba, az áthaladó térerősségvektor
. A polarizátor után mérhető fényintenzitás arányos a térerősség négyzetével, vagyis az E és a polarizátor áteresztési síkja közötti szög koszinuszának négyzetével (Malus-törvény). Ha a térerősségvektor a MO-rétegről reflektálódva θk szöggel elfordul az analizátor áteresztési síkja irányába, vagy a tér átfordításakor az ellenkező irányba, az áthaladó térerősségvektor
![\[E_t = E\cdot \cos(\alpha - \Theta_k) \qquad vagy \qquad E_t = E\cdot \cos(\alpha + \Theta_k)\]](/images/math/f/a/f/faf67997f00dadb67a2750546ab0dc6c.png)
lesz a két esetnek megfelelően. A polarizátor utáni fényintenzitások méréséből a Kerr-szög elvileg meghatározható. Kis szögű elfordulások esetén az intenzitás csak másodrendben változik, így ez a módszer meglehetősen pontatlan.
Pontosabb mérést tesz lehetővé az ún. Wollaston-féle polarizációs osztóprizma alkalmazása. Ez az eszköz a ráeső fényt két merőleges lineáris polarizációjú nyalábra bontja, mintha két merőleges állású polarizátort egyszerre alkalmaznánk ugyanarra a nyalábra. Az 5. ábra a prizma hatását szemléleti.
Akár lineárisan-, akár elliptikusan poláros fény esik a Wollaston prizmára, a prizma megfelelő elforgatásával elérhető, hogy két azonos intenzitású nyalábot kapjunk. Az elforgatás szöge a cirkulárisan poláros esetet leszámítva egyértelmű. A 6. ábrán nyomon követhető, mikor kapunk két egyenlő intenzitású nyalábot.
Elliptikus esetben ehhez értelemszerűen az ellipszis főtengelyének 45° fokos szöget kell bezárnia az osztóprizma által kijelölt két egymásra merőleges (x', y') síkkal. A mérés elve tehát az, hogy a két merőleges polarizációjú nyaláb intenzitásának különbségét minimalizáljuk a prizma megfelelő forgatásával, nulla jelet keresve. A gyakorlatban az elektronika miatt (műveleti erősítők) a mért intenzitások különbsége sosem lesz pontosan nulla. Ez esetben az osztóprizma szöge tehát meghatározott −45° fokos szöget zár be az ellipszis főtengelyével, amelynek helyzetéből adódik a Kerr-szög. Ha a polarizátort úgy állítjuk be, hogy a Kerr-szöggel elfordult térerősségvektort a polarizátor két azonos nagyságú, egymásra merőleges polarizációjú komponensre bontsa, majd a mágneses tér átfordításakor a polarizátort addig forgatjuk, míg ismételten két azonos térerősség-komponenst tudunk előállítani, a polarizátor szögelfordulása éppen a Kerr-szög kétszeresét adja.
A Kerr-szögmérő műszer
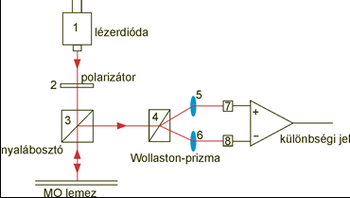
A műszer optikai rendszere a 7. ábrán látható. Az 1 fényforrás egy Philips lézerdióda modul (lézerdióda + kollimátor optika + meghajtó elektronika), amely homogén, párhuzamos nyalábot bocsát ki 820 nm-es hullámhosszon. Ezt úgy érik el, hogy a lézerdióda erősen széttartó (divergens) és aszimmetrikus fényét megfelelő optikai rendszerrel egybeépítik, mely elvégzi a nyalábformálást és a kollimálást (párhuzamosítást). A lézerdióda fénye csak kis mértékben polarizált, a polarizációs arány ennél a típusnál 35:1-hez. (A polarizációs arány egyszerű polarizátorral mérhető. A 4. ábra szerint az α szög függvényében mérve az áteresztett intenzitást, a maximális és minimális intenzitások aránya.) Emiatt a fény polarizáltságát a minta előtt javítani kell. Ezt végzi el a 2 polarizátor, mely egy Nicol-féle prizma. A Nicol-prizma kettőstörő anyagból (mészpátból) készül, és úgy van kialakítva, hogy csak egy bizonyos lineáris polarizációjú fényt engedjen át. A 2 polarizátor után a polarizációs arány jobb, mint 1000:1-hez.
A 3 nyalábosztó prizma segítségével lehet a Kerr-effektust merőleges beesés mellett vizsgálni. A 3 nyalábosztó két 45°-os félprizmából áll, melyek közül az egyik felületén lévő dielektrikum réteg kb. 50 %-os áteresztést, illetve reflexiót enged meg polarizációtól függetlenül az alkalmazott 820 nm-es hullámhosszon. Ezután következik a 4 Wollaston-típusú polarizációs prizma, mely szintén kettőstörő anyagból készül, de úgy van kialakítva, hogy mindkét egymásra merőleges polarizációjú fénykomponenst átengedi kb. 20° szögeltéréssel. A kettéválasztott sugarakat az 5 - 6 lencsék fókuszálják rá a 7 - 8 detektorokra, melyek jeleit a különbségképző erősítőre vezetjük. A Wollaston-prizma, a lencsék és a detektorok együtt egy forgatható asztalra vannak felszerelve, mely lehetővé teszi az előző fejezetben említett módszer alkalmazását. A mintaasztal alatt egy elektromágnes található. A mágneses indukció irányát és nagyságát a tekercsben folyó áram irányával és erősségével változtathatjuk.
Az elektronika feladata a különbségi jel előállítása lehetőleg minimális zaj (háttérfény, detektorzaj, elektronika zaja) mellett. A lézerdióda áramát ezért ~1 kHz frekvenciával moduláljuk, és a különbségi jelet egy erre a frekvenciára hangolt keskenysávú szűrőn engedjük át. Ezzel a módszerrel csak az erre a keskeny sávra eső zaj marad a hasznos jelben. A különbségképző erősítésének függvényében a jel néhányszor 10 mV. (A detektorok áramainak különbsége csak ~ 0,03 µA.) A jelet érzékeny AC voltmérővel mérjük.
A műszer kezelése
A mérendő mintát a készülék elején lévő asztalra kell helyezni. Az asztal síkja az asztal szélein található csavarokkal állítható. Az asztal fölött egy fém henger található, melynek kettős szerepe van. A Kerr-mérőből kilépő 820 nm-es fény emberi szemmel nem látható. A fény a henger belsejében halad. A minta mérni kívánt pontját kell a henger alá helyezni. A henger megakadályozza, hogy a mintát helytelen szögben helyezzük az asztal fölé, s így a káros reflexiókat is kiszűri. A műszer jobb oldalán található a forgatható asztal mikrométerorsója, amely a 8. ábrán (5) is látható. A mikrométerorsó egy osztása 0,5 perc szögértéknek felel meg. Egy teljes körbefordulás (50∙0,5 =) 25 percnek felel meg. Fontos megjegyzés: a mikrométerorsó 6 rögzítő elemét ne oldjuk ki, mert akkor a Wollaston prizma a műszerben szabadon elfordulhat!
A 230V-os hálózati csatlakozó és a biztosíték a készülék hátlapján helyezkedik el. A készüléket a baloldalon lévő kapcsolóval lehet bekapcsolni. A készülék bekapcsolt állapotát a műszer mutatós kijelzője (a különbségi jel indikátor) fölötti LED jelzi. Közvetlenül a bekapcsolás után a lézerdióda még nem működik, azt külön kell bekapcsolni a 4 jelű potenciométer elforgatásával (ON). A készülék kikapcsolását is a potenciométer OFF helyzetbe való forgatásával kell kezdeni! Erre azért van szükség, mert a lézerdióda zaj impulzusokra, ki-be kapcsolási tranziensekre nagyon érzékeny. A lézerdióda kontrol jele a 2 BNC csatlakozóról (LD CONTR. SIGNAL) levehető. A különbségi jel, amely az indikátort is vezérli, a 3 BNC csatlakozóról vehető le. A két kimenet révén lehetőség van a különbségi jelet és a kontrol jelet egyszerre oszcilloszkópon figyelni, így a jel fázisváltását is láthatjuk, melyet az indikátor nem jelez.
Az 1 kapcsoló segítségével lehet a kijelzést szabályozni. LOG állásban a kijelzés a vezérlő jellel logaritmikus, LIN állásban pedig lineáris kapcsolatban van. Mikor a nulla helyzetet keressük, a kapcsolót először LOG állásba kell állítani, a nulla helyzet finom állításakor a kapcsolót LIN állásba kell kapcsolni.
Mérési feladatok
- 1. feladat
Kapcsolja be a Kerr-mérő műszert, ekkor a lézerdióda meghajtó áramát szabályzó 4 potméter OFF állásban van. Csatlakoztassa a lézerdióda kontrol kimenetét az oszcilloszkóp 2. csatornájához! A 4 potméter ON állásba való forgatása mellett ellenőrizze oszcilloszkópon a lézer működését. Határozza meg a modulációs frekvenciát!
- 2. feladat
Határozza meg az üveghordozós MO minta Kerr-forgatási szögét! A minta asztalra helyezése előtt győződjön meg róla, hogy a mintaasztal vízszintes helyzetben van. Ha állításra van szükség, kérje a laborvezető segítségét, ugyanis a minta állítás közben könnyen eltörhet! Ezután csatlakoztassa az elektromágnes kivezetéseit a DC feszültséggenerátor + és − kimenetére a labortápegység kikapcsolt állapotában. A műszer bal oldali kijelzője az áramot, a jobb oldali pedig a feszültséget mutatja amper illetve volt egységekben. Ellenőrizze, hogy a szabályozó gombok balra kitekert állapotban vannak (nulla feszültség és áram), majd kapcsolja be a tápegységet. Figyelem! A balesetveszély elkerülése érdekében áramfelvétel mellett soha ne húzza ki az elektromágnes kivezetéseit a tápegységből, mivel ekkor a hirtelen változás nagyfeszültséget indukálhat a kivezetéseken! Az árammérőt figyelve növelje a feszültséget addig, hogy a tekercs áramfelvétele 400 mA legyen. Csatlakoztassa a detektorok felerősített különbségi jelét (DIFF. SIGNAL) az oszcilloszkóp 1. csatornájára. Ezután forgassa az 5 forgatható asztal segítségével a Wollaston-prizmát olyan helyzetbe, hogy a null-indikátoron az 1. kapcsoló LIN állása mellett minimum legyen. A jelminimum precíz megkeresése legkönnyebben az oszcilloszkópot figyelve történhet. Olvassa le a forgató mikrométerorsóján lévő értéket! (egy század miliméter a mikrométeren 0.5’ szögelfordulásnak felel meg) Ezután tekerje le nullára a feszültséget a tápegységen és kapcsolja ki a tápegységet! Fordítsa meg a polaritást a banándugók felcserélésével, majd állítson be ellenkező irányú, 400 mA értékű áramot! Ismét határozza meg a nulla helyzetnek megfelelő szögértéket! Számítsa ki a Kerr-szög értékét!
- 3. feladat
Ismételje meg a 2. feladat szerinti mérést még két különböző pontban a mintán! Határozza meg az átlagos Kerr-szöget és a mérések hibáját!
- 4. feladat
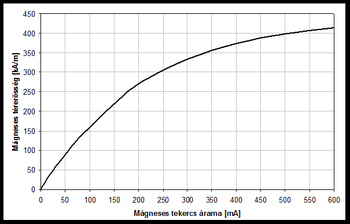
Határozza meg a MO minta koercitív erejét (ld. 9.ábra)! A koercitív erő definíciója a 9. ábrán látható: az a külső mágneses térerősség, amely mellett a minta saját mágneses tere nulla. Meghatározásához meg kell mérni a Kerr-szöget a mágneses tér függvényében. A mágneses tér nagysága az áram függvényében a mérőhelyen lévő grafikonról leolvasható, illetve a 10. ábrán látható. Mérje ki a Kerr-szög változását a tekercs áramának függvényében! Induljon el 400 mA-ről! Keresse meg a minimális különbségi jelnek megfelelő szögértéket. Csökkentse az áram értékét, figyelve a nullindikátor mutatóját. Eleinte 50 mA -enként, később kb. 5 mA -enként álljon meg, és állítsa be a minimális különbségi jelet. Az adatokból számítsa ki a relatív szögértékeket, valamint a grafikonról olvassa le a mágneses tér nagyságát! Növekvő és csökkenő áramértékekre az átbillenés más-más áramértékeknél következik be. Ábrázolja a hiszterézis görbét (Kerr-szög értékeket) a mágneses tér függvényében! Adja meg a koercitív erő értékét!
Adatok:
x = [0 20 75 100 140 200 300 400 500 600];
y = [0 40 127 159 207 271 334 374 398 414];
PDF formátum
Magneto-optikai Kerr-szög mérése