„Kvantumpöttyök” változatai közötti eltérés
| 3. sor: | 3. sor: | ||
===Kvantum pöttyök, energia skálák=== | ===Kvantum pöttyök, energia skálák=== | ||
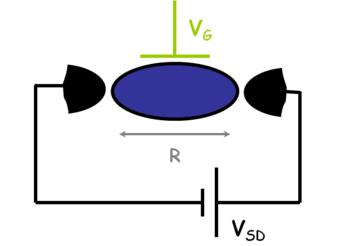
| − | + | {{fig|QD_1.png|fig:1|1. ábra}} | |
===Elektrosztatikus energia kvantum pöttyökben=== | ===Elektrosztatikus energia kvantum pöttyökben=== | ||
A lap 2013. április 11., 16:14-kori változata
Hát erről lesz szó, csak kicsit bővebben.
Tartalomjegyzék |
Kvantum pöttyök, energia skálák
Elektrosztatikus energia kvantum pöttyökben
Coulomb gyémántok
Mesterséges atomok és kvantum bezártság
Pauli spin blokád
Cotunneling és Kondo effektus
Kvantum pöttyök felhasználása
Egy elektron pumpa, spin kvantum bit
| |
| 1. ábra |
A korábbiakban láttuk, hogy egy egycsatornás kvantumvezeték vezetőképessége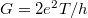 
, ahol 
a vezeték közepén elhelyezett szórócentrum transzmissziós valószínűsége. Ez a vezetőképesség abból adódik, hogy a bejövő elektronhullám parciálisan transzmittálódik illetve reflektálódik. A fotonokkal végzett kétrés kísérlethez hasonlóan ha megmérjük, hogy egy elektron áthaladt vagy visszaverődött a szórócentrumon, akkor csak azt kaphatjuk, hogy vagy az egész elektron áthaladt vagy az egész elektron visszaverődött, parciális töltés transzmisszióját nem mérhetjük. Így a mért áram (ill. vezetőképesség) abból adódik, hogy az elektronok -ed része teljesen transzmittálódik,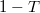 
-ed része pedig reflektálódik. Innen már rögtön látszik, hogy a véletlenszerűen transzmittálódó töltéscsomagok árama a várható érték körül fluktuálni fog.
 |
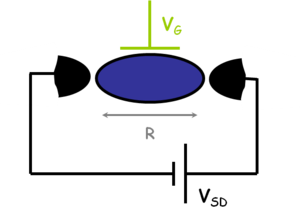
| 1. ábra |
Egy elektronra vonatkoztatva az áthaladt töltés valószínűséggel 
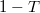, valószínűséggel pedig 
, így várhatóértékben
![\[<Q>=T\cdot e+(1-T)\cdot 0=T\cdot e,\]](/images/math/5/b/a/5bab70164556df83b81d56389eb1de9a.png)
azaz a Landauer formulának megfelelően az áram -vel arányos. Hasonlóan kiszámolhatjuk az áthaladt töltés szórásnégyzetét:
![\[<(\Delta Q)^2>=<Q^2>-<Q>^2=T\cdot e^2 - (T\cdot e)^2=T(1-T)e^2,\]](/images/math/3/b/9/3b94398b6e8943b375dd70cef5a3dc35.png)
azaz az áram szórásnégyzete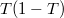 
-vel arányos, ami 
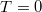és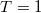 
kivételével mindig véges, azaz egy részlegesen transzmittáló nanovezeték mindig véges áramfluktuációt, véges zajt mutat.
A zaj, azaz egy mennyiség várható érték körüli fluktuációja sok esetben lényeges többlet információt hordozhat a várható értékhez (pl. vezetőképességhez) képest, amire a későbbiekben pár egyszerű példát mutatunk. Mindenek előtt azonban definiáljuk pontosabban a zaj fogalmát.
Az áram időbeli fluktuációja
A korábbiakban l
A zaj, azaz egy mennyiség várható érték körüli fluktuációja sok esetben lényeges többlet információt hordozhat a várható értékhez (pl. vezetőképességhez) képest, amire a későbbiekben pár egyszerű példát mutatunk. Mindenek előtt azonban definiáljuk pontosabban a zaj fogalmát.
