„Spintronika” változatai közötti eltérés

A Fizipedia wikiből
(→‎Spinpolarizált vezetés nanoszerkezetekben)
(→‎Spinpolarizált transzport alkalmazása: spinszelep)
 
(egy szerkesztő 48 közbeeső változata nincs mutatva)
1. sor: 1. sor:
−
 
+
==Spindiffúziós hossz==
−
==Bevezetés==
+
 
<wlatex>
 
<wlatex>
−
The spin dependence of electronic transport is hidden in most metals. However,
+
Egy makroszkopikus vezetőben az elektronok számtalanszor szóródnak miközben eljutnak az egyik elektródából a másikba. Ahogy a [[Transzport_nanovezetékekben:_Landauer_formula,_vezetőképesség-kvantálás|nanovezetékek tárgyalásának bevezetésekor láttuk,]] a szennyezőkön és rácshibákon történő ''rugalmas'' szórás az elektronok elektromos tértől nyert impulzusának elvesztéséhez vezet. Ennek a folyamatnak a karakterisztikus skáláját az átlagos momentumrelaxációs szabadúthossz, $l_m$ jellemzi. Rugalmatlan szórások esetén (pl. kölcsönhatás rácsrezgésekkel) az elektronok energiája megváltozik, és így elveszik a fázisinformáció, azaz [[Interferencia_és_dekoherencia_nanoszerkezetekben|megszűnik az interferenciaképesség]]. Ennek a folyamatnak a karakterisztikus skálája az ún. fázisdiffúziós hossz, $L_{\phi}$. Megfelelő távolságon belül az elektronok a mágneses momentumuk, azaz a spinjükhöz tartozó információt is elvesztik, amit a spindiffúziós hosszal, $L_s$ jellemezhetünk.
−
spin polarized current injected to a nonmagnetic conductor keeps the spin memory
+
Egy spindiffúziós hossznál kisebb, mágnesesen rendezett építőelemeket tartalmazó nanoszerkezetben azonban számos érdekes, az elektronok spin szerinti ''polarizáltságához'' kötődő jelenséggel találkozhatunk.  
−
within a certain distance, typically in the submicron range. By now, nanoscale
+
−
devices have been prepared where the size of the components is well below the
+
−
distance of the spin-memory, and both the control of the spin states and the
+
−
utilization of the spin information have been
+
−
demonstrated.\cite{Wolf16112001,Awschalom2007} In most of these electronic
+
−
applications ferromagnetic components act as spin filter and detector,
+
−
\cite{RevModPhys.76.323,0022-3727-35-18-201} while a nonmagnetic metal mediates
+
−
the spin information: this is the simplest spin-valve structure. For the design
+
−
of such nanodevices a proper understanding of spin dependent transport is
+
−
necessary, including the knowledge of the carriers' spin-polarization, or the
+
−
determination of the spin diffusion length.
+
−
 
+
−
In the first part of this review we present a simple model for the spin
+
−
dependent transmission through a nanostructure based on the Landauer
+
−
formalism widely applied in the field of nanophysics. In the
+
−
second part a special measurement technique is reviewed, which allows the
+
−
direct determination of the current spin polarization, and with which even the
+
−
decay of the spin polarization i.e.~the spin diffusion length can be determined
+
−
in a nonmagnetic layer. In the last part the nanoscale spin-valve architecture
+
−
is discussed, demonstrating how the results of basic research find broad
+
−
technical application and trigger an intensive development of novel memory
+
−
elements.
+
 
</wlatex>
 
</wlatex>
−
==Spinpolarizált vezetés nanoszerkezetekben==
+
==Spinpolarizáció ideális nanovezetékekben==
−
<wlatex>
+
<wlatex>  
−
In a macroscopic conductor the electrons suffer numerous scattering processes as
+
A [[Transzport_nanovezet%C3%A9kekben:_Landauer_formula,_vezet%C5%91k%C3%A9pess%C3%A9g-kvant%C3%A1l%C3%A1s#Kvantumvezet.C3.A9k_ellen.C3.A1ll.C3.A1sa|korábbiakban láttuk]], hogy ha két elektróda közé egy ideális, szórásmentes nanovezetéket helyezünk, akkor abban keresztirányban állóhullámok, hosszirányban pedig síkhullám terjedés alakul ki, a vezetőképesség pedig $G=(2e^2/h)M$, ahol M a nyitott vezetési csatornák száma, azaz azon különböző keresztmódusokhoz tartozó egydimenziós parabolikus diszperziók száma, melyek metszik a Fermi-energiát. A kettes szorzó a spin szerinti degenerációból adódott.
−
they move from one electrode towards the other. Due to the scattering on
+
−
impurities and lattice defects the drift momentum of the electrons gained from
+
−
the electric field is lost. This process is described by the characteristic
+
−
length scale of the momentum relaxation mean free path, $l_m$. Inelastic
+
−
scattering processes like the scattering on lattice vibrations lead to a change
+
−
of energy, which results in the loss of phase coherence for electron waves. The
+
−
corresponding characteristic length scale is called phase diffusion length,
+
−
$l_{\phi}$.\cite{nazarov_book,datta_book} Within a large enough distance the
+
−
electrons also loose their spin information, as characterized by the spin diffusion length,
+
−
$l_s$.\cite{RevModPhys.76.323,fabian:1708} In a nanostructure, however, all
+
−
these length scales may become comparable to, or even larger than the characteristic size of the structure,
+
−
$L$. For instance, in small enough structures ($L<l_s$) the spin information is
+
−
preserved, which is a key ingredient for spintronic
+
−
applications.\cite{PhysRevB.48.7099} For structures smaller than $l_{\phi}$
+
−
coherent quantummechanical features appear, whereas for $L<l_m$ a ballistic
+
−
transport is observed, i.e.~the electrons scatter only on the edges of the
+
−
structure, but not inside.
+
  
−
Here we give a simple model to demonstrate how spin-polarized current may arise
+
Egy ferromágneses nanovezetékben azonban különbséget kell tenni a fel és a le spinű elektronok között.
−
in ferromagnetic nanostructures, which are smaller than the spin diffusion
+
A vezeték mágnesezettségét legegyszerűbben Stoner-képben vehetjük figyelembe, azaz az energidiszperziókhoz hozzáadjuk a kicserőlédési energiát, mely $\varepsilon_{\mathrm{ex}}$-el különbözik a fel illetve le spinű ($\sigma =\pm 1/2$) elektronokra:
−
length. In order to provide a microscopic insight to the relevant processes we
+
$$\varepsilon_n^{\sigma}(k)=\varepsilon(k)+\varepsilon_n-\sigma\varepsilon_{\mathrm{ex}}.$$
−
use the well established approach of the Landauer
+
Emlékeztetőül: $\varepsilon(k)$ a hosszirányú terjedést, $\varepsilon_n$ pedig a keresztirányú állóhullámok energiáját írja le. Fontos megjegyezni, hogy $\varepsilon(k)$ lehet tetszőleges Bloch-állapot diszperziója, nem kell feltétlenül szabad elektronoknak megfelelő parabolikus diszperziót feltételezni. 
−
formalism,\cite{Landauer_form,datta_book} which has been successfully applied to
+
−
describe several nanoscale systems, like atomic-sized
+
−
conductors\cite{Agrait200381} or semiconductor
+
−
nanostructures.\cite{PhysRevLett.60.848,ihn_book}
+
  
 
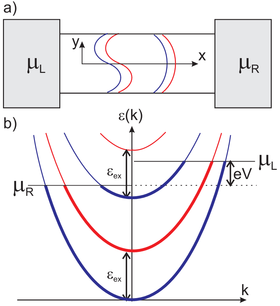
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Spintronika1.png|közép|300px|]]
+
| align="center"|[[Fájl:Spintronika1.png|közép|280px|]]
 
|-
 
|-
−
| align="center"|1. ábra  
+
| align="center"|1. ábra. ''Ferromágneses nanovezetékben a le spinű elektronok diszperziós relációja (piros) a kicserélődési energiával eltolódik a fel spinű elektronokéhoz képest (kék)'' 
 
|}
 
|}
  
−
Panel (a) demonstrates an ideal 2D quantum wire with parallel
+
Az 1. ábra parabolikus szabad elektron diszperzió esetén szemlélteti az energiaviszonyokat. A kék görbék a fel, a piros görbék pedig a le spinű elektronokhoz tartoznak, azaz a piros parabolák mindig $\varepsilon_{\mathrm{ex}}$ energiával a megfelelő kék parabola felett helyezkednek el. [[Transzport_nanovezet%C3%A9kekben:_Landauer_formula,_vezet%C5%91k%C3%A9pess%C3%A9g-kvant%C3%A1l%C3%A1s#Kvantumvezet.C3.A9k_ellen.C3.A1ll.C3.A1sa|A korábbiaknak megfelelően]] a $k>0$ állapotok a bal oldali elektródából származnak, így annak a $\mu_L$ kémiai potenciáljáig vannak betöltve, míg a $k<0$ állapotok a jobb oldali, $\mu_R$ kémiai potenciálú elektródából származnak.
−
walls and the absence of scattering inside the wire. The standing waves
+
−
demonstrate the quantized transverse modes in the wire. Panel (b) demonstrates
+
−
the dispersion of the conductance channels inside the wire in a free electron
+
−
picture. The blue parabolas correspond to spin up electrons, whereas the red
+
−
parabolas stand for the spin down electrons. The two spin subbands are shifted
+
−
by an energy $\varepsilon_{ex}$. The thick/thin lines denote the
+
−
occupied/unoccupied states. Note, that right going states ($k>0$) are occupied
+
−
up to an energy higher by $eV$ than the left moving states ($k<0$).
+
−
 
+
−
As a simplified model first we consider an ideal two dimensional wire with
+
−
parallel walls (Fig.~\ref{Qwire}(a)). In the ballistic limit no scattering occurs
+
−
in the wire, and an electron entering into the wire from one side will propagate
+
−
to the other side without changing its energy and spin state. Along
+
−
the wire ($x$-direction) the electrons exhibit a free, reflectionless
+
−
propagation, whereas perpendicular to the wire ($y$-direction) quantized
+
−
transverse modes are formed. In this simple geometry the wavefunction factorizes
+
−
to the product of a longitudinal and a transverse wave function, and the
+
−
energies corresponding to the transverse standing waves and the longitudinal
+
−
propagation are simply added. After including magnetism in a Stoner type picture
+
−
the energy dispersion for this system can be written as:
+
−
$$\varepsilon_n^{\sigma}(k)=\varepsilon(k)+\varepsilon_n-\sigma\varepsilon_{\mathrm{ex}},$$
+
−
where $\varepsilon_n$ is the energy corresponding to the quantized transverse
+
−
modes, $\varepsilon(k)$ is the dispersion of the extended Bloch states in the $x$
+
−
direction ($k$=$k_x$), $\sigma =\pm 1/2$ is the spin index, and
+
−
$\varepsilon_{\mathrm{ex}}$ is the exchange energy. The resulting dispersion is a
+
−
set of one dimensional dispersion curves, which are vertically shifted by the
+
−
transverse energies and the exchange energy (Fig.~\ref{Qwire}(b)). The discrete
+
−
one dimensional dispersions are called \emph{conductance
+
−
channels}.\cite{PhysRevB.31.6207,datta_book}
+
−
 
+
−
In such an ideal wire the states with positive and negative $k$ are well
+
−
separated, the former are all coming from the left electrode, while the latter are all
+
−
coming from the right electrode. In a symmetric situation no net current flows.
+
−
Application of a bias voltage between the two sides of the wire, however, shifts
+
−
the chemical potentials of the right and left moving electron states by $eV$
+
−
with respect to each other, and this imbalance results in a finite current. For
+
−
a selected conductance channel the velocity of the electrons and the density of
+
−
states is respectively given as
+
−
$$
+
−
v_n^{\sigma}=\frac{1}{\hbar}\frac{\partial \varepsilon_n^{\sigma}(k)}{\partial k},\ \ \ \ g_n^{\sigma}=\frac{L}{2\pi}\left(\frac{\partial \varepsilon_n^{\sigma}(k)}{\partial k}\right)^{-1},
+
−
$$
+
−
where $L$ is the length of the nanowire. The spacial density for the electron
+
−
states in the $eV$ energy window is obtained as
+
−
$$
+
−
n_n^{\sigma}=eV g_n^{\sigma}/L.
+
−
$$
+
−
The current is then calculated as a product of charge, velocity and electron
+
−
density, summing over the spins and all the conductance channels:
+
−
$$
+
−
I=\sum_\sigma \sum_{n=1}^{M^{\sigma}}e v_n^{\sigma} n_n^{\sigma} =\sum_\sigma\frac{e^2}{h}M^{\sigma}V.
+
−
$$
+
−
Here $M^{\sigma}$ is the number of open conductance channels, i.e. the number of
+
−
1D dispersion curves crossing the Fermi energy for a given spin orientation.
+
−
Note that $\partial \varepsilon / \partial k$ cancels in the product of $v$ and
+
−
$n$, thus the above result is valid for any shape of the dispersion curve.
+
−
Furthermore, the two dimensional model only simplifies the visualization, but
+
−
the above arguments also hold for any perfect three dimensional nanowire with
+
−
uniform cross section along the $x$ axis.
+
−
 
+
−
Here we have taken advantage of the assumption that the spin state is conserved,
+
−
i.e. the structure is smaller than the spin diffusion length. This has allowed
+
−
the separation of the current to a purely spin up and a purely spin down component
+
−
being two independent \emph{routes} of the transport:
+
−
$I=I^{\uparrow}+I^{\downarrow}=(e^2/h)(M^{\uparrow}+M^{\downarrow})V$. The
+
−
total current is determined by the number of open conductance channels, and the
+
−
conductance ($G=I/V$) is an integer multiple  of $e^2/h=(25.8\,$k$\Omega)^{-1}$.
+
  
 
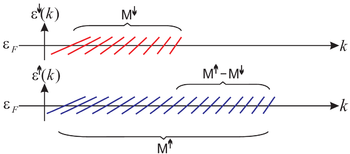
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Spintronika2.png|közép|300px|]]
+
| align="center"|[[Fájl:Spintronika2.png|közép|350px]]
 
|-
 
|-
−
| align="center"|2. ábra  
+
| align="center"|2. ábra. ''Diszperziós görbék ferromágneses nanovezetékben a Fermi-energia körül. Fel spinű elektronoknak (kék) több nyitott vezetési csatorna áll rendelkezésre mint le spinű elektronoknak (piros).'' 
 
|}
 
|}
  
−
\begin{figure} [!h]
+
Értelemszerűen egy ferromágneses nanovezetékben a nyitott csatornák száma különbözhet a különböző spinű elektronokra (2. ábra), így
−
\centering
+
az áram
−
\includegraphics[width=\columnwidth]{fig2.eps}
+
$$
−
\caption{\it The dispersion curves around the Fermi energy
+
I=\sum_{\sigma =\frac{1}{2},-\frac{1}{2}} \frac{e^2}{h}M^{\sigma}V
−
for the different conductance channels. The bottom and top panels
+
$$
−
correspond to spin up and spin down electrons, respectively. Due to the exchange
+
alakban írható, ahol $M^{\sigma}$ (illetve máshogy jelölve $M^{\uparrow}$ és $M^{\downarrow}$) a fel és le spinű elektronokhoz tartozó nyitott csatornák száma.
−
splitting the number of open conductance channels differs for the two spin subbands.}
+
−
\label{linear}
+
−
\end{figure}
+
  
−
Due to the shifted spin subbands, $M^{\uparrow}$ not necessarily equals
+
Fontos megjegyezni, hogy itt figyelembe vettük, hogy a nanovezetéken belül az elektronok spinállapota nem változik, ennek köszönhető hogy a fel és le spinű elektronokat egymástól független ''csatornaként'' kezelhetjük az áram felírásakor:
−
$M^{\downarrow}$. This is indicated by Fig.~\ref{linear}, where only the
+
$I=I^{\uparrow}+I^{\downarrow}=(e^2/h)(M^{\uparrow}+M^{\downarrow})V$. Látjuk, hogy ferromágneses ideális nanovezetékben a vezetőképesség $e^2/h$ szerint kvantált.
−
linearized part of the 1D dispersions around the Fermi energy is shown
+
 
−
demonstrating that the free electron dispersions in Fig.~\ref{Qwire}(b) are only
+
Az elektronok spin szerinti polarizáltságának fokát
−
illustrations and are generally not considered in this model. The degree of the
+
−
resulting spin polarization can be characterized by the ratio of the spin
+
−
polarized current and the total current:
+
 
$$
 
$$
−
P_c=\frac{I^{\uparrow}-I^{\downarrow}}{I^{\uparrow}+I^{\downarrow}}=\frac{M^{\uparrow}-M^{\downarrow}}{M^{\uparrow}+M^{\downarrow}}.
+
P_c=\frac{I^{\uparrow}-I^{\downarrow}}{I^{\uparrow}+I^{\downarrow}}
 
$$
 
$$
−
This normalized current spin polarization can reach even $100\%$ ($P_c=1$) in
+
képlettel definiálhatjuk, ami ideális nanovezetékben $P_c=(M^{\uparrow}-M^{\downarrow})/(M^{\uparrow}+M^{\downarrow})$ formában is írható. Ez a ''spinpolarizáció'' $-1$ és $1$ közötti értékeket vehet föl, tökéletes spinpolarizáció ($P_c=\pm 1$) félfémben érhető el, amikor csak fel (vagy le) spinű elektronok találhatók a Fermi-energia környékén. Fontos megjegyezni, hogy mindig a fel spint vesszük többségi spinorientációnak, mely a ferromágneses tartomány mágnesezettség-irányának felel meg. Később látni fogjuk, hogy a spinpolarizáció lehet a mágnesezettséggel ellentétes előjelű.
−
case of a half-metal, where only one type of carrier is present at the
+
</wlatex>
−
Fermi level.
+
 
 +
==Landauer formula spinpolarizált esetben==
 +
<wlatex>
 +
Egy mágneses nanovezeték valósághűbb leírását kapjuk, ha szórást is megengedünk a vezetéken belül. Ezt a legegyszerűbben a [[Transzport_nanovezetékekben:_Landauer_formula,_vezetőképesség-kvantálás#Landauer formula|korábban megismert]] Landauer formalizmus keretében tehetjük meg. A Landauer képben az elektrontranszportot $\mathcal{T}_{m,n}$ transzmisszós valószínűségekkel írjuk le, melyek a bal oldali $n$-edik vezetési csatornából a jobb oldali $m$-edik csatornába történő szóródás valószínűségét adják meg. Míg $\mathcal{T}_{m,n}=\delta_{m,n}$ a fent tárgyalt ideális kvantumvezetéknek felel meg, ha  a vezetéken belül az elektronok rácshibákon, illetve szennyezőkön szóródnak, akkor $\mathcal{T}<1$ transzmissziós valószínűségeket kapunk. Fontos megjegyezni, hogy a Landauer-kép inelasztikus szórásokat (pl. elektron-fonon kölcsönhatás) és spinszórásokat nem tud figyelembe venni.
 +
 
 +
Vizsgáljuk meg a 3. ábrán szemléltetett rendszer vezetési tulajdonságait: a nanovezeték két nemmágneses ideális kvantumvezeték között egy ferromágneses tartományt tartalmaz, melyben szóródhatnak az elektronok.
  
 
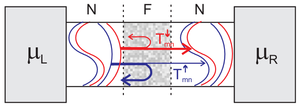
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Spintronika3.png|közép|300px|]]
+
| align="center"|[[Fájl:Spintronika3.png|közép|300px|]]
 
|-
 
|-
−
| align="center"|3. ábra  
+
| align="center"|3. ábra. ''Ferromágneses nanovezetékben a fel és le spinű elektronok transzmissziós valószínűségei különbözhetnek''
 
|}
 
|}
  
−
\begin{figure} [!h]
+
Mivel spinszórás nem történik, az áramot továbbra is egymástól függetlenül számolhatjuk a két spincsatornára a transzmissziós valószínűségek figyelembe vételével:  
−
\centering
+
−
\includegraphics[width=0.7\columnwidth]{fig3.eps}
+
−
\caption{\it A diffusive ferromagnetic region is sandwiched between two normal
+
−
metal ideal quantum wires. The transport is determined by spin dependent
+
−
transmission probabilities between the conductance channels at the two sides.}
+
−
\label{landauer}
+
−
\end{figure}
+
−
 
+
−
A more realistic description can be given for the conductance of a piece of
+
−
magnetic nanowire inserted between nonmagnetic reservoirs by taking also into
+
−
account elastic scatterings (Fig.~\ref{landauer}). According to the Landauer
+
−
picture the transport in this system can be be described by the transmission
+
−
probabilities $T_{nm}$, i.e. the probability for the transmission of an electron
+
−
from channel $n$ on the left side to channel $m$ on the right side. These
+
−
transmission probabilities depend on the ``waveguide'' parameters of the wire.
+
−
While $T_{nm}=\delta_{nm}$ corresponds to the previous model of an ideal wire,
+
−
$T<1$ represents scatterings in the wire due to defects, impurities, etc.
+
−
 
+
−
As no spin mixing occurs between the spin up and spin down states, the current
+
−
can still be calculated for each spin state independently taking into account
+
−
the finite transmissions of the
+
−
channels:\cite{PhysRevB.31.6207,Agrait200381,datta_book}
+
 
$$
 
$$
−
I^\sigma=\frac{e^2}{h}\sum_{n,m=1}^{M^\sigma}T_{nm}^\sigma V.
+
I^\sigma=\frac{e^2}{h}\sum_{n,m=1}^{M^\sigma}T_{m,n}^\sigma V.
 
$$
 
$$
−
The values of $T_{nm}$ depend on the Fermi wave numbers of the involved
+
A $\mathcal{T}_{m,n}$ értékek függnek az elektronok Fermi-hullámhosszától, ami egy adott $n$-edik csatorna esetén jelentősen eltérhet a két spin-orientációra a kicserélődési felhasadás miatt. Ez alapján spinszórás (pl. spin-pálya kölcsönhatás) nélkül is a transzmisszós valószínűségek különböznek a két spincsatornára, ezt vesszük figyelembe a $\sigma$ indexszel.
−
channels. Due to the spin-dependent shift of the dispersions the spin up and the
+
−
spin down channels have different wave numbers at the Fermi energy. Thus, in
+
−
general, the transmission probability may become spin dependent even without any
+
−
direct spin-interaction, like spin-orbit coupling.
+
  
−
 
+
A spinfüggő áramot átírhatjuk
−
The spin dependent current can be rewritten in the form:
+
 
$$
 
$$
−
I^\sigma=\frac{e^2}{h}M^\sigma \bar{T}^\sigma V,
+
I^\sigma=\frac{e^2}{h}M^\sigma \bar{T}^\sigma V
 
$$
 
$$
−
where $\bar{T}^\sigma$ is the average transmission probability for all the
+
formába, ahol $\bar{\mathcal{T}}^\sigma$ az átlagos transzmissziós valószínűség a $\sigma$ spin-orientációhoz tartozó összes nyitott vezetési csatornára. Ezzel a jelöléssel az áram spin szerinti polarizáltságát
−
conductance channels with a given spin direction. With this notation the spin
+
−
polarization of the current can be written as:
+
 
$$
 
$$
 
P_c=\frac{I^{\uparrow}-I^{\downarrow}}{I^{\uparrow}+I^{\downarrow}}=\frac{M^{\uparrow}\bar{T}^\uparrow-M^{\downarrow}\bar{T}^\downarrow}{M^{\uparrow}\bar{T}^\uparrow+M^{\downarrow}\bar{T}^\downarrow}.
 
P_c=\frac{I^{\uparrow}-I^{\downarrow}}{I^{\uparrow}+I^{\downarrow}}=\frac{M^{\uparrow}\bar{T}^\uparrow-M^{\downarrow}\bar{T}^\downarrow}{M^{\uparrow}\bar{T}^\uparrow+M^{\downarrow}\bar{T}^\downarrow}.
 
$$
 
$$
−
It is evident from this formula, that either the difference of the transmission
+
formában írhatjuk. Spinpolarizált áramot a két spincsatorna között a nyitott vezetési csatornák számában illetve az az átlagos transzmissziós valószínűségben fellépő különbség egyaránt eredményezhet.
−
probabilities for the two spin channels, or the difference in the number of open
+
−
channels for spin up and spin down electrons gives contribution to the spin
+
−
polarization of the current.
+
  
−
In case of a few conductance channels the difference in $\bar{T}^\uparrow$ and
+
Kevés vezetési csatorna (pl. [[Nanoszerkezetek_előállítási_és_vizsgálati_technikái#Önszerveződő_nanoszerkezetek|egyatomos kontaktus]]) esetén a $\bar{T}^\uparrow$ és $\bar{T}^\downarrow$ közötti különbség jelentős spinpolaizációt okozhat akkor is, ha a vezetési csatornák száma megegyezik a két spinirányra. Sok csatornás struktúrákban viszont $\bar{T}^\sigma$ sok, különböző Fermi-hullámszámú csatornára vett átlag, így a spindiffúziós hossznál kisebb struktúrákban, ahol csak a rugalmas szórásokat vesszük figyelembe, az átlagos transzmisszós valószínűséget közel azonosnak várjuk a két spinirányra. Ennek megfelelően
−
$\bar{T}^\downarrow$ may introduce a spin polarized current even for the same
+
az áram spinpolarizációjához az elsődleges járulékot a vezetési csatornák számának különbsége adja:
−
number of open channels. Indeed, for ferromagnetic atomic point contacts, the
+
$$
−
transmission probabilities for the two spin channels are expected to differ
+
P_c\approx \frac{M^{\uparrow}-M^{\downarrow}}{M^{\uparrow}+M^{\downarrow}},
−
significantly.\cite{PhysRevB.77.104409}
+
$$
−
 
+
akkor is ha nem ideális a vezeték, azaz $\bar{T}^\uparrow\approx\bar{T}^\downarrow<1$.
−
However, for larger structures, where
+
−
many conductance channels are present (Fig.~\ref{linear}), $\bar{T}^\sigma$ is
+
−
an average over a broad ensemble of different wavenumbers, and for diffusive
+
−
junctions random matrix theory (RMT) predicts a universal value of
+
−
\(\bar{T}^{\sigma}=l_m^{\sigma}/L\),\cite{RevModPhys.69.731} where \(L\) is the
+
−
length of the diffusive region. As the momentum relaxation
+
−
mean free path is expected to be similar for the two spin subbands, $\bar{T}^\uparrow \approx
+
−
\bar{T}^\downarrow$ can be assumed. Accordingly the key contribution to the spin
+
−
polarization is given solely by the difference of $M^\uparrow$ and $M^\downarrow$. In this limit, Eq.~\ref{Pc}
+
−
gives a reasonable approximation for the spin polarization, even for non-ideal transmission probabilities
+
−
($\bar{T}^\uparrow\approx\bar{T}^\downarrow<1$).
+
  
−
According to Eq.~\ref{vn} the number of conductance channels can be formally
+
[[Transzport_nanovezetékekben:_Landauer-formula,_vezetőképesség-kvantálás#Kvantumvezeték_ellenállása|Korábbi megfontolások alapján]] a vezetési csatornák számát formálisan:
−
written as:
+
 
$$
 
$$
−
M^\sigma=\frac{2\pi\hbar}{L}\sum_{n=1}^{M^\sigma}v_n^{\sigma}g_n^{\sigma}.
+
M^\sigma=\frac{2\pi\hbar}{L}\sum_{n=1}^{M^\sigma}v_n^{\sigma}g_n^{\sigma}
 
$$
 
$$
−
Introducing a mean Fermi velocity, which is the average of the Fermi velocities for the different conductance channels weighted by the density of states of the channels,
+
alakban írhatjuk. Vezessünk be egy átlagos Fermi-sebességet, mely a különböző csatornák Fermi-sebességeinek átlaga a csatornák állapotsűrűségével súlyozva,
 
$$
 
$$
−
\bar{v}_F^\sigma=\frac{\sum_{n} g_n^\sigma v_n^\sigma}{\sum_{n} g_n^\sigma},
+
\bar{v}_F^\sigma=\frac{\sum_{n} g_n^\sigma v_n^\sigma}{\sum_{n} g_n^\sigma}.
 
$$
 
$$
−
and noting that $\sum_{n} g_n^\sigma=g_F^\sigma$ is the total density of states at the Fermi level, the formula for the current spin polarization can be rewritten as:
+
Figyelembe véve, hogy $\sum_{n} g_n^\sigma=g_F^\sigma$ a Fermi szint teljes állapotsűrűsége, az áram spinpolarizációjára vonatkozó formulánkat átírhatjuk
 
$$
 
$$
−
P_c\approx\frac{M^{\uparrow}-M^{\downarrow}}{M^{\uparrow}+M^{\downarrow}}=\frac{g_F^{\uparrow}\bar{v}_F^{\uparrow}-g_F^{\downarrow}\bar{v}_F^{\downarrow}}{g_F^{\uparrow}\bar{v}_F^{\uparrow}+g_F^{\downarrow}\bar{v}_F^{\downarrow}}.
+
P_c\approx\frac{M^{\uparrow}-M^{\downarrow}}{M^{\uparrow}+M^{\downarrow}}=\frac{g_F^{\uparrow}\bar{v}_F^{\uparrow}-g_F^{\downarrow}\bar{v}_F^{\downarrow}}{g_F^{\uparrow}\bar{v}_F^{\uparrow}+g_F^{\downarrow}\bar{v}_F^{\downarrow}}
 
$$
 
$$
−
This formula supplies a microscopic background for the conventional
+
alakba. Ez a formula lehetőséget ad arra, hogy a spinpolarizációt sávszerkezet-parameterek (Fermi-felület állapotsűrűsége és Fermi-sebesség) alapján értelmezzük.
−
formulation of the current spin polarization\cite{PhysRevB.70.054416} expressed
+
−
by Fermi surface parameters of the two spin subbands: density of states and Fermi velocity.
+
  
 +
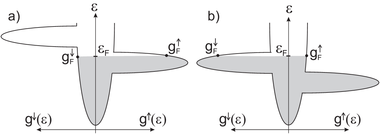
Ferromágneses anyag sávmodelljét szemlélteti a 4. ábra. Mindkét panelen az energiatengelytől jobbra a fel, míg balra a le spinű elektronok állapotsűrűsége látszik. Az $s$-elektronokhoz tartozó parabolikus energiafüggésű állapotsűrűség mellett a keskeny $d$ (vagy $f$) sávokhoz tartozó állapotűrűség-csúcsokat láthatjuk, az utóbbi energiában felhasad a kicserélődési kölcsönhatás miatt.
 +
Az anyag mágnesezettsége a betöltött (Fermi-energia alatti) fel és le spinű elektronok számának különbségéből adódik. Mindkét panelen a fel spinű elektronok vannak nagyobb számban, azaz a fel spint tekintjük többségi spinorientációnak. Ezzel szemben a transzport-tulajdonságokhoz, így az áram spinpolarizációjához csak a Fermi-felület közelében levő elektronok adnak járulékot. Az a) panelen a fel spinű elektronok vannak jelen nagyobb számban a Fermi-szintnél, így pozitív a spinpolarizáció. Ezzel szemben a b) panelen a Fermi-energia máshol helyezkedik el a $d$-sávokhoz képest, így végül a le spinű elektronok állnak rendelkezésre nagyobb számban a Fermi-energiánál, azaz a pozitív mágnesezettség ellenére negatív spinpolarizációt kapunk. Negatív spinpolarizációt valós anyagokban is tapasztalhatunk, pl. Co és Ni esetében.
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Spintronika4.png|közép|300px|]]
+
| align="center"|[[Fájl:Spintronika4.png|közép|380px|]]
 
|-
 
|-
−
| align="center"|4. ábra  
+
| align="center"|4. ábra. ''Pozitív (a) és negatív (b) spinpolarizációval rendelkező mágnesesen rendezett anyagok sávszerkezetének szemléltetése''
 
|}
 
|}
 +
</wlatex>
  
−
\begin{figure} [!h]
+
==Spinpolarizált transzport alkalmazása: spinszelep==
−
\centering
+
<wlatex>
−
\includegraphics[width=\columnwidth]{fig4.eps}
+
A spin szabadsági fok kihasználásával számos érdekes eszközt építhetünk. A továbbiakban a gyakorlati felhasználás szempontjából legelterjedtebb, merevlemezek olvasófejében alkalmazott eszközt, a spinszelepet mutatjuk be.
−
\caption{\it  Illustration for the density of states in ferromagnets. The
+
−
magnetism is related to the exchange splitting of the narrow $d$ (or $f$)
+
−
bands. Panel (a) demonstrates the DOS in Fe: for minority spins (left side) the
+
−
$d$ band is above the Fermi level, whereas for majority spins (right side) the
+
−
Fermi level lies inside the $d$ band. Accordingly the DOS is significantly
+
−
larger for the majority spins. Panel (b) demonstrates the DOS for Co and Ni type
+
−
band filling. In this case $\varepsilon_F$ is above the $d$ band for majority
+
−
spins, whereas it lies inside the $d$ band for minority spins resulting in a
+
−
negative Fermi surface spin polarization with respect to the positive
+
−
magnetization.}
+
−
\label{DOS}
+
−
\end{figure}
+
  
−
In real ferromagnets the exchange splitting of narrow $d$ (or $f$) bands and the
+
Az alapötlet, az óriás mágneses ellenállást mutató nanoszerkezet felfedezése, Albert Fert<sup>[http://prl.aps.org/abstract/PRL/v61/i21/p2472_1 1]</sup> és Peter Grünberg<sup>[http://prb.aps.org/abstract/PRB/v39/i7/p4828_1 2]</sup> nevéhez kötődik, akik 2007-ben Nobel-díjat kaptak felfedezésükért. A szerkezet két ferromágneses rétegből áll, melyeket egy, a spindiffúziós hossznál vékonyabb paramágneses réteg köt össze (lásd 5. ábra, illetve 6/a. ábra). A tapasztalatok alapján ennek a nanostruktúrának az ellenállása lényegesen kisebb akkor, ha a két mágneses réteg mágnesezettsége azonos irányba mutat, mint ha ellentétes irányba mutatnak. Ezt a jelenséget lehet kihasználni mágnesesen tárolt információ kiolvasására, ha a felső réteg mágnesezettségét rögzítjük, az alsó réteg mágnesezettsége pedig az alatta mozgatott adattároló lemez mágnesezettségének megfelelően áll be, így az információ egyszerű ellenállás-méréssel kiolvasható (5. ábra). Ezzel a módszerrel a merevlemezek tárolókapacitásának jelentős növekedését lehetett elérni az eredeti induktív, illetve a későbbi anizotróp mágneses ellenállás mérésen alapuló módszerekhez képest.
−
filling of the bands determine the magnetic properties (see Fig.~\ref{DOS}). The
+
−
integral of the density of states up to the Fermi energy is different for the
+
−
two spin orientations, which results in a finite magnetization, conventionally
+
−
selecting the up spin as the majority spin orientation. However, the electron
+
−
transport is determined by the Fermi surface properties. The spin polarized
+
−
transport is not characterized by the magnetization, rather it is described by
+
−
the spin polarization of the current as described by Eq.~\ref{PcDOS}. An
+
−
interesting example is supplied by the Co or Ni type band fillings: the density
+
−
of states at the Fermi level is much larger for the down spin, leading to a
+
−
situation where the current spin polarization may take a sign opposite to that
+
−
of the magnetization (Fig.~\ref{DOS}b).
+
  
−
\section{The spin valve structure}
+
{|  cellpadding="5" cellspacing="0" align="center"
−
 
+
|-
−
The knowledge of current spin polarization and spin diffusion length is
+
| align="center"|[[Fájl:merevlemez.png|közép|400px|]]
−
essential for the design of spintronic devices. In the previous part we have
+
|-
−
shown an experimental method which allows the determination of both quantities.
+
| align="center"|5. ábra. ''Merevlemezek spinszelep struktúrán alapuló olvasófeje, forrás: [http://pl.wikipedia.org/wiki/Plik:Head_of_disc.svg Wikipedia]
−
In the following we turn to the application of spin polarized transport by
+
|}
−
discussing the most widely utilized spintronic device, the nanoscale spin-valve
+
−
structure. First we give simple demonstrative models for this structure, and
+
−
then we briefly discuss possible applications for next generation data storage
+
−
devices.
+
  
−
The basic idea of this structure dates back to the discovery of the giant magnetoresistance (GMR)
+
Először tegyük fel, hogy mindkét ferromágneses réteg mágnesezettsége felfelé mutat. Az 6/b. ábra szemlélteti a fenti Stoner-modell keretében a kicserélődési energia alakulását a fel spinű elektronokra (kék görbe) illetve a le spinű elektronokra (piros görbe). A kicserélődési felhasadás hatását legegyszerűbben úgy szemléltethetjük, hogy mind a normál mind a ferromágneses tartományokat [[Transzport_nanovezet%C3%A9kekben:_Landauer_formula,_vezet%C5%91k%C3%A9pess%C3%A9g-kvant%C3%A1l%C3%A1s#Kvantumvezet.C3.A9k_ellen.C3.A1ll.C3.A1sa|ideális nanovezetéknek]] tekintjük. Ebben az esetben a pozitív kicserélődési energia ekvivalens azzal, mintha egy nemmágneses tartományban a keresztirányú $\varepsilon_n$ energia megnőne, azaz a vezeték összeszűkülne, míg a negatív kicserélődési energiát úgy tekinthetjük, mintha $\varepsilon_n$ csökkenne, azaz a vezeték szélessége megnőne. Ezt az ekvivalens képet szemlélteti az 6/c. ábra az 6/b. ábrának megfelelő mágnesezettség-irányok mellett, illetve az 6/e. ábra abban az esetben, ha a két mágneses réteg mágnesezettsége ellentétes irányba mutat (6/d. ábra).  
−
effect by Albert Fert \cite{PhysRevLett.61.2472} and Peter Gr\"unberg
+
−
\cite{PhysRevB.39.4828}, for which the Nobel price in
+
−
physics was awarded in 2007. The architecture is based on two ferromagnetic
+
−
layers, which are separated by a paramagnetic layer being thinner than the spin
+
−
diffusion length (Fig.~\ref{GMR1}(a)). It was found that the conductance of this device is larger for
+
−
the parallel orientation of the two magnetic layers than for the antiparallel
+
−
orientation.
+
  
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Spintronika5.png|közép|300px|]]
+
| align="center"|[[Fájl:Spintronika5.png|közép|300px|]]
 
|-
 
|-
−
| align="center"|5. ábra  
+
| align="center"|6. ábra ''GMR-jelenség ballisztikus modellje''
 
|}
 
|}
  
−
\begin{figure} [!h]
+
Ebben az ekvivalens képben a fel és a le spinű elektronok is egy adiabatikus nanovezetéket látnak, így a legkisebb keresztmetszetben ''elférő'' nyitott csatornák száma fogja meghatározni a vezetőképességet.
−
\centering
+
Jelöljük a nyitott csatornák számát $M^0$-al a normál vezetékdarabban, $M^\uparrow$-el ha az elektronok spinje a többségi spinorientációnak felel meg (azaz $\uparrow$ spinű elektronok mennek $\uparrow$ mágnesezettésű tartományban vagy $\downarrow$ elektronok mennek $\downarrow$ tartományban), illetve $M^\downarrow$-vel, ha egy adott mágnesezettségű tartományban ellentétes spinű (kisebbségi spinorientációjú) elektronok haladnak. A mágneses rétegek azonos irányú (parallel, $P$) beállása esetén a fel spinű elektronokra $M^0$, míg a le spinű elektronokra $M^\downarrow$ a csatornák száma a legkisebb keresztmetszetben, azaz a
−
\includegraphics[width=\columnwidth]{fig9.eps}
+
a vezetőképesség $G^\mathrm{P}=(e^2/h)(M^\downarrow+M^0)$. Ellentétes mágnesezettségű rétegek esetén (antiparallel, $AP$) mindkét spinirányra $M^\downarrow$ számú csatorna fér el a legkisebb keresztmetszetben, azaz a vezetőképesség $G^\mathrm{AP}=2(e^2/h)M^\downarrow$. Így a relatív vezetőképességváltozás a két beállás között:
−
\caption{\it Panel (a) demonstrates the basic idea of a spin valve structure:
+
$$
−
two ferromagnetic regions are separated by a narrow normal region, and this
+
\frac{\Delta G}{G^\mathrm{P}}=\frac{G^\mathrm{P}-G^\mathrm{AP}}{G^\mathrm{P}}=\frac{M^0-M^\downarrow}{M^0+M^\downarrow},
−
structure is connected to normal leads at both sides. Panels (b,d) demonstrate
+
$$
−
the variation of the exchange energy along the structure. Panel (b) corresponds
+
ami mindig pozitív érték. Kis vezetőképesség-változás esetén ($\Delta G \ll G^\mathrm{P}$), és feltételezve hogy $M^0-M^\downarrow \approx M^\uparrow-M^0$
−
to the parallel magnetic orientation of the layers (both layers have $\uparrow$
+
−
magnetic orientation), whereas panel (d) demonstrates the antiparallel
+
−
orientation ($\uparrow$ in the first layer and $\downarrow$ in the second one).
+
−
Panels (c) and (e) respectively show the equivalent ballistic model, where the
+
−
change of the exchange energy is replaced by an effective narrowing or widening
+
−
of the channel.}
+
−
\label{GMR1}
+
−
\end{figure}
+
−
 
+
−
To understand this phenomenon, as the simplest model we can consider an ideal
+
−
quantum wire, in which the exchange coupling is switched on adiabatically in two
+
−
regions (Fig.~\ref{GMR1}(b,d)). The parallel orientation is modeled by a
+
−
positive exchange in both regions, whereas the antiparallel orientation
+
−
corresponds to opposite signs of the exchange in the two regions. Similarly to
+
−
the previous situations the current can be divided to two independent components
+
−
corresponding to spin up and spin down electrons. For a given spin orientation
+
−
the effect of the exchange energy is very similar to an effective spatial
+
−
narrowing or widening of the channel, which would increase/decrease the
+
−
transverse quantized energies (Fig.~\ref{GMR1}(c,e)). Therefore the system can
+
−
be considered as serial connected quantum point contacts. For electrons with
+
−
majority spin direction (spin direction parallel to the magnetization direction)
+
−
the number of open channels is denoted by $M^\uparrow$, whereas for minority
+
−
spins (antiparallel spin direction to the magnetization direction) the number of
+
−
open channels is $M^\downarrow(<M^\uparrow)$. (Note, that here the superscript
+
−
$\uparrow$ denotes majority orientation instead of the real spin direction,
+
−
and the number of open channels is also $M^\uparrow$ for down spins in down
+
−
oriented magnetization of the magnetic layer.)
+
−
 
+
−
In such ballistic quantum point contacts the conductance is determined by the
+
−
number of modes at the narrowest cross section. If the two magnetic layers have
+
−
antiparallel (AP) orientation either the first or the second layer restricts the
+
−
number of channels to $M^\downarrow$, and so the conductance for both spin
+
−
channels is $(e^2/h)M^\downarrow$, i.e. the total conductance is
+
−
$G^\mathrm{AP}=2(e^2/h)M^\downarrow$. For parallel orientation of the magnetic
+
−
layers the conductance is $(e^2/h)M^\uparrow$ if the spin direction of the
+
−
carriers is the same as the magnetization, and it is $(e^2/h)M^\downarrow$ if
+
−
the magnetization has opposite orientation to the spin orientation of the
+
−
carriers. The net conductance is
+
−
$G^\mathrm{P}=(e^2/h)(M^\downarrow+M^\uparrow)$. The magnitude of the
+
−
magnetoresistance effect can be characterized by $\Delta G/G^\mathrm{P}$, where
+
−
$\Delta G=G^\mathrm{P}-G^\mathrm{AP}$. With this notation the relative change of
+
−
the conductance turns out to be equal to the current spin polarization
+
−
characteristic to the ferromagnetic metal applied,
+
 
$$
 
$$
−
\frac{\Delta G}{G^\mathrm{P}}=\frac{M^\uparrow-M^\downarrow}{M^\uparrow+M^\downarrow}=P_c.
+
\frac{\Delta G}{G^\mathrm{P}}\approx\frac{1}{2}\frac{M^\uparrow-M^\downarrow}{M^\uparrow+M^\downarrow} \approx \frac{P_c}{2}
 
$$
 
$$
−
This simplified model corresponds to the perfectly ballistic limit, where no
+
adódik. Ez az egyszerűsített, ideális kvantumvezetékeken alapuló kép természetesen nem írja le valósághűen a merevlemezben használt spinszelepek vezetési tulajdonságait.  
−
backscatterings are considered inside the quantum wire.
+
  
−
In a more realistic model the scattering inside the nanostructure should also be
+
Valósághűbb képet kapunk, ha a különböző tartományokban szórási folyamatokat is megengedünk.
−
considered. If the structure is smaller than the phase diffusion length,
+
Ha a spin-szelep struktúra kisebb a fázisdiffúziós hossznál ($L_\phi$), akkor a két réteg közötti oda-visza szórásokat koherensen kell összeadni, így a teljes vezetőképesség interferencia-jelenségek finom részleteitől függ.  
−
$l_\phi$ the scattering in the two layers are added coherently, and accordingly
+
−
the total resistance relies on the fine details of quantum interference
+
−
phenomena.
+
  
 +
A fázisdiffúziós hossznál nagyobb (de a spindiffúziós hossznál kisebb) spin-szelep esetén viszont könnyen számolhatunk, mert elvész a koherencia, és így a sorosan kötött ellenállások egyszerűen összeadódnak. Hogy eredményeinket összehasonlíthassuk az ideális kvantumvezetékek modelljével, a számolást vezetőképességekkel végezzük: többségi spinorientáció esetén a vezetőképesség $G^\uparrow$, kisebbségi spinorientáció esetén pedig $G^\downarrow$ (7. ábra).
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| [[Fájl:Spintronika6.png|közép|300px|]]
+
| align="center"|[[Fájl:Spintronika6.png|közép|300px|]]
 
|-
 
|-
−
| align="center"|6. ábra  
+
| align="center"|7. ábra ''GMR-jelenség diffúzív, inkoherens modellje''
 
|}
 
|}
−
 
+
A rétegek $P$ beállása esetén a teljes vezetőképesség $G^{P}=G^\uparrow/2+G^\downarrow/2$, míg $AP$ beállás esetén $G^{AP}=2G^\uparrow G^\downarrow/(G^\uparrow+G^\downarrow)$, azaz a relatív vezetőképesség-változás:
−
 
+
−
\begin{figure} [!h]
+
−
\centering
+
−
\includegraphics[width=\columnwidth]{fig10.eps}
+
−
\caption{\it Resistive model of the GMR effect. The two magnetic layers are
+
−
separated by an incoherent nonmagnetic region. The top panel demonstrates the
+
−
parallel alignment of the magnetic layers (both layers have $\uparrow$
+
−
magnetization direction), whereas the bottom panel demonstrates the
+
−
antiparallel alignment (the left layer has $\uparrow$ and the right layer has
+
−
$\downarrow$ magnetization direction). $G^\uparrow$ and $G^\downarrow$ denote
+
−
the conductance of a layer for electrons with majority and minority spin
+
−
direction, respectively.}
+
−
\label{GMR2}
+
−
\end{figure}
+
−
 
+
−
For even larger junctions, where phase coherence between the two magnetic layers
+
−
is already lost ($L>l_\phi$), but the spin information is still preserved
+
−
($L<l_s$), the two scattering regions are connected \emph{incoherently}
+
−
(Fig.~\ref{GMR2}), and accordingly their  resistances are simply summed to get
+
−
the total resistance.\cite{note1} In this limit the magnetoresistance of the
+
−
spin valve structure is also easily calculated. To compare with the previous
+
−
ballistic model we calculate with conductances: the conductance for majority
+
−
spin states is $G^\uparrow$, whereas for minority spins it is $G^\downarrow$.
+
−
For antiparallel oriented magnetic layers the total conductance is
+
−
$G^{AP}=2G^\uparrow G^\downarrow/(G^\uparrow+G^\downarrow)$, whereas for
+
−
parallel oriented layers it is $G^{P}=G^\uparrow/2+G^\downarrow/2$. From these
+
 
$$
 
$$
−
\begin{equation}
+
\frac{\Delta G}{G^\mathrm{P}}=\left(\frac{G^\uparrow-G^\downarrow}{G^\uparrow+G^\downarrow}\right)^2=P_c^2.
−
\frac{\Delta G}{G^\mathrm{P}}=\left(\frac{G^\uparrow-G^\downarrow}{G^\uparrow+G^\downarrow}\right)^2=P_c^2
+
 
$$
 
$$
−
follows. Note, that this model is equivalent with the common resistor model of the GMR phenomenon.\cite{0022-3727-35-18-201}
+
Látszik, hogy mindkét modellben a relatív vezetőképesség-változás a spinpolarizációval skálázódik. Tökéletes spinpolarizáció esetén $M^\downarrow =0$ és $G^\downarrow = 0$, így mindkét modell esetén $\Delta G/G^\mathrm{P}=1$ adódik, ami jól megközelíthető valós, jelentős spin-polarizációval rendelkező eszközökben.
 +
</wlatex>
  
−
Both of the above simple models show that $\Delta G$ is positive, i.e. the
+
==Hivatkozások==
−
parallel orientation has higher conductance than the antiparallel one. Depending
+
−
on the model, the relative conductance change ranges between $P_c$ and $P_c^2$
+
−
which indicates that a more complicated model based on the coherent
+
−
superposition of two scattering regions would also give a result between the
+
−
above two extreme limits. These considerations show that for typical values of
+
−
$P_c\approx0.2-0.6$, the relative amplitude of the GMR effect is expected to be
+
−
significant regardless of the details of the model. Note, however, that this
+
−
is only valid if the spin information is fully preserved in the spacer layer. As
+
−
the separation of the magnetic layers becomes larger than the spin diffusion length the GMR
+
−
effect exponentially decays.\cite{PhysRevB.48.7099,0953-8984-19-18-183201}
+
  
−
The magnetic layers of a spin valve are decoupled by paramagnetic spacer, and
+
===Fent hivatkozott szakcikkek===
−
this allows switching between parallel and antiparallel alignments. As the
+
[1] [http://prl.aps.org/abstract/PRL/v61/i21/p2472_1 M. N. Baibich, J. M. Broto, A. Fert, F. Nguyen Van Dau, F. Petroff, P. Etienne, G. Creuzet, A. Friederich, J. Chazelas: ''Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices'', '''Phys. Rev. Lett. 61''' p2472–2475 (1988)]
−
relative alignment depends on the external magnetic field, the GMR effect can be
+
−
used for magnetic sensing. For this purpose the orientation of one layer is
+
−
pinned by growing it on top of an antiferromagnet, while the unpinned free layer
+
−
can rotate even under the influence of a weak magnetic field. Spin valves are
+
−
extensively applied as the read head of hard disks, which utilizes the fast and
+
−
reliable reading of the magnetic information by an electric signal.
+
  
−
The spin valve structure can also be used to store magnetic information. This
+
[2] [http://prb.aps.org/abstract/PRB/v39/i7/p4828_1 G. Binasch, P. Grünberg, F. Saurenbach, W. Zinn: ''Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange'', '''Phys. Rev. B 39''' p4828–4830 (1989)]
−
type of non-volatile memory consists of a large number of spin valves, each of
+
===Ajánlott könyvek és összefoglaló cikkek===
−
them being addressed separately in a crossbar wire architecture. The
+
*[http://rmp.aps.org/abstract/RMP/v76/i2/p323_1 Igor Žutić, Jaroslav Fabian, S. Das Sarma: ''Spintronics: Fundamentals and applications'', '''Rev. Mod. Phys. 76''' p323–410 (2004)]
−
orientation of the free layer defines bit ``0'' and bit ``1'', which can be
+
*[http://books.google.hu/books/about/Semiconductor_Nanostructures.html?id=qD6623gfAZgC&redir_esc=y Thomas Ihn: ''Semiconducting nanosctructures'', OUP Oxford (2010)]
−
changed by the stray field of the nearby crossing wires. The information written in
+
*[http://books.google.hu/books?id=YNr4OcCExUcC&printsec=frontcover&dq=Nazarov+quantum+transport&hl=hu&sa=X&ei=2SzZUfGCMYna4ASDq4DQBQ&ved=0CDIQ6AEwAA Yuli V. Nazarov, Yaroslav M. Blanter: ''Quantum Transport: Introduction to Nanoscience'', Cambridge University Press (2009)]
−
this way is red out by the GMR effect. However, the areal density of this type
+
−
of magnetoresistive random access memories (MRAM) is limited by the length scale
+
−
of the slowly decreasing stray fields.
+
  
−
 
+
===Ajánlott kurzusok===
−
In the most advanced novel MRAMs no external field (and extra wiring) is
+
*[[Új kísérletek a nanofizikában|''Új kísérletek a nanofizikában'', Halbritter András és Csonka Szabolcs, BME Fizika Tanszék]]
−
required to write information in a spin valve memory element. In these devices
+
*[[Transzport komplex nanoszerkezetekben|''Transzport komplex nanoszerkezetekben'', Halbritter András, Csonka Szabolcs, Csontos Miklós, Makk Péter, BME Fizika Tanszék]]
−
the orientation of the free layer is manipulated by high density spin polarized
+
*[[Alkalmazott szilárdtestfizika|''Alkalmazott szilárdtestfizika'', Mihály György, BME Fizika Tanszék]]
−
currents, while the magnetic information is obtained by low current GMR
+
*[[Fizika 3 - Villamosmérnöki mesterszak|''Fizika 3'', Mihály György, BME Fizika Tanszék (mérnök hallgatóknak)]]
−
measurements. The writing is based on the spin-flip electron scattering
+
*[http://www.phy.bme.hu/~zarand/mezoszkopia.html ''Mezoszkopikus rendszerek fizikája'', Zaránd Gergely, BME Elméleti Fizika Tanszék]
−
processes occurring in the free layer, which exert a torque on the
+
*''Mezoszkopikus rendszerek fizikája'', Cserti József, ELTE Komplex Rendszerek Fizikája Tanszék
−
magnetization. Even though such spin-flips are rare events (the spin diffusion
+
−
length is much larger than the characteristic size of the nanodomain), at
+
−
current densities of about \(10^9 -10^{10}\, \textrm{A/cm}^2\), the induced
+
−
torque becomes large enough to reverse the magnetization. The details of the spin transfer torque
+
−
phenomenon are reviewed in Ref.~\cite{Ralph20081190}. Here we just point
+
−
out the importance of the strongly non-equilibrium state of this nanoscale
+
−
device: while the above current densities would lead to melting in any macroscopic metal, in this device the
+
−
length scales which determine its transparency (i.e. its resistance) are well
+
−
below the inelastic mean free path, and as a consequence the Joule heat is
+
−
produced outside the device, in a much larger volume. In spite of the huge
+
−
current densities, the nanoscale electronics defines appropriate signal levels
+
−
for practical applications (below \(100\,\mu\)A, and around \(1\,\)V).  Finally
+
−
it is to be noted that the spin transfer torque magnetoresistive random access memory
+
−
(STT-MRAM) is one of the most promising candidate for future spintronic
+
−
applications.
+
−
 
+
−
\section{Conclusions}
+
−
 
+
−
Nanoscale phenomena of spin related transport were discussed both theoretically
+
−
and experimentally. Based on the spin dependent band structure of a magnetic
+
−
metal, we discussed the propagation of electrons in the ballistic and diffusive
+
−
limits, and by applying the Landauer formalism, we supplied a \emph{nanoscopic}
+
−
background for the conventional expression of the current spin polarization. As
+
−
the most direct experimental method for spin polarization measurements, the
+
−
Andreev reflection spectroscopy was introduced, and experimental results on Fe
+
−
and Co were shown. The analysis demonstrated the reliability of measurements carried out in
+
−
the ballistic limit. The method was also extended for the determination of the
+
−
spin diffusion length, one of the most important parameters of metals in
+
−
spintronic applications. The operation of spin valves was described in terms of
+
−
the Landauer formalism and the magnitude of the GMR effect was determined in
+
−
the coherent ballistic and the incoherent diffusive limits. Finally a short
+
−
overview on spin valve applications was given.
+
−
 
+
−
</wlatex>
+

A lap jelenlegi, 2013. október 8., 13:34-kori változata

Tartalomjegyzék

Spindiffúziós hossz


Egy makroszkopikus vezetőben az elektronok számtalanszor szóródnak miközben eljutnak az egyik elektródából a másikba. Ahogy a nanovezetékek tárgyalásának bevezetésekor láttuk, a szennyezőkön és rácshibákon történő rugalmas szórás az elektronok elektromos tértől nyert impulzusának elvesztéséhez vezet. Ennek a folyamatnak a karakterisztikus skáláját az átlagos momentumrelaxációs szabadúthossz, 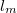\setbox0\hbox{$l_m$}% \message{//depth:\the\dp0//}% \box0% jellemzi. Rugalmatlan szórások esetén (pl. kölcsönhatás rácsrezgésekkel) az elektronok energiája megváltozik, és így elveszik a fázisinformáció, azaz megszűnik az interferenciaképesség. Ennek a folyamatnak a karakterisztikus skálája az ún. fázisdiffúziós hossz, 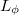\setbox0\hbox{$L_{\phi}$}% \message{//depth:\the\dp0//}% \box0%. Megfelelő távolságon belül az elektronok a mágneses momentumuk, azaz a spinjükhöz tartozó információt is elvesztik, amit a spindiffúziós hosszal, 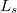\setbox0\hbox{$L_s$}% \message{//depth:\the\dp0//}% \box0% jellemezhetünk. Egy spindiffúziós hossznál kisebb, mágnesesen rendezett építőelemeket tartalmazó nanoszerkezetben azonban számos érdekes, az elektronok spin szerinti polarizáltságához kötődő jelenséggel találkozhatunk.

Spinpolarizáció ideális nanovezetékekben


A korábbiakban láttuk, hogy ha két elektróda közé egy ideális, szórásmentes nanovezetéket helyezünk, akkor abban keresztirányban állóhullámok, hosszirányban pedig síkhullám terjedés alakul ki, a vezetőképesség pedig 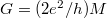\setbox0\hbox{$G=(2e^2/h)M$}% \message{//depth:\the\dp0//}% \box0%, ahol M a nyitott vezetési csatornák száma, azaz azon különböző keresztmódusokhoz tartozó egydimenziós parabolikus diszperziók száma, melyek metszik a Fermi-energiát. A kettes szorzó a spin szerinti degenerációból adódott.

Egy ferromágneses nanovezetékben azonban különbséget kell tenni a fel és a le spinű elektronok között. A vezeték mágnesezettségét legegyszerűbben Stoner-képben vehetjük figyelembe, azaz az energidiszperziókhoz hozzáadjuk a kicserőlédési energiát, mely 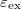\setbox0\hbox{$\varepsilon_{\mathrm{ex}}$}% \message{//depth:\the\dp0//}% \box0%-el különbözik a fel illetve le spinű (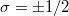\setbox0\hbox{$\sigma =\pm 1/2$}% \message{//depth:\the\dp0//}% \box0%) elektronokra:

\[\varepsilon_n^{\sigma}(k)=\varepsilon(k)+\varepsilon_n-\sigma\varepsilon_{\mathrm{ex}}.\]

Emlékeztetőül: 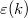\setbox0\hbox{$\varepsilon(k)$}% \message{//depth:\the\dp0//}% \box0% a hosszirányú terjedést, 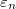\setbox0\hbox{$\varepsilon_n$}% \message{//depth:\the\dp0//}% \box0% pedig a keresztirányú állóhullámok energiáját írja le. Fontos megjegyezni, hogy 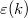\setbox0\hbox{$\varepsilon(k)$}% \message{//depth:\the\dp0//}% \box0% lehet tetszőleges Bloch-állapot diszperziója, nem kell feltétlenül szabad elektronoknak megfelelő parabolikus diszperziót feltételezni.

Spintronika1.png
1. ábra. Ferromágneses nanovezetékben a le spinű elektronok diszperziós relációja (piros) a kicserélődési energiával eltolódik a fel spinű elektronokéhoz képest (kék)

Az 1. ábra parabolikus szabad elektron diszperzió esetén szemlélteti az energiaviszonyokat. A kék görbék a fel, a piros görbék pedig a le spinű elektronokhoz tartoznak, azaz a piros parabolák mindig 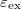\setbox0\hbox{$\varepsilon_{\mathrm{ex}}$}% \message{//depth:\the\dp0//}% \box0% energiával a megfelelő kék parabola felett helyezkednek el. A korábbiaknak megfelelően a 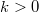\setbox0\hbox{$k>0$}% \message{//depth:\the\dp0//}% \box0% állapotok a bal oldali elektródából származnak, így annak a 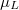\setbox0\hbox{$\mu_L$}% \message{//depth:\the\dp0//}% \box0% kémiai potenciáljáig vannak betöltve, míg a 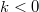\setbox0\hbox{$k<0$}% \message{//depth:\the\dp0//}% \box0% állapotok a jobb oldali, 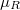\setbox0\hbox{$\mu_R$}% \message{//depth:\the\dp0//}% \box0% kémiai potenciálú elektródából származnak.

Spintronika2.png
2. ábra. Diszperziós görbék ferromágneses nanovezetékben a Fermi-energia körül. Fel spinű elektronoknak (kék) több nyitott vezetési csatorna áll rendelkezésre mint le spinű elektronoknak (piros).

Értelemszerűen egy ferromágneses nanovezetékben a nyitott csatornák száma különbözhet a különböző spinű elektronokra (2. ábra), így az áram

\[ I=\sum_{\sigma =\frac{1}{2},-\frac{1}{2}} \frac{e^2}{h}M^{\sigma}V \]

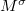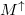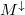alakban írható, ahol \setbox0\hbox{$M^{\sigma}$}% \message{//depth:\the\dp0//}% \box0% (illetve máshogy jelölve \setbox0\hbox{$M^{\uparrow}$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$M^{\downarrow}$}% \message{//depth:\the\dp0//}% \box0%) a fel és le spinű elektronokhoz tartozó nyitott csatornák száma.

Fontos megjegyezni, hogy itt figyelembe vettük, hogy a nanovezetéken belül az elektronok spinállapota nem változik, ennek köszönhető hogy a fel és le spinű elektronokat egymástól független csatornaként kezelhetjük az áram felírásakor: 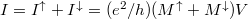\setbox0\hbox{$I=I^{\uparrow}+I^{\downarrow}=(e^2/h)(M^{\uparrow}+M^{\downarrow})V$}% \message{//depth:\the\dp0//}% \box0%. Látjuk, hogy ferromágneses ideális nanovezetékben a vezetőképesség 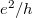\setbox0\hbox{$e^2/h$}% \message{//depth:\the\dp0//}% \box0% szerint kvantált.

Az elektronok spin szerinti polarizáltságának fokát

\[ P_c=\frac{I^{\uparrow}-I^{\downarrow}}{I^{\uparrow}+I^{\downarrow}} \]

képlettel definiálhatjuk, ami ideális nanovezetékben 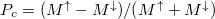\setbox0\hbox{$P_c=(M^{\uparrow}-M^{\downarrow})/(M^{\uparrow}+M^{\downarrow})$}% \message{//depth:\the\dp0//}% \box0% formában is írható. Ez a spinpolarizáció 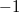\setbox0\hbox{$-1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$1$}% \message{//depth:\the\dp0//}% \box0% közötti értékeket vehet föl, tökéletes spinpolarizáció (\setbox0\hbox{$P_c=\pm 1$}% \message{//depth:\the\dp0//}% \box0%) félfémben érhető el, amikor csak fel (vagy le) spinű elektronok találhatók a Fermi-energia környékén. Fontos megjegyezni, hogy mindig a fel spint vesszük többségi spinorientációnak, mely a ferromágneses tartomány mágnesezettség-irányának felel meg. Később látni fogjuk, hogy a spinpolarizáció lehet a mágnesezettséggel ellentétes előjelű.

Landauer formula spinpolarizált esetben


Egy mágneses nanovezeték valósághűbb leírását kapjuk, ha szórást is megengedünk a vezetéken belül. Ezt a legegyszerűbben a korábban megismert Landauer formalizmus keretében tehetjük meg. A Landauer képben az elektrontranszportot 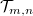\setbox0\hbox{$\mathcal{T}_{m,n}$}% \message{//depth:\the\dp0//}% \box0% transzmisszós valószínűségekkel írjuk le, melyek a bal oldali \setbox0\hbox{$n$}% \message{//depth:\the\dp0//}% \box0%-edik vezetési csatornából a jobb oldali \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%-edik csatornába történő szóródás valószínűségét adják meg. 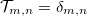Míg \setbox0\hbox{$\mathcal{T}_{m,n}=\delta_{m,n}$}% \message{//depth:\the\dp0//}% \box0% a fent tárgyalt ideális kvantumvezetéknek felel meg, ha a vezetéken belül az elektronok rácshibákon, illetve szennyezőkön szóródnak, akkor 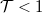\setbox0\hbox{$\mathcal{T}<1$}% \message{//depth:\the\dp0//}% \box0% transzmissziós valószínűségeket kapunk. Fontos megjegyezni, hogy a Landauer-kép inelasztikus szórásokat (pl. elektron-fonon kölcsönhatás) és spinszórásokat nem tud figyelembe venni.

Vizsgáljuk meg a 3. ábrán szemléltetett rendszer vezetési tulajdonságait: a nanovezeték két nemmágneses ideális kvantumvezeték között egy ferromágneses tartományt tartalmaz, melyben szóródhatnak az elektronok.

Spintronika3.png
3. ábra. Ferromágneses nanovezetékben a fel és le spinű elektronok transzmissziós valószínűségei különbözhetnek

Mivel spinszórás nem történik, az áramot továbbra is egymástól függetlenül számolhatjuk a két spincsatornára a transzmissziós valószínűségek figyelembe vételével:

\[ I^\sigma=\frac{e^2}{h}\sum_{n,m=1}^{M^\sigma}T_{m,n}^\sigma V. \]

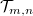A \setbox0\hbox{$\mathcal{T}_{m,n}$}% \message{//depth:\the\dp0//}% \box0% értékek függnek az elektronok Fermi-hullámhosszától, ami egy adott \setbox0\hbox{$n$}% \message{//depth:\the\dp0//}% \box0%-edik csatorna esetén jelentősen eltérhet a két spin-orientációra a kicserélődési felhasadás miatt. Ez alapján spinszórás (pl. spin-pálya kölcsönhatás) nélkül is a transzmisszós valószínűségek különböznek a két spincsatornára, ezt vesszük figyelembe a \setbox0\hbox{$\sigma$}% \message{//depth:\the\dp0//}% \box0% indexszel.

A spinfüggő áramot átírhatjuk

\[ I^\sigma=\frac{e^2}{h}M^\sigma \bar{T}^\sigma V \]

formába, ahol 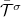\setbox0\hbox{$\bar{\mathcal{T}}^\sigma$}% \message{//depth:\the\dp0//}% \box0% az átlagos transzmissziós valószínűség a \setbox0\hbox{$\sigma$}% \message{//depth:\the\dp0//}% \box0% spin-orientációhoz tartozó összes nyitott vezetési csatornára. Ezzel a jelöléssel az áram spin szerinti polarizáltságát

\[ P_c=\frac{I^{\uparrow}-I^{\downarrow}}{I^{\uparrow}+I^{\downarrow}}=\frac{M^{\uparrow}\bar{T}^\uparrow-M^{\downarrow}\bar{T}^\downarrow}{M^{\uparrow}\bar{T}^\uparrow+M^{\downarrow}\bar{T}^\downarrow}. \]

formában írhatjuk. Spinpolarizált áramot a két spincsatorna között a nyitott vezetési csatornák számában illetve az az átlagos transzmissziós valószínűségben fellépő különbség egyaránt eredményezhet.

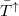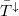Kevés vezetési csatorna (pl. egyatomos kontaktus) esetén a \setbox0\hbox{$\bar{T}^\uparrow$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\bar{T}^\downarrow$}% \message{//depth:\the\dp0//}% \box0% közötti különbség jelentős spinpolaizációt okozhat akkor is, ha a vezetési csatornák száma megegyezik a két spinirányra. Sok csatornás struktúrákban viszont 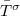\setbox0\hbox{$\bar{T}^\sigma$}% \message{//depth:\the\dp0//}% \box0% sok, különböző Fermi-hullámszámú csatornára vett átlag, így a spindiffúziós hossznál kisebb struktúrákban, ahol csak a rugalmas szórásokat vesszük figyelembe, az átlagos transzmisszós valószínűséget közel azonosnak várjuk a két spinirányra. Ennek megfelelően az áram spinpolarizációjához az elsődleges járulékot a vezetési csatornák számának különbsége adja:

\[ P_c\approx \frac{M^{\uparrow}-M^{\downarrow}}{M^{\uparrow}+M^{\downarrow}}, \]

akkor is ha nem ideális a vezeték, azaz 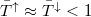\setbox0\hbox{$\bar{T}^\uparrow\approx\bar{T}^\downarrow<1$}% \message{//depth:\the\dp0//}% \box0%.

Korábbi megfontolások alapján a vezetési csatornák számát formálisan:

\[ M^\sigma=\frac{2\pi\hbar}{L}\sum_{n=1}^{M^\sigma}v_n^{\sigma}g_n^{\sigma} \]

alakban írhatjuk. Vezessünk be egy átlagos Fermi-sebességet, mely a különböző csatornák Fermi-sebességeinek átlaga a csatornák állapotsűrűségével súlyozva,

\[ \bar{v}_F^\sigma=\frac{\sum_{n} g_n^\sigma v_n^\sigma}{\sum_{n} g_n^\sigma}. \]

Figyelembe véve, hogy 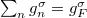\setbox0\hbox{$\sum_{n} g_n^\sigma=g_F^\sigma$}% \message{//depth:\the\dp0//}% \box0% a Fermi szint teljes állapotsűrűsége, az áram spinpolarizációjára vonatkozó formulánkat átírhatjuk

\[ P_c\approx\frac{M^{\uparrow}-M^{\downarrow}}{M^{\uparrow}+M^{\downarrow}}=\frac{g_F^{\uparrow}\bar{v}_F^{\uparrow}-g_F^{\downarrow}\bar{v}_F^{\downarrow}}{g_F^{\uparrow}\bar{v}_F^{\uparrow}+g_F^{\downarrow}\bar{v}_F^{\downarrow}} \]

alakba. Ez a formula lehetőséget ad arra, hogy a spinpolarizációt sávszerkezet-parameterek (Fermi-felület állapotsűrűsége és Fermi-sebesség) alapján értelmezzük.

Ferromágneses anyag sávmodelljét szemlélteti a 4. ábra. Mindkét panelen az energiatengelytől jobbra a fel, míg balra a le spinű elektronok állapotsűrűsége látszik. Az \setbox0\hbox{$s$}% \message{//depth:\the\dp0//}% \box0%-elektronokhoz tartozó parabolikus energiafüggésű állapotsűrűség mellett a keskeny \setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0% (vagy \setbox0\hbox{$f$}% \message{//depth:\the\dp0//}% \box0%) sávokhoz tartozó állapotűrűség-csúcsokat láthatjuk, az utóbbi energiában felhasad a kicserélődési kölcsönhatás miatt. Az anyag mágnesezettsége a betöltött (Fermi-energia alatti) fel és le spinű elektronok számának különbségéből adódik. Mindkét panelen a fel spinű elektronok vannak nagyobb számban, azaz a fel spint tekintjük többségi spinorientációnak. Ezzel szemben a transzport-tulajdonságokhoz, így az áram spinpolarizációjához csak a Fermi-felület közelében levő elektronok adnak járulékot. Az a) panelen a fel spinű elektronok vannak jelen nagyobb számban a Fermi-szintnél, így pozitív a spinpolarizáció. Ezzel szemben a b) panelen a Fermi-energia máshol helyezkedik el a \setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0%-sávokhoz képest, így végül a le spinű elektronok állnak rendelkezésre nagyobb számban a Fermi-energiánál, azaz a pozitív mágnesezettség ellenére negatív spinpolarizációt kapunk. Negatív spinpolarizációt valós anyagokban is tapasztalhatunk, pl. Co és Ni esetében.

Spintronika4.png
4. ábra. Pozitív (a) és negatív (b) spinpolarizációval rendelkező mágnesesen rendezett anyagok sávszerkezetének szemléltetése

Spinpolarizált transzport alkalmazása: spinszelep


A spin szabadsági fok kihasználásával számos érdekes eszközt építhetünk. A továbbiakban a gyakorlati felhasználás szempontjából legelterjedtebb, merevlemezek olvasófejében alkalmazott eszközt, a spinszelepet mutatjuk be.

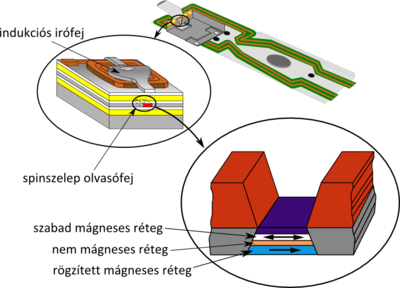
Az alapötlet, az óriás mágneses ellenállást mutató nanoszerkezet felfedezése, Albert Fert1 és Peter Grünberg2 nevéhez kötődik, akik 2007-ben Nobel-díjat kaptak felfedezésükért. A szerkezet két ferromágneses rétegből áll, melyeket egy, a spindiffúziós hossznál vékonyabb paramágneses réteg köt össze (lásd 5. ábra, illetve 6/a. ábra). A tapasztalatok alapján ennek a nanostruktúrának az ellenállása lényegesen kisebb akkor, ha a két mágneses réteg mágnesezettsége azonos irányba mutat, mint ha ellentétes irányba mutatnak. Ezt a jelenséget lehet kihasználni mágnesesen tárolt információ kiolvasására, ha a felső réteg mágnesezettségét rögzítjük, az alsó réteg mágnesezettsége pedig az alatta mozgatott adattároló lemez mágnesezettségének megfelelően áll be, így az információ egyszerű ellenállás-méréssel kiolvasható (5. ábra). Ezzel a módszerrel a merevlemezek tárolókapacitásának jelentős növekedését lehetett elérni az eredeti induktív, illetve a későbbi anizotróp mágneses ellenállás mérésen alapuló módszerekhez képest.

Merevlemez.png
5. ábra. Merevlemezek spinszelep struktúrán alapuló olvasófeje, forrás: Wikipedia

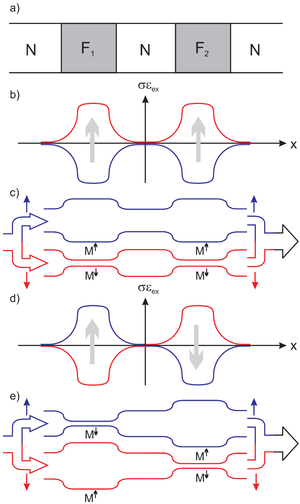
Először tegyük fel, hogy mindkét ferromágneses réteg mágnesezettsége felfelé mutat. Az 6/b. ábra szemlélteti a fenti Stoner-modell keretében a kicserélődési energia alakulását a fel spinű elektronokra (kék görbe) illetve a le spinű elektronokra (piros görbe). A kicserélődési felhasadás hatását legegyszerűbben úgy szemléltethetjük, hogy mind a normál mind a ferromágneses tartományokat ideális nanovezetéknek tekintjük. Ebben az esetben a pozitív kicserélődési energia ekvivalens azzal, mintha egy nemmágneses tartományban a keresztirányú 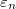\setbox0\hbox{$\varepsilon_n$}% \message{//depth:\the\dp0//}% \box0% energia megnőne, azaz a vezeték összeszűkülne, míg a negatív kicserélődési energiát úgy tekinthetjük, mintha 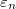\setbox0\hbox{$\varepsilon_n$}% \message{//depth:\the\dp0//}% \box0% csökkenne, azaz a vezeték szélessége megnőne. Ezt az ekvivalens képet szemlélteti az 6/c. ábra az 6/b. ábrának megfelelő mágnesezettség-irányok mellett, illetve az 6/e. ábra abban az esetben, ha a két mágneses réteg mágnesezettsége ellentétes irányba mutat (6/d. ábra).

Spintronika5.png
6. ábra GMR-jelenség ballisztikus modellje

Ebben az ekvivalens képben a fel és a le spinű elektronok is egy adiabatikus nanovezetéket látnak, így a legkisebb keresztmetszetben elférő nyitott csatornák száma fogja meghatározni a vezetőképességet. 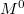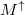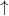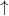Jelöljük a nyitott csatornák számát \setbox0\hbox{$M^0$}% \message{//depth:\the\dp0//}% \box0%-al a normál vezetékdarabban, \setbox0\hbox{$M^\uparrow$}% \message{//depth:\the\dp0//}% \box0%-el ha az elektronok spinje a többségi spinorientációnak felel meg (azaz \setbox0\hbox{$\uparrow$}% \message{//depth:\the\dp0//}% \box0% spinű elektronok mennek \setbox0\hbox{$\uparrow$}% \message{//depth:\the\dp0//}% \box0% mágnesezettésű tartományban vagy \setbox0\hbox{$\downarrow$}% \message{//depth:\the\dp0//}% \box0% elektronok mennek \setbox0\hbox{$\downarrow$}% \message{//depth:\the\dp0//}% \box0% tartományban), illetve \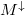setbox0\hbox{$M^\downarrow$}% \message{//depth:\the\dp0//}% \box0%-vel, ha egy adott mágnesezettségű tartományban ellentétes spinű (kisebbségi spinorientációjú) elektronok haladnak. 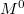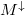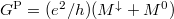A mágneses rétegek azonos irányú (parallel, \setbox0\hbox{$P$}% \message{//depth:\the\dp0//}% \box0%) beállása esetén a fel spinű elektronokra \setbox0\hbox{$M^0$}% \message{//depth:\the\dp0//}% \box0%, míg a le spinű elektronokra \setbox0\hbox{$M^\downarrow$}% \message{//depth:\the\dp0//}% \box0% a csatornák száma a legkisebb keresztmetszetben, azaz a a vezetőképesség \setbox0\hbox{$G^\mathrm{P}=(e^2/h)(M^\downarrow+M^0)$}% \message{//depth:\the\dp0//}% \box0%. Ellentétes mágnesezettségű rétegek esetén (antiparallel, 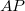\setbox0\hbox{$AP$}% \message{//depth:\the\dp0//}% \box0%) mindkét spinirányra 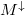\setbox0\hbox{$M^\downarrow$}% \message{//depth:\the\dp0//}% \box0% számú csatorna fér el a legkisebb keresztmetszetben, azaz a vezetőképesség 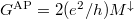\setbox0\hbox{$G^\mathrm{AP}=2(e^2/h)M^\downarrow$}% \message{//depth:\the\dp0//}% \box0%. Így a relatív vezetőképességváltozás a két beállás között:

\[ \frac{\Delta G}{G^\mathrm{P}}=\frac{G^\mathrm{P}-G^\mathrm{AP}}{G^\mathrm{P}}=\frac{M^0-M^\downarrow}{M^0+M^\downarrow}, \]

ami mindig pozitív érték. Kis vezetőképesség-változás esetén (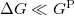\setbox0\hbox{$\Delta G \ll G^\mathrm{P}$}% \message{//depth:\the\dp0//}% \box0%), és feltételezve hogy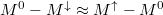 \setbox0\hbox{$M^0-M^\downarrow \approx M^\uparrow-M^0$}% \message{//depth:\the\dp0//}% \box0%

\[ \frac{\Delta G}{G^\mathrm{P}}\approx\frac{1}{2}\frac{M^\uparrow-M^\downarrow}{M^\uparrow+M^\downarrow} \approx \frac{P_c}{2} \]

adódik. Ez az egyszerűsített, ideális kvantumvezetékeken alapuló kép természetesen nem írja le valósághűen a merevlemezben használt spinszelepek vezetési tulajdonságait.

Valósághűbb képet kapunk, ha a különböző tartományokban szórási folyamatokat is megengedünk. Ha a spin-szelep struktúra kisebb a fázisdiffúziós hossznál (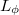\setbox0\hbox{$L_\phi$}% \message{//depth:\the\dp0//}% \box0%), akkor a két réteg közötti oda-visza szórásokat koherensen kell összeadni, így a teljes vezetőképesség interferencia-jelenségek finom részleteitől függ.

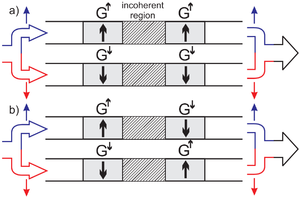
A fázisdiffúziós hossznál nagyobb (de a spindiffúziós hossznál kisebb) spin-szelep esetén viszont könnyen számolhatunk, mert elvész a koherencia, és így a sorosan kötött ellenállások egyszerűen összeadódnak. 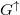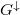Hogy eredményeinket összehasonlíthassuk az ideális kvantumvezetékek modelljével, a számolást vezetőképességekkel végezzük: többségi spinorientáció esetén a vezetőképesség \setbox0\hbox{$G^\uparrow$}% \message{//depth:\the\dp0//}% \box0%, kisebbségi spinorientáció esetén pedig \setbox0\hbox{$G^\downarrow$}% \message{//depth:\the\dp0//}% \box0% (7. ábra).

Spintronika6.png
7. ábra GMR-jelenség diffúzív, inkoherens modellje

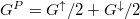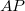A rétegek \setbox0\hbox{$P$}% \message{//depth:\the\dp0//}% \box0% beállása esetén a teljes vezetőképesség \setbox0\hbox{$G^{P}=G^\uparrow/2+G^\downarrow/2$}% \message{//depth:\the\dp0//}% \box0%, míg \setbox0\hbox{$AP$}% \message{//depth:\the\dp0//}% \box0% beállás esetén 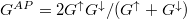\setbox0\hbox{$G^{AP}=2G^\uparrow G^\downarrow/(G^\uparrow+G^\downarrow)$}% \message{//depth:\the\dp0//}% \box0%, azaz a relatív vezetőképesség-változás:

\[ \frac{\Delta G}{G^\mathrm{P}}=\left(\frac{G^\uparrow-G^\downarrow}{G^\uparrow+G^\downarrow}\right)^2=P_c^2. \]

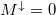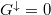Látszik, hogy mindkét modellben a relatív vezetőképesség-változás a spinpolarizációval skálázódik. Tökéletes spinpolarizáció esetén \setbox0\hbox{$M^\downarrow =0$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$G^\downarrow = 0$}% \message{//depth:\the\dp0//}% \box0%, így mindkét modell esetén 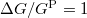\setbox0\hbox{$\Delta G/G^\mathrm{P}=1$}% \message{//depth:\the\dp0//}% \box0% adódik, ami jól megközelíthető valós, jelentős spin-polarizációval rendelkező eszközökben.

Hivatkozások

Fent hivatkozott szakcikkek

[1] M. N. Baibich, J. M. Broto, A. Fert, F. Nguyen Van Dau, F. Petroff, P. Etienne, G. Creuzet, A. Friederich, J. Chazelas: Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices, Phys. Rev. Lett. 61 p2472–2475 (1988)

[2] G. Binasch, P. Grünberg, F. Saurenbach, W. Zinn: Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange, Phys. Rev. B 39 p4828–4830 (1989)

Ajánlott könyvek és összefoglaló cikkek

Ajánlott kurzusok

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Spintronika&oldid=13225”