„Kvantált Hall-jelenség” változatai közötti eltérés
(→Elektrontranszport egyetlen Landau-nívó esetén) |
(→Mach-Zehnder interferométer kvantált Hall-élállapotokkal) |
||
| (egy szerkesztő 36 közbeeső változata nincs mutatva) | |||
| 10. sor: | 10. sor: | ||
|} | |} | ||
| − | A Hall-jelenséget általában az 1. ábrán bemutatott Hall-elrendezésben szokták mérni. Az | + | A Hall-jelenséget általában az 1. ábrán bemutatott Hall-elrendezésben szokták mérni. Az x irányú $I$ áram az 1. és 2. kontaktus között folyik. Ha a mérést zérus mágneses térben végezzük, akkor a 4. és 5. kontaktus között (y irányban) nem mérünk feszültséget. A 3. és 4. kontaktus között mért $V_{xx}$ ''longitudinális feszültség'' és az áram arányából pedig a minta [http://en.wikipedia.org/wiki/Four-terminal_sensing négypont ellenállását] kapjuk meg. |
| − | A minta síkjára merőleges ( | + | A minta síkjára merőleges (z irányú) mágneses teret kapcsolva a 4. és 5. kontaktus között $V_H$ Hall-feszültség jelenik meg, melynek az értéke a mágneses tér nagyságával lineárisan változik (2. ábra, piros görbe). A 3. és 4. kontaktus között (kismértékű mágneses ellenállástól eltekintve) továbbra is a zérus térben tapasztalt longitudinális ellenállást mérjük (2. ábra, kék görbe). |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 29. sor: | 29. sor: | ||
$$\left( \begin{array}{c} E_x \\ E_y \end{array} \right) = \left( \begin{array}{cc} m/e^2 n \tau_m & B/e n \\ -B/e n & m/e^2 n \tau_m \end{array} \right) \left( \begin{array}{c} j_x \\ j_y \end{array} \right) = \left( \begin{array}{cc} \rho_{xx} & \rho_{xy} \\ \rho_{yx} & \rho_{yy} \end{array} \right) \left( \begin{array}{c} j_x \\ j_y \end{array} \right).$$ | $$\left( \begin{array}{c} E_x \\ E_y \end{array} \right) = \left( \begin{array}{cc} m/e^2 n \tau_m & B/e n \\ -B/e n & m/e^2 n \tau_m \end{array} \right) \left( \begin{array}{c} j_x \\ j_y \end{array} \right) = \left( \begin{array}{cc} \rho_{xx} & \rho_{xy} \\ \rho_{yx} & \rho_{yy} \end{array} \right) \left( \begin{array}{c} j_x \\ j_y \end{array} \right).$$ | ||
| − | Az áramot | + | Az áramot x irányba folyatva és x irányú feszültséget mérve a minta longitudinális ellenállását a $\rho_{xx}=m/e^2 n \tau_m$ fajlagos ellenállásból kaphatjuk meg a geometriai faktorokkal történő skálázás után. |
| − | A fenti számolásból jól látszik, hogy véges mágneses térben | + | A fenti számolásból jól látszik, hogy véges mágneses térben x irányú áram esetén y irányú feszültség is megjelenik. A Hall-ellenállást a 4. és 5. kontaktusok között megjelenő $V_H$ Hall-feszültség és az $I$ áram hányadosaként definiáljuk. Két dimenzióban ez megegyezik az y irányú elektromos tér és az x irányú áramsűrűség arányával: |
| − | $$R_H=\frac{V_H}{I}=\frac{E_y}{j_x}=\rho_{yx}=-\frac{B}{e n}$$ | + | $$R_H=\frac{V_H}{I}=\frac{E_y}{j_x}=\rho_{yx}=-\frac{B}{e n}.$$ |
| − | Egyszerű számolásunkból jól látszik, hogy a Hall-ellenállás a $B$ mágneses térrel egyenesen arányos, és ezen kívül csak az elektronok sűrűségétől függ, azaz az $\tau_m$ relaxációs idő a longitudinális ellenállástól eltérően a Hall-ellenállásban ''nem jelenik meg''. Ennek köszönhetően a Hall-ellenállás mérése általánosan bevett módszer félvezetők elektronsűrűségének meghatározására. Érdemes megjegyezni, hogy $p$-típusú félvezetőkben, azaz amikor az áramot nem elektronok, hanem lyukak vezetik, a Hall-ellenállás előjelet vált. A Hall-jelenséget -amellett hogy a szilárdtestfizika alapvető mérési módszerei közé tartozik- a hétköznapokban is gyakran használjuk különböző elektronikai eszközökben elhelyezett [http://en.wikipedia.org/wiki/Hall_effect_sensor mágneses tér szenzorok] formájában. | + | Egyszerű számolásunkból jól látszik, hogy a Hall-ellenállás a $B$ mágneses térrel egyenesen arányos, és ezen kívül csak az elektronok sűrűségétől függ, azaz az $\tau_m$ relaxációs idő a longitudinális ellenállástól eltérően a Hall-ellenállásban ''nem jelenik meg''. Ennek köszönhetően a Hall-ellenállás mérése általánosan bevett módszer félvezetők elektronsűrűségének meghatározására. Érdemes megjegyezni, hogy $p$-típusú félvezetőkben, azaz amikor az áramot nem elektronok, hanem lyukak vezetik, a Hall-ellenállás előjelet vált. A Hall-jelenséget - amellett hogy a szilárdtestfizika alapvető mérési módszerei közé tartozik - a hétköznapokban is gyakran használjuk különböző elektronikai eszközökben elhelyezett [http://en.wikipedia.org/wiki/Hall_effect_sensor mágneses tér szenzorok] formájában. |
Hall-jelenséget elsősorban félvezetőkben szoktak tanulmányozni, hiszen az alacsony elektronsűrűség miatt a Hall-ellenállás viszonylag könnyen mérhető. Fémekben a nagy elektronsűrűség miatt a Hall-ellenállás értéke sokkal kisebb, de precíziós műszerekkel fémekben is vizsgálható a Hall-jelenség. Mindezekről a fizikushallgatók maguk is meggyőződhetnek a [[Hall-effektus]] c. hallgatói mérés során. | Hall-jelenséget elsősorban félvezetőkben szoktak tanulmányozni, hiszen az alacsony elektronsűrűség miatt a Hall-ellenállás viszonylag könnyen mérhető. Fémekben a nagy elektronsűrűség miatt a Hall-ellenállás értéke sokkal kisebb, de precíziós műszerekkel fémekben is vizsgálható a Hall-jelenség. Mindezekről a fizikushallgatók maguk is meggyőződhetnek a [[Hall-effektus]] c. hallgatói mérés során. | ||
| 42. sor: | 42. sor: | ||
===Klaus von Klitzing meglepő felfedezése=== | ===Klaus von Klitzing meglepő felfedezése=== | ||
<wlatex> | <wlatex> | ||
| − | A Hall-jelenséget megfelelően nagy tisztaságú kétdimenziós elektrongázban (2DEG) és elegendően nagy mágneses térben vizsgálva nagyon meglepő viselkedést tapasztalunk. A Hall-ellenállás a lineáris térfüggés helyett lépcsőszerűen változik, a longitudinális ellenállás pedig zérus értéket vesz fel ($V_{xx}=0$) azokban a mágneses tér tartományokban, ahol a Hall-ellenállás vízszintes platót mutat (lásd | + | A Hall-jelenséget megfelelően nagy tisztaságú kétdimenziós elektrongázban (2DEG) és elegendően nagy mágneses térben vizsgálva nagyon meglepő viselkedést tapasztalunk. A Hall-ellenállás a lineáris térfüggés helyett lépcsőszerűen változik, a longitudinális ellenállás pedig zérus értéket vesz fel ($V_{xx}=0$) azokban a mágneses tér tartományokban, ahol a Hall-ellenállás vízszintes platót mutat (lásd 3. ábra). |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 54. sor: | 54. sor: | ||
$$R_H=\frac{h}{e^2 n}, \;\;\;n=0,1,2,\dots,$$ | $$R_H=\frac{h}{e^2 n}, \;\;\;n=0,1,2,\dots,$$ | ||
ami a spindegeneráció miatti 2-es szorzótól eltekintve a [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Vezetőképesség-kvantálás kvantum-pontkontaktusban|vezetőképesség kvantálás]] képletének felel meg. | ami a spindegeneráció miatti 2-es szorzótól eltekintve a [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Vezetőképesség-kvantálás kvantum-pontkontaktusban|vezetőképesség kvantálás]] képletének felel meg. | ||
| − | A tapasztalatok szerint a kvantált $R_H$ értékek függetlenek a minta alakjától, méretétől, anyagától, és $R_H$ kísérletileg meghatározott értékei akár $10^{-7}$ pontossággal leírhatók a fenti egyszerű képlettel, azaz a kvantált Hall platók ellenállás-standardként is jól használhatók. | + | A tapasztalatok szerint a kvantált $R_H$ értékek függetlenek a minta alakjától, méretétől, anyagától, és $R_H$ kísérletileg meghatározott értékei akár $10^{-7}$ pontossággal leírhatók a fenti egyszerű képlettel, azaz a kvantált Hall-platók ellenállás-standardként is jól használhatók. |
| − | A kvantált Hall jelenséget [http://en.wikipedia.org/wiki/Klaus_von_Klitzing Klaus von Klitzing] fedezte fel 1980-ban.<sup>[http://prl.aps.org/abstract/PRL/v45/i6/p494_1 1]</sup> Pár évvel később (1985-ben) felfedezését Nobel díjjal jutalmazták. | + | A kvantált Hall-jelenséget [http://en.wikipedia.org/wiki/Klaus_von_Klitzing Klaus von Klitzing] fedezte fel 1980-ban.<sup>[http://prl.aps.org/abstract/PRL/v45/i6/p494_1 1]</sup> Pár évvel később (1985-ben) felfedezését Nobel-díjjal jutalmazták. |
</wlatex> | </wlatex> | ||
| − | ===A következő Nobel díj: tört számú kvantált Hall-effektus=== | + | ===A következő Nobel-díj: tört számú kvantált Hall-effektus=== |
<wlatex> | <wlatex> | ||
| − | A kvantált Hall-jelenség felfedezése óriási érdeklődést váltott ki, és nem kellett sokat várni újabb meglepő kísérleti eredményekre. [http://en.wikipedia.org/wiki/Daniel_C._Tsui Daniel Tsui] és [http://en.wikipedia.org/wiki/Horst_Ludwig_St%C3%B6rmer Horst Störmer] kísérletei 1982-ben megmutatták,<sup>[http://prl.aps.org/abstract/PRL/v48/i22/p1559_1 2],[http:// | + | A kvantált Hall-jelenség felfedezése óriási érdeklődést váltott ki, és nem kellett sokat várni újabb meglepő kísérleti eredményekre. [http://en.wikipedia.org/wiki/Daniel_C._Tsui Daniel Tsui] és [http://en.wikipedia.org/wiki/Horst_Ludwig_St%C3%B6rmer Horst Störmer] kísérletei 1982-ben megmutatták,<sup>[http://prl.aps.org/abstract/PRL/v48/i22/p1559_1 2],[http://rmp.aps.org/abstract/RMP/v71/i4/p875_1 3]</sup> hogy még tisztább kétdimenziós elektrongázban és még nagyobb mágneses térben a Hall-ellenállás |
$$R_H=\frac{h}{e^2 \nu},\;\;\; \nu=\frac{p}{q}, \;\;\; p,q=0,1,2,\dots$$ | $$R_H=\frac{h}{e^2 \nu},\;\;\; \nu=\frac{p}{q}, \;\;\; p,q=0,1,2,\dots$$ | ||
értékeket vehet fel, ahol $\nu$ már nem egész szám, hanem bizonyos egész számok hányadosa. A Hall-platók tartományában | értékeket vehet fel, ahol $\nu$ már nem egész szám, hanem bizonyos egész számok hányadosa. A Hall-platók tartományában | ||
| 83. sor: | 83. sor: | ||
|} | |} | ||
| − | A továbbiakban az egész számú kvantált Hall jelenség leírását szemléltetjük. A grafén fizikájáról egy külön fejezet keretében adunk leírást. | + | A továbbiakban az egész számú kvantált Hall-jelenség leírását szemléltetjük. A grafén fizikájáról egy külön fejezet keretében adunk leírást. |
</wlatex> | </wlatex> | ||
| 92. sor: | 92. sor: | ||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | align="center"|[[Fájl:2DEG.jpg|közép| | + | | align="center"|[[Fájl:2DEG.jpg|közép|120px]] |
|- | |- | ||
| align="center"|5. ábra. ''Ciklotronpálya mágneses térbe helyezett 2DEG-ben'' | | align="center"|5. ábra. ''Ciklotronpálya mágneses térbe helyezett 2DEG-ben'' | ||
| 118. sor: | 118. sor: | ||
$$[\hat{a},\hat{a}^+]=\frac{1}{2 \alpha}[i\hat{v}_x+\hat{v}_y, -i\hat{v}_x+\hat{v}_y]=1.$$ | $$[\hat{a},\hat{a}^+]=\frac{1}{2 \alpha}[i\hat{v}_x+\hat{v}_y, -i\hat{v}_x+\hat{v}_y]=1.$$ | ||
Látszik, hogy az új operátorok segítségével az egydimenziós harmonikus oszcillátor problémájára vezettük vissza a Schrödinger egyenletet, így további számolás nélkül megállapíthatjuk, hogy a mágneses térben mozgó elektronok lehetséges energiái a harmonikus oszcillátorhoz hasonlóan kvantáltak: | Látszik, hogy az új operátorok segítségével az egydimenziós harmonikus oszcillátor problémájára vezettük vissza a Schrödinger egyenletet, így további számolás nélkül megállapíthatjuk, hogy a mágneses térben mozgó elektronok lehetséges energiái a harmonikus oszcillátorhoz hasonlóan kvantáltak: | ||
| − | $$E=\hbar \omega_c (n+\frac{1}{2}).$$ | + | $$E=\hbar \omega_c \left( n+\frac{1}{2}\right).$$ |
| − | A kvantált energiaszinteket Landau nívóknak hívjuk. | + | A kvantált energiaszinteket Landau-nívóknak hívjuk. |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 132. sor: | 132. sor: | ||
ahol $\Phi=B A$ a teljes fluxus$, \Phi_0=h/e$ pedig a fluxuskvantum. Egy teljesen betöltött Landau-szinten a fentiek alapján az elektronsűrűség: $n=2 e B/h$. | ahol $\Phi=B A$ a teljes fluxus$, \Phi_0=h/e$ pedig a fluxuskvantum. Egy teljesen betöltött Landau-szinten a fentiek alapján az elektronsűrűség: $n=2 e B/h$. | ||
| − | A Landau-szintek magasfokú degenerációja mögött szemléletesen az áll, hogy egy ciklotronsugárnak megfelelő tipikus kiterjedésű elektronállapotot a minta $A$ felületén összesen$N\approx 2A/r_c^2\pi$ különböző helyre tehetünk le (a spin szerinti degenerációt is figyelembe véve). Ez alapján kis átalakítással $N=4\Phi/\Phi_0$ adódik, azaz naiv számolásunkkal egy egy kettes szorzó eltéréssel visszakaptuk a Landau nívók fent kiszámolt degenerációs fokát. | + | A Landau-szintek magasfokú degenerációja mögött szemléletesen az áll, hogy egy ciklotronsugárnak megfelelő tipikus kiterjedésű elektronállapotot a minta $A$ felületén összesen$N\approx 2A/r_c^2\pi$ különböző helyre tehetünk le (a spin szerinti degenerációt is figyelembe véve). Ez alapján kis átalakítással $N=4\Phi/\Phi_0$ adódik, azaz naiv számolásunkkal egy egy kettes szorzó eltéréssel visszakaptuk a Landau-nívók fent kiszámolt degenerációs fokát. |
| − | A Landau-szintek kialakulásának fontos feltétele, hogy az elektronok a ciklotronpályát két ütközés között sokszor bejárják, azaz a cikotronpálya periódusideje a momentumrelaxációs időnél sokkal | + | A Landau-szintek kialakulásának fontos feltétele, hogy az elektronok a ciklotronpályát két ütközés között sokszor bejárják, azaz a cikotronpálya periódusideje a momentumrelaxációs időnél sokkal kisebb legyen, $\omega_c^{-1} \ll \tau_m$. Ez akkor teljesül, ha $B \gg \mu^{-1}$, ahol $\mu=e \tau_m /m$ az elektronok mobilitása a 2DEG-ben, azaz Landau-szinteket csak kellően tiszta mintában és kellően nagy mágneses térben látunk. További fontos feltétel, hogy Landau-szintek közötti energiakülönbség nagyobb legyen a hőmérsékletnél és a feszültségnél, $\hbar \omega_c >> k T,\; eV$. |
</wlatex> | </wlatex> | ||
===Ciklotronpályák középpontjának mozgása=== | ===Ciklotronpályák középpontjának mozgása=== | ||
<wlatex> | <wlatex> | ||
Nagy mágneses térben azt várjuk, hogy az elektronok egy középponti $r$ kordináta körül nagyon kis, $\approx r_c$ sugarú ciklotronmozgást végeznek. Klasszikusan az elektron éppen aktuális $r$ helyzetét | Nagy mágneses térben azt várjuk, hogy az elektronok egy középponti $r$ kordináta körül nagyon kis, $\approx r_c$ sugarú ciklotronmozgást végeznek. Klasszikusan az elektron éppen aktuális $r$ helyzetét | ||
| − | $r = r_0 + \Delta r$ alakban írhatjuk, ahol $\Delta r$ a középpontból az aktuális ponta mutató vektor (7. ábra). | + | $r = r_0 + \Delta r$ alakban írhatjuk, ahol $\Delta r$ a középpontból az aktuális ponta mutató vektor (7. ábra). |
| − | + | ||
| − | + | ||
| − | + | ||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| 149. sor: | 146. sor: | ||
| align="center"|7. ábra. | | align="center"|7. ábra. | ||
|} | |} | ||
| + | Körmozgás esetén az elektront körpályán tartó centripetális erőt $F_{cp} = -m\omega^2\Delta r = - e v \times B$ alakban írhatjuk, ami jelen esetben értelemszerűen a Lorentz-erővel egyezik meg. Ez alapján a körpálya középpontját formálisan | ||
| + | $$r_0 = r-\frac{e}{m \omega^2} v \times B$$ | ||
| + | alakban írhatjuk. | ||
| + | |||
Játsszunk el a gondolattal, hogy az $r_0$ koordinátát kvantummechanikai tartalommal ruházzuk fel a ciklotronpályák középpontjának helyét leíró operátorként! Komponensenként kifejtve: | Játsszunk el a gondolattal, hogy az $r_0$ koordinátát kvantummechanikai tartalommal ruházzuk fel a ciklotronpályák középpontjának helyét leíró operátorként! Komponensenként kifejtve: | ||
| 165. sor: | 166. sor: | ||
adódik, azaz a ciklotronpálya középpontjának x és y írányú kvantummechanikai bizonytalanságát összeszorozva pont az $r_c$ ciklotronsugár négyzete köszön vissza, egy elektron legalább $r_c^2/2$ ''helyet foglal''. Ez alapján körszimmetrikus hullámfüggvényt feltételezve a ciklotron pályák x és y irányban is $\approx r_c$ kiterjedésűek. | adódik, azaz a ciklotronpálya középpontjának x és y írányú kvantummechanikai bizonytalanságát összeszorozva pont az $r_c$ ciklotronsugár négyzete köszön vissza, egy elektron legalább $r_c^2/2$ ''helyet foglal''. Ez alapján körszimmetrikus hullámfüggvényt feltételezve a ciklotron pályák x és y irányban is $\approx r_c$ kiterjedésűek. | ||
</wlatex> | </wlatex> | ||
| + | |||
===Bezáró és random potenciál=== | ===Bezáró és random potenciál=== | ||
<wlatex> | <wlatex> | ||
| 174. sor: | 176. sor: | ||
| align="center"|[[Fájl:QHall_potential.png|közép|350px]] | | align="center"|[[Fájl:QHall_potential.png|közép|350px]] | ||
|- | |- | ||
| − | | align="center"|8. ábra. ''Landau-szintek módosulása a a minta szélénél a bezáró potenciál, illetve a minta | + | | align="center"|8. ábra. ''Landau-szintek módosulása a a minta szélénél a bezáró potenciál, illetve a minta belsejében jelentkező fluktuáló potenciál miatt'' |
|} | |} | ||
| − | Az U potenciált perturbációként kezelve, és feltételezve hogy U lassan változik a hullámfüggvény tipikus kiterjedéséhez, $r_c$-hez képest (azaz elegendően nagy a mágneses tér) az energiária egyszerűen | + | Az $U$ potenciált perturbációként kezelve, és feltételezve hogy $U$ lassan változik a hullámfüggvény tipikus kiterjedéséhez, $r_c$-hez képest (azaz elegendően nagy a mágneses tér) az energiária egyszerűen |
$$E=\hbar \omega_c (n+\frac{1}{2}) + \langle \Psi | U | \Psi \rangle \approx E=\hbar \omega_c(n+\frac{1}{2}) + U(x_0,y_0)$$ | $$E=\hbar \omega_c (n+\frac{1}{2}) + \langle \Psi | U | \Psi \rangle \approx E=\hbar \omega_c(n+\frac{1}{2}) + U(x_0,y_0)$$ | ||
| − | adódik, azaz a kvantált Landau szintek energiáit a hullámfüggvény középpontjánál vett potenciál értékével korrigáljuk. | + | adódik, azaz a kvantált Landau-szintek energiáit a hullámfüggvény középpontjánál vett potenciál értékével korrigáljuk. |
| − | Véges U esetén az elektronok mozgását úgy képzeljük el, hogy a gyors ($\omega_c$ körfrekvenciájú) és kis ($\sim r_c^2 \sim 1/B$) területre koncentrált ciklotronmozgás mellett a ciklotronpályák középpontjának koordinátái a potenciál hatására haladó mozgást végeznek. Írjuk fel a mozgásegyenletet $x_0$ és $y_0$-ra: | + | Véges $U$ esetén az elektronok mozgását úgy képzeljük el, hogy a gyors ($\omega_c$ körfrekvenciájú) és kis ($\sim r_c^2 \sim 1/B$) területre koncentrált ciklotronmozgás mellett a ciklotronpályák középpontjának koordinátái a potenciál hatására haladó mozgást végeznek. Írjuk fel a mozgásegyenletet $x_0$ és $y_0$-ra: |
| − | $$\frac{d}{d t}\langle\hat{x}_0\rangle = \frac{i}{\hbar} \langle[\hat{H},\hat{x}_0]\rangle = \frac{i}{\hbar} \langle[\hat{H}_0,\hat{x}_0]\rangle + \frac{i}{\hbar} \langle[\hat{U},\hat{x}_0]\rangle = - \frac{i}{\hbar m \omega_c} \langle[\hat{U},\hat{p}_y]\rangle = - \frac{1}{m \omega_c} \langle[U,\partial_x]\rangle = \frac{1}{e B} \ | + | $$\frac{d}{d t}\langle\hat{x}_0\rangle = \frac{i}{\hbar} \langle[\hat{H},\hat{x}_0]\rangle = \frac{i}{\hbar} \langle[\hat{H}_0,\hat{x}_0]\rangle + \frac{i}{\hbar} \langle[\hat{U},\hat{x}_0]\rangle = - \frac{i}{\hbar m \omega_c} \langle[\hat{U},\hat{p}_y]\rangle = - \frac{1}{m \omega_c} \langle[U,\partial_x]\rangle = \frac{1}{e B} \left< \frac{\partial U}{\partial y}\right> \approx \frac{1}{e B} \frac{\partial U(x_0,y_0)}{\partial y_0},$$ |
| − | ahol megintcsak feltételeztük, hogy a hullámfüggvény kiterjedése kicsi U változásának skáláján. Hasonlóan: | + | ahol megintcsak feltételeztük, hogy a hullámfüggvény kiterjedése kicsi $U$ változásának skáláján. Hasonlóan: |
| − | $$\frac{d}{d t}\ | + | $$\frac{d}{d t}\left< \hat{y}_0\right> = -\frac{1}{e B} \left< \frac{\partial U}{\partial x}\right> \approx -\frac{1}{e B} \frac{\partial U(x_0,y_0)}{\partial x_0}.$$ |
| − | A fentiek alapján számoljuk ki a potenciál változását a pálya mentén, azaz U idő szerinti teljes deriváltját: | + | A fentiek alapján számoljuk ki a potenciál változását a pálya mentén, azaz $U$ idő szerinti teljes deriváltját: |
$$\frac{d U}{d t}=\frac{\partial U}{\partial x_0} \cdot \dot{x}_0 + \frac{\partial U}{\partial y_0} \cdot \dot{y}_0 = \frac{c}{e H} \left( \frac{\partial U}{\partial x_0} \frac{\partial U}{\partial y_0} - \frac{\partial U}{\partial y_0} \frac{\partial U}{\partial x_0} \right) = 0.$$ | $$\frac{d U}{d t}=\frac{\partial U}{\partial x_0} \cdot \dot{x}_0 + \frac{\partial U}{\partial y_0} \cdot \dot{y}_0 = \frac{c}{e H} \left( \frac{\partial U}{\partial x_0} \frac{\partial U}{\partial y_0} - \frac{\partial U}{\partial y_0} \frac{\partial U}{\partial x_0} \right) = 0.$$ | ||
Számolásunk alapján a ''ciklotronpályák középpontja ekvipotenciális felületek mentén mozog''! | Számolásunk alapján a ''ciklotronpályák középpontja ekvipotenciális felületek mentén mozog''! | ||
</wlatex> | </wlatex> | ||
| + | |||
==Elektrontranszport egyetlen Landau-nívó esetén== | ==Elektrontranszport egyetlen Landau-nívó esetén== | ||
<wlatex> | <wlatex> | ||
| − | Tételezzünk fel olyan mágneses teret, melynél a Fermi-energia az első és második Landau szint között helyezkedik el, azaz az első Landau szint teljesen betöltött, a második pedig betöltetlen (lásd 9. ábra, bal oldal). Ebben az esetben a Fermi-energiánál | + | Tételezzünk fel olyan mágneses teret, melynél a Fermi-energia az első és második Landau-szint között helyezkedik el, azaz az első Landau-szint teljesen betöltött, a második pedig betöltetlen (lásd 9. ábra, bal oldal). Ebben az esetben a Fermi-energiánál |
| − | a minta széleinél találunk csak állapotokat a bezáró potenciálnak köszönhetően, a minta belsejében egy ''tiltott sávot'' tapasztalunk a Fermi-energia és a betöltött Landau-szint között. Ebben az esetben elektrontranszport csak a minta szélei mentén megengedett, ahol az elektronok energiája metszi a Fermi energiát. Mivel a minta két szélét elválasztó makroszkopikus méretű tartományban az elektrontranszport nem megengedett, így a minta két széle között nem történhet átszóródás (9. ábra, jobb oldal). | + | a minta széleinél találunk csak állapotokat a bezáró potenciálnak köszönhetően, a minta belsejében egy ''tiltott sávot'' tapasztalunk a Fermi-energia és a betöltött Landau-szint között. Ebben az esetben elektrontranszport csak a minta szélei mentén megengedett, ahol az elektronok energiája metszi a Fermi-energiát. Mivel a minta két szélét elválasztó makroszkopikus méretű tartományban az elektrontranszport nem megengedett, így a minta két széle között nem történhet átszóródás (9. ábra, jobb oldal). |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 210. sor: | 213. sor: | ||
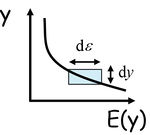
A Hall-ellenállás meghatározásához az élállapotokon keresztül folyó áramot is meg kell határoznunk. Először számoljuk ki, hogy egy élállapot $d\varepsilon$ szélességű energiatartománya mekkora járulékot ad az áramhoz. | A Hall-ellenállás meghatározásához az élállapotokon keresztül folyó áramot is meg kell határoznunk. Először számoljuk ki, hogy egy élállapot $d\varepsilon$ szélességű energiatartománya mekkora járulékot ad az áramhoz. | ||
| − | A $d\varepsilon$ energiatartomány $dy$ szélességű térbeli tartománynak felel meg az él mentén, ahol $d\varepsilon/dy$ a potenciál y szerinti deriváltja (10 | + | A $d\varepsilon$ energiatartomány $dy$ szélességű térbeli tartománynak felel meg az él mentén, ahol $d\varepsilon/dy$ a potenciál y szerinti deriváltja (10. ábra). |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| 229. sor: | 232. sor: | ||
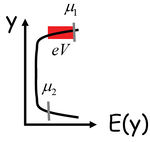
Mivel $\mu_1-\mu_2=e V$ esetén a felső él mentén $eV$-vel magasabb energiáig vannak betöltve az állapotok mint az alsó él mentén (11. ábra), így a mintán folyó teljes áram | Mivel $\mu_1-\mu_2=e V$ esetén a felső él mentén $eV$-vel magasabb energiáig vannak betöltve az állapotok mint az alsó él mentén (11. ábra), így a mintán folyó teljes áram | ||
$$I=\frac{2 e}{h} e V.$$ | $$I=\frac{2 e}{h} e V.$$ | ||
| − | Ennek megfelelően a Hall ellenállás illetve a Hall vezetőképesség: | + | Ennek megfelelően a Hall-ellenállás illetve a Hall-vezetőképesség: |
$$R_H=\frac{V_H}{I}=\frac{h}{2 e^2}, \ \ \ G_H=\frac{I}{V_H}=\frac{2 e^2}{h}$$ | $$R_H=\frac{V_H}{I}=\frac{h}{2 e^2}, \ \ \ G_H=\frac{I}{V_H}=\frac{2 e^2}{h}$$ | ||
| 237. sor: | 240. sor: | ||
== Több Landau-nívó, Zeeman-felhasadás == | == Több Landau-nívó, Zeeman-felhasadás == | ||
<wlatex> | <wlatex> | ||
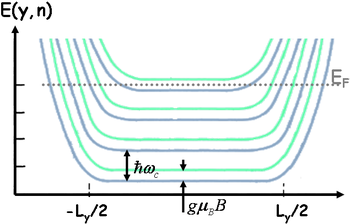
| − | A korábbiakban a Landau nívókat spin szerint degeneráltnak tekintettük. Természetesen mágneses térben az energiák spin szerinti Zeeman-felhasadását is figyelembe kell venni: | + | A korábbiakban a Landau-nívókat spin szerint degeneráltnak tekintettük. Természetesen mágneses térben az energiák spin szerinti Zeeman-felhasadását is figyelembe kell venni: |
| − | $$E=\hbar \omega_c (n+\frac{1}{2})+U_{bezaro} + g \mu_B B S_z,$$ | + | $$E=\hbar \omega_c \left(n+\frac{1}{2} \right) +U_\mathrm{bezaro} + g \mu_B B S_z,$$ |
ahol $S_z=\pm1/2$ az elektronspin z irányú komponense. | ahol $S_z=\pm1/2$ az elektronspin z irányú komponense. | ||
| − | Félvezetőkben a kis effektív tömeg miatt tipikusan $\hbar \omega_c | + | Félvezetőkben a kis effektív tömeg miatt tipikusan $\hbar \omega_c \gg g \mu_B B$ ($\hbar \omega_c [K] \approx 20 B [T],\;\; g \mu_B B [K] \approx 0.3 \cdot B [T]$), de ha a $B$ tér elegendően nagy akkor a Landau-szintek fel és le spinű elektronjai elkülönült energiaszinteket tudnak létrehozni, ezek a spinpolarizált Landau-szintek (12. ábra). |
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| − | [[Fájl:QHall_splitting.png|közép|350px | + | |- |
| − | + | | align="center"|[[Fájl:QHall_splitting.png|közép|350px]] | |
| + | |- | ||
| + | | align="center"|12. ábra. ''Spinpolarizált Landau-szintek'' | ||
| + | |} | ||
| − | Egyetlen teljesen | + | Egyetlen teljesen betöltött spinpolarizált Landau-szint esetén a minta két szélén kialakuló élállapot értelemszerűen $G_H=e^2/h$ vezetőképességet ad, hiszen csak a spindegenerációból adódó kettes faktort kell elhagyni az állapotsűrűségből. |
| − | Ha a Fermi energia alatt M db. | + | Ha a Fermi-energia alatt M db. spinpolarizált Landau-szint található, és a minta belsejében a Fermi-energia két Landau-szint közé esik, akkor a Hall-vezetőképesség: |
| − | + | $$G_H=\frac{e^2}{h} M,$$ | |
| − | $$G_H | + | azaz visszakaptuk a kísérletekben megfigyelt értékeket. A mérések szerint $R_H$ relatív pontossága akár $\sim 10^{-7}$ is lehet, ami a visszaszórás hiányának tökéletességét mutatja. Fontos megjegyezni, hogy a minta egyik oldalán különböző Landau-szintek közötti átszórás nem változtat a vezetőképességen, hiszen csak az számít, hogy egy adott élállapotban elinduló elektron - még ha át is szóródik másik élállapotba - biztosan nem jut vissza a kiinduló elektródába. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
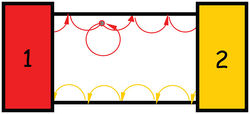
| + | A jelenség megértését segíti a 13. ábrán bemutatott klasszikus kép is: az élek mentén hiába szóródik szennyezőkön egy elektron, az 1. elektródából induló elektron végül mindig a 2. elektródába érkezik! | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | align="center"|[[Fájl:HallClassic.jpg|közép|250px]] | ||
| + | |- | ||
| + | | align="center"|13. ábra. ''Élállapotok klasszikus ciklotronpályákkal szemléltetve'' | ||
| + | |} | ||
</wlatex> | </wlatex> | ||
==A Fermi-energia helyzete == | ==A Fermi-energia helyzete == | ||
<wlatex> | <wlatex> | ||
| − | A fenti megfontolások alapján pontosan kijön a Hall-ellenállás kvantáltsága, azonban a számolások azon a feltételezésen alapulnak, hogy a Fermi energia két Landau-szint közé esik, ami nem feltétlenül igaz. Vizsgáljuk meg pontosabban, hogy mikor is esik a Fermi | + | A fenti megfontolások alapján pontosan kijön a Hall-ellenállás kvantáltsága, azonban a számolások azon a feltételezésen alapulnak, hogy a Fermi-energia két Landau-szint közé esik, ami nem feltétlenül igaz. Vizsgáljuk meg pontosabban, hogy mikor is esik a Fermi-energia két Landau-szint közé! |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | align="center"|[[Fájl:Ef.jpg|közép|250px]] | ||
| + | |- | ||
| + | | align="center"|14. ábra. ''Felső panel: a Fermi energia változása 1/B függvényében. Általában a Fermi energia valamelyik tömbi, spinpolarizált Landau-szintnél található (vízszintes platók), és csak nagyon szűk mágneses tér tartományokban kerül $\varepsilon_F$ két Landau-szint közé. Az alsó panel azt szemlélteti, hogy a Hall-vezetőképesség kvantált értékeit csak azokban a diszkrét (zöld) pontokban várjuk, ahol $\varepsilon_F$ két Landau-szint között helyezkedik el.'' | ||
| + | |} | ||
| + | 1/B növelésével egymás után töltjük be a spinpolarizált Landau-szinteket. A Landau-szintek óriási degenerációja miatt a Fermi-energia szinte mindig az egyik Landau-szintre esik, kivéve amikor éppen egy teljesen betöltött és egy betöltetlen Landau-szint közötti élállapotokat töltünk fel. Az élállapotok száma azonban elhanyagolható a Landau-szintek belső állapotainak számához képest: egyszerű becslésként e két állapotszám úgy aránylik egymáshoz mint a minta makroszkopikus szélessége az élállapot nanométeres skálájú y irányú kiterjedéséhez. Ennek megfelelően csak nagyon szűk mágneses tér tartományokban várjuk, hogy a Fermi-energia két tömbi Landau-szint energiája között legyen (14. ábra, felső panel). Ha viszont a Fermi-energia egy tömbi Landau-szintnél helyezkedik el, akkor ezen a Landau-szinten keresztül már átszóródhatnak az elektronok a két él között (15. ábra), azaz a korábbi érvelésünk érvénytelen. Azaz azt a lehangoló eredményt kaptuk, hogy a Hall-vezetőképesség csak nagyon szűk, szinte pontszerű mágneses-tér tartományokban veszi fel a várt kvantált értékeket, ráadásul ezek a pontok jól illeszkednek a klasszikus Hall-vezetőképesség 1/B-vel lineárisan arányos változására (14. ábra alsó panel), azaz a kiterjedt Hall-platókra eddig nem kaptunk magyarázatot. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | align="center"|[[Fájl:QHall_E_Fermi.png|közép|150px]] | ||
| + | |- | ||
| + | | align="center"|15. ábra. ''Ha a Fermi-energia egy tömbi Landau-szintnél található, akkor a két oldalon haladó élállapotok között az eletronok át tudnak szóródni a tömbi Landau-szinten keresztül'' | ||
| + | |} | ||
</wlatex> | </wlatex> | ||
== Rendezetlenség szerepe == | == Rendezetlenség szerepe == | ||
<wlatex> | <wlatex> | ||
| + | Az eddigi számolásokban csak az élállapotok kialakulásáért felelős bezáró potenciált vettük figyelembe. A kiterjedt kvantált Hall-platók megértéséhez a minta belsejében kialakuló fluktuáló potenciált is figyelembe kell venni. Tökéletlen minta (azaz véges fluktuáló potenciál) esetén a tömbi Landau-szintektől eltérő energiánál az elektronok nem csak az élállapot mentén mozoghatnak, hanem a minta belsejében a fluktuáló potenciál adott energiának megfelelő ekvipotenciális vonalai mentén is. Ha az energia kellőképpen eltér a tömbi Landau-szintektől, akkor az elektronok a fluktuáló potenciál hegyei vagy völgyei mentén kis kiterjedésű zárt pályákra kényszerülnek (16. ábra bal oldal), azaz a minta belsejében vannak a Landau-szintektől eltérő energiájú állapotok, de ezek lokalizált állapotok, a minta két széle közötti transzporthoz nem járulnak hozzá. A tömbi Landau-szinteknek megfelelő energiáknál az elektronok már találnak az ekvipotenciális vonalak mentén olyan trajektróriákat, melyek mentén átszóródhatnak a minta két széle között (16. ábra jobb oldal). | ||
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| + | |- | ||
| + | | align="center"|[[Fájl:QHall_equipotential.png|közép|450px]] | ||
| + | |- | ||
| + | | align="center"|16. ábra. ''Elektronok mozgása ekvipotenciális felületek mentén'' | ||
| + | |} | ||
| − | + | A fentiek gondolatmenet alapján megállapíthatjuk, hogy tökéletlen minta esetén a Landau-szintek körüli véges energiatartományban véges állapotsűrűséget tapasztalunk (17. ábra), azonban a Landau-szintektől távolabb ez a véges állapotsűrűség a tömbi tartomány potenciáljában lokalizált állapotoknak felel meg. Ennek megfelelően a Fermi-energia kiterjedt mágneses tér tartományokban eltér Landau-szintek energiájától, de ezeknél az energiáknál továbbra is igaz a két oldalon kialakuló élállapotok közötti átszórás tilalma, azaz valóban véges szélességű kvantált Hall-platókat várunk. | |
| − | + | ||
| − | + | ||
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| − | + | |- | |
| − | + | | align="center"|[[Fájl:szennyezesek.jpg|közép|450px]] | |
| − | [[Fájl:szennyezesek.jpg|közép|450px | + | |- |
| − | + | | align="center"|17. ábra. ''Szennyezők hatása az állapotsűrűségre: a Landau-szintek körüli szélesebb energiatartományban lokalizált elektronállapotok jelennek meg'' | |
| − | + | |} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | A fentiek alapján látjuk, hogy a rendezetlenségnek kettős szerepe van a kvantált Hall-jelenség szempontjából. Egyrészt túl nagy szennyező-koncentráció, melynél a szórások közötti átlagos idő összemérhető a ciklotronmozgás periódusidejével ($B \sim 1/\mu$) lerombolja a kvantált Hall-jelenséget. Másrészt ha a minta túl tökéletes, akkor szintén nem várunk kiterjedt kvantált Hall-platókat, azaz a minta tökéletlensége teszi lehetővé, hogy $R_H=h/e^2$ legyen a létező legpontosabb ellenállás standard. Ez utóbbi egyértelműen látszik a tört számú kvantált Hall-effektust bemutató kísérletekben.<sup>[http://prl.aps.org/abstract/PRL/v48/i22/p1559_1 2],[http://prl.aps.org/abstract/PRL/v50/i18/p1395_1 3]</sup> Ezekhez a mérésekhez nagyon jó minőségű (nagy szabad úthosszal rendelkező) kétdimenziós elektrongáz rendszerek kellettek (epitaxiálisan növesztett GaAs/AlGaAs 2DEG + delta dópolás + nagyon alacsony hőmérséklet), és ennek megfelelően az egész számú kvantált Hall-platók sokkal ''csúnyábbak'', kevésbé kiterjedtek mint Klaus von Klitzing IQHE mérései.<sup>[http://prl.aps.org/abstract/PRL/v45/i6/p494_1 1]</sup> | ||
</wlatex> | </wlatex> | ||
| − | + | ==Mach-Zehnder interferométer kvantált Hall-élállapotokkal== | |
| − | == Mach-Zehnder interferométer | + | |
<wlatex> | <wlatex> | ||
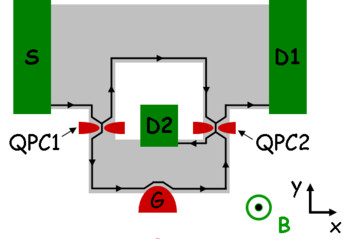
| + | A kvantált Hall-effektus - azon túl, hogy önmagában is érdekes jelenség - a nanofizika eszköztárát is fontos kísérleti technikával bővítette. Az kvantált Hall-élállapotok a visszaszórás hiánya miatt kifejezetten jól használhatók arra, hogy kvantum elektronikai kísérleteket végezzünk. Az alábbiakban a legalapvetőbb példát mutatjuk be: egy Mach Zehnder interferométer kialakítását élállapotokkal.<sup>[http://www.nature.com/nature/journal/v422/n6930/full/nature01503.html 7]</sup> | ||
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| + | |- | ||
| + | | align="center"|[[Fájl:QHall_interferometer.png|közép|350px]] | ||
| + | |- | ||
| + | | align="center"|18. ábra. ''Mach-Zehnder interferométer kvantált Hall-élállapotokkal'' | ||
| + | |} | ||
| − | + | Az optikában jól ismert Mach-Zehnder interferométer elvét elektronokkal a 18. ábrán szemléltetett módon, pár mikrométer méretű áramkörben lehet megvalósítani. Az elektronok egy 2DEG-ben, a szürkével jelzett tartományokban mozoghatnak. Nagy mágneses térrel az elektronokot élállapotokra kényszerítjük, a $B$ teret úgy állítjuk be, hogy csak egy Landau-szint legyen betöltve. Az S elektródára feszültséget kapcsolunk, a D1 elektródán a föld felé folyó áramot mérünk, a D2 elektródát leföldeljük. Az S elektródából induló élállapotban az elektronok eljutnak a QPC1 [[Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás#Vezetőképesség-kvantálás kvantum-pontkontaktusban|kvantum-pontkontaktushoz]], mely félig áteresztő tükérként van beállítva, azaz a nyaláb felét visszaveri, a másik felét átengedi ($\mathcal{T}=0.5$). A két parciális elektronhullám a QPC2 kvantum-pontkontaktusnál találkozik, mely mindkét nyalábot $\mathcal{T}=0.5$ valószínűséggel a D1 elektróda felé haladó élállapotba szórja, így a D1-nél mért áramban láthatjuk a két nyaláb közti interferenciát. A két nyaláb közötti fázisviszony kétféleképpen is hangolható: egyrészt a G kapuelektródára helyezett feszültséggel hangolhatjuk az alsó ágon haladó elektronok trajektóriájának hosszát, másrészt a mágneses tér enyhe változtatásával hangolhatjuk a két nyaláb közti [[Interferencia_és_dekoherencia_nanoszerkezetekben#Aharonov-Bohm_gyűrű|Aharonov-Bohm fázisból]] adódó fáziskülönbséget. Mind a G-re adott feszültség, mind a mágneses tér változtatásával közel 100%-os kontrasztú oszcilláció látható a D1 elektróda áramában.<sup>[http://www.nature.com/nature/journal/v422/n6930/full/nature01503.html 7]</sup> | |
| + | </wlatex> | ||
| − | + | ==Hivatkozások== | |
| − | + | ||
| − | + | ===Fent hivatkozott szakcikkek=== | |
| − | [[ | + | [1] [http://prl.aps.org/abstract/PRL/v45/i6/p494_1 K. v. Klitzing, G. Dorda, M. Pepper: ''New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance'', '''Phys. Rev. Lett. 45''' p494–497 (1980)] |
| − | + | ||
| − | + | [2] [http://prl.aps.org/abstract/PRL/v48/i22/p1559_1 D. C. Tsui, H. L. Stormer, A. C. Gossard: ''Two-Dimensional Magnetotransport in the Extreme Quantum Limit'', '''Phys. Rev. Lett. 48''' p1559–1562 (1982)] | |
| − | + | [3] [http://rmp.aps.org/abstract/RMP/v71/i4/p875_1 Horst L. Stormer: ''Nobel Lecture: The fractional quantum Hall effect'', '''Rev. Mod. Phys. 71''' p875–889 (1999)] | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | [4] [http://prl.aps.org/abstract/PRL/v50/i18/p1395_1 R. B. Laughlin: ''Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations'', '''Phys. Rev. Lett. 50''' p1395–1398 (1983)] | ||
| + | [5] [http://www.nature.com/nature/journal/v438/n7065/full/nature04233.html K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos, A. A. Firsov: ''Two-dimensional gas of massless Dirac fermions in graphene'', '''Nature 438''' p197-200 (2005)] | ||
| − | + | [6] [http://www.sciencemag.org/content/315/5817/1379.abstract K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim, A. K. Geim: ''Room-Temperature Quantum Hall Effect in Graphene'', '''Science 315''' p. 1379 (2007)] | |
| − | + | [7] [http://www.nature.com/nature/journal/v422/n6930/full/nature01503.html Yang Ji, Yunchul Chung, D. Sprinzak, M. Heiblum, D. Mahalu, Hadas Shtrikman: ''An electronic Mach–Zehnder interferometer'', '''Nature 422''' p415-418 (2003)] | |
| − | [ | + | ===Ajánlott könyvek és összefoglaló cikkek=== |
| − | + | *[http://books.google.hu/books/about/Electronic_Transport_in_Mesoscopic_Syste.html?id=28BC-ofEhvUC&redir_esc=y S. Datta: ''Electronic Transport in Mesoscopic Systems'', Cambridge University Press (1997)] | |
| + | *[http://books.google.hu/books/about/Semiconductor_Nanostructures.html?id=qD6623gfAZgC&redir_esc=y Thomas Ihn: ''Semiconducting nanosctructures'', OUP Oxford (2010)] | ||
| + | *[http://books.google.hu/books?id=YNr4OcCExUcC&printsec=frontcover&dq=Nazarov+quantum+transport&hl=hu&sa=X&ei=2SzZUfGCMYna4ASDq4DQBQ&ved=0CDIQ6AEwAA Yuli V. Nazarov, Yaroslav M. Blanter: ''Quantum Transport: Introduction to Nanoscience'', Cambridge University Press (2009)] | ||
| − | + | ===Ajánlott kurzusok=== | |
| − | + | *[[Új kísérletek a nanofizikában|''Új kísérletek a nanofizikában'', Halbritter András és Csonka Szabolcs, BME Fizika Tanszék]] | |
| − | + | *[[Transzport komplex nanoszerkezetekben|''Transzport komplex nanoszerkezetekben'', Halbritter András, Csonka Szabolcs, Csontos Miklós, Makk Péter, BME Fizika Tanszék]] | |
| + | *[[Alkalmazott szilárdtestfizika|''Alkalmazott szilárdtestfizika'', Mihály György, BME Fizika Tanszék]] | ||
| + | *[[Fizika 3 - Villamosmérnöki mesterszak|''Fizika 3'', Mihály György, BME Fizika Tanszék (mérnök hallgatóknak)]] | ||
| + | *[http://www.phy.bme.hu/~zarand/mezoszkopia.html ''Mezoszkopikus rendszerek fizikája'', Zaránd Gergely, BME Elméleti Fizika Tanszék] | ||
| + | *''Mezoszkopikus rendszerek fizikája'', Cserti József, ELTE Komplex Rendszerek Fizikája Tanszék | ||
A lap jelenlegi, 2013. július 11., 16:17-kori változata
Klasszikus Hall-effektus
A Hall-effektust 1879-ben Edwin Hall fedezte fel. A jelenség lényege, hogy ha egy síkszerű elektromos vezetőben a síkra merőleges mágneses tér jelenlétében áram folyik, akkor a vezető két oldala között az elektronokra ható Lorentz-erő miatt feszültség jelenik meg.
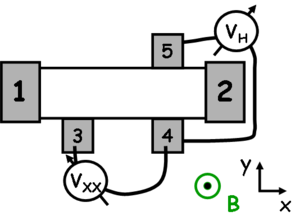
| 1. ábra. Hall-jelenség méréséhez használt elrendezés |
A Hall-jelenséget általában az 1. ábrán bemutatott Hall-elrendezésben szokták mérni. Az x irányú  áram az 1. és 2. kontaktus között folyik. Ha a mérést zérus mágneses térben végezzük, akkor a 4. és 5. kontaktus között (y irányban) nem mérünk feszültséget. A 3. és 4. kontaktus között mért
áram az 1. és 2. kontaktus között folyik. Ha a mérést zérus mágneses térben végezzük, akkor a 4. és 5. kontaktus között (y irányban) nem mérünk feszültséget. A 3. és 4. kontaktus között mért 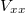 longitudinális feszültség és az áram arányából pedig a minta négypont ellenállását kapjuk meg.
A minta síkjára merőleges (z irányú) mágneses teret kapcsolva a 4. és 5. kontaktus között
longitudinális feszültség és az áram arányából pedig a minta négypont ellenállását kapjuk meg.
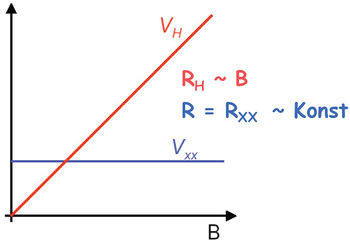
A minta síkjára merőleges (z irányú) mágneses teret kapcsolva a 4. és 5. kontaktus között 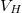 Hall-feszültség jelenik meg, melynek az értéke a mágneses tér nagyságával lineárisan változik (2. ábra, piros görbe). A 3. és 4. kontaktus között (kismértékű mágneses ellenállástól eltekintve) továbbra is a zérus térben tapasztalt longitudinális ellenállást mérjük (2. ábra, kék görbe).
Hall-feszültség jelenik meg, melynek az értéke a mágneses tér nagyságával lineárisan változik (2. ábra, piros görbe). A 3. és 4. kontaktus között (kismértékű mágneses ellenállástól eltekintve) továbbra is a zérus térben tapasztalt longitudinális ellenállást mérjük (2. ábra, kék görbe).
| 2. ábra. Hall-feszültség és longitudinális feszültség változása a mágneses térrel |
A Hall-jelenség jól leírható klasszikus, Drude-közelítésben. Az egyszerűség kedvéért számoljunk két dimenzióban. Az elektronok 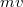 impulzusának idő szerinti deriváltját az elektronokra ható erők összegeként kapjuk meg. A
impulzusának idő szerinti deriváltját az elektronokra ható erők összegeként kapjuk meg. A 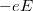 elektromos, illetve
elektromos, illetve 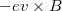 Lorentz erő mellett figyelembe vesszük azt is, hogy a a kristályban történő szóródások következtében az elektronok átlagosan
Lorentz erő mellett figyelembe vesszük azt is, hogy a a kristályban történő szóródások következtében az elektronok átlagosan 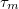 momentumrelaxációs idő alatt elveszítik impulzusukat:
momentumrelaxációs idő alatt elveszítik impulzusukat:
![\[m \frac{dv}{dt}=-eE-ev \times B - m \frac{v}{\tau_m}.\]](/images/math/a/4/0/a40d7310b8c331638a3c505446d0b0ac.png)
A sebesség helyett vezessük be a 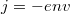 áramsűrűséget, ahol
áramsűrűséget, ahol  az elektronok (kétdimenziós) sűrűsége.
Az egyenletet átrendezve az alábbi mátrixegyenletet kapjuk az elektromos tér és az áramsűrűség komponensei között:
az elektronok (kétdimenziós) sűrűsége.
Az egyenletet átrendezve az alábbi mátrixegyenletet kapjuk az elektromos tér és az áramsűrűség komponensei között:
![\[\left( \begin{array}{c} E_x \\ E_y \end{array} \right) = \left( \begin{array}{cc} m/e^2 n \tau_m & B/e n \\ -B/e n & m/e^2 n \tau_m \end{array} \right) \left( \begin{array}{c} j_x \\ j_y \end{array} \right) = \left( \begin{array}{cc} \rho_{xx} & \rho_{xy} \\ \rho_{yx} & \rho_{yy} \end{array} \right) \left( \begin{array}{c} j_x \\ j_y \end{array} \right).\]](/images/math/a/f/f/affb8c8691fb45b35bac75ddd96f23ca.png)
Az áramot x irányba folyatva és x irányú feszültséget mérve a minta longitudinális ellenállását a 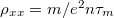 fajlagos ellenállásból kaphatjuk meg a geometriai faktorokkal történő skálázás után.
fajlagos ellenállásból kaphatjuk meg a geometriai faktorokkal történő skálázás után.
A fenti számolásból jól látszik, hogy véges mágneses térben x irányú áram esetén y irányú feszültség is megjelenik. A Hall-ellenállást a 4. és 5. kontaktusok között megjelenő 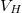 Hall-feszültség és az
Hall-feszültség és az  áram hányadosaként definiáljuk. Két dimenzióban ez megegyezik az y irányú elektromos tér és az x irányú áramsűrűség arányával:
áram hányadosaként definiáljuk. Két dimenzióban ez megegyezik az y irányú elektromos tér és az x irányú áramsűrűség arányával:
![\[R_H=\frac{V_H}{I}=\frac{E_y}{j_x}=\rho_{yx}=-\frac{B}{e n}.\]](/images/math/2/0/8/20880a9554882e5cebff4b0f5b2ac003.png)
Egyszerű számolásunkból jól látszik, hogy a Hall-ellenállás a  mágneses térrel egyenesen arányos, és ezen kívül csak az elektronok sűrűségétől függ, azaz az
mágneses térrel egyenesen arányos, és ezen kívül csak az elektronok sűrűségétől függ, azaz az 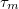 relaxációs idő a longitudinális ellenállástól eltérően a Hall-ellenállásban nem jelenik meg. Ennek köszönhetően a Hall-ellenállás mérése általánosan bevett módszer félvezetők elektronsűrűségének meghatározására. Érdemes megjegyezni, hogy
relaxációs idő a longitudinális ellenállástól eltérően a Hall-ellenállásban nem jelenik meg. Ennek köszönhetően a Hall-ellenállás mérése általánosan bevett módszer félvezetők elektronsűrűségének meghatározására. Érdemes megjegyezni, hogy  -típusú félvezetőkben, azaz amikor az áramot nem elektronok, hanem lyukak vezetik, a Hall-ellenállás előjelet vált. A Hall-jelenséget - amellett hogy a szilárdtestfizika alapvető mérési módszerei közé tartozik - a hétköznapokban is gyakran használjuk különböző elektronikai eszközökben elhelyezett mágneses tér szenzorok formájában.
-típusú félvezetőkben, azaz amikor az áramot nem elektronok, hanem lyukak vezetik, a Hall-ellenállás előjelet vált. A Hall-jelenséget - amellett hogy a szilárdtestfizika alapvető mérési módszerei közé tartozik - a hétköznapokban is gyakran használjuk különböző elektronikai eszközökben elhelyezett mágneses tér szenzorok formájában.
Hall-jelenséget elsősorban félvezetőkben szoktak tanulmányozni, hiszen az alacsony elektronsűrűség miatt a Hall-ellenállás viszonylag könnyen mérhető. Fémekben a nagy elektronsűrűség miatt a Hall-ellenállás értéke sokkal kisebb, de precíziós műszerekkel fémekben is vizsgálható a Hall-jelenség. Mindezekről a fizikushallgatók maguk is meggyőződhetnek a Hall-effektus c. hallgatói mérés során.
Kvantált Hall-effektus
Klaus von Klitzing meglepő felfedezése
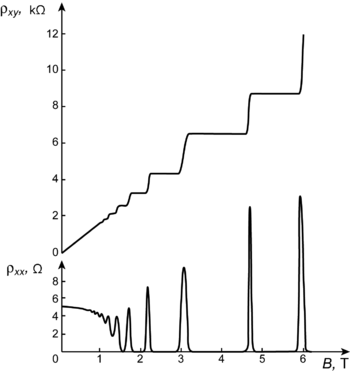
A Hall-jelenséget megfelelően nagy tisztaságú kétdimenziós elektrongázban (2DEG) és elegendően nagy mágneses térben vizsgálva nagyon meglepő viselkedést tapasztalunk. A Hall-ellenállás a lineáris térfüggés helyett lépcsőszerűen változik, a longitudinális ellenállás pedig zérus értéket vesz fel (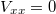 ) azokban a mágneses tér tartományokban, ahol a Hall-ellenállás vízszintes platót mutat (lásd 3. ábra).
) azokban a mágneses tér tartományokban, ahol a Hall-ellenállás vízszintes platót mutat (lásd 3. ábra).
| 3. ábra. Kvantált Hall-jelenség, forrás: Wikipedia |
A kvantált Hall-ellenállás értékeket egy univerzális állandó és egy egész szám hányadosaként kapjuk meg:
![\[R_H=\frac{h}{e^2 n}, \;\;\;n=0,1,2,\dots,\]](/images/math/9/8/2/98210ceb9358c0a152f4f1b27ddc3485.png)
ami a spindegeneráció miatti 2-es szorzótól eltekintve a vezetőképesség kvantálás képletének felel meg.
A tapasztalatok szerint a kvantált 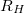 értékek függetlenek a minta alakjától, méretétől, anyagától, és
értékek függetlenek a minta alakjától, méretétől, anyagától, és 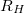 kísérletileg meghatározott értékei akár
kísérletileg meghatározott értékei akár 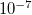 pontossággal leírhatók a fenti egyszerű képlettel, azaz a kvantált Hall-platók ellenállás-standardként is jól használhatók.
pontossággal leírhatók a fenti egyszerű képlettel, azaz a kvantált Hall-platók ellenállás-standardként is jól használhatók.
A kvantált Hall-jelenséget Klaus von Klitzing fedezte fel 1980-ban.1 Pár évvel később (1985-ben) felfedezését Nobel-díjjal jutalmazták.
A következő Nobel-díj: tört számú kvantált Hall-effektus
A kvantált Hall-jelenség felfedezése óriási érdeklődést váltott ki, és nem kellett sokat várni újabb meglepő kísérleti eredményekre. Daniel Tsui és Horst Störmer kísérletei 1982-ben megmutatták,2,3 hogy még tisztább kétdimenziós elektrongázban és még nagyobb mágneses térben a Hall-ellenállás
![\[R_H=\frac{h}{e^2 \nu},\;\;\; \nu=\frac{p}{q}, \;\;\; p,q=0,1,2,\dots\]](/images/math/2/c/8/2c80ed0473db25bb0c2e968af88c9c06.png)
értékeket vehet fel, ahol  már nem egész szám, hanem bizonyos egész számok hányadosa. A Hall-platók tartományában
a longitudinális feszültség továbbra is zérus,
már nem egész szám, hanem bizonyos egész számok hányadosa. A Hall-platók tartományában
a longitudinális feszültség továbbra is zérus, 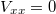 .
.
A későbbiekben látni fogjuk, hogy Klaus von Klitzing felfedezése, az egész számú kvantált Hall-effektus (IQHE, integer quantum Hall effect) egy viszonylag egyszerű modellel magyarázható, melyben az elektronok kölcsönhatását nem kell figyelembe venni. Ezzel szemben Tsui és Störmer méréseiben tapasztalt tört számú kvantált Hall-effektus (FQHE, fractional quantum Hall effect) magyarázatában az elektronok kölcsönhatása fontos szerepet kap, a jelenség úgynevezett kompozit fermion részecskék bevezetésével írható le, mely Robert Laughlin nevéhez kötődik.4
Tsui és Störmer kísérleti felfedezését, illetve Laughlin kísérletekre adott elméleti magyarázatát 1998-ban Nobel-díjjal jutalmazták.
A harmadik Nobel-díj: anomális kvantált Hall-effektus grafénban
A kvantált Hall-effektus egy közelmúltban kiosztott Nobel-díjjal kapcsolatban is előtérbe került. 2010-ben Andre Geim és Konstantin Novoselov grafénon, azaz egyetlen grafit síkon végzett kísérleteit jutalmazták Nobel-díjjal, melynek keretében alapvető jelentőségű volt a grafénon tapasztalható anomális kvantált Hall-jelenség megmutatása.5 Grafénon a Hall-ellenállás az elektrosztatikus potenciáltól függően egyaránt lehet pozitív és negatív, a kvantált értékek pedig
![\[R_H=\pm\frac{h}{e^2}\frac{1}{4(m+1/2)}, \;\;\; m=0,1,2,\dots \]](/images/math/b/a/6/ba64c8e52cbc399217766186f9a65046.png)
képlet segítségével írhatók le. A kétdimenziós elektrongáz rendszerekkel ellentétben grafénban a kvantált Hall-effektus szobahőmérsékleten is megfigyelhető.6
| 4. ábra. Anomális kvantált Hall-jelenség grafénban, forrás: Tóvári Endre diplomamunka, BME Fizika Tanszék, 2011. |
A továbbiakban az egész számú kvantált Hall-jelenség leírását szemléltetjük. A grafén fizikájáról egy külön fejezet keretében adunk leírást.
Kétdimenziós elektrongáz mágneses térben, Landau-nívók
Vizsgáljuk egy kétdimenziós szabad elektrongáz viselkedését a 2DEG síkjára merőleges mágneses térben!
| 5. ábra. Ciklotronpálya mágneses térbe helyezett 2DEG-ben |
Klasszikusan az elektronok ciklotronpályákon mozognak (5. ábra) 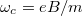 körfrekvenciával, azaz a körfrekvencia nem függ az elektronok sebességétől, csak a mágneses tértől.
A körpálya sugara klasszikusan tetszőleges lehet az elektron sebességétől függően, kvantummechanikai tárgyalásban viszont a körpálya sugarának (illetve a mozgás energiájának) kvantáltságát várjuk. A Bohr - Sommerfeld kvantálási feltétel alapján meghatározhatjuk a lehetséges legkisebb sugarat (ciklotronsugár):
körfrekvenciával, azaz a körfrekvencia nem függ az elektronok sebességétől, csak a mágneses tértől.
A körpálya sugara klasszikusan tetszőleges lehet az elektron sebességétől függően, kvantummechanikai tárgyalásban viszont a körpálya sugarának (illetve a mozgás energiájának) kvantáltságát várjuk. A Bohr - Sommerfeld kvantálási feltétel alapján meghatározhatjuk a lehetséges legkisebb sugarat (ciklotronsugár):
![\[2 \pi r_c = \lambda = \frac{2 \pi \hbar}{p} = \frac{2 \pi \hbar}{m \omega_c r} \;\; \Longrightarrow \;\; r_c=\sqrt{\frac{\hbar}{m\omega_c}}.\]](/images/math/6/6/f/66f1261a573a1cde84b323dcee029c7a.png)
A kvantummechanikai viselkedés részletesebb leírásához oldjuk meg a rendszer Schrödinger-egyenletét. A Hamilton-operátor:
![\[\hat{H}=\frac{1}{2}m(\hat{v}_x^2+\hat{v}_y^2),\]](/images/math/0/4/c/04c528a1e299169f635a16f257773bab.png)
ahol a sebességoperátor a 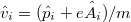 képlettel származtatható a kanonikus impulzus operátorból, illetve a vektorpotenciálból. A minta síkjára (x,y) merőleges (z irányú) B térnél
a vektorpotenciál az általánosság megszorítása nélkül vehető úgy, hogy csak x és y komponenssel rendelkezzen, azaz
képlettel származtatható a kanonikus impulzus operátorból, illetve a vektorpotenciálból. A minta síkjára (x,y) merőleges (z irányú) B térnél
a vektorpotenciál az általánosság megszorítása nélkül vehető úgy, hogy csak x és y komponenssel rendelkezzen, azaz 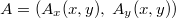 .
.
Számoljuk ki a sebességoperátor x és y komponensének a kommutátorát!
![\[[\hat{v}_x,\hat{v}_y]=\frac{1}{m^2}[\hat{p}_x+e\hat{A}_x,\;\hat{p}_y+e\hat{A}_y]=\frac{\hbar e}{i m^2}\left([\partial_x,A_y]+[A_x,\partial_y] \right)=\frac{\hbar e}{i m^2}\left(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)=\frac{\hbar e B}{i m^2},\]](/images/math/2/b/d/2bd4327b0894bd1f06a3771b988ffb71.png)
azaz:
![\[[\hat{v}_x,\hat{v}_y]=\frac{\alpha}{i},\;\;\;\alpha=\frac{\hbar \omega_c}{m}.\]](/images/math/a/6/0/a602195e6a8162ff96a8e478f8d0d4ab.png)
Vezessünk be új operátorokat: 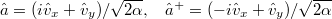 .
Az új operátorok segítségével a Hamilton operátor
.
Az új operátorok segítségével a Hamilton operátor
![\[\hat{H}=\hbar \omega_c \left(\hat{a}^+\hat{a}+\frac{1}{2}\right)=\frac{1}{2}\hbar \omega_c + \frac{\hbar \omega_c}{2 \alpha}(\hat{v}_x^2+\hat{v}_y^2-i\hat{v}_x\hat{v}_y+i\hat{v}_x\hat{v}_y)=\frac{1}{2}m(\hat{v}_x^2+\hat{v}_y^2)\]](/images/math/5/9/c/59cc717e76eb2820629c684fd6baa5c2.png)
formában írható fel, a két új operátor kommutátora pedig:
![\[[\hat{a},\hat{a}^+]=\frac{1}{2 \alpha}[i\hat{v}_x+\hat{v}_y, -i\hat{v}_x+\hat{v}_y]=1.\]](/images/math/7/a/a/7aada3231166cd64b2cf3ed14682e191.png)
Látszik, hogy az új operátorok segítségével az egydimenziós harmonikus oszcillátor problémájára vezettük vissza a Schrödinger egyenletet, így további számolás nélkül megállapíthatjuk, hogy a mágneses térben mozgó elektronok lehetséges energiái a harmonikus oszcillátorhoz hasonlóan kvantáltak:
![\[E=\hbar \omega_c \left( n+\frac{1}{2}\right).\]](/images/math/f/6/5/f6521c2748fdbeb33991a5bb430cb921.png)
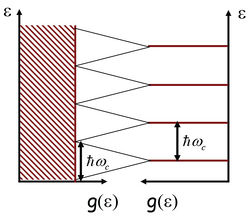
A kvantált energiaszinteket Landau-nívóknak hívjuk.
6. ábra. 2DEG állapotsűrűségének energiafüggése zérus  térben, illetve nagy mágneses térben kialakult Landau-nívók esetén térben, illetve nagy mágneses térben kialakult Landau-nívók esetén
|
Ahogy a 6. ábra mutatja, a mágneses tér bekapcsolása alapvetően megváltoztatja az elektronok állapotsűrűségének energia szerinti eloszlását. Mágneses tér nélkül az elektronok állapotsűrűsége konstans (energiafüggetlen), 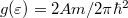 . Nagy mágneses térben csak a kvantált Landau-szinteken helyezkedhetnek el elektronok, ezek a diszkrét energiaszintek viszont szükségszerűen sokszorosan degenerált állapotok. D-szeres degenerációt feltételezve az állapotsűrűség:
. Nagy mágneses térben csak a kvantált Landau-szinteken helyezkedhetnek el elektronok, ezek a diszkrét energiaszintek viszont szükségszerűen sokszorosan degenerált állapotok. D-szeres degenerációt feltételezve az állapotsűrűség: 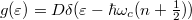 . Mivel az elektronok száma a mágneses tér bekapcsolásával nem változik, így feltételezhető hogy egy Landau-szinten levő állapotok zérus térben
. Mivel az elektronok száma a mágneses tér bekapcsolásával nem változik, így feltételezhető hogy egy Landau-szinten levő állapotok zérus térben 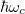 szélességű energiatartományban helyezkednek el. Így egy Landau-szint degenerációja (a spin szerinti degenerációt is figyelembe véve):
szélességű energiatartományban helyezkednek el. Így egy Landau-szint degenerációja (a spin szerinti degenerációt is figyelembe véve):
![\[D=\hbar \omega_c 2 \frac{A m}{2 \pi \hbar^2}=\frac{2 e B A}{h} \;\; \Longrightarrow \;\; D=\frac{2 \Phi}{\Phi_0},\]](/images/math/7/c/a/7ca63f5401af4876b36b9ff370f71497.png)
ahol 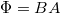 a teljes fluxus
a teljes fluxus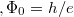 pedig a fluxuskvantum. Egy teljesen betöltött Landau-szinten a fentiek alapján az elektronsűrűség:
pedig a fluxuskvantum. Egy teljesen betöltött Landau-szinten a fentiek alapján az elektronsűrűség: 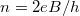 .
.
A Landau-szintek magasfokú degenerációja mögött szemléletesen az áll, hogy egy ciklotronsugárnak megfelelő tipikus kiterjedésű elektronállapotot a minta  felületén összesen
felületén összesen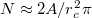 különböző helyre tehetünk le (a spin szerinti degenerációt is figyelembe véve). Ez alapján kis átalakítással
különböző helyre tehetünk le (a spin szerinti degenerációt is figyelembe véve). Ez alapján kis átalakítással 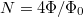 adódik, azaz naiv számolásunkkal egy egy kettes szorzó eltéréssel visszakaptuk a Landau-nívók fent kiszámolt degenerációs fokát.
adódik, azaz naiv számolásunkkal egy egy kettes szorzó eltéréssel visszakaptuk a Landau-nívók fent kiszámolt degenerációs fokát.
A Landau-szintek kialakulásának fontos feltétele, hogy az elektronok a ciklotronpályát két ütközés között sokszor bejárják, azaz a cikotronpálya periódusideje a momentumrelaxációs időnél sokkal kisebb legyen, 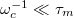 . Ez akkor teljesül, ha
. Ez akkor teljesül, ha 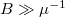 , ahol
, ahol 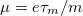 az elektronok mobilitása a 2DEG-ben, azaz Landau-szinteket csak kellően tiszta mintában és kellően nagy mágneses térben látunk. További fontos feltétel, hogy Landau-szintek közötti energiakülönbség nagyobb legyen a hőmérsékletnél és a feszültségnél,
az elektronok mobilitása a 2DEG-ben, azaz Landau-szinteket csak kellően tiszta mintában és kellően nagy mágneses térben látunk. További fontos feltétel, hogy Landau-szintek közötti energiakülönbség nagyobb legyen a hőmérsékletnél és a feszültségnél, 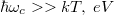 .
.
Ciklotronpályák középpontjának mozgása
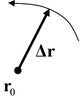
Nagy mágneses térben azt várjuk, hogy az elektronok egy középponti  kordináta körül nagyon kis,
kordináta körül nagyon kis, 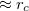 sugarú ciklotronmozgást végeznek. Klasszikusan az elektron éppen aktuális
sugarú ciklotronmozgást végeznek. Klasszikusan az elektron éppen aktuális  helyzetét
helyzetét
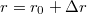 alakban írhatjuk, ahol
alakban írhatjuk, ahol 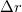 a középpontból az aktuális ponta mutató vektor (7. ábra).
a középpontból az aktuális ponta mutató vektor (7. ábra).
| 7. ábra. |
Körmozgás esetén az elektront körpályán tartó centripetális erőt 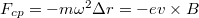 alakban írhatjuk, ami jelen esetben értelemszerűen a Lorentz-erővel egyezik meg. Ez alapján a körpálya középpontját formálisan
alakban írhatjuk, ami jelen esetben értelemszerűen a Lorentz-erővel egyezik meg. Ez alapján a körpálya középpontját formálisan
![\[r_0 = r-\frac{e}{m \omega^2} v \times B\]](/images/math/c/2/d/c2d6543730e1c3734b301f0156562cf9.png)
alakban írhatjuk.
Játsszunk el a gondolattal, hogy az 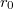 koordinátát kvantummechanikai tartalommal ruházzuk fel a ciklotronpályák középpontjának helyét leíró operátorként! Komponensenként kifejtve:
koordinátát kvantummechanikai tartalommal ruházzuk fel a ciklotronpályák középpontjának helyét leíró operátorként! Komponensenként kifejtve:
![\[\hat{x}_0=\hat{x}-\frac{\hat{v}_y}{\omega_c},\;\; \hat{y}_0=\hat{y}-\frac{\hat{v}_x}{\omega_c}.\]](/images/math/a/2/a/a2a8559ef48c3d1672aa9d7f896105ae.png)
Vizsgáljuk meg, hogy a középponti koordináta várható értéke hogyan változik az idő függvényében:
![\[\frac{d}{d t}\langle\hat{x}_0\rangle = \frac{i}{\hbar} \langle[\hat{H},\hat{x}]\rangle - \frac{i m}{2\hbar\omega_c} \langle[\hat{v}^2_x+\hat{v}^2_y,\hat{v}_y]\rangle = \hat{v}_x - \frac{i m}{2\hbar\omega_c} \langle[\hat{v}^2_x,\hat{v}_y]\rangle = 0,\]](/images/math/d/e/d/deda0c25fb1f424e062d7d7480cf74a5.png)
![\[\frac{d}{d t}\langle\hat{y}_0\rangle = 0,\]](/images/math/6/1/d/61d29b01f81f90dd06e86a2dfc324837.png)
azaz a várakozásoknak megfelelően a ciklotronpályák középpontja nem mozog.
Érdemes kiszámolni a középponti koordináták operátorainak kommutátorát is:
![\[[\hat{y}_0,\hat{x}_0] = \left[\hat{y} + \frac{\hat{v}_x}{\omega_c}, \hat{x} - \frac{\hat{v}_y}{\omega_c} \right] = -\left[\hat{y}, \frac{\hat{p}_y}{m \omega_c} \right] + \left[\frac{\hat{p}_x}{m \omega_c}, \hat{x}\right] - \left[ \frac{\hat{v}_x}{\omega_c}, \frac{\hat{v}_y}{\omega_c} \right] = \frac{\hbar}{i m \omega_c} = \frac{r_c^2}{i}.\]](/images/math/c/5/3/c53a60723b4b27cfcc165f0643c8b465.png)
Tetszőleges két fizikai mennyiség operátorára fennáll az általános Heisenberg-féle határozatlansági reláció, azaz:
![\[\Delta A \cdot \Delta B \geq \frac{1}{2}|\langle[ \hat{A}, \hat{B} ]\rangle|.\]](/images/math/7/b/c/7bc1dd0c823a339b9b1a68dabaccd8b6.png)
Ezt az összefüggést a középponti koordináta két komponensének operátorára vonatkoztatva
![\[\Delta x_0 \cdot \Delta y_0 \geq \frac{r^2_c}{2}\]](/images/math/5/5/3/553157cd43fd417eeb10d946dbecc99e.png)
adódik, azaz a ciklotronpálya középpontjának x és y írányú kvantummechanikai bizonytalanságát összeszorozva pont az 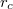 ciklotronsugár négyzete köszön vissza, egy elektron legalább
ciklotronsugár négyzete köszön vissza, egy elektron legalább 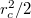 helyet foglal. Ez alapján körszimmetrikus hullámfüggvényt feltételezve a ciklotron pályák x és y irányban is
helyet foglal. Ez alapján körszimmetrikus hullámfüggvényt feltételezve a ciklotron pályák x és y irányban is 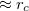 kiterjedésűek.
kiterjedésűek.
Bezáró és random potenciál
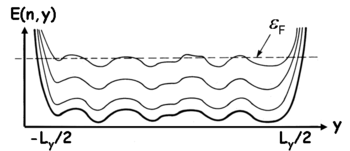
Az eddigiekben a Schrödinger-egyenletben csak az elektronok kinetikus energiáját vettük figyelembe. Egy valós, véges méretű mintában a minta széleinél jelentkező bezáró potenciált, illetve a felületi töltések és szennyezők hatásaként a minta belsejében jelentkező potenciálfluktuációkat is figyelembe kell venni (8. ábra):
![\[\hat{H} = \hat{H}_0 + \hat{U} = \hat{H}_0 + \hat{U}_\mathrm{bezaro} + \hat{U}_\mathrm{flukt}.\]](/images/math/3/9/c/39c1d2fa81b6b53685b74add091624f4.png)
| 8. ábra. Landau-szintek módosulása a a minta szélénél a bezáró potenciál, illetve a minta belsejében jelentkező fluktuáló potenciál miatt |
Az  potenciált perturbációként kezelve, és feltételezve hogy
potenciált perturbációként kezelve, és feltételezve hogy  lassan változik a hullámfüggvény tipikus kiterjedéséhez,
lassan változik a hullámfüggvény tipikus kiterjedéséhez, 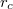 -hez képest (azaz elegendően nagy a mágneses tér) az energiária egyszerűen
-hez képest (azaz elegendően nagy a mágneses tér) az energiária egyszerűen
![\[E=\hbar \omega_c (n+\frac{1}{2}) + \langle \Psi | U | \Psi \rangle \approx E=\hbar \omega_c(n+\frac{1}{2}) + U(x_0,y_0)\]](/images/math/d/a/5/da5f08672e4054bb95629d9a327b26c1.png)
adódik, azaz a kvantált Landau-szintek energiáit a hullámfüggvény középpontjánál vett potenciál értékével korrigáljuk.
Véges  esetén az elektronok mozgását úgy képzeljük el, hogy a gyors (
esetén az elektronok mozgását úgy képzeljük el, hogy a gyors (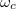 körfrekvenciájú) és kis (
körfrekvenciájú) és kis (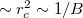 ) területre koncentrált ciklotronmozgás mellett a ciklotronpályák középpontjának koordinátái a potenciál hatására haladó mozgást végeznek. Írjuk fel a mozgásegyenletet
) területre koncentrált ciklotronmozgás mellett a ciklotronpályák középpontjának koordinátái a potenciál hatására haladó mozgást végeznek. Írjuk fel a mozgásegyenletet 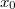 és
és 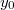 -ra:
-ra:
![\[\frac{d}{d t}\langle\hat{x}_0\rangle = \frac{i}{\hbar} \langle[\hat{H},\hat{x}_0]\rangle = \frac{i}{\hbar} \langle[\hat{H}_0,\hat{x}_0]\rangle + \frac{i}{\hbar} \langle[\hat{U},\hat{x}_0]\rangle = - \frac{i}{\hbar m \omega_c} \langle[\hat{U},\hat{p}_y]\rangle = - \frac{1}{m \omega_c} \langle[U,\partial_x]\rangle = \frac{1}{e B} \left< \frac{\partial U}{\partial y}\right> \approx \frac{1}{e B} \frac{\partial U(x_0,y_0)}{\partial y_0},\]](/images/math/f/3/5/f3569d783edabad9f2f2c9776532d77b.png)
ahol megintcsak feltételeztük, hogy a hullámfüggvény kiterjedése kicsi  változásának skáláján. Hasonlóan:
változásának skáláján. Hasonlóan:
![\[\frac{d}{d t}\left< \hat{y}_0\right> = -\frac{1}{e B} \left< \frac{\partial U}{\partial x}\right> \approx -\frac{1}{e B} \frac{\partial U(x_0,y_0)}{\partial x_0}.\]](/images/math/7/a/c/7ac9a04be1f26b0870cddd26ee2dcc19.png)
A fentiek alapján számoljuk ki a potenciál változását a pálya mentén, azaz  idő szerinti teljes deriváltját:
idő szerinti teljes deriváltját:
![\[\frac{d U}{d t}=\frac{\partial U}{\partial x_0} \cdot \dot{x}_0 + \frac{\partial U}{\partial y_0} \cdot \dot{y}_0 = \frac{c}{e H} \left( \frac{\partial U}{\partial x_0} \frac{\partial U}{\partial y_0} - \frac{\partial U}{\partial y_0} \frac{\partial U}{\partial x_0} \right) = 0.\]](/images/math/7/f/1/7f1c676f027034ba47413a9fcb82bb38.png)
Számolásunk alapján a ciklotronpályák középpontja ekvipotenciális felületek mentén mozog!
Elektrontranszport egyetlen Landau-nívó esetén
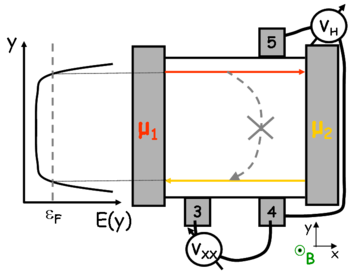
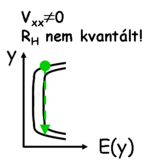
Tételezzünk fel olyan mágneses teret, melynél a Fermi-energia az első és második Landau-szint között helyezkedik el, azaz az első Landau-szint teljesen betöltött, a második pedig betöltetlen (lásd 9. ábra, bal oldal). Ebben az esetben a Fermi-energiánál
a minta széleinél találunk csak állapotokat a bezáró potenciálnak köszönhetően, a minta belsejében egy tiltott sávot tapasztalunk a Fermi-energia és a betöltött Landau-szint között. Ebben az esetben elektrontranszport csak a minta szélei mentén megengedett, ahol az elektronok energiája metszi a Fermi-energiát. Mivel a minta két szélét elválasztó makroszkopikus méretű tartományban az elektrontranszport nem megengedett, így a minta két széle között nem történhet átszóródás (9. ábra, jobb oldal).
| 9. ábra. A tömbi Landau-szintektől távol áram csak az élállapotok mentén folyhat, a két él között nincs átszóródás |
Vizsgáljuk meg a minta felső széle mentén az elektronpályák középpontjának mozgását. Korábban kiszámolt képletünk alapján:
![\[\dot{x}_0=\frac{1}{e B} \frac{\partial U_\mathrm{bezaro}}{\partial y_0} > 0,\]](/images/math/4/a/e/4aeab7cc082c07a636f6e28fea7c947f.png)
azaz, mivel a felső élnél a bezáró potenciál y szerinti deriváltja pozitív, így az elektronok pozitív x irányban mozognak. Y irányban a bezáró potenciál nem változik, így az elektronok középpontjának y irányú sebessége zérus. Hasonlóan megállapítható, hogy a minta alsó szélénél az elektronok negatív x irányú mozgást végeznek.
Az előbbi megállapítás önmagában elég ahhoz, hogy a kvantált Hall-effektus egyik meglepő tulajdonságát megértsük. Mivel a felső él mentén csak pozitív irányban haladhatnak az elektronok, és az alsó és felső élállapotok között nem megengedett az átszórás, így a felső él mentén mozgó elektronok mind a baloldali elektródából származnak, azaz kémiai potenciáljuk 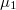 . Hasonlóképpen az alsó él mentén mozgó elektronok mind a jobb oldali elketródából származnak, azaz
. Hasonlóképpen az alsó él mentén mozgó elektronok mind a jobb oldali elketródából származnak, azaz 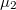 kémiai potenciállal rendelkeznek (9. ábra, jobb oldal). Így érthető, hogy egy él mentén mért hosszirányú feszültség zérus, a két él között pedig a két elektróda kémiai potenciál különbségének megfelelő Hall-feszültség jelentkezik,
kémiai potenciállal rendelkeznek (9. ábra, jobb oldal). Így érthető, hogy egy él mentén mért hosszirányú feszültség zérus, a két él között pedig a két elektróda kémiai potenciál különbségének megfelelő Hall-feszültség jelentkezik,
![\[V_{xx}=0,\;\; V_H=(\mu_1-\mu_2)/e.\]](/images/math/3/4/9/349170341559ea0ff96bfbb28a3945c8.png)
A Hall-ellenállás meghatározásához az élállapotokon keresztül folyó áramot is meg kell határoznunk. Először számoljuk ki, hogy egy élállapot 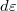 szélességű energiatartománya mekkora járulékot ad az áramhoz.
A
szélességű energiatartománya mekkora járulékot ad az áramhoz.
A 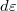 energiatartomány
energiatartomány 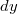 szélességű térbeli tartománynak felel meg az él mentén, ahol
szélességű térbeli tartománynak felel meg az él mentén, ahol 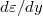 a potenciál y szerinti deriváltja (10. ábra).
a potenciál y szerinti deriváltja (10. ábra).
| 10. ábra. |
Korábbi számolásaink alapján az elektronok sebessége 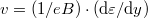 , az elektronsűrűség pedig
, az elektronsűrűség pedig 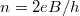 , így az áramra
, így az áramra
![\[I=j \mathrm{d} y = n e v \mathrm{d} y = \frac{2 e}{h} \mathrm{d} \varepsilon\]](/images/math/3/a/a/3aafd214827f4dfdb93fcdbad99ca4a4.png)
adódik.
| 11. ábra. |
Mivel 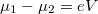 esetén a felső él mentén
esetén a felső él mentén 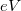 -vel magasabb energiáig vannak betöltve az állapotok mint az alsó él mentén (11. ábra), így a mintán folyó teljes áram
-vel magasabb energiáig vannak betöltve az állapotok mint az alsó él mentén (11. ábra), így a mintán folyó teljes áram
![\[I=\frac{2 e}{h} e V.\]](/images/math/4/9/9/499eee5d0128a9c6ec6f93e59c0aee99.png)
Ennek megfelelően a Hall-ellenállás illetve a Hall-vezetőképesség:
![\[R_H=\frac{V_H}{I}=\frac{h}{2 e^2}, \ \ \ G_H=\frac{I}{V_H}=\frac{2 e^2}{h}\]](/images/math/f/f/7/ff7c9f71dda1342c1cc8529198bb826b.png)
A Hall-vezetőképességre kapott eredmény megegyezik egy egycsatornás tökéletes kvantumvezeték ellenállásával, azaz a vezetőképesség kvantummal. Fontos azonban megemlíteni, hogy nanovezetékekben a vezetőképesség-kvantálás csak a hullámhosszal összemérhető méreteknél és simán változó (visszaszórásmentes) potenciálban figyelhető meg, addig a kvantált Hall-effektus a jobbra és balra haladó állapotok térbeli szeparációjának köszönhetően egy makroszkopikus mintán megfigyelhető jelenség.
Több Landau-nívó, Zeeman-felhasadás
A korábbiakban a Landau-nívókat spin szerint degeneráltnak tekintettük. Természetesen mágneses térben az energiák spin szerinti Zeeman-felhasadását is figyelembe kell venni:
![\[E=\hbar \omega_c \left(n+\frac{1}{2} \right) +U_\mathrm{bezaro} + g \mu_B B S_z,\]](/images/math/a/1/f/a1fbb9183a7ec0169d43c1b5d5668e32.png)
ahol 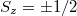 az elektronspin z irányú komponense.
az elektronspin z irányú komponense.
Félvezetőkben a kis effektív tömeg miatt tipikusan 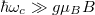 (
(![\setbox0\hbox{$\hbar \omega_c [K] \approx 20 B [T],\;\; g \mu_B B [K] \approx 0.3 \cdot B [T]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/a/e/d/aede3cb72dc611fb7781497ae0a0ddeb.png) ), de ha a
), de ha a  tér elegendően nagy akkor a Landau-szintek fel és le spinű elektronjai elkülönült energiaszinteket tudnak létrehozni, ezek a spinpolarizált Landau-szintek (12. ábra).
tér elegendően nagy akkor a Landau-szintek fel és le spinű elektronjai elkülönült energiaszinteket tudnak létrehozni, ezek a spinpolarizált Landau-szintek (12. ábra).
| 12. ábra. Spinpolarizált Landau-szintek |
Egyetlen teljesen betöltött spinpolarizált Landau-szint esetén a minta két szélén kialakuló élállapot értelemszerűen 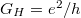 vezetőképességet ad, hiszen csak a spindegenerációból adódó kettes faktort kell elhagyni az állapotsűrűségből.
vezetőképességet ad, hiszen csak a spindegenerációból adódó kettes faktort kell elhagyni az állapotsűrűségből.
Ha a Fermi-energia alatt M db. spinpolarizált Landau-szint található, és a minta belsejében a Fermi-energia két Landau-szint közé esik, akkor a Hall-vezetőképesség:
![\[G_H=\frac{e^2}{h} M,\]](/images/math/9/b/2/9b2856acf63d749244f5b97051f0e262.png)
azaz visszakaptuk a kísérletekben megfigyelt értékeket. A mérések szerint 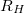 relatív pontossága akár
relatív pontossága akár 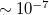 is lehet, ami a visszaszórás hiányának tökéletességét mutatja. Fontos megjegyezni, hogy a minta egyik oldalán különböző Landau-szintek közötti átszórás nem változtat a vezetőképességen, hiszen csak az számít, hogy egy adott élállapotban elinduló elektron - még ha át is szóródik másik élállapotba - biztosan nem jut vissza a kiinduló elektródába.
is lehet, ami a visszaszórás hiányának tökéletességét mutatja. Fontos megjegyezni, hogy a minta egyik oldalán különböző Landau-szintek közötti átszórás nem változtat a vezetőképességen, hiszen csak az számít, hogy egy adott élállapotban elinduló elektron - még ha át is szóródik másik élállapotba - biztosan nem jut vissza a kiinduló elektródába.
A jelenség megértését segíti a 13. ábrán bemutatott klasszikus kép is: az élek mentén hiába szóródik szennyezőkön egy elektron, az 1. elektródából induló elektron végül mindig a 2. elektródába érkezik!
| 13. ábra. Élállapotok klasszikus ciklotronpályákkal szemléltetve |
A Fermi-energia helyzete
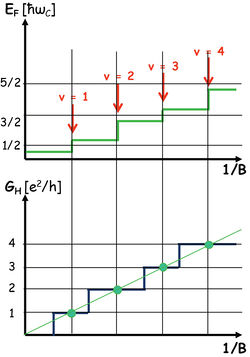
A fenti megfontolások alapján pontosan kijön a Hall-ellenállás kvantáltsága, azonban a számolások azon a feltételezésen alapulnak, hogy a Fermi-energia két Landau-szint közé esik, ami nem feltétlenül igaz. Vizsgáljuk meg pontosabban, hogy mikor is esik a Fermi-energia két Landau-szint közé!
14. ábra. Felső panel: a Fermi energia változása 1/B függvényében. Általában a Fermi energia valamelyik tömbi, spinpolarizált Landau-szintnél található (vízszintes platók), és csak nagyon szűk mágneses tér tartományokban kerül 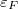 két Landau-szint közé. Az alsó panel azt szemlélteti, hogy a Hall-vezetőképesség kvantált értékeit csak azokban a diszkrét (zöld) pontokban várjuk, ahol két Landau-szint közé. Az alsó panel azt szemlélteti, hogy a Hall-vezetőképesség kvantált értékeit csak azokban a diszkrét (zöld) pontokban várjuk, ahol 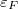 két Landau-szint között helyezkedik el. két Landau-szint között helyezkedik el.
|
1/B növelésével egymás után töltjük be a spinpolarizált Landau-szinteket. A Landau-szintek óriási degenerációja miatt a Fermi-energia szinte mindig az egyik Landau-szintre esik, kivéve amikor éppen egy teljesen betöltött és egy betöltetlen Landau-szint közötti élállapotokat töltünk fel. Az élállapotok száma azonban elhanyagolható a Landau-szintek belső állapotainak számához képest: egyszerű becslésként e két állapotszám úgy aránylik egymáshoz mint a minta makroszkopikus szélessége az élállapot nanométeres skálájú y irányú kiterjedéséhez. Ennek megfelelően csak nagyon szűk mágneses tér tartományokban várjuk, hogy a Fermi-energia két tömbi Landau-szint energiája között legyen (14. ábra, felső panel). Ha viszont a Fermi-energia egy tömbi Landau-szintnél helyezkedik el, akkor ezen a Landau-szinten keresztül már átszóródhatnak az elektronok a két él között (15. ábra), azaz a korábbi érvelésünk érvénytelen. Azaz azt a lehangoló eredményt kaptuk, hogy a Hall-vezetőképesség csak nagyon szűk, szinte pontszerű mágneses-tér tartományokban veszi fel a várt kvantált értékeket, ráadásul ezek a pontok jól illeszkednek a klasszikus Hall-vezetőképesség 1/B-vel lineárisan arányos változására (14. ábra alsó panel), azaz a kiterjedt Hall-platókra eddig nem kaptunk magyarázatot.
| 15. ábra. Ha a Fermi-energia egy tömbi Landau-szintnél található, akkor a két oldalon haladó élállapotok között az eletronok át tudnak szóródni a tömbi Landau-szinten keresztül |
Rendezetlenség szerepe
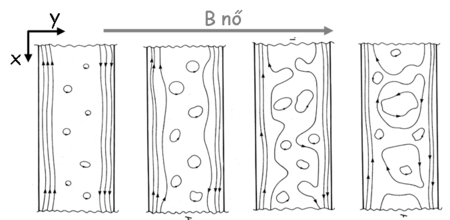
Az eddigi számolásokban csak az élállapotok kialakulásáért felelős bezáró potenciált vettük figyelembe. A kiterjedt kvantált Hall-platók megértéséhez a minta belsejében kialakuló fluktuáló potenciált is figyelembe kell venni. Tökéletlen minta (azaz véges fluktuáló potenciál) esetén a tömbi Landau-szintektől eltérő energiánál az elektronok nem csak az élállapot mentén mozoghatnak, hanem a minta belsejében a fluktuáló potenciál adott energiának megfelelő ekvipotenciális vonalai mentén is. Ha az energia kellőképpen eltér a tömbi Landau-szintektől, akkor az elektronok a fluktuáló potenciál hegyei vagy völgyei mentén kis kiterjedésű zárt pályákra kényszerülnek (16. ábra bal oldal), azaz a minta belsejében vannak a Landau-szintektől eltérő energiájú állapotok, de ezek lokalizált állapotok, a minta két széle közötti transzporthoz nem járulnak hozzá. A tömbi Landau-szinteknek megfelelő energiáknál az elektronok már találnak az ekvipotenciális vonalak mentén olyan trajektróriákat, melyek mentén átszóródhatnak a minta két széle között (16. ábra jobb oldal).
| 16. ábra. Elektronok mozgása ekvipotenciális felületek mentén |
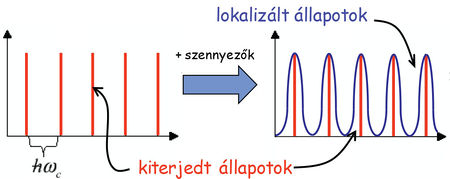
A fentiek gondolatmenet alapján megállapíthatjuk, hogy tökéletlen minta esetén a Landau-szintek körüli véges energiatartományban véges állapotsűrűséget tapasztalunk (17. ábra), azonban a Landau-szintektől távolabb ez a véges állapotsűrűség a tömbi tartomány potenciáljában lokalizált állapotoknak felel meg. Ennek megfelelően a Fermi-energia kiterjedt mágneses tér tartományokban eltér Landau-szintek energiájától, de ezeknél az energiáknál továbbra is igaz a két oldalon kialakuló élállapotok közötti átszórás tilalma, azaz valóban véges szélességű kvantált Hall-platókat várunk.
| 17. ábra. Szennyezők hatása az állapotsűrűségre: a Landau-szintek körüli szélesebb energiatartományban lokalizált elektronállapotok jelennek meg |
A fentiek alapján látjuk, hogy a rendezetlenségnek kettős szerepe van a kvantált Hall-jelenség szempontjából. Egyrészt túl nagy szennyező-koncentráció, melynél a szórások közötti átlagos idő összemérhető a ciklotronmozgás periódusidejével (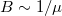 ) lerombolja a kvantált Hall-jelenséget. Másrészt ha a minta túl tökéletes, akkor szintén nem várunk kiterjedt kvantált Hall-platókat, azaz a minta tökéletlensége teszi lehetővé, hogy
) lerombolja a kvantált Hall-jelenséget. Másrészt ha a minta túl tökéletes, akkor szintén nem várunk kiterjedt kvantált Hall-platókat, azaz a minta tökéletlensége teszi lehetővé, hogy 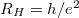 legyen a létező legpontosabb ellenállás standard. Ez utóbbi egyértelműen látszik a tört számú kvantált Hall-effektust bemutató kísérletekben.2,3 Ezekhez a mérésekhez nagyon jó minőségű (nagy szabad úthosszal rendelkező) kétdimenziós elektrongáz rendszerek kellettek (epitaxiálisan növesztett GaAs/AlGaAs 2DEG + delta dópolás + nagyon alacsony hőmérséklet), és ennek megfelelően az egész számú kvantált Hall-platók sokkal csúnyábbak, kevésbé kiterjedtek mint Klaus von Klitzing IQHE mérései.1
legyen a létező legpontosabb ellenállás standard. Ez utóbbi egyértelműen látszik a tört számú kvantált Hall-effektust bemutató kísérletekben.2,3 Ezekhez a mérésekhez nagyon jó minőségű (nagy szabad úthosszal rendelkező) kétdimenziós elektrongáz rendszerek kellettek (epitaxiálisan növesztett GaAs/AlGaAs 2DEG + delta dópolás + nagyon alacsony hőmérséklet), és ennek megfelelően az egész számú kvantált Hall-platók sokkal csúnyábbak, kevésbé kiterjedtek mint Klaus von Klitzing IQHE mérései.1
Mach-Zehnder interferométer kvantált Hall-élállapotokkal
A kvantált Hall-effektus - azon túl, hogy önmagában is érdekes jelenség - a nanofizika eszköztárát is fontos kísérleti technikával bővítette. Az kvantált Hall-élállapotok a visszaszórás hiánya miatt kifejezetten jól használhatók arra, hogy kvantum elektronikai kísérleteket végezzünk. Az alábbiakban a legalapvetőbb példát mutatjuk be: egy Mach Zehnder interferométer kialakítását élállapotokkal.7
| 18. ábra. Mach-Zehnder interferométer kvantált Hall-élállapotokkal |
Az optikában jól ismert Mach-Zehnder interferométer elvét elektronokkal a 18. ábrán szemléltetett módon, pár mikrométer méretű áramkörben lehet megvalósítani. Az elektronok egy 2DEG-ben, a szürkével jelzett tartományokban mozoghatnak. Nagy mágneses térrel az elektronokot élállapotokra kényszerítjük, a  teret úgy állítjuk be, hogy csak egy Landau-szint legyen betöltve. Az S elektródára feszültséget kapcsolunk, a D1 elektródán a föld felé folyó áramot mérünk, a D2 elektródát leföldeljük. Az S elektródából induló élállapotban az elektronok eljutnak a QPC1 kvantum-pontkontaktushoz, mely félig áteresztő tükérként van beállítva, azaz a nyaláb felét visszaveri, a másik felét átengedi (
teret úgy állítjuk be, hogy csak egy Landau-szint legyen betöltve. Az S elektródára feszültséget kapcsolunk, a D1 elektródán a föld felé folyó áramot mérünk, a D2 elektródát leföldeljük. Az S elektródából induló élállapotban az elektronok eljutnak a QPC1 kvantum-pontkontaktushoz, mely félig áteresztő tükérként van beállítva, azaz a nyaláb felét visszaveri, a másik felét átengedi (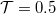 ). A két parciális elektronhullám a QPC2 kvantum-pontkontaktusnál találkozik, mely mindkét nyalábot
). A két parciális elektronhullám a QPC2 kvantum-pontkontaktusnál találkozik, mely mindkét nyalábot 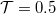 valószínűséggel a D1 elektróda felé haladó élállapotba szórja, így a D1-nél mért áramban láthatjuk a két nyaláb közti interferenciát. A két nyaláb közötti fázisviszony kétféleképpen is hangolható: egyrészt a G kapuelektródára helyezett feszültséggel hangolhatjuk az alsó ágon haladó elektronok trajektóriájának hosszát, másrészt a mágneses tér enyhe változtatásával hangolhatjuk a két nyaláb közti Aharonov-Bohm fázisból adódó fáziskülönbséget. Mind a G-re adott feszültség, mind a mágneses tér változtatásával közel 100%-os kontrasztú oszcilláció látható a D1 elektróda áramában.7
valószínűséggel a D1 elektróda felé haladó élállapotba szórja, így a D1-nél mért áramban láthatjuk a két nyaláb közti interferenciát. A két nyaláb közötti fázisviszony kétféleképpen is hangolható: egyrészt a G kapuelektródára helyezett feszültséggel hangolhatjuk az alsó ágon haladó elektronok trajektóriájának hosszát, másrészt a mágneses tér enyhe változtatásával hangolhatjuk a két nyaláb közti Aharonov-Bohm fázisból adódó fáziskülönbséget. Mind a G-re adott feszültség, mind a mágneses tér változtatásával közel 100%-os kontrasztú oszcilláció látható a D1 elektróda áramában.7
Hivatkozások
Fent hivatkozott szakcikkek
Ajánlott könyvek és összefoglaló cikkek
- S. Datta: Electronic Transport in Mesoscopic Systems, Cambridge University Press (1997)
- Thomas Ihn: Semiconducting nanosctructures, OUP Oxford (2010)
- Yuli V. Nazarov, Yaroslav M. Blanter: Quantum Transport: Introduction to Nanoscience, Cambridge University Press (2009)
Ajánlott kurzusok
- Új kísérletek a nanofizikában, Halbritter András és Csonka Szabolcs, BME Fizika Tanszék
- Transzport komplex nanoszerkezetekben, Halbritter András, Csonka Szabolcs, Csontos Miklós, Makk Péter, BME Fizika Tanszék
- Alkalmazott szilárdtestfizika, Mihály György, BME Fizika Tanszék
- Fizika 3, Mihály György, BME Fizika Tanszék (mérnök hallgatóknak)
- Mezoszkopikus rendszerek fizikája, Zaránd Gergely, BME Elméleti Fizika Tanszék
- Mezoszkopikus rendszerek fizikája, Cserti József, ELTE Komplex Rendszerek Fizikája Tanszék