„Későneutron-paraméterek vizsgálata, uránkoncentráció meghatározása” változatai közötti eltérés
| (egy szerkesztő 7 közbeeső változata nincs mutatva) | |||
| 69. sor: | 69. sor: | ||
A görbékből megállapítható, hogy a későneutron-hozam a 0 ≤ E<sub>n</sub> ≤ 4 MeV intervallumban gyakorlatilag független a hasadást kiváltó neutronok energiájától. | A görbékből megállapítható, hogy a későneutron-hozam a 0 ≤ E<sub>n</sub> ≤ 4 MeV intervallumban gyakorlatilag független a hasadást kiváltó neutronok energiájától. | ||
| − | A | + | A teljes későneutron-hozamok értékei jelentősen függnek a hasadóképes izotóptól. Az 1. táblázatban bemutatott értékekből azonban kétféle szabályt mégis megfigyelhetünk: |
* Egy adott elemre vonatkozóan a későneutron-hozam növekszik a tömegszámmal ${(A)}$. | * Egy adott elemre vonatkozóan a későneutron-hozam növekszik a tömegszámmal ${(A)}$. | ||
| 175. sor: | 175. sor: | ||
===A késő neutronok hatása a neutronfluxus időbeni változására=== | ===A késő neutronok hatása a neutronfluxus időbeni változására=== | ||
| − | + | <ref>Ez a fejezet azoknak szóló összefoglalás, akik nem hallgatták a ''Reaktorfizika'' előadást, a többieknek könnyű olvasmány.</ref> | |
| − | + | ||
Ha egy termikus reaktor időben állandósult állapotban üzemel, akkor az egymást követő neutrongenerációk neutronszámának hányadosát jelentő ''effektív sokszorozási tényező'', ${k_\textrm{eff}}$ éppen egységnyi. A reaktor teljesítményének növelésekor vagy csökkenésekor a sokszorozási tényező 1-től eltér: | Ha egy termikus reaktor időben állandósult állapotban üzemel, akkor az egymást követő neutrongenerációk neutronszámának hányadosát jelentő ''effektív sokszorozási tényező'', ${k_\textrm{eff}}$ éppen egységnyi. A reaktor teljesítményének növelésekor vagy csökkenésekor a sokszorozási tényező 1-től eltér: | ||
| 356. sor: | 355. sor: | ||
|} | |} | ||
| − | A fenti számpéldában ez a közelítés ${T}$<sub>1</sub> = 20,26 s-t ad, tehát a közelítő képlet elég pontos. Minőségileg megváltozik azonban a helyzet, amikor ${\rho/\beta}$ > 1. Ekkor ugyanis (9)-ben a második tag együtthatója pozitívra vált, és az egyenlet pozitív gyökét más képlettel kell közelíteni:Az Olvasó számára hasznos gyakorlat a közelítő képlet levezetése, így ugyanis ellenőrizheti, mennyire sikerült az eddigieket megértenie. | + | A fenti számpéldában ez a közelítés ${T}$<sub>1</sub> = 20,26 s-t ad, tehát a közelítő képlet elég pontos. Minőségileg megváltozik azonban a helyzet, amikor ${\rho/\beta}$ > 1. Ekkor ugyanis (9)-ben a második tag együtthatója pozitívra vált, és az egyenlet pozitív gyökét más képlettel kell közelíteni:<ref>Az Olvasó számára hasznos gyakorlat a közelítő képlet levezetése, így ugyanis ellenőrizheti, mennyire sikerült az eddigieket megértenie.</ref> |
{| width = "100%" | {| width = "100%" | ||
| 367. sor: | 366. sor: | ||
Például, ${\rho/\beta}$=1,1 esetén (${ k_\mathrm{eff} }$ = 1,0071) a (12b) képlet szerint ${T_{1}}$ = 0,109 s, azaz a reaktor ismét szabályozhatatlanná válik. A pontos érték ${T_{1}}$ = 0,099 s Azt találtuk tehát, a reaktor csak addig szabályozható, amíg ${\rho/\beta}$ < 1, vagyis ${k_\mathrm{eff}}$ < 1+${\beta}$ (közelítőleg). Más szavakkal a szabályozhatóság szükséges feltételét úgy szoktuk kifejezni, hogy ''a reaktor a késő neutronok nélkül legyen szubkritikus''. Ha azonban a reaktor már a késő neutronok nélkül is szuperkritikus (vagyis ha ${\rho/\beta}$ > 1), a reaktor szabályozhatatlanná válik, ''megszalad''. Az ilyen reaktorállapotot ''prompt szuperkritikus állapotnak'' nevezzük, amelynek a fellépte súlyos reaktorbalesetnek minősül. | Például, ${\rho/\beta}$=1,1 esetén (${ k_\mathrm{eff} }$ = 1,0071) a (12b) képlet szerint ${T_{1}}$ = 0,109 s, azaz a reaktor ismét szabályozhatatlanná válik. A pontos érték ${T_{1}}$ = 0,099 s Azt találtuk tehát, a reaktor csak addig szabályozható, amíg ${\rho/\beta}$ < 1, vagyis ${k_\mathrm{eff}}$ < 1+${\beta}$ (közelítőleg). Más szavakkal a szabályozhatóság szükséges feltételét úgy szoktuk kifejezni, hogy ''a reaktor a késő neutronok nélkül legyen szubkritikus''. Ha azonban a reaktor már a késő neutronok nélkül is szuperkritikus (vagyis ha ${\rho/\beta}$ > 1), a reaktor szabályozhatatlanná válik, ''megszalad''. Az ilyen reaktorállapotot ''prompt szuperkritikus állapotnak'' nevezzük, amelynek a fellépte súlyos reaktorbalesetnek minősül. | ||
| − | Az elmondottakból következik, hogy a $\beta$ későneutron-hányadnak a reaktorszabályozás szempontjából döntő jelentősége van. Erre való tekintettel ezt választjuk a reaktivitás egységének is. Ennek az egységnek a neve: ''dollár'' | + | Az elmondottakból következik, hogy a $\beta$ későneutron-hányadnak a reaktorszabályozás szempontjából döntő jelentősége van. Erre való tekintettel ezt választjuk a reaktivitás egységének is. Ennek az egységnek a neve: ''dollár'', egy reaktor reaktivitása 1 dollár, ha ${\rho/\beta}$=1. Mint láttuk, a gyakorlatban ezt a reaktorállapotot kerülni kell, ezért a gyakorlatban ennek az egységnek a 100-ad részét, a centet (<big> ˘ </big>) használjuk, egy reaktor reaktivitása 1<big>˘</big>, ha ${\rho/\beta}$ = 0,01. |
==Későneutron paraméterek meghatározása== | ==Későneutron paraméterek meghatározása== | ||
| 437. sor: | 436. sor: | ||
A polietilén csőpostatokban az ismeretlen mintából, a standardokéhoz hasonló mennyiséget, kb. 100 mg-ot helyezünk el. A besugárzást 10 kW reaktorteljesítményen végezzük. Az analizátor beállítása megegyezik a korábbival (vö. A mérés menete rész). A mérés alapgondolata: ''a standardokban és az ismeretlen mintában a besugárzott urán bomlásgörbéjét ugyanaz a (2) szerinti függvény írja le, legfeljebb az egyes görbék ${n_\textrm{f}}$ együtthatója térhet el.'' Ebből következik, hogy a lecsengő későneutron-intenzitási görbe bármelyik szakaszának összevetése alkalmas a minták összehasonlítására. Elvileg egy adott időpontbeli intenzitás - akár egy csatorna - is elegendő lenne, de több csatorna összegzésével a kiértékelés alapjául szolgáló impulzusszám relatív szórását csökkenthetjük. Az összegzett csatornák kiválasztásában az alábbi szempontokat vesszük figyelembe. | A polietilén csőpostatokban az ismeretlen mintából, a standardokéhoz hasonló mennyiséget, kb. 100 mg-ot helyezünk el. A besugárzást 10 kW reaktorteljesítményen végezzük. Az analizátor beállítása megegyezik a korábbival (vö. A mérés menete rész). A mérés alapgondolata: ''a standardokban és az ismeretlen mintában a besugárzott urán bomlásgörbéjét ugyanaz a (2) szerinti függvény írja le, legfeljebb az egyes görbék ${n_\textrm{f}}$ együtthatója térhet el.'' Ebből következik, hogy a lecsengő későneutron-intenzitási görbe bármelyik szakaszának összevetése alkalmas a minták összehasonlítására. Elvileg egy adott időpontbeli intenzitás - akár egy csatorna - is elegendő lenne, de több csatorna összegzésével a kiértékelés alapjául szolgáló impulzusszám relatív szórását csökkenthetjük. Az összegzett csatornák kiválasztásában az alábbi szempontokat vesszük figyelembe. | ||
| − | Mind a standardok, mind az ismeretlen minta tartalmaz oxigént, amelyben a besugárzás során az <sup>17</sup>O(n,p)<sup>17</sup>N magreakció eredményeként 4,1 s felezési idejű neutronemitter mag, <sup>17</sup>N keletkezik. Mivel az oxigén mennyisége mintánként változik (továbbá nem is ismert), a besugárzás után, a mérés megkezdése előtt célszerű 20 s ún. ''hűtési idő''t várni, mialatt az <sup>17</sup>N-től származó neutronok gyakorlatilag eltűnnek, és így a minta és a standardok oxigéntartalmának különbsége nem zavaró. Ebből következik, hogy a 2. táblázat szerinti | + | Mind a standardok, mind az ismeretlen minta tartalmaz oxigént, amelyben a besugárzás során az <sup>17</sup>O(n,p)<sup>17</sup>N magreakció eredményeként 4,1 s felezési idejű neutronemitter mag, <sup>17</sup>N keletkezik. Mivel az oxigén mennyisége mintánként változik (továbbá nem is ismert), a besugárzás után, a mérés megkezdése előtt célszerű 20 s ún. ''hűtési idő''t várni, mialatt az <sup>17</sup>N-től származó neutronok gyakorlatilag eltűnnek, és így a minta és a standardok oxigéntartalmának különbsége nem zavaró. Ebből következik, hogy a 2. táblázat szerinti 3.÷6. későneutron-csoportok a mérés kezdetére szintén eltűnnek, tehát az urántartalom meghatározását a 22,72 s felezési idejű, elegendően nagy hozamú későneutron-csoportra érdemes alapozni. A hűtési idő növelése egyébként más szempontból is hasznos lehet, mivel rövid hűtési idők esetében az időmérés bizonytalansága (1 s-os felbontás) is nagyobb. A mérési időt úgy kell megválasztani, hogy a mérési idő végén a csökkenő későneutron-intenzitás még mindig jelentősen kiemelkedjék a háttérből. (A javasolt mérési időintervallum 20÷80 s.) |
A szórás és a kimutatási határ számításához a háttér mérése is szükséges: üres tok | A szórás és a kimutatási határ számításához a háttér mérése is szükséges: üres tok | ||
| 445. sor: | 444. sor: | ||
| − | + | '''''Egy standard mérése''''' | |
| − | A kiértékelés célja az ismeretlen minta uránkoncentrációjának meghatározása. Jelölje a mintára, illetve a standardra vonatkozó impulzusszámok összegét rendre | + | A kiértékelés célja az ismeretlen minta uránkoncentrációjának meghatározása. Jelölje a mintára, illetve a standardra vonatkozó impulzusszámok összegét rendre ${N_\mathrm{x}}$ és ${N_\mathrm{std}}$: |
{| width = "100%" | {| width = "100%" | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ N_{x} = \sum_{i=20}^{80}n_{i,x} \hspace{20mm} N_{std} = \sum_{i=20}^{80}n_{i,std} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ N_\mathrm{x} = \sum_{i=20}^{80}n_\mathrm{i,x} \hspace{20mm} N_\mathrm{std} = \sum_{i=20}^{80}n_\mathrm{i,std} \]</latex></div> |
| align = "right" | <span id="eq2"> (15) </span> | | align = "right" | <span id="eq2"> (15) </span> | ||
|} | |} | ||
| 458. sor: | 457. sor: | ||
| − | ahol ${n_\ | + | ahol ${n_\mathrm{i,x}}$ és ${n_\mathrm{i,std}}$ az i-edik csatorna tartalma az ismeretlen mintára, illetve a standardra vonatkozóan. Hasonló módon kapjuk az ezekből levonandó hátteret: |
{| width = "100%" | {| width = "100%" | ||
| 467. sor: | 466. sor: | ||
|} | |} | ||
| − | ahol ${h_\ | + | ahol ${h_\mathrm{i,x}}$ az i-edik csatorna tartalma az ismeretlen mintához tartozó háttér mérésekor. Ha a |
| − | standardot és az ismeretlen mintát időben egymáshoz közel mérjük, fel lehet tételezni, hogy ez a háttér érvényes a standardra is. Az általánosság kedvéért azonban megengedjük, hogy az utóbbihoz külön háttér, ${ | + | standardot és az ismeretlen mintát időben egymáshoz közel mérjük, fel lehet tételezni, hogy ez a háttér érvényes a standardra is. Az általánosság kedvéért azonban megengedjük, hogy az utóbbihoz külön háttér, ${H_\mathrm{std}}$ tartozzon. Az ismeretlen koncentrációt azzal a feltételezéssel határozzuk meg, hogy a minta ''fajlagos'' (egységnyi tömegre vonatkozó) beütésszáma a ''C uránkoncentrációval arányos:'' |
{| width = "100%" | {| width = "100%" | ||
| 485. sor: | 484. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \tilde{a} = \frac{N_{std}-H_{std}}{m_{std}-C_{std}} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \tilde{a} = \frac{N_\mathrm{std}-H_\mathrm{std}}{m_\mathrm{std}-C_\mathrm{std}} \]</latex></div> |
| align = "right" | <span id="eq2"> (18) </span> | | align = "right" | <span id="eq2"> (18) </span> | ||
|} | |} | ||
| − | ahol az "std" index a standardra vonatkozóan mért adatokra utal. ${ | + | ahol az "${\mathrm{std}}$" index a standardra vonatkozóan mért adatokra utal. ${C_\mathrm{std}}$ a kiválasztott |
standard bizonylati koncentrációja (tömeg%, vö. 3. táblázat). Ennek alapján az ismeretlen | standard bizonylati koncentrációja (tömeg%, vö. 3. táblázat). Ennek alapján az ismeretlen | ||
minta uránkoncentrációját a | minta uránkoncentrációját a | ||
| 502. sor: | 501. sor: | ||
képlettel becsüljük. Ha csak egy standardot mérünk, ez a képlet jelenti a kiértékelés végét. Mielőtt a két standard esetét tárgyalnánk, adjuk meg a (19)-hez tartozó hibaszámítási képleteket. | képlettel becsüljük. Ha csak egy standardot mérünk, ez a képlet jelenti a kiértékelés végét. Mielőtt a két standard esetét tárgyalnánk, adjuk meg a (19)-hez tartozó hibaszámítási képleteket. | ||
| − | Tekintve, hogy tömeget (az egyéb hibaforrásokhoz képest) nagy pontossággal tudunk mérni, ${m_{x}}$ és ${m_{std}}$ mérési hibáját elhanyagoljuk. A háttérrel csökkentett beütésszámok szórásnégyzetét a Poisson-eloszlás alapján becsüljük: | + | Tekintve, hogy tömeget (az egyéb hibaforrásokhoz képest) nagy pontossággal tudunk mérni, ${m_\mathrm{x}}$ és ${m_\mathrm{std}}$ mérési hibáját elhanyagoljuk. A háttérrel csökkentett beütésszámok szórásnégyzetét a Poisson-eloszlás alapján becsüljük: |
{| width = "100%" | {| width = "100%" | ||
| 533. sor: | 532. sor: | ||
| − | + | '''''Két standard mérése''''' | |
| + | |||
Amikor mindkét standardot mérjük, több kiértékelési módszer kínálkozik. A legegyszerűbb az a paraméternek mindkét standard alapján való független becslése: | Amikor mindkét standardot mérjük, több kiértékelési módszer kínálkozik. A legegyszerűbb az a paraméternek mindkét standard alapján való független becslése: | ||
| 544. sor: | 544. sor: | ||
|} | |} | ||
| − | ahol az "i" index az egyes standard mintákra mért adatokat jelöli. Az így kapott értékek | + | ahol az "${i}$" index az egyes standard mintákra mért adatokat jelöli. Az így kapott értékek |
szórásnégyzetét (21a) mintájára becsülhetjük: | szórásnégyzetét (21a) mintájára becsülhetjük: | ||
| 550. sor: | 550. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \sigma^{2}_{ | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \sigma^{2}_{ai} = {\tilde{a}_{i}}^2 \Bigg(\frac{N_{i}+H_{i}}{(N_{i}-H_{i})^2}+\frac{\sigma^2_{Ci}}{C^2_{i}}\Bigg) \hspace{20mm} (i = 1,2) \]</latex></div> |
| align = "right" | <span id="eq2"> (23) </span> | | align = "right" | <span id="eq2"> (23) </span> | ||
|} | |} | ||
| 572. sor: | 572. sor: | ||
|} | |} | ||
| − | Kevésbé heurisztikus becslést kapunk, ha a (17) képletre alapozva az a paramétert lineáris regresszióval becsüljük. Ez azt jelenti, hogy az ${a}$ paraméter függvényében keressük a | + | Kevésbé heurisztikus becslést kapunk, ha a (17) képletre alapozva az ${a}$ paramétert lineáris regresszióval becsüljük. Ez azt jelenti, hogy az ${a}$ paraméter függvényében keressük a |
{| width = "100%" | {| width = "100%" | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ Q=\sum_{i=1}^{2}w_{i}\Bigg(\frac{N_{i} | + | | width = "80%" | <div class="texdisplay"><latex display >\[ Q=\sum_{i=1}^{2}w_{i}\Bigg(\frac{N_{i}-H_{i}}{m_{i}}-aC_{i}\Bigg)^2 \]</latex></div> |
| align = "right" | <span id="eq2"> (25a) </span> | | align = "right" | <span id="eq2"> (25a) </span> | ||
|} | |} | ||
| 608. sor: | 608. sor: | ||
|} | |} | ||
| − | Tekintve, hogy a ${w_{i}}$ i súlyok a (25b) képlet szerint függnek az ${a}$ paramétertől, a (26a) képlet alkalmazása ${a}$-ra nézve iterációt igényel. Ennek az iterációnak a tulajdonságai erősen függnek az egyes szórások értékeitől. Ajánlatos, hogy az Olvasó a konkrét mérés esetében közelebbről ismerkedjen meg vele. Általános tendencia, hogy a (25b) szerinti súlyozás csökkenteni igyekszik a becsült értékét. A (24a) szerinti módszer ilyen iterációt nem tesz szükségessé. | + | Tekintve, hogy a ${w_{i}}$ i súlyok a (25b) képlet szerint függnek az ${a}$ paramétertől, a (26a) képlet alkalmazása ${a}$-ra nézve iterációt igényel.<ref>Ennek az iterációnak a tulajdonságai erősen függnek az egyes szórások értékeitől. Ajánlatos, hogy az Olvasó a konkrét mérés esetében közelebbről ismerkedjen meg vele. Általános tendencia, hogy a (25b) szerinti súlyozás csökkenteni igyekszik a becsült értékét.</ref> A (24a) szerinti módszer ilyen iterációt nem tesz szükségessé. |
Akár a (22)÷(24) formulákat, akár a (25)÷(26) formulákat használjuk, az ismeretlen uránkoncentráció meghatározására a (19) és (21b) képleteket kell alkalmaznunk. A két kiértékelési mód egymással egyenértékű. Ajánlatos, hogy az Olvasó ezt bizonyítsa be. Útmutatás: a (23) képletben (de csak ott!) írjunk ${\tilde{a}^2_{i}}$ helyébe ${\tilde{a}^2}$ -t; ezután egyszerű algebrai átalakításokkal beláthatjuk, hogy (24a) és (24b) pontosan ugyanazt adja, mint (26a), illetve (26b). Kérdés: miért elég ennek bizonyítása a két becslés egyenértékűségének a belátásához? | Akár a (22)÷(24) formulákat, akár a (25)÷(26) formulákat használjuk, az ismeretlen uránkoncentráció meghatározására a (19) és (21b) képleteket kell alkalmaznunk. A két kiértékelési mód egymással egyenértékű. Ajánlatos, hogy az Olvasó ezt bizonyítsa be. Útmutatás: a (23) képletben (de csak ott!) írjunk ${\tilde{a}^2_{i}}$ helyébe ${\tilde{a}^2}$ -t; ezután egyszerű algebrai átalakításokkal beláthatjuk, hogy (24a) és (24b) pontosan ugyanazt adja, mint (26a), illetve (26b). Kérdés: miért elég ennek bizonyítása a két becslés egyenértékűségének a belátásához? | ||
| − | + | '''''Kimutatási határ''''' | |
A kimutatási határ definíciójánál az urán mennyiség meghatározás alapjául szolgáló nettó impulzusszám háttérből való szignifikáns kiemelkedését kell biztosítani statisztikai kritériumok alapján, másként megfogalmazva azt kell eldöntenünk, hogy van-e effektus vagy nincs, és ennek a döntésnek a mennyiségi megalapozását kell megadnunk. A döntés során alapvetően kétféle hibát követhetünk el. Az első az úgynevezett elsőfajú hiba melynél azt feltételezzük, hogy a mért összegzett intenzitás egy része a minta urán tartalmától származik, pedig csak a háttér pozitív fluktuációjáról van szó. Másodfajú hibát akkor követünk el, ha mért impulzusszám egy része urántól származik, de úgy gondoljuk hogy ez csak a háttér véletlen fluktuációja. | A kimutatási határ definíciójánál az urán mennyiség meghatározás alapjául szolgáló nettó impulzusszám háttérből való szignifikáns kiemelkedését kell biztosítani statisztikai kritériumok alapján, másként megfogalmazva azt kell eldöntenünk, hogy van-e effektus vagy nincs, és ennek a döntésnek a mennyiségi megalapozását kell megadnunk. A döntés során alapvetően kétféle hibát követhetünk el. Az első az úgynevezett elsőfajú hiba melynél azt feltételezzük, hogy a mért összegzett intenzitás egy része a minta urán tartalmától származik, pedig csak a háttér pozitív fluktuációjáról van szó. Másodfajú hibát akkor követünk el, ha mért impulzusszám egy része urántól származik, de úgy gondoljuk hogy ez csak a háttér véletlen fluktuációja. | ||
| 657. sor: | 657. sor: | ||
# Mi a periódus idő? | # Mi a periódus idő? | ||
# Mi a szerepe a késő neutronoknak a reaktor szabályzásban? | # Mi a szerepe a késő neutronoknak a reaktor szabályzásban? | ||
| − | # Ismertesse a késő neutronok mérésénél alkalmazott módszert | + | # Ismertesse a késő neutronok mérésénél alkalmazott módszert! |
# Milyen csoportokba sorolhatjuk a késő neutronokat és minek alapján? | # Milyen csoportokba sorolhatjuk a késő neutronokat és minek alapján? | ||
# Ismertesse az uránkoncentráció meghatározás elvét! | # Ismertesse az uránkoncentráció meghatározás elvét! | ||
| 674. sor: | 674. sor: | ||
==Lábjegyzetek== | ==Lábjegyzetek== | ||
| + | |||
<references /> | <references /> | ||
A lap jelenlegi, 2018. november 15., 12:32-kori változata
Tartalomjegyzék |
Bevezetés
Az 235U atommag egy neutron befogását követő hasadása során keletkező instabil közbenső mag két hasadványmagra[1] hasad, ezenkívül hasadásonként néhány (235U esetében átlagosan 2,47) neutron szabadul fel. A keletkező neutronok több mint 99%-a a hasadást követő 10-12 s-on belül emittálódik. Ezeket a neutronokat prompt neutronoknak nevezzük. Az ezt követően - akár néhány perccel később - kibocsátott neutronok az ún. késő neutronok. Bár ezek mennyisége a prompt neutronokéhoz viszonyítva kicsi (235U esetében az össz-neutronszámnak csupán 0,64%-a), jelentőségük igen nagy a reaktorok szabályozhatósága szempontjából.
Elméleti összefoglalás
Az 235U termikus befogását követően létrejött közbenső mag sokféle (több 100) különböző módon hasadhat szét. Egy ilyen lehetőség például a következő:
235U+n ⇒ 236U* ⇒ 90Kr+143Ba+3n
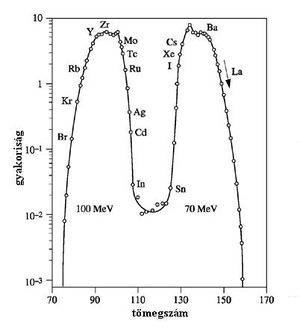
A hasadási termékek száma igen nagy. A hasadványok relatív gyakoriságának tömegszám szerinti eloszlását az 1. ábrán láthatjuk. Megállapítható, hogy a görbének a 95 és a 140 tömegszám közelében egy-egy maximuma van. A hasadásban közvetlenül keletkező primer hasadási termékek nagy neutronfelesleggel rendelkeznek az azonos tömegszámú stabil atommagokhoz képest. A hasadási termékek az esetek döntő többségében sorozatos izobár magátalakulással, 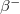 -bomlással szabadulnak meg neutronfeleslegüktől, és így közelítik meg a stabil
-bomlással szabadulnak meg neutronfeleslegüktől, és így közelítik meg a stabil 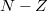 görbét. A fent bemutatott hasadványpár esetében a következő két bomlássorozat megy végbe:
görbét. A fent bemutatott hasadványpár esetében a következő két bomlássorozat megy végbe:
![\[ {^{90}Kr\frac{\beta^{-}}{33s}} \to {^{90}Rb\frac{\beta^{-}}{2.7min}} \to {^{90}Sr\frac{\beta^{-}}{28y}} \to {^{90}Y\frac{\beta^{-}}{64h}} \to {^{90}Zr} (stabil) \]](/images/math/6/f/8/6f8401cb5bd99b244d786b290549776a.png) |
![\[ {^{143}Ba\frac{\beta^{-}}{0.5min}} \to {^{143}La\frac{\beta^{-}}{12min}} \to {^{143}Ce\frac{\beta^{-}}{33h}} \to {^{143}Pr\frac{\beta^{-}}{13.7d}} \to {^{143}}Nd (stabil) \]](/images/math/8/2/0/8202044b21b5058a3a15172daaf42b31.png) |
A vonalak alatti idők a 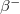 -bomlások felezési idejét jelentik.
-bomlások felezési idejét jelentik.
A prompt és késő neutronok keletkezése a hasadás során
Amint a bevezetőben említettük, a hasadás során keletkező neutronok csaknem mindegyike - több mint 99%-a - a hasadást követően szinte azonnal, számottevő késés nélkül keletkezik. Ezek a prompt neutronok, amelyeket a hasadványok bocsátják ki. Gerjesztési energiájuk ugyanis általában sokkal nagyobb mint egy neutron szeparációs energiája. Az ilyen gerjesztett állapotok neutronemisszióval történő bomlásának az ideje 10-15 s (10-14 s - 10-12 s) vagy kisebb. Nem minden hasadvány emittál neutronokat, néhányuk esetében a legerjesztődés történhet 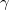 emisszióval is.
emisszióval is.
Ezt követően a hasadási termékek 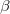 -bomlással szabadulnak meg neutronfeleslegüktől, és további neutron-kibocsátás általában már nem történik. Némelyikük izobár átalakulása azonban olyan leányelem képződéséhez vezet, amelyikben a gerjesztési energia nagyobb, mint a neutron szeparációs energiája. Ekkor a
-bomlással szabadulnak meg neutronfeleslegüktől, és további neutron-kibocsátás általában már nem történik. Némelyikük izobár átalakulása azonban olyan leányelem képződéséhez vezet, amelyikben a gerjesztési energia nagyobb, mint a neutron szeparációs energiája. Ekkor a 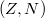 rendszámú, illetve neutronszámú hasadási termék magjából magasan gerjesztett állapotú
rendszámú, illetve neutronszámú hasadási termék magjából magasan gerjesztett állapotú 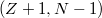 mag keletkezik, amely "azonnal" kibocsát egy neutront, és átalakul a
mag keletkezik, amely "azonnal" kibocsát egy neutront, és átalakul a 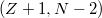 maggá. Így keletkeznek az ún. késő neutronok. A
maggá. Így keletkeznek az ún. késő neutronok. A 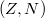 magot későneutron-anyamagnak, a
magot későneutron-anyamagnak, a 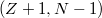 magot pedig későneutron-emitternek nevezzük. Az ily módon keletkező késő neutronok esetében a maghasadás pillanatától számított teljes késési idő várható értékét az anyamag
magot pedig későneutron-emitternek nevezzük. Az ily módon keletkező késő neutronok esetében a maghasadás pillanatától számított teljes késési idő várható értékét az anyamag 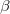 -bomlásának felezési ideje szabja meg. Megállapíthatjuk továbbá, hogy az anyamagok
-bomlásának felezési ideje szabja meg. Megállapíthatjuk továbbá, hogy az anyamagok 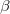 -bomlását követően létrejött emitter magok esetében a gerjesztési energia kisebb, mint a közvetlen hasadási termékek esetében, emiatt a késő neutronok átlagos energiája számottevően kisebb (300÷600 keV), mint a prompt neutronoké (átlagosan 2 MeV).
-bomlását követően létrejött emitter magok esetében a gerjesztési energia kisebb, mint a közvetlen hasadási termékek esetében, emiatt a késő neutronok átlagos energiája számottevően kisebb (300÷600 keV), mint a prompt neutronoké (átlagosan 2 MeV).
A hasadásban keletkező neutronok teljes hozama (száma,  ) a prompt neutronok és a késő neutronok hozamából (
) a prompt neutronok és a késő neutronok hozamából (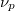 , illetve
, illetve 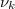 ) tevődik össze.
) tevődik össze.
![\[ \nu =\nu_{p}+\nu_{k} \]](/images/math/d/7/d/d7d6b485715f468e9bd705a1e2c537c9.png) |
A késő neutronok mennyiségét szokás még az ún. későneutron-hányad formájában is kifejezni:
![\[ \beta=\frac{\nu_{k}}{\nu} \]](/images/math/e/d/1/ed144f9e9c69e0926541d6dd81999ebb.png) |
(1) |
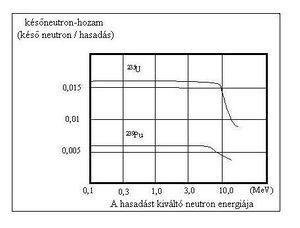
A 2. ábrán a későneutron-hozamnak a hasadást kiváltó neutron energiájától való függését mutatjuk be 235U és 239Pu esetére.
A görbékből megállapítható, hogy a későneutron-hozam a 0 ≤ En ≤ 4 MeV intervallumban gyakorlatilag független a hasadást kiváltó neutronok energiájától.
A teljes későneutron-hozamok értékei jelentősen függnek a hasadóképes izotóptól. Az 1. táblázatban bemutatott értékekből azonban kétféle szabályt mégis megfigyelhetünk:
- Egy adott elemre vonatkozóan a későneutron-hozam növekszik a tömegszámmal
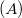 .
.
- A későneutron-hozam csökken a protonszámmal
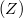 .
.
Teljes későneutron-hozamok (későneutron-szám per 100 hasadás) különböző
izotópoknak termikus neutronok által kiváltott hasadásaira| hasadóképes mag |  k (neutron/100 hasadás) k (neutron/100 hasadás)
|
| 233U | 0,667 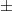 0,0029 0,0029
|
| 235U | 1,621 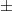 0,0500 0,0500
|
| 238U* | 4,390 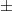 0,1000 0,1000
|
| 239Pu | 0,628 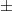 0,0380 0,0380
|
| 240Pu* | 0,950 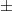 0,0800 0,0800
|
| 241Pu | 1,520 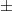 0,1100 0,1100
|
| 242Pu* | 2,210 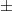 0,2600 0,2600
|
* Gyors neutron által kiváltott hasadásokra vonatkozó adat
A későneutron-csoportok
A magfizikusok eddig 66 különböző későneutron-anyamagot azonosítottak.[2] Felezési időik 0,12 s és 78 s között változik, emiatt az általuk keltett késő neutronok jelentősen különböző késleltetési időkkel jelennek meg. Reaktorkinetikai számításokban a késő neutronok korrekt kezelése ennek megfelelően az lenne, ha valamennyi anyamagot a saját felezési idejével és hozamával vennénk figyelembe. Ezzel kapcsolatban két fő probléma merül fel:
- Az anyamagok nagy száma miatt a feladat nagyon elbonyolódna.
- Az egyes anyamagok bomlási sémája, felezési ideje, részaránya nem kellő pontossággal ismert.
G. R. Keepin dolgozta ki kísérleti úton a számítások számára kielégítő közelítést a későneutron-adatok kondenzált kezelésével, azaz a későneutron-csoportok létrehozásával. Hasonlóan a mai gyakorlaton elvégzendő méréshez, hasadóanyagból készített mintát rövid ideig tartó neutron-besugárzásnak tett ki. A besugárzott mintában bekövetkezett hasadások révén nagy számú anyamag keletkezett, amelyek a besugárzást követően felezési idejük szerint lecsengő későneutron-forrásként működtek - 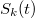 . Ha a mintában a besugárzás során bekövetkezett hasadási reakciók száma
. Ha a mintában a besugárzás során bekövetkezett hasadási reakciók száma 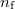 volt, akkor a keltett anyamagok száma
volt, akkor a keltett anyamagok száma 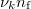 . Az
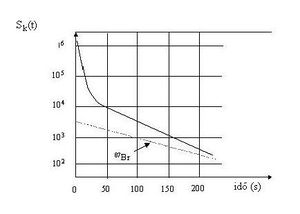
. Az 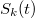 függvény ezen anyamagok lebomlását, és ennélfogva a késő neutronok keletkezésének időbeli alakulását írja le. A 3. ábrán egy ilyen görbe látható a 87Br izotópnak, egy tipikus anyamagnak a bomlási-görbéjével együtt.
függvény ezen anyamagok lebomlását, és ennélfogva a késő neutronok keletkezésének időbeli alakulását írja le. A 3. ábrán egy ilyen görbe látható a 87Br izotópnak, egy tipikus anyamagnak a bomlási-görbéjével együtt.
Az 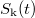 bomlási görbe az összes anyamag járulékos bomlásgörbéinek bonyolult szuperpoziciója. Keepin szerint az
bomlási görbe az összes anyamag járulékos bomlásgörbéinek bonyolult szuperpoziciója. Keepin szerint az 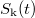 jól közelíthető hat exponenciális függvény összegével:
jól közelíthető hat exponenciális függvény összegével:
![\[ S_\textrm{k}(t) = n_\textrm{f}\sum_{i=1}^6\nu_\textrm{ki}\lambda_\textrm{ki}e^{{-\lambda_\textrm{ki}}t} \]](/images/math/9/0/a/90ae9e1f574e0d3ec8787ab993f4596d.png) |
(2) |
ahol
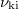 |
: az i-edik későneutron-csoport hozama |
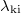 |
: az i-edik későneutron-csoport bomlási állandója |
Az 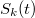 függvény a fenti közelítésben olyan későneutron-forrásfüggvényt reprezentál, amelyben mindegyik csoport saját
függvény a fenti közelítésben olyan későneutron-forrásfüggvényt reprezentál, amelyben mindegyik csoport saját 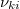 későneutron-hozammal, átlagos
későneutron-hozammal, átlagos 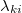 bomlási állandóval, ill. az ennek megfelelő átlagos felezési idővel rendelkezik. Három különböző hasadóképes izotópra (235U, 239Pu, 233U) a későneutron-csoportok főbb adatait a 2. táblázatban foglaltuk össze. Ez a hatcsoportos későneutron-struktúra általánosan használatos a reaktorkinetikában.
bomlási állandóval, ill. az ennek megfelelő átlagos felezési idővel rendelkezik. Három különböző hasadóképes izotópra (235U, 239Pu, 233U) a későneutron-csoportok főbb adatait a 2. táblázatban foglaltuk össze. Ez a hatcsoportos későneutron-struktúra általánosan használatos a reaktorkinetikában.
A későneutron-csoportok adatai három hasadóképes izotópra
| késő neutronok lehetséges anyamagjai | közepes energia (MeV) | anyamagok átlagos felezési ideje (s) | késő neutronok részaránya az összes hasadási neutronhoz viszonyítva (%) | |||||
| 235U | 239Pu | 233U | 235U | 239Pu | 233U | |||
| 1 | 87Br, 142Cs | 0,25 | 55,72 | 54,28 | 55,0 | 0,021 | 0,0072 | 0,0226 |
| 2 | 137I, 88Br | 0,56 | 22,72 | 23,04 | 20,57 | 0,140 | 0,0626 | 0,0786 |
| 3 | 138I, 89Br, (93, 94)Rb | 0,43 | 6,22 | 5,60 | 5,00 | 0,126 | 0,0444 | 0,0658 |
| 4 | 139I, (93, 94)Kr, 143Xe, (90, 92)Br | 0,62 | 2,3 | 2,13 | 2,13 | 0,252 | 0,0685 | 0,0730 |
| 5 | 140I, 145Cs | 0,42 | 0,61 | 0,618 | 0,615 | 0,074 | 0,018 | 0,0135 |
| 6 | (Br, Rb, As stb.) | - | 0,23 | 0,257 | 0,277 | 0,027 | 0,0093 | 0,0087 |
| összesen: | 0,64 | 0,21 | 0,26 | |||||
A késő neutronok hatása a neutronfluxus időbeni változására
Ha egy termikus reaktor időben állandósult állapotban üzemel, akkor az egymást követő neutrongenerációk neutronszámának hányadosát jelentő effektív sokszorozási tényező, 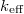 éppen egységnyi. A reaktor teljesítményének növelésekor vagy csökkenésekor a sokszorozási tényező 1-től eltér:
éppen egységnyi. A reaktor teljesítményének növelésekor vagy csökkenésekor a sokszorozási tényező 1-től eltér:
![\[ \Delta k_\mathrm{eff} = k_\mathrm{eff}-1 \]](/images/math/d/5/1/d51b63c8aa4281e3c4e68cc4d30b4805.png) |
A  reaktivitás definíció szerint a következő:
reaktivitás definíció szerint a következő:
![\[ \rho = \frac{\Delta k_\mathrm{eff}}{k_\mathrm{eff}} = \frac{k_\mathrm{eff}-1}{k_\mathrm{eff}} \]](/images/math/e/4/6/e46e5226d5cc365f057d9b959734c1be.png) |
(3) |
Időben állandósult állapotban  = 0. A szokásos körülmények közötti teljesítményváltoztatások az állandósult állapothoz közeli állapotokon keresztül mennek végbe, és ekkor jó közelítéssel
= 0. A szokásos körülmények közötti teljesítményváltoztatások az állandósult állapothoz közeli állapotokon keresztül mennek végbe, és ekkor jó közelítéssel
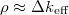 . Minthogy
. Minthogy 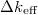 jelenti a neutronszám növekedési arányát az egyik generáció és a soron következő generáció között, a teljes neutronszámnak egy generáció élete során bekövetkező növekedése
jelenti a neutronszám növekedési arányát az egyik generáció és a soron következő generáció között, a teljes neutronszámnak egy generáció élete során bekövetkező növekedése 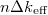 -fel egyenlő, ahol
-fel egyenlő, ahol 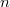 a neutronszám az induló neutronpopulációban. Ha a neutronok átlagos élettartama
a neutronszám az induló neutronpopulációban. Ha a neutronok átlagos élettartama 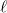 , akkor a neutronszám időegység alatti változását a következő differenciálegyenlet adja meg:
, akkor a neutronszám időegység alatti változását a következő differenciálegyenlet adja meg:
![\[ \frac{dn}{dt} = \frac{n\Delta k_\mathrm{eff}}{\ell}. \]](/images/math/2/b/f/2bf6113259e4186e583c33c2827e8565.png) |
(4) |
Feltételezve azt, hogy 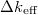 nem függ az időtől, integrálással kapjuk:
nem függ az időtől, integrálással kapjuk:
![\[ n(t) = n(t_0) \exp \Big( \frac{\Delta k_\mathrm{eff}}{\ell}t \Big) \]](/images/math/7/6/2/7622c9b81bcf48eff4fbc3c97637b197.png) |
(5) |
Az oktatóreaktorban 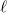 = 7
= 7  10-5 sec. Definiáljuk a reaktor periódusidejét
10-5 sec. Definiáljuk a reaktor periódusidejét 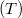 : az az idő, amely alatt a neutronszám az
: az az idő, amely alatt a neutronszám az  -szeresére változik (
-szeresére változik ( = 2,7172...), (5) alapján tehát:
= 2,7172...), (5) alapján tehát:
![\[ T = \frac{\ell}{\Delta{k}_\mathrm{eff}}. \]](/images/math/7/e/e/7ee8eedb48349dd91b74c42b7f2c5d4c.png) |
(6) |
A neutronszámra felírt összefüggés átvihető közelítőleg (egycsoportos elmélet) a neutronsűrűségre és ezen keresztül a neutronfluxusra és a reaktorteljesítményre is:
![\[ n(t)=n(t_{0})e^{\frac{t}{T}} \]](/images/math/2/a/d/2adf850255977b9a5e08357c91d7fbf1.png) |
(5a) |
Az időben állandó, stacioner üzemű reaktorban 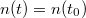 = konst., tehát
= konst., tehát 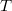 végtelen. A reaktor periódusideje rendkívül fontos mennyiség a változó teljesítményű reaktor biztonsága szempontjából. Minden reaktorba beépítenek olyan biztonságvédelmi rendszert, amely azonnal leállítja a reaktort, ha a periódusidő a szabályozhatóság lehetőségeit tekintve túlságosan kicsiny. Ha nem üzemelne periódusidő-védelem, a 7÷10 s-nál rövidebb periódusidő már kifejezetten veszélyes állapotot jelentene.
végtelen. A reaktor periódusideje rendkívül fontos mennyiség a változó teljesítményű reaktor biztonsága szempontjából. Minden reaktorba beépítenek olyan biztonságvédelmi rendszert, amely azonnal leállítja a reaktort, ha a periódusidő a szabályozhatóság lehetőségeit tekintve túlságosan kicsiny. Ha nem üzemelne periódusidő-védelem, a 7÷10 s-nál rövidebb periódusidő már kifejezetten veszélyes állapotot jelentene.
A késő neutronok fontosságának a kidomborítása érdekében határozzuk meg a periódusidőt abban az esetben, amikor a reaktivitás 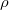 = 0,25%[4], de csak a prompt neutronokat figyelembe véve. Mivel
= 0,25%[4], de csak a prompt neutronokat figyelembe véve. Mivel 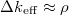 = 0,0025, (6) alapján a periódusidőre a következő adódik:
= 0,0025, (6) alapján a periódusidőre a következő adódik:
![\[ T = \frac{\ell}{\Delta{k}_\mathrm{eff}} = \frac{0,00007}{0,0025} = 0,028 s \]](/images/math/0/0/4/004a30240278cfb38b29464316160b18.png) |
Ezt azt jelenti, hogy 1 s alatt a neutronszám
![\[ \frac{n(1s)}{n(0)} = e^{\frac{1s}{0,028s}}= e^{35,7}=3\times 10^{15} \]](/images/math/a/0/8/a0826017db7dc284d2be7460d806590d.png) |
szeresére nő. Semmilyen szabályozórendszer (amely mechanikus elemeket is tartalmaz) nem tudja követni ezt a gyors felfutást. "Szerencsére" a késő neutronok bizonyos feltételek között jelentősen lelassítják a növekedési ütemet, és ezzel lehetővé teszik a reaktorok szabályozását.
A késő neutronok hatásának a megvilágítása érdekében leegyszerűsítjük a tárgyalást: csak egyetlen, átlagos későneutron-csoportot veszünk figyelembe[5] Ha a 2. táblázatban az 235U-ra adott felezési időket átlagoljuk, 9 s-t kapunk, vagyis a (2) alatti hat bomlási állandót az átlagos
![\[ \bar{\lambda}=\frac{\log 2}{9s}=0,077s^{-1} \]](/images/math/2/a/0/2a067f4636fee34e7a4e854ade4085da.png) |
bomlási állandóval helyettesítjük. Ha 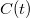 -vel jelöljük a t időpillanatban a reaktorban levő
későneutron-anyamagok számát, akkor 1 s alatt
-vel jelöljük a t időpillanatban a reaktorban levő
későneutron-anyamagok számát, akkor 1 s alatt 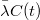 késő neutron keletkezik. Ennek megfelelően a (4) egyenlet az alábbi alakba megy át:
késő neutron keletkezik. Ennek megfelelően a (4) egyenlet az alábbi alakba megy át:
![\[ \frac{dn}{dt}=\frac{nk_{\mathrm{eff}}(1-\beta)-n}{\ell}+\bar{\lambda}\textit{C(t)} \]](/images/math/1/c/f/1cf6622b8b5aa471469c8fe8e333b27b.png) |
(7a) |
amelynek a jobb oldalán az első tag a prompt, a második tag pedig a késő neutronok által képviselt neutronsokszorozást fejezi ki. Ezt az egyenletet ki kell egészítenünk a későneutron-anyamagok számát megszabó egyenlettel:
![\[ \frac{dC}{dt}=-\bar{{\lambda}}\textit{C(t)}+\frac{nk_{\mathrm{eff}}{\beta}}{\ell} \]](/images/math/8/7/c/87c1ed5c391e2b4684ab30ec04bb66af.png) |
(7b) |
A jobboldal első tagja az 1 s alatt elbomló, a második tag pedig az 1 s alatt a hasadásokban keletkező anyamagok számát adja meg.[6] Nézzük meg ezután, mennyiben növelik a késő neutronok a reaktorperiódust!
(5a) mintájára a (7) egyenletrendszer megoldását az alábbi alakban keressük:
![\[ n(t) = n_{0}e^{t/T} \quad \quad \textrm{és} \quad \quad C(t)=C_{0}e^{t/T} \]](/images/math/1/e/5/1e53d4f55d8582e44b48664227eed3f5.png) |
Ha ezt (7)-be helyettesítjük, elemi számolás után 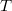 -re a következő egyenletet kapjuk:
-re a következő egyenletet kapjuk:
![\[ \frac{\rho}{\beta}=\frac{\ell/(\mathrm{k}_{\mathrm{eff}}\beta)}{T}+\frac{1}{1+\bar{\lambda}T} \]](/images/math/c/8/7/c873c1a93512582f9c606e1a36a7d012.png) |
(8) |
ahol felhasználtuk a (3) alatt definiált reaktivitást. Amikor ennek az egyenletnek a megfelelőjét 6 későneutron-csoport figyelembe vételével vezetjük le, akkor a kapott egyenletet reciprokóra egyenletnek nevezzük.
Adott reaktivitás mellett a (8) egyenlet a 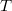 periódusidőre vonatkozóan másodfokú egyenlet:
periódusidőre vonatkozóan másodfokú egyenlet:
![\[ \frac{\rho}{\beta}\bar{\lambda}T^{2}+\Big(\frac{\rho}{\beta}-\frac{\ell\bar{\lambda}}{\mathrm{k}_{e\mathrm{ff}}\beta}-1\Big)T-\frac{\ell}{k_{e\mathrm{ff}}\beta}=0 \]](/images/math/3/0/1/301c5095ac1f90506661c2732443a083.png) |
(9) |
Jelöljük a két gyököt 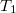 -gyel és
-gyel és 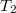 -vel. Ezek felhasználásával a neutronszám időfüggése
-vel. Ezek felhasználásával a neutronszám időfüggése
![\[ n(t)=n_{1}e^{t/T_{1}}+n_{2}e^{t/T_{2}} \]](/images/math/c/b/a/cba8ef580adbcf9328e88729694c675f.png) |
(10) |
alakban adódik, ahol az 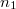 és
és 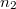 állandók a kezdeti feltételektől függnek. Ha a
állandók a kezdeti feltételektől függnek. Ha a 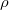 reaktivitás negatív (vagyis
reaktivitás negatív (vagyis 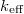 < 1, tehát a reaktor szubkritikus), a (9) egyenlet mindhárom együtthatója negatív, tehát mindkét gyök negatív[7], vagyis a neutronszám (10) szerint a kezdeti feltételektől függetlenül időben csökken. Ha azonban a
< 1, tehát a reaktor szubkritikus), a (9) egyenlet mindhárom együtthatója negatív, tehát mindkét gyök negatív[7], vagyis a neutronszám (10) szerint a kezdeti feltételektől függetlenül időben csökken. Ha azonban a 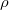 reaktivitás pozitív (vagyis
reaktivitás pozitív (vagyis 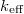 > 1, tehát a reaktor szuperkritikus), a (9) egyenlet első együtthatója pozitív, a harmadik pedig továbbra is negatív. A reaktivitástól függően a második együttható lehet negatív is, pozitív is. Mindkét esetben azonban van egy előjelváltás és egy előjelkövetés, vagyis a két gyök közül az egyik negatív, a másik pozitív. Legyen az utóbbi
> 1, tehát a reaktor szuperkritikus), a (9) egyenlet első együtthatója pozitív, a harmadik pedig továbbra is negatív. A reaktivitástól függően a második együttható lehet negatív is, pozitív is. Mindkét esetben azonban van egy előjelváltás és egy előjelkövetés, vagyis a két gyök közül az egyik negatív, a másik pozitív. Legyen az utóbbi 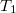 . Ekkor elegendően nagy
. Ekkor elegendően nagy 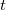 idő elteltével (10) átmegy az
idő elteltével (10) átmegy az
![\[ n(t)=n_{1}e^{t/T_{1}} \hspace{20mm} (\textit{t}\gg\textit{T}_{2}) \]](/images/math/c/0/d/c0dcf7dca2aa5ae6d7b7cfbdf4950880.png) |
(11) |
alakba. A késő neutronok jelenlétében is igaz marad tehát, hogy egy magára hagyott szuperkritikus reaktorban a neutronszám exponenciálisan nő. Döntő viszont az időállandó nagysága. Vegyük fel a következő számértékeket:
![\[ \beta=0,0064 \hspace{10mm} \ell=7 \times 10^{-5} \hspace{10mm} \rho=0,0025 \hspace{10mm} \bar\lambda=0,077s^{-1} \hspace{10mm} k_{\textrm{eff}} = 1,0025 \]](/images/math/5/4/7/547ad323c0a75d6c78c9379602277c79.png) |
Ezeket (9)-be helyettesítve 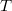 1 = 20,31 s adódik, ami lényegesen nagyobb idő, mint a késő neutronok nélkül kapott 0,028 s. Ez a számpélda jól mutatja a lényeget: a késő neutronok hatására a periódusidő olyan mértékben megnő, hogy a neutronszám növekedését külső eszközökkel biztonságosan befolyásolni lehet.
1 = 20,31 s adódik, ami lényegesen nagyobb idő, mint a késő neutronok nélkül kapott 0,028 s. Ez a számpélda jól mutatja a lényeget: a késő neutronok hatására a periódusidő olyan mértékben megnő, hogy a neutronszám növekedését külső eszközökkel biztonságosan befolyásolni lehet.
Ez az állítás azonban csak addig érvényes, amíg a reaktivitás nem túlságosan nagy, pontosabban, amíg 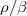 < 1. Amíg ez fennáll, a (9) egyenletben az
< 1. Amíg ez fennáll, a (9) egyenletben az 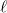 -et tartalmazó tagok elhanyagolhatók, vagyis a pozitív periódus közelítőleg így írható:
-et tartalmazó tagok elhanyagolhatók, vagyis a pozitív periódus közelítőleg így írható:
![\[ T_{1} \approx \frac{\beta-\rho}{\rho\bar{\lambda}} \hspace{30mm} (\rho/\beta<1) \]](/images/math/0/d/9/0d992a59b72ba15ccc8f984373984ed7.png) |
(12a) |
A fenti számpéldában ez a közelítés 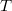 1 = 20,26 s-t ad, tehát a közelítő képlet elég pontos. Minőségileg megváltozik azonban a helyzet, amikor
1 = 20,26 s-t ad, tehát a közelítő képlet elég pontos. Minőségileg megváltozik azonban a helyzet, amikor 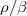 > 1. Ekkor ugyanis (9)-ben a második tag együtthatója pozitívra vált, és az egyenlet pozitív gyökét más képlettel kell közelíteni:[8]
> 1. Ekkor ugyanis (9)-ben a második tag együtthatója pozitívra vált, és az egyenlet pozitív gyökét más képlettel kell közelíteni:[8]
![\[ T_{1} \approx \frac{\ell}{k_{\textrm{eff}}(\rho-\beta)} \hspace{20mm} (\rho/\beta>1) \]](/images/math/6/c/6/6c6affd6e88145feba44dd79664d0a56.png) |
(12b) |
Például, 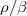 =1,1 esetén (
=1,1 esetén (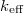 = 1,0071) a (12b) képlet szerint
= 1,0071) a (12b) képlet szerint 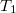 = 0,109 s, azaz a reaktor ismét szabályozhatatlanná válik. A pontos érték
= 0,109 s, azaz a reaktor ismét szabályozhatatlanná válik. A pontos érték 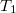 = 0,099 s Azt találtuk tehát, a reaktor csak addig szabályozható, amíg
= 0,099 s Azt találtuk tehát, a reaktor csak addig szabályozható, amíg 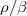 < 1, vagyis
< 1, vagyis 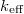 < 1+
< 1+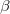 (közelítőleg). Más szavakkal a szabályozhatóság szükséges feltételét úgy szoktuk kifejezni, hogy a reaktor a késő neutronok nélkül legyen szubkritikus. Ha azonban a reaktor már a késő neutronok nélkül is szuperkritikus (vagyis ha
(közelítőleg). Más szavakkal a szabályozhatóság szükséges feltételét úgy szoktuk kifejezni, hogy a reaktor a késő neutronok nélkül legyen szubkritikus. Ha azonban a reaktor már a késő neutronok nélkül is szuperkritikus (vagyis ha 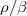 > 1), a reaktor szabályozhatatlanná válik, megszalad. Az ilyen reaktorállapotot prompt szuperkritikus állapotnak nevezzük, amelynek a fellépte súlyos reaktorbalesetnek minősül.
> 1), a reaktor szabályozhatatlanná válik, megszalad. Az ilyen reaktorállapotot prompt szuperkritikus állapotnak nevezzük, amelynek a fellépte súlyos reaktorbalesetnek minősül.
Az elmondottakból következik, hogy a  későneutron-hányadnak a reaktorszabályozás szempontjából döntő jelentősége van. Erre való tekintettel ezt választjuk a reaktivitás egységének is. Ennek az egységnek a neve: dollár, egy reaktor reaktivitása 1 dollár, ha
későneutron-hányadnak a reaktorszabályozás szempontjából döntő jelentősége van. Erre való tekintettel ezt választjuk a reaktivitás egységének is. Ennek az egységnek a neve: dollár, egy reaktor reaktivitása 1 dollár, ha 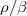 =1. Mint láttuk, a gyakorlatban ezt a reaktorállapotot kerülni kell, ezért a gyakorlatban ennek az egységnek a 100-ad részét, a centet ( ˘ ) használjuk, egy reaktor reaktivitása 1˘, ha
=1. Mint láttuk, a gyakorlatban ezt a reaktorállapotot kerülni kell, ezért a gyakorlatban ennek az egységnek a 100-ad részét, a centet ( ˘ ) használjuk, egy reaktor reaktivitása 1˘, ha 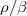 = 0,01.
= 0,01.
Későneutron paraméterek meghatározása
A méréshez szükséges eszközök, anyagok
- Reaktor és besugárzó csőposta
- besugárzandó urán fólia csőposta-tokban
- moderátorral töltött mérőedény
- neutrondetektor-gyűrű 6 db detektorból (3He)
- mérő elektronika (tápegység, diszkriminátor)
- PC sokcsatornás analizátorkártyával (multiscaler - időanalizátor)
A mérés menete
A reaktor aktív zónájában besugárzott természetes urán fólia a csőposta segítségével (kb. 3 s-os szállítási idő után) a mérőhelyre kerül. A besugárzást követően a mérőedényben elhelyezett neutrondetektorok mérik a fólia időben csökkenő későneutron-intenzitását. Az intenzitás időbeli változásának rögzítése az analizátorkártyával történik, amely a detektorok diszkriminált jeleit összegzi a megadott léptetési időtartam alatt (1 s). A léptetési időtartam alatt gyűjtött impulzusok időbeli sorrendjüknek megfelelően egymás utáni csatornákban tárolódnak. Amint azt az elméleti összefoglalóban láttuk, a későneutron-intenzitásnak ez a változása nem más, mint különböző felezési idejű exponenciális bomlási görbék lineáris szuperpozíciója. A későneutron-intenzitás mért értékeiből a kiértékeléskor lépésről-lépésre meghatározzuk és levonjuk a leghosszabb felezési idejű exponenciális komponenseket.
A reaktor 1 kW-os teljesítményénél az urán fóliát tartalmazó tok a csőposta segítségével az aktív zónába kerül. A meghatározott besugárzási idő elteltével a minta automatikusan kerül a mérő pozícióba. A minta mozgását érzékelő, és a csőpostát vezérlő fotocella jele a méréshez startjelként használható. (Figyelem: a mozgásérzékelő befelé menet is jelez!)
A paraffin moderátorral töltött mérőedényben 6 db, párhuzamosan kapcsolt 3He töltésű neutron-számlálócső van elhelyezve. A termikus neutronenergiák tartományában érzékeny detektorok miatt a detektálandó késő neutronokat le kell lassítani. Éppen erre szolgál a mérőedényben levő moderátor. A neutronok lelassulási ideje elhanyagolhatóan kicsi (kb. 1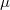 s.), még a gyakorlatilag mérhető legrövidebb felezési idejű késő neutronok késleltetési idejéhez képest is.
s.), még a gyakorlatilag mérhető legrövidebb felezési idejű késő neutronok késleltetési idejéhez képest is.
A neutrondetektorok esetében fordítsunk gondot a jelamplitúdó diszkriminációs szint helyes megválasztására! Mint ismeretes, az említett detektortípusnál az amplitúdódiszkriminációval jelentősen csökkenthető a 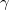 és zajháttér. A diszkriminációs szint beállításhoz először keressük meg azt a maximális diszkriminációs értéket, amelynél
még jelentős a számlálási sebesség, és válasszuk ennek kb. 1/8-át. A mérést maximum 300 s-ig érdemes folytatni. A kapott eredmény a PC-ben elhelyezett analizátor memóriájában hozzáférhető, elmenthető és kinyomtatható.
és zajháttér. A diszkriminációs szint beállításhoz először keressük meg azt a maximális diszkriminációs értéket, amelynél
még jelentős a számlálási sebesség, és válasszuk ennek kb. 1/8-át. A mérést maximum 300 s-ig érdemes folytatni. A kapott eredmény a PC-ben elhelyezett analizátor memóriájában hozzáférhető, elmenthető és kinyomtatható.
Kiértékelés
A későneutron-intenzitás időbeli csökkenését leíró függvény közelítőleg 6 db exponenciális összegének tekinthető. A kiértékelés célja a felezési idők és a relatív intenzitások meghatározása az adott körülmények között mérhető későneutron-csoportokra. Az eljárás első lépéseként a leghosszabb felezési idejű komponens paramétereit határozzuk meg abban az időtartományban, ahol a rövidebb felezési idejű komponensek már nem észlelhetők, de a mért intenzitások még kiemelkednek a háttérből. Az intenzitások logaritmikus transzformációja után egyenest illesztünk a kiválasztott időintervallum pontjaira. Meredekségének abszolút értéke a leghosszabb felezési idejű csoport bomlási állandóját adja, míg a tengelymetszet a relatív intenzitás logaritmusa.
A meghatározott paraméterekkel megadott exponenciális komponenst levonjuk az eredeti intenzitásokból, ahol így már csak a maradék csoportoktól származó intenzitás időbeli függvénye marad, majd megismételjük az eljárást. A kiértékelésre szánt időintervallumok között célszerű pontokat kihagyni, hogy a levonást követően a véletlen zaj miatt megjelenő esetleges negatív értékek ne zavarjanak (például a logaritmusképzés miatt). Megjegyezzük, hogy az eljárás csak közelítő pontosságú, mivel az illesztés előtti logaritmikus transzformálás az eltéréseket is transzformálja. A számításoknál referencia időpontnak azt az időpontot kell venni, amikor a minta az aktív zónát elhagyja. (Ennek az időpontnak felel meg a startjel.)
Pontosabb eredmény kapható a teljes adatsoron végrehajtott súlyozott legkisebb négyzetes illesztéssel.
Urántartalom meghatározása
A mérés során egy olyan mintában, amelyik ismeretlen mennyiségben tartalmaz természetes izotóp-összetételű urániumot, meg kívánjuk határozni a tömeg százalékában mért uránkoncentrációt. Az ismeretlen összetételű minta teljes tömege 105,5 mg.
A méréshez szükséges eszközök, anyagok
- A későneutron-paraméterek meghatározásánál használt berendezés (lásd 3.1. rész)
- analitikai mérleg
- polietilén csőposta besugárzó tokok
- reaktor és besugárzó csőposta
- két darab, a Nemzetközi Atomenergia Ügynökségtől (NAÜ) származó uránstandard
Az uránstandardok adatai
| jel | természetes izotóp összetételű U-koncentráció a mintában | a minta teljes tömege (mg) | |
| bizonylati koncentrációk szélső értékei (tömeg%) | U-koncentráció: átlagérték±szórás (tömeg%) | ||
| S-7 | 0,475 ÷ 0,527 | 0,501±0,013 | 93,3 |
| S-8 | 0,128 ÷ 0,142 | 0,135±0,0035 | 85,1 |
A mérés menete
A mérés a relatív későneutron-intenzitás mérésén alapul, amely az urántartalom gyors, pontos, roncsolásmentes meghatározását teszi lehetővé. A módszer gyorsasága és egyszerű kivitelezhetősége miatt ércminták sorozatelemzésére, érzékenysége folytán pedig az érckutatásban az urán dúsulásainak nyomozására szolgálhat. A mérés célja ismeretlen koncentrációjú minta urántartalmának meghatározása a NAÜ két uránstandardjával történő összehasonlítás alapján, továbbá a mérési hibának, valamint a kimutatási határnak a számítása. Ismeretlen mintaként uránszurokérc tartalmú kőzetet használunk.
A polietilén csőpostatokban az ismeretlen mintából, a standardokéhoz hasonló mennyiséget, kb. 100 mg-ot helyezünk el. A besugárzást 10 kW reaktorteljesítményen végezzük. Az analizátor beállítása megegyezik a korábbival (vö. A mérés menete rész). A mérés alapgondolata: a standardokban és az ismeretlen mintában a besugárzott urán bomlásgörbéjét ugyanaz a (2) szerinti függvény írja le, legfeljebb az egyes görbék 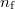 együtthatója térhet el. Ebből következik, hogy a lecsengő későneutron-intenzitási görbe bármelyik szakaszának összevetése alkalmas a minták összehasonlítására. Elvileg egy adott időpontbeli intenzitás - akár egy csatorna - is elegendő lenne, de több csatorna összegzésével a kiértékelés alapjául szolgáló impulzusszám relatív szórását csökkenthetjük. Az összegzett csatornák kiválasztásában az alábbi szempontokat vesszük figyelembe.
együtthatója térhet el. Ebből következik, hogy a lecsengő későneutron-intenzitási görbe bármelyik szakaszának összevetése alkalmas a minták összehasonlítására. Elvileg egy adott időpontbeli intenzitás - akár egy csatorna - is elegendő lenne, de több csatorna összegzésével a kiértékelés alapjául szolgáló impulzusszám relatív szórását csökkenthetjük. Az összegzett csatornák kiválasztásában az alábbi szempontokat vesszük figyelembe.
Mind a standardok, mind az ismeretlen minta tartalmaz oxigént, amelyben a besugárzás során az 17O(n,p)17N magreakció eredményeként 4,1 s felezési idejű neutronemitter mag, 17N keletkezik. Mivel az oxigén mennyisége mintánként változik (továbbá nem is ismert), a besugárzás után, a mérés megkezdése előtt célszerű 20 s ún. hűtési időt várni, mialatt az 17N-től származó neutronok gyakorlatilag eltűnnek, és így a minta és a standardok oxigéntartalmának különbsége nem zavaró. Ebből következik, hogy a 2. táblázat szerinti 3.÷6. későneutron-csoportok a mérés kezdetére szintén eltűnnek, tehát az urántartalom meghatározását a 22,72 s felezési idejű, elegendően nagy hozamú későneutron-csoportra érdemes alapozni. A hűtési idő növelése egyébként más szempontból is hasznos lehet, mivel rövid hűtési idők esetében az időmérés bizonytalansága (1 s-os felbontás) is nagyobb. A mérési időt úgy kell megválasztani, hogy a mérési idő végén a csökkenő későneutron-intenzitás még mindig jelentősen kiemelkedjék a háttérből. (A javasolt mérési időintervallum 20÷80 s.)
A szórás és a kimutatási határ számításához a háttér mérése is szükséges: üres tok besugárzásával a kiértékelésre szánt intervallumra vegyük fel a háttér-intenzitás értékeit.
A mérés kiértékelése
Egy standard mérése
A kiértékelés célja az ismeretlen minta uránkoncentrációjának meghatározása. Jelölje a mintára, illetve a standardra vonatkozó impulzusszámok összegét rendre 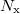 és
és 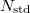 :
:
![\[ N_\mathrm{x} = \sum_{i=20}^{80}n_\mathrm{i,x} \hspace{20mm} N_\mathrm{std} = \sum_{i=20}^{80}n_\mathrm{i,std} \]](/images/math/e/1/0/e104509d36dbdca4278bf1b905d0e44d.png) |
(15) |
ahol 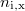 és
és 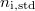 az i-edik csatorna tartalma az ismeretlen mintára, illetve a standardra vonatkozóan. Hasonló módon kapjuk az ezekből levonandó hátteret:
az i-edik csatorna tartalma az ismeretlen mintára, illetve a standardra vonatkozóan. Hasonló módon kapjuk az ezekből levonandó hátteret:
![\[ H_{x} = \sum_{i=20}^{80}h_{i,x} \]](/images/math/b/a/9/ba9a052a45493321129d1ddaf388b01c.png) |
(16) |
ahol 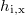 az i-edik csatorna tartalma az ismeretlen mintához tartozó háttér mérésekor. Ha a
standardot és az ismeretlen mintát időben egymáshoz közel mérjük, fel lehet tételezni, hogy ez a háttér érvényes a standardra is. Az általánosság kedvéért azonban megengedjük, hogy az utóbbihoz külön háttér,
az i-edik csatorna tartalma az ismeretlen mintához tartozó háttér mérésekor. Ha a
standardot és az ismeretlen mintát időben egymáshoz közel mérjük, fel lehet tételezni, hogy ez a háttér érvényes a standardra is. Az általánosság kedvéért azonban megengedjük, hogy az utóbbihoz külön háttér, 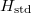 tartozzon. Az ismeretlen koncentrációt azzal a feltételezéssel határozzuk meg, hogy a minta fajlagos (egységnyi tömegre vonatkozó) beütésszáma a C uránkoncentrációval arányos:
tartozzon. Az ismeretlen koncentrációt azzal a feltételezéssel határozzuk meg, hogy a minta fajlagos (egységnyi tömegre vonatkozó) beütésszáma a C uránkoncentrációval arányos:
![\[ \frac{N-H}{m} = aC \]](/images/math/2/5/9/259d996c3cd9d628d4ca8869f0d96e7a.png) |
(17) |
ahol 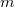 a minta tömege, és
a minta tömege, és  valamilyen (ismeretlen) arányossági tényező. Természetesen
a (17) összefüggés nem a mért adatokra, hanem csak azok várható értékére érvényes.
Viszont a (17) összefüggés lehetővé teszi, hogy az egyik standardra kapott mérési adatok
alapján becslést adjunk az ismeretlen a paraméterre:
valamilyen (ismeretlen) arányossági tényező. Természetesen
a (17) összefüggés nem a mért adatokra, hanem csak azok várható értékére érvényes.
Viszont a (17) összefüggés lehetővé teszi, hogy az egyik standardra kapott mérési adatok
alapján becslést adjunk az ismeretlen a paraméterre:
![\[ \tilde{a} = \frac{N_\mathrm{std}-H_\mathrm{std}}{m_\mathrm{std}-C_\mathrm{std}} \]](/images/math/5/2/b/52bd5147f4ba6b7701f915b239cc5f14.png) |
(18) |
ahol az "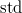 " index a standardra vonatkozóan mért adatokra utal.
" index a standardra vonatkozóan mért adatokra utal. 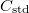 a kiválasztott
standard bizonylati koncentrációja (tömeg%, vö. 3. táblázat). Ennek alapján az ismeretlen
minta uránkoncentrációját a
a kiválasztott
standard bizonylati koncentrációja (tömeg%, vö. 3. táblázat). Ennek alapján az ismeretlen
minta uránkoncentrációját a
![\[ C_{x} = \frac{N_{x}-H_{x}}{m_{x}\tilde{a}} \]](/images/math/1/5/4/154fd4d248e1a547c48157b579c0b322.png) |
(19) |
képlettel becsüljük. Ha csak egy standardot mérünk, ez a képlet jelenti a kiértékelés végét. Mielőtt a két standard esetét tárgyalnánk, adjuk meg a (19)-hez tartozó hibaszámítási képleteket.
Tekintve, hogy tömeget (az egyéb hibaforrásokhoz képest) nagy pontossággal tudunk mérni, 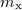 és
és 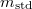 mérési hibáját elhanyagoljuk. A háttérrel csökkentett beütésszámok szórásnégyzetét a Poisson-eloszlás alapján becsüljük:
mérési hibáját elhanyagoljuk. A háttérrel csökkentett beütésszámok szórásnégyzetét a Poisson-eloszlás alapján becsüljük:
![\[ \sigma^{2}_{std} \approx N_{std}+H_{std} \hspace{20mm} \acute{e}s \hspace{20mm} \sigma^{2}_{x} \approx N_{x}+H_{x} \]](/images/math/3/a/d/3adad408159533eefb3f987e2004d5bd.png) |
(20) |
Az  paraméter (18) szerint becsült értékének a szórásnégyzete:
paraméter (18) szerint becsült értékének a szórásnégyzete:
![\[ \sigma^{2}_{a} = {\tilde{a}}^2 \Bigg(\frac{N_{std}+H_{std}}{(N_{std}-H_{std})^2}+\frac{\sigma^2_{C_{std}}}{C^2_{std}}\Bigg) \]](/images/math/a/c/c/acc19c645d347095bf34dddde9a7c410.png) |
(21a) |
továbbá a (19) szerint számolt uránkoncentrációé:
![\[ \sigma^{2}_{C_{x}} = C^2_{x} \Bigg(\frac{N_{x}+H_{x}}{(N_{x}-H_{x})^2}+\frac{\sigma^2_{a}}{\tilde{a}^2}\Bigg) \]](/images/math/1/d/5/1d5cefc9db2ccb73531294e9a24457a4.png) |
(21b) |
A (21) képletek levezetése a matematikai statisztikai elemeiből következik, ezért nem is részletezzük.
Két standard mérése
Amikor mindkét standardot mérjük, több kiértékelési módszer kínálkozik. A legegyszerűbb az a paraméternek mindkét standard alapján való független becslése:
![\[ \tilde{a}_{i} = \frac{N_{i}-H_{i}}{m_{i}C_{i}} \hspace{20mm} (i = 1,2) \]](/images/math/c/b/1/cb1ecd9abd7f98bd29015b7d799d83d5.png) |
(22) |
ahol az "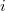 " index az egyes standard mintákra mért adatokat jelöli. Az így kapott értékek
szórásnégyzetét (21a) mintájára becsülhetjük:
" index az egyes standard mintákra mért adatokat jelöli. Az így kapott értékek
szórásnégyzetét (21a) mintájára becsülhetjük:
![\[ \sigma^{2}_{ai} = {\tilde{a}_{i}}^2 \Bigg(\frac{N_{i}+H_{i}}{(N_{i}-H_{i})^2}+\frac{\sigma^2_{Ci}}{C^2_{i}}\Bigg) \hspace{20mm} (i = 1,2) \]](/images/math/d/0/f/d0fd3bfc46eabb4519300acc34c2f060.png) |
(23) |
Az  paraméter végső értékét ezek súlyozott átlagolásával becsülhetjük:
paraméter végső értékét ezek súlyozott átlagolásával becsülhetjük:
![\[ \tilde{a} = \frac{\displaystyle\sum_{i=1}^{2}\tilde{a}_{i}/\sigma^2_{ai}}{\displaystyle\sum_{i=1}^{2}1/\sigma^2_{ai}} \]](/images/math/f/2/1/f215c6ffaccebc26857b217e40505b7b.png) |
(24a) |
amelynek a szórásnégyzete:
![\[ \sigma^2_{a} = \frac{1}{\displaystyle\sum_{i=1}^{2}1/\sigma^2_{ai}} \]](/images/math/3/e/4/3e4e0b840a79d405df3ac224c640827a.png) |
(24b) |
Kevésbé heurisztikus becslést kapunk, ha a (17) képletre alapozva az  paramétert lineáris regresszióval becsüljük. Ez azt jelenti, hogy az
paramétert lineáris regresszióval becsüljük. Ez azt jelenti, hogy az  paraméter függvényében keressük a
paraméter függvényében keressük a
![\[ Q=\sum_{i=1}^{2}w_{i}\Bigg(\frac{N_{i}-H_{i}}{m_{i}}-aC_{i}\Bigg)^2 \]](/images/math/5/6/0/560a8bedc9cde6e039bf7ba6012266c9.png) |
(25a) |
négyzetösszeg minimumát, amelyben a súlyok a mért mennyiségek szórásnégyzeteivel fejezhetők ki:
![\[ w^{-1}_{i} = \frac{N_{i}+H_{i}}{m^2_{i}}+a^2\sigma^2_{C_{i}} \]](/images/math/0/e/6/0e691e7fcc6b66b217ee78e90c2ffb0c.png) |
(25b) |
Ennek a minimumproblémának a megoldása könnyen levezethető:
![\[ \tilde{a} = \frac{\displaystyle\sum_{i=1}^{2}w_{i}C_{i}\frac{N_{i}-H_{i}}{m_{i}}}{\displaystyle\sum_{i=1}^{2}w_{i}C^2_{i}} \]](/images/math/6/8/6/68673bc04a9448c6759c41265fc3e24c.png) |
(26a) |
amelynek a szórásnégyzete:
![\[ \sigma^2_{a} = \frac{1}{\displaystyle\sum_{i=1}^{2}w_{i}C^2_{i}} \]](/images/math/6/8/0/680b042c853a3b20c55a516f561504ae.png) |
(26b) |
Tekintve, hogy a 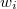 i súlyok a (25b) képlet szerint függnek az
i súlyok a (25b) képlet szerint függnek az  paramétertől, a (26a) képlet alkalmazása
paramétertől, a (26a) képlet alkalmazása  -ra nézve iterációt igényel.[9] A (24a) szerinti módszer ilyen iterációt nem tesz szükségessé.
-ra nézve iterációt igényel.[9] A (24a) szerinti módszer ilyen iterációt nem tesz szükségessé.
Akár a (22)÷(24) formulákat, akár a (25)÷(26) formulákat használjuk, az ismeretlen uránkoncentráció meghatározására a (19) és (21b) képleteket kell alkalmaznunk. A két kiértékelési mód egymással egyenértékű. Ajánlatos, hogy az Olvasó ezt bizonyítsa be. Útmutatás: a (23) képletben (de csak ott!) írjunk 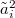 helyébe
helyébe 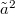 -t; ezután egyszerű algebrai átalakításokkal beláthatjuk, hogy (24a) és (24b) pontosan ugyanazt adja, mint (26a), illetve (26b). Kérdés: miért elég ennek bizonyítása a két becslés egyenértékűségének a belátásához?
-t; ezután egyszerű algebrai átalakításokkal beláthatjuk, hogy (24a) és (24b) pontosan ugyanazt adja, mint (26a), illetve (26b). Kérdés: miért elég ennek bizonyítása a két becslés egyenértékűségének a belátásához?
Kimutatási határ
A kimutatási határ definíciójánál az urán mennyiség meghatározás alapjául szolgáló nettó impulzusszám háttérből való szignifikáns kiemelkedését kell biztosítani statisztikai kritériumok alapján, másként megfogalmazva azt kell eldöntenünk, hogy van-e effektus vagy nincs, és ennek a döntésnek a mennyiségi megalapozását kell megadnunk. A döntés során alapvetően kétféle hibát követhetünk el. Az első az úgynevezett elsőfajú hiba melynél azt feltételezzük, hogy a mért összegzett intenzitás egy része a minta urán tartalmától származik, pedig csak a háttér pozitív fluktuációjáról van szó. Másodfajú hibát akkor követünk el, ha mért impulzusszám egy része urántól származik, de úgy gondoljuk hogy ez csak a háttér véletlen fluktuációja.
Az elsőfajú hiba ellen bizonyos megbízhatósági szinten - centrált normális zaj feltételezéssel - , úgy védhetjük magunkat, hogy a hasznos jel komponenstől elvárjuk, hogy a háttér szórását a konfidencia szinttől függő mértékben haladja meg.
![\[ L_{c1} = k_{1}\sigma_{h} = k_{1}\sqrt{N_{h}} \]](/images/math/b/d/3/bd3446d5f0d8fd2c3d0b01851678dcea.png) |
Ahol 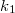 az elsőfajú hibára vonatkozó szignifikancia szinttől függő egyoldali kvantilis.
az elsőfajú hibára vonatkozó szignifikancia szinttől függő egyoldali kvantilis.
A másodfajú hiba valószínűsége általában valamilyen konkrét ellenhipotézis formájában fogalmazható meg. Itt ésszerű kiindulás az, hogy feltételezünk egy 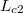 nagyságú nettó effektust, melynek meg kell haladnia az előbb definiált
nagyságú nettó effektust, melynek meg kell haladnia az előbb definiált 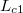 szintet olyan mértékben, hogy az alá
szintet olyan mértékben, hogy az alá 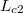 bizonyos szintű negatív fluktuációi révén se kerülhessen. Azaz
bizonyos szintű negatív fluktuációi révén se kerülhessen. Azaz 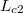 legyen
legyen 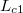 plusz
plusz 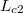 szórásának megfelelő kvantilissel vett szorzata:
szórásának megfelelő kvantilissel vett szorzata:
![\[ L_{c2} = L_{c1} + k_{2}\sqrt{\sigma^2_{L_{c2}}+\sigma^2_{h}} \]](/images/math/4/4/e/44e0f39c61fa15aa2ed5c72f36690d52.png) |
Ahol 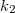 a másodfajú hibára vonatkozó szignifikancia szinthez tartozó kvantilis. Ha
a másodfajú hibára vonatkozó szignifikancia szinthez tartozó kvantilis. Ha 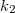 =
= 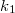 feltételből indulunk ki (ettől való eltérés a kétféle hibából eredő kockázat alapján lehetséges), akkor a háttérből még szignifikánsan kiemelkedő impulzusszám:
feltételből indulunk ki (ettől való eltérés a kétféle hibából eredő kockázat alapján lehetséges), akkor a háttérből még szignifikánsan kiemelkedő impulzusszám:
![\[ L_{c2} = k^2 + 2L_{c1} = k^2 + 2k\sqrt{N_{h}} \]](/images/math/c/0/5/c059f72131890b5433eea1d50c86b0f8.png) |
E mennyiséget kell a standardnál mérhető impulzusszámhoz hasonlítani, hogy a urán mennyiségre vonatkozó kimutatási határ értéket megkapjuk.
Ellenőrző kérdések
- Mik a késő neutronok?
- Ismertesse a késő neutronok keletkezési mechanizmusát!
- Mik az anyamagok?
- Mik a prompt neutronok?
- Ismertesse a prompt neutronok keletkezési mechanizmusát!
- Mi a különbség a prompt és a későneutronok energia eloszlása között?
- Mi a periódus idő?
- Mi a szerepe a késő neutronoknak a reaktor szabályzásban?
- Ismertesse a késő neutronok mérésénél alkalmazott módszert!
- Milyen csoportokba sorolhatjuk a késő neutronokat és minek alapján?
- Ismertesse az uránkoncentráció meghatározás elvét!
Irodalom
- G. R. Keepin: Physics of Nuclear Reactors, Addison-Wesley Publishing Co., Massachusetts (1965)
- G. R. Keepin: Interpretation of Delayed Neutron Phenomena, J. Nucl. Energy, 7, 13 (1958)
- G. R. Keepin, T. F. Wimmet, R. K. Zeigler: Delayed Neutron from Fissionable Isotopes of Uranium, Plutonium and Thorium, Phys. Rev., 107, 1044 (1957)
- Kiss D., Quittner P., Neutronfizika, Akadémiai Kiadó, Budapest 1971.
- Szatmáry Z., Bevezetés a reaktorfizikába, Egyetemi jegyzet (ELTE), 1991.
Külső hivatkozások
A Későneutron-paraméterek vizsgálata, uránkoncentráció meghatározása laborjegyzet forrása elérhető a [1] linken:
Lábjegyzetek
- ↑ A hasadás pillanatában (azaz 10-14 s-on belül) keletkező atommagokat hasadványoknak nevezzük. Ezek később elektronokat szednek fel, majd radioaktív bomlások révén új atomokká alakulnak át. Ez utóbbiakat hasadási termékeknek nevezzük.
- ↑ Ezek a Ga, As, Se, Br, Kr, Rb, Sr, Y, In, Sn, Sb, Te, I, Xe, Cs, Ba, La és Tl egyes izotópjai.
- ↑ Ez a fejezet azoknak szóló összefoglalás, akik nem hallgatták a Reaktorfizika előadást, a többieknek könnyű olvasmány.
- ↑ A reaktivitást (amely dimenzió nélküli szám) gyakran fejezzük ki %-ban. Például
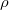 = 0,25% azt jelenti, hogy
= 0,25% azt jelenti, hogy 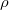 = 0,0025 (vagyis (3) alapján
= 0,0025 (vagyis (3) alapján 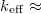 1,0025).
1,0025).
- ↑ A részletest tárgyalását lásd az [5] jegyzetben.
- ↑ Vegyük észre, hogy éppen ezzel az utóbbi taggal csökkent (7a) jobb oldalának első tagja a (4) egyenlethez képest.
- ↑ Emlékeztetünk arra az elemi algebrai szabályra, hogy két egymást követő együttható azonos előjele negatív, különböző előjele pedig pozitív gyököt jelent.
- ↑ Az Olvasó számára hasznos gyakorlat a közelítő képlet levezetése, így ugyanis ellenőrizheti, mennyire sikerült az eddigieket megértenie.
- ↑ Ennek az iterációnak a tulajdonságai erősen függnek az egyes szórások értékeitől. Ajánlatos, hogy az Olvasó a konkrét mérés esetében közelebbről ismerkedjen meg vele. Általános tendencia, hogy a (25b) szerinti súlyozás csökkenteni igyekszik a becsült értékét.