„UV-látható és NIR spektrofotometria” változatai közötti eltérés

A Fizipedia wikiből
a
a
 
(2 szerkesztő 23 közbeeső változata nincs mutatva)
21. sor: 21. sor:
 
''A mérés célja:''
 
''A mérés célja:''
  
−
A spektrofotometriai mérések széles körben elterjedt érintésmentes vizsgálati módszerek a legkülönfélébb kvalitatív illetve kvantitatív célokra mind a laboratóriumi mind az ipari területeken fizikai tulajdonságok (vastagság, törésmutató, szemcseméret, …) illetve analitikai információk (koncentráció, összetétel) megállapítására. A különböző spektrofotométerek igen eltérő tulajdonságokkal rendelkeznek nemcsak a működési hullámhossztartomány (látható, UV, IR, …) vagy a detektált sugárzás típusa (emittált, transzmittált vagy reflektált), hanem a mérések minősége (fotometriai pontosság, hullámhossz pontosság, reprodukálhatóság, dinamika, …), az elviselt mérési körülmények (labor, ipari: tág hőmérséklettűrés, nedvességtűrés, robbanásbiztosság) és az áruk alapján. Ezért nagyon fontos a kívánt alkalmazás és a választott készülék egymáshoz illesztése.
+
A spektrofotometriai mérések széles körben elterjedt érintésmentes vizsgálati módszerek a legkülönfélébb kvalitatív illetve kvantitatív célokra mind a laboratóriumi mind az ipari területeken fizikai tulajdonságok (vastagság, törésmutató, szemcseméret …) illetve analitikai információk (koncentráció, összetétel) megállapítására. A különböző spektrofotométerek igen eltérő tulajdonságokkal rendelkeznek nemcsak a működési hullámhossztartomány (látható, UV, IR …) vagy a detektált sugárzás típusa (emittált, transzmittált vagy reflektált), hanem a mérések minősége (fotometriai pontosság, hullámhossz pontosság, reprodukálhatóság, dinamika …), az elviselt mérési körülmények (labor, ipari: tág hőmérséklettűrés, nedvességtűrés, robbanásbiztosság) és az áruk alapján. Ezért nagyon fontos a kívánt alkalmazás és a választott készülék egymáshoz illesztése.
  
 
A hallgatói mérés természetesen csak a spektroszkópia egy kis szeletének (optikai tartomány) kis szeletébe enged bepillantást. A hallgatók az UV, látható, NIR (közeli infravörös) tartományban működő két utas, rácsos monokromátorral rendelkező, számítógéppel vezérelt spektrofotométerrel ismerkednek meg a készülékek néhány jellemző tulajdonságának meghatározásán és konkrét alkalmazásán keresztül. E rácsos spektrofotométer nagy pontosságú, de lassú, laboratóriumi körülmények között végrehajtható méréseket tesznek lehetővé.  
 
A hallgatói mérés természetesen csak a spektroszkópia egy kis szeletének (optikai tartomány) kis szeletébe enged bepillantást. A hallgatók az UV, látható, NIR (közeli infravörös) tartományban működő két utas, rácsos monokromátorral rendelkező, számítógéppel vezérelt spektrofotométerrel ismerkednek meg a készülékek néhány jellemző tulajdonságának meghatározásán és konkrét alkalmazásán keresztül. E rácsos spektrofotométer nagy pontosságú, de lassú, laboratóriumi körülmények között végrehajtható méréseket tesznek lehetővé.  
133. sor: 133. sor:
  
 
====Kezelőszervek a készüléken====
 
====Kezelőszervek a készüléken====
−
* ''Hálózati kapcsoló'' (I/O) a bekapcsolás után automatikus hullámhossz kalibráció történik (kb 3 perc).   
+
* ''Hálózati kapcsoló (I/O)'' a bekapcsolás után automatikus hullámhossz kalibráció történik (kb 3 perc).   
 
* ''Küvettatér'' küvetták, mérendő anyagok behelyezése, kivétele.
 
* ''Küvettatér'' küvetták, mérendő anyagok behelyezése, kivétele.
  
156. sor: 156. sor:
 
A monokromátorok egy-egy beállított hullámhosszon egy viszonylag keskeny (de nem végtelen keskeny) fénysávot enged tovább, illetve monokromátortól függően kisebb-nagyobb mértékben más, távolabb eső hullámhosszakat is. Ez azt jelenti, hogy egy elméletileg egyetlen vonalat tartalmazó spektrumot mérve nem vonalat, hanem valamilyen véges $\Delta \lambda$ félértékszélességű spektrumot kapunk, melyet a rendszertechnikában a készülék impulzus-válaszfüggvényének, vagy súlyfüggvényének hívnak (a spektroszkópiában: vonalalak-függvény). Tetszőleges elméleti spektrum (bemeneti jel) esetén a mért spektrum (kimeneti jel) a súlyfüggvény és a bemeneti függvény konvolúciójaként áll elő. Ennek következtében egyrészt a mérés végeredményeként az elméleti abszorpciós csúcsok ellaposodnak, kiszélesednek, az egymáshoz közeli abszorpciós csúcsok kevésbé élesen különböztethetőek meg, vagyis romlik a felbontás. Másrészt a mért adatok dinamikája véges lesz, hiszen nem tudunk tetszőlegesen kicsiny transzmissziós értéket mérni amiatt, hogy az adott hullámhosszhoz tartozó elméletileg nulla transzmisszió mellett a közeli hullámhosszakhoz tartozó nem nulla transzmissziót is hozzámérjük.
 
A monokromátorok egy-egy beállított hullámhosszon egy viszonylag keskeny (de nem végtelen keskeny) fénysávot enged tovább, illetve monokromátortól függően kisebb-nagyobb mértékben más, távolabb eső hullámhosszakat is. Ez azt jelenti, hogy egy elméletileg egyetlen vonalat tartalmazó spektrumot mérve nem vonalat, hanem valamilyen véges $\Delta \lambda$ félértékszélességű spektrumot kapunk, melyet a rendszertechnikában a készülék impulzus-válaszfüggvényének, vagy súlyfüggvényének hívnak (a spektroszkópiában: vonalalak-függvény). Tetszőleges elméleti spektrum (bemeneti jel) esetén a mért spektrum (kimeneti jel) a súlyfüggvény és a bemeneti függvény konvolúciójaként áll elő. Ennek következtében egyrészt a mérés végeredményeként az elméleti abszorpciós csúcsok ellaposodnak, kiszélesednek, az egymáshoz közeli abszorpciós csúcsok kevésbé élesen különböztethetőek meg, vagyis romlik a felbontás. Másrészt a mért adatok dinamikája véges lesz, hiszen nem tudunk tetszőlegesen kicsiny transzmissziós értéket mérni amiatt, hogy az adott hullámhosszhoz tartozó elméletileg nulla transzmisszió mellett a közeli hullámhosszakhoz tartozó nem nulla transzmissziót is hozzámérjük.
  
−
A készülék felbontását a $\frac{\lambda}{d \lambda}$-val definiáljuk. Amennyiben mind a készülék válaszfüggvényét (félértékszélessége: $\Delta \lambda_k$) , mind az interferencia-szűrő áteresztését (félértékszélessége: $\Delta \lambda_{sz}$, maximumhelye: $\lambda_{max}$) Gauss-görbével közelítjük a szűrőn mért spektrum szintén Gauss-görbe lesz $\Delta \lambda_m {{=}} \sqrt{\Delta \lambda_{sz}^2 + \Delta \lambda_k^2}$ félértékszélességgel. Ha a szűrőhöz áteresztésének félértékszélessége ismert, a $\lambda_{max}$-hoz tartozó $\frac{\lambda_{max}}{\Delta \lambda}$ felbontást becsülni tudjuk. Egyszerű geometriai optikai megfontolásokkal azt kapjuk, hogy a készülék válaszfüggvényének félértékszélessége (a spektroszkópiában: vonalszórás) a résszélességgel arányos. Ha ez így lenne tetszőlegesen kicsiny vonalszórást érhetnénk el a résszélesség megfelelő mértékű csökkentésével. A valóságban természetesen van egy alsó határ, melynél kisebb vonalszórást nem érhetünk el. Vagy másképp: a felbontásnak van egy elméleti felső határa.
+
A készülék felbontását $\frac{\lambda}{d \lambda}$-val definiáljuk, ami az adott hullámhosszon (λ) megkülönböztethető legközelebbi spektrális információ (dλ) (pl két csúcs). A dλ értéke közelíthető az impulzus válaszfüggvény félértékszélességével. A készülék impulzus válaszfüggvényének félértékszélessége meghatározható egy ismert spektrumú minta mérésével. Amennyiben mind a készülék válaszfüggvényét (félértékszélessége: Δλ<sub>k</sub>) , mind a minta, ami legtöbbször egy  interferencia-szűrő áteresztését (félértékszélessége: Δλ<sub>sz</sub>, maximumhelye: λ<sub>max</sub>) Gauss-görbével közelítjük a szűrőn mért spektrum szintén Gauss-görbe lesz, amelynek a félértékszélessége $\Delta \lambda_m {{=}} \sqrt{\Delta \lambda_{sz}^2 + \Delta \lambda_k^2}$ képlettel számítható. Ha az interferencia-szűrő áteresztésének félértékszélessége ismert, az interferencia-szűrő áteresztési maximumához tartozó hullámhosszhoz, λ<sub>max</sub>-hoz tartozó felbontást becsülni tudjuk $\frac{\lambda_{max}}{\Delta \lambda}$ számításával a mérés alapján. Egyszerű geometriai optikai megfontolásokkal azt kapjuk, hogy a készülék válaszfüggvényének félértékszélessége (λ<sub>k</sub>) a résszélességgel arányos. Az elérhető legnagyobb felbontást a rács véges mérete által okozott diffrakció korlátozza, így tetszőlegesen kicsiny vonalszórást nem tudunk elérni a résszélesség csökkentésével.  
 +
 
 +
A monokromátor által létrehozott diffrakciós képből a réssel kiszűrt próbanyaláb az összes spektrális komponenst tartalmazza különböző arányokban, ami korlátozza az egy spektrális komponens mérésekor elérhető legkisebb és legnagyobb jelszint arányát, amit dinamikának (OD) neveznek. Továbbá az optikai elemek alakhibái miatt szintén fellép bizonyos mértékű szóródás, ami tovább csökkenti a dinamikát. A véges dinamika eredményeképpen a Lambert-Beer törvény által meghatározott összefüggés kis transzmisszió esetén nem lesz lineáris, hanem a szórt fény által korlátozott dinamikához tartozó abszorbancia értékhez telítődik.  
 +
 
 +
Adott anyag különböző koncentrációk mellett felvett spektrumaiban az abszorpciós csúcsnál mérhető abszorbancia értékeket a koncentráció függvényében ábrázolva a dinamika meghatározható optikai denzitás (OD=-lg(T<sub>min</sub>)) egységekben. Ez az érték hullámhosszfüggő.
  
−
Az optikai és mechanikai elemeken szintén fellép bizonyos mértékű szóródás, ami a dinamikát még tovább csökkenti. Végeredményben a Lambert-Beer törvény követelte $–lg(T){{=}} \alpha hc$ összefüggés nem lesz lineáris, egy adott abszorbancia értéknél nagyobbat mérni nem tudunk.
 
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
 
| {{fig|UVNIR_04.png|fig:4|4. ábra}}
 
| {{fig|UVNIR_04.png|fig:4|4. ábra}}
−
|}  
+
|}
−
Anyagpáron különböző koncentrációk mellett felvett spektrumok abszorpciós csúcsain az abszorbancia értékeket a koncentráció függvényében ábrázolva a dinamika meghatározható optikai denzitás (OD) egységekben. Ez az érték kis mértékben anyag- és hullámhosszfüggő, az érték mellett ezeket is meg kell adni.
+
  
 
====Mérési feladat====
 
====Mérési feladat====
178. sor: 180. sor:
 
===Vékonyréteg vizsgálat az UV-látható spektrofotométeren===
 
===Vékonyréteg vizsgálat az UV-látható spektrofotométeren===
 
====Elmélet====
 
====Elmélet====
−
A transzmisszió és reflexió számolt, illetve spektroszkópon mért értékeinek összehasonlításával a rácsos UV-látható spektrométer jó lehetőséget ad a különböző rétegszerkezetek vizsgálatára. Az elméleti értékek számolására a történelem folyamán többféle módszert találtak ki. Ezek közül a legelterjedtebb az ún. mátrixos-leírás módszere, melyet sugárátvezetéssel a Maxwell-egyenletekből és a hozzájuk tartozó határfeltételekből származtathatunk.  Megvizsgálhatjuk például, hogy a tervezett antireflexiós réteg a gyártás után az elvártnak megfelelően sikerült-e. Mivel a labormérés keretei nem engedik meg a réteg megtervezésének – elkészíttetésének – ellenőrzésének elvégzését egy már elkészült, enyhén abszorbeáló, vékony (melynek transzmissziós spektrumán interferencia-mintázat figyelhető meg) réteget vizsgálnak a hallgatók. A felvett transzmissziós spektrum alapján a réteg törésmutatója, extinkciója, és vastagsága kerül meghatározásra.
+
A transzmisszió és reflexió számolt, illetve spektroszkópon mért értékeinek összehasonlításával a rácsos UV-látható spektrométer jó lehetőséget ad a különböző rétegszerkezetek vizsgálatára. Az elméleti értékek számolására a történelem folyamán többféle módszert találtak ki. Ezek közül a legelterjedtebb az ún. mátrixos-leírás módszere, melyet sugárátvezetéssel a Maxwell-egyenletekből és a hozzájuk tartozó határfeltételekből származtathatunk.  Megvizsgálhatjuk például, hogy a tervezett antireflexiós réteg a gyártás után az elvártnak megfelelően sikerült-e. Mivel a labormérés keretei nem engedik meg a réteg megtervezésének – elkészíttetésének – ellenőrzésének elvégzését egy már elkészült, enyhén abszorbeáló, vékony (melynek transzmissziós spektrumán interferencia-mintázat figyelhető meg) réteget vizsgálnak a hallgatók. A felvett transzmissziós spektrum alapján a réteg törésmutatója, extinkciója, és vastagsága kerül meghatározásra. Az extinkció a mintán áthaladó fény gyengülését adja meg, tartalmazza az elnyelést és a rugalmas és rugalmatlan szórásokat. Ha a szórás kicsi, akkor az extinkció közelítően megegyezik az abszorpcióval.
  
 
Tekintsünk egy $n_h$ valós törésmutatójú végtelen vastag hordozón egy h vastagságú, enyhén abszorbeáló $n + i\kappa (\kappa \ll n)$ törésmutatójú réteget!  
 
Tekintsünk egy $n_h$ valós törésmutatójú végtelen vastag hordozón egy h vastagságú, enyhén abszorbeáló $n + i\kappa (\kappa \ll n)$ törésmutatójú réteget!  
185. sor: 187. sor:
  
 
A teljes (hordozó + réteg) transzmisszióját az alábbi képlet adja meg és az ábrán látható módon néz ki:  
 
A teljes (hordozó + réteg) transzmisszióját az alábbi képlet adja meg és az ábrán látható módon néz ki:  
 +
$$T {{=}} \frac{Ax}{B - Cx\cos\phi + Dx^2}$$
 +
ahol: $x {{=}} e^{-\frac{4\pi }{\lambda }\kappa h}$ az extinkció a rétegen, $\qquad \phi{{=}} \frac{4\pi}{\lambda}nh$ a fázistolás  a rétegen, $\qquad A {{=}} 16n_hn^2 \qquad B {{=}} (n+1)^3(n+n_h^2) \qquad C {{=}} 2(n^2 - 1)(n^2 - n_h^2) \qquad D {{=}} (n-1)^3(n-n_h^2)$ törésmutatófüggő változók.
 +
 
{|  cellpadding="5" cellspacing="0" align="center"
 
{|  cellpadding="5" cellspacing="0" align="center"
 
|-
 
|-
−
| {{fig|UVNIR_05.png|fig:5|5. ábra}}
+
| {{fig|UVNIR_05.png|fig:5|5. ábra Tipikus transzmissziós spektrum}}
 
|}  
 
|}  
−
$$T {{=}} \frac{Ax}{B - Cx\cos\phi + Dx^2}$$
+
A rétegszerkezeten való áthaladáskor hullámhossztól függően változó fázistolás jön létre, ami transzmissziós spektrumban minimumokat és maximumokat hoz létre attól függően, hogy konstruktív vagy destruktív interferencia tapasztalható az adott hullámhosszon a réteg felületéről és a réteg-hordozó határon reflektálódó nyalábok között. Az interferencia-mintázat maximumaira és minimumaira egy-egy burkoló görbe illeszthető, ezek a T<sub>M</sub> maximum és T<sub>m</sub> minimum görbék:
−
ahol: $x {{=}} e^{-\frac{4\pi }{\lambda }\kappa h} \qquad \phi{{=}} \frac{4\pi}{\lambda}nh \qquad A {{=}} 16n_hn^2 \qquad B {{=}} (n+1)^3(n+n_h^2) \qquad C {{=}} 2(n^2 - 1)(n^2 - n_h^2) \qquad D {{=}} (n-1)^3(n-n_h^2)$
+
−
 
+
−
Az interferencia-mintázatot burkoló T<sub>M</sub> maximum és T<sub>m</sub> minimum görbékre:
+
 
$$T_M {{=}} \frac{Ax}{B - Cx + Dx^2} \qquad T_m {{=}} \frac{Ax}{B + Cx + Dx^2}$$
 
$$T_M {{=}} \frac{Ax}{B - Cx + Dx^2} \qquad T_m {{=}} \frac{Ax}{B + Cx + Dx^2}$$
 
A burkoló görbék reciprokait egymásból kivonva csak a törésmutatótól (az abszorpciótól független) egyenletet kapunk, így belőle a réteg törésmutatója a hullámhossz függvényében meghatározható:
 
A burkoló görbék reciprokait egymásból kivonva csak a törésmutatótól (az abszorpciótól független) egyenletet kapunk, így belőle a réteg törésmutatója a hullámhossz függvényében meghatározható:
  
−
$\frac{1}{T_m} - \frac{1}{T_M} {{=}} \frac{2C}{A} \quad \to \quad n {{=}} \sqrt{N + \sqrt{N^2 - n_h^2}}$, ahol $N {{=}} 2\cdot n_h \cdot \frac{T_M - T_m}{T_M \cdot T_m} + \frac{n_h^2 + 1}{2}$.
+
$\frac{1}{T_m} - \frac{1}{T_M} {{=}} \frac{2C}{A} \quad \to \quad n {{=}} \sqrt{N + \sqrt{N^2 - n_h^2}}$, ahol $N {{=}} 2\cdot n_h \cdot \frac{T_M - T_m}{T_M \cdot T_m} + \frac{n_h^2 + 1}{2}$ egy fizikai tartalom  nélküli változó.
 +
 
 +
Ha már n(λ)-t ismerjük x (extinkció), illetve a törésmutató komplex része (κ) többféle módon számolható. A burkoló-görbék egyenletei például x-től négyzetesen függenek és így x-re megoldhatók (a TM-ből számolt érték pontosabb).
 +
 
 +
A maximumokból számolva:
 +
 
 +
$x {{=}} \frac{E_{M}-\sqrt{E_{M}^2-(n^2-1)^3\cdot (n^2-n_h^4)}}{(n-1)^3\cdot(n-n_h^2)}$, ahol $E_{M} {{=}} \frac{8\cdot n^2\cdot n_h}{T_{M}}+ (n^2-1)(n^2-n_h^2)$
  
−
Ha már $n(\lambda)$-t ismerjük x, illetve az extinkció többféle módon számolható. A burkoló-görbék egyenletei például x-től négyzetesen függenek és így x-re megoldhatók (a T<sub>M</sub>-ből számolt érték pontosabb):
+
a minimumból számolva:
  
−
$x {{=}} \frac{E_{M,m}-\sqrt{E_{M,m}^2-(n^2-1)^3\cdot (n^2-n_h^4)}}{(n-1)^3\cdot(n-n_h^2)}$, ahol $E_{M,m} {{=}} \frac{8\cdot n^2\cdot n_h}{T_{M,m}}\pm (n^2-1)(n^2-n_h^2)$.
+
$x {{=}} \frac{E_{m}-\sqrt{E_{m}^2-(n^2-1)^3\cdot (n^2-n_h^4)}}{(n-1)^3\cdot(n-n_h^2)}$, ahol $E_{m} {{=}} \frac{8\cdot n^2\cdot n_h}{T_{m}}- (n^2-1)(n^2-n_h^2)$ E<sub>M</sub> és E<sub>m</sub> fizika tartalom nélküli változók.
  
−
A törésmutató és extinkció számolásához T<sub>M</sub> és T<sub>m</sub> különböző hullámhosszhoz tartozó értékeinek ismeretére van szükségünk. A közbeeső értékeket számítógépen parabolikus interpoláció segítségével számolhatjuk. A görbékre függvényt illesztve a pontosságot rontanánk. A labormérésen a hallgatók csak a minimum- illetve maximumhelyeken vett törésmutatót és extinkciót számolják oly módon, hogy a minimumhelyen vett T<sub>M</sub>-értéket a két szomszédos maximumérték átlagolásával számolják, és fordítva.
+
A törésmutató és extinkció számolásához T<sub>M</sub> és T<sub>m</sub> különböző hullámhosszhoz tartozó értékeinek ismeretére van szükségünk. A labormérésen csak a minimum- illetve maximumhelyeken vett törésmutatót és extinkciót kell kiszámolni oly módon, hogy a minimumhelyen vett T<sub>M</sub>-értéket a két szomszédos maximumérték közötti lineáris interpolációval lehet meghatározni, és fordítva.
  
 
A rétegvastagság meghatározása a szélsőértékek helyéből lehetséges.  
 
A rétegvastagság meghatározása a szélsőértékek helyéből lehetséges.  
225. sor: 233. sor:
 
Így, ha l/2-t ábrázoljuk $n/\lambda$ függvényében az egyenes meredeksége 2h.
 
Így, ha l/2-t ábrázoljuk $n/\lambda$ függvényében az egyenes meredeksége 2h.
  
−
<u>Megjegyzés</u>: a spektrométer véges spektrális vonalszórása ezt a mérést is jelentősen befolyásolja, mégpedig a spektrumban megfigyelhető interferencia-mintázat összenyomásához vezet, ezért a gyakorlatban a résszélességnek megfelelően korrigálni kell a mért spektrumokat.
+
<u>Megjegyzés</u>: a spektrométer véges spektrális vonalszórása ezt a mérést is jelentősen befolyásolhatja, mégpedig a spektrumban megfigyelhető interferencia-mintázat összenyomásához vezethet, ezért szükséges lehet a spektrumok dekonvoluciója a résszélességnek megfelelően.
  
 
====Mérési feladat====
 
====Mérési feladat====
231. sor: 239. sor:
 
* A tiszta hordozó transzmissziós spektruma alapján számolja ki annak törésmutatóját a hullámhossz függvényében!
 
* A tiszta hordozó transzmissziós spektruma alapján számolja ki annak törésmutatóját a hullámhossz függvényében!
 
* Adja meg a rétegezett minta transzmissziós spektrumának maximum- és minimumhelyeit, majd határozza meg az összes szélsőértékhez tartozó T<sub>M</sub> és T<sub>m</sub> értékeket!
 
* Adja meg a rétegezett minta transzmissziós spektrumának maximum- és minimumhelyeit, majd határozza meg az összes szélsőértékhez tartozó T<sub>M</sub> és T<sub>m</sub> értékeket!
−
* Határozza meg ezekben a pontokban a réteg törésmutatóját és extinkcióját!
+
* Határozza meg ezekben a pontokban a réteg törésmutatóját és extinkcióját(n+iκ)!
 
* Határozza meg a vastagságot valamelyik (iterációs ill. grafikus) módszerrel!
 
* Határozza meg a vastagságot valamelyik (iterációs ill. grafikus) módszerrel!
  
 
==PDF formátum==
 
==PDF formátum==
−
*[[Media:Spektrofotometer_PE_2.pdf|UV-látható és NIR spektrofotometria (nem korrigált)]]
+
*[[Media:Spektrofotometer2017.pdf|UV-látható és NIR spektrofotometria]]
  
 
</wlatex>
 
</wlatex>
−
<!--Utolso szerkesztes: 2012.12.19-->
+
<!--Utolso szerkesztes: 2017.02.10-->

A lap jelenlegi, 2017. február 14., 09:38-kori változata


A mérés célja:

A spektrofotometriai mérések széles körben elterjedt érintésmentes vizsgálati módszerek a legkülönfélébb kvalitatív illetve kvantitatív célokra mind a laboratóriumi mind az ipari területeken fizikai tulajdonságok (vastagság, törésmutató, szemcseméret …) illetve analitikai információk (koncentráció, összetétel) megállapítására. A különböző spektrofotométerek igen eltérő tulajdonságokkal rendelkeznek nemcsak a működési hullámhossztartomány (látható, UV, IR …) vagy a detektált sugárzás típusa (emittált, transzmittált vagy reflektált), hanem a mérések minősége (fotometriai pontosság, hullámhossz pontosság, reprodukálhatóság, dinamika …), az elviselt mérési körülmények (labor, ipari: tág hőmérséklettűrés, nedvességtűrés, robbanásbiztosság) és az áruk alapján. Ezért nagyon fontos a kívánt alkalmazás és a választott készülék egymáshoz illesztése.

A hallgatói mérés természetesen csak a spektroszkópia egy kis szeletének (optikai tartomány) kis szeletébe enged bepillantást. A hallgatók az UV, látható, NIR (közeli infravörös) tartományban működő két utas, rácsos monokromátorral rendelkező, számítógéppel vezérelt spektrofotométerrel ismerkednek meg a készülékek néhány jellemző tulajdonságának meghatározásán és konkrét alkalmazásán keresztül. E rácsos spektrofotométer nagy pontosságú, de lassú, laboratóriumi körülmények között végrehajtható méréseket tesznek lehetővé.

Tartalomjegyzék


Elméleti összefoglaló

A spektroszkópia fogalma

A spektroszkópia tudománya valamely közeg atomjai, molekulái vagy egyéb kémiai elemei által abszorbeált, szórt (reflektált) vagy emittált elektromágneses sugárzás hullámhossz függvényében történő mérésével és vizsgálatával foglalkozik. Mivel az abszorpció vagy az emisszió a kölcsönható részecske (atom, molekula) energiaállapotában bekövetkező változással van összefüggésben és minden egyes anyagnak karakterisztikus energiaállapotai vannak, a kölcsönható anyagot azonosítani lehet. Mint később kiderül kvantitatív információk szerzésére is van lehetőség.

Az elektromágneses hullám

Az anyag és a fény kölcsönhatása az elektromágneses sugárzás teljes tartományát átfogja a kozmikus sugárzás 10-9 nm-es hullámaitól a rádióhullámok 1000 km-es hullámáig. Az optikai hullámhossz tartomány határai ~ 10 és 105 nm. A sugárzások a hullámhosszon kívül az anyagban előidézett kémiai és fizikai változásokban különböznek.

1. ábra

UV-látható tartomány

A látható és UV tartományban a gerjesztő foton energiája a külső elektronok kötési energiájának megváltoztatására fordítódik. Ebben a tartományban a spektrofotometriát legfőképpen laboratóriumi vizsgálatokra használják. Érintésmentességének köszönhetően kedvelt kémiai analitikai (minőségi és mennyiségi) vizsgálatokra, reakciók nyomon követésére (keveredés, egyensúly, fotometriai titrálás, …). Megfelelő előkészítéssel fémes, nemfémes és szerves vegyületek egyaránt vizsgálhatóak segítségével. Az optikai alkalmazások terén elsősorban vékonyréteg vizsgálatokra, ellenőrzésre használják.

NIR tartomány jellegzetességei

A közeli infravörös spektroszkópiával a legtöbb szerves és néhány szervetlen molekula vizsgálható. Ezen molekulák infravörös tartománybeli alaprezgései a NIR tartományban kisebb intenzitású és kiszélesedett felhangokat és kombinációs sávokat eredményeznek, melyek egymással gyakran átlapolódnak. Az átlapolódás következtében a hagyományos értelemben vett, Lambert-Beer törvényen alapuló kalibráció általában nem lehetséges, ennél bonyolultabb matematikai módszerekre, a többváltozós lineáris regresszió módszerére van szükség. Erre születtek az un. kemometriai szoftverek. Egy-egy jó kalibrációs modell elkészítéséhez 100-1000 nagyságrendű mintára van szükség. Az ipari alkalmazásra fejlesztett készülékek a kemometriai szoftverekkel kiegészítve az utóbbi 25-30 évben rohamosan növekvő népszerűséget vívtak ki maguknak a legkülönbözőbb kvalitatív illetve kvantitatív analitikai információt kívánó alkalmazási területeken az egyszerű nyersanyagtól a komplex termékek vizsgálatáig, így például az élelmiszer-, a textil-, a kozmetikai, a gyógyszer , a vegy- és a műanyagiparban.

Spektrofotométerek felépítése

Egy spektroszkóp alapvető optikai fő egységei: a fényforrás(ok), a spektrális bontóelem(ek)-et magába foglaló monokromátor(ok), az érzékelő(k) és maga a minta. A berendezés része még valamilyen megjelenítő/rögzítőegység: lapíró, vagy korszerűbb esetben számítógép. A hallgatói mérésben használt spektrofotométer Perkin-Elmer Lambda 35 típusú. A készülék monokromátora egy konkáv holografikus rácsot használ (1053 vonalpár/mm). Félvezető fotodióda a detektor. Két fényforrást alkalmaz a készülék egy Deutérium lámpát (<326nm) és egy wolfram izzót (>326nm).

Monokromátor felépítése

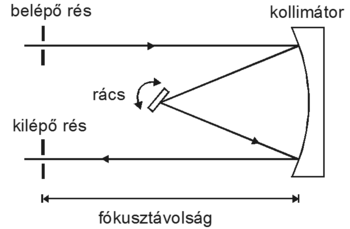
A spektrométerek azon elemei, ahol az összetett fényt spektrális komponenseire bontjuk. A spektrális bontóelemen kívül (szűrő, prizma, rács) bemeneti rést, kimeneti rést és leképező optikát tartalmaz. Működésének lényege, hogy a bemeneti rés ’fehér’ fénnyel kivilágított képét oly módon képezi a kimeneti résre, hogy azon keresztül már csak olyan komponensek jutnak át, melyek hullámhossza egy keskeny, monokromatikusnak tekinthető tartományba esnek. Az alábbi ábra egy tipikus (Ebert-féle) monokromátor elrendezést mutat.

2. ábra

Diffrakciós rács

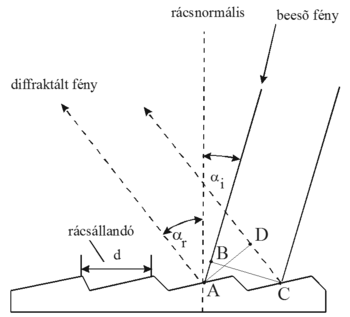
Az optikai diffrakciós rács nem más, mint N darab egyforma szélességű rácsprofil közvetlen egymás mellett, d távolságban melyek vagy átvezetik (transzmissziós rács) vagy reflektálják (reflexiós rács) a beeső sugárzást. A rács felületére érkező fény hullámfrontja diffraktálódik, és különböző irányokban szórtan folytatja útját. Egy adott irányba adott beesési szög mellett bizonyos hullámhosszakra konstruktív interferencia lép fel. A rács forgatásával az erősítés feltétele más-más hullámhosszakra teljesül.

3. ábra
\[\delta {{=}} \frac{2\pi }{\lambda }\left (AB - DC\right ) {{=}}\frac{2\pi d\left ( sin\alpha_i – sin\alpha_r\right )}{\lambda} {{=}} 2\pi m\]
\[d\left (sin\alpha_i - sin\alpha_r\right ) {{=}} m\lambda\]

ahol d rácsállandó

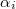\setbox0\hbox{$\alpha_i$}% \message{//depth:\the\dp0//}% \box0% beesési szög

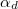\setbox0\hbox{$\alpha_d$}% \message{//depth:\the\dp0//}% \box0% konstruktív interferencia irányába diffraktált sugár szöge

m diffrakciós rendszám.

Az elhajlási rendek átfedéséből adódó átlapolódások zavaró hatását sáváteresztő- illetve élszűrőkkel kerülhetjük el. Rácsos monokromátor sávszélességét a rácsbarázda sűrűsége, az optikai rendszer fókusztávolsága és a be- illetve kilépő rés szélessége határozza meg. A zajnak (nemkívánt sugárzás) két forrása van: szellemek és szórt fény. A szellemek forrása a barázdák elhelyezkedésében lévő periodikus hibák, a szóródásé pedig a nemperiodikus pozícióhibák és a felületek nem tökéletes síksága.

Kétutas spektrofotométerek

Kétutas készülékben a monokromatikus hullám két részre van osztva, általában egyenlő teljesítménnyel. Az egyik nyaláb a mintán halad keresztül, a másik pedig üresen vagy a referencia oldaton. E módszerrel az időbeli instabilitások (például a lámpáé) kiküszöbölődnek. A spektrumfelvétel előtt, a két ágat össze kell kalibrálni (például egy szürke ék segítségével) úgy, hogy a minta nélkül a transzmisszió 100 % legyen.

Spektrofotométer jellemzői

P-E Lambda 35
hullámhossztartomány 190-1100 nm
lépésköz 10-0,1 nm
felbontás 0,5-4 nm
transzmisszió/ reflexió pontosság ± 0,05 T%
hullámhossz/ -szám pontosság ± 0,3 nm
transzmisszió/ reflexió reprodukálhatóság ±0,1 T%
hullámhossz/ -szám reprodukálhatóság ± 0,1 nm
körülmények 15..35 °C

Felbontás: az a hullámhossz /-szám távolság, amelyen belül két szomszédos abszorpciós csúcs felbontható, megkülönböztethető (hullámhosszfüggő).

Dinamika: abszorbancia skálán a minimális és maximális érték különbsége (hullámhossz és anyagfüggő).

Analitikai mérések alapja: a Lambert-Beer törvény

Ha monokromatikus nyaláb h vastagságú elnyelő rétegbe hatol a beérkező P0 sugárzási teljesítménynek egy része elnyelődik (a fotonok ütköznek a közeg molekuláival és gerjesztik azt), illetve szóródik, és a teljesítmény fokozatosan lecsökken. Igen vékony, dh vastagságú rétegen bekövetkező teljesítménycsökkenésre:

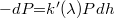\setbox0\hbox{$-dP {{=}} k’(\lambda)Pdh$}% \message{//depth:\the\dp0//}% \box0%, ahol 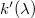\setbox0\hbox{$k'(\lambda ) \qquad $}% \message{//depth:\the\dp0//}% \box0% arányossági tényező

A h vastagságú anyagon áthaladott fény P teljesítményét a változók szétválasztásával, majd integrálással kapjuk meg.

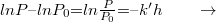\setbox0\hbox{$lnP – lnP_0 {{=}} ln\frac{P}{P_0} {{=}} –k’h \qquad \to $}% \message{//depth:\the\dp0//}% \box0% Lambert törvény

Amennyiben az egyes összetevők koncentrációjától való függést is figyelembe vesszük, és tízes alapú logaritmusra térünk át:

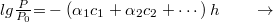\setbox0\hbox{$lg\frac{P}{P_0} {{=}} -\left ( \alpha_1c_1 + \alpha_2c_2 + \cdots\right )h \qquad \to $}% \message{//depth:\the\dp0//}% \box0% Lambert-Beer törvény

Amennyiben a fényszóródásból adódó vesztesség elhanyagolható 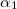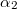\setbox0\hbox{$\alpha_1$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$\alpha_2$}% \message{//depth:\the\dp0//}% \box0%, … együtthatókat az összetevők abszorpciós koefficienseinek hívjuk.

Az abszorbancia definíció szerint 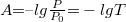\setbox0\hbox{$A {{=}} –lg\frac{P}{P_0} {{=}} -lgT$}% \message{//depth:\the\dp0//}% \box0%, ahol T a transzmittancia.

A Lambert-Beer törvény teszi lehetővé a mennyiségi analitikai vizsgálatok elvégzését.

Mérésben használt spektrofotométer használati utasítása

Bekapcsolás

Korszerűsített, kétsugaras, automatikus kalibrációs, számítógépről vezérelhető spektrofotométer. A kényelmes kezelhetőséget és a mérések utólagos kiértékelését a hozzákapcsolt számítógépen Windows alatt futó UVwinlab nevű program biztosítja.

Kezelőszervek a készüléken

  • Hálózati kapcsoló (I/O) a bekapcsolás után automatikus hullámhossz kalibráció történik (kb 3 perc).
  • Küvettatér küvetták, mérendő anyagok behelyezése, kivétele.

UVwinlab program ismertetése

  • Autozero : E gombot megnyomva tudjuk elvégezni a két fényutas kalibrálást a beállított mérési módszernek (method) megfelelő hullámhossz tartományban. Ha az UV tartományban is akarunk mérni, akkor a deutérium lámpát is be kell kapcsolni (method) és melegíteni.
  • Start: A mérési módszernek megfelelő tartományon elvégzi a mérést a készülék.
  • Spektrum lista mentés: a felvett spektrumokat a készülék egyedi formátumban menti, de lehetőség van a mérési eredmények lista szerű elmentésére is a SAVE AS parancs indítása után ASCII formátum kiválasztásával.

Mérési feladatok

UV-látható spektrofotométer

Kalibrálás (a készülék bemelegítéséről már előre gondoskodott a mérésvezető)

  • Válassza a SCANVIS mérési módszert a METHOD ablakban.
  • Győződjön meg róla, hogy nincs semmi minta a küvettatérben!
  • Klikkeljen a PC-n az AUTOZERO gombra.
  • A kalibrálás végén az aktuális transzmisszió és hullámhossz érték megjelenik az alsó kék státusz sorban.
  • Helyezzük be a mintát a küvettatérbe!
  • A mérés a START gomb megnyomásával indul!
  • A mérés elindulása utána képernyőn megjelenő koordinátarendszerben követhetjük nyomon a spektrumfelvétel alakulását.

Felbontás és dinamika mérése

Elmélet

A monokromátorok egy-egy beállított hullámhosszon egy viszonylag keskeny (de nem végtelen keskeny) fénysávot enged tovább, illetve monokromátortól függően kisebb-nagyobb mértékben más, távolabb eső hullámhosszakat is. Ez azt jelenti, hogy egy elméletileg egyetlen vonalat tartalmazó spektrumot mérve nem vonalat, hanem valamilyen véges 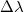\setbox0\hbox{$\Delta \lambda$}% \message{//depth:\the\dp0//}% \box0% félértékszélességű spektrumot kapunk, melyet a rendszertechnikában a készülék impulzus-válaszfüggvényének, vagy súlyfüggvényének hívnak (a spektroszkópiában: vonalalak-függvény). Tetszőleges elméleti spektrum (bemeneti jel) esetén a mért spektrum (kimeneti jel) a súlyfüggvény és a bemeneti függvény konvolúciójaként áll elő. Ennek következtében egyrészt a mérés végeredményeként az elméleti abszorpciós csúcsok ellaposodnak, kiszélesednek, az egymáshoz közeli abszorpciós csúcsok kevésbé élesen különböztethetőek meg, vagyis romlik a felbontás. Másrészt a mért adatok dinamikája véges lesz, hiszen nem tudunk tetszőlegesen kicsiny transzmissziós értéket mérni amiatt, hogy az adott hullámhosszhoz tartozó elméletileg nulla transzmisszió mellett a közeli hullámhosszakhoz tartozó nem nulla transzmissziót is hozzámérjük.

A készülék felbontását 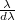\setbox0\hbox{$\frac{\lambda}{d \lambda}$}% \message{//depth:\the\dp0//}% \box0%-val definiáljuk, ami az adott hullámhosszon (λ) megkülönböztethető legközelebbi spektrális információ (dλ) (pl két csúcs). A dλ értéke közelíthető az impulzus válaszfüggvény félértékszélességével. A készülék impulzus válaszfüggvényének félértékszélessége meghatározható egy ismert spektrumú minta mérésével. Amennyiben mind a készülék válaszfüggvényét (félértékszélessége: Δλk) , mind a minta, ami legtöbbször egy interferencia-szűrő áteresztését (félértékszélessége: Δλsz, maximumhelye: λmax) Gauss-görbével közelítjük a szűrőn mért spektrum szintén Gauss-görbe lesz, amelynek a félértékszélessége 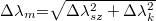\setbox0\hbox{$\Delta \lambda_m {{=}} \sqrt{\Delta \lambda_{sz}^2 + \Delta \lambda_k^2}$}% \message{//depth:\the\dp0//}% \box0% képlettel számítható. Ha az interferencia-szűrő áteresztésének félértékszélessége ismert, az interferencia-szűrő áteresztési maximumához tartozó hullámhosszhoz, λmax-hoz tartozó felbontást becsülni tudjuk 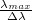\setbox0\hbox{$\frac{\lambda_{max}}{\Delta \lambda}$}% \message{//depth:\the\dp0//}% \box0% számításával a mérés alapján. Egyszerű geometriai optikai megfontolásokkal azt kapjuk, hogy a készülék válaszfüggvényének félértékszélessége (λk) a résszélességgel arányos. Az elérhető legnagyobb felbontást a rács véges mérete által okozott diffrakció korlátozza, így tetszőlegesen kicsiny vonalszórást nem tudunk elérni a résszélesség csökkentésével.

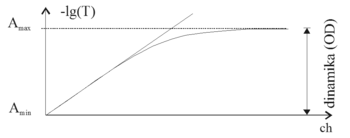
A monokromátor által létrehozott diffrakciós képből a réssel kiszűrt próbanyaláb az összes spektrális komponenst tartalmazza különböző arányokban, ami korlátozza az egy spektrális komponens mérésekor elérhető legkisebb és legnagyobb jelszint arányát, amit dinamikának (OD) neveznek. Továbbá az optikai elemek alakhibái miatt szintén fellép bizonyos mértékű szóródás, ami tovább csökkenti a dinamikát. A véges dinamika eredményeképpen a Lambert-Beer törvény által meghatározott összefüggés kis transzmisszió esetén nem lesz lineáris, hanem a szórt fény által korlátozott dinamikához tartozó abszorbancia értékhez telítődik.

Adott anyag különböző koncentrációk mellett felvett spektrumaiban az abszorpciós csúcsnál mérhető abszorbancia értékeket a koncentráció függvényében ábrázolva a dinamika meghatározható optikai denzitás (OD=-lg(Tmin)) egységekben. Ez az érték hullámhosszfüggő.

4. ábra

Mérési feladat

A felbontás meghatározása a mérésvezető által adott interferencia-szűrőn történik 4 különböző résbeállítás (0,5, 1, 2, 4) mellett. Minden egyes réshez külön kell kalibrálni a készüléket.

  • Mérje meg az interferencia-szűrő spektrumát 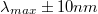\setbox0\hbox{$\lambda_{max} \pm 10 nm$}% \message{//depth:\the\dp0//}% \box0% tartományban 0,1 nm lépésközzel!
  • Határozza meg az egyes résszélesség értékek mellett a készülék vonalszórását és felbontását, valamint a szűrő félérték szélességét (azt felhasználva, hogy az egyes beállított résszélességek aránya adott)!

A dinamika meghatározása a Nd:YAG kristály 6 különböző vastagságánál felvett abszorpciós spektrum csúcsain kerül meghatározásra.

  • Mérje meg a kristály transzmissziós spektrumát 2 nm-es résszélesség mellett a 400-1100 nm tartományban 1 nm lépésközzel!
  • Válasszon ki 5 eltérő abszorbanciával rendelkező elnyelési csúcsot!
  • Hozzon létre eltérő vastagságokat a fényútba egymás utáni behelyezett azonos méretű kristályok segítségével és mindegyikről vegyen fel spektrumot.
  • A választott csúcsoknál ábrázolja az abszorbancia vastagságfüggését és határozza meg a dinamikát! A reflexió miatt bekövetkezett alapvonal eltolódást kompenzálja!

Vékonyréteg vizsgálat az UV-látható spektrofotométeren

Elmélet

A transzmisszió és reflexió számolt, illetve spektroszkópon mért értékeinek összehasonlításával a rácsos UV-látható spektrométer jó lehetőséget ad a különböző rétegszerkezetek vizsgálatára. Az elméleti értékek számolására a történelem folyamán többféle módszert találtak ki. Ezek közül a legelterjedtebb az ún. mátrixos-leírás módszere, melyet sugárátvezetéssel a Maxwell-egyenletekből és a hozzájuk tartozó határfeltételekből származtathatunk. Megvizsgálhatjuk például, hogy a tervezett antireflexiós réteg a gyártás után az elvártnak megfelelően sikerült-e. Mivel a labormérés keretei nem engedik meg a réteg megtervezésének – elkészíttetésének – ellenőrzésének elvégzését egy már elkészült, enyhén abszorbeáló, vékony (melynek transzmissziós spektrumán interferencia-mintázat figyelhető meg) réteget vizsgálnak a hallgatók. A felvett transzmissziós spektrum alapján a réteg törésmutatója, extinkciója, és vastagsága kerül meghatározásra. Az extinkció a mintán áthaladó fény gyengülését adja meg, tartalmazza az elnyelést és a rugalmas és rugalmatlan szórásokat. Ha a szórás kicsi, akkor az extinkció közelítően megegyezik az abszorpcióval.

Tekintsünk egy 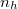\setbox0\hbox{$n_h$}% \message{//depth:\the\dp0//}% \box0% valós törésmutatójú végtelen vastag hordozón egy h vastagságú, enyhén abszorbeáló 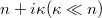\setbox0\hbox{$n + i\kappa (\kappa \ll n)$}% \message{//depth:\the\dp0//}% \box0% törésmutatójú réteget!

A tiszta hordozó transzmissziója: 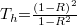\setbox0\hbox{$T_h {{=}} \frac{{\left (1 - R\right )}^2}{1 - R^2}$}% \message{//depth:\the\dp0//}% \box0%, ahol 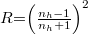\setbox0\hbox{$R {{=}} {\left (\frac{n_h - 1}{n_h +1 }\right )}^2$}% \message{//depth:\the\dp0//}% \box0% . Az összefüggés alapján, a transzmissziót mérve a hordozó törésmutatója számolható.

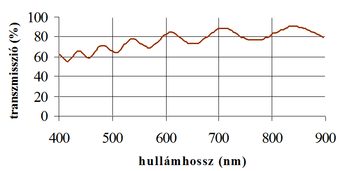
A teljes (hordozó + réteg) transzmisszióját az alábbi képlet adja meg és az ábrán látható módon néz ki:

\[T {{=}} \frac{Ax}{B - Cx\cos\phi + Dx^2}\]

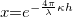ahol: \setbox0\hbox{$x {{=}} e^{-\frac{4\pi }{\lambda }\kappa h}$}% \message{//depth:\the\dp0//}% \box0% az extinkció a rétegen, 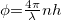\setbox0\hbox{$\qquad \phi{{=}} \frac{4\pi}{\lambda}nh$}% \message{//depth:\the\dp0//}% \box0% a fázistolás a rétegen, 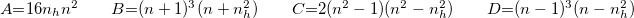\setbox0\hbox{$\qquad A {{=}} 16n_hn^2 \qquad B {{=}} (n+1)^3(n+n_h^2) \qquad C {{=}} 2(n^2 - 1)(n^2 - n_h^2) \qquad D {{=}} (n-1)^3(n-n_h^2)$}% \message{//depth:\the\dp0//}% \box0% törésmutatófüggő változók.

5. ábra Tipikus transzmissziós spektrum

A rétegszerkezeten való áthaladáskor hullámhossztól függően változó fázistolás jön létre, ami transzmissziós spektrumban minimumokat és maximumokat hoz létre attól függően, hogy konstruktív vagy destruktív interferencia tapasztalható az adott hullámhosszon a réteg felületéről és a réteg-hordozó határon reflektálódó nyalábok között. Az interferencia-mintázat maximumaira és minimumaira egy-egy burkoló görbe illeszthető, ezek a TM maximum és Tm minimum görbék:

\[T_M {{=}} \frac{Ax}{B - Cx + Dx^2} \qquad T_m {{=}} \frac{Ax}{B + Cx + Dx^2}\]

A burkoló görbék reciprokait egymásból kivonva csak a törésmutatótól (az abszorpciótól független) egyenletet kapunk, így belőle a réteg törésmutatója a hullámhossz függvényében meghatározható:

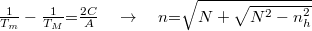\setbox0\hbox{$\frac{1}{T_m} - \frac{1}{T_M} {{=}} \frac{2C}{A} \quad \to \quad n {{=}} \sqrt{N + \sqrt{N^2 - n_h^2}}$}% \message{//depth:\the\dp0//}% \box0%, ahol 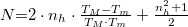\setbox0\hbox{$N {{=}} 2\cdot n_h \cdot \frac{T_M - T_m}{T_M \cdot T_m} + \frac{n_h^2 + 1}{2}$}% \message{//depth:\the\dp0//}% \box0% egy fizikai tartalom nélküli változó.

Ha már n(λ)-t ismerjük x (extinkció), illetve a törésmutató komplex része (κ) többféle módon számolható. A burkoló-görbék egyenletei például x-től négyzetesen függenek és így x-re megoldhatók (a TM-ből számolt érték pontosabb).

A maximumokból számolva:

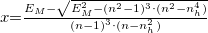\setbox0\hbox{$x {{=}} \frac{E_{M}-\sqrt{E_{M}^2-(n^2-1)^3\cdot (n^2-n_h^4)}}{(n-1)^3\cdot(n-n_h^2)}$}% \message{//depth:\the\dp0//}% \box0%, ahol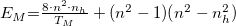 \setbox0\hbox{$E_{M} {{=}} \frac{8\cdot n^2\cdot n_h}{T_{M}}+ (n^2-1)(n^2-n_h^2)$}% \message{//depth:\the\dp0//}% \box0%

a minimumból számolva:

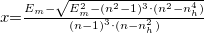\setbox0\hbox{$x {{=}} \frac{E_{m}-\sqrt{E_{m}^2-(n^2-1)^3\cdot (n^2-n_h^4)}}{(n-1)^3\cdot(n-n_h^2)}$}% \message{//depth:\the\dp0//}% \box0%, ahol 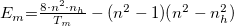\setbox0\hbox{$E_{m} {{=}} \frac{8\cdot n^2\cdot n_h}{T_{m}}- (n^2-1)(n^2-n_h^2)$}% \message{//depth:\the\dp0//}% \box0% EM és Em fizika tartalom nélküli változók.

A törésmutató és extinkció számolásához TM és Tm különböző hullámhosszhoz tartozó értékeinek ismeretére van szükségünk. A labormérésen csak a minimum- illetve maximumhelyeken vett törésmutatót és extinkciót kell kiszámolni oly módon, hogy a minimumhelyen vett TM-értéket a két szomszédos maximumérték közötti lineáris interpolációval lehet meghatározni, és fordítva.

A rétegvastagság meghatározása a szélsőértékek helyéből lehetséges. A transzmisszió maximumra:

 
\[\frac{4\pi}{\lambda}\cdot n\cdot h = \pi + 2\cdot \pi \cdot m\]
(1.a)

illetve minimumra:

 
\[\frac{4\pi}{\lambda}\cdot n\cdot h = 2\cdot \pi \cdot m\]
(1.b)

Például két szomszédos maximum vagy minimum helyéből

 
\[h = \frac{\lambda_1\cdot \lambda_2}{2\cdot (\lambda_1\cdot n_2 - \lambda_2\cdot n_1)}\]
(2)

Az így számolt vastagságérték elég érzékeny a törésmutató meghatározás hibájára és így nem túl pontos.

A pontosság növelhető, a következő iteráció elvégzésével:

  • több szomszédos csúcsra kiszámoljuk a vastagságértéket (2)-vel, majd átlagoljuk ezeket,
  • a kapott vastagságértéket használva, az egyes szélsőértékekre a rendeket számoljuk (1)-ből és kerekítjük egész számra,
  • a kerekített rendeket használva újból vastagságot számolunk (1)-ből.

\setbox0\hbox{$\cdots$}% \message{//depth:\the\dp0//}% \box0%

A vastagságot egyszerű grafikus úton is meghatározhatjuk, mivel a szélsőhelyekre:

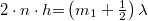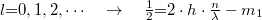\setbox0\hbox{$2\cdot n\cdot h {{=}} \left (m_1 + \frac{1}{2}\right )\lambda$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$l {{=}} 0,1,2, \cdots \quad \to \quad \frac{1}{2} {{=}} 2\cdot h\cdot\frac{n}{\lambda}-m_1$}% \message{//depth:\the\dp0//}% \box0% az egyenes egyenlete.

Így, ha l/2-t ábrázoljuk 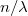\setbox0\hbox{$n/\lambda$}% \message{//depth:\the\dp0//}% \box0% függvényében az egyenes meredeksége 2h.

Megjegyzés: a spektrométer véges spektrális vonalszórása ezt a mérést is jelentősen befolyásolhatja, mégpedig a spektrumban megfigyelhető interferencia-mintázat összenyomásához vezethet, ezért szükséges lehet a spektrumok dekonvoluciója a résszélességnek megfelelően.

Mérési feladat

  • Mérje meg a kapott hordozó illetve a teljes rendszer (hordozó+réteg) transzmissziós spektrumát a 400-1100 nm tartományban a 2 nm-es résszélesség mellett 1 nm lépésközzel!
  • A tiszta hordozó transzmissziós spektruma alapján számolja ki annak törésmutatóját a hullámhossz függvényében!
  • Adja meg a rétegezett minta transzmissziós spektrumának maximum- és minimumhelyeit, majd határozza meg az összes szélsőértékhez tartozó TM és Tm értékeket!
  • Határozza meg ezekben a pontokban a réteg törésmutatóját és extinkcióját(n+iκ)!
  • Határozza meg a vastagságot valamelyik (iterációs ill. grafikus) módszerrel!

PDF formátum


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=UV-látható_és_NIR_spektrofotometria&oldid=19983”