„Pásztázó alagútmikroszkóp (STM) alkalmazása” változatai közötti eltérés
(Új oldal, tartalma: „<wlatex> Szerkesztés alatt! __TOC__ ==Információk== '''A gyakorlatnak otthont adó intézmény:''' [http://www.mfa.kfki.hu/hu MTA TTK MFA] (Műszaki Fizikai és …”) |
|||
| (egy szerkesztő 7 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
<wlatex> | <wlatex> | ||
| − | |||
| − | |||
__TOC__ | __TOC__ | ||
| 15. sor: | 13. sor: | ||
Az egyetem déli részéről: 212-es busszal Svábhegyig, onnan a 21-es busszal a végállomásig. <br /> | Az egyetem déli részéről: 212-es busszal Svábhegyig, onnan a 21-es busszal a végállomásig. <br /> | ||
'''Gyakorlatvezetők:''' | '''Gyakorlatvezetők:''' | ||
| − | '' | + | ''Kun Péter'' (kun@mfa.kfki.hu, telefon: xxxx-es mellék), ''Pálinkás András'' (palinkas@mfa.kfki.hu, telefon: xxxx-ös mellék) |
<br /> | <br /> | ||
==Elméleti összefoglaló== | ==Elméleti összefoglaló== | ||
| − | === | + | ===Bevezetés=== |
| + | |||
| + | <span id="fig:1">[[Fájl:STM HOPG.jpg|bélyegkép|400px|jobb|'''1.1. ábra.''' Atomi felbontású STM kép HOPG (Highly Oriented Pyrolytic Graphite) felületéről.]]</span> | ||
| + | |||
| + | A gyakorlat célja hozzásegíteni a hallgatókat ahhoz, hogy megismerkedhessenek napjaink talán legizgalmasabb felületvizsgáló eszközcsoportjának (SPM, Scanning Probe Microscope) egyikével, az STM-mel (Scanning Tunneling Microscope, pásztázó alagútmikroszkóp), mérések végzésével és a nyert képek számítógépes kiértékelésével. | ||
| + | Az STM elektromosan vezető felületek atomi léptékű vizsgálatára és módosítására alkalmas eszköz. Az alagútmikroszkópban egy igen hegyes tűt mozgatunk a felülettől nanométeres távolságra, miközben a tű és a minta közé volt nagyságrendű feszültséget kapcsolunk. Az STM leggyakrabban alkalmazott üzemmódjában (állandó áramú leképezés) miközben a minta síkjában a tűvel pásztázó mozgást végzünk, egy visszacsatoló hurokkal a tű felület fölötti magasságát úgy szabályozzuk, hogy a tű és a minta közötti, általában nanoamper nagyságrendű alagútáram állandó értéken maradjon. A tű így kialakuló háromdimenziós mozgása adja az STM képet. A megfelelő módon zajvédett (elektromos és mechanikai zajok szempontjából egyaránt) STM elegendően sima felületeken - pl. hasított egykristály - rutinszerűen képes elérni az atomi felbontást, lásd az [[#fig:1|1.1 ábrán]]. | ||
| + | |||
| + | ===Az alagúteffektus=== | ||
| + | |||
| + | <span id="fig:2">[[Fájl:STM potencialgat.jpg|bélyegkép|300px|jobb|'''1.2. ábra.''' $V_0$ magasságú és $d$ szélességü potenciálgát. Az $E$ energiával érkező részecske $P$ valószínűséggel hatol át a potenciálgáton és $(1-P)$ valószínűséggel verődik vissza.]]</span> | ||
| + | |||
| + | |||
| + | Ha két vezető anyag közé elektromos feszültséget kapcsolunk, és ezeket összeérintjük, áram folyik. Az elektródákat eltávolítva egymástól az áram megszűnik. Az áram megszűnése azonban nem ugrásszerűen, hanem fokozatosan történik, az elektródákat távolítva az áram exponenciálisan csökken. Makroszkópikus elektróda távolságoknál az áram mérhetetlenül kicsivé válik, tehát minden gyakorlati szempontból nullának tekinthető. Viszont ha az elektródák távolsága elegendően kicsi, azaz a nanométer (''nm'') tartományba esik, akkor jól mérhető áram fog folyni. Ezt a jelenséget kvantummechanikai alagúteffektusnak nevezzük. | ||
| + | Az alagúteffektus elmélete szerint egy részecske egy $d$ szélességű és $V_0$ magasságú potenciálgáton ([[#fig:2|1.2. ábra]]) akkor is véges valószínűséggel képes áthatolni, ha az $E$ energiája kisebb a potenciálgát magasságánál, $E < V_0$. Az áthaladás valószínűsége: | ||
| + | |||
| + | |||
| + | {{eq| P {{=}} \frac{16E\left( V_0 - E\right)}{V_0^2}\cdot e^{-2\kappa d} |eq:1|(1)}} | ||
| + | |||
| + | |||
| + | ahol <math>\kappa = \sqrt{\dfrac{2m}{\hbar^2 \left(V_0-E \right)}}</math> (Ez a képlet csak aszimptotikusan,$\kappa d >> 1$ határesetben igaz.) | ||
| + | |||
| + | Fém elektródák esetén a potenciálgát $V_0$ magassága elektronvolt ($eV$) nagyságrendű. Ilyenkor az [[#eq:1|(1)]] képlet szerint az átmeneti valószínűség kb. tizedére csökken, ha az elektródák távolságát $0.1 nm$-rel növeljük. Az STM-ben szokásos $nm$ nagyságrendű $d$ értékek esetén $P$ jellegzetes értéke kb. $10^{-5}$. | ||
| + | |||
| + | |||
| + | ===Az alagútáram=== | ||
| + | |||
| + | <span id="fig:3">[[Fájl:STM potencialkad.jpg|bélyegkép|200px|jobb|'''1.3. ábra.''' Potenciálkád modell. A <math>\left[ \frac{-L}{2},\frac{L}{2} \right]</math> intervallumban elhelyezkedő fémben az elektron <math> -\left( \Phi+E_F \right) </math>potenciált, az intervallumon kívüli vákuumban nulla potenciált érzékel. A <math> \left[-\left( \Phi+E_F \right),-\Phi \right] </math>közötti energiaszintek betöltöttek, az e fölötti szintek üresek. A bal oldali ábra egy hipotetikus állapotsűrűség függvényt mutat. A piros szaggatott vonal jelöli a Fermi szint helyét.]]</span> | ||
| + | |||
| + | |||
| + | Ha a két elektróda közé $U_t$ előfeszítést kapcsolunk, akkor az $I_t$ alagútáram nagysága ettől a feszültségértéktől, az elektródák anyagától és az elektródák közti távolságtól fog függeni. Az alagútáram az alábbi módon becsülhető meg. | ||
| + | |||
| + | A fémes vezetés legegyszerűbb modellje, a szabadelektron gáz modell szerint a vezetési elektronok a fém belsejében szabadon mozoghatnak, de a határfelületnek belülről nekiütközve visszaverődnek a fém belsejébe. Mivel a fémek tipikus elektronsűrűsége <math> n = 10^{29}\frac{1}{m^3} </math> körüli és az elektronok átlagos sebessége <math> v_F = 10^{6}\frac{m}{s} </math>, időegységenként kb. <math> \frac{n \cdot v_F}{6} = 1.7 \cdot 10^{34} db </math> elektron ütközik a határfelület egységnyi felületén. Ha az [[#eq:1|(1)]] képletet figyelembe véve feltesszük, hogy ezeknek $P$-ed része jut át a másik elektródába, nulladik közelítésként az alagútáramra <math> \frac{n \cdot v_F \cdot A \cdot P \cdot e}{6} = 2.6 nA </math> adódik, ahol $e$ az elektron töltése, továbbá föltételeztük, hogy az áram egy <math> A = 0.1 nm^2 </math> területű alagút csatornán át folyik. (Ez utóbbi érték megfelel egy egyatomos STM tű csúcs felületének.) Bár a kapott alagútáram nagyságrendileg valóban az STM esetén szokásos $nA$ tartományba esik, ez a durva becslés több szempontból is pontosításra szorul. Elsősorban figyelembe kell venni a ''Pauli elvet'', ugyanis egy adott $E$ energiájú elektron csak akkor juthat át a másik elektródába, ha azon az energián rendelkezésre áll ott nem betöltött energiaállapot. Másodsorban az is lényeges módon befolyásolja az alagútáramot, hogy milyen az elektronok energia szerinti eloszlása az elektródákban. Ezen hatások figyelembevétele a következő módon lehetséges. | ||
| + | A fémek legegyszerűbb kvantumfizikai modellje, a potenciálkád modell ([[#fig:3|1.3. ábra]]) feltételezi, hogy a vezetési elektronok egy potenciál dobozba vannak zárva. Ebben a modellben a fém vezetési elektronjainak (azaz a fémben szabad mozgásra képes, ún. delokalizált, tehát nem valamely atomhoz kötött elektronoknak) két leglényegesebb tulajdonságát vesszük figyelembe: | ||
| + | *''a)'' az elektronok a fémben kötöttek, kiszabadításukhoz munkát kell befektetni, ennek a legkisebb nagysága a $\Phi$ kilépési munka | ||
| + | *''b)'' az elektronok egy véges energiasávot foglalnak el, melynek szélessége az $E_F$ ''Fermi energia'' és a legmagasabb energiájú betöltött állapot energiája a ''Fermi szint''. | ||
| + | |||
| + | Ennek az energiasávnak a szerkezetét a <math> \rho \left( E \right) </math> állapotsűrűség függvény (''Density of States, DOS'') írja le, definíció szerint <math>\rho \left( E \right)dE </math>az $E$ energia körüli $dE$ infinitezimális energiaintervallumban található elektronállapotok száma. Az állapotsűrűség függvény ismeretében az adott szilárdtest legtöbb fontos adata (pl. elektromos, optikai, mechanikai, termodinamikai jellemzők) kiszámítható, és mint alább megmutatjuk, az alagútáram nagyságát is a DOS határozza meg. | ||
| + | |||
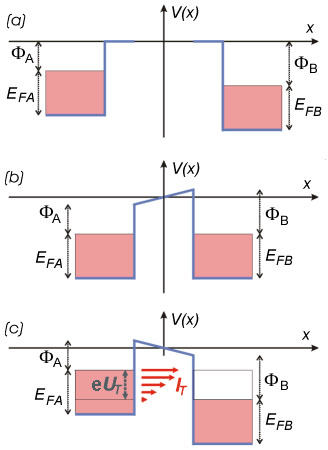
| + | <span id="fig:4">[[Fájl:STM alagutaram.jpg|bélyegkép|400px|közép|'''1.4. ábra.''' Az alagútáram kialakulásának sávszerkezeti modellje. ''(a)'' Az ''A'' és a ''B'' elektróda távol van egymástól. ''(b)'' Az elektródákat $nm$ közelségbe hozzuk, a ''Fermi szintek'' kiegyenlítődnek és kialakul a kontaktpotenciál. ''(c)'' Az elektródák közé $U_t$ előfeszítést kapcsolunk. Az $I_t$ alagútáram az <math> e \cdot U_t </math> szélességű energiaintervallumban folyik, az ''A'' elektróda betőltőtt állapotaiból a ''B'' elektróda üres állapotaiba. A nagyobb energiájú komponensek áram járuléka nagyobb, a nagyobb átmeneti valószínűségük miatt.]]</span> | ||
| + | |||
| + | |||
| + | A [[#fig:4|1.4/a. ábrán]] a két, egymástól kezdetben makroszkópikus távolságban lévő elektróda potenciálkád sávszerkezetét ábrázoltuk. Általános esetben a két elektróda (''A'' és ''B'') különböző anyagú, ezért Fermi energiájuk és kilépési munkájuk is eltérő, az ábrán az ''A'' elektróda Fermi szintje magasabban helyezkedik el a ''B'' Fermi szintjénél. Ha az elektródákat olyan közelségbe hozzuk egymáshoz, hogy az elektronok számottevő valószínűséggel közlekedhessenek egyikből a másikba (alagúteffektus által), akkor az ''A'' elektródából elektronok kezdenek átfolyni a ''B'' elektródába. Ez azt jelenti, hogy ''A'' pozitív, ''B'' pedig negatív töltést nyer, minek hatására mindkét elektróda a vákuumszinthez képest elektrosztatikus potenciális energiára tesz szert. Mivel ahhoz, hogy a végtelenből a "+" töltésű A felületéig vigyünk egy elektront "-" munkát, ahhoz viszont, hogy a "-" töltésű ''B'' felületéig vigyünk egy elektront "+" munkát kell végezni, ''A'' energiaszintjei "-", ''B'' energiaszintjei pedig "+" irányban tolódnak el a vákuumszinthez képest. Következésképpen a két elektróda közt létrejön az ún. kontaktpotenciál. A töltésátfolyás mindaddig tart, amíg a két elektróda Fermi szintje ki nem egyenlítődik ([[#fig:4|1.4/b. ábra]]). Mint arról egyszerű számolással meggyőződhetünk, a kiegyenlítődés eléréséhez (fémek esetében) a vezetési elektronok összes számához képest elegendő igen kevés elektronnak átjutnia ''A''-ból ''B''-be, tehát a sávszélességek változása teljesen elhanyagolható. | ||
| + | |||
| + | Ha ezután a két, $d$ távolságban lévő elektróda közé $U_t$ előfeszítést kapcsolunk, a [[#fig:4|1.4/c. ábrán]] vázolt helyzet áll elő. Ilyenkor csak az ábrán jelölt, $U_t$ szélességű energiasávba eső elektronok juthatnak át az ''A'' elektródából a ''B'' elektródába, mert csak ezeken az energiákon vannak az ''A'' elektródában betöltött, a ''B'' elektródában pedig üres állapotok. Mivel adott $E$ energia körüli $dE$ intervallumban átjutó elektronok száma a $P$ átmeneti valószínűségtől, valamint attól függ, hogy a két elektródában hány állapot van ebben a $dE$ intervallumban, a teljes <math>e \cdot U_t </math> energiaintervallumban folyó $I_t$ alagútáram: | ||
| + | |||
| + | |||
| + | {{eq| I_t \propto \int_{E_F}^{E_F+eU_t} \rho_{tu} \left( E-eU_t \right) \cdot \rho_{minta} \left( E \right) \cdot P \left( E,U_t \right)\,\mathrm{d}E |eq:2|(2)}} | ||
| + | |||
| + | |||
| + | Ha feltesszük, hogy a $P$ és a tű DOS értékek csak elhanyagolható módon függenek az energiától, a következő összefüggést kapjuk: | ||
| + | |||
| + | |||
| + | {{eq| I_t \propto \int_{E_F}^{E_F+eU_t} \rho_{minta}\left( E \right) \,\mathrm{d}E |eq:3|(3)}} | ||
| + | |||
| + | |||
| + | |||
| + | ===Az alagútmikroszkóp=== | ||
| + | |||
| + | <span id="fig:5">[[Fájl:STM felepites.jpg|bélyegkép|300px|jobb|'''1.5. ábra.''' A pásztázó alagútmikroszkóp elvi működése. Az alsó kis ábra azt mutatja be, milyen három dimenziós mozgást végez a tű a pásztázás alatt.]]</span> | ||
| + | |||
| + | |||
| + | Az STM, mint eszköz ([[#fig:5|1.5. ábra]]) az alábbi módon működik. | ||
| + | *Az egyik elektródát igen hegyes tűnek képezzük ki. Ekkor az alagútáram csak a tű hegye körüli keskeny csatornában fog folyni, mivel az alagutazási valószínűség exponenciális távolságfüggése miatt a tű távolabbi részei és a minta közötti áram elhanyagolhatóan kicsi. Ennek az alagút csatornának a szélessége körülbelül akkora, mint a tű csúcsának a görbületi sugara. Tehát műszerünk felbontását elsősorban az alkalmazott tű hegyessége határozza meg. Ha atomi skálán hegyes tűt alkalmazunk, akkor a felbontás is atomi léptékű lesz. | ||
| + | *A tűt egy olyan háromdimenziós mechanikai mozgató rendszerre szereljük, amely igen finom (század nanométeres, vagy finomabb) pontossággal képes mozgatni a tűt a minta felett. A gyakorlatban erre a célra általában piezoelektromos mozgatókat alkalmaznak. | ||
| + | *A tű és a minta közé $V$ nagyságrendű előfeszítést kapcsolunk. | ||
| + | *Ezután a tűt óvatosan addig közelítjük a felülethez, amíg megjelenik az alagútáram és elér egy előre beállított $I_{Referencia}$ értéket. Minél nagyobb az $I_{Referencia}$, annál közelebb kerül a tű a felülethez, gyakorlatban a tipikus nagysága $nA$ körüli. | ||
| + | *A minta ''X-Y'' síkjában a tűvel pásztázó mozgást végzünk, hasonlóan a TV készülékekben alkalmazott vezérléshez ([[#fig:5|1.5. ábra]]). Természetesen, mivel itt nem elektronsugarat, hanem makroszkopikus tömegeket mozgatunk, a mechanikai rendszer tehetetlensége és rezonanciái miatt az alkalmazható kép- illetve sorfrekvencia kisebb, mint a TV esetén megszokott. Ezért egy STM kép fölvétele általában másodpercekig vagy percekig tart. | ||
| + | *Pásztázás közben a tű minta feletti magasságát (Z pozícióját) egy visszacsatoló hurokkal úgy szabályozzuk, hogy a mért alagútáram állandóan megegyezzen az $I_{Referencia}$ értékkel. | ||
| + | *Ily módon a tű minden egyes ''(X,Y)'' pozíciójához egy meghatározott Z érték fog tartozni. Ezeket a ''Z(X,Y)'' értékeket számítógéppel rögzítjük. (A módszer hőskorában a ''Z(X,Y)'' felületet úgy jelenítették meg, hogy az egyes ''Z(X,Y=const)'' pásztázási sorokat analóg rajzgéppel vastag papírra rögzítették, majd a papírból kivágták és egymás mögé ragasztották.) | ||
| + | *Az STM-ben igen gondos rezgéscsillapításra van szükség, mivel a tűt a minta fölött nanométeres távolságban kell mozgatnunk. Ha a tű beleütközik a mintába, az általában a tű hegyének és a mintának a sérülését okozza, továbbá, az alagútköz szélességének véletlenszerű változásai "zajként" jelennek meg a felvett képen. A nagyamplitúdójú zaj elfedi a jellemzően <math> 0.01 - 0.1 nm </math> -es atomi korrugációt. | ||
| + | *Bár az első STM kísérleteket ultra nagy vákuumban (UHV) végezték, később megállapították, hogy az alagútmikroszkóp normál levegőn, sőt még (szigetelő) folyadékban is kiválóan működik! Ezért a költséges és nehézkes vákuumrendszereket csak akkor szükséges alkalmazni, ha a mérendő felület tulajdonságai ezt megkívánják, azaz ha a vizsgált minta a levegőn oxidálódna, illetve szennyeződne. Mivel a nem oxidálódó minták (pl. a szén) levegőn vizsgálhatóak, az alagútmikroszkóp egy viszonylag olcsó eszköz, összehasonlítva a modern fizika egyéb mérőeszközeivel, például az elektronmikroszkóppal. | ||
| + | |||
| + | |||
| + | ===STM üzemmódok=== | ||
| + | |||
| + | A gyakorlatban az alagútmikroszkópot általában vagy ún. topográfiai, vagy ún. ''spektroszkópiai'' üzemmódban használjuk. | ||
| + | *'''Topográfiai üzemmódban''' rögzített $U_t$ előfeszítés és $I_{Referencia}$ alagútáram érték mellett a ''Z(X,Y)'' felületet vesszük fel. Ha feltételezzük, hogy a $P$ átmeneti valószínűség és a minta állapotsűrűsége mindegyik ''(X,Y)'' pontban egyforma, a ''Z(X,Y)'' felület nulladik közelítésben a minta geometriai felületét, topográfiáját fogja megadni. Azonban a gyakorlatban ezek a mennyiségek a helytől is függhetnek, tehát a mért ''Z(X,Y)'' felület együttesen tartalmazza a topográfiai és az elektronszerkezeti információt. A topográfiai üzemmódban leggyakrabban kicsi előfeszítést alkalmazunk. Ha $U_t$ infinitezimálisan kicsi, a [[#eq:2|(2)]] képlet integrandusában a DOS és $P$ energiafüggése elhanyagolható. Mivel a DOS helyfüggése mellett az átmeneti valószínűség helyfüggése kisebb szerepet játszik, az alagútáram mindenhol a minta állapotsűrűség Fermi szintnek megfelelő értékével lesz arányos: | ||
| + | |||
| + | |||
| + | {{eq| I_t \left( \overrightarrow{r}, U_t \right) \propto U_t \cdot \rho_{minta} \left( E {{=}} E_{F},\overrightarrow{r} \right) |eq:4|(4)}} | ||
| + | |||
| + | |||
| + | *'''Spektroszkópiai üzemmódban''' ''(Scanning Tunneling Spectroscopy, STS)'' egy, kiválasztott ''(X,Y)'' pontban megállunk a tűvel és ideiglenesen kikapcsoljuk a visszacsatoló hurkot is. Ebben a rögzített <math>\mathbf{r_0}</math> tű helyzetben felvesszük az alagútátmenet áram-feszültség karakterisztikáját, azaz az $U_t$ előfeszítést változtatva megmérjük az $I_t$ alagútáram változását. Mivel $U_t$ változtatása a [[#eq:3|(3)]] képlet integrálási határa változtatásának felel meg, a mért áram feszültség szerinti deriválásával a képlet integrandusának energiafüggését kapjuk: | ||
| + | |||
| + | |||
| + | {{eq| \frac{I_t \left( U_t \right)}{dU_t} \propto \rho_{minta} \left( E {{=}} E_F + eU_t,\overrightarrow{r} {{=}} \overrightarrow{r_0}\right)|eq:5|(5)}} | ||
| + | |||
| + | |||
| + | ===Az STM családja=== | ||
| + | |||
| + | A zseniális ötletek általában megtermékenyítően hatnak a tudomány fejlődésére. Az STM esetén is így történt, ez vezetett az ún. pásztázó szondás módszerek családjának létrejöttéhez. Mindegyik ilyen eszközben egy hegyes szondát pásztáznak a minta fölött és a szonda és a minta valamiféle kölcsönhatását mérik. A legfontosabb ezek közül az atomerő mikroszkóp ''(Atomic Force Microscope, AFM)''. Az AFM-ben, hasonlóan az STM-hez, egy hegyes tűt mozgatunk a minta fölött és közben a tűre ható erőt a visszacsatoló hurok segítségével állandó értéken tartjuk. Mivel ez a műszer szigetelő felületek vizsgálatát is lehetővé teszi, az ipari kutatásokban is gyakran használják. | ||
| + | |||
| + | |||
| + | ==Műszerek== | ||
| + | |||
| + | A mérésekhez egy [http://www.veeco.com/ Veeco] (DI) gyártmányú '''Nanoscope 3''' STM/AFM készülékkel rendelkezünk. Ennek jellemzője a moduláris felépítés, ami lehetővé teszi, hogy különféle pásztázó fejeket, vezérlő elektronikákat és számítógépeket illeszthessünk össze. A berendezés szabad levegőn működik. Esetünkben a mérőfej 15x15 mikron vízszintes és 3 mikron függőleges tartomány pásztázását teszi lehetővé, de ez egyszerűen kicserélhető nagyobb tartomány pásztázására képes fejre is. A rendszer blokkvázlatát a következő ábrán láthatjuk: | ||
| + | |||
| + | <span id="fig:6">[[Fájl:STM merorendszer.jpg|bélyegkép|300px|jobb|'''2.1. ábra.''' Az STM mérőrendszer blokkvázlata.]]</span> | ||
| + | |||
| + | |||
| + | A '''rezgéscsillapító''' alapvető feladata, hogy a külvilág felől érkező mechanikai vibrációkat távol tartsa a tulajdonképpeni STM-től, illetőleg elfogadható szintűre csillapítsa azokat. Ez nagyon fontos része a készüléknek, hiszen a mintát letapogató tűt mindössze $nm$-es ($10^{-9} m$) távolságban kell a minta felületétől mozgatnunk, ezért ha a rezgések ennél nagyobb amplitúdójú relatív elmozdulását okozzák a tűnek és a mintának, akkor a tű beleszaladhat a mintába, ami természetesen a tű hegyének letompulását és a minta lokális roncsolódását okozza. Egészen kisfrekvenciás zavarok esetén a helyzet azért drámainak nem mondható, ugyanis a mindenkori tű-minta távolságot egy néhány $kHz$ frekvenciával reagálni képes negatív visszacsatolás szabályozza. Tehát amíg a rázkódásból eredő relatív elmozdulások nem túl gyorsak és nem lépik túl a szabályozási tartományt, addig az STM megőrzi működőképességét. Sajnos azonban a működőképesség megőrzése még nem jelent optimális működést, ugyanis a sikeresen kompenzált mechanikai rezgés esetén is hozzáadódik a hasznos jelhez a zavaró jel, ami különféle, nem valós periodikus struktúrák megjelenését eredményezi az STM képen. Így tehát elsőrendű feladatunk, hogy a hangfrekvenciás rezgések szintjét ''nagyságrendekkel '' csillapítsuk, az infrahangokét pedig annyira, amennyire módunkban áll. A csillapítás elvi alapja az, hogy mérsékeljük az STM fejre ható, a külső vibrációkból eredő ''gyorsító erőt'', rugalmas felfüggesztés közbeiktatásával. | ||
| + | |||
| + | Az '''STM mikroszkóp fejben''' ([[#fig:7|2.2. ábra]]) található a készülék "lelke", amely nem más, mint a letapogató tű. Ez voltaképpen egy, az egyik végén atomi léptékben hegyes vékony wolfram, platina-ródium vagy platina-irídium drót. Az STM tűt a mérőfejen található csövecskébe helyezzük. Felvetődik a kérdés, hogy hogyan lehet ilyen jól kihegyezni egy drótot? Nos, erre léteznek különféle módszerek (pl. elektrokémiai maratás). Mi a közönséges mechanikai hegyezéshez folyamodunk, a drótot egy éles ollóval, távolító mozdulattal kombináltan elvágjuk. A tűket optikai mikroszkóp alatt ellenőrizzük. Természetesen, nincs arra garancia, hogy az optikailag tökéletesnek látszó tű akárcsak elfogadható is legyen, hiszen az optikai mikroszkópban csak kb. mikronos felbontásban láthatjuk a tű végét, vagyis mintegy 3-4 nagyságrenddel durvábban a kelleténél. A gyakorlat azonban azt mutatja, hogy egy ügyes kezű ember minden második-harmadik hegyezése bizonyos mérésekhez elfogadható tűt eredményez. A tű végének keresztmetszete általában nem körszimmetrikus, hanem valamilyen irányban elnyújtott. A mindkét irányban ''(X, Y)'' egyformán hegyes tű sokkal ritkábban sikerül. A mechanikai hegyezéssel előállított tűk jellegzetes hibája, hogy a végükön egymás mellett több ún. nano-csúcs is lehet, amelyek közül az alagútáram az erős távolságfüggés miatt lényegében csak azon át folyik, amelyik a minta felületéhez a legközelebb van. Kellően sík mintánál (pl. HOPG) a mérés alatt végig ugyanaz maradhat az aktív nano-csúcs, miközben tagoltabb felületűeknél (pl. csiszolt fémeknél) akár többször is megváltozhat egyetlen mérés alatt. (Ilyenkor a pásztázás kissé máshol folytatódik, mint "hiszi" azt az adatgyűjtő program.) Az előbbi tűhibákra a felvett képek minőségéből következtethetünk. Vagyis egy tű jóságát végső fokon onnan tudjuk megítélni, hogy milyen képeket tudunk vele készíteni. Ezért a megfelelő tű elkészítése meglehetősen időigényes eljárás, hiszen egy-egy próba mérés előkészítése és elvégzése sok-sok percre rúghat. Akár egy teljes napot is igénybe vehet a kísérletezés, amíg végre szert teszünk egy kiváló minőségű tűre. Ráadásul a tű egy szempillantás alatt bármikor tönkre is mehet, hiszen elegendő egy icipicit beleütköznie a minta felületébe. A helyzet orvoslására a méréshez 1-1 megfelelően jól hegyezett tűt eleve biztosítunk, de természetesen a diákok is próbálkozhatnak a tűhegyezéssel. A tű közvetlenül egy előerősítőhöz csatlakozik, így lecsökkenthető az alagútáramra tevődő zaj. A berendezés minimum $200 pA$ alagútáramon képes dolgozni, ennél kisebb áramokon látványosan lelassul az előerősítő. | ||
| + | |||
| + | <span id="fig:7">[[Fájl:STM mikroszkopfej.jpg|bélyegkép|400px|közép|'''2.2. ábra.''' STM mikroszkóp fej.]]</span> | ||
| + | |||
| + | |||
| + | A minta mechanikai mozgatását (pásztáztatását) egy piezokerámia szkenner cső végzi, megfelelő (maximum $\pm 220 V$-os) feszültség hatására. A tű durva közelítését és távolítását egy mikrométer csavar végzi, melyet motor működtet. Minta- illetve tűcsere esetén a tű az előerősítővel együtt levehető. Tűcsere után az előerősítőt rugókkal rögzítjük, a tűt a csavarral kb. $0,1 mm$ távolságra közelítjük a mintához, majd a számítógép segítségével folytatjuk a tű mozgatását. | ||
| + | |||
| + | A mérés vezérlését és az adatok gyűjtését számítógép végzi. Az egyszerűbb kezelhetőség miatt két monitort használunk, a vezérlő monitoron a mérési paraméterek állíthatók, a kijelző monitoron pedig az STM kép látható. | ||
| + | |||
| + | A mérés üzemmód (Realtime) a [[Fájl:STM icon microscope.jpg]] gomb segítségével indítható, a rögzített képek (Offline) pedig a [[Fájl:STM icon monitor.jpg]] gomb megnyomásával érhetők el. Mérés üzemmódban [[Fájl:STM icon microscope.jpg]] ([[#fig:8|2.3. ábra]]) a '''Scan Controls''' ablakban állítható a pásztázási ablak mérete, a pásztázás helye, szöge, frekvenciája, sebessége és felbontása. A pásztázási sebesség (frekvencia) megválasztásánál figyelembe kell venni a visszacsatoló rendszer tehetetlenségét és a minta durvaságát, mivel a nagy sebesség a minta és/vagy a tű sérülését eredményezheti. Az STM kép felbontása 128, 256 vagy 512 <math>\dfrac{pont}{vonal}</math> lehet. A '''Feedback Controls''' ablakban állítható az alagútáram, a tű-minta feszültség és a visszacsatolás erőssége. Nagyobb Integral és Proportional Gain értékek gyorsabb pásztázást tesznek lehetővé, viszont túl nagy értékek esetén a visszacsatoló hurok begerjed. A maximális függőleges pásztázási tartomány és a színskála az '''Other Controls''' ablakban állítható. Ismeretlen minta esetén érdemes a maximális függőleges tartományt használni, viszont ez gyengébb függőleges felbontást eredményez (felbontás <math>{{=}}\dfrac{Z limit}{2^{16}}</math>). A '''Channel''' ablakokban választható a rögzített adatok típusa (magasság vagy áram), skála mérete, pásztázás iránya és a dőléskiegyenlítés módja. | ||
| + | |||
| + | <span id="fig:8">[[Fájl:STM nanoscope1.jpg|bélyegkép|300px|közép|'''2.3. ábra.''' STM mikroszkóp fej.]]</span> | ||
| + | |||
| + | A mérésvezérlő program felépítése hasonlít a Windows programokhoz. Az utasítások menükbe vannak csoportosítva, a gyakran használt utasítások közvetlenül elérhetők. [[Fájl:STM icon pin-down.jpg]] a tűt addig közelíti a mintához, amíg a beállított áram meg nem jelenik. [[Fájl:STM icon pin-up.jpg]] hatására a tű eltávolodik a mintától. [[Fájl:STM icon eye.jpg]] megnyomásával a készülő képet,[[Fájl:STM icon wave.jpg]] megnyomásával pedig az utolsó pásztázási vonalat jelenítjük meg a képernyőn. [[Fájl:STM icon up-down.jpg]] lentről vagy fentről indítja a pásztázást. [[Fájl:STM icon camera-nocamera.jpg]] be vagy ki kapcsolja a kép rögzítését. A képernyő alján látható a mérőfej típusa, az üzemmód, a tű állapota, képrögzítés állapota, a file neve és az idő. A file neve a '''Capture->Capture Filename''' paranccsal állítható be. | ||
| + | Mérés közben a kijelző képernyőn ([[#fig:9|2.4. ábra]]) követhető a pásztázás. A képernyő bal oldalán az 1-es csatorna (jobbról balra pásztázás) adatai láthatók, a képernyő jobb oldalán pedig a 2-es csatorna adatai. FONTOS folyamatosan figyelni a képernyő bal alsó sarkában található '''Z Center Position''' kijelzőt, amely a piezo kerámiára kapcsolt feszültséget jelzi. Ha a piros nyíllal jelzett fehér függőleges vonal a zöld téglalap végéhez ér, akkor a kerémia maximálisan összehúzódott vagy kinyúlt és képtelen a felületet követni. A maximális függőleges tartomány ('''Z limit''') növelésével vagy a pásztázási ablak ('''Scan size''') csökkentésével általában javítható a helyzet. Ha ez nem sikerül, akkor a tűt ki kell húzni [[Fájl:STM icon pin-up.jpg]]. | ||
| + | |||
| + | <span id="fig:9">[[Fájl:STM kijelzo.jpg|bélyegkép|300px|közép|'''2.4. ábra.''' Kijelző képernyő.]]</span> | ||
| + | |||
| + | |||
| + | ==Minták== | ||
| + | |||
| + | Ahhoz, hogy az STM-mel meg tudjunk mérni egy mintát, szükséges, hogy a felülete elektromosan vezető legyen. Mint tudjuk, a fémek általában kiváló elektromos vezetők, ezért joggal reménykedhetünk abban, hogy az STM-mel jól meg tudjuk mérni őket. Sajnos azonban ez még sincs mindig így. Pl. az ''alumínium'' kiváló elektromos vezető, de a felületén a szabad levegőn a legrövidebb időn belül is kialakul egy vékony oxid réteg ($Al_2O_3$), amely viszont a legkiválóbb szigetelők közé tartozik (olyannyira, hogy nagyfeszültségű szigetelő kerámiák legfőbb alapanyaga), és mindennek a tetejében még nagyon kemény is (csiszolóanyag és drágakő, lásd korund, zafír). Hasonlóan tudjuk a ''vas''ról is, hogy igen hajlamos a rozsdásodásra (oxid és hidroxid vegyesen), és a rozsda egykettőre olyan vastag lehet, hogy a letapogató tűt teljesen elfedi, beszennyezi. | ||
| + | Logikus arra gondolni, hogy a nemesfémekkel talán több szerencsénk lesz. És valóban, pl. az ''arany'' és a ''platina'' szabad levegőn is egészen jól mérhetők STM-mel, de pl. az egyébként legkiválóbb elektromos vezető ''ezüst'' nem! Ennek oka nem az oxigén, hanem az oxigén csoportjába tartozó másik kémiai elem, a ''kén''. Ez ugyanis az ipari szennyezés miatt mindig jelen van a levegőben, az ezüst pedig igen könnyen alkot vele szulfidot. (Ez adja az ezüst tárgyak sötétszürke színét is.) A félnemes fémnek tekinthető ''vörösréz'' sem problémamentes, ugyanis elég könnyen oxidálódik (barna szín), illetve képződik rajta zöldes-kékes színű patina (nitrátok, hidrokarbonátok, stb.). Segítségünkre van viszont, hogy a réz oxidja ($CuO$) félvezető természetű (a század elején fel is használták egyenirányítási célokra), ilyenformán az alagútáram kialakulását nem akadályozza meg, feltéve, hogy az oxid réteg nem túl vastag. (A frissen vákuumpárologtatott réz réteg napokig is mérhető maradhat szabad levegőn STM-mel.) Bizonyos fémek jól mérhetők szabad levegőn, pl. a ''nikkel'', a ''króm'' és a ''molibdén''. Ezeken csak vékony a kialakuló oxid réteg, és ráadásul eléggé félvezető természetű is. (Nem véletlen, hogy tükröző felületek készítésére is használják őket.) Egyes anyagok egyáltalán nem fémek, pl. az $SnO_2$, de szép és stabil félvezető kristályokat alkotnak, így remekül mérhetők. A legfontosabb félvezetővel, a ''szilícium''mal viszont problémánk van, ugyanis igen gyorsan (a másodperc töredéke alatt) oxidálódik, és az oxidja, a kvarc ($SiO_2$) a legkiválóbb szigetelők és legkeményebb anyagok közé tartozik. Ezért a szilícium megfelelő STM-es vizsgálata csak ultranagy-vákuumban lehetséges, az ott alkalmazott ("in situ") tisztítást követő korlátozott ideig. A különlegesebb anyagok közül a ''fémüvegek'' elsősorban akkor mérhetők jól, ha elég nagy mennyiségben tartalmaznak nemesfém összetevőt is. A mágneses szempontból fontos ''permalloy'' sem reménytelen eset, miután akár <math>\frac{3}{4}</math> résznyi nikkelt is tartalmazhat. Azonban a szabadlevegős STM-es vizsgálatok kétségtelenül legnagyobb sztárja a ''grafit''. Ez az anyag úgy él hétköznapi szemléletünkben, mint egy elektromosan vezető, enyhén fémes csillogású, gyenge, könnyen szétmorzsolható anyag. Azonban a könnyű szétmorzsolhatósága kizárólag a rétegeinek egymáshoz képesti könnyű elcsúszásból fakad, miközben az egyes rétegeken belül a szénatomokat nagyon erős kovalens kötések tartják a helyükön. Ezért a grafit kémiailag nagyon kevéssé reaktív elem (nem oxidálódik), elektromosan vezet, és a pásztázott felületének számottevő mechanikai tartása is van. Mindezekért viszonylag könnyen elérhetünk rajta akár ''atomi felbontást'' is. Ehhez legcélszerűbb HOPG-t (Highly Oriented Pyrolitic Graphite) használnunk, amely ránézésre a csillámhoz hasonló réteges szerkezetű anyag, csak sötétebb. Minthogy a grafit szén atomjainak kötéstávolságát más módszerekkel is meg tudjuk mérni, így a grafit az STM kalibrációjára is felhasználható. | ||
| + | A konkrét mérésekhez a következő mintákat fogjuk megnézni: | ||
| + | |||
| + | *1.) HOPG grafit (atomi felbontáshoz); | ||
| + | *2.) párologtatott arany réteg (a szemcseméret statisztikai vizsgálatához); | ||
| + | *3.) esetleges hozott minta (pl. arany vagy platina nyaklánc egy különálló szeme). | ||
| + | |||
| + | A minták mérete tipikusan nem haladhatja meg a $10 mm$-es átmérőt és $2-3 mm$-es vastagságot. A legkisebb még kényelmesen kezelhető méret kb. $3 mm$-es átmérőjű és $0.2-1$ mm-es vastagságú. A mintákat egy-egy mintatartóra kell rögzítenünk. A rögzítésnek egyszerre kell biztosítania az elektromos vezetést és a mechanikai stabilitást. Mindkét feltételnek megvannak a maga nehézségei, ugyanis egy kicsit is bizonytalan mechanikai illesztést minden "bolygatás" után hosszadalmas (akár órákra rúgó!) relaxációs mozgás követhet. Elektromos kontaktust pedig nem könnyű biztosítani pl. egy olyan párologtatott fémfelülethez, amely esetleg csak néhány $nm$ vastag. | ||
| + | |||
| + | |||
| + | ==Mérés== | ||
| + | |||
| + | A mérés egymást követő lépései a minta konkrét fajtájától függetlenül hasonlóak. Az általános eljárás a következő: <br /> | ||
| + | |||
| + | '''1.)''' Ellenőrizzük, hogy az egyes egységek helyesen vannak-e összekapcsolva, majd a főkapcsolóval egyszerre bekapcsoljuk a vezérlő elektronikát és számítógépet (hogy mielőbb felvegye az üzemi hőmérsékletet). (Ezt a gyakorlatvezető elvégzi a mérés megkezdése előtt.)<br /> | ||
| + | |||
| + | '''2.)''' Előkészítjük a mérendő mintát (hogy mielőbb bekövetkezhessen a mechanikai relaxációja). (Általában a gyakorlatvezető ezt is elvégzi a mérés megkezdése előtt.)<br /> | ||
| + | |||
| + | '''3.)''' Következő lépésként megpróbálunk előállítani egy elfogadhatóan hegyes tűt. (Bár lesz a gyakorlatvezető által előzetesen meghegyezett tű is, a diákoknak is meg kell kísérelniük a hegyezést.)<br /> | ||
| + | |||
| + | '''4.)''' Ezután egy csipesszel behelyezzük a tűt a foglalatába, a tű-minta távolságot kb. $0.1 mm$-re csökkentjük, majd a mérőfejet rezgésmentes asztalra helyezzük. (Első alkalommal ezt megmutatja a gyakorlatvezető, később a diákoknak célszerű megtenniük.)<br /> | ||
| + | |||
| + | '''5.)''' Beállítjuk a kívánt pásztázási paramétereket (ablakméret, soronkénti pixelszám, pásztázási sebesség, alagútfeszültség és áram), majd aktiváljuk a durva közelítő mechanizmust [[Fájl:STM icon pin-down.jpg]].<br /> | ||
| + | |||
| + | '''6.)''' A mérésvezérlő szoftver automatikusan elindítja az adatgyűjtést. Amennyiben a kép megfelelő, úgy elmentjük a HDD-re [[Fájl:STM icon camera.jpg]]. Ha a kép nem megfelelő, akkor a paraméterek állításával megpróbálunk javítani rajta. Ha ez semmiképp sem sikerül, annak leggyakoribb oka, hogy a tű szennyezett, vagy tompa. Ekkor leállítjuk a mérést [[Fájl:STM icon pin-up.jpg]],<br /> | ||
| + | |||
| + | '''7.)''' A tű-minta távolságot legalább $2 mm$-re növeljük. <br /> | ||
| + | |||
| + | '''8.)''' Kivesszük a tűt és visszatérünk a 3.)-es ponthoz, vagyis a tű újbóli meghegyezéshez, vagy cseréjéhez.<br /> | ||
| + | |||
| + | |||
| + | ==Képfeldolgozás== | ||
| + | |||
| + | A rögzített képek Offline üzemmódban [[Fájl:STM icon monitor.jpg]] a ! meghajtón találhatók ([[#fig:10|5.1 ábra]]). | ||
| + | |||
| + | <span id="fig:10">[[Fájl:STM nanoscope2.jpg|bélyegkép|300px|jobb|'''5.1. ábra.''' Offline üzemmód.]]</span> | ||
| + | |||
| + | A mérési file általában két képet tartalmaz (Channel1 és Channel2), egyiket jobbról balra, a másikat balról jobbra pásztázva készítjük. A kép szűrése előtt ki kell választani egyik képet az '''Image->Select Left Image''' vagy '''Image->Select Right Image''' parancs segítségével. A kép kiválasztása után elérhetővé válnak a szűrési, mérési és megjelenítési lehetőségek ([[#fig:|5.2 ábra]]). | ||
| + | |||
| + | <span id="fig:11">[[Fájl:STM nanoscope3.jpg|bélyegkép|300px|jobb|'''5.2. ábra.''' Képfeldolgozás.]]</span> | ||
| + | |||
| + | A képfeldolgozást ajánlott a '''Modify->Plane fit Auto'''[[Fájl:STM icon autofit.jpg]](felület illesztése a rögzített képhez) vagy '''Modify->Flatten''' [[Fájl:STM icon flatten.jpg]] (görbe illesztése a pásztázási vonalakhoz) utasításokkal kezdeni. A képen található tüskék '''Modify->Median''' (mátrix szűrő) vagy '''Modify->Lowpass''' (nagy frekvenciákat levágó) szűrővel távolíthatók el. A különösen zajos pásztázási vonalak eltávolíthatók a '''Modify->Erase Scan Lines''' paranccsal. A periodikus struktúrák '''Modify->Spectrum 2D''' Fourier szűrővel emelhetők ki. A szűrőket minden esetben körültekintően kell használni, mivel azok eltorzíthatják a képet. Távolságokat és magasságokat az '''Analyze->Section''' (vonalmetszet) [[Fájl:STM icon section.jpg]] utasítás segítségével mérhetünk. A képek két vagy három dimenziós ábrázolásban a '''View->Top View'''[[Fájl:STM icon topview.jpg]] vagy a '''View->Surface Plot''' [[Fájl:STM icon surfaceplot.jpg]] utasításokkal jeleníthetők meg. A képek kontrasztja bármely szűrő használatakor állítható. A képek mentésére a '''Utility->TIFF Export''' utasítás használható. A Nanoscope program saját formátuma a megszokott képfeldolgozó programok segítségével nem nyitható ki, viszont a [http://www.nanotec.es/ Nanotec Electronica] cég ingyenes [http://www.nanotec.es/products/wsxm/thanks.php?code=3_1 WSxM] 3.1-es vagy újabb programja képes kinyitni és feldolgozni a Nanoscope fileokat. A WSxM program működése hasonlít a Nanoscope program működéséhez, viszont a megjelenése és az utasítások megnevezése eltér. A kép dőlését a teljes képhez ('''Process-> Plane-> Global''') vagy a kép egy részéhez ('''Process-> Plane-> Local''') illesztett sík kivonásával tudjuk eltávolítani. Szükség esetén a '''Process-> Filter-> Fit2nd''' utasítással másodfokú felületet vonhatunk ki a képből. Az egyes pásztázási vonalak magassága gyakran eltér, ezért általában érdemes végrehajtani a '''Process-> Filter-> Flatten''' parancsot. Ezzel az utasítással minden pásztázási vonalhoz egyenest ('''Offset''' - nincs dőlés és '''Line''' - van dőlés) vagy parabolát (Parabola) illesztünk, és azt kivonjuk a pásztázási vonalból. '''Process->Filter->Flatten->Line''' a '''Process-> Plane-> Global''' parancsot is helyettesíti. A képen tálalható tüskék eltávolíthatók például a '''Process-> Filter-> Matrix convolution-> Smooth_3x3''' átlagoló mátrixszűrővel. A kép egy részlete a Process-> Zoom paranccsal nagyítható ki. Vonalmetszetet a '''Process-> Profile''' paranccsal készíthetünk. A metszeten '''Process-> Measure''' distance utasítással lehet megmérni két pont távolságát. A kép 3D megjelenítése a '''Display-> 3D Settings and Preview''' utasítással módosítható. Itt lehetőség van a kép döntésére és forgatására, valamint a megvilágítás irányának a változtatására is. 2D ábrázolásban ('''Display-> Top View''') fontos színskálát használni. A színskála a '''Display-> Info''' paranccsal érhető el. | ||
</wlatex> | </wlatex> | ||
A lap jelenlegi, 2016. február 19., 01:49-kori változata
Tartalomjegyzék[elrejtés] |
Információk
A gyakorlatnak otthont adó intézmény:
MTA TTK MFA (Műszaki Fizikai és Anyagtudományi Kutatóintézet),Nanoszerkezetek Osztály
Helyszíne:
KFKI telephely (Csillebérc), Budapest XII., Konkoly-Thege M. út 29-33., 26-os épület, f.sz. 1-es labor.
Megközelítése:
Az egyetem északi részéről: 18-as villamossal a Széll Kálmán térig, onnan a 21-es busszal a végállomásig.
Az egyetem déli részéről: 212-es busszal Svábhegyig, onnan a 21-es busszal a végállomásig.
Gyakorlatvezetők:
Kun Péter (kun@mfa.kfki.hu, telefon: xxxx-es mellék), Pálinkás András (palinkas@mfa.kfki.hu, telefon: xxxx-ös mellék)
Elméleti összefoglaló
Bevezetés
A gyakorlat célja hozzásegíteni a hallgatókat ahhoz, hogy megismerkedhessenek napjaink talán legizgalmasabb felületvizsgáló eszközcsoportjának (SPM, Scanning Probe Microscope) egyikével, az STM-mel (Scanning Tunneling Microscope, pásztázó alagútmikroszkóp), mérések végzésével és a nyert képek számítógépes kiértékelésével. Az STM elektromosan vezető felületek atomi léptékű vizsgálatára és módosítására alkalmas eszköz. Az alagútmikroszkópban egy igen hegyes tűt mozgatunk a felülettől nanométeres távolságra, miközben a tű és a minta közé volt nagyságrendű feszültséget kapcsolunk. Az STM leggyakrabban alkalmazott üzemmódjában (állandó áramú leképezés) miközben a minta síkjában a tűvel pásztázó mozgást végzünk, egy visszacsatoló hurokkal a tű felület fölötti magasságát úgy szabályozzuk, hogy a tű és a minta közötti, általában nanoamper nagyságrendű alagútáram állandó értéken maradjon. A tű így kialakuló háromdimenziós mozgása adja az STM képet. A megfelelő módon zajvédett (elektromos és mechanikai zajok szempontjából egyaránt) STM elegendően sima felületeken - pl. hasított egykristály - rutinszerűen képes elérni az atomi felbontást, lásd az 1.1 ábrán.
Az alagúteffektus
Ha két vezető anyag közé elektromos feszültséget kapcsolunk, és ezeket összeérintjük, áram folyik. Az elektródákat eltávolítva egymástól az áram megszűnik. Az áram megszűnése azonban nem ugrásszerűen, hanem fokozatosan történik, az elektródákat távolítva az áram exponenciálisan csökken. Makroszkópikus elektróda távolságoknál az áram mérhetetlenül kicsivé válik, tehát minden gyakorlati szempontból nullának tekinthető. Viszont ha az elektródák távolsága elegendően kicsi, azaz a nanométer (nm) tartományba esik, akkor jól mérhető áram fog folyni. Ezt a jelenséget kvantummechanikai alagúteffektusnak nevezzük.
Az alagúteffektus elmélete szerint egy részecske egy  szélességű és
szélességű és 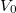 magasságú potenciálgáton (1.2. ábra) akkor is véges valószínűséggel képes áthatolni, ha az
magasságú potenciálgáton (1.2. ábra) akkor is véges valószínűséggel képes áthatolni, ha az  energiája kisebb a potenciálgát magasságánál,
energiája kisebb a potenciálgát magasságánál, 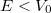 . Az áthaladás valószínűsége:
. Az áthaladás valószínűsége:
![\[ P = \frac{16E\left( V_0 - E\right)}{V_0^2}\cdot e^{-2\kappa d} \]](/images/math/8/5/9/8593addce489e1eb2e03882003c42f22.png)
ahol 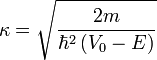 (Ez a képlet csak aszimptotikusan,
(Ez a képlet csak aszimptotikusan,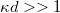 határesetben igaz.)
határesetben igaz.)
Fém elektródák esetén a potenciálgát 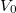 magassága elektronvolt (
magassága elektronvolt (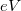 ) nagyságrendű. Ilyenkor az (1) képlet szerint az átmeneti valószínűség kb. tizedére csökken, ha az elektródák távolságát
) nagyságrendű. Ilyenkor az (1) képlet szerint az átmeneti valószínűség kb. tizedére csökken, ha az elektródák távolságát 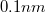 -rel növeljük. Az STM-ben szokásos
-rel növeljük. Az STM-ben szokásos 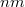 nagyságrendű
nagyságrendű  értékek esetén
értékek esetén  jellegzetes értéke kb.
jellegzetes értéke kb. 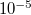 .
.
Az alagútáram
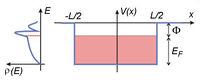
![\left[ \frac{-L}{2},\frac{L}{2} \right]](/images/math/5/8/d/58d9dd56c26f5c3724cfd82bde14cb36.png) intervallumban elhelyezkedő fémben az elektron
intervallumban elhelyezkedő fémben az elektron 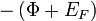 potenciált, az intervallumon kívüli vákuumban nulla potenciált érzékel. A
potenciált, az intervallumon kívüli vákuumban nulla potenciált érzékel. A ![\left[-\left( \Phi+E_F \right),-\Phi \right]](/images/math/c/8/e/c8e946ef670885e121b5fd0ddbcad97c.png) közötti energiaszintek betöltöttek, az e fölötti szintek üresek. A bal oldali ábra egy hipotetikus állapotsűrűség függvényt mutat. A piros szaggatott vonal jelöli a Fermi szint helyét.
közötti energiaszintek betöltöttek, az e fölötti szintek üresek. A bal oldali ábra egy hipotetikus állapotsűrűség függvényt mutat. A piros szaggatott vonal jelöli a Fermi szint helyét.
Ha a két elektróda közé 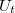 előfeszítést kapcsolunk, akkor az
előfeszítést kapcsolunk, akkor az 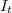 alagútáram nagysága ettől a feszültségértéktől, az elektródák anyagától és az elektródák közti távolságtól fog függeni. Az alagútáram az alábbi módon becsülhető meg.
alagútáram nagysága ettől a feszültségértéktől, az elektródák anyagától és az elektródák közti távolságtól fog függeni. Az alagútáram az alábbi módon becsülhető meg.
A fémes vezetés legegyszerűbb modellje, a szabadelektron gáz modell szerint a vezetési elektronok a fém belsejében szabadon mozoghatnak, de a határfelületnek belülről nekiütközve visszaverődnek a fém belsejébe. Mivel a fémek tipikus elektronsűrűsége 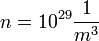 körüli és az elektronok átlagos sebessége
körüli és az elektronok átlagos sebessége 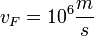 , időegységenként kb.
, időegységenként kb. 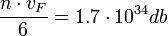 elektron ütközik a határfelület egységnyi felületén. Ha az (1) képletet figyelembe véve feltesszük, hogy ezeknek
elektron ütközik a határfelület egységnyi felületén. Ha az (1) képletet figyelembe véve feltesszük, hogy ezeknek  -ed része jut át a másik elektródába, nulladik közelítésként az alagútáramra
-ed része jut át a másik elektródába, nulladik közelítésként az alagútáramra 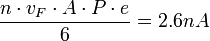 adódik, ahol
adódik, ahol  az elektron töltése, továbbá föltételeztük, hogy az áram egy
az elektron töltése, továbbá föltételeztük, hogy az áram egy 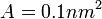 területű alagút csatornán át folyik. (Ez utóbbi érték megfelel egy egyatomos STM tű csúcs felületének.) Bár a kapott alagútáram nagyságrendileg valóban az STM esetén szokásos
területű alagút csatornán át folyik. (Ez utóbbi érték megfelel egy egyatomos STM tű csúcs felületének.) Bár a kapott alagútáram nagyságrendileg valóban az STM esetén szokásos 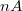 tartományba esik, ez a durva becslés több szempontból is pontosításra szorul. Elsősorban figyelembe kell venni a Pauli elvet, ugyanis egy adott
tartományba esik, ez a durva becslés több szempontból is pontosításra szorul. Elsősorban figyelembe kell venni a Pauli elvet, ugyanis egy adott  energiájú elektron csak akkor juthat át a másik elektródába, ha azon az energián rendelkezésre áll ott nem betöltött energiaállapot. Másodsorban az is lényeges módon befolyásolja az alagútáramot, hogy milyen az elektronok energia szerinti eloszlása az elektródákban. Ezen hatások figyelembevétele a következő módon lehetséges.
A fémek legegyszerűbb kvantumfizikai modellje, a potenciálkád modell (1.3. ábra) feltételezi, hogy a vezetési elektronok egy potenciál dobozba vannak zárva. Ebben a modellben a fém vezetési elektronjainak (azaz a fémben szabad mozgásra képes, ún. delokalizált, tehát nem valamely atomhoz kötött elektronoknak) két leglényegesebb tulajdonságát vesszük figyelembe:
energiájú elektron csak akkor juthat át a másik elektródába, ha azon az energián rendelkezésre áll ott nem betöltött energiaállapot. Másodsorban az is lényeges módon befolyásolja az alagútáramot, hogy milyen az elektronok energia szerinti eloszlása az elektródákban. Ezen hatások figyelembevétele a következő módon lehetséges.
A fémek legegyszerűbb kvantumfizikai modellje, a potenciálkád modell (1.3. ábra) feltételezi, hogy a vezetési elektronok egy potenciál dobozba vannak zárva. Ebben a modellben a fém vezetési elektronjainak (azaz a fémben szabad mozgásra képes, ún. delokalizált, tehát nem valamely atomhoz kötött elektronoknak) két leglényegesebb tulajdonságát vesszük figyelembe:
- a) az elektronok a fémben kötöttek, kiszabadításukhoz munkát kell befektetni, ennek a legkisebb nagysága a
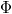 kilépési munka
kilépési munka
- b) az elektronok egy véges energiasávot foglalnak el, melynek szélessége az
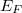 Fermi energia és a legmagasabb energiájú betöltött állapot energiája a Fermi szint.
Fermi energia és a legmagasabb energiájú betöltött állapot energiája a Fermi szint.
Ennek az energiasávnak a szerkezetét a 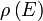 állapotsűrűség függvény (Density of States, DOS) írja le, definíció szerint
állapotsűrűség függvény (Density of States, DOS) írja le, definíció szerint 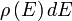 az
az  energia körüli
energia körüli 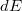 infinitezimális energiaintervallumban található elektronállapotok száma. Az állapotsűrűség függvény ismeretében az adott szilárdtest legtöbb fontos adata (pl. elektromos, optikai, mechanikai, termodinamikai jellemzők) kiszámítható, és mint alább megmutatjuk, az alagútáram nagyságát is a DOS határozza meg.
infinitezimális energiaintervallumban található elektronállapotok száma. Az állapotsűrűség függvény ismeretében az adott szilárdtest legtöbb fontos adata (pl. elektromos, optikai, mechanikai, termodinamikai jellemzők) kiszámítható, és mint alább megmutatjuk, az alagútáram nagyságát is a DOS határozza meg.
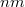 közelségbe hozzuk, a Fermi szintek kiegyenlítődnek és kialakul a kontaktpotenciál. (c) Az elektródák közé
közelségbe hozzuk, a Fermi szintek kiegyenlítődnek és kialakul a kontaktpotenciál. (c) Az elektródák közé 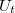 előfeszítést kapcsolunk. Az
előfeszítést kapcsolunk. Az 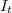 alagútáram az
alagútáram az 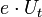 szélességű energiaintervallumban folyik, az A elektróda betőltőtt állapotaiból a B elektróda üres állapotaiba. A nagyobb energiájú komponensek áram járuléka nagyobb, a nagyobb átmeneti valószínűségük miatt.
szélességű energiaintervallumban folyik, az A elektróda betőltőtt állapotaiból a B elektróda üres állapotaiba. A nagyobb energiájú komponensek áram járuléka nagyobb, a nagyobb átmeneti valószínűségük miatt.
A 1.4/a. ábrán a két, egymástól kezdetben makroszkópikus távolságban lévő elektróda potenciálkád sávszerkezetét ábrázoltuk. Általános esetben a két elektróda (A és B) különböző anyagú, ezért Fermi energiájuk és kilépési munkájuk is eltérő, az ábrán az A elektróda Fermi szintje magasabban helyezkedik el a B Fermi szintjénél. Ha az elektródákat olyan közelségbe hozzuk egymáshoz, hogy az elektronok számottevő valószínűséggel közlekedhessenek egyikből a másikba (alagúteffektus által), akkor az A elektródából elektronok kezdenek átfolyni a B elektródába. Ez azt jelenti, hogy A pozitív, B pedig negatív töltést nyer, minek hatására mindkét elektróda a vákuumszinthez képest elektrosztatikus potenciális energiára tesz szert. Mivel ahhoz, hogy a végtelenből a "+" töltésű A felületéig vigyünk egy elektront "-" munkát, ahhoz viszont, hogy a "-" töltésű B felületéig vigyünk egy elektront "+" munkát kell végezni, A energiaszintjei "-", B energiaszintjei pedig "+" irányban tolódnak el a vákuumszinthez képest. Következésképpen a két elektróda közt létrejön az ún. kontaktpotenciál. A töltésátfolyás mindaddig tart, amíg a két elektróda Fermi szintje ki nem egyenlítődik (1.4/b. ábra). Mint arról egyszerű számolással meggyőződhetünk, a kiegyenlítődés eléréséhez (fémek esetében) a vezetési elektronok összes számához képest elegendő igen kevés elektronnak átjutnia A-ból B-be, tehát a sávszélességek változása teljesen elhanyagolható.
Ha ezután a két,  távolságban lévő elektróda közé
távolságban lévő elektróda közé 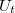 előfeszítést kapcsolunk, a 1.4/c. ábrán vázolt helyzet áll elő. Ilyenkor csak az ábrán jelölt,
előfeszítést kapcsolunk, a 1.4/c. ábrán vázolt helyzet áll elő. Ilyenkor csak az ábrán jelölt, 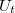 szélességű energiasávba eső elektronok juthatnak át az A elektródából a B elektródába, mert csak ezeken az energiákon vannak az A elektródában betöltött, a B elektródában pedig üres állapotok. Mivel adott
szélességű energiasávba eső elektronok juthatnak át az A elektródából a B elektródába, mert csak ezeken az energiákon vannak az A elektródában betöltött, a B elektródában pedig üres állapotok. Mivel adott  energia körüli
energia körüli 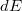 intervallumban átjutó elektronok száma a
intervallumban átjutó elektronok száma a  átmeneti valószínűségtől, valamint attól függ, hogy a két elektródában hány állapot van ebben a
átmeneti valószínűségtől, valamint attól függ, hogy a két elektródában hány állapot van ebben a 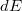 intervallumban, a teljes
intervallumban, a teljes 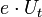 energiaintervallumban folyó
energiaintervallumban folyó 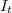 alagútáram:
alagútáram:
![\[ I_t \propto \int_{E_F}^{E_F+eU_t} \rho_{tu} \left( E-eU_t \right) \cdot \rho_{minta} \left( E \right) \cdot P \left( E,U_t \right)\,\mathrm{d}E \]](/images/math/9/2/a/92a58663b9c9f5f1a2042fd197198705.png)
Ha feltesszük, hogy a  és a tű DOS értékek csak elhanyagolható módon függenek az energiától, a következő összefüggést kapjuk:
és a tű DOS értékek csak elhanyagolható módon függenek az energiától, a következő összefüggést kapjuk:
![\[ I_t \propto \int_{E_F}^{E_F+eU_t} \rho_{minta}\left( E \right) \,\mathrm{d}E \]](/images/math/6/8/3/6837ead8492dcd174981a9bbf048b595.png)
Az alagútmikroszkóp
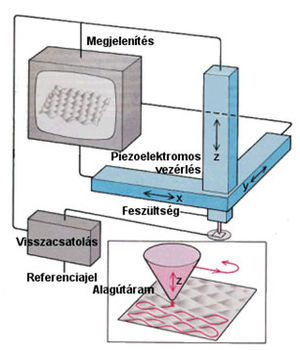
Az STM, mint eszköz (1.5. ábra) az alábbi módon működik.
- Az egyik elektródát igen hegyes tűnek képezzük ki. Ekkor az alagútáram csak a tű hegye körüli keskeny csatornában fog folyni, mivel az alagutazási valószínűség exponenciális távolságfüggése miatt a tű távolabbi részei és a minta közötti áram elhanyagolhatóan kicsi. Ennek az alagút csatornának a szélessége körülbelül akkora, mint a tű csúcsának a görbületi sugara. Tehát műszerünk felbontását elsősorban az alkalmazott tű hegyessége határozza meg. Ha atomi skálán hegyes tűt alkalmazunk, akkor a felbontás is atomi léptékű lesz.
- A tűt egy olyan háromdimenziós mechanikai mozgató rendszerre szereljük, amely igen finom (század nanométeres, vagy finomabb) pontossággal képes mozgatni a tűt a minta felett. A gyakorlatban erre a célra általában piezoelektromos mozgatókat alkalmaznak.
- A tű és a minta közé
 nagyságrendű előfeszítést kapcsolunk.
nagyságrendű előfeszítést kapcsolunk.
- Ezután a tűt óvatosan addig közelítjük a felülethez, amíg megjelenik az alagútáram és elér egy előre beállított
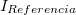 értéket. Minél nagyobb az
értéket. Minél nagyobb az 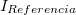 , annál közelebb kerül a tű a felülethez, gyakorlatban a tipikus nagysága
, annál közelebb kerül a tű a felülethez, gyakorlatban a tipikus nagysága 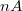 körüli.
körüli.
- A minta X-Y síkjában a tűvel pásztázó mozgást végzünk, hasonlóan a TV készülékekben alkalmazott vezérléshez (1.5. ábra). Természetesen, mivel itt nem elektronsugarat, hanem makroszkopikus tömegeket mozgatunk, a mechanikai rendszer tehetetlensége és rezonanciái miatt az alkalmazható kép- illetve sorfrekvencia kisebb, mint a TV esetén megszokott. Ezért egy STM kép fölvétele általában másodpercekig vagy percekig tart.
- Pásztázás közben a tű minta feletti magasságát (Z pozícióját) egy visszacsatoló hurokkal úgy szabályozzuk, hogy a mért alagútáram állandóan megegyezzen az
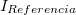 értékkel.
értékkel.
- Ily módon a tű minden egyes (X,Y) pozíciójához egy meghatározott Z érték fog tartozni. Ezeket a Z(X,Y) értékeket számítógéppel rögzítjük. (A módszer hőskorában a Z(X,Y) felületet úgy jelenítették meg, hogy az egyes Z(X,Y=const) pásztázási sorokat analóg rajzgéppel vastag papírra rögzítették, majd a papírból kivágták és egymás mögé ragasztották.)
- Az STM-ben igen gondos rezgéscsillapításra van szükség, mivel a tűt a minta fölött nanométeres távolságban kell mozgatnunk. Ha a tű beleütközik a mintába, az általában a tű hegyének és a mintának a sérülését okozza, továbbá, az alagútköz szélességének véletlenszerű változásai "zajként" jelennek meg a felvett képen. A nagyamplitúdójú zaj elfedi a jellemzően
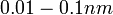 -es atomi korrugációt.
-es atomi korrugációt.
- Bár az első STM kísérleteket ultra nagy vákuumban (UHV) végezték, később megállapították, hogy az alagútmikroszkóp normál levegőn, sőt még (szigetelő) folyadékban is kiválóan működik! Ezért a költséges és nehézkes vákuumrendszereket csak akkor szükséges alkalmazni, ha a mérendő felület tulajdonságai ezt megkívánják, azaz ha a vizsgált minta a levegőn oxidálódna, illetve szennyeződne. Mivel a nem oxidálódó minták (pl. a szén) levegőn vizsgálhatóak, az alagútmikroszkóp egy viszonylag olcsó eszköz, összehasonlítva a modern fizika egyéb mérőeszközeivel, például az elektronmikroszkóppal.
STM üzemmódok
A gyakorlatban az alagútmikroszkópot általában vagy ún. topográfiai, vagy ún. spektroszkópiai üzemmódban használjuk.
- Topográfiai üzemmódban rögzített
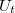 előfeszítés és
előfeszítés és 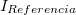 alagútáram érték mellett a Z(X,Y) felületet vesszük fel. Ha feltételezzük, hogy a
alagútáram érték mellett a Z(X,Y) felületet vesszük fel. Ha feltételezzük, hogy a  átmeneti valószínűség és a minta állapotsűrűsége mindegyik (X,Y) pontban egyforma, a Z(X,Y) felület nulladik közelítésben a minta geometriai felületét, topográfiáját fogja megadni. Azonban a gyakorlatban ezek a mennyiségek a helytől is függhetnek, tehát a mért Z(X,Y) felület együttesen tartalmazza a topográfiai és az elektronszerkezeti információt. A topográfiai üzemmódban leggyakrabban kicsi előfeszítést alkalmazunk. Ha
átmeneti valószínűség és a minta állapotsűrűsége mindegyik (X,Y) pontban egyforma, a Z(X,Y) felület nulladik közelítésben a minta geometriai felületét, topográfiáját fogja megadni. Azonban a gyakorlatban ezek a mennyiségek a helytől is függhetnek, tehát a mért Z(X,Y) felület együttesen tartalmazza a topográfiai és az elektronszerkezeti információt. A topográfiai üzemmódban leggyakrabban kicsi előfeszítést alkalmazunk. Ha 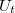 infinitezimálisan kicsi, a (2) képlet integrandusában a DOS és
infinitezimálisan kicsi, a (2) képlet integrandusában a DOS és  energiafüggése elhanyagolható. Mivel a DOS helyfüggése mellett az átmeneti valószínűség helyfüggése kisebb szerepet játszik, az alagútáram mindenhol a minta állapotsűrűség Fermi szintnek megfelelő értékével lesz arányos:
energiafüggése elhanyagolható. Mivel a DOS helyfüggése mellett az átmeneti valószínűség helyfüggése kisebb szerepet játszik, az alagútáram mindenhol a minta állapotsűrűség Fermi szintnek megfelelő értékével lesz arányos:
![\[ I_t \left( \overrightarrow{r}, U_t \right) \propto U_t \cdot \rho_{minta} \left( E = E_{F},\overrightarrow{r} \right) \]](/images/math/6/a/4/6a44c57136f2fb35671422ff36d07248.png)
- Spektroszkópiai üzemmódban (Scanning Tunneling Spectroscopy, STS) egy, kiválasztott (X,Y) pontban megállunk a tűvel és ideiglenesen kikapcsoljuk a visszacsatoló hurkot is. Ebben a rögzített
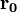 tű helyzetben felvesszük az alagútátmenet áram-feszültség karakterisztikáját, azaz az
tű helyzetben felvesszük az alagútátmenet áram-feszültség karakterisztikáját, azaz az 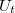 előfeszítést változtatva megmérjük az
előfeszítést változtatva megmérjük az 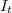 alagútáram változását. Mivel
alagútáram változását. Mivel 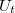 változtatása a (3) képlet integrálási határa változtatásának felel meg, a mért áram feszültség szerinti deriválásával a képlet integrandusának energiafüggését kapjuk:
változtatása a (3) képlet integrálási határa változtatásának felel meg, a mért áram feszültség szerinti deriválásával a képlet integrandusának energiafüggését kapjuk:
![\[ \frac{I_t \left( U_t \right)}{dU_t} \propto \rho_{minta} \left( E = E_F + eU_t,\overrightarrow{r} = \overrightarrow{r_0}\right)\]](/images/math/1/8/0/1809f389c11ff265899c40030e39184f.png)
Az STM családja
A zseniális ötletek általában megtermékenyítően hatnak a tudomány fejlődésére. Az STM esetén is így történt, ez vezetett az ún. pásztázó szondás módszerek családjának létrejöttéhez. Mindegyik ilyen eszközben egy hegyes szondát pásztáznak a minta fölött és a szonda és a minta valamiféle kölcsönhatását mérik. A legfontosabb ezek közül az atomerő mikroszkóp (Atomic Force Microscope, AFM). Az AFM-ben, hasonlóan az STM-hez, egy hegyes tűt mozgatunk a minta fölött és közben a tűre ható erőt a visszacsatoló hurok segítségével állandó értéken tartjuk. Mivel ez a műszer szigetelő felületek vizsgálatát is lehetővé teszi, az ipari kutatásokban is gyakran használják.
Műszerek
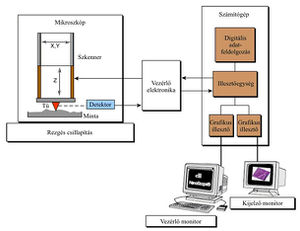
A mérésekhez egy Veeco (DI) gyártmányú Nanoscope 3 STM/AFM készülékkel rendelkezünk. Ennek jellemzője a moduláris felépítés, ami lehetővé teszi, hogy különféle pásztázó fejeket, vezérlő elektronikákat és számítógépeket illeszthessünk össze. A berendezés szabad levegőn működik. Esetünkben a mérőfej 15x15 mikron vízszintes és 3 mikron függőleges tartomány pásztázását teszi lehetővé, de ez egyszerűen kicserélhető nagyobb tartomány pásztázására képes fejre is. A rendszer blokkvázlatát a következő ábrán láthatjuk:
A rezgéscsillapító alapvető feladata, hogy a külvilág felől érkező mechanikai vibrációkat távol tartsa a tulajdonképpeni STM-től, illetőleg elfogadható szintűre csillapítsa azokat. Ez nagyon fontos része a készüléknek, hiszen a mintát letapogató tűt mindössze 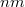 -es (
-es (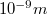 ) távolságban kell a minta felületétől mozgatnunk, ezért ha a rezgések ennél nagyobb amplitúdójú relatív elmozdulását okozzák a tűnek és a mintának, akkor a tű beleszaladhat a mintába, ami természetesen a tű hegyének letompulását és a minta lokális roncsolódását okozza. Egészen kisfrekvenciás zavarok esetén a helyzet azért drámainak nem mondható, ugyanis a mindenkori tű-minta távolságot egy néhány
) távolságban kell a minta felületétől mozgatnunk, ezért ha a rezgések ennél nagyobb amplitúdójú relatív elmozdulását okozzák a tűnek és a mintának, akkor a tű beleszaladhat a mintába, ami természetesen a tű hegyének letompulását és a minta lokális roncsolódását okozza. Egészen kisfrekvenciás zavarok esetén a helyzet azért drámainak nem mondható, ugyanis a mindenkori tű-minta távolságot egy néhány 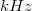 frekvenciával reagálni képes negatív visszacsatolás szabályozza. Tehát amíg a rázkódásból eredő relatív elmozdulások nem túl gyorsak és nem lépik túl a szabályozási tartományt, addig az STM megőrzi működőképességét. Sajnos azonban a működőképesség megőrzése még nem jelent optimális működést, ugyanis a sikeresen kompenzált mechanikai rezgés esetén is hozzáadódik a hasznos jelhez a zavaró jel, ami különféle, nem valós periodikus struktúrák megjelenését eredményezi az STM képen. Így tehát elsőrendű feladatunk, hogy a hangfrekvenciás rezgések szintjét nagyságrendekkel csillapítsuk, az infrahangokét pedig annyira, amennyire módunkban áll. A csillapítás elvi alapja az, hogy mérsékeljük az STM fejre ható, a külső vibrációkból eredő gyorsító erőt, rugalmas felfüggesztés közbeiktatásával.
frekvenciával reagálni képes negatív visszacsatolás szabályozza. Tehát amíg a rázkódásból eredő relatív elmozdulások nem túl gyorsak és nem lépik túl a szabályozási tartományt, addig az STM megőrzi működőképességét. Sajnos azonban a működőképesség megőrzése még nem jelent optimális működést, ugyanis a sikeresen kompenzált mechanikai rezgés esetén is hozzáadódik a hasznos jelhez a zavaró jel, ami különféle, nem valós periodikus struktúrák megjelenését eredményezi az STM képen. Így tehát elsőrendű feladatunk, hogy a hangfrekvenciás rezgések szintjét nagyságrendekkel csillapítsuk, az infrahangokét pedig annyira, amennyire módunkban áll. A csillapítás elvi alapja az, hogy mérsékeljük az STM fejre ható, a külső vibrációkból eredő gyorsító erőt, rugalmas felfüggesztés közbeiktatásával.
Az STM mikroszkóp fejben (2.2. ábra) található a készülék "lelke", amely nem más, mint a letapogató tű. Ez voltaképpen egy, az egyik végén atomi léptékben hegyes vékony wolfram, platina-ródium vagy platina-irídium drót. Az STM tűt a mérőfejen található csövecskébe helyezzük. Felvetődik a kérdés, hogy hogyan lehet ilyen jól kihegyezni egy drótot? Nos, erre léteznek különféle módszerek (pl. elektrokémiai maratás). Mi a közönséges mechanikai hegyezéshez folyamodunk, a drótot egy éles ollóval, távolító mozdulattal kombináltan elvágjuk. A tűket optikai mikroszkóp alatt ellenőrizzük. Természetesen, nincs arra garancia, hogy az optikailag tökéletesnek látszó tű akárcsak elfogadható is legyen, hiszen az optikai mikroszkópban csak kb. mikronos felbontásban láthatjuk a tű végét, vagyis mintegy 3-4 nagyságrenddel durvábban a kelleténél. A gyakorlat azonban azt mutatja, hogy egy ügyes kezű ember minden második-harmadik hegyezése bizonyos mérésekhez elfogadható tűt eredményez. A tű végének keresztmetszete általában nem körszimmetrikus, hanem valamilyen irányban elnyújtott. A mindkét irányban (X, Y) egyformán hegyes tű sokkal ritkábban sikerül. A mechanikai hegyezéssel előállított tűk jellegzetes hibája, hogy a végükön egymás mellett több ún. nano-csúcs is lehet, amelyek közül az alagútáram az erős távolságfüggés miatt lényegében csak azon át folyik, amelyik a minta felületéhez a legközelebb van. Kellően sík mintánál (pl. HOPG) a mérés alatt végig ugyanaz maradhat az aktív nano-csúcs, miközben tagoltabb felületűeknél (pl. csiszolt fémeknél) akár többször is megváltozhat egyetlen mérés alatt. (Ilyenkor a pásztázás kissé máshol folytatódik, mint "hiszi" azt az adatgyűjtő program.) Az előbbi tűhibákra a felvett képek minőségéből következtethetünk. Vagyis egy tű jóságát végső fokon onnan tudjuk megítélni, hogy milyen képeket tudunk vele készíteni. Ezért a megfelelő tű elkészítése meglehetősen időigényes eljárás, hiszen egy-egy próba mérés előkészítése és elvégzése sok-sok percre rúghat. Akár egy teljes napot is igénybe vehet a kísérletezés, amíg végre szert teszünk egy kiváló minőségű tűre. Ráadásul a tű egy szempillantás alatt bármikor tönkre is mehet, hiszen elegendő egy icipicit beleütköznie a minta felületébe. A helyzet orvoslására a méréshez 1-1 megfelelően jól hegyezett tűt eleve biztosítunk, de természetesen a diákok is próbálkozhatnak a tűhegyezéssel. A tű közvetlenül egy előerősítőhöz csatlakozik, így lecsökkenthető az alagútáramra tevődő zaj. A berendezés minimum 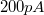 alagútáramon képes dolgozni, ennél kisebb áramokon látványosan lelassul az előerősítő.
alagútáramon képes dolgozni, ennél kisebb áramokon látványosan lelassul az előerősítő.
A minta mechanikai mozgatását (pásztáztatását) egy piezokerámia szkenner cső végzi, megfelelő (maximum 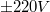 -os) feszültség hatására. A tű durva közelítését és távolítását egy mikrométer csavar végzi, melyet motor működtet. Minta- illetve tűcsere esetén a tű az előerősítővel együtt levehető. Tűcsere után az előerősítőt rugókkal rögzítjük, a tűt a csavarral kb.
-os) feszültség hatására. A tű durva közelítését és távolítását egy mikrométer csavar végzi, melyet motor működtet. Minta- illetve tűcsere esetén a tű az előerősítővel együtt levehető. Tűcsere után az előerősítőt rugókkal rögzítjük, a tűt a csavarral kb. 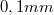 távolságra közelítjük a mintához, majd a számítógép segítségével folytatjuk a tű mozgatását.
távolságra közelítjük a mintához, majd a számítógép segítségével folytatjuk a tű mozgatását.
A mérés vezérlését és az adatok gyűjtését számítógép végzi. Az egyszerűbb kezelhetőség miatt két monitort használunk, a vezérlő monitoron a mérési paraméterek állíthatók, a kijelző monitoron pedig az STM kép látható.
A mérés üzemmód (Realtime) a ![]() gomb segítségével indítható, a rögzített képek (Offline) pedig a
gomb segítségével indítható, a rögzített képek (Offline) pedig a ![]() gomb megnyomásával érhetők el. Mérés üzemmódban
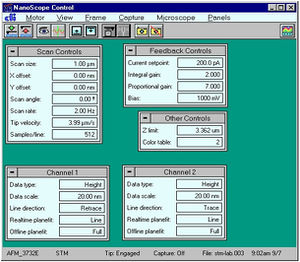
gomb megnyomásával érhetők el. Mérés üzemmódban ![]() (2.3. ábra) a Scan Controls ablakban állítható a pásztázási ablak mérete, a pásztázás helye, szöge, frekvenciája, sebessége és felbontása. A pásztázási sebesség (frekvencia) megválasztásánál figyelembe kell venni a visszacsatoló rendszer tehetetlenségét és a minta durvaságát, mivel a nagy sebesség a minta és/vagy a tű sérülését eredményezheti. Az STM kép felbontása 128, 256 vagy 512
(2.3. ábra) a Scan Controls ablakban állítható a pásztázási ablak mérete, a pásztázás helye, szöge, frekvenciája, sebessége és felbontása. A pásztázási sebesség (frekvencia) megválasztásánál figyelembe kell venni a visszacsatoló rendszer tehetetlenségét és a minta durvaságát, mivel a nagy sebesség a minta és/vagy a tű sérülését eredményezheti. Az STM kép felbontása 128, 256 vagy 512 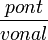 lehet. A Feedback Controls ablakban állítható az alagútáram, a tű-minta feszültség és a visszacsatolás erőssége. Nagyobb Integral és Proportional Gain értékek gyorsabb pásztázást tesznek lehetővé, viszont túl nagy értékek esetén a visszacsatoló hurok begerjed. A maximális függőleges pásztázási tartomány és a színskála az Other Controls ablakban állítható. Ismeretlen minta esetén érdemes a maximális függőleges tartományt használni, viszont ez gyengébb függőleges felbontást eredményez (felbontás
lehet. A Feedback Controls ablakban állítható az alagútáram, a tű-minta feszültség és a visszacsatolás erőssége. Nagyobb Integral és Proportional Gain értékek gyorsabb pásztázást tesznek lehetővé, viszont túl nagy értékek esetén a visszacsatoló hurok begerjed. A maximális függőleges pásztázási tartomány és a színskála az Other Controls ablakban állítható. Ismeretlen minta esetén érdemes a maximális függőleges tartományt használni, viszont ez gyengébb függőleges felbontást eredményez (felbontás 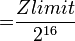 ). A Channel ablakokban választható a rögzített adatok típusa (magasság vagy áram), skála mérete, pásztázás iránya és a dőléskiegyenlítés módja.
). A Channel ablakokban választható a rögzített adatok típusa (magasság vagy áram), skála mérete, pásztázás iránya és a dőléskiegyenlítés módja.
A mérésvezérlő program felépítése hasonlít a Windows programokhoz. Az utasítások menükbe vannak csoportosítva, a gyakran használt utasítások közvetlenül elérhetők. ![]() a tűt addig közelíti a mintához, amíg a beállított áram meg nem jelenik.
a tűt addig közelíti a mintához, amíg a beállított áram meg nem jelenik. ![]() hatására a tű eltávolodik a mintától.
hatására a tű eltávolodik a mintától. ![]() megnyomásával a készülő képet,
megnyomásával a készülő képet,![]() megnyomásával pedig az utolsó pásztázási vonalat jelenítjük meg a képernyőn.
megnyomásával pedig az utolsó pásztázási vonalat jelenítjük meg a képernyőn. ![]() lentről vagy fentről indítja a pásztázást.
lentről vagy fentről indítja a pásztázást. ![]() be vagy ki kapcsolja a kép rögzítését. A képernyő alján látható a mérőfej típusa, az üzemmód, a tű állapota, képrögzítés állapota, a file neve és az idő. A file neve a Capture->Capture Filename paranccsal állítható be.
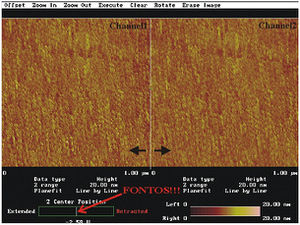
Mérés közben a kijelző képernyőn (2.4. ábra) követhető a pásztázás. A képernyő bal oldalán az 1-es csatorna (jobbról balra pásztázás) adatai láthatók, a képernyő jobb oldalán pedig a 2-es csatorna adatai. FONTOS folyamatosan figyelni a képernyő bal alsó sarkában található Z Center Position kijelzőt, amely a piezo kerámiára kapcsolt feszültséget jelzi. Ha a piros nyíllal jelzett fehér függőleges vonal a zöld téglalap végéhez ér, akkor a kerémia maximálisan összehúzódott vagy kinyúlt és képtelen a felületet követni. A maximális függőleges tartomány (Z limit) növelésével vagy a pásztázási ablak (Scan size) csökkentésével általában javítható a helyzet. Ha ez nem sikerül, akkor a tűt ki kell húzni
be vagy ki kapcsolja a kép rögzítését. A képernyő alján látható a mérőfej típusa, az üzemmód, a tű állapota, képrögzítés állapota, a file neve és az idő. A file neve a Capture->Capture Filename paranccsal állítható be.
Mérés közben a kijelző képernyőn (2.4. ábra) követhető a pásztázás. A képernyő bal oldalán az 1-es csatorna (jobbról balra pásztázás) adatai láthatók, a képernyő jobb oldalán pedig a 2-es csatorna adatai. FONTOS folyamatosan figyelni a képernyő bal alsó sarkában található Z Center Position kijelzőt, amely a piezo kerámiára kapcsolt feszültséget jelzi. Ha a piros nyíllal jelzett fehér függőleges vonal a zöld téglalap végéhez ér, akkor a kerémia maximálisan összehúzódott vagy kinyúlt és képtelen a felületet követni. A maximális függőleges tartomány (Z limit) növelésével vagy a pásztázási ablak (Scan size) csökkentésével általában javítható a helyzet. Ha ez nem sikerül, akkor a tűt ki kell húzni ![]() .
.
Minták
Ahhoz, hogy az STM-mel meg tudjunk mérni egy mintát, szükséges, hogy a felülete elektromosan vezető legyen. Mint tudjuk, a fémek általában kiváló elektromos vezetők, ezért joggal reménykedhetünk abban, hogy az STM-mel jól meg tudjuk mérni őket. Sajnos azonban ez még sincs mindig így. Pl. az alumínium kiváló elektromos vezető, de a felületén a szabad levegőn a legrövidebb időn belül is kialakul egy vékony oxid réteg (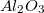 ), amely viszont a legkiválóbb szigetelők közé tartozik (olyannyira, hogy nagyfeszültségű szigetelő kerámiák legfőbb alapanyaga), és mindennek a tetejében még nagyon kemény is (csiszolóanyag és drágakő, lásd korund, zafír). Hasonlóan tudjuk a vasról is, hogy igen hajlamos a rozsdásodásra (oxid és hidroxid vegyesen), és a rozsda egykettőre olyan vastag lehet, hogy a letapogató tűt teljesen elfedi, beszennyezi.
Logikus arra gondolni, hogy a nemesfémekkel talán több szerencsénk lesz. És valóban, pl. az arany és a platina szabad levegőn is egészen jól mérhetők STM-mel, de pl. az egyébként legkiválóbb elektromos vezető ezüst nem! Ennek oka nem az oxigén, hanem az oxigén csoportjába tartozó másik kémiai elem, a kén. Ez ugyanis az ipari szennyezés miatt mindig jelen van a levegőben, az ezüst pedig igen könnyen alkot vele szulfidot. (Ez adja az ezüst tárgyak sötétszürke színét is.) A félnemes fémnek tekinthető vörösréz sem problémamentes, ugyanis elég könnyen oxidálódik (barna szín), illetve képződik rajta zöldes-kékes színű patina (nitrátok, hidrokarbonátok, stb.). Segítségünkre van viszont, hogy a réz oxidja (
), amely viszont a legkiválóbb szigetelők közé tartozik (olyannyira, hogy nagyfeszültségű szigetelő kerámiák legfőbb alapanyaga), és mindennek a tetejében még nagyon kemény is (csiszolóanyag és drágakő, lásd korund, zafír). Hasonlóan tudjuk a vasról is, hogy igen hajlamos a rozsdásodásra (oxid és hidroxid vegyesen), és a rozsda egykettőre olyan vastag lehet, hogy a letapogató tűt teljesen elfedi, beszennyezi.
Logikus arra gondolni, hogy a nemesfémekkel talán több szerencsénk lesz. És valóban, pl. az arany és a platina szabad levegőn is egészen jól mérhetők STM-mel, de pl. az egyébként legkiválóbb elektromos vezető ezüst nem! Ennek oka nem az oxigén, hanem az oxigén csoportjába tartozó másik kémiai elem, a kén. Ez ugyanis az ipari szennyezés miatt mindig jelen van a levegőben, az ezüst pedig igen könnyen alkot vele szulfidot. (Ez adja az ezüst tárgyak sötétszürke színét is.) A félnemes fémnek tekinthető vörösréz sem problémamentes, ugyanis elég könnyen oxidálódik (barna szín), illetve képződik rajta zöldes-kékes színű patina (nitrátok, hidrokarbonátok, stb.). Segítségünkre van viszont, hogy a réz oxidja (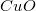 ) félvezető természetű (a század elején fel is használták egyenirányítási célokra), ilyenformán az alagútáram kialakulását nem akadályozza meg, feltéve, hogy az oxid réteg nem túl vastag. (A frissen vákuumpárologtatott réz réteg napokig is mérhető maradhat szabad levegőn STM-mel.) Bizonyos fémek jól mérhetők szabad levegőn, pl. a nikkel, a króm és a molibdén. Ezeken csak vékony a kialakuló oxid réteg, és ráadásul eléggé félvezető természetű is. (Nem véletlen, hogy tükröző felületek készítésére is használják őket.) Egyes anyagok egyáltalán nem fémek, pl. az
) félvezető természetű (a század elején fel is használták egyenirányítási célokra), ilyenformán az alagútáram kialakulását nem akadályozza meg, feltéve, hogy az oxid réteg nem túl vastag. (A frissen vákuumpárologtatott réz réteg napokig is mérhető maradhat szabad levegőn STM-mel.) Bizonyos fémek jól mérhetők szabad levegőn, pl. a nikkel, a króm és a molibdén. Ezeken csak vékony a kialakuló oxid réteg, és ráadásul eléggé félvezető természetű is. (Nem véletlen, hogy tükröző felületek készítésére is használják őket.) Egyes anyagok egyáltalán nem fémek, pl. az 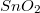 , de szép és stabil félvezető kristályokat alkotnak, így remekül mérhetők. A legfontosabb félvezetővel, a szilíciummal viszont problémánk van, ugyanis igen gyorsan (a másodperc töredéke alatt) oxidálódik, és az oxidja, a kvarc (
, de szép és stabil félvezető kristályokat alkotnak, így remekül mérhetők. A legfontosabb félvezetővel, a szilíciummal viszont problémánk van, ugyanis igen gyorsan (a másodperc töredéke alatt) oxidálódik, és az oxidja, a kvarc (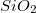 ) a legkiválóbb szigetelők és legkeményebb anyagok közé tartozik. Ezért a szilícium megfelelő STM-es vizsgálata csak ultranagy-vákuumban lehetséges, az ott alkalmazott ("in situ") tisztítást követő korlátozott ideig. A különlegesebb anyagok közül a fémüvegek elsősorban akkor mérhetők jól, ha elég nagy mennyiségben tartalmaznak nemesfém összetevőt is. A mágneses szempontból fontos permalloy sem reménytelen eset, miután akár
) a legkiválóbb szigetelők és legkeményebb anyagok közé tartozik. Ezért a szilícium megfelelő STM-es vizsgálata csak ultranagy-vákuumban lehetséges, az ott alkalmazott ("in situ") tisztítást követő korlátozott ideig. A különlegesebb anyagok közül a fémüvegek elsősorban akkor mérhetők jól, ha elég nagy mennyiségben tartalmaznak nemesfém összetevőt is. A mágneses szempontból fontos permalloy sem reménytelen eset, miután akár  résznyi nikkelt is tartalmazhat. Azonban a szabadlevegős STM-es vizsgálatok kétségtelenül legnagyobb sztárja a grafit. Ez az anyag úgy él hétköznapi szemléletünkben, mint egy elektromosan vezető, enyhén fémes csillogású, gyenge, könnyen szétmorzsolható anyag. Azonban a könnyű szétmorzsolhatósága kizárólag a rétegeinek egymáshoz képesti könnyű elcsúszásból fakad, miközben az egyes rétegeken belül a szénatomokat nagyon erős kovalens kötések tartják a helyükön. Ezért a grafit kémiailag nagyon kevéssé reaktív elem (nem oxidálódik), elektromosan vezet, és a pásztázott felületének számottevő mechanikai tartása is van. Mindezekért viszonylag könnyen elérhetünk rajta akár atomi felbontást is. Ehhez legcélszerűbb HOPG-t (Highly Oriented Pyrolitic Graphite) használnunk, amely ránézésre a csillámhoz hasonló réteges szerkezetű anyag, csak sötétebb. Minthogy a grafit szén atomjainak kötéstávolságát más módszerekkel is meg tudjuk mérni, így a grafit az STM kalibrációjára is felhasználható.
A konkrét mérésekhez a következő mintákat fogjuk megnézni:
résznyi nikkelt is tartalmazhat. Azonban a szabadlevegős STM-es vizsgálatok kétségtelenül legnagyobb sztárja a grafit. Ez az anyag úgy él hétköznapi szemléletünkben, mint egy elektromosan vezető, enyhén fémes csillogású, gyenge, könnyen szétmorzsolható anyag. Azonban a könnyű szétmorzsolhatósága kizárólag a rétegeinek egymáshoz képesti könnyű elcsúszásból fakad, miközben az egyes rétegeken belül a szénatomokat nagyon erős kovalens kötések tartják a helyükön. Ezért a grafit kémiailag nagyon kevéssé reaktív elem (nem oxidálódik), elektromosan vezet, és a pásztázott felületének számottevő mechanikai tartása is van. Mindezekért viszonylag könnyen elérhetünk rajta akár atomi felbontást is. Ehhez legcélszerűbb HOPG-t (Highly Oriented Pyrolitic Graphite) használnunk, amely ránézésre a csillámhoz hasonló réteges szerkezetű anyag, csak sötétebb. Minthogy a grafit szén atomjainak kötéstávolságát más módszerekkel is meg tudjuk mérni, így a grafit az STM kalibrációjára is felhasználható.
A konkrét mérésekhez a következő mintákat fogjuk megnézni:
- 1.) HOPG grafit (atomi felbontáshoz);
- 2.) párologtatott arany réteg (a szemcseméret statisztikai vizsgálatához);
- 3.) esetleges hozott minta (pl. arany vagy platina nyaklánc egy különálló szeme).
A minták mérete tipikusan nem haladhatja meg a 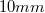 -es átmérőt és
-es átmérőt és 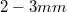 -es vastagságot. A legkisebb még kényelmesen kezelhető méret kb.
-es vastagságot. A legkisebb még kényelmesen kezelhető méret kb. 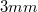 -es átmérőjű és
-es átmérőjű és 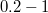 mm-es vastagságú. A mintákat egy-egy mintatartóra kell rögzítenünk. A rögzítésnek egyszerre kell biztosítania az elektromos vezetést és a mechanikai stabilitást. Mindkét feltételnek megvannak a maga nehézségei, ugyanis egy kicsit is bizonytalan mechanikai illesztést minden "bolygatás" után hosszadalmas (akár órákra rúgó!) relaxációs mozgás követhet. Elektromos kontaktust pedig nem könnyű biztosítani pl. egy olyan párologtatott fémfelülethez, amely esetleg csak néhány
mm-es vastagságú. A mintákat egy-egy mintatartóra kell rögzítenünk. A rögzítésnek egyszerre kell biztosítania az elektromos vezetést és a mechanikai stabilitást. Mindkét feltételnek megvannak a maga nehézségei, ugyanis egy kicsit is bizonytalan mechanikai illesztést minden "bolygatás" után hosszadalmas (akár órákra rúgó!) relaxációs mozgás követhet. Elektromos kontaktust pedig nem könnyű biztosítani pl. egy olyan párologtatott fémfelülethez, amely esetleg csak néhány 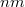 vastag.
vastag.
Mérés
A mérés egymást követő lépései a minta konkrét fajtájától függetlenül hasonlóak. Az általános eljárás a következő:
1.) Ellenőrizzük, hogy az egyes egységek helyesen vannak-e összekapcsolva, majd a főkapcsolóval egyszerre bekapcsoljuk a vezérlő elektronikát és számítógépet (hogy mielőbb felvegye az üzemi hőmérsékletet). (Ezt a gyakorlatvezető elvégzi a mérés megkezdése előtt.)
2.) Előkészítjük a mérendő mintát (hogy mielőbb bekövetkezhessen a mechanikai relaxációja). (Általában a gyakorlatvezető ezt is elvégzi a mérés megkezdése előtt.)
3.) Következő lépésként megpróbálunk előállítani egy elfogadhatóan hegyes tűt. (Bár lesz a gyakorlatvezető által előzetesen meghegyezett tű is, a diákoknak is meg kell kísérelniük a hegyezést.)
4.) Ezután egy csipesszel behelyezzük a tűt a foglalatába, a tű-minta távolságot kb. 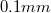 -re csökkentjük, majd a mérőfejet rezgésmentes asztalra helyezzük. (Első alkalommal ezt megmutatja a gyakorlatvezető, később a diákoknak célszerű megtenniük.)
-re csökkentjük, majd a mérőfejet rezgésmentes asztalra helyezzük. (Első alkalommal ezt megmutatja a gyakorlatvezető, később a diákoknak célszerű megtenniük.)
5.) Beállítjuk a kívánt pásztázási paramétereket (ablakméret, soronkénti pixelszám, pásztázási sebesség, alagútfeszültség és áram), majd aktiváljuk a durva közelítő mechanizmust ![]() .
.
6.) A mérésvezérlő szoftver automatikusan elindítja az adatgyűjtést. Amennyiben a kép megfelelő, úgy elmentjük a HDD-re ![]() . Ha a kép nem megfelelő, akkor a paraméterek állításával megpróbálunk javítani rajta. Ha ez semmiképp sem sikerül, annak leggyakoribb oka, hogy a tű szennyezett, vagy tompa. Ekkor leállítjuk a mérést
. Ha a kép nem megfelelő, akkor a paraméterek állításával megpróbálunk javítani rajta. Ha ez semmiképp sem sikerül, annak leggyakoribb oka, hogy a tű szennyezett, vagy tompa. Ekkor leállítjuk a mérést ![]() ,
,
7.) A tű-minta távolságot legalább 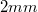 -re növeljük.
-re növeljük.
8.) Kivesszük a tűt és visszatérünk a 3.)-es ponthoz, vagyis a tű újbóli meghegyezéshez, vagy cseréjéhez.
Képfeldolgozás
A rögzített képek Offline üzemmódban ![]() a ! meghajtón találhatók (5.1 ábra).
a ! meghajtón találhatók (5.1 ábra).
A mérési file általában két képet tartalmaz (Channel1 és Channel2), egyiket jobbról balra, a másikat balról jobbra pásztázva készítjük. A kép szűrése előtt ki kell választani egyik képet az Image->Select Left Image vagy Image->Select Right Image parancs segítségével. A kép kiválasztása után elérhetővé válnak a szűrési, mérési és megjelenítési lehetőségek (5.2 ábra).
A képfeldolgozást ajánlott a Modify->Plane fit Auto![]() (felület illesztése a rögzített képhez) vagy Modify->Flatten
(felület illesztése a rögzített képhez) vagy Modify->Flatten ![]() (görbe illesztése a pásztázási vonalakhoz) utasításokkal kezdeni. A képen található tüskék Modify->Median (mátrix szűrő) vagy Modify->Lowpass (nagy frekvenciákat levágó) szűrővel távolíthatók el. A különösen zajos pásztázási vonalak eltávolíthatók a Modify->Erase Scan Lines paranccsal. A periodikus struktúrák Modify->Spectrum 2D Fourier szűrővel emelhetők ki. A szűrőket minden esetben körültekintően kell használni, mivel azok eltorzíthatják a képet. Távolságokat és magasságokat az Analyze->Section (vonalmetszet)
(görbe illesztése a pásztázási vonalakhoz) utasításokkal kezdeni. A képen található tüskék Modify->Median (mátrix szűrő) vagy Modify->Lowpass (nagy frekvenciákat levágó) szűrővel távolíthatók el. A különösen zajos pásztázási vonalak eltávolíthatók a Modify->Erase Scan Lines paranccsal. A periodikus struktúrák Modify->Spectrum 2D Fourier szűrővel emelhetők ki. A szűrőket minden esetben körültekintően kell használni, mivel azok eltorzíthatják a képet. Távolságokat és magasságokat az Analyze->Section (vonalmetszet) ![]() utasítás segítségével mérhetünk. A képek két vagy három dimenziós ábrázolásban a View->Top View
utasítás segítségével mérhetünk. A képek két vagy három dimenziós ábrázolásban a View->Top View![]() vagy a View->Surface Plot
vagy a View->Surface Plot ![]() utasításokkal jeleníthetők meg. A képek kontrasztja bármely szűrő használatakor állítható. A képek mentésére a Utility->TIFF Export utasítás használható. A Nanoscope program saját formátuma a megszokott képfeldolgozó programok segítségével nem nyitható ki, viszont a Nanotec Electronica cég ingyenes WSxM 3.1-es vagy újabb programja képes kinyitni és feldolgozni a Nanoscope fileokat. A WSxM program működése hasonlít a Nanoscope program működéséhez, viszont a megjelenése és az utasítások megnevezése eltér. A kép dőlését a teljes képhez (Process-> Plane-> Global) vagy a kép egy részéhez (Process-> Plane-> Local) illesztett sík kivonásával tudjuk eltávolítani. Szükség esetén a Process-> Filter-> Fit2nd utasítással másodfokú felületet vonhatunk ki a képből. Az egyes pásztázási vonalak magassága gyakran eltér, ezért általában érdemes végrehajtani a Process-> Filter-> Flatten parancsot. Ezzel az utasítással minden pásztázási vonalhoz egyenest (Offset - nincs dőlés és Line - van dőlés) vagy parabolát (Parabola) illesztünk, és azt kivonjuk a pásztázási vonalból. Process->Filter->Flatten->Line a Process-> Plane-> Global parancsot is helyettesíti. A képen tálalható tüskék eltávolíthatók például a Process-> Filter-> Matrix convolution-> Smooth_3x3 átlagoló mátrixszűrővel. A kép egy részlete a Process-> Zoom paranccsal nagyítható ki. Vonalmetszetet a Process-> Profile paranccsal készíthetünk. A metszeten Process-> Measure distance utasítással lehet megmérni két pont távolságát. A kép 3D megjelenítése a Display-> 3D Settings and Preview utasítással módosítható. Itt lehetőség van a kép döntésére és forgatására, valamint a megvilágítás irányának a változtatására is. 2D ábrázolásban (Display-> Top View) fontos színskálát használni. A színskála a Display-> Info paranccsal érhető el.
utasításokkal jeleníthetők meg. A képek kontrasztja bármely szűrő használatakor állítható. A képek mentésére a Utility->TIFF Export utasítás használható. A Nanoscope program saját formátuma a megszokott képfeldolgozó programok segítségével nem nyitható ki, viszont a Nanotec Electronica cég ingyenes WSxM 3.1-es vagy újabb programja képes kinyitni és feldolgozni a Nanoscope fileokat. A WSxM program működése hasonlít a Nanoscope program működéséhez, viszont a megjelenése és az utasítások megnevezése eltér. A kép dőlését a teljes képhez (Process-> Plane-> Global) vagy a kép egy részéhez (Process-> Plane-> Local) illesztett sík kivonásával tudjuk eltávolítani. Szükség esetén a Process-> Filter-> Fit2nd utasítással másodfokú felületet vonhatunk ki a képből. Az egyes pásztázási vonalak magassága gyakran eltér, ezért általában érdemes végrehajtani a Process-> Filter-> Flatten parancsot. Ezzel az utasítással minden pásztázási vonalhoz egyenest (Offset - nincs dőlés és Line - van dőlés) vagy parabolát (Parabola) illesztünk, és azt kivonjuk a pásztázási vonalból. Process->Filter->Flatten->Line a Process-> Plane-> Global parancsot is helyettesíti. A képen tálalható tüskék eltávolíthatók például a Process-> Filter-> Matrix convolution-> Smooth_3x3 átlagoló mátrixszűrővel. A kép egy részlete a Process-> Zoom paranccsal nagyítható ki. Vonalmetszetet a Process-> Profile paranccsal készíthetünk. A metszeten Process-> Measure distance utasítással lehet megmérni két pont távolságát. A kép 3D megjelenítése a Display-> 3D Settings and Preview utasítással módosítható. Itt lehetőség van a kép döntésére és forgatására, valamint a megvilágítás irányának a változtatására is. 2D ábrázolásban (Display-> Top View) fontos színskálát használni. A színskála a Display-> Info paranccsal érhető el.

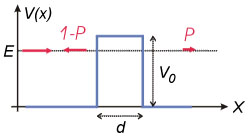
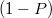 valószínűséggel verődik vissza.
valószínűséggel verődik vissza.