„Sugárvédelmi anyagok vizsgálata” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „==Bevezetés== A védelemkutatás célja a különböző minőségű és összetételű anyagok, ill. az ezek felhasználásával felépített védelmi konfigurációk…”)
 
 
(egy szerkesztő 12 közbeeső változata nincs mutatva)
1. sor: 1. sor:
 
==Bevezetés==
 
==Bevezetés==
 +
 +
Minta
 +
 +
Ezek alapanyaga nagy tisztaságú, ${n}$ típusú Si egykristályból készült lap.
 +
Így jön létre a ${p - n}$ ''átmenet''.
 +
(kb. 50 μg/cm<sup>2</sup>)
 +
4${\pi}$ térszögbe
 +
Legyen az ${E}$ és ${E+dE}$ közé eső energiájú neutronok sűrűsége a reaktor ${r}$ pontjának közelében ${n(r,E)dE}$.
 +
 +
 +
  
 
A védelemkutatás célja a különböző minőségű és összetételű anyagok, ill. az ezek felhasználásával felépített védelmi konfigurációk sugárgyengítő képességének meghatározása elméleti, vagy kísérleti úton, majd az eredmények ismeretében olyan konkrét védelmek tervezése, amelyek alkalmazásával az atomtechnikai létesítményekben dolgozókat maximális biztonsággal megvédhetjük a külső sugárterheléstől.
 
A védelemkutatás célja a különböző minőségű és összetételű anyagok, ill. az ezek felhasználásával felépített védelmi konfigurációk sugárgyengítő képességének meghatározása elméleti, vagy kísérleti úton, majd az eredmények ismeretében olyan konkrét védelmek tervezése, amelyek alkalmazásával az atomtechnikai létesítményekben dolgozókat maximális biztonsággal megvédhetjük a külső sugárterheléstől.
12. sor: 23. sor:
 
===A neutronok kölcsönhatása az anyaggal===
 
===A neutronok kölcsönhatása az anyaggal===
  
−
A neutronok az anyagon való áthaladásuk során az atommagokkal lépnek kölcsönhatásba: részint szóródnak, részint elnyelődnek. Valamennyi reakciófajta végbemenetelének valószínűségét leírhatjuk a megfelelő hatáskeresztmetszetek segítségével. Valamely magreakció hatáskeresztmetszete adott anyag esetén a neutronenergiától függ:  
+
A neutronok az anyagon való áthaladásuk során az atommagokkal lépnek kölcsönhatásba: részint szóródnak, részint elnyelődnek. Valamennyi reakciófajta végbemenetelének valószínűségét leírhatjuk a megfelelő hatáskeresztmetszetek segítségével. Valamely magreakció hatáskeresztmetszete adott anyag esetén a neutronenergiától függ: <math> sigma = sigma(E)</math>. A mikroszkopikus hatáskeresztmetszetek az adott kölcsönhatás valószínűségét az anyag egyetlen atommagjára adják meg: a neutron szóródás valószínűségét a mikroszkopikus szórási hatáskeresztmetszet (s,), a neutronabszorpcióét a mikroszkópikus abszorpciós hatáskeresztmetszet (a) fejezi ki. A szóródási folyamat lehet rugalmas (hatáskeresztmetszete es) és rugalmatlan (hatáskeresztmetszete is). A neutronabszorpciós folyamatok közül reaktor környezetben a védelem szempontjából a radiációs befogás (capture, hatáskeresztmetszete c) és a maghasadás - amennyiben a vizsgált térben hasadó anyag is jelen van - (hatáskeresztmetszete f) a legfontosabb. Fentiekből következően, a teljes mikroszkopikus hatáskeresztmetszet:
−
= ( En ) . A mikroszkopikus hatáskeresztmetszetek az adott kölcsönhatás valószínűségét az anyag egyetlen atommagjára adják meg: a neutron szóródás valószínűségét a mikroszkopikus szórási hatáskeresztmetszet (s,), a neutronabszorpcióét a mikroszkópikus abszorpciós hatáskeresztmetszet (a) fejezi ki. A szóródási folyamat lehet rugalmas (hatáskeresztmetszete es) és rugalmatlan (hatáskeresztmetszete is). A neutronabszorpciós folyamatok közül reaktor környezetben a védelem szempontjából a radiációs befogás (capture, hatáskeresztmetszete c) és a maghasadás - amennyiben a vizsgált térben hasadó anyag is jelen van - (hatáskeresztmetszete f) a legfontosabb. Fentiekből következően, a teljes mikroszkopikus hatáskeresztmetszet:
+
 
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \sigma_{tot} = \sigma_{s} + \sigma_{a} = \sigma_{es} + \sigma_{is} + \sigma_{c} + \sigma_{f}  \hspace{15mm} (cm^{2}) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (1) </span>
 +
|}
  
−
tot = s + a = es+is+c +f      (cm2) (1)
 
  
 
Ennek megfelelően, a teljes makroszkopikus hatáskeresztmetszet (amely a kérdéses anyag 1 cm3-nyi mennyiségére adja meg az adott magreakció végbemenetelének valószínűségét):
 
Ennek megfelelően, a teljes makroszkopikus hatáskeresztmetszet (amely a kérdéses anyag 1 cm3-nyi mennyiségére adja meg az adott magreakció végbemenetelének valószínűségét):
  
−
tot  = Ntot (cm-1 ) (2)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \sum{_{tot}} = N\sigma_{tot} \hspace{15mm} (cm^{-1}) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (2) </span>
 +
|}
  
 
ahol N a minta 1 cm3-ében lévő atomok száma. Egyetlen elemből álló anyag esetén:
 
ahol N a minta 1 cm3-ében lévő atomok száma. Egyetlen elemből álló anyag esetén:
  
−
N =          (cm-3)   (3)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ N = \frac{L\rho}{A} \alpha \hspace{15mm} (cm^{-3})\]</latex></div>
 +
| align = "right" | <span id="eq2"> (3) </span>
 +
|}
  
−
L = 6.023 x 1023,   az anyag sürüsége (gcm-3),   a kérdéses izotóp előfordulási gyakorisága az adott elemben, A - a kérdéses elem atomsúlya (~tömegszáma). Amennyiben a vizsgált védelmi anyag összetett, több elem keveréke, akkor az eredő makroszkopikus hatáskeresztmetszet:
 
  
−
=  Nitot,i (4)
+
L = 6.023 x 1023,  az anyag sürüsége (gcm-3),   a kérdéses izotóp előfordulási gyakorisága az adott elemben, A - a kérdéses elem atomsúlya (~tömegszáma). Amennyiben a vizsgált védelmi anyag összetett, több elem keveréke, akkor az eredő makroszkopikus hatáskeresztmetszet:
  
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \sum_{tot}^{ered\textrm{ő}} = \sum_{i=1}^{n} N_{i}\sigma_{tot,i} \]</latex></div>
 +
| align = "right" | <span id="eq2"> (4) </span>
 +
|}
 
ahol n a komponensek száma a keverékben.
 
ahol n a komponensek száma a keverékben.
  
 
Ha egy Io intenzitású, monoenergiás, párhuzamos neutronnyaláb egy x vastagságú anyagon áthalad, akkor intenzitása az
 
Ha egy Io intenzitású, monoenergiás, párhuzamos neutronnyaláb egy x vastagságú anyagon áthalad, akkor intenzitása az
  
−
I(x) = Io exp(-tot x)   (5)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ I(x) = I_{o}\textrm{exp}(-\sum{_{tot}}x) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (5) </span>
 +
|}
  
 
sugárgyengülési törvény szerint változik, ahol I(x) az induló energiájú neutronok intenzitása az x vastagságú közeg mögött, Io a neutron intenzitás ugyanazon a helyen, de a gyengítő anyag nélkül mérve, tot az illető anyag teljes makroszkopikus hatáskeresztmetszete.
 
sugárgyengülési törvény szerint változik, ahol I(x) az induló energiájú neutronok intenzitása az x vastagságú közeg mögött, Io a neutron intenzitás ugyanazon a helyen, de a gyengítő anyag nélkül mérve, tot az illető anyag teljes makroszkopikus hatáskeresztmetszete.
51. sor: 87. sor:
  
 
Különböző rendszámú anyagok és különböző fotonenergiák esetén az 1. ábrán láthatjuk, hogy a három folyamat közül melyiknek a végbemenetele a legvalószínűbb az adott esetben.
 
Különböző rendszámú anyagok és különböző fotonenergiák esetén az 1. ábrán láthatjuk, hogy a három folyamat közül melyiknek a végbemenetele a legvalószínűbb az adott esetben.
−
+
 
 +
{|
 +
| <span id="fig:1">[[Fájl:HaladoLab_SA_01.jpg|közép|bélyegkép|500px|1.ábra: A gamma-sugárzás és az anyag kölcsönhatási folyamatai ]]</span>
 +
|}
 
   
 
   
−
1. ábra
 
−
A gamma-sugárzás és az anyag kölcsönhatási folyamatai
 
  
 
A teljes mikroszkopikus hatáskeresztmetszet (tot) a három részfolyamat hatáskeresztmetszetének összege:
 
A teljes mikroszkopikus hatáskeresztmetszet (tot) a három részfolyamat hatáskeresztmetszetének összege:
  
−
tot =f + c + p (6)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \sigma_{tot} = \sigma_{f} + \sigma_{c} + \sigma_{p} \]</latex></div>
 +
| align = "right" | <span id="eq2"> (6) </span>
 +
|}
  
 
A makroszkopikus totális hatáskeresztmetszetet gamma sugárzás esetében a szakirodalom általában -vel jelöli, és lineáris sugárgyengítési tényezőnek nevezi:
 
A makroszkopikus totális hatáskeresztmetszetet gamma sugárzás esetében a szakirodalom általában -vel jelöli, és lineáris sugárgyengítési tényezőnek nevezi:
  
−
=tot = N(f + c + p) (cm-1) (7)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \mu = \sum{_{tot}} = N(\sigma_{f} + \sigma_{c} + \sigma_{p}) \hspace{15mm} (cm^{-1})\]</latex></div>
 +
| align = "right" | <span id="eq2"> (7) </span>
 +
|}
  
 
A  lineáris sugárgyengítési tényező arányos az abszorbáló közeg sűrűségével (). Gyakorlatban a  helyett használatosabb az un. tömeggyengítési tényező, amely a lineáris sugárgyengítési tényezővel, ill. a mikroszkopikus hatáskeresztmetszettel az alábbi kapcsolatban van:
 
A  lineáris sugárgyengítési tényező arányos az abszorbáló közeg sűrűségével (). Gyakorlatban a  helyett használatosabb az un. tömeggyengítési tényező, amely a lineáris sugárgyengítési tényezővel, ill. a mikroszkopikus hatáskeresztmetszettel az alábbi kapcsolatban van:
  
−
m =   =   tot (cm2g-1) (8)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \mu_{m} = \frac{\mu}{\rho} = \frac{6,023\mathrm{x}10^{23}}{A} \sigma_{tot} \hspace{15mm} (cm^{2}g^{-1}) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (8) </span>
 +
|}
 
 
 
A tömeggyengítési tényező ilymódon független az anyag sűrűségétől, ezért is a vonatkozó táblázatok nagy része ezt közli. A tömegabszorpciós tényező bevezetése megkívánja, hogy az abszorbensvastagságot a sűrűséggel szorozva adjuk meg, amelyet felületi sűrűségnek nevezünk:
 
A tömeggyengítési tényező ilymódon független az anyag sűrűségétől, ezért is a vonatkozó táblázatok nagy része ezt közli. A tömegabszorpciós tényező bevezetése megkívánja, hogy az abszorbensvastagságot a sűrűséggel szorozva adjuk meg, amelyet felületi sűrűségnek nevezünk:
  
−
                      d = . x (g cm-2) (9)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ d = \rho.\mathrm{x} \hspace{15mm} (g\mathrm{ }cm^{-2}) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (9) </span>
 +
|}
  
 
A gamma-sugárzás gyengülését monoenergiás, párhuzamos sugárnyaláb esetén valamely x vastagságú anyagon való áthatolás során a jól ismert sugárgyengülési törvény írja le:
 
A gamma-sugárzás gyengülését monoenergiás, párhuzamos sugárnyaláb esetén valamely x vastagságú anyagon való áthatolás során a jól ismert sugárgyengülési törvény írja le:
  
−
I(x) =Io exp( - x) = Io exp(-md) (10)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ I(x) = I_{o}\mathrm{exp}(-\mu x) = I_{o}\mathrm{exp}(-\mu_{m}d) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (10) </span>
 +
|}
  
 
Az intenzitás változását az anyagvastagság függvényében mérve, (10)-ből  m értéke meghatározható.
 
Az intenzitás változását az anyagvastagság függvényében mérve, (10)-ből  m értéke meghatározható.
83. sor: 145. sor:
 
A fentiekben a neutron - ill. gammasugárzás gyengülésére vonatkozóan bemutatott (5) és (10) összefüggések csak egydimenziós folyamatokra érvényesek, azaz akkor, ha a részecskék áramlása párhuzamos. A gyakorlati számításokhoz gyakran a  "relaxációs hosszat"-at (közepes szabad úthossz) használják. Ennek definíciója:
 
A fentiekben a neutron - ill. gammasugárzás gyengülésére vonatkozóan bemutatott (5) és (10) összefüggések csak egydimenziós folyamatokra érvényesek, azaz akkor, ha a részecskék áramlása párhuzamos. A gyakorlati számításokhoz gyakran a  "relaxációs hosszat"-at (közepes szabad úthossz) használják. Ennek definíciója:
  
−
ln = -1   (xo tetszőleges) (11)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \mathrm{ln} \Bigg( \frac{I(x_{0}+\lambda)}{I(x_{0})} \Bigg)= -1 \hspace{15mm} (x_{0}\textrm{ } tetsz\textrm{ő}leges) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (11) </span>
 +
|}
 
   
 
   
 
azaz  az a falvastagság, melyen áthatolva, a sugárzás intenzitása e-ed részére csökken. Hasonló értelmezéssel kapjuk a felezési ill. tizedelési rétegvastagságokat. Ezek -ból In(2)-vel, ill. In(10)-zel való szorzással nyerhetők.
 
azaz  az a falvastagság, melyen áthatolva, a sugárzás intenzitása e-ed részére csökken. Hasonló értelmezéssel kapjuk a felezési ill. tizedelési rétegvastagságokat. Ezek -ból In(2)-vel, ill. In(10)-zel való szorzással nyerhetők.
89. sor: 156. sor:
 
A (5) képlet alapján:
 
A (5) képlet alapján:
  
−
neutron = (12)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \lambda_{neutron} = \frac{1}{\sum{_{tot}}} \]</latex></div>
 +
| align = "right" | <span id="eq2"> (12) </span>
 +
|}
 +
 
 
illetőleg a (10) összefüggésből
 
illetőleg a (10) összefüggésből
−
gamma = (13)
+
 
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \lambda_{gamma} = \frac{1}{\mu} \]</latex></div>
 +
| align = "right" | <span id="eq2"> (13) </span>
 +
|}
 +
 
 
Adott, homogén anyagú védőfal sugárgyengítő képességét tehát a  relaxációs hosszal lehet jellemezni. Ennek meghatározásához elegendő egy tetszőleges vastagságú fal előtt és mögött megmérni a sugárzás intenzitását.
 
Adott, homogén anyagú védőfal sugárgyengítő képességét tehát a  relaxációs hosszal lehet jellemezni. Ennek meghatározásához elegendő egy tetszőleges vastagságú fal előtt és mögött megmérni a sugárzás intenzitását.
  
106. sor: 186. sor:
 
Ha a "tiszta" geometriai feltételek nem teljesülnek, a detektorba a már szóródott részecskék is bejutnak (2. ábra, B eset). Az ilyen "rossz" geometriában végzett mérések I(x) megnövekedéséhez vezetnek:
 
Ha a "tiszta" geometriai feltételek nem teljesülnek, a detektorba a már szóródott részecskék is bejutnak (2. ábra, B eset). Az ilyen "rossz" geometriában végzett mérések I(x) megnövekedéséhez vezetnek:
  
−
I(x) =Io exp(-m  x) B(x) (14)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ I(x) = I_{o}\mathrm{exp}(-\mu_{m}\rho x)B(x) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (14) </span>
 +
|}
  
 
ahol B (értéke>1) a felhalmozódási tényező ("build-up faktor"). A szóródások hatására   látszólag megnő.
 
ahol B (értéke>1) a felhalmozódási tényező ("build-up faktor"). A szóródások hatására   látszólag megnő.
112. sor: 197. sor:
 
B közelítésére számos empirikus függvény használatos. Egydimenziós gamma-gyengítési esetben talán legelterjedtebb ezek közül a Taylor-formula:
 
B közelítésére számos empirikus függvény használatos. Egydimenziós gamma-gyengítési esetben talán legelterjedtebb ezek közül a Taylor-formula:
  
−
B = A exp + (1-A) + exp (15)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ B = A_{ }\mathrm{exp} \Bigg(-\frac{\alpha_{1}X}{\lambda} \Bigg) + (1-A) + \mathrm{exp} \Bigg(-\frac{\alpha_{2}X}{\lambda} \Bigg) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (15) </span>
 +
|}
  
 
A (15) összefüggés A, 1 és 2 paramétereinek nagysága függ attól, hogy a formulát
 
A (15) összefüggés A, 1 és 2 paramétereinek nagysága függ attól, hogy a formulát
119. sor: 209. sor:
 
- milyen a részecskék energia-eloszlása (spektruma).
 
- milyen a részecskék energia-eloszlása (spektruma).
 
A paraméterek értéke táblázatosan vagy diagramokban sok helyen hozzáférhető.
 
A paraméterek értéke táblázatosan vagy diagramokban sok helyen hozzáférhető.
−
A Taylor-formula tipikus hibája a gamma-energiától függően normálbetonra 5-10%, ha  = 2... 4.
+
A Taylor-formula tipikus hibája a gamma-energiától függően normálbetonra 5-10%,
 +
 
  
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ ha \frac{X}{\lambda} = 2...4 \]</latex></div>
 +
| align = "right" | <span id="eq2"> </span>
 +
|}
  
  

A lap jelenlegi, 2015. március 4., 09:25-kori változata

Tartalomjegyzék

Bevezetés

Minta

Ezek alapanyaga nagy tisztaságú, ${n}$ típusú Si egykristályból készült lap. Így jön létre a ${p - n}$ átmenet. (kb. 50 μg/cm2) 4${\pi}$ térszögbe Legyen az ${E}$ és ${E+dE}$ közé eső energiájú neutronok sűrűsége a reaktor ${r}$ pontjának közelében ${n(r,E)dE}$.



A védelemkutatás célja a különböző minőségű és összetételű anyagok, ill. az ezek felhasználásával felépített védelmi konfigurációk sugárgyengítő képességének meghatározása elméleti, vagy kísérleti úton, majd az eredmények ismeretében olyan konkrét védelmek tervezése, amelyek alkalmazásával az atomtechnikai létesítményekben dolgozókat maximális biztonsággal megvédhetjük a külső sugárterheléstől. A kutató atomreaktorok körül elsősorban a vízszintes csatornák környezetében találhatunk - a végzett munkától, ill. a reaktor teljesítményétől függően kisebb-nagyobb sugárzási teret. A többnyire kevert (neutron-gamma) sugárzási térben tartózkodó dolgozók sugárterhelésének megakadályozására egyrészt előre meg kell határozni a várható dózisszinteket, másrészről szükség esetén alkalmas árnyékoló anyaggal kell csökkenteni a várható sugárterhelést a lehető legkisebb szintre. A mérési gyakorlat keretében megvizsgáljuk néhány árnyékolásra használt védelmi anyag sugárgyengítő tulajdonságát. A méréseket a reaktor valamelyik vízszintes csatornájánál végezzük kevert (neutron-gamma) sugártérben, párhuzamos sugárnyaláb esetén.

Elméleti összefoglalás

Egy termikus reaktor aktív zónájában a maghasadás során különböző sugárzások keletkeznek, de a fűtőelem burkolat, a moderátor, a reaktortartály és a tartály körüli betonvédelem következtében a reaktor környezetében csak a neutron és a gamma-sugárzás a reális veszélyeztető tényező. Ezért a továbbiakban ezekkel foglalkozunk.

A neutronok kölcsönhatása az anyaggal

A neutronok az anyagon való áthaladásuk során az atommagokkal lépnek kölcsönhatásba: részint szóródnak, részint elnyelődnek. Valamennyi reakciófajta végbemenetelének valószínűségét leírhatjuk a megfelelő hatáskeresztmetszetek segítségével. Valamely magreakció hatáskeresztmetszete adott anyag esetén a neutronenergiától függ: 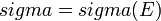sigma = sigma(E). A mikroszkopikus hatáskeresztmetszetek az adott kölcsönhatás valószínűségét az anyag egyetlen atommagjára adják meg: a neutron szóródás valószínűségét a mikroszkopikus szórási hatáskeresztmetszet (s,), a neutronabszorpcióét a mikroszkópikus abszorpciós hatáskeresztmetszet (a) fejezi ki. A szóródási folyamat lehet rugalmas (hatáskeresztmetszete es) és rugalmatlan (hatáskeresztmetszete is). A neutronabszorpciós folyamatok közül reaktor környezetben a védelem szempontjából a radiációs befogás (capture, hatáskeresztmetszete c) és a maghasadás - amennyiben a vizsgált térben hasadó anyag is jelen van - (hatáskeresztmetszete f) a legfontosabb. Fentiekből következően, a teljes mikroszkopikus hatáskeresztmetszet:

\[ \sigma_{tot} = \sigma_{s} + \sigma_{a} = \sigma_{es} + \sigma_{is} + \sigma_{c} + \sigma_{f} \hspace{15mm} (cm^{2}) \]
 (1)


Ennek megfelelően, a teljes makroszkopikus hatáskeresztmetszet (amely a kérdéses anyag 1 cm3-nyi mennyiségére adja meg az adott magreakció végbemenetelének valószínűségét):

\[ \sum{_{tot}} = N\sigma_{tot} \hspace{15mm} (cm^{-1}) \]
 (2)

ahol N a minta 1 cm3-ében lévő atomok száma. Egyetlen elemből álló anyag esetén:

\[ N = \frac{L\rho}{A} \alpha \hspace{15mm} (cm^{-3})\]
 (3)


L = 6.023 x 1023,  az anyag sürüsége (gcm-3),  a kérdéses izotóp előfordulási gyakorisága az adott elemben, A - a kérdéses elem atomsúlya (~tömegszáma). Amennyiben a vizsgált védelmi anyag összetett, több elem keveréke, akkor az eredő makroszkopikus hatáskeresztmetszet:

\[ \sum_{tot}^{ered\textrm{ő}} = \sum_{i=1}^{n} N_{i}\sigma_{tot,i} \]
 (4)

ahol n a komponensek száma a keverékben.

Ha egy Io intenzitású, monoenergiás, párhuzamos neutronnyaláb egy x vastagságú anyagon áthalad, akkor intenzitása az

\[ I(x) = I_{o}\textrm{exp}(-\sum{_{tot}}x) \]
 (5)

sugárgyengülési törvény szerint változik, ahol I(x) az induló energiájú neutronok intenzitása az x vastagságú közeg mögött, Io a neutron intenzitás ugyanazon a helyen, de a gyengítő anyag nélkül mérve, tot az illető anyag teljes makroszkopikus hatáskeresztmetszete. tot ismeretében a neutronsugárzás gyengülése meghatározható az adott anyagra; vagy megfordítva: a neutronsugárzás intenzitásának változását a védelem anyagvastagság függvényében mérve, tot az (5) összefüggésből adódik.

Az (5) alatti összefüggés korlátozottan és bizonyos közelítéssel nem monoenergiás neutronnyalábra is alkalmazható, ebben az esetben azonban tot érékét nem az (1) és (2) összefüggések adják meg.


Gamma-sugárzás kölcsönhatása az anyaggal

A gamma sugárzás az anyagon való áthaladás során elsősorban az atomokkal, közelebbről azoknak héjelektronjaival lép kölcsönhatásba. A kölcsönhatást három alapvető folyamat határozza meg (bővebben l. pl. [1]):

a) fotoelektromos abszorpció (fotoeffektus: mikroszkopikus hatáskeresztmetszete f); b) Compton-szórás (mikroszkopikus hatáskeresztmetszete c); c) párkeltés (mikroszkopikus hatáskeresztmetszete p).

Különböző rendszámú anyagok és különböző fotonenergiák esetén az 1. ábrán láthatjuk, hogy a három folyamat közül melyiknek a végbemenetele a legvalószínűbb az adott esetben.

1.ábra: A gamma-sugárzás és az anyag kölcsönhatási folyamatai


A teljes mikroszkopikus hatáskeresztmetszet (tot) a három részfolyamat hatáskeresztmetszetének összege:

\[ \sigma_{tot} = \sigma_{f} + \sigma_{c} + \sigma_{p} \]
 (6)

A makroszkopikus totális hatáskeresztmetszetet gamma sugárzás esetében a szakirodalom általában -vel jelöli, és lineáris sugárgyengítési tényezőnek nevezi:

\[ \mu = \sum{_{tot}} = N(\sigma_{f} + \sigma_{c} + \sigma_{p}) \hspace{15mm} (cm^{-1})\]
 (7)

A  lineáris sugárgyengítési tényező arányos az abszorbáló közeg sűrűségével (). Gyakorlatban a  helyett használatosabb az un. tömeggyengítési tényező, amely a lineáris sugárgyengítési tényezővel, ill. a mikroszkopikus hatáskeresztmetszettel az alábbi kapcsolatban van:

\[ \mu_{m} = \frac{\mu}{\rho} = \frac{6,023\mathrm{x}10^{23}}{A} \sigma_{tot} \hspace{15mm} (cm^{2}g^{-1}) \]
 (8)

A tömeggyengítési tényező ilymódon független az anyag sűrűségétől, ezért is a vonatkozó táblázatok nagy része ezt közli. A tömegabszorpciós tényező bevezetése megkívánja, hogy az abszorbensvastagságot a sűrűséggel szorozva adjuk meg, amelyet felületi sűrűségnek nevezünk:

\[ d = \rho.\mathrm{x} \hspace{15mm} (g\mathrm{ }cm^{-2}) \]
 (9)

A gamma-sugárzás gyengülését monoenergiás, párhuzamos sugárnyaláb esetén valamely x vastagságú anyagon való áthatolás során a jól ismert sugárgyengülési törvény írja le:

\[ I(x) = I_{o}\mathrm{exp}(-\mu x) = I_{o}\mathrm{exp}(-\mu_{m}d) \]
 (10)

Az intenzitás változását az anyagvastagság függvényében mérve, (10)-ből m értéke meghatározható.


Sugárgyengülés a szórások figyelembevételével

A fentiekben a neutron - ill. gammasugárzás gyengülésére vonatkozóan bemutatott (5) és (10) összefüggések csak egydimenziós folyamatokra érvényesek, azaz akkor, ha a részecskék áramlása párhuzamos. A gyakorlati számításokhoz gyakran a  "relaxációs hosszat"-at (közepes szabad úthossz) használják. Ennek definíciója:

\[ \mathrm{ln} \Bigg( \frac{I(x_{0}+\lambda)}{I(x_{0})} \Bigg)= -1 \hspace{15mm} (x_{0}\textrm{ } tetsz\textrm{ő}leges) \]
 (11)

azaz  az a falvastagság, melyen áthatolva, a sugárzás intenzitása e-ed részére csökken. Hasonló értelmezéssel kapjuk a felezési ill. tizedelési rétegvastagságokat. Ezek -ból In(2)-vel, ill. In(10)-zel való szorzással nyerhetők.

A (5) képlet alapján:

\[ \lambda_{neutron} = \frac{1}{\sum{_{tot}}} \]
 (12)

illetőleg a (10) összefüggésből

\[ \lambda_{gamma} = \frac{1}{\mu} \]
 (13)

Adott, homogén anyagú védőfal sugárgyengítő képességét tehát a  relaxációs hosszal lehet jellemezni. Ennek meghatározásához elegendő egy tetszőleges vastagságú fal előtt és mögött megmérni a sugárzás intenzitását.

Valós, háromdimenziós esetben a viszonyok természetesen bonyolultabbak. Mivel a neutron-sugárzás gyengülését nemcsak az elnyelés okozza, meg kell vizsgálni a szóródások szerepét is. Hasonlóképpen: a gamma¬foton csak a fotoeffektus során "nyelődik el", a Compton-szóródásból (egy kisebb energiájú) foton lép ki, párkeltés esetén a pozitron megsemmisülését újabb foton születése kíséri. Gamma-gyengítés esetén is figyelemmel kell tehát kísérni a szóródások hatását.

Az egydimenziós eset kísérleti megvalósítását "jó" vagy "tiszta" geometriának nevezik (2. ábra, A eset). A sugárforrás-detektor egyenes irányból kiszóródott részecskéket a kollimátorok elnyelik, így a detektorba csak az (5), ill. a (10) függvényekkel modellezett folyamat szerinti részecskék jutnak el.


2. ábra A B "Jó" mérési geometria megvalósítása "Rossz" mérési geometria

Ha a "tiszta" geometriai feltételek nem teljesülnek, a detektorba a már szóródott részecskék is bejutnak (2. ábra, B eset). Az ilyen "rossz" geometriában végzett mérések I(x) megnövekedéséhez vezetnek:

\[ I(x) = I_{o}\mathrm{exp}(-\mu_{m}\rho x)B(x) \]
 (14)

ahol B (értéke>1) a felhalmozódási tényező ("build-up faktor"). A szóródások hatására  látszólag megnő.

B közelítésére számos empirikus függvény használatos. Egydimenziós gamma-gyengítési esetben talán legelterjedtebb ezek közül a Taylor-formula:

\[ B = A_{ }\mathrm{exp} \Bigg(-\frac{\alpha_{1}X}{\lambda} \Bigg) + (1-A) + \mathrm{exp} \Bigg(-\frac{\alpha_{2}X}{\lambda} \Bigg) \]
 (15)

A (15) összefüggés A, 1 és 2 paramétereinek nagysága függ attól, hogy a formulát - milyen folyamatra vonatkoztathatjuk (dimenziógyengítés stb), - mi a védőfal anyaga, - milyen a részecskék energia-eloszlása (spektruma). A paraméterek értéke táblázatosan vagy diagramokban sok helyen hozzáférhető. A Taylor-formula tipikus hibája a gamma-energiától függően normálbetonra 5-10%,


\[ ha \frac{X}{\lambda} = 2...4 \]


A mérési feladat

1. Határozzuk meg néhány védelmi anyag (paraffin, beton, ólom, stb.) neutron-, ill. gamma-sugárzás gyengítő képességét! 2. Határozzuk meg a felezési, ill. tizedelési rétegvastagságokat, és hasonlítsuk össze értéküket az egyes anyagok esetén!


A méréshez szükséges eszközök és anyagok

- Reaktor + valamelyik vízszintes besugárzó csatorna; - Neutron detektáláshoz: impulzus üzemben működő neutrondetektor és impulzus-számláló berendezés; - Gamma detektáláshoz: gamma detektor impulzus üzemben működtetve és impulzus-számláló berendezés; - Különböző védelmi anyagok (paraffin, ólom, beton, fa).


A mérés menete

A vázolt mérési feladatokat a 2.sz. vízszintes csatornánál végezzük. A mérés kezdetekor a gyakorlatvezető engedélyt kér a mérés megkezdésére. A csatornából el kell távolítani először a vas-zárat, majd a vízzárat. Ez utóbbira akkor van mód, ha az operátor a csatorna nyitását engedélyezi, azaz a leürítő kapcsolóján és a reaktortömbön fehér fény világít. 40-150 W reaktorteljesítmény mellett elvégezzük a különböző védelmi anyagok neutron, ill. gamma sugárgyengítő képességének vizsgálatát. Az egyes védelmi anyagok vastagságának függvényében mérjük a neutron- ill. gamma-sugárzás intenzitását. Minden mérési sorozat kezdetén ellenőrizzük az abszorbens nélküli neutron- ill. gamma-intenzitást (lo).

A mérések kiértékelése

A különböző védelmi anyagok esetében mért neutron- ill. gamma-sugárzás intenzitásának csökkenéséből az (5) illetve (10) számú összefüggések alkalmazásával meghatározzuk a megfelelő sugárgyengítési tényezőket. A kiértékeléshez illesszünk a fenti összefüggések szerinti (exponenciális) függvényt a mért pontokra. A sugárgyengítési tényezők ismeretében meghatározzuk a relaxációs hosszakat ((12), (13) összefüggés) és a felezési (tizedelési) rétegvastagságokat a különböző védelmi anyagokra nézve.

Irodalom

Bódizs Dénes: Atommag sugárzások méréstechnikái. Typotex Kiadó, Budapest, 2006.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Sugárvédelmi_anyagok_vizsgálata&oldid=16250”