„Nagyfrekvenciás jelek terjedésének fizikai alapjai” változatai közötti eltérés
(→Duplexerrel) |
(→Mérési feladatok) |
||
| (3 szerkesztő 59 közbeeső változata nincs mutatva) | |||
| 3. sor: | 3. sor: | ||
==Bevezetés== | ==Bevezetés== | ||
<wlatex> | <wlatex> | ||
| − | A laborgyakorlat célja, hogy a nagyfrekvenciás ($f>1-10 | + | A laborgyakorlat célja, hogy a nagyfrekvenciás ($f>1-10~\textrm{MHz}$) méréstechnika és jelátvitel területén felmerülő alapfogalmakat és jelenségeket bemutassa. A legfontosabb amit érdemes megjegyezni az, hogy az alacsony frekvenciás hálózatok vizsgálatakor megszokott leírásmódok nagyobb frekvenciákon érvényüket vesztik, és a hagyományos áramköri jelenségeken túlmutató, szokatlan jelenségek lépnek fel, mint pl. a jelek reflexiója. A fizika szempontjából itt a Maxwell-egyenletek nagyfrekvenciás, azaz hullámjelenségeket is figyelembe vevő alkalmazásáról van szó kábelek esetére. |
A XIX. század közepén felmerült az igény a nagy távolságokra történő adattovábbításra, akár kontinensnyi távolságokban, pl. tenger alatti kábelek segítségével. (Az első transzatlanti kábelt 1858-ban helyezték üzembe.) Hamar kiderült, hogy a vezetékben történő jeltovábbításánál lényeges a hullámjelenségek figyelembevétele. Ez a technológiai fejlődés és igény az elméleti leírásra időben közel volt a Maxwell-egyenletek (1861) megszületéséhez. A vezetékben terjedő hullámjelenségek leírását ma mint az ún. ''távíróegyenleteket'' ismerjük. Ez a Maxwell-egyenletek által megjósolt elektromágneses hullámjelenségek egyik gyakorlati alkalmazása, és e leírás gyakorlati sikere is inspirálóan hatott az elektromágneses sugárzás későbbi felfedezésére (Hertz, 1886). | A XIX. század közepén felmerült az igény a nagy távolságokra történő adattovábbításra, akár kontinensnyi távolságokban, pl. tenger alatti kábelek segítségével. (Az első transzatlanti kábelt 1858-ban helyezték üzembe.) Hamar kiderült, hogy a vezetékben történő jeltovábbításánál lényeges a hullámjelenségek figyelembevétele. Ez a technológiai fejlődés és igény az elméleti leírásra időben közel volt a Maxwell-egyenletek (1861) megszületéséhez. A vezetékben terjedő hullámjelenségek leírását ma mint az ún. ''távíróegyenleteket'' ismerjük. Ez a Maxwell-egyenletek által megjósolt elektromágneses hullámjelenségek egyik gyakorlati alkalmazása, és e leírás gyakorlati sikere is inspirálóan hatott az elektromágneses sugárzás későbbi felfedezésére (Hertz, 1886). | ||
| − | A fizikus tanulmányok során eddigiekben felmerült egyenáramú (DC) és alacsony frekvenciás váltóáramú (AC) hálózatok vizsgálatakor nem törődtünk azzal, hogy a jel terjedési sebessége véges. Feltételeztük, hogy adott ponton feszültséget kapcsolva egy áramkörre az pillanatszerűen megjelenik minden azonos potenciálú helyen. Mindez | + | A fizikus tanulmányok során eddigiekben felmerült egyenáramú (DC) és alacsony frekvenciás váltóáramú (AC) hálózatok vizsgálatakor nem törődtünk azzal, hogy a jel terjedési sebessége véges. Feltételeztük, hogy adott ponton feszültséget kapcsolva egy áramkörre az pillanatszerűen megjelenik minden azonos potenciálú helyen. Mindez nyilvánvalóan érvényét veszíti, amikor a jel számára szükséges terjedési idő, $t=d/c$ (itt $d$ a kábel hossza, $c$ a közegben érvényes fénysebesség), összemérhető a jel periódusidejével: $t \approx 1/f$ (a gyakorlatban inkább a $10 \cdot t \approx 1/f$ feltétel a használatos). Például a transzatlanti kábel esetére az így kapott frekvencia $f=6~\textrm{Hz}$. Ez az eredmény azt jelenti, hogy a hullámjelenségek figyelembe vétele nélkül a transzatlanti kommunikáció csak ennél lényegesen alacsonyabb frekvencián, mai szóhasználattal kb. $6~\textrm{Hz}$ ''sávszélességen'' (azaz 6 bit/sec) mehetne csak végbe. |
| − | A hullámjelenségek figyelembevétele a modern kommunikációs eszközöknél még fontosabb, mivel pl. 9 GHz-es vivőfrekvenciára (ami egy elterjedt kommunikációs sáv) a hullámhossz mindössze 3 cm. Egy másik gyakorlati példánk a számítógépek, melyek tipikusan 2-3 GHz-es jelekkel dolgoznak ($\lambda \approx 10~\textrm{cm}$), melyeket 10-20 cm távolságra juttatnak el, így itt nyilvánvalóan szükséges a hullámjelenségek figyelembevétele az áramkörök tervezésekor. A későbbi tanulmányaink során hasonló jelenségekkel találkozhatunk az ''Önálló labor'' tárgy NMR (magmágneses-rezonancia) és ESR (elektronspin-rezonancia) laborgyakorlatain.</wlatex> | + | A hullámjelenségek figyelembevétele a modern kommunikációs eszközöknél még fontosabb, mivel pl. 9 GHz-es vivőfrekvenciára (ami egy elterjedt kommunikációs sáv) a hullámhossz mindössze 3 cm. Egy másik gyakorlati példánk a számítógépek, melyek tipikusan 2-3 GHz-es jelekkel dolgoznak ($\lambda \approx 10~\textrm{cm}$), melyeket 10-20 cm távolságra juttatnak el, így itt nyilvánvalóan szükséges a hullámjelenségek figyelembevétele az áramkörök tervezésekor. A későbbi tanulmányaink során hasonló jelenségekkel találkozhatunk az ''Önálló labor'' tárgy NMR (magmágneses-rezonancia) és ESR (elektronspin-rezonancia) laborgyakorlatain. |
| + | </wlatex> | ||
| − | |||
| − | == | + | ==Elméleti háttér== |
<wlatex> | <wlatex> | ||
| + | ===A távíróegyenletek=== | ||
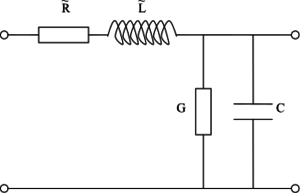
Tekintsük a jelet továbbító vezeték egy infinitezimálisan kicsi darabját, ami az 1. ábrán látható. Ezt legáltalánosabban egy soros, ún. ''elosztott ellenállás'', $\widetilde{R}$ (egysége Ohm per méter), ''elosztott induktivitás'', $\widetilde{L}$ (egysége Henry per méter), ''elosztott kapacitás'', $\widetilde{C}$ (egysége Farád per méter), és a két drót közti ''elosztott vezetés'', $\widetilde{G}$ (egysége Siemens per méter) jellemzi. | Tekintsük a jelet továbbító vezeték egy infinitezimálisan kicsi darabját, ami az 1. ábrán látható. Ezt legáltalánosabban egy soros, ún. ''elosztott ellenállás'', $\widetilde{R}$ (egysége Ohm per méter), ''elosztott induktivitás'', $\widetilde{L}$ (egysége Henry per méter), ''elosztott kapacitás'', $\widetilde{C}$ (egysége Farád per méter), és a két drót közti ''elosztott vezetés'', $\widetilde{G}$ (egysége Siemens per méter) jellemzi. | ||
A soros ellenállás oka a vezetékdarabokban lévő veszteség, az induktivitás oka pedig az, hogy az egyes drótdarabokat mágneses tér veszi körbe, ezért lesz egyetlen drótszálnak is önindukciója. A $\widetilde{G}$ írja le a két vezetékdarab közti elektromos vezetést, ami akkor is jelen van, ha nagyon jó dielektrikum választja el a két vezetőt egymástól. Mivel a két drót nincs azonos potenciálon, ezért lesz köztük a $\widetilde{C}$ kapacitás. | A soros ellenállás oka a vezetékdarabokban lévő veszteség, az induktivitás oka pedig az, hogy az egyes drótdarabokat mágneses tér veszi körbe, ezért lesz egyetlen drótszálnak is önindukciója. A $\widetilde{G}$ írja le a két vezetékdarab közti elektromos vezetést, ami akkor is jelen van, ha nagyon jó dielektrikum választja el a két vezetőt egymástól. Mivel a két drót nincs azonos potenciálon, ezért lesz köztük a $\widetilde{C}$ kapacitás. | ||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | [[Fájl:vezetek_sema. | + | | [[Fájl:vezetek_sema.png|közép|300px|]] |
|- | |- | ||
| align="center"|1. ábra: A jelterjedésben vizsgált vezeték egy darabjának áramköri modellje. | | align="center"|1. ábra: A jelterjedésben vizsgált vezeték egy darabjának áramköri modellje. | ||
|} | |} | ||
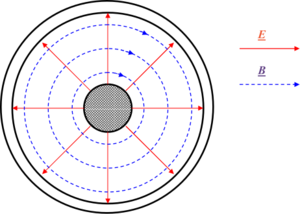
| − | Látható, hogy a fenti értékek közül $\widetilde{R}$ értéke elsősorban a vezető anyagi minőségétől függ (értéke nagyfrekvencián a ''skin-effektus'' miatt megnő), azonban $\widetilde{L}$, $\widetilde{C}$ és $\widetilde{G}$ értéke nagyban függ attól, hogy a két drót egymáshoz képest hogyan helyezkedik el (pl. sodort érpárra $\widetilde{L}=0$, de $\widetilde{C}$ értéke nagy). Egymástól adott távolságra elhelyezkedő drótpár esetére $\widetilde{L}$ értéke fix, viszont $\widetilde{C}$ nagyban függ a környező dielektrikumtól (utóbbi probléma a sós víz miatt a transzatlanti kábelnél merült fel). Mindezen problémákra kínál megoldást a koaxiális kábel (Heaviside, 1880), amiben a földelt külső vezetéken belül helyezkedik el a másik drót. Ennek előnye, hogy minden paramétere jól definiált, mind az elektromos, mind a mágneses erővonalak belül a két koaxiális vezeték között helyezkednek el, amint azt a 2. ábra mutatja. A korábbi merev falú, levegővel kitöltött koaxiális kábeleket mára a rugalmas dielektrikummal kitöltött kábelek váltották fel (tipikusan $\varepsilon_{\text{r}}=2-3$ és $\mu_{\text{r}}=1 | + | Látható, hogy a fenti értékek közül $\widetilde{R}$ értéke elsősorban a vezető anyagi minőségétől függ (értéke nagyfrekvencián a ''skin-effektus'' miatt megnő), azonban $\widetilde{L}$, $\widetilde{C}$ és $\widetilde{G}$ értéke nagyban függ attól, hogy a két drót egymáshoz képest hogyan helyezkedik el (pl. sodort érpárra $\widetilde{L}=0$, de $\widetilde{C}$ értéke nagy). Egymástól adott távolságra elhelyezkedő drótpár esetére $\widetilde{L}$ értéke fix, viszont $\widetilde{C}$ nagyban függ a környező dielektrikumtól (utóbbi probléma a sós víz miatt a transzatlanti kábelnél merült fel). Mindezen problémákra kínál megoldást a koaxiális kábel (Heaviside, 1880), amiben a földelt külső vezetéken belül helyezkedik el a másik drót. Ennek előnye, hogy minden paramétere jól definiált, mind az elektromos, mind a mágneses erővonalak belül a két koaxiális vezeték között helyezkednek el, amint azt a 2. ábra mutatja. A korábbi merev falú, levegővel kitöltött koaxiális kábeleket mára a rugalmas dielektrikummal kitöltött kábelek váltották fel (tipikusan $\varepsilon_{\text{r}}=2-3$ és $\mu_{\text{r}}=1,0$). |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | [[Fájl:koax_abra. | + | | [[Fájl:koax_abra.png|közép|300px|]] |
|- | |- | ||
| align="center"|2. ábra: A koaxiális vezeték keresztmetszete az elektromos és mágneses tér $\underline{\textit{\textbf{E}}}$, ill. $\underline{\textit{\textbf{B}}}$ vonalaival a kábel alapvető, ún. TEM00 módusára. A belső vezetéken változó feszültség van, míg a külső leggyakrabban le van földelve. | | align="center"|2. ábra: A koaxiális vezeték keresztmetszete az elektromos és mágneses tér $\underline{\textit{\textbf{E}}}$, ill. $\underline{\textit{\textbf{B}}}$ vonalaival a kábel alapvető, ún. TEM00 módusára. A belső vezetéken változó feszültség van, míg a külső leggyakrabban le van földelve. | ||
|} | |} | ||
| − | A koaxiális kábelek hosszegységre eső kapacitására és önindukciós együtthatójára e két paraméter | + | A koaxiális kábelek hosszegységre eső kapacitására és önindukciós együtthatójára e két paraméter definíciójából adódik: |
| − | + | ||
$$ | $$ | ||
\widetilde{C}=\frac{2 \pi \varepsilon_0 \varepsilon_{\text{r}}}{\ln(D/d)}, \qquad \widetilde{L}=\frac{\mu_0 \mu_{\text{r}}\ln(D/d)}{2\pi}, | \widetilde{C}=\frac{2 \pi \varepsilon_0 \varepsilon_{\text{r}}}{\ln(D/d)}, \qquad \widetilde{L}=\frac{\mu_0 \mu_{\text{r}}\ln(D/d)}{2\pi}, | ||
$$ | $$ | ||
| − | + | ahol $D$ az árnyékolás belső átmérője és $d$ a kábel belső vezetőjének külső átmérője, $\varepsilon_0$ és $\mu_0$ az ismert fizika állandók, $\varepsilon_{\text{r}}$ és $\mu_{\text{r}}$ az anyagra jellemző paraméterek. | |
| − | + | ||
A távíróegyenletek bemutatásához a legegyszerűbb eset tárgyalásához feltesszük, hogy mindkét drót tökéletes vezető ($\widetilde{R}=0$) és tökéletesen szigetelt egymástól ($\widetilde{G}=0$), tehát a jelenség csak $\widetilde{L}$ és $\widetilde{C}$-től fog függeni. (A teljesen általános eset is megoldható, csak bonyolultabb eredményekre vezet.) Ekkor mind a feszültség ($U(x,t)$), mind az áram ($I(x,t)$) hely- és időfüggő lesz, és leírásukra a következő két csatolt, lineáris, elsőrendű parciális-differenciálegyenlet adódik (Heaviside, 1880): | A távíróegyenletek bemutatásához a legegyszerűbb eset tárgyalásához feltesszük, hogy mindkét drót tökéletes vezető ($\widetilde{R}=0$) és tökéletesen szigetelt egymástól ($\widetilde{G}=0$), tehát a jelenség csak $\widetilde{L}$ és $\widetilde{C}$-től fog függeni. (A teljesen általános eset is megoldható, csak bonyolultabb eredményekre vezet.) Ekkor mind a feszültség ($U(x,t)$), mind az áram ($I(x,t)$) hely- és időfüggő lesz, és leírásukra a következő két csatolt, lineáris, elsőrendű parciális-differenciálegyenlet adódik (Heaviside, 1880): | ||
| 73. sor: | 72. sor: | ||
\frac{U(x,t)}{I(x,t)}=\sqrt{\frac{\widetilde{L}}{\widetilde{C}}}=Z_0, | \frac{U(x,t)}{I(x,t)}=\sqrt{\frac{\widetilde{L}}{\widetilde{C}}}=Z_0, | ||
$$ | $$ | ||
| − | ahol a $Z_0$ ellenállás dimenziójú mennyiséget a kábel | + | ahol a $Z_0$ ellenállás dimenziójú mennyiséget a kábel hullámimpedanciájának nevezzük. |
</wlatex> | </wlatex> | ||
| + | |||
===Visszaverődések a kábel végéről=== | ===Visszaverődések a kábel végéről=== | ||
<wlatex> | <wlatex> | ||
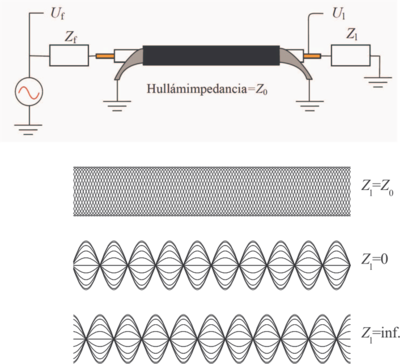
| − | + | A hullámegyenlet konkrét megoldását a kezdeti és peremfeltételek (pl. a drót végén előírt amplitúdó) ismeretében kaphatjuk meg. Középiskolás hangtani jelenségekkel analóg a következő két eset: amikor a koax kábel végét rövidre zárjuk ($Z_{\text{l}}=0$), ill. amikor a koax kábel végén szakadás van ($Z_{\text{l}}=\infty$). E két esetet szemlélteti a 3. ábra. Amennyiben a vezeték hossza és a gerjesztő hullám frekvenciája között jól meghatározható összefüggések állnak fenn ($d=n \cdot \lambda/2$ a zárt végre és $d=(2n+1) \cdot \lambda/4$ nyitott végre, $n$ egész), a vezeték mentén feszültség állóhullámok alakulnak ki. A csomó- és duzzadóhelyeket a jól ismert bezárt illetve nyitott végű síppal való analógia alapján kaphatjuk meg. E két esetet a hanghullámokra vonatkozó analógia alapján úgy érthetjük meg, hogy mind a lezárt, mind a nyitott végről visszaverődik a hullám, és a kábelmenti feszültségben látható állóhullám kép az odafelé haladó és visszavert hullámok interferenciájának eredménye. A DC áramköröknél szerzett ismeretek azt mondanák, hogy a feszültség a rövidre zárt drótpárban végig 0, míg a szakadásos végű drótpárra végig a meghajtó generátor feszültségét veszi fel. | |
| − | A hullámegyenlet konkrét megoldását a kezdeti és peremfeltételek (pl. a drót végén előírt amplitúdó) ismeretében kaphatjuk meg. Középiskolás hangtani jelenségekkel analóg a következő két eset: amikor a koax kábel végét rövidre zárjuk ($Z_{\text{l}}=0$), ill. amikor a koax kábel végén szakadás van ($Z_{\text{l}}=\infty$). E két esetet szemlélteti a 3. ábra. Amennyiben a vezeték hossza és a gerjesztő hullám frekvenciája között jól meghatározható összefüggések állnak fenn ($d=n \cdot \lambda/2$ a zárt végre és $d=(2n+1) \cdot \lambda/4$ nyitott végre, $n$ egész), a vezeték mentén feszültség állóhullámok alakulnak ki. A csomó- és duzzadóhelyeket a jól ismert bezárt illetve nyitott végű síppal való analógia alapján kaphatjuk meg. E két esetet a hanghullámokra vonatkozó analógia alapján úgy érthetjük meg, hogy mind a lezárt, mind a nyitott végről visszaverődik a hullám, és a kábelmenti feszültségben látható állóhullám kép az odafelé haladó és visszavert hullámok interferenciájának eredménye. A DC áramköröknél szerzett ismeretek azt mondanák, hogy a feszültség a | + | |
| − | + | ||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | [[Fájl:aramkor_lezarassal_new. | + | | [[Fájl:aramkor_lezarassal_new.png|közép|400px|]] |
|- | |- | ||
| align="center"|3. ábra: Sematikus áramkör szinuszos meghajtó generátorral aminek $Z_{\textrm{f}}$ kimenő ellenállása van, koaxiális vezeték aminek a végén $Z_{\textrm{l}}$ lezáró impedancia van. A generátorból jön ki a teljes teljesítmény ha $Z_{\textrm{f}}=Z_0$. A lezárás három értékére vonatkozó vezetékbeli feszültség eloszlást is mutatjuk 20 pillanatfelvételre, amikor $d=5 \lambda$. Vegyük észre, hogy $Z_{\textrm{f}}=Z_0$ esetén a vezetékben homogén a feszültség maximuma, $Z_{\textrm{f}}=0$ esetén mindkét végén csomópont van (ekkor forráson is 0 feszültséget mérünk), és $Z_{\textrm{f}}=\inf$ esetén mindkét végén duzzadóhely van. | | align="center"|3. ábra: Sematikus áramkör szinuszos meghajtó generátorral aminek $Z_{\textrm{f}}$ kimenő ellenállása van, koaxiális vezeték aminek a végén $Z_{\textrm{l}}$ lezáró impedancia van. A generátorból jön ki a teljes teljesítmény ha $Z_{\textrm{f}}=Z_0$. A lezárás három értékére vonatkozó vezetékbeli feszültség eloszlást is mutatjuk 20 pillanatfelvételre, amikor $d=5 \lambda$. Vegyük észre, hogy $Z_{\textrm{f}}=Z_0$ esetén a vezetékben homogén a feszültség maximuma, $Z_{\textrm{f}}=0$ esetén mindkét végén csomópont van (ekkor forráson is 0 feszültséget mérünk), és $Z_{\textrm{f}}=\inf$ esetén mindkét végén duzzadóhely van. | ||
|} | |} | ||
| − | |||
A nagyfrekvenciás adat- vagy energiaátvitel nyilvánvalóan azt követeli meg, hogy a kábel végéről ne legyen visszaverődés. Az A. függelékben megmutatjuk, hogy ez akkor lép fel, amennyiben a lezáró impedanciára fennáll: | A nagyfrekvenciás adat- vagy energiaátvitel nyilvánvalóan azt követeli meg, hogy a kábel végéről ne legyen visszaverődés. Az A. függelékben megmutatjuk, hogy ez akkor lép fel, amennyiben a lezáró impedanciára fennáll: | ||
$$ | $$ | ||
| 96. sor: | 93. sor: | ||
\Gamma=\frac{Z_{\text{l}}-Z_0}{Z_{\text{l}}+Z_0}, | \Gamma=\frac{Z_{\text{l}}-Z_0}{Z_{\text{l}}+Z_0}, | ||
$$ | $$ | ||
| − | ahol $\Gamma$ az ún. reflexiós tényező; $Z_{\text{l}}$ komplex értéke mellett $\Gamma$ is komplex, ami azt fejezi ki, hogy a visszavert hullám fázisa nem többszöröse $\pi$-nek. Vegyük észre, hogy a két fentebb tárgyalt határesetben, $Z_{\text{l}}=0$ és $Z_{\text{l}}=\infty$, amikor is maximális a reflexió $\pi$ ill. 0 fokos fázistolással visszavert hullámmal. | + | ahol $\Gamma$ az ún. reflexiós tényező; $Z_{\text{l}}$ komplex értéke mellett $\Gamma$ is komplex, ami azt fejezi ki, hogy a visszavert hullám fázisa nem többszöröse $\pi$-nek. Vegyük észre, hogy a két fentebb tárgyalt határesetben, $Z_{\text{l}}=0$ és $Z_{\text{l}}=\infty$, amikor is maximális a reflexió $\pi$, ill. 0 fokos fázistolással visszavert hullámmal. |
A leggyakrabban használt koaxiális kábelek hullámimpedanciája $50~\Omega$. Ez az érték megállapodásból született, és a 60-as évektől kezdve elterjedt ipari sztenderd lett. Néhány helyen találkozhatunk még $75~\Omega$-os koaxiális kábelekkel is. Érdekességképp ezen értékek és az $50~\Omega$ történeti hátteréről olvashatunk a B. függelékben. | A leggyakrabban használt koaxiális kábelek hullámimpedanciája $50~\Omega$. Ez az érték megállapodásból született, és a 60-as évektől kezdve elterjedt ipari sztenderd lett. Néhány helyen találkozhatunk még $75~\Omega$-os koaxiális kábelekkel is. Érdekességképp ezen értékek és az $50~\Omega$ történeti hátteréről olvashatunk a B. függelékben. | ||
| − | A DC és alacsony frekvenciájú (néhány kHz-es AC) eszközöknél megszokhattuk, hogy egy ideális feszültség forrás belső ellenállása $0~\Omega$, míg ideális feszültségmérő bemenő ellenállása végtelen. A nagyfrekvenciás hálózatoknál minden mérőeszköz bemenő és kimenő ellenállása $50~\Omega$, mivel ekkora | + | A DC és alacsony frekvenciájú (néhány kHz-es AC) eszközöknél megszokhattuk, hogy egy ideális feszültség forrás belső ellenállása $0~\Omega$, míg ideális feszültségmérő bemenő ellenállása végtelen. A nagyfrekvenciás hálózatoknál minden mérőeszköz bemenő és kimenő ellenállása $50~\Omega$, mivel ekkora hullámimpedanciájú kábeleket csatlakoztatunk hozzájuk. Amennyiben egy adott hullámimpedanciájú vezetéket az ennek megfelelő ellenállással zárunk le, úgy nem alakulnak ki állóhullámok (hiszen nincs reflexió a végről), és a teljes vezeték hosszában azonos feszültséget mérhetünk. |
| − | + | ||
</wlatex> | </wlatex> | ||
| + | |||
===A lezáró impedancia=== | ===A lezáró impedancia=== | ||
| + | <wlatex> | ||
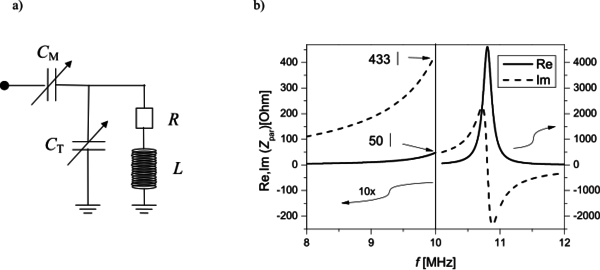
| + | A kábelt lezáró impedancia megvalósításának egy érdekes esetét mutatja a 4.a ábra. Az áramkör sajátossága, hogy valós 50 Ω impedanciájú lezárást valósít meg, miközben nem tartalmaz jelentős rezisztív elemet a tekercs kis ellenállásán kívül. A 4.b ábra mutatja az áramkörben párhuzamosan kapcsolt $C_{\text{T}}$ és $L$ impedanciájának $Z_{\text{par}}$, valós és képzetes részeit $C_{\text{T}}=217~\textrm{pF}$ és $L=1~\mu\textrm{H}$ esetére, és feltettük, hogy a tekercsnek van egy kicsi, kb. 1 Ω-os valós ellenállása is. (A gyakorlaton használt vörösréz ($\varrho=1,7\cdot 10^{-8}\Omega\text{m}$) tekercsünk 0,5 m hosszú, 1 mm átmérőjű, ennek DC ellenállása 11 mΩ. 10 MHz-en a behatolási mélység 20 μm, ezért az ellenállása felmegy 130 mΩ-ra.) Az áramkör ezen részére 10 MHz-en az impedancia valós része 50 Ω, míg a képzetes rész nagy pozitív értékű (440 Ω), amit a sorba kötött $C_{\text{M}}=36~\textrm{pF}$-os kondenzátorral tudunk kompenzálni. Így el tudjuk érni azt, hogy ez az áramkör valós 50 Ω impedanciájú lezárásnak tűnjön. Ezt az áramkört a magmágneses rezonancia spektroszkópiában használják rádiófrekvenciás pulzusok adás-vételére. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:NMR_aramkor_uj.png|közép|600px|]] | ||
| + | |- | ||
| + | | align="center"|4. ábra: a) Rezisztív elemet nem tartalmazó áramkör, ami behangolható a kábel hullámimpedanciájára. A példánkban csak a $C_{\text{M}}$ értékét változtatjuk. b) Az áramkörbeli párhuzamosan kapcsolt $C_{\text{T}}$ és $L$ rész impedanciájának, $Z_{\text{par}}$ valós és képzetes része a frekvencia függvényében konkrét értékekre (a 10 MHz alatti rész 10 szeresre van nagyítva). Vegyük észre, hogy 10 MHz-en a képzetes rész nagy pozitív értékű miközben a valós rész 50 Ω. | ||
| + | |} | ||
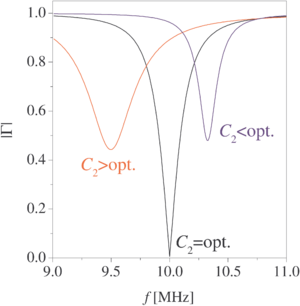
| + | Az 5. ábrán mutatjuk a 4.a ábra áramkörének reflexióját, $\left|\Gamma\right|$, a frekvencia függvényében a | ||
| + | $C_{\text{M}}$ illesztő kondenzátor három értékére. Az optimálisan beállított $C_{\text{M}}$ érték mellett a reflexió nullává válik. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:NMR_aramkor_reflexio.png|közép|300px|]] | ||
| + | |- | ||
| + | | align="center"|5. ábra: A bemutatott áramkörről történő reflexiós tényező, $\left|\Gamma\right|$, a frekvencia függvényében a szövegben megadott paraméterekkel a $C_{\text{M}}$ három értékére: optimális (36 pF), annál kisebb (20 pF), illetve nagyobb (65 pF). Utóbbi két esetet nevezik alul- , ill. túl-csatolt esetnek is. Vegyük észre, hogy a $C_{\text{M}}$ optimális értéke mellett a reflexió 0-vá válik egy adott frekvencián, míg egyébként véges értékű minden frekvencián. | ||
| + | |} | ||
| + | </wlatex> | ||
| + | |||
===Visszaverődések vizsgálata=== | ===Visszaverődések vizsgálata=== | ||
| + | <wlatex> | ||
| + | A reflexiók jelenlétét kétféleképpen vizsgálhatjuk, a forrás kimenő feszültségének vizsgálatával és ún. ''duplexer'' segítségével. Az első esetben az oszcillátor forrás kimenetére BNC T elosztót teszünk, majd az így kettéosztott jelet küldjük egy hosszú (pl. 10-25 m) vezetékbe, egy rövidebb (pl. 0,5 m) BNC kábellel pedig egy oszcilloszkópra tesszük a jelet. Az oszcilloszkóp bemenetére is egy másik T-vel 50 Ω-os lezárást teszünk. A forrás frekvenciájának függvényében a hosszú vezeték lezárásának értékétől függően az oszcilloszkópon lévő jel nagysága változik. Ebből pl. a jel terjedési sebességét a kábelen vagy ennek ismeretében a kábel hosszát meg tudjuk határozni. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:hybrid_tee_uj.png|közép|300px|]] | ||
| + | |- | ||
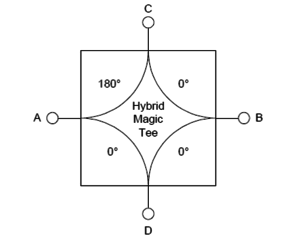
| + | | align="center"|6. ábra: Az esetünkben használt duplexer, vagy ''hybrid magic tee'' (típusa Anzac HH107, 2-200 MHz) sematikus ábrája. A duplexeren a csatlakozók másképp helyezkednek el, mint ezen a sematikus ábrán, figyeljünk a jelölésekre! | ||
| + | |} | ||
| + | A duplexer egy általános fogalom, lényege, hogy lehetőséget ad arra, hogy egy forrásból egy kábel felé elküldött jelre meghatározhassuk a kábel felől reflektált feszültséget. Esetünkben a rádiófrekvenciás duplexer egy ún. ''hybrid magic tee'', amit a 6. ábra mutat és működését a C. függelékben mutatjuk meg. A duplexer lényege, hogy pl. az $A$ bemenetére adott feszültséget elosztja a $C$ és $D$ portok között, miközben a $C$ port felé a fázist is elforgatja. (A ''hybrid magic tee''-re jellemző, hogy a portok között van egy kismértékű (10%) áthallás is.) A jel terjedési irányát megfordítva: az $A$ porton a $C$ és $D$ portokra adott feszültségek különbsége jelenik meg: $D-C$. A mi esetünkben a reflexiók vizsgálatára a ''hybrid magic tee'' használatakor $A$: a forrás, $D$: az oszcilloszkóp CH1, 50 Ω-os lezárással, $C$: a reflexióra bevizsgált kábel, $B$: az oszcilloszkóp másik bemenete 50 Ω-mal lezárva. Ha a $B$ porton 0 feszültséget mérünk, akkor a bevizsgált kábelen nincs reflexió. | ||
| + | </wlatex> | ||
| + | |||
===A Smith chart=== | ===A Smith chart=== | ||
| + | <wlatex> | ||
| + | Az ún. ''Smith chart'' egy gyakran használt grafikus segédeszköz a az áramkörök frekvenciafüggő tulajdonságainak vizsgálatára és a felmerülő problémák megoldására. A ''Smith chart''-on többféle mennyiséget is megjeleníthetünk, mint pl. impedancia, admittancia, reflexiós tényező, állóhullámarány stb. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:Smith_chart_reflexio_uj2.png|közép|600px|]] | ||
| + | |- | ||
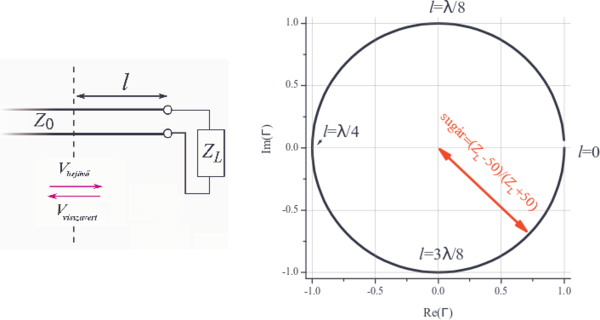
| + | | align="center"|7. ábra: A kábelvégről történő reflexió esetén kapott ''Smith chart'', a kör sugarának és a körív nevezetes pontjainak bejelölésével. Az ábrához tartozó kísérleti elrendezést is mutatjuk. A vízszintes és függőleges tengelyek a sugár egységeiben vannak mérve. | ||
| + | |} | ||
| + | A 7. ábrán mutatjuk a $Z_{\text{L}}$ terhelő ellenállással lezárt kábelvégről történő reflexió esetén a reflexiós tényező képzetes részét a valós rész függvényében: | ||
| + | $$ | ||
| + | \Gamma=\frac{V_{\text{visszavert}}}{V_{\text{bejövõ}}}. | ||
| + | $$ | ||
| + | A kapott görbét a kábel $l$ hossza parametrizálja, a nevezetes pontjait az ábrán bejelöltük, azaz amikor $l$ értéke a hullámhosszhoz képest megadott értékeket vesz fel. A kör sugara $r=\frac{Z_{\text{L}}-50}{Z_{\text{L}}+50}$, itt a sugár előjeles mennyiségként értendő, tehát negatív előjel esetén a $\Gamma=0$ pontra tükröződik a kör. A reflexiós tényező valós és képzetes részeit a kábel végéről visszavert jel -- kiadott jelhez képesti -- fázisának mérésével kaphatjuk meg. | ||
| + | |||
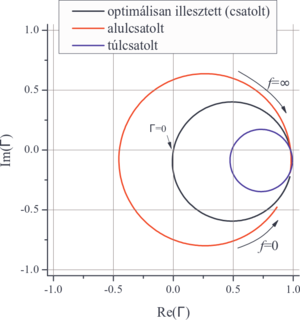
| + | A 4.a ábrai áramkörrel történő lezárás esetére mutatjuk a reflexiós tényező képzetes részét a valós rész függvényében. Jól láthatóan kör alakul ki, aminek a frekvencia a paramétere. Az optimális (vagy kritikus) csatolás esetén a kör átmegy a Smith chart origóján. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:Smith_chart_NMR_uj.png|közép|300px|]] | ||
| + | |- | ||
| + | | align="center"|8. ábra: A reflexiós tényező valós és képzetes részei ábrázolva egymás függvényében a 4.a áramkör esetére az impedanciaillesztés három esetére. A körök paramétere a frekvencia, aminek a határértékeit bejelöltük. | ||
| + | |} | ||
| + | A 8. ábrán a 4.a ábrai áramkörrel történő lezárás esetére mutatjuk a reflexiós tényező képzetes részét a valós rész függvényében. Jól láthatóan kör alakul ki, aminek a frekvencia a paramétere. Az optimális (vagy kritikus) csatolás esetén a kör átmegy a Smith chart origóján. | ||
| + | </wlatex> | ||
| + | |||
==Mérési feladatok== | ==Mérési feladatok== | ||
| 114. sor: | 164. sor: | ||
===I. A kábelvégi reflexió vizsgálata (első mérési alkalom)=== | ===I. A kábelvégi reflexió vizsgálata (első mérési alkalom)=== | ||
| − | |||
| − | |||
<wlatex> | <wlatex> | ||
| + | ====1. Oszcilloszkóppal==== | ||
| + | |||
Itt oszcilloszkóppal mérjük meg a kábelvégi reflexió hatását a forrás kimenetére. | Itt oszcilloszkóppal mérjük meg a kábelvégi reflexió hatását a forrás kimenetére. | ||
| − | + | *1. Vegyük fel oszcilloszkóp segítségével a nagyfrekvenciás jelgenerátor kimenetének feszültségét a lezáró impedancia három esetére (0, 50 Ω és szakadás) a frekvencia (0,001 MHz-15 MHz) függvényében a mérőprogrammal. (''Segítség:'' BNC T a forrás kimenetén, egyik vége oszcilloszkópon minél rövidebb dróttal 50 Ω-mal lezárva, másik végén egy ismert hosszúságú BNC kábel, mérőeszköz leírás a D. függelékben. A forrás 2-es kimenetére triggereljük az oszcilloszkópot. A mérőprogramban a ''rflabor <startfreq> <stopfreq> <numberofpoints>'' paranccsal tudjuk a frekvencia változtatása mellett felvenni az oszcilloszkóp 1-es csatornáján mért jel nagyságát és az 1-es és 2-es csatornán mért jel egymáshoz viszonyított fázisát. A ''save'' paranccsal tudjuk elmenteni a mérésünk eredményét. A ''readscope'' paranccsal fel tudjuk venni az oszcilloszkópon éppen látható jelet.) | |
| − | + | *2. A kapott görbék segítségével határozzuk meg a kábelbeli jel terjedési sebességét. Ebből határozzuk meg a BNC kábelben lévő dielektrikum $\epsilon_{\text{r}}$ relatív dielektromos állandóját ($\mu_{\text{r}}=1$), és írjuk le röviden, hogy a módszer hogyan használható egy elszakadt kábelban a szakadás helyének meghatározására. | |
| + | ====2. Duplexerrel==== | ||
| + | |||
| + | Itt a ''hybrid magic tee'' (Tee a továbbiakban) segítségével vizsgáljuk a kábelvégi reflexiót. A vizsgált frekvenciatartomány: 2-20 MHz. | ||
| + | |||
| + | *3. A Tee bekötése: $A$ - a forrás, $D$ - a oszcilloszkóp CH2 (trigger forrás), 50 Ω-os lezárással, $C$ - az oszcilloszkóp másik bemenete, CH1 50 Ω-mal lezárva. Ekkor a CH1 és CH2-n ellentétes fázisú jelet kell látunk, amit vegyünk is fel (''readscope'' parancs)! A következő esetben: $A$ - a forrás, $D$ - oszcilloszkóp CH2, 50 Ω-os lezárással, $C$ - 50 Ω-mal lezárva, $B$ - az oszcilloszkóp másik bemenete, CH1 50 Ω-mal lezárva. Ideális esetben ekkor 0 jelet kellene látnunk, azonban a duplexer tökéletlensége miatt mégis látunk egy kis jelet CH1-en, amit vegyünk is fel! | ||
| + | *4. A Tee segítségével vegyük fel a kábel végéről visszavert jel nagyságát a frekvencia függvényében (2-15 MHz), úgy mint az előző feladatban, de a $C$-re a reflexióra bevizsgált kábelt helyezzük, rövidre zárva, lezáratlanul és 50 Ω-mal lezárva. Milyen az oszcilloszkóp CH1-en mért jele a frekvencia függvényében erre a három esetre és miért? (''Segítség:'' a duplexer mindhárom esetben a visszavert jel nagyságát mutatja meg, ami nem interferál a forrás jelével. Ezért itt nem várjuk olyan állóhullámképek kialakulását mint az I/1/1. feladatban.) Vizsgáljuk meg, hogy 10 MHz-es frekvencián a CH1 csatornán látható jelhez képest hogyan változik CH2-n látható jel fázisa akkor, amikor a kábel végét rövidre zárjuk, vagy lezáratlanul hagyjuk. Ehhez vegyük fel e két esetre az oszcilloszkóp jelét! | ||
| + | Az első feladatban 1 kHz-15 MHz intervallumban vizsgáltuk a jelterjedést, a negyedikben, a duplexerrel a 2 MHz-15 MHz intervallumon. Mi miért szűkítettük a sávot? Az előző feladatot végezzük el az 1 kHz-15 MHz sávban is. Mit tapasztalunk? | ||
| + | |||
| + | ====3. Pulzus kábelvégi reflexiójának vizsgálata==== | ||
| + | |||
| + | *5. A jelgenerátoron állítsunk be 1 MHz-es frekvenciájú szinusz jelet. A BURST megnyomása után beállítható, hogy a generátor e jel hány periódusát küldje ki milyen ismétlési idővel. Az I/2/4. mérési feladatbeli összeállítást használjuk fel arra, hogy a 25 m-es kábel végéről történő reflexiót megmérjük. Az oszcilloszkóp jelét vegyük fel, és a visszavert pulzus időkésésének tekintsük az összetartozó fázisú jelek közti időkülönbséget. Mit látunk a rövidzár, szakadás és 50 Ω-os lezárás eseteire? Az impulzus visszaverődési idejéből határozzuk meg a kábelbeli fénysebességet, és a kapott eredményt hasonlítsuk össze I/1/2. mérési feladat eredményével. Próbáljuk ki ugyanezt, ha nem szinusz, hanem négyszögjelet használunk, és az így kapott jelalakokat is vegyük fel! A szakadást tartalmazó koaxiális kábelen látott reflexióból számoljuk ki a szakadás helyzetét. | ||
</wlatex> | </wlatex> | ||
| − | === | + | ===II. A lezáró impedancia vizsgálata (első alkalom)=== |
| + | <wlatex> | ||
| + | *6. A 4.a ábrán látható áramkört csatlakoztassuk a Tee segítségével a forrásra az eddigi ismeretek alapján úgy, hogy az áramkörről történő reflexiót vizsgálhassuk. Állítsuk be a $C_{\text{M}}$ trimmer kondenzátor értékét úgy, hogy az áramkörről minimális legyen a reflexió egy adott frekvencián! Ekkor olyan reflexiós görbét kellene kapnunk mint amit az 5. ábrán mutatunk. Segítség: a multiméter segítségével állítsuk a $C_{\text{M}}$-et úgy, hogy kb. 30 pF-on legyen. (A forgókondenzátor a doboz hátoldalán levő banánhüvelyekhez van csatlakoztatva.) Ekkor látnunk kell egy reflexió minimumot 10 MHz körül. Közel erre a frekvenciára álljunk rá, és a jelgenerátor frekvenciája és a trimmer kondenzátor együttes állításával érjük el, hogy a minimális reflexió értéke kisebb legyen mint a minimumtól távoli frekvencián mért reflexió 10%-a! Alternatív, bár lassabb módszer az, ha folyamatosan a ''freqswe'' paranccsal felvesszük a reflexiót úgy, hogy közben a $C_{\text{M}}$ értékét változtatjuk, ekkor az 5. ábrán mutatottakhoz hasonló görbéket figyelhetünk meg. | ||
| + | *7. Vegyük fel az áramkörről reflektálódó jelet a frekvencia függvényében legfeljebb 1-2 MHz szélességben! Mérjük meg a $C_{\text{M}}$ értékét. Számítsuk ki, hogy mekkora $C_{\text{M}}$ érték mellett lesz az áramkör impedanciája $50+i\cdot 0~\Omega$ , és hasonlítsuk össze a két értéket. A tekercs és a párhuzamos kapacitás adatai az alkatrészeket tartalmazó dobozról leolvashatók. | ||
| + | </wlatex> | ||
| − | + | ===III. Szórt kapacitás mérése koaxiális kábelen (második alkalom)=== | |
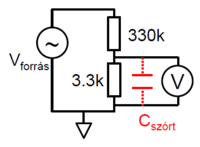
| + | <wlatex> | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:szortkapacitas_uj.png|közép|200px|]] | ||
| + | |- | ||
| + | | align="center"|9. ábra: Kábel szórt kapacitásának mérésére alkalmas összeállítás | ||
| + | |} | ||
| + | *8. Egy koaxiális kábel két vezetője egy kis kapacitású kondenzátort alakít ki. Rakjuk össze a 9. ábrán látható kapcsolást egy rövid és egy 20 m-es koaxiális kábellel. A mérőprogram segítségével mérjük meg az átviteli karakterisztikáját több bemenő frekvenciára. Figyeljük meg, hogy a hosszabb kábel használata esetén a kapcsolás mint aluláteresztő szűrő viselkedik. Mérjük meg ugyanezt a két kábelt négyszögjelet használva. Figyeljük meg, hogy a felfutás ideje különbözik a két kábelre. A mérések eredményéből határozzuk meg a kábel hosszegységre eső kapacitását. | ||
| + | </wlatex> | ||
| − | + | ===IV. Fénysebesség mérése szabad térben (második alkalom)=== | |
| − | + | <wlatex> | |
| + | *9. Rakjuk össze az adó egységet a függvénygenerátor és az adó antennaként használt tekercsből. A függvénygenerátoron állítsunk be egy négszögjelet. A függvénygenerátor másik kimenetére kössük a kb. 20 m-es kábellel az oszcilloszkóp egyik bemenetét. Az oszcilloszkóp másik bemenetére kössük a vevő antennát. A négyszögjel felfutásához és lefutásához kapcsolódó jelet mérünk a vevőnkkel. | ||
| + | *10. Rögzítsük a jelet az adó és vevő közeli helyzete mellett, majd távolítsuk egymástól az adót és a vevőt, amennyire a kábelek engedik. Figyeljük meg, hogy a referencia és az antennával mért jel helyzete változik egymáshoz képest. Mérjük a meg az elmozdulás miatti eltolódás idejét és az adó és a vevő távolságát. A kapott értékekből számoljuk számoljuk az elektromágneses hullám szabadtéri terjedési sebességét. | ||
| + | </wlatex> | ||
| − | ==== | + | ==Függelék== |
| + | ===A. A reflexiós tényező származtatása=== | ||
| + | <wlatex> | ||
| + | Korábban láthattuk, hogy a kábelen egy irányban haladó jelre a feszültség és áram aránya minden időpillanatban és a kábel minden helyén a $Z_0$ hullámimpedancia. Azonban amikor a kábel vége egy tetszőleges $Z_{\textrm{l}}$ impedanciával van lezárva, akkor a lezáráson a feszültség és áram hányadosának ekkora értéket kell felvennie. Ezért alakul ki reflektált hullám, mert ez biztosítja, hogy a lezáráson ez a feltétel matematikailag fennálljon. | ||
| − | === | + | Vegyük fel úgy az $x$ koordinátát, hogy a lezáráson legyen $x=0$. Erre az esetre a távíróegyenletek megoldásai két egymással szemben terjedő haladó hullám mind a feszültségre mind az áramra, úgy, hogy a két iránybeli amplitúdók nem feltétlenül azonosak: |
| + | $$ | ||
| + | U(x)=U^+_0 e^{i(\omega t +k x)}+U^-_0 e^{i(\omega t -k x)}\\ | ||
| + | I(x)=\frac{U^+_0}{Z_0} e^{i(\omega t +k x)}-\frac{U^-_0}{Z_0} e^{i(\omega t -k x)}, | ||
| + | $$ | ||
| + | ahol $U^+_0$ és $U^-_0$ a lezárás felé, illetve attól távolodva haladó hullám. Vegyük észre az áram kifejezésében a második tag negatív előjelét, ami a távíróegyenletből adódik. Ennek a megoldásnak teljesítenie kell az $\frac{U(x=0)}{I(x=0)}=Z_{\textrm{l}}$ feltételt, azaz: | ||
| + | $$ | ||
| + | Z_{\textrm{l}}=\frac{U^+_0+U^-_0}{U^+_0-U^-_0} Z_0, | ||
| + | $$ | ||
| + | amiből adódik a visszavert hullám amplitúdójára: | ||
| + | $$ | ||
| + | U^-_0=\frac{Z_{\textrm{l}}-Z_0}{Z_{\textrm{l}}+Z_0} U^+_0. | ||
| + | $$ | ||
| + | Ebből közvetlenül adódik a korábbiakban bevezetett $\Gamma$ reflexiós tényező, ami a $ | ||
| + | \Gamma=\frac{U_{\text{visszavert}}}{U_{\text{bejövõ}}}$ képlet szerint adódik. | ||
| + | </wlatex> | ||
| − | === | + | ===B. Érdekességek a témakörből=== |
| + | <wlatex> | ||
| + | ====A kábelek impedanciaillesztésének szerepe==== | ||
| − | === | + | A reflexiókat kábelvégi szakadások vizsgálatára lehet felhasználni. Kémregényekben ezzel a módszerrel vizsgálják meg, hogy egy kábelra valaki rámért-e, illetve azt is meg lehet vele határozni, hogy hol történt a rámérés. A mérés lényege, hogy akármennyire is kis perturbációként történik meg a kábelra a rámérés, az meg fogja változtatni egy adott ponton a vezeték hullámimpedanciáját, ami a kábelról történő reflexió megváltozásához vezet. A rámérés helye a frekvenciafüggő reflexiós együtthatóból határozható meg. |
| + | |||
| + | A fizikában semmi sem véletlen: ha két fizikai állandóból származtatható egy adott dimenziójú harmadik állandó, akkor annak legtöbbször van valami fizikai tartalma. Így van ez pl. a fluxuskvantummal (h/2e), vagy a Bohr-magnetonnal ($e\hbar/2m_{\text{e}}$), melyek a megfelelő fizikai mennyiségek kvantumai. Ismert a $c=1/\sqrt{\varepsilon_0 \mu_0}$ összefüggés, ami a fénysebesség és az elektromágneses egységek kapcsolatát írja le. Hasonlóan, a $\sqrt{\mu_0/\varepsilon_0}$ mennyiségnek is van fizikai tartalma. Ennek dimenziója Ohm, értéke kb. 377 Ω és a vákuum impedanciájának nevezzük. | ||
| + | |||
| + | A vákuum hullámimpedancia fizikai jelentése a következő. Az elektromos és mágneses térerősségek hányadosából vákuumban terjedő elektromágneses sugárzásra: $Z_0=|\textbf{E}|/|\textbf{H}|=\sqrt{\mu_0/\varepsilon_0}$ ez azt jelenti, hogy a vákuumba kisugárzó és onnan vevő antennáknak ilyen impedanciával kell ideálisan rendelkeznie. Másfelől ez az összefüggés, összehasonlítva a koaxiális kábelekkel azt jelenti, hogy utóbbiban kisebb az elektromos tér nagysága a mágneseshez képest mint a szabad térben terjedő elektromágneses sugárzás, ennek elsődleges oka, hogy a koaxiális kábelekben $\varepsilon_{\text{r}}>1$ (tipikusan 2,5 körüli). | ||
| + | |||
| + | Láttuk a bevezetőben, hogy a jelterjedés számára előnyös a koaxiális kábelek használata, azonban néhány helyen, pl. audiotechnikában, távközlésben találkozunk egyéb preferált impedanciákkal pl. 8, 150, vagy 600 Ω. Mindezeknek történeti háttere van, pl. a 600 Ω oka, hogy a hagyományos, nem koaxiális távíró vonalaknak (két rézdrót egymástól 1 láb távolságra) ekkora volt a hullámimpedanciája. Az első távolsági telefonok ezeket a vezetékeket használták, ezért egy időben a 600 Ω volt a távközlési sztenderd. Később a csavart rézdrótpár terjedt el aminek 150 Ω a hullámimpedanciája. Napjainkban igen elterjedt az ún. UTP (''unshielded twisted pair'') kábel a számítógépes hálózati alkalmazásokhoz, melynek 100 Ω a hullámimpedanciája. | ||
| + | |||
| + | A koaxiális kábelek elterjedésével felmerült a kérdés, hogy melyik hullámimdepancia legyen a sztenderd. Érdekes módon erre nem kapunk egyértelmű választ, több forrásból merítve ([http://www.highfrequencyelectronics.com/Archives/Jun07/HFE0607\_Editorial.pdf [1]], [http://www.rfcafe.com/references/electrical/history-of-50-ohms.htm [2]],[http://www.microwaves101.com/encyclopedia/why50ohms.cfm [3]],[http://en.wikipedia.org/wiki/Coaxial\_cable [4]]) a következő történetet találjuk. | ||
| + | |||
| + | A hullámimpedancia három egymástól független, technikailag fontos paraméterben jelenik meg: a maximális teljesítményátvitelben (optimális ha $Z_0=30~\Omega$), a nagyfeszültségű elektromos letörés maximumában (optimális ha $Z_0=60~\Omega$), és az átvitt jel veszteségének minimumában (optimális ha $Z_0=77~\Omega$). A korai (1920-as évek) rádiófrekvenciás gyakorlatban a források teljesítménye alacsony volt, ezért a 77 Ω-os kábelek terjedtek el. Mivel nem léteztek jó és rugalmas dielektrikumok, ezért a vezetékek két egymásba helyezett koaxiális csőből álltak, melyeket levegő töltött ki. | ||
| + | |||
| + | 50 Ω-os vezetéket kapunk ha egy 3/4 colos rézcsövet egy 2 colos rézcsőbe helyezünk (mindkettő elterjedt méret az USA-ban), ezért ez a megoldás az 1930-as évektől elterjedt a nagyteljesítményű rádiófrekvenciás adások kisugárzására. Amikor egy 77 Ω-os vezetéket feltöltünk polietilénnel ($\varepsilon_{\text{r}}=2.3$) akkor az impedanciája 51 Ω lesz, ami szintén az 50 Ω felé mutat. Egy másik szempont az, hogy a két fent emlitett érték, 30 és 77 Ω, számtani közepe 53,5 Ω, mértani közepe 48 Ω, ezért az 50 Ω egy jó kompromisszum a veszteség és teljesítményátvitel között: ugyanazzal a kábellel tudunk nagyenegeriájú jelet adni és venni. Egy érdekes szempont még az, hogy egy koaxiális kábel amire a belső vezető és külső árnyékolás átmérőjének aránya ránézésre "szép", kb. 50 Ω-os hullámimpedanciájú lesz. | ||
| + | |||
| + | Az 50 Ω elterjedtsége ellenére találunk még gyenge videójelek átvitelénél 75 Ω-os kábelt, ami a veszteségre optimális, illetve 93 Ω-os kábelt pl. számítógép és monitorok összekötésére. A 93 Ω-os hullámimpedanciájú kábelnél a hosszegységre eső kapacitás a legalacsonyabb, ezért ennek a nagyfrekvenciás levágási frekvenciája a legnagyobb. Emiatt a négyszögjelek is jobban, torzításmentesen kerülnek átvitelre. | ||
| + | |||
| + | ====Egyéb példák impedanciaillesztésre, mechanika és optikai területéről==== | ||
| + | |||
| + | Impedanciaillesztéssel nem csak kábelekben terjedő elektromágneses hullámok, hanem fény és hanghullámok esetén is találkozhatunk. Hanghullámok terjedésekor nagyon különböző törésmutatójú közegek határára érkezve a hanghullámok visszaverődnek, ahelyett, hogy áthaladnának. Az orvosi ultrahangos vizsgálatokban használt zselé tölti be azt a szerepet, hogy az emberi test és a hanghullámot adó berendezés között illeszti az impedanciát. A bizonyos hangszereken található tölcsér és a hangszórók geometriai kialakítása is a hangadó és a környező levegő közötti impedancia illesztést végzik. | ||
| + | |||
| + | Az egyik sokat vizsgált mechanikai példánkban, két test rugalmas ütközésekor, a maximális energiaátadás a két test között akkor történik meg, amikor a két test tömege egyenlő. Ez is felfogható, mint "mechanikai impedancia illesztés". | ||
| + | |||
| + | Optikai problémáknál azt találjuk, hogy a fény visszaverődik olyan közegek határáról, melyek törésmutatója nem azonos. A törésmutató, $n$, reciprokát azonosíthatjuk az optikai vagy hullámimpedanciával: $Z=n^{-1}$. Az $n_1$ törésmutatójú közegből $n_2$ törésmutatójú közegbe haladó hullámra a reflektált hullám amplitúdójára azt kapjuk, hogy $r=\frac{Z_2-Z_1}{Z_1+Z_2}$. Ezt az összefüggést az optikában Fresnel-egyenletekként ismerik. Egy hétköznapi példája a szemüvegek lencséjéről történő reflexió (csillogás) ami megfelelő, ún. ''antireflex'' burkolattal szüntethető meg. Ebben az esetben az antireflex réteg végzi az impedanciaillesztés szerepét. | ||
| + | </wlatex> | ||
| + | |||
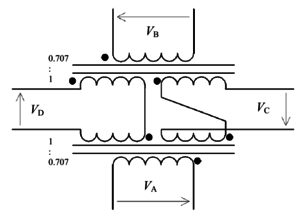
| + | ===C. A rádiófrekvenciás duplexer=== | ||
| + | <wlatex> | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:duplexer_transformator_uj.png|közép|300px|]] | ||
| + | |- | ||
| + | | align="center"|C1. ábra: Az esetünkben használt rádiófrekvenciás duplexer megvalósítása. A fekete pontok a transzformátorok tekercsein az azonos fázisban lévő pontokat mutatják. Vegyük észre, hogy a menetszámok aránya nem 1:1, hanem minél jobban megközelíti az $1:1/\sqrt{2}$ arányt. | ||
| + | |} | ||
| + | |||
| + | A rádiófrekvenciás duplexer megvalósításának sémáját a C1. ábrán mutatjuk. Lényege, hogy a feszültségeket ferritmagos transzformátorokkal választjuk a portok között szét, vagy éppenséggel egyesítjük két port bemenő jelét. A transzformátorok tulajdonsága alapján az egyes portokon mérhető feszültségek között a következő összefüggések adódnak: | ||
| + | |||
| + | $$ | ||
| + | V_{\text{A}}=\left(V_{\text{D}}-V_{\text{C}}\right)/\sqrt{2}\\ | ||
| + | V_{\text{B}}=\left(V_{\text{C}}+V_{\text{D}}\right)/\sqrt{2}\\ | ||
| + | V_{\text{C}}=\left(V_{\text{B}}-V_{\text{A}}\right)/\sqrt{2}\\ | ||
| + | V_{\text{D}}=\left(V_{\text{A}}+V_{\text{B}}\right)/\sqrt{2}. | ||
| + | $$ | ||
| + | |||
| + | Látható, hogy ezen feszültségek közötti összefüggések éppen annak a sematikának felelnek meg, amit a 6. ábrán mutatunk. Tehát pl. a $C$ port feszültsége az $A$ és $B$ portok feszültségeinek különbsége. Az energiamegmaradást megvizsgálva azt láthatjuk, hogy ha pl. $A$ és $B$ portokon érkezik be jel, akkor az a $C$ és $D$ portok között oszlik el, de nem egyenlően hanem attól függő intenzitás aránnyal, hogy a két jel fáziskülönbsége mekkora egymáshoz képest. Ha a fáziskülönbség éppen $\pi/2$, akkor az intenzitások egyenlően oszlanak el. | ||
| + | </wlatex> | ||
| + | |||
| + | ===D. A mérőeszközök használata=== | ||
| + | <wlatex> | ||
| + | '''Tektronix oszcilloszkóp'''. A digitális oszcilloszkóp alapvető használatát ismertnek tételezzük fel. A ''TRIGGER'' gomb megnyomása után választható ki a csatorna, amire triggerelünk (kijelző alatti gombokkal érhető el a trigger menü almenüje), a ''VERTICAL MENU''-ben a kijelzőtől jobbra elhelyezett gombokkal tudjuk a megfelelő kijelzett csatornákat beállítani. Célszerű a forrásból kijövő referencia jelre triggerelni, vagy a duplexerrel történő méréseknél a duplexer referencia (általában $D$) kimenetére. Az oszcilloszkóppal akkor tudjuk a lehető legkisebb hibával megmérni a feszültséget ha a mérendő jel éppen kitölti a képernyőt, vagy annál kis mértékben (maximum 20%) nagyobb. A frekvenciabeállítás akkor optimális ha a szinuszos jel néhány (2-5) periódusát látjuk. | ||
| + | |||
| + | '''Siglent SDG1025 jelgenerátor'''. A megfelelő jelalak az erre dedikált funkciógombokkal érhetőek el. A függvény paraméterei (''frequency'', ''amplitude'' stb.) a kijelző melletti gombok megnyomása után megadható. A két csatorna közti váltást a ''CH1/2'' gombbal tudjuk megtenni. A beállított jelalak kimeneten való megjelenítéséhez a kimeneti csatlakozók feletti ''OUTPUT'' gombokat kell megnyomni. | ||
| + | |||
| + | '''A mérőprogram'''. A Desktopon lévő ''RF\_Labor.Ink'' nevű parancsikont elindítva a program menüsora alatt találunk egy parancssort (''command line'') ahová az ''rflabor'', ''readscope'' vagy ''save'' parancsokat írhatjuk be. | ||
| + | |||
| + | Az '''''rflabor''''' paranccsal mérhetjük meg a frekvencia sweepet. A program beállítja a generátort a megfelelő értékekre, majd mindig kiolvassa az oszcilloszkóp 1-es csatornájára kötött jel nagyságát, majd az 1-es és 2-es csatorna közti fáziskülönbséget. A parancs elindításához 3 paraméter szüksége, melyeket egy szünettel kell elválasztani: a kezdő frekvencia, a végső frekvencia és a mérési pontok száma. | ||
| + | |||
| + | A '''''readscope''''' paranccsal beolvashatjuk az oszcilloszkóp által mért jelalakot. | ||
| + | |||
| + | Az '''''save''''' paranccsal elmenthetjük a mérésünk eredményeit egy ASCII fájlba. | ||
| + | </wlatex> | ||
| + | |||
| + | ===E. A mérőkód=== | ||
| + | <wlatex> | ||
| + | A mérőkód C# nyelven készült el a Visual Studio 2013-as verzióját használva. A program USB porton keresztül VISA protokolt használva kommunikál a mérőműszerekkel. A VISA protokoll használatakor rövid szöveges parancsokat adunk a műszereknek, amik szintén szöveges üzenetekkel válaszolnak. Példának következik az oszcilloszkópot kiolvasó függvény kódja: | ||
| + | A mérőkód C# nyelven készült el a Visual Studio 2013-as verzióját használva. A program USB porton keresztül VISA protokolt használva kommunikál a mérőműszerekkel. A VISA protokoll használatakor rövid szöveges parancsokat adunk a műszereknek, amik szintén szöveges üzenetekkel válaszolnak. Példának következik az oszcilloszkópot kiolvasó függvény kódja: | ||
| + | <syntaxhighlight lang="csharp"> | ||
| + | public static Curve read() | ||
| + | { | ||
| + | Curve r = new Curve(); | ||
| + | |||
| + | double ch1scale = double.Parse(VISA.Query(VISAaddress, "CH1:SCAL?")); | ||
| + | double ch1offset = double.Parse(VISA.Query(VISAaddress, "CH1:POS?")); | ||
| + | double ch2offset = double.Parse(VISA.Query(VISAaddress, "CH2:POS?")); | ||
| + | double ch2scale = double.Parse(VISA.Query(VISAaddress, "CH2:SCAL?")); | ||
| + | double timebase = double.Parse(VISA.Query(VISAaddress, "HOR:MAI:SCALE?")); | ||
| + | double timeoffset = double.Parse(VISA.Query(VISAaddress, "HOR:MAI:POS?")); | ||
| + | |||
| + | VISA.Write(VISAaddress, "DATA:SOURCE CH1"); | ||
| + | VISA.Write(VISAaddress, "DATA:ENC ASCII"); | ||
| + | VISA.Write(VISAaddress, "DATA:WIDTH 1"); | ||
| + | VISA.Write(VISAaddress, "DATA:START 1"); | ||
| + | VISA.Write(VISAaddress, "DATA:STOP 25000"); | ||
| + | string instring1 = VISA.Query(VISAaddress, "CURV?"); | ||
| + | VISA.Write(VISAaddress, "DATA:SOURCE CH2");\\ | ||
| + | string instring2 = VISA.Query(VISAaddress, "CURV?"); | ||
| + | |||
| + | string[] ch1strings = instring1.Split(','); | ||
| + | string[] ch2strings = instring2.Split(','); | ||
| + | |||
| + | for (int i = 0; i < ch1strings.Length; i++) | ||
| + | r.Add(\\ | ||
| + | (double)i / (ch1strings.Length) * timebase * 10 + timeoffset - 5 * timebase, | ||
| + | (double.Parse(ch1strings[i]) - ch1offset * 25) / 25 * ch1scale, | ||
| + | (double.Parse(ch2strings[i]) - ch2offset * 25) / 25 * ch2scale | ||
| + | ); | ||
| + | |||
| + | return r; | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | </wlatex> | ||
A lap jelenlegi, 2020. január 28., 15:56-kori változata
Tartalomjegyzék |
Bevezetés
A laborgyakorlat célja, hogy a nagyfrekvenciás (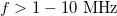 ) méréstechnika és jelátvitel területén felmerülő alapfogalmakat és jelenségeket bemutassa. A legfontosabb amit érdemes megjegyezni az, hogy az alacsony frekvenciás hálózatok vizsgálatakor megszokott leírásmódok nagyobb frekvenciákon érvényüket vesztik, és a hagyományos áramköri jelenségeken túlmutató, szokatlan jelenségek lépnek fel, mint pl. a jelek reflexiója. A fizika szempontjából itt a Maxwell-egyenletek nagyfrekvenciás, azaz hullámjelenségeket is figyelembe vevő alkalmazásáról van szó kábelek esetére.
) méréstechnika és jelátvitel területén felmerülő alapfogalmakat és jelenségeket bemutassa. A legfontosabb amit érdemes megjegyezni az, hogy az alacsony frekvenciás hálózatok vizsgálatakor megszokott leírásmódok nagyobb frekvenciákon érvényüket vesztik, és a hagyományos áramköri jelenségeken túlmutató, szokatlan jelenségek lépnek fel, mint pl. a jelek reflexiója. A fizika szempontjából itt a Maxwell-egyenletek nagyfrekvenciás, azaz hullámjelenségeket is figyelembe vevő alkalmazásáról van szó kábelek esetére.
A XIX. század közepén felmerült az igény a nagy távolságokra történő adattovábbításra, akár kontinensnyi távolságokban, pl. tenger alatti kábelek segítségével. (Az első transzatlanti kábelt 1858-ban helyezték üzembe.) Hamar kiderült, hogy a vezetékben történő jeltovábbításánál lényeges a hullámjelenségek figyelembevétele. Ez a technológiai fejlődés és igény az elméleti leírásra időben közel volt a Maxwell-egyenletek (1861) megszületéséhez. A vezetékben terjedő hullámjelenségek leírását ma mint az ún. távíróegyenleteket ismerjük. Ez a Maxwell-egyenletek által megjósolt elektromágneses hullámjelenségek egyik gyakorlati alkalmazása, és e leírás gyakorlati sikere is inspirálóan hatott az elektromágneses sugárzás későbbi felfedezésére (Hertz, 1886).
A fizikus tanulmányok során eddigiekben felmerült egyenáramú (DC) és alacsony frekvenciás váltóáramú (AC) hálózatok vizsgálatakor nem törődtünk azzal, hogy a jel terjedési sebessége véges. Feltételeztük, hogy adott ponton feszültséget kapcsolva egy áramkörre az pillanatszerűen megjelenik minden azonos potenciálú helyen. Mindez nyilvánvalóan érvényét veszíti, amikor a jel számára szükséges terjedési idő, 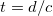 (itt
(itt  a kábel hossza,
a kábel hossza,  a közegben érvényes fénysebesség), összemérhető a jel periódusidejével:
a közegben érvényes fénysebesség), összemérhető a jel periódusidejével: 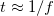 (a gyakorlatban inkább a
(a gyakorlatban inkább a 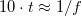 feltétel a használatos). Például a transzatlanti kábel esetére az így kapott frekvencia
feltétel a használatos). Például a transzatlanti kábel esetére az így kapott frekvencia 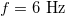 . Ez az eredmény azt jelenti, hogy a hullámjelenségek figyelembe vétele nélkül a transzatlanti kommunikáció csak ennél lényegesen alacsonyabb frekvencián, mai szóhasználattal kb.
. Ez az eredmény azt jelenti, hogy a hullámjelenségek figyelembe vétele nélkül a transzatlanti kommunikáció csak ennél lényegesen alacsonyabb frekvencián, mai szóhasználattal kb. 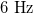 sávszélességen (azaz 6 bit/sec) mehetne csak végbe.
sávszélességen (azaz 6 bit/sec) mehetne csak végbe.
A hullámjelenségek figyelembevétele a modern kommunikációs eszközöknél még fontosabb, mivel pl. 9 GHz-es vivőfrekvenciára (ami egy elterjedt kommunikációs sáv) a hullámhossz mindössze 3 cm. Egy másik gyakorlati példánk a számítógépek, melyek tipikusan 2-3 GHz-es jelekkel dolgoznak (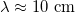 ), melyeket 10-20 cm távolságra juttatnak el, így itt nyilvánvalóan szükséges a hullámjelenségek figyelembevétele az áramkörök tervezésekor. A későbbi tanulmányaink során hasonló jelenségekkel találkozhatunk az Önálló labor tárgy NMR (magmágneses-rezonancia) és ESR (elektronspin-rezonancia) laborgyakorlatain.
), melyeket 10-20 cm távolságra juttatnak el, így itt nyilvánvalóan szükséges a hullámjelenségek figyelembevétele az áramkörök tervezésekor. A későbbi tanulmányaink során hasonló jelenségekkel találkozhatunk az Önálló labor tárgy NMR (magmágneses-rezonancia) és ESR (elektronspin-rezonancia) laborgyakorlatain.
Elméleti háttér
A távíróegyenletek
Tekintsük a jelet továbbító vezeték egy infinitezimálisan kicsi darabját, ami az 1. ábrán látható. Ezt legáltalánosabban egy soros, ún. elosztott ellenállás, 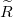 (egysége Ohm per méter), elosztott induktivitás,
(egysége Ohm per méter), elosztott induktivitás, 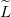 (egysége Henry per méter), elosztott kapacitás,
(egysége Henry per méter), elosztott kapacitás, 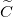 (egysége Farád per méter), és a két drót közti elosztott vezetés,
(egysége Farád per méter), és a két drót közti elosztott vezetés, 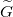 (egysége Siemens per méter) jellemzi.
A soros ellenállás oka a vezetékdarabokban lévő veszteség, az induktivitás oka pedig az, hogy az egyes drótdarabokat mágneses tér veszi körbe, ezért lesz egyetlen drótszálnak is önindukciója. A
(egysége Siemens per méter) jellemzi.
A soros ellenállás oka a vezetékdarabokban lévő veszteség, az induktivitás oka pedig az, hogy az egyes drótdarabokat mágneses tér veszi körbe, ezért lesz egyetlen drótszálnak is önindukciója. A 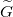 írja le a két vezetékdarab közti elektromos vezetést, ami akkor is jelen van, ha nagyon jó dielektrikum választja el a két vezetőt egymástól. Mivel a két drót nincs azonos potenciálon, ezért lesz köztük a
írja le a két vezetékdarab közti elektromos vezetést, ami akkor is jelen van, ha nagyon jó dielektrikum választja el a két vezetőt egymástól. Mivel a két drót nincs azonos potenciálon, ezért lesz köztük a 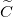 kapacitás.
kapacitás.
| 1. ábra: A jelterjedésben vizsgált vezeték egy darabjának áramköri modellje. |
Látható, hogy a fenti értékek közül 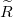 értéke elsősorban a vezető anyagi minőségétől függ (értéke nagyfrekvencián a skin-effektus miatt megnő), azonban
értéke elsősorban a vezető anyagi minőségétől függ (értéke nagyfrekvencián a skin-effektus miatt megnő), azonban 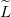 ,
, 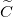 és
és 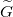 értéke nagyban függ attól, hogy a két drót egymáshoz képest hogyan helyezkedik el (pl. sodort érpárra
értéke nagyban függ attól, hogy a két drót egymáshoz képest hogyan helyezkedik el (pl. sodort érpárra 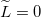 , de
, de 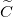 értéke nagy). Egymástól adott távolságra elhelyezkedő drótpár esetére
értéke nagy). Egymástól adott távolságra elhelyezkedő drótpár esetére 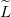 értéke fix, viszont
értéke fix, viszont 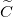 nagyban függ a környező dielektrikumtól (utóbbi probléma a sós víz miatt a transzatlanti kábelnél merült fel). Mindezen problémákra kínál megoldást a koaxiális kábel (Heaviside, 1880), amiben a földelt külső vezetéken belül helyezkedik el a másik drót. Ennek előnye, hogy minden paramétere jól definiált, mind az elektromos, mind a mágneses erővonalak belül a két koaxiális vezeték között helyezkednek el, amint azt a 2. ábra mutatja. A korábbi merev falú, levegővel kitöltött koaxiális kábeleket mára a rugalmas dielektrikummal kitöltött kábelek váltották fel (tipikusan
nagyban függ a környező dielektrikumtól (utóbbi probléma a sós víz miatt a transzatlanti kábelnél merült fel). Mindezen problémákra kínál megoldást a koaxiális kábel (Heaviside, 1880), amiben a földelt külső vezetéken belül helyezkedik el a másik drót. Ennek előnye, hogy minden paramétere jól definiált, mind az elektromos, mind a mágneses erővonalak belül a két koaxiális vezeték között helyezkednek el, amint azt a 2. ábra mutatja. A korábbi merev falú, levegővel kitöltött koaxiális kábeleket mára a rugalmas dielektrikummal kitöltött kábelek váltották fel (tipikusan 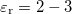 és
és 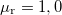 ).
).
2. ábra: A koaxiális vezeték keresztmetszete az elektromos és mágneses tér 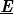 , ill. , ill. 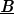 vonalaival a kábel alapvető, ún. TEM00 módusára. A belső vezetéken változó feszültség van, míg a külső leggyakrabban le van földelve. vonalaival a kábel alapvető, ún. TEM00 módusára. A belső vezetéken változó feszültség van, míg a külső leggyakrabban le van földelve.
|
A koaxiális kábelek hosszegységre eső kapacitására és önindukciós együtthatójára e két paraméter definíciójából adódik:
![\[ \widetilde{C}=\frac{2 \pi \varepsilon_0 \varepsilon_{\text{r}}}{\ln(D/d)}, \qquad \widetilde{L}=\frac{\mu_0 \mu_{\text{r}}\ln(D/d)}{2\pi}, \]](/images/math/6/9/0/690a2bceed2cc1530ee78e457e0c9a56.png)
ahol  az árnyékolás belső átmérője és
az árnyékolás belső átmérője és  a kábel belső vezetőjének külső átmérője,
a kábel belső vezetőjének külső átmérője, 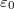 és
és 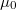 az ismert fizika állandók,
az ismert fizika állandók, 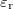 és
és 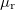 az anyagra jellemző paraméterek.
az anyagra jellemző paraméterek.
A távíróegyenletek bemutatásához a legegyszerűbb eset tárgyalásához feltesszük, hogy mindkét drót tökéletes vezető (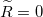 ) és tökéletesen szigetelt egymástól (
) és tökéletesen szigetelt egymástól (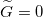 ), tehát a jelenség csak
), tehát a jelenség csak 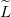 és
és 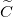 -től fog függeni. (A teljesen általános eset is megoldható, csak bonyolultabb eredményekre vezet.) Ekkor mind a feszültség (
-től fog függeni. (A teljesen általános eset is megoldható, csak bonyolultabb eredményekre vezet.) Ekkor mind a feszültség (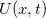 ), mind az áram (
), mind az áram (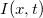 ) hely- és időfüggő lesz, és leírásukra a következő két csatolt, lineáris, elsőrendű parciális-differenciálegyenlet adódik (Heaviside, 1880):
) hely- és időfüggő lesz, és leírásukra a következő két csatolt, lineáris, elsőrendű parciális-differenciálegyenlet adódik (Heaviside, 1880):
![\[ \begin{aligned} \frac{\partial U(x,t)}{\partial x}=-\widetilde{L} \frac{\partial I(x,t)}{\partial t}\\ \frac{\partial I(x,t)}{\partial x}=-\widetilde{C} \frac{\partial U(x,t)}{\partial t}. \end{aligned} \]](/images/math/b/4/2/b42c7453324b14212652250b1c030ea8.png)
Ezek a távíróegyenletek a Maxwell-egyenletekből véges differenciák segítségével elemi úton levezethetők. További összevonással két ekvivalens hullámegyenletet kapunk mind az áramra, mind a feszültségre:
![\[ \begin{aligned} \frac{\partial^2 U(x,t)}{\partial t^2}=\frac{1}{\widetilde{L}\widetilde{C}}\frac{\partial^2 U(x,t)}{\partial x^2}\\ \frac{\partial^2 I(x,t)}{\partial t^2}=\frac{1}{\widetilde{L}\widetilde{C}}\frac{\partial^2 I(x,t)}{\partial x^2}. \end{aligned} \]](/images/math/7/b/2/7b2d296fb325fdba98591229785c26e2.png)
Az ismert alakú hullámegyenletekből leolvasható, hogy a kábelben terjedő zavar sebessége 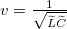 , és a legáltalánosabb megoldás a feszültségre és áramra:
, és a legáltalánosabb megoldás a feszültségre és áramra:
![\[ \begin{aligned} U(x,t)=U^+ f(\omega t- k x)+U^-f(\omega t+ k x)\\ I(x,t)=I^+ f(\omega t- k x)+I^-f(\omega t+ k x), \end{aligned} \]](/images/math/c/d/d/cdd1833774e27b35ce35085d1bddd450.png)
ahol  a terjedő hullám körfrekvenciája,
a terjedő hullám körfrekvenciája, 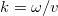 pedig a hullámszáma.
pedig a hullámszáma. 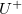 és
és 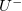 a pozitív, illetve negatív
a pozitív, illetve negatív  irányba terjedő jel amplitúdója,
irányba terjedő jel amplitúdója,  egy tetszőleges függvény. Vegyük észre, hogy a
egy tetszőleges függvény. Vegyük észre, hogy a  mennyiség dimenziója valóban m/s.
mennyiség dimenziója valóban m/s.
Egy speciális eset az, amikor a kábelen csak egy irányba haladó hullám van jelen. Ez a megoldás:
![\[ \begin{aligned} U(x,t)=U_0 e^{i(\omega t- k x)}\\ I(x,t)=I_0 e^{i(\omega t- k x)}. \end{aligned} \]](/images/math/1/7/b/17bda5e19986fa1b178bd4606ac94bcb.png)
Ezt a speciális megoldást a távíróegyenletekbe visszaírva azt kapjuk, hogy a feszültség és áram aránya a haladó hullámra:
![\[ \frac{U(x,t)}{I(x,t)}=\sqrt{\frac{\widetilde{L}}{\widetilde{C}}}=Z_0, \]](/images/math/4/2/0/42092ec1c6d0285584f917e078fd290a.png)
ahol a 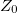 ellenállás dimenziójú mennyiséget a kábel hullámimpedanciájának nevezzük.
ellenállás dimenziójú mennyiséget a kábel hullámimpedanciájának nevezzük.
Visszaverődések a kábel végéről
A hullámegyenlet konkrét megoldását a kezdeti és peremfeltételek (pl. a drót végén előírt amplitúdó) ismeretében kaphatjuk meg. Középiskolás hangtani jelenségekkel analóg a következő két eset: amikor a koax kábel végét rövidre zárjuk (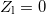 ), ill. amikor a koax kábel végén szakadás van (
), ill. amikor a koax kábel végén szakadás van (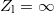 ). E két esetet szemlélteti a 3. ábra. Amennyiben a vezeték hossza és a gerjesztő hullám frekvenciája között jól meghatározható összefüggések állnak fenn (
). E két esetet szemlélteti a 3. ábra. Amennyiben a vezeték hossza és a gerjesztő hullám frekvenciája között jól meghatározható összefüggések állnak fenn (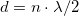 a zárt végre és
a zárt végre és 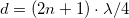 nyitott végre,
nyitott végre,  egész), a vezeték mentén feszültség állóhullámok alakulnak ki. A csomó- és duzzadóhelyeket a jól ismert bezárt illetve nyitott végű síppal való analógia alapján kaphatjuk meg. E két esetet a hanghullámokra vonatkozó analógia alapján úgy érthetjük meg, hogy mind a lezárt, mind a nyitott végről visszaverődik a hullám, és a kábelmenti feszültségben látható állóhullám kép az odafelé haladó és visszavert hullámok interferenciájának eredménye. A DC áramköröknél szerzett ismeretek azt mondanák, hogy a feszültség a rövidre zárt drótpárban végig 0, míg a szakadásos végű drótpárra végig a meghajtó generátor feszültségét veszi fel.
egész), a vezeték mentén feszültség állóhullámok alakulnak ki. A csomó- és duzzadóhelyeket a jól ismert bezárt illetve nyitott végű síppal való analógia alapján kaphatjuk meg. E két esetet a hanghullámokra vonatkozó analógia alapján úgy érthetjük meg, hogy mind a lezárt, mind a nyitott végről visszaverődik a hullám, és a kábelmenti feszültségben látható állóhullám kép az odafelé haladó és visszavert hullámok interferenciájának eredménye. A DC áramköröknél szerzett ismeretek azt mondanák, hogy a feszültség a rövidre zárt drótpárban végig 0, míg a szakadásos végű drótpárra végig a meghajtó generátor feszültségét veszi fel.
3. ábra: Sematikus áramkör szinuszos meghajtó generátorral aminek 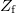 kimenő ellenállása van, koaxiális vezeték aminek a végén kimenő ellenállása van, koaxiális vezeték aminek a végén 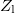 lezáró impedancia van. A generátorból jön ki a teljes teljesítmény ha lezáró impedancia van. A generátorból jön ki a teljes teljesítmény ha 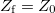 . A lezárás három értékére vonatkozó vezetékbeli feszültség eloszlást is mutatjuk 20 pillanatfelvételre, amikor . A lezárás három értékére vonatkozó vezetékbeli feszültség eloszlást is mutatjuk 20 pillanatfelvételre, amikor 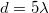 . Vegyük észre, hogy . Vegyük észre, hogy 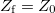 esetén a vezetékben homogén a feszültség maximuma, esetén a vezetékben homogén a feszültség maximuma, 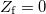 esetén mindkét végén csomópont van (ekkor forráson is 0 feszültséget mérünk), és esetén mindkét végén csomópont van (ekkor forráson is 0 feszültséget mérünk), és 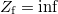 esetén mindkét végén duzzadóhely van. esetén mindkét végén duzzadóhely van.
|
A nagyfrekvenciás adat- vagy energiaátvitel nyilvánvalóan azt követeli meg, hogy a kábel végéről ne legyen visszaverődés. Az A. függelékben megmutatjuk, hogy ez akkor lép fel, amennyiben a lezáró impedanciára fennáll:
![\[ Z_{\text{l}}=Z_0\,, \]](/images/math/1/d/6/1d645ae2a5758b9be2e2e9eabed95f2b.png)
ahol 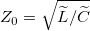 a vezeték hullámimpedanciája. Amennyiben ez a feltétel nem teljesül, akkor a visszavert és a kábel végére érkező hullámok amplitúdójának arányára fennáll:
a vezeték hullámimpedanciája. Amennyiben ez a feltétel nem teljesül, akkor a visszavert és a kábel végére érkező hullámok amplitúdójának arányára fennáll:
![\[ \Gamma=\frac{Z_{\text{l}}-Z_0}{Z_{\text{l}}+Z_0}, \]](/images/math/e/7/0/e70ce2a45531aa4098b85dbb1e85ffd7.png)
ahol 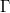 az ún. reflexiós tényező;
az ún. reflexiós tényező; 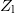 komplex értéke mellett
komplex értéke mellett 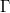 is komplex, ami azt fejezi ki, hogy a visszavert hullám fázisa nem többszöröse
is komplex, ami azt fejezi ki, hogy a visszavert hullám fázisa nem többszöröse 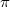 -nek. Vegyük észre, hogy a két fentebb tárgyalt határesetben,
-nek. Vegyük észre, hogy a két fentebb tárgyalt határesetben, 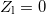 és
és 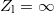 , amikor is maximális a reflexió
, amikor is maximális a reflexió 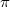 , ill. 0 fokos fázistolással visszavert hullámmal.
, ill. 0 fokos fázistolással visszavert hullámmal.
A leggyakrabban használt koaxiális kábelek hullámimpedanciája 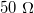 . Ez az érték megállapodásból született, és a 60-as évektől kezdve elterjedt ipari sztenderd lett. Néhány helyen találkozhatunk még
. Ez az érték megállapodásból született, és a 60-as évektől kezdve elterjedt ipari sztenderd lett. Néhány helyen találkozhatunk még 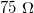 -os koaxiális kábelekkel is. Érdekességképp ezen értékek és az
-os koaxiális kábelekkel is. Érdekességképp ezen értékek és az 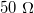 történeti hátteréről olvashatunk a B. függelékben.
történeti hátteréről olvashatunk a B. függelékben.
A DC és alacsony frekvenciájú (néhány kHz-es AC) eszközöknél megszokhattuk, hogy egy ideális feszültség forrás belső ellenállása 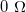 , míg ideális feszültségmérő bemenő ellenállása végtelen. A nagyfrekvenciás hálózatoknál minden mérőeszköz bemenő és kimenő ellenállása
, míg ideális feszültségmérő bemenő ellenállása végtelen. A nagyfrekvenciás hálózatoknál minden mérőeszköz bemenő és kimenő ellenállása 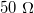 , mivel ekkora hullámimpedanciájú kábeleket csatlakoztatunk hozzájuk. Amennyiben egy adott hullámimpedanciájú vezetéket az ennek megfelelő ellenállással zárunk le, úgy nem alakulnak ki állóhullámok (hiszen nincs reflexió a végről), és a teljes vezeték hosszában azonos feszültséget mérhetünk.
, mivel ekkora hullámimpedanciájú kábeleket csatlakoztatunk hozzájuk. Amennyiben egy adott hullámimpedanciájú vezetéket az ennek megfelelő ellenállással zárunk le, úgy nem alakulnak ki állóhullámok (hiszen nincs reflexió a végről), és a teljes vezeték hosszában azonos feszültséget mérhetünk.
A lezáró impedancia
A kábelt lezáró impedancia megvalósításának egy érdekes esetét mutatja a 4.a ábra. Az áramkör sajátossága, hogy valós 50 Ω impedanciájú lezárást valósít meg, miközben nem tartalmaz jelentős rezisztív elemet a tekercs kis ellenállásán kívül. A 4.b ábra mutatja az áramkörben párhuzamosan kapcsolt 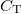 és
és  impedanciájának
impedanciájának 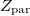 , valós és képzetes részeit
, valós és képzetes részeit 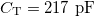 és
és 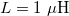 esetére, és feltettük, hogy a tekercsnek van egy kicsi, kb. 1 Ω-os valós ellenállása is. (A gyakorlaton használt vörösréz (
esetére, és feltettük, hogy a tekercsnek van egy kicsi, kb. 1 Ω-os valós ellenállása is. (A gyakorlaton használt vörösréz (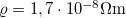 ) tekercsünk 0,5 m hosszú, 1 mm átmérőjű, ennek DC ellenállása 11 mΩ. 10 MHz-en a behatolási mélység 20 μm, ezért az ellenállása felmegy 130 mΩ-ra.) Az áramkör ezen részére 10 MHz-en az impedancia valós része 50 Ω, míg a képzetes rész nagy pozitív értékű (440 Ω), amit a sorba kötött
) tekercsünk 0,5 m hosszú, 1 mm átmérőjű, ennek DC ellenállása 11 mΩ. 10 MHz-en a behatolási mélység 20 μm, ezért az ellenállása felmegy 130 mΩ-ra.) Az áramkör ezen részére 10 MHz-en az impedancia valós része 50 Ω, míg a képzetes rész nagy pozitív értékű (440 Ω), amit a sorba kötött 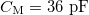 -os kondenzátorral tudunk kompenzálni. Így el tudjuk érni azt, hogy ez az áramkör valós 50 Ω impedanciájú lezárásnak tűnjön. Ezt az áramkört a magmágneses rezonancia spektroszkópiában használják rádiófrekvenciás pulzusok adás-vételére.
-os kondenzátorral tudunk kompenzálni. Így el tudjuk érni azt, hogy ez az áramkör valós 50 Ω impedanciájú lezárásnak tűnjön. Ezt az áramkört a magmágneses rezonancia spektroszkópiában használják rádiófrekvenciás pulzusok adás-vételére.
4. ábra: a) Rezisztív elemet nem tartalmazó áramkör, ami behangolható a kábel hullámimpedanciájára. A példánkban csak a 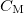 értékét változtatjuk. b) Az áramkörbeli párhuzamosan kapcsolt értékét változtatjuk. b) Az áramkörbeli párhuzamosan kapcsolt 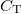 és és  rész impedanciájának, rész impedanciájának, 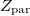 valós és képzetes része a frekvencia függvényében konkrét értékekre (a 10 MHz alatti rész 10 szeresre van nagyítva). Vegyük észre, hogy 10 MHz-en a képzetes rész nagy pozitív értékű miközben a valós rész 50 Ω. valós és képzetes része a frekvencia függvényében konkrét értékekre (a 10 MHz alatti rész 10 szeresre van nagyítva). Vegyük észre, hogy 10 MHz-en a képzetes rész nagy pozitív értékű miközben a valós rész 50 Ω.
|
Az 5. ábrán mutatjuk a 4.a ábra áramkörének reflexióját, 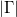 , a frekvencia függvényében a
, a frekvencia függvényében a
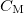 illesztő kondenzátor három értékére. Az optimálisan beállított
illesztő kondenzátor három értékére. Az optimálisan beállított 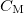 érték mellett a reflexió nullává válik.
érték mellett a reflexió nullává válik.
5. ábra: A bemutatott áramkörről történő reflexiós tényező, 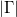 , a frekvencia függvényében a szövegben megadott paraméterekkel a , a frekvencia függvényében a szövegben megadott paraméterekkel a 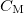 három értékére: optimális (36 pF), annál kisebb (20 pF), illetve nagyobb (65 pF). Utóbbi két esetet nevezik alul- , ill. túl-csatolt esetnek is. Vegyük észre, hogy a három értékére: optimális (36 pF), annál kisebb (20 pF), illetve nagyobb (65 pF). Utóbbi két esetet nevezik alul- , ill. túl-csatolt esetnek is. Vegyük észre, hogy a 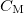 optimális értéke mellett a reflexió 0-vá válik egy adott frekvencián, míg egyébként véges értékű minden frekvencián. optimális értéke mellett a reflexió 0-vá válik egy adott frekvencián, míg egyébként véges értékű minden frekvencián.
|
Visszaverődések vizsgálata
A reflexiók jelenlétét kétféleképpen vizsgálhatjuk, a forrás kimenő feszültségének vizsgálatával és ún. duplexer segítségével. Az első esetben az oszcillátor forrás kimenetére BNC T elosztót teszünk, majd az így kettéosztott jelet küldjük egy hosszú (pl. 10-25 m) vezetékbe, egy rövidebb (pl. 0,5 m) BNC kábellel pedig egy oszcilloszkópra tesszük a jelet. Az oszcilloszkóp bemenetére is egy másik T-vel 50 Ω-os lezárást teszünk. A forrás frekvenciájának függvényében a hosszú vezeték lezárásának értékétől függően az oszcilloszkópon lévő jel nagysága változik. Ebből pl. a jel terjedési sebességét a kábelen vagy ennek ismeretében a kábel hosszát meg tudjuk határozni.
| 6. ábra: Az esetünkben használt duplexer, vagy hybrid magic tee (típusa Anzac HH107, 2-200 MHz) sematikus ábrája. A duplexeren a csatlakozók másképp helyezkednek el, mint ezen a sematikus ábrán, figyeljünk a jelölésekre! |
A duplexer egy általános fogalom, lényege, hogy lehetőséget ad arra, hogy egy forrásból egy kábel felé elküldött jelre meghatározhassuk a kábel felől reflektált feszültséget. Esetünkben a rádiófrekvenciás duplexer egy ún. hybrid magic tee, amit a 6. ábra mutat és működését a C. függelékben mutatjuk meg. A duplexer lényege, hogy pl. az  bemenetére adott feszültséget elosztja a
bemenetére adott feszültséget elosztja a  és
és  portok között, miközben a
portok között, miközben a  port felé a fázist is elforgatja. (A hybrid magic tee-re jellemző, hogy a portok között van egy kismértékű (10%) áthallás is.) A jel terjedési irányát megfordítva: az
port felé a fázist is elforgatja. (A hybrid magic tee-re jellemző, hogy a portok között van egy kismértékű (10%) áthallás is.) A jel terjedési irányát megfordítva: az  porton a
porton a  és
és  portokra adott feszültségek különbsége jelenik meg:
portokra adott feszültségek különbsége jelenik meg: 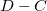 . A mi esetünkben a reflexiók vizsgálatára a hybrid magic tee használatakor
. A mi esetünkben a reflexiók vizsgálatára a hybrid magic tee használatakor  : a forrás,
: a forrás,  : az oszcilloszkóp CH1, 50 Ω-os lezárással,
: az oszcilloszkóp CH1, 50 Ω-os lezárással,  : a reflexióra bevizsgált kábel,
: a reflexióra bevizsgált kábel,  : az oszcilloszkóp másik bemenete 50 Ω-mal lezárva. Ha a
: az oszcilloszkóp másik bemenete 50 Ω-mal lezárva. Ha a  porton 0 feszültséget mérünk, akkor a bevizsgált kábelen nincs reflexió.
porton 0 feszültséget mérünk, akkor a bevizsgált kábelen nincs reflexió.
A Smith chart
Az ún. Smith chart egy gyakran használt grafikus segédeszköz a az áramkörök frekvenciafüggő tulajdonságainak vizsgálatára és a felmerülő problémák megoldására. A Smith chart-on többféle mennyiséget is megjeleníthetünk, mint pl. impedancia, admittancia, reflexiós tényező, állóhullámarány stb.
| 7. ábra: A kábelvégről történő reflexió esetén kapott Smith chart, a kör sugarának és a körív nevezetes pontjainak bejelölésével. Az ábrához tartozó kísérleti elrendezést is mutatjuk. A vízszintes és függőleges tengelyek a sugár egységeiben vannak mérve. |
A 7. ábrán mutatjuk a 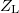 terhelő ellenállással lezárt kábelvégről történő reflexió esetén a reflexiós tényező képzetes részét a valós rész függvényében:
terhelő ellenállással lezárt kábelvégről történő reflexió esetén a reflexiós tényező képzetes részét a valós rész függvényében:
![\[ \Gamma=\frac{V_{\text{visszavert}}}{V_{\text{bejövõ}}}. \]](/images/math/f/f/d/ffd5f7af651bcca512d56182b7f39acd.png)
A kapott görbét a kábel  hossza parametrizálja, a nevezetes pontjait az ábrán bejelöltük, azaz amikor
hossza parametrizálja, a nevezetes pontjait az ábrán bejelöltük, azaz amikor  értéke a hullámhosszhoz képest megadott értékeket vesz fel. A kör sugara
értéke a hullámhosszhoz képest megadott értékeket vesz fel. A kör sugara 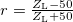 , itt a sugár előjeles mennyiségként értendő, tehát negatív előjel esetén a
, itt a sugár előjeles mennyiségként értendő, tehát negatív előjel esetén a 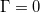 pontra tükröződik a kör. A reflexiós tényező valós és képzetes részeit a kábel végéről visszavert jel -- kiadott jelhez képesti -- fázisának mérésével kaphatjuk meg.
pontra tükröződik a kör. A reflexiós tényező valós és képzetes részeit a kábel végéről visszavert jel -- kiadott jelhez képesti -- fázisának mérésével kaphatjuk meg.
A 4.a ábrai áramkörrel történő lezárás esetére mutatjuk a reflexiós tényező képzetes részét a valós rész függvényében. Jól láthatóan kör alakul ki, aminek a frekvencia a paramétere. Az optimális (vagy kritikus) csatolás esetén a kör átmegy a Smith chart origóján.
| 8. ábra: A reflexiós tényező valós és képzetes részei ábrázolva egymás függvényében a 4.a áramkör esetére az impedanciaillesztés három esetére. A körök paramétere a frekvencia, aminek a határértékeit bejelöltük. |
A 8. ábrán a 4.a ábrai áramkörrel történő lezárás esetére mutatjuk a reflexiós tényező képzetes részét a valós rész függvényében. Jól láthatóan kör alakul ki, aminek a frekvencia a paramétere. Az optimális (vagy kritikus) csatolás esetén a kör átmegy a Smith chart origóján.
Mérési feladatok
A mérést két alkalomra bontva fogjuk elvégezni.
I. A kábelvégi reflexió vizsgálata (első mérési alkalom)
1. Oszcilloszkóppal
Itt oszcilloszkóppal mérjük meg a kábelvégi reflexió hatását a forrás kimenetére.
- 1. Vegyük fel oszcilloszkóp segítségével a nagyfrekvenciás jelgenerátor kimenetének feszültségét a lezáró impedancia három esetére (0, 50 Ω és szakadás) a frekvencia (0,001 MHz-15 MHz) függvényében a mérőprogrammal. (Segítség: BNC T a forrás kimenetén, egyik vége oszcilloszkópon minél rövidebb dróttal 50 Ω-mal lezárva, másik végén egy ismert hosszúságú BNC kábel, mérőeszköz leírás a D. függelékben. A forrás 2-es kimenetére triggereljük az oszcilloszkópot. A mérőprogramban a rflabor <startfreq> <stopfreq> <numberofpoints> paranccsal tudjuk a frekvencia változtatása mellett felvenni az oszcilloszkóp 1-es csatornáján mért jel nagyságát és az 1-es és 2-es csatornán mért jel egymáshoz viszonyított fázisát. A save paranccsal tudjuk elmenteni a mérésünk eredményét. A readscope paranccsal fel tudjuk venni az oszcilloszkópon éppen látható jelet.)
- 2. A kapott görbék segítségével határozzuk meg a kábelbeli jel terjedési sebességét. Ebből határozzuk meg a BNC kábelben lévő dielektrikum
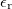 relatív dielektromos állandóját (
relatív dielektromos állandóját (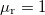 ), és írjuk le röviden, hogy a módszer hogyan használható egy elszakadt kábelban a szakadás helyének meghatározására.
), és írjuk le röviden, hogy a módszer hogyan használható egy elszakadt kábelban a szakadás helyének meghatározására.
2. Duplexerrel
Itt a hybrid magic tee (Tee a továbbiakban) segítségével vizsgáljuk a kábelvégi reflexiót. A vizsgált frekvenciatartomány: 2-20 MHz.
- 3. A Tee bekötése:
 - a forrás,
- a forrás,  - a oszcilloszkóp CH2 (trigger forrás), 50 Ω-os lezárással,
- a oszcilloszkóp CH2 (trigger forrás), 50 Ω-os lezárással,  - az oszcilloszkóp másik bemenete, CH1 50 Ω-mal lezárva. Ekkor a CH1 és CH2-n ellentétes fázisú jelet kell látunk, amit vegyünk is fel (readscope parancs)! A következő esetben:
- az oszcilloszkóp másik bemenete, CH1 50 Ω-mal lezárva. Ekkor a CH1 és CH2-n ellentétes fázisú jelet kell látunk, amit vegyünk is fel (readscope parancs)! A következő esetben:  - a forrás,
- a forrás,  - oszcilloszkóp CH2, 50 Ω-os lezárással,
- oszcilloszkóp CH2, 50 Ω-os lezárással,  - 50 Ω-mal lezárva,
- 50 Ω-mal lezárva,  - az oszcilloszkóp másik bemenete, CH1 50 Ω-mal lezárva. Ideális esetben ekkor 0 jelet kellene látnunk, azonban a duplexer tökéletlensége miatt mégis látunk egy kis jelet CH1-en, amit vegyünk is fel!
- az oszcilloszkóp másik bemenete, CH1 50 Ω-mal lezárva. Ideális esetben ekkor 0 jelet kellene látnunk, azonban a duplexer tökéletlensége miatt mégis látunk egy kis jelet CH1-en, amit vegyünk is fel!
- 4. A Tee segítségével vegyük fel a kábel végéről visszavert jel nagyságát a frekvencia függvényében (2-15 MHz), úgy mint az előző feladatban, de a
 -re a reflexióra bevizsgált kábelt helyezzük, rövidre zárva, lezáratlanul és 50 Ω-mal lezárva. Milyen az oszcilloszkóp CH1-en mért jele a frekvencia függvényében erre a három esetre és miért? (Segítség: a duplexer mindhárom esetben a visszavert jel nagyságát mutatja meg, ami nem interferál a forrás jelével. Ezért itt nem várjuk olyan állóhullámképek kialakulását mint az I/1/1. feladatban.) Vizsgáljuk meg, hogy 10 MHz-es frekvencián a CH1 csatornán látható jelhez képest hogyan változik CH2-n látható jel fázisa akkor, amikor a kábel végét rövidre zárjuk, vagy lezáratlanul hagyjuk. Ehhez vegyük fel e két esetre az oszcilloszkóp jelét!
-re a reflexióra bevizsgált kábelt helyezzük, rövidre zárva, lezáratlanul és 50 Ω-mal lezárva. Milyen az oszcilloszkóp CH1-en mért jele a frekvencia függvényében erre a három esetre és miért? (Segítség: a duplexer mindhárom esetben a visszavert jel nagyságát mutatja meg, ami nem interferál a forrás jelével. Ezért itt nem várjuk olyan állóhullámképek kialakulását mint az I/1/1. feladatban.) Vizsgáljuk meg, hogy 10 MHz-es frekvencián a CH1 csatornán látható jelhez képest hogyan változik CH2-n látható jel fázisa akkor, amikor a kábel végét rövidre zárjuk, vagy lezáratlanul hagyjuk. Ehhez vegyük fel e két esetre az oszcilloszkóp jelét!
Az első feladatban 1 kHz-15 MHz intervallumban vizsgáltuk a jelterjedést, a negyedikben, a duplexerrel a 2 MHz-15 MHz intervallumon. Mi miért szűkítettük a sávot? Az előző feladatot végezzük el az 1 kHz-15 MHz sávban is. Mit tapasztalunk?
3. Pulzus kábelvégi reflexiójának vizsgálata
- 5. A jelgenerátoron állítsunk be 1 MHz-es frekvenciájú szinusz jelet. A BURST megnyomása után beállítható, hogy a generátor e jel hány periódusát küldje ki milyen ismétlési idővel. Az I/2/4. mérési feladatbeli összeállítást használjuk fel arra, hogy a 25 m-es kábel végéről történő reflexiót megmérjük. Az oszcilloszkóp jelét vegyük fel, és a visszavert pulzus időkésésének tekintsük az összetartozó fázisú jelek közti időkülönbséget. Mit látunk a rövidzár, szakadás és 50 Ω-os lezárás eseteire? Az impulzus visszaverődési idejéből határozzuk meg a kábelbeli fénysebességet, és a kapott eredményt hasonlítsuk össze I/1/2. mérési feladat eredményével. Próbáljuk ki ugyanezt, ha nem szinusz, hanem négyszögjelet használunk, és az így kapott jelalakokat is vegyük fel! A szakadást tartalmazó koaxiális kábelen látott reflexióból számoljuk ki a szakadás helyzetét.
II. A lezáró impedancia vizsgálata (első alkalom)
- 6. A 4.a ábrán látható áramkört csatlakoztassuk a Tee segítségével a forrásra az eddigi ismeretek alapján úgy, hogy az áramkörről történő reflexiót vizsgálhassuk. Állítsuk be a
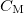 trimmer kondenzátor értékét úgy, hogy az áramkörről minimális legyen a reflexió egy adott frekvencián! Ekkor olyan reflexiós görbét kellene kapnunk mint amit az 5. ábrán mutatunk. Segítség: a multiméter segítségével állítsuk a
trimmer kondenzátor értékét úgy, hogy az áramkörről minimális legyen a reflexió egy adott frekvencián! Ekkor olyan reflexiós görbét kellene kapnunk mint amit az 5. ábrán mutatunk. Segítség: a multiméter segítségével állítsuk a 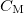 -et úgy, hogy kb. 30 pF-on legyen. (A forgókondenzátor a doboz hátoldalán levő banánhüvelyekhez van csatlakoztatva.) Ekkor látnunk kell egy reflexió minimumot 10 MHz körül. Közel erre a frekvenciára álljunk rá, és a jelgenerátor frekvenciája és a trimmer kondenzátor együttes állításával érjük el, hogy a minimális reflexió értéke kisebb legyen mint a minimumtól távoli frekvencián mért reflexió 10%-a! Alternatív, bár lassabb módszer az, ha folyamatosan a freqswe paranccsal felvesszük a reflexiót úgy, hogy közben a
-et úgy, hogy kb. 30 pF-on legyen. (A forgókondenzátor a doboz hátoldalán levő banánhüvelyekhez van csatlakoztatva.) Ekkor látnunk kell egy reflexió minimumot 10 MHz körül. Közel erre a frekvenciára álljunk rá, és a jelgenerátor frekvenciája és a trimmer kondenzátor együttes állításával érjük el, hogy a minimális reflexió értéke kisebb legyen mint a minimumtól távoli frekvencián mért reflexió 10%-a! Alternatív, bár lassabb módszer az, ha folyamatosan a freqswe paranccsal felvesszük a reflexiót úgy, hogy közben a 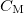 értékét változtatjuk, ekkor az 5. ábrán mutatottakhoz hasonló görbéket figyelhetünk meg.
értékét változtatjuk, ekkor az 5. ábrán mutatottakhoz hasonló görbéket figyelhetünk meg.
- 7. Vegyük fel az áramkörről reflektálódó jelet a frekvencia függvényében legfeljebb 1-2 MHz szélességben! Mérjük meg a
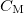 értékét. Számítsuk ki, hogy mekkora
értékét. Számítsuk ki, hogy mekkora 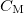 érték mellett lesz az áramkör impedanciája
érték mellett lesz az áramkör impedanciája 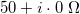 , és hasonlítsuk össze a két értéket. A tekercs és a párhuzamos kapacitás adatai az alkatrészeket tartalmazó dobozról leolvashatók.
, és hasonlítsuk össze a két értéket. A tekercs és a párhuzamos kapacitás adatai az alkatrészeket tartalmazó dobozról leolvashatók.
III. Szórt kapacitás mérése koaxiális kábelen (második alkalom)
| 9. ábra: Kábel szórt kapacitásának mérésére alkalmas összeállítás |
- 8. Egy koaxiális kábel két vezetője egy kis kapacitású kondenzátort alakít ki. Rakjuk össze a 9. ábrán látható kapcsolást egy rövid és egy 20 m-es koaxiális kábellel. A mérőprogram segítségével mérjük meg az átviteli karakterisztikáját több bemenő frekvenciára. Figyeljük meg, hogy a hosszabb kábel használata esetén a kapcsolás mint aluláteresztő szűrő viselkedik. Mérjük meg ugyanezt a két kábelt négyszögjelet használva. Figyeljük meg, hogy a felfutás ideje különbözik a két kábelre. A mérések eredményéből határozzuk meg a kábel hosszegységre eső kapacitását.
IV. Fénysebesség mérése szabad térben (második alkalom)
- 9. Rakjuk össze az adó egységet a függvénygenerátor és az adó antennaként használt tekercsből. A függvénygenerátoron állítsunk be egy négszögjelet. A függvénygenerátor másik kimenetére kössük a kb. 20 m-es kábellel az oszcilloszkóp egyik bemenetét. Az oszcilloszkóp másik bemenetére kössük a vevő antennát. A négyszögjel felfutásához és lefutásához kapcsolódó jelet mérünk a vevőnkkel.
- 10. Rögzítsük a jelet az adó és vevő közeli helyzete mellett, majd távolítsuk egymástól az adót és a vevőt, amennyire a kábelek engedik. Figyeljük meg, hogy a referencia és az antennával mért jel helyzete változik egymáshoz képest. Mérjük a meg az elmozdulás miatti eltolódás idejét és az adó és a vevő távolságát. A kapott értékekből számoljuk számoljuk az elektromágneses hullám szabadtéri terjedési sebességét.
Függelék
A. A reflexiós tényező származtatása
Korábban láthattuk, hogy a kábelen egy irányban haladó jelre a feszültség és áram aránya minden időpillanatban és a kábel minden helyén a 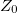 hullámimpedancia. Azonban amikor a kábel vége egy tetszőleges
hullámimpedancia. Azonban amikor a kábel vége egy tetszőleges 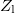 impedanciával van lezárva, akkor a lezáráson a feszültség és áram hányadosának ekkora értéket kell felvennie. Ezért alakul ki reflektált hullám, mert ez biztosítja, hogy a lezáráson ez a feltétel matematikailag fennálljon.
impedanciával van lezárva, akkor a lezáráson a feszültség és áram hányadosának ekkora értéket kell felvennie. Ezért alakul ki reflektált hullám, mert ez biztosítja, hogy a lezáráson ez a feltétel matematikailag fennálljon.
Vegyük fel úgy az  koordinátát, hogy a lezáráson legyen
koordinátát, hogy a lezáráson legyen 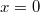 . Erre az esetre a távíróegyenletek megoldásai két egymással szemben terjedő haladó hullám mind a feszültségre mind az áramra, úgy, hogy a két iránybeli amplitúdók nem feltétlenül azonosak:
. Erre az esetre a távíróegyenletek megoldásai két egymással szemben terjedő haladó hullám mind a feszültségre mind az áramra, úgy, hogy a két iránybeli amplitúdók nem feltétlenül azonosak:
![\[ U(x)=U^+_0 e^{i(\omega t +k x)}+U^-_0 e^{i(\omega t -k x)}\\ I(x)=\frac{U^+_0}{Z_0} e^{i(\omega t +k x)}-\frac{U^-_0}{Z_0} e^{i(\omega t -k x)}, \]](/images/math/d/d/5/dd5a22ad4f1c46b7c3fbd3b7bba0d4cf.png)
ahol 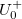 és
és 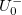 a lezárás felé, illetve attól távolodva haladó hullám. Vegyük észre az áram kifejezésében a második tag negatív előjelét, ami a távíróegyenletből adódik. Ennek a megoldásnak teljesítenie kell az
a lezárás felé, illetve attól távolodva haladó hullám. Vegyük észre az áram kifejezésében a második tag negatív előjelét, ami a távíróegyenletből adódik. Ennek a megoldásnak teljesítenie kell az 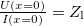 feltételt, azaz:
feltételt, azaz:
![\[ Z_{\textrm{l}}=\frac{U^+_0+U^-_0}{U^+_0-U^-_0} Z_0, \]](/images/math/7/1/5/7159dbf05afddbfdc74f1f7e72418ac2.png)
amiből adódik a visszavert hullám amplitúdójára:
![\[ U^-_0=\frac{Z_{\textrm{l}}-Z_0}{Z_{\textrm{l}}+Z_0} U^+_0. \]](/images/math/c/8/2/c829bdf3b75a5f9b719c1665329ae795.png)
Ebből közvetlenül adódik a korábbiakban bevezetett 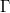 reflexiós tényező, ami a
reflexiós tényező, ami a 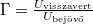 képlet szerint adódik.
képlet szerint adódik.
B. Érdekességek a témakörből
A kábelek impedanciaillesztésének szerepe
A reflexiókat kábelvégi szakadások vizsgálatára lehet felhasználni. Kémregényekben ezzel a módszerrel vizsgálják meg, hogy egy kábelra valaki rámért-e, illetve azt is meg lehet vele határozni, hogy hol történt a rámérés. A mérés lényege, hogy akármennyire is kis perturbációként történik meg a kábelra a rámérés, az meg fogja változtatni egy adott ponton a vezeték hullámimpedanciáját, ami a kábelról történő reflexió megváltozásához vezet. A rámérés helye a frekvenciafüggő reflexiós együtthatóból határozható meg.
A fizikában semmi sem véletlen: ha két fizikai állandóból származtatható egy adott dimenziójú harmadik állandó, akkor annak legtöbbször van valami fizikai tartalma. Így van ez pl. a fluxuskvantummal (h/2e), vagy a Bohr-magnetonnal (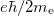 ), melyek a megfelelő fizikai mennyiségek kvantumai. Ismert a
), melyek a megfelelő fizikai mennyiségek kvantumai. Ismert a 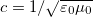 összefüggés, ami a fénysebesség és az elektromágneses egységek kapcsolatát írja le. Hasonlóan, a
összefüggés, ami a fénysebesség és az elektromágneses egységek kapcsolatát írja le. Hasonlóan, a 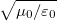 mennyiségnek is van fizikai tartalma. Ennek dimenziója Ohm, értéke kb. 377 Ω és a vákuum impedanciájának nevezzük.
mennyiségnek is van fizikai tartalma. Ennek dimenziója Ohm, értéke kb. 377 Ω és a vákuum impedanciájának nevezzük.
A vákuum hullámimpedancia fizikai jelentése a következő. Az elektromos és mágneses térerősségek hányadosából vákuumban terjedő elektromágneses sugárzásra:  ez azt jelenti, hogy a vákuumba kisugárzó és onnan vevő antennáknak ilyen impedanciával kell ideálisan rendelkeznie. Másfelől ez az összefüggés, összehasonlítva a koaxiális kábelekkel azt jelenti, hogy utóbbiban kisebb az elektromos tér nagysága a mágneseshez képest mint a szabad térben terjedő elektromágneses sugárzás, ennek elsődleges oka, hogy a koaxiális kábelekben
ez azt jelenti, hogy a vákuumba kisugárzó és onnan vevő antennáknak ilyen impedanciával kell ideálisan rendelkeznie. Másfelől ez az összefüggés, összehasonlítva a koaxiális kábelekkel azt jelenti, hogy utóbbiban kisebb az elektromos tér nagysága a mágneseshez képest mint a szabad térben terjedő elektromágneses sugárzás, ennek elsődleges oka, hogy a koaxiális kábelekben 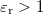 (tipikusan 2,5 körüli).
(tipikusan 2,5 körüli).
Láttuk a bevezetőben, hogy a jelterjedés számára előnyös a koaxiális kábelek használata, azonban néhány helyen, pl. audiotechnikában, távközlésben találkozunk egyéb preferált impedanciákkal pl. 8, 150, vagy 600 Ω. Mindezeknek történeti háttere van, pl. a 600 Ω oka, hogy a hagyományos, nem koaxiális távíró vonalaknak (két rézdrót egymástól 1 láb távolságra) ekkora volt a hullámimpedanciája. Az első távolsági telefonok ezeket a vezetékeket használták, ezért egy időben a 600 Ω volt a távközlési sztenderd. Később a csavart rézdrótpár terjedt el aminek 150 Ω a hullámimpedanciája. Napjainkban igen elterjedt az ún. UTP (unshielded twisted pair) kábel a számítógépes hálózati alkalmazásokhoz, melynek 100 Ω a hullámimpedanciája.
A koaxiális kábelek elterjedésével felmerült a kérdés, hogy melyik hullámimdepancia legyen a sztenderd. Érdekes módon erre nem kapunk egyértelmű választ, több forrásból merítve ([1], [2],[3],[4]) a következő történetet találjuk.
A hullámimpedancia három egymástól független, technikailag fontos paraméterben jelenik meg: a maximális teljesítményátvitelben (optimális ha 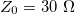 ), a nagyfeszültségű elektromos letörés maximumában (optimális ha
), a nagyfeszültségű elektromos letörés maximumában (optimális ha 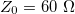 ), és az átvitt jel veszteségének minimumában (optimális ha
), és az átvitt jel veszteségének minimumában (optimális ha 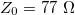 ). A korai (1920-as évek) rádiófrekvenciás gyakorlatban a források teljesítménye alacsony volt, ezért a 77 Ω-os kábelek terjedtek el. Mivel nem léteztek jó és rugalmas dielektrikumok, ezért a vezetékek két egymásba helyezett koaxiális csőből álltak, melyeket levegő töltött ki.
). A korai (1920-as évek) rádiófrekvenciás gyakorlatban a források teljesítménye alacsony volt, ezért a 77 Ω-os kábelek terjedtek el. Mivel nem léteztek jó és rugalmas dielektrikumok, ezért a vezetékek két egymásba helyezett koaxiális csőből álltak, melyeket levegő töltött ki.
50 Ω-os vezetéket kapunk ha egy 3/4 colos rézcsövet egy 2 colos rézcsőbe helyezünk (mindkettő elterjedt méret az USA-ban), ezért ez a megoldás az 1930-as évektől elterjedt a nagyteljesítményű rádiófrekvenciás adások kisugárzására. Amikor egy 77 Ω-os vezetéket feltöltünk polietilénnel (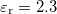 ) akkor az impedanciája 51 Ω lesz, ami szintén az 50 Ω felé mutat. Egy másik szempont az, hogy a két fent emlitett érték, 30 és 77 Ω, számtani közepe 53,5 Ω, mértani közepe 48 Ω, ezért az 50 Ω egy jó kompromisszum a veszteség és teljesítményátvitel között: ugyanazzal a kábellel tudunk nagyenegeriájú jelet adni és venni. Egy érdekes szempont még az, hogy egy koaxiális kábel amire a belső vezető és külső árnyékolás átmérőjének aránya ránézésre "szép", kb. 50 Ω-os hullámimpedanciájú lesz.
) akkor az impedanciája 51 Ω lesz, ami szintén az 50 Ω felé mutat. Egy másik szempont az, hogy a két fent emlitett érték, 30 és 77 Ω, számtani közepe 53,5 Ω, mértani közepe 48 Ω, ezért az 50 Ω egy jó kompromisszum a veszteség és teljesítményátvitel között: ugyanazzal a kábellel tudunk nagyenegeriájú jelet adni és venni. Egy érdekes szempont még az, hogy egy koaxiális kábel amire a belső vezető és külső árnyékolás átmérőjének aránya ránézésre "szép", kb. 50 Ω-os hullámimpedanciájú lesz.
Az 50 Ω elterjedtsége ellenére találunk még gyenge videójelek átvitelénél 75 Ω-os kábelt, ami a veszteségre optimális, illetve 93 Ω-os kábelt pl. számítógép és monitorok összekötésére. A 93 Ω-os hullámimpedanciájú kábelnél a hosszegységre eső kapacitás a legalacsonyabb, ezért ennek a nagyfrekvenciás levágási frekvenciája a legnagyobb. Emiatt a négyszögjelek is jobban, torzításmentesen kerülnek átvitelre.
Egyéb példák impedanciaillesztésre, mechanika és optikai területéről
Impedanciaillesztéssel nem csak kábelekben terjedő elektromágneses hullámok, hanem fény és hanghullámok esetén is találkozhatunk. Hanghullámok terjedésekor nagyon különböző törésmutatójú közegek határára érkezve a hanghullámok visszaverődnek, ahelyett, hogy áthaladnának. Az orvosi ultrahangos vizsgálatokban használt zselé tölti be azt a szerepet, hogy az emberi test és a hanghullámot adó berendezés között illeszti az impedanciát. A bizonyos hangszereken található tölcsér és a hangszórók geometriai kialakítása is a hangadó és a környező levegő közötti impedancia illesztést végzik.
Az egyik sokat vizsgált mechanikai példánkban, két test rugalmas ütközésekor, a maximális energiaátadás a két test között akkor történik meg, amikor a két test tömege egyenlő. Ez is felfogható, mint "mechanikai impedancia illesztés".
Optikai problémáknál azt találjuk, hogy a fény visszaverődik olyan közegek határáról, melyek törésmutatója nem azonos. A törésmutató,  , reciprokát azonosíthatjuk az optikai vagy hullámimpedanciával:
, reciprokát azonosíthatjuk az optikai vagy hullámimpedanciával: 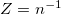 . Az
. Az 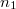 törésmutatójú közegből
törésmutatójú közegből 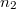 törésmutatójú közegbe haladó hullámra a reflektált hullám amplitúdójára azt kapjuk, hogy
törésmutatójú közegbe haladó hullámra a reflektált hullám amplitúdójára azt kapjuk, hogy 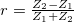 . Ezt az összefüggést az optikában Fresnel-egyenletekként ismerik. Egy hétköznapi példája a szemüvegek lencséjéről történő reflexió (csillogás) ami megfelelő, ún. antireflex burkolattal szüntethető meg. Ebben az esetben az antireflex réteg végzi az impedanciaillesztés szerepét.
. Ezt az összefüggést az optikában Fresnel-egyenletekként ismerik. Egy hétköznapi példája a szemüvegek lencséjéről történő reflexió (csillogás) ami megfelelő, ún. antireflex burkolattal szüntethető meg. Ebben az esetben az antireflex réteg végzi az impedanciaillesztés szerepét.
C. A rádiófrekvenciás duplexer
C1. ábra: Az esetünkben használt rádiófrekvenciás duplexer megvalósítása. A fekete pontok a transzformátorok tekercsein az azonos fázisban lévő pontokat mutatják. Vegyük észre, hogy a menetszámok aránya nem 1:1, hanem minél jobban megközelíti az 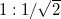 arányt. arányt.
|
A rádiófrekvenciás duplexer megvalósításának sémáját a C1. ábrán mutatjuk. Lényege, hogy a feszültségeket ferritmagos transzformátorokkal választjuk a portok között szét, vagy éppenséggel egyesítjük két port bemenő jelét. A transzformátorok tulajdonsága alapján az egyes portokon mérhető feszültségek között a következő összefüggések adódnak:
![\[ V_{\text{A}}=\left(V_{\text{D}}-V_{\text{C}}\right)/\sqrt{2}\\ V_{\text{B}}=\left(V_{\text{C}}+V_{\text{D}}\right)/\sqrt{2}\\ V_{\text{C}}=\left(V_{\text{B}}-V_{\text{A}}\right)/\sqrt{2}\\ V_{\text{D}}=\left(V_{\text{A}}+V_{\text{B}}\right)/\sqrt{2}. \]](/images/math/3/0/3/303252e587c00c3a53e8c8f3086fd034.png)
Látható, hogy ezen feszültségek közötti összefüggések éppen annak a sematikának felelnek meg, amit a 6. ábrán mutatunk. Tehát pl. a  port feszültsége az
port feszültsége az  és
és  portok feszültségeinek különbsége. Az energiamegmaradást megvizsgálva azt láthatjuk, hogy ha pl.
portok feszültségeinek különbsége. Az energiamegmaradást megvizsgálva azt láthatjuk, hogy ha pl.  és
és  portokon érkezik be jel, akkor az a
portokon érkezik be jel, akkor az a  és
és  portok között oszlik el, de nem egyenlően hanem attól függő intenzitás aránnyal, hogy a két jel fáziskülönbsége mekkora egymáshoz képest. Ha a fáziskülönbség éppen
portok között oszlik el, de nem egyenlően hanem attól függő intenzitás aránnyal, hogy a két jel fáziskülönbsége mekkora egymáshoz képest. Ha a fáziskülönbség éppen 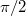 , akkor az intenzitások egyenlően oszlanak el.
, akkor az intenzitások egyenlően oszlanak el.
D. A mérőeszközök használata
Tektronix oszcilloszkóp. A digitális oszcilloszkóp alapvető használatát ismertnek tételezzük fel. A TRIGGER gomb megnyomása után választható ki a csatorna, amire triggerelünk (kijelző alatti gombokkal érhető el a trigger menü almenüje), a VERTICAL MENU-ben a kijelzőtől jobbra elhelyezett gombokkal tudjuk a megfelelő kijelzett csatornákat beállítani. Célszerű a forrásból kijövő referencia jelre triggerelni, vagy a duplexerrel történő méréseknél a duplexer referencia (általában  ) kimenetére. Az oszcilloszkóppal akkor tudjuk a lehető legkisebb hibával megmérni a feszültséget ha a mérendő jel éppen kitölti a képernyőt, vagy annál kis mértékben (maximum 20%) nagyobb. A frekvenciabeállítás akkor optimális ha a szinuszos jel néhány (2-5) periódusát látjuk.
) kimenetére. Az oszcilloszkóppal akkor tudjuk a lehető legkisebb hibával megmérni a feszültséget ha a mérendő jel éppen kitölti a képernyőt, vagy annál kis mértékben (maximum 20%) nagyobb. A frekvenciabeállítás akkor optimális ha a szinuszos jel néhány (2-5) periódusát látjuk.
Siglent SDG1025 jelgenerátor. A megfelelő jelalak az erre dedikált funkciógombokkal érhetőek el. A függvény paraméterei (frequency, amplitude stb.) a kijelző melletti gombok megnyomása után megadható. A két csatorna közti váltást a CH1/2 gombbal tudjuk megtenni. A beállított jelalak kimeneten való megjelenítéséhez a kimeneti csatlakozók feletti OUTPUT gombokat kell megnyomni.
A mérőprogram. A Desktopon lévő RF\_Labor.Ink nevű parancsikont elindítva a program menüsora alatt találunk egy parancssort (command line) ahová az rflabor, readscope vagy save parancsokat írhatjuk be.
Az rflabor paranccsal mérhetjük meg a frekvencia sweepet. A program beállítja a generátort a megfelelő értékekre, majd mindig kiolvassa az oszcilloszkóp 1-es csatornájára kötött jel nagyságát, majd az 1-es és 2-es csatorna közti fáziskülönbséget. A parancs elindításához 3 paraméter szüksége, melyeket egy szünettel kell elválasztani: a kezdő frekvencia, a végső frekvencia és a mérési pontok száma.
A readscope paranccsal beolvashatjuk az oszcilloszkóp által mért jelalakot.
Az save paranccsal elmenthetjük a mérésünk eredményeit egy ASCII fájlba.
E. A mérőkód
A mérőkód C# nyelven készült el a Visual Studio 2013-as verzióját használva. A program USB porton keresztül VISA protokolt használva kommunikál a mérőműszerekkel. A VISA protokoll használatakor rövid szöveges parancsokat adunk a műszereknek, amik szintén szöveges üzenetekkel válaszolnak. Példának következik az oszcilloszkópot kiolvasó függvény kódja:
A mérőkód C# nyelven készült el a Visual Studio 2013-as verzióját használva. A program USB porton keresztül VISA protokolt használva kommunikál a mérőműszerekkel. A VISA protokoll használatakor rövid szöveges parancsokat adunk a műszereknek, amik szintén szöveges üzenetekkel válaszolnak. Példának következik az oszcilloszkópot kiolvasó függvény kódja:
public static Curve read() { Curve r = new Curve(); double ch1scale = double.Parse(VISA.Query(VISAaddress, "CH1:SCAL?")); double ch1offset = double.Parse(VISA.Query(VISAaddress, "CH1:POS?")); double ch2offset = double.Parse(VISA.Query(VISAaddress, "CH2:POS?")); double ch2scale = double.Parse(VISA.Query(VISAaddress, "CH2:SCAL?")); double timebase = double.Parse(VISA.Query(VISAaddress, "HOR:MAI:SCALE?")); double timeoffset = double.Parse(VISA.Query(VISAaddress, "HOR:MAI:POS?")); VISA.Write(VISAaddress, "DATA:SOURCE CH1"); VISA.Write(VISAaddress, "DATA:ENC ASCII"); VISA.Write(VISAaddress, "DATA:WIDTH 1"); VISA.Write(VISAaddress, "DATA:START 1"); VISA.Write(VISAaddress, "DATA:STOP 25000"); string instring1 = VISA.Query(VISAaddress, "CURV?"); VISA.Write(VISAaddress, "DATA:SOURCE CH2");\\ string instring2 = VISA.Query(VISAaddress, "CURV?"); string[] ch1strings = instring1.Split(','); string[] ch2strings = instring2.Split(','); for (int i = 0; i < ch1strings.Length; i++) r.Add(\\ (double)i / (ch1strings.Length) * timebase * 10 + timeoffset - 5 * timebase, (double.Parse(ch1strings[i]) - ch1offset * 25) / 25 * ch1scale, (double.Parse(ch2strings[i]) - ch2offset * 25) / 25 * ch2scale ); return r; }