„Spektrumanalízis szerkesztőlap” változatai közötti eltérés
(→A zaj definíciója) |
(→A zaj definíciója) |
||
| (egy szerkesztő 6 közbeeső változata nincs mutatva) | |||
| 25. sor: | 25. sor: | ||
A fenti mennyiség abszolútérték négyzete pedig nem más, mint a mért jel teljesítményspektruma (''Power Spectrum''): | A fenti mennyiség abszolútérték négyzete pedig nem más, mint a mért jel teljesítményspektruma (''Power Spectrum''): | ||
| − | $$PS=|f_W(\omega)|^2=|\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t|^2 | + | $$PS=|f_W(\omega)|^2=|\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t|^2.$$ |
| 33. sor: | 33. sor: | ||
</wlatex> | </wlatex> | ||
| − | ==A zaj definíciója== | + | ===A zaj definíciója=== |
<wlatex> | <wlatex> | ||
| − | Egy $V(t)$ időben fluktuáló zaj jellegű (azaz széles frekvenciaspektrumú) jelet egy $f_0$ középfrekvencia körüli $\Delta f$ szélességű sávszűrűn keresztül vizsgálva azt találjuk, hogy a szűrt jel szórásnégyzete arányos a frekvenciatartomány $\Delta f$ szélességével, az arányossági tényező a feszültségzaj spektrális sűrűsége (spectral density of noise), azaz a teljesítmény spektrális sűrűsége (Power | + | Egy $V(t)$ időben fluktuáló zaj jellegű (azaz széles frekvenciaspektrumú) jelet egy $f_0$ középfrekvencia körüli $\Delta f$ szélességű sávszűrűn keresztül vizsgálva azt találjuk, hogy a szűrt jel szórásnégyzete arányos a frekvenciatartomány $\Delta f$ szélességével, az arányossági tényező a feszültségzaj spektrális sűrűsége (spectral density of noise), azaz a teljesítmény spektrális sűrűsége (Power Spectral Density - PSD): |
$$\left\langle (\Delta V(t|f_0,\Delta f))^2 \right\rangle=s_V(f_0)\Delta f.$$ | $$\left\langle (\Delta V(t|f_0,\Delta f))^2 \right\rangle=s_V(f_0)\Delta f.$$ | ||
| 51. sor: | 51. sor: | ||
$$C(0)=\langle(\Delta V(t))^2 \rangle.$$ | $$C(0)=\langle(\Delta V(t))^2 \rangle.$$ | ||
Most fejezzük ki a korrelációs függvényt a Fourier-transzformáltja segítségével: | Most fejezzük ki a korrelációs függvényt a Fourier-transzformáltja segítségével: | ||
| − | $$ | + | $$C(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega e^{i\omega t}c(\omega).$$ |
Ez alapján a feszültség szórásnégyzete: | Ez alapján a feszültség szórásnégyzete: | ||
| 58. sor: | 58. sor: | ||
mivel $c(\omega)=c(-\omega)$. | mivel $c(\omega)=c(-\omega)$. | ||
| − | Másrészt a | + | Másrészt a szórásnégyzet és a zaj közötti összefüggésből következik: |
$$\langle(\Delta V(t))^2 \rangle=\frac{1}{2\pi} \int_{0}^{\infty} d\omega s_V(\omega).$$ | $$\langle(\Delta V(t))^2 \rangle=\frac{1}{2\pi} \int_{0}^{\infty} d\omega s_V(\omega).$$ | ||
| 87. sor: | 87. sor: | ||
Innen könnyen kifejezhető a zaj teljesítménysűrűsége, felhasználva, hogy az a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese. | Innen könnyen kifejezhető a zaj teljesítménysűrűsége, felhasználva, hogy az a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese. | ||
| − | $$s_V(\omega)=\lim\limits_{T->\infty} \frac{2}{T}\left\langle | + | $$s_V(\omega)=\lim\limits_{T->\infty} \frac{2}{T}\left\langle |\int_{-T/2}^{T/2} dt \Delta V(t)e^{-i\omega t}|^2\right\rangle.$$ |
A mérésünk során diszkrét pontokon történik a mintavételezés, így ugyanez a számolás DFT segítségével a következő módon fejezhető ki: | A mérésünk során diszkrét pontokon történik a mintavételezés, így ugyanez a számolás DFT segítségével a következő módon fejezhető ki: | ||
| − | $$s_V(\omega)\approx\frac{2}{N\Delta t} | + | $$s_V(\omega)\approx\frac{2}{N\Delta t}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}\Delta t|^2=\frac{2\Delta t}{N}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}|^2.$$ |
A fentiekben sikerült megállapítanunk, hogy a vizsgált $\Delta V(t)$ jel Fourier-transzformáltjából hogyan számolható a zaj spektrális sűrűsége. Azonban ennél a számolásnál nem vettünk figyelembe ablakfüggvényt, vagy fogalmazhatunk úgy is, hogy téglalap ablakkal számoltunk. | A fentiekben sikerült megállapítanunk, hogy a vizsgált $\Delta V(t)$ jel Fourier-transzformáltjából hogyan számolható a zaj spektrális sűrűsége. Azonban ennél a számolásnál nem vettünk figyelembe ablakfüggvényt, vagy fogalmazhatunk úgy is, hogy téglalap ablakkal számoltunk. | ||
| 113. sor: | 113. sor: | ||
$$\langle|\Delta v_W(\omega)|^2\rangle=\frac{s_0}{2}\int_{-\infty}^{\infty}W^2(t)dt.$$ | $$\langle|\Delta v_W(\omega)|^2\rangle=\frac{s_0}{2}\int_{-\infty}^{\infty}W^2(t)dt.$$ | ||
| − | Azaz a | + | Azaz a zajsűrűség számolása: |
$$s_0=\frac{2\langle|v_W(\omega)|^2\rangle}{\int_{-\infty}^{\infty}W^2(t)dt}.$$ | $$s_0=\frac{2\langle|v_W(\omega)|^2\rangle}{\int_{-\infty}^{\infty}W^2(t)dt}.$$ | ||
| 123. sor: | 123. sor: | ||
A zajsűrűség Hanning-ablakot használva: | A zajsűrűség Hanning-ablakot használva: | ||
| − | $$s_0=\frac{ | + | $$s_0=\frac{4\langle|v_W(\omega)|^2\rangle}{3T}.$$ |
Diszkrét mérési pontok esetén a következőképpen módosul a kifejezés: | Diszkrét mérési pontok esetén a következőképpen módosul a kifejezés: | ||
| − | $$s_0\approx\dfrac{2}{\sum_{n=0}^{N-1}W^2(n\Delta t)\Delta t} | + | $$s_0\approx\dfrac{2}{\sum_{n=0}^{N-1}W^2(n\Delta t)\Delta t}|\sum_{n=0}^{N-1}W(n\Delta t) V(N\Delta t)e^{-i\omega n\Delta t}\Delta t|^2.$$ |
Hanning-ablakkal számolva: | Hanning-ablakkal számolva: | ||
| − | $$s_0\approx\frac{ | + | $$s_0\approx\frac{4\Delta t}{3N}|\sum_{n=0}^{N-1}W(n\Delta t)\Delta V(n\Delta t)e^{-i\omega n\Delta t}|^2.$$ |
| − | Így frekvenciafüggetlen zajsűrűségek esetén sikerült meghatározni, hogy a mérési pontokból miképpen számolható ki a zaj spektrális sűrűsége. | + | Így frekvenciafüggetlen zajsűrűségek esetén sikerült analitikusan meghatározni, hogy a mérési pontokból miképpen számolható ki a zaj spektrális sűrűsége. |
</wlatex> | </wlatex> | ||
A lap jelenlegi, 2018. május 16., 21:32-kori változata
Fourier-transzformáció
Egy időben változó jel spektrumát a Fourier-transzformáció segítségével ismerhetjük meg.
![\[f(\omega)=\int_{-\infty}^{\infty}F(t)e^{-i\omega t}dt.\]](/images/math/8/5/e/85ef324eb4aa203303778f249b1a850f.png)
Azonban mivel a mérést véges időintervallumban végezzük a spektrum felbontása nem tökéletes. A véges ideig mért jel spektrumára gyakorlatilag úgy tekinthetünk, mintha az a T ideig mért jel periodikus kiterjesztésének a spektruma lenne. Ha a mért jelünk a T időablakban nem periodikus, akkor a periodikusan kiterjesztett jel az időablak határain ugrásokat mutathat, melyek miatt fals nagyfrekvenciás komponensek jelennek meg a spektrumban. Ezen probléma kiküszöbölésére olyan ablakfüggvények használatára van szükség, amelyek a mérési intervallum szélén eltűnnek. A Fourier-transzformációt tehát a vizsgált jel és az ablakfüggvény szorzatán végezzük
![\[f_W(\omega)=\int_{-\infty}^{\infty}W(t)F(t)e^{-i\omega t}dt,\]](/images/math/3/5/8/358e08414d5fd63a56b0bd3f383c0404.png)
ahol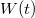 
súlyfüggvény egy T időablakon kívül zérus.
Két függvény szorzata a Fourier-térben a függvények Fourier-transzfor-máltjának konvolúciójával egyezik meg:
![\[f_W(\omega)=\int_{-\infty}^{\infty}f(\omega')w(\omega-\omega')\frac{d\omega'}{2\pi},\]](/images/math/3/b/b/3bbabc3324c3fcc7a2837a36d2369ce3.png)
azaz a spektrum 
frekvenciájához az ablakfüggvény bekever jelet az 
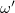frekvenciából is. Ezt a jelenséget spektrális szivárgásnak nevezzük.
DFT, FFT
A gyakorlati spektrumanalizáláshoz nem csak a véges időintervallumban végzett mérést kell figyelembe venni, hanem azt is, hogy a mért jelet nem folytonosan, hanem diszkrét pontokon mintavételezzük.
Az ablakfüggvénnyel szorzott jel integrálját ennek megfelelően egy diszkrét összeggel közelítjük:
![\[f_W(\omega)=\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t,\]](/images/math/8/1/e/81e072541760e95c8c13a9926ef052ec.png)
ahol 
a két diszkrét mintavételezés között eltelt idő (a mérési idő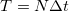 
). A diszkrét Fourier-transzformáció (DFT) tehát a diszkrét pontokon felvett függvény spektrumát adja meg.A Nyquist-Shannon mintavételezési törvény értelmében mintavételezési idővel legfeljebb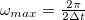 
maximális frekvenciáig lehetséges a jel rekonstrukciója.
A fenti mennyiség abszolútérték négyzete pedig nem más, mint a mért jel teljesítményspektruma (Power Spectrum):
![\[PS=|f_W(\omega)|^2=|\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t|^2.\]](/images/math/5/0/f/50f366f3f72a866eebfab2a5c8074cc3.png)
Nem csak a mintavételezés történik diszkrét időnként, hanem a DFT kiszámítása is diszkrét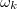 
értéken valósul meg. A diszkrét Fourier-transzformáció műveletigénye egyszerű "brute force" eljárással N frekvencia pont esetén 
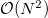műveletet igényel. Ez rendkívül időigényes, ezért egy más számítási algoritmust használnak a szoftverek a jel feldolgozásához. Ez a gyors Fourier-transzformáció (FFT), amelynek működési alapelve, hogy a mintát kettéválasztja páros és páratlan pontokra, így az N pontos DFT két N/2 pontos DFT-re bomlik. Ezt követően ezeket tovább felezi, és azokat is tovább, stb. Ehhez természetesen szükséges, hogy a mérési pontok száma kettő hatványa legyen. Könnyen belátható, hogy ennek az algoritmusnak a műveletigénye 
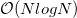nagyságrendű. Az FFT algoritmus az 
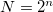adatpontból álló jel Fourier-spektrumát 
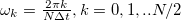diszkrét körfrekvenciapontokon adja meg.
Most a DFT definiálását követően megvizsgálhatjuk az ablakfüggvények különböző tulajdonságát. Tételezzük fel, hogy egy egykomponensű 
jelet vizsgálunk. Könnyen belátható, hogy ha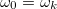 
bármelyik értékére, akkor a spektrális szivárgás nulla lesz. Ez pontosan annak felel meg, amikor a jelünk a T időablakban periodikus. Azonban az esetek többségében értelemszerűen ez nem teljesül. Ekkor a spektrális szivárgáson kívül romlik a jel frekvenciafelbontása és amplitúdópontossága is. Ez előbbi a centrális csúcs keskenységével jellemezhető, míg az utóbbinál éppen ellenkezőleg arra van szükség, hogy megfelelően lapos legyen az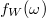 
jelünk környékén.
A zaj definíciója
Egy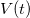 
időben fluktuáló zaj jellegű (azaz széles frekvenciaspektrumú) jelet egy 
középfrekvencia körüli 
szélességű sávszűrűn keresztül vizsgálva azt találjuk, hogy a szűrt jel szórásnégyzete arányos a frekvenciatartomány szélességével, az arányossági tényező a feszültségzaj spektrális sűrűsége (spectral density of noise), azaz a teljesítmény spektrális sűrűsége (Power Spectral Density - PSD):
![\[\left\langle (\Delta V(t|f_0,\Delta f))^2 \right\rangle=s_V(f_0)\Delta f.\]](/images/math/f/c/e/fcef50d6c156742a0f491cc490623688.png)
Ez a zaj kísérleti definíciója. A feszültség szórásnégyzete a zajsűrűség teljes frekvenciatartományra vett integráljával egyenlő.
![\[\langle(\Delta V(t))^2 \rangle=\int_{0}^{\infty} df s_V(f).\]](/images/math/4/e/5/4e5f54e003163e2b26ac0e5c132ede8d.png)
Ez a képlet közvetlenül is használható a zajspektrum kísérleti meghatározásához, azonban emellett jó kiindulópontként szolgál más fizikai mennyiségekkel való kapcsolatának vizsgálatára is. Érdemes megvizsgálni a zajsűrűség és a feszültség korrelációs függvény kapcsolatát. Ez utóbbi a következőképpen definiálható:
![\[C(\Delta t)=\langle\Delta V(t)\cdotp\Delta V(t+\Delta t) \rangle=\lim\limits_{T\rightarrow\infty}\frac{1}{T}\int_{0}^{T}dt\Delta V(t)\cdotp\Delta V(t+\Delta t).\]](/images/math/2/2/4/2249b4df683368d4b8351cadfb3df188.png)
Könnyen belátható, hogy a korrelációs függvény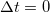 
-ban megegyezik a feszültség szórásnégyzetével.
![\[C(0)=\langle(\Delta V(t))^2 \rangle.\]](/images/math/a/b/5/ab573547effc08d355afcf78edbf2b69.png)
Most fejezzük ki a korrelációs függvényt a Fourier-transzformáltja segítségével:
![\[C(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega e^{i\omega t}c(\omega).\]](/images/math/9/2/d/92d0898595e749cda299df5939826fab.png)
Ez alapján a feszültség szórásnégyzete:
![\[\langle(\Delta V(t))^2 \rangle=C(0)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega c(\omega)=\frac{1}{\pi}\int_{0}^{\infty}d\omega c(\omega),\]](/images/math/1/e/f/1eff86c194f06c16f8941773197552b2.png)
mivel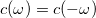 
.
Másrészt a szórásnégyzet és a zaj közötti összefüggésből következik:
![\[\langle(\Delta V(t))^2 \rangle=\frac{1}{2\pi} \int_{0}^{\infty} d\omega s_V(\omega).\]](/images/math/7/9/7/7975f3b4b9d91fc7591790411d47208e.png)
Az utóbbi két egyenletből látható, hogy a zaj teljesítménysűrűsége a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese.
Sikerült kapcsolatot teremteni a zajsűrűség és a feszültség korrelációs függvény között. Most vizsgáljuk meg a feszültség korrelációs függvény és a feszültség mint mérhető fizikai mennyiségek kapcsolatát. A feszültség átlagtól való eltérésének (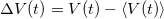
) a Fourier-transzformáltja szerint:
![\[\Delta v(\omega)= \int_{-\infty}^{\infty} dt \Delta V(t)e^{-i\omega t}.\]](/images/math/2/9/6/2965fd4ba4a7bbef8a3053293de74505.png)
Vizsgáljuk ezen Fourier-transzformált abszolút érték négyzetének várható értékét:
![\[\langle|(\Delta v(\omega))|^2 \rangle= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} dt' dt \langle\Delta V(t)\Delta V(t') \rangle e^{-i\omega t} e^{i\omega t'}.\]](/images/math/4/c/e/4ce29a8e2825fd676032ef5e4d3274cb.png)
Az egyenlet jobb oldalán látható korrelációs függvény kifejezhető a következőképpen:
![\[ \langle\Delta V(t)\Delta V(t')\rangle=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega'c(\omega')e^{i\omega'(t-t')}.\]](/images/math/0/2/0/020ed4a8570c778e72bfcb56197a4710.png)
Továbbá az exponenciális tagokat átcsoportosítva a következő tag integrálja egy Dirac-deltát ad:
![\[\int_{-\infty}^{\infty}dt'\frac{e^{i(\omega+\omega')t'}}{2\pi}=\delta(\omega+\omega').\]](/images/math/0/9/5/095ca08f79957cdab9fa2f6b7d38b462.png)
Így a feszültség Fourier-transzformált abszolút érték négyzetének várható értéke könnyen belátható, hogy arányos a korrelációs függvény Fourier-transzformáltjával, illetve az időablak szélességével:
![\[\langle|(\Delta v(\omega))|^2 \rangle= c(\omega) \int_{-\infty}^{\infty} dt.\]](/images/math/b/e/7/be72f26b149e5ab64d53d20f46b4bc31.png)
Innen könnyen kifejezhető a zaj teljesítménysűrűsége, felhasználva, hogy az a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese.
![\[s_V(\omega)=\lim\limits_{T->\infty} \frac{2}{T}\left\langle |\int_{-T/2}^{T/2} dt \Delta V(t)e^{-i\omega t}|^2\right\rangle.\]](/images/math/f/6/2/f62535c4ffea081a318dd4bd7ac2a654.png)
A mérésünk során diszkrét pontokon történik a mintavételezés, így ugyanez a számolás DFT segítségével a következő módon fejezhető ki:
![\[s_V(\omega)\approx\frac{2}{N\Delta t}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}\Delta t|^2=\frac{2\Delta t}{N}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}|^2.\]](/images/math/6/0/3/603ab5b3fd96cfbcbb85edb29268c6af.png)
A fentiekben sikerült megállapítanunk, hogy a vizsgált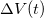 
jel Fourier-transzformáltjából hogyan számolható a zaj spektrális sűrűsége. Azonban ennél a számolásnál nem vettünk figyelembe ablakfüggvényt, vagy fogalmazhatunk úgy is, hogy téglalap ablakkal számoltunk.
Nézzük meg, hogy egy tetszőleges ablakfüggvény esetén hogyan származtatható a zajsűrűség. Sajnos tetszőleges spektrumú zajra és tetszőleges ablakfüggvényre általános összefüggés nem adható, viszont ha 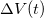fehér zaj, akkor tetszőleges ablakfüggvényre egyszerűen számolható a konverziós faktor.
Az ablakfüggvénnyel szorzott jel Fourier-transzformáltja:
![\[\Delta v_W(\omega)=\int_{-\infty}^{\infty}dt\Delta V(t)W(t)e^{-i\omega t}.\]](/images/math/7/e/f/7efc09e6fe1e8b10c418e39ae67c31c9.png)
Vizsgáljuk meg ezen Fourier-transzformált abszolút érték négyzetének várható értékét, ekkor a következőt kapjuk:
![\[\langle|\Delta v(\omega)|^2\rangle=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}dtdt'W(t)W(t')\langle\Delta V(t)\Delta V(t')\rangle e^{-i\omega t}e^{-i\omega t'}.\]](/images/math/7/d/3/7d3c7333af2e34f077367ef15237c488.png)
A fehér zaj jellegéből következik, hogy:
![\[\langle\Delta V(t)\Delta V(t')\rangle=C(t-t')=\frac{s_0}{2}\delta(t-t').\]](/images/math/7/2/c/72c3ab5d9e5160ea1cc93ce4aa1e97ae.png)
Így a Fourier-transzformált abszolút érték négyzetének várható értéke a következőképpen egyszerűsödik:
![\[\langle|\Delta v_W(\omega)|^2\rangle=\frac{s_0}{2}\int_{-\infty}^{\infty}W^2(t)dt.\]](/images/math/6/3/5/6356a96296e2b3eca8d114d91dae4d48.png)
Azaz a zajsűrűség számolása:
![\[s_0=\frac{2\langle|v_W(\omega)|^2\rangle}{\int_{-\infty}^{\infty}W^2(t)dt}.\]](/images/math/9/1/7/917c7b49524f91ef5d3aee98385f13b5.png)
A feszültségzaj spektrális sűrűsége egy normálási faktor erejéig egyenlő a mért feszültségpontok diszkrét Fourier-transzformáltjának abszolútérték-négyzetének kétszeresével. A normálási faktor az ablakfüggvény négyzetének a mérési időablakra vett integrálja. Láttuk, hogy ez téglalap ablakkal számolva 
. Most vizsgáljuk meg a zajméréshez leggyakrabban használt Hanning-ablakot, melynek ablakfüggvénye:
![\[W(t)=2\sin^2\left(\frac{t\pi}{T}\right).\]](/images/math/d/5/8/d58104d67248c78d0d25e0feb8d3b3ac.png)
A zajsűrűség Hanning-ablakot használva:
![\[s_0=\frac{4\langle|v_W(\omega)|^2\rangle}{3T}.\]](/images/math/b/d/e/bdee8db481fad34233895abf370d61ae.png)
Diszkrét mérési pontok esetén a következőképpen módosul a kifejezés:
![\[s_0\approx\dfrac{2}{\sum_{n=0}^{N-1}W^2(n\Delta t)\Delta t}|\sum_{n=0}^{N-1}W(n\Delta t) V(N\Delta t)e^{-i\omega n\Delta t}\Delta t|^2.\]](/images/math/c/7/9/c798b690d1d9023a3a2741285d12ca1c.png)
Hanning-ablakkal számolva:
![\[s_0\approx\frac{4\Delta t}{3N}|\sum_{n=0}^{N-1}W(n\Delta t)\Delta V(n\Delta t)e^{-i\omega n\Delta t}|^2.\]](/images/math/e/1/1/e11505f5d483e5c169ac48ae35cc33ba.png)
Így frekvenciafüggetlen zajsűrűségek esetén sikerült analitikusan meghatározni, hogy a mérési pontokból miképpen számolható ki a zaj spektrális sűrűsége.
