„Hőmérsékleti sugárzás vizsgálata” változatai közötti eltérés
a (Helyesírás) |
|||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 216. sor: | 216. sor: | ||
<span id="fig:10">[[Fájl:Mérési_elrendezés_2_homsug.jpg|bélyegkép|közép|400px|10. ábra]]</span> | <span id="fig:10">[[Fájl:Mérési_elrendezés_2_homsug.jpg|bélyegkép|közép|400px|10. ábra]]</span> | ||
*<span id="4.fel">4. </span>Ellenőrizze a Stefan–Boltzmann-törvényt alacsony hőmérsékletű sugárforrás esetén! Határozza meg a sugárforrás felületeit jellemző abszorpciós és emissziós tényezőket! ''Mérőeszközök'': Alacsonyhőmérsékletű sugárforrás, sugárzásérzékelő + állvány, 2 db multiméter, stopper. | *<span id="4.fel">4. </span>Ellenőrizze a Stefan–Boltzmann-törvényt alacsony hőmérsékletű sugárforrás esetén! Határozza meg a sugárforrás felületeit jellemző abszorpciós és emissziós tényezőket! ''Mérőeszközök'': Alacsonyhőmérsékletű sugárforrás, sugárzásérzékelő + állvány, 2 db multiméter, stopper. | ||
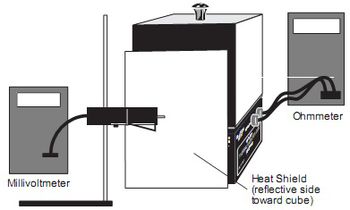
| − | **Állítsa össze a [[#fig:11|11. ábrán]] látható elrendezést! A sugárzásérzékelő mérőfeje a sugárforrás lapjainak közepénél, attól kb. 3 - 4 cm távolságban legyen! A fűtés bekapcsolása előtt határozzuk meg a termisztor ellenállása alapján a környezet hőmérsékletét $(T_0)$ ! Kapcsolja a sugárforrás fűtését HIGH-állásba! 1 perc eltelte után olvassa le a fekete oldallal szembe állított detektor feszültségét (nyitott és zárt ablakkal), valamint a sugárforrás termisztorának ellenállását! | + | **Állítsa össze a [[#fig:11|11. ábrán]] látható elrendezést! A sugárzásérzékelő mérőfeje a sugárforrás lapjainak közepénél, attól kb. 3 - 4 cm távolságban legyen! A fűtés bekapcsolása előtt határozzuk meg a termisztor ellenállása alapján a környezet hőmérsékletét $(T_0)$ ! Kapcsolja a sugárforrás fűtését HIGH-állásba! 1 perc eltelte után olvassa le a fekete oldallal szembe állított detektor feszültségét (nyitott és zárt ablakkal), valamint a sugárforrás termisztorának ellenállását! Fél perc múlva ismételje meg a mérést a szomszédos felületen! Fél percenként váltogatva a vizsgált felületet folytassa a vizsgálatot kb. fél órán keresztül! (Az egyes felületek 2 percenként kerülnek sorra.) A méréssorozat végére a sugárforrás eléri a véghőmérsékletet. '''A fűtést még ne kapcsolja ki!''' |
{| | {| | ||
| 223. sor: | 223. sor: | ||
|} | |} | ||
| − | **Ábrázolja az egyes felületekre külön-külön $E_f$ $(T_f^4-T_0^4)$ | + | **Ábrázolja az egyes felületekre külön-külön $E_f$ -et $(T_f^4-T_0^4)$ függvényében! Határozza meg a felületek relatív emissziós tényezőit! Értékelje ki a fekete felületen mért adatokból a detektor $c$ együtthatóját (ld. alább)! |
**''Megjegyzések'': A detektor hőmérsékletét a ráeső sugárzási teljesítmény és a leadott sugárzási teljesítmény különbsége határozza meg. Az előbbi a forrás hőmérsékletének $(T_f)$ negyedik hatványával arányos, míg az utóbbi a detektorhőmérséklet $(T_0)$ negyedik hatványával. Így a kimenőjel $U_{ki} = c(T_f^4-T_0^4)$, ahol c állandó. [A 2. és 3. feladatoknál, ahol a forrás hőmérséklete 1000 - 3000 K között változott a detektor által kibocsátott sugárzást elhanyagolhattuk. Most azonban, a sugárforrás hőmérséklete 120ºC alatt van, így ez nem tehető meg.] Feltesszük, hogy az érzékelő szobahőmérsékleten van, aminek értékét az 1. pontban mért termisztor ellenállásból határozhatjuk meg. A sugárforrás hőmérséklete az alumíniumkockában levő izzó áramával szabályozható. A skálával ellátott forgatógomb 5; 6,5; 8 és “HIGH” állásaihoz tartozó állandósult hőmérsékletek rendre ~ 80, 90, 100 és 110ºC. | **''Megjegyzések'': A detektor hőmérsékletét a ráeső sugárzási teljesítmény és a leadott sugárzási teljesítmény különbsége határozza meg. Az előbbi a forrás hőmérsékletének $(T_f)$ negyedik hatványával arányos, míg az utóbbi a detektorhőmérséklet $(T_0)$ negyedik hatványával. Így a kimenőjel $U_{ki} = c(T_f^4-T_0^4)$, ahol c állandó. [A 2. és 3. feladatoknál, ahol a forrás hőmérséklete 1000 - 3000 K között változott a detektor által kibocsátott sugárzást elhanyagolhattuk. Most azonban, a sugárforrás hőmérséklete 120ºC alatt van, így ez nem tehető meg.] Feltesszük, hogy az érzékelő szobahőmérsékleten van, aminek értékét az 1. pontban mért termisztor ellenállásból határozhatjuk meg. A sugárforrás hőmérséklete az alumíniumkockában levő izzó áramával szabályozható. A skálával ellátott forgatógomb 5; 6,5; 8 és “HIGH” állásaihoz tartozó állandósult hőmérsékletek rendre ~ 80, 90, 100 és 110ºC. | ||
A lap jelenlegi, 2019. szeptember 16., 13:46-kori változata
A mérés célja:
- a hőmérsékleti sugárzás legfontosabb tulajdonságainak és törvényeinek megismerése.
Ennek érdekében:
- összefoglaljuk a hőmérsékleti sugárzásra vonatkozó ismereteket,
- kimérjük egy pontszerű forrás sugárzási intenzitásának távolságfüggését,
- meghatározzuk a fekete test sugárzási intenzitásának hőmérsékletfüggését (Stefan–Boltzmann-törvény),
- megvizsgáljuk különböző anyagok abszorpció- és emisszióképességét.
Tartalomjegyzék |
Elméleti összefoglaló
A tapasztalat szerint két különböző hőmérsékletű test között akkor is végbemegy energiaátadás, ha a hővezetés és a konvektív hőcsere gyakorlatilag elhanyagolható. Az energia ilyenkor elektromágneses sugárzás révén jut át az egyik testről a másikra. Ezt az anyagoknak két alapvető tulajdonsága teszi lehetővé: egyrészt az anyagok külső behatás nélkül - a bennük atomi, molekuláris szinten lezajló mozgások következtében - szünet nélkül, és minden hőmérsékleten elektromágneses sugárzást bocsátanak ki, másrészt az anyagok a rájuk eső elektromágneses sugárzást - ugyancsak atomi, molekuláris mechanizmusok révén - képesek elnyelni. Így egy A test által kibocsátott sugárzásnak egy részét (és az általa szállított energiát) a sugárzás útjába eső B test elnyeli, de ugyanígy, a B test által kibocsátott sugárzás (energia) egy részét az A test nyeli el: szakkifejezéssel élve, az A és B test sugárzási kölcsönhatásban áll egymással. A tapasztalat azt mutatja, hogy az energiacsere eredményeképpen végül is a melegebb testről a hidegebbre megy át energia, tehát a melegebb test hűlni fog, a hidegebb pedig melegedni. Azt azonban, hogy ez a folyamat részleteiben hogyan zajlik le, tehát például adott idő alatt mennyi az átadott energia, csak a sugárzás kibocsátásának, illetve elnyelésének részletes tanulmányozásával tudhatjuk meg.
Hőmérsékleti sugárzás és a jellemzésére szolgáló mennyiségek
A testek által külső behatás nélkül kibocsátott elektromágneses sugárzás intenzitását a tapasztalat szerint alapvetően a test hőmérséklete határozza meg, és az intenzitás a test hőmérsékletétől igen erősen függ. A hőmérsékleti sugárzás során létrejött elektromágneses hullámban különböző hullámhosszú összetevők terjednek. A kibocsátott energiának a különböző hullámhosszú összetevők közötti eloszlása - a sugárzás spektrális eloszlása - szintén függ a test hőmérsékletétől. Ezek a tények indokolják azt, hogy az ilyen sugárzást hőmérsékleti sugárzásnak nevezik. A sugárzás kibocsátásának és elnyelésének vizsgálatánál fontos szerepet játszik néhány alapvető fogalom és mennyiség, ezért először ezekkel foglalkozunk.
Egy test által sugárzás útján kibocsátott energiát az emisszióképességgel jellemezzük. Ha a 
hőmérsékletű test egy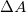 
nagyságú felületéről 
idő alatt egy 
és 
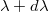közé eső hullámhossztartományban 
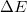energiát sugároz ki, akkor az adott hullámhosszra és hőmérsékletre vonatkozó emisszióképessége:
![\[ \varepsilon (\lambda ,T)= \frac{\Delta E}{\Delta A \Delta t \Delta \lambda}. \]](/images/math/8/9/2/892db9763be064f048ee1a461dc60d04.png)
Ha a kibocsátott energia hullámhossz szerinti (spektrális) eloszlása nem fontos számunkra, akkor a teljes spektrumban kibocsátott, ún. integrált emisszióképességet használhatjuk, amely
![\[ E(T)= \int_0^\infty \varepsilon (\lambda ,T) \, \mathrm{d} \lambda. \]](/images/math/a/f/0/af064e02c7ad9f40ef561cb5a8553b9c.png)
Megjegyezzük, hogy az integrált emisszióképesség értelmezhető a spektrum egyes részeire (pl. infravörös, látható, stb.) is, ilyenkor az integrálás a megfelelő hullámhossztartományra terjed ki.
A már kibocsátott, térben terjedő sugárzás energetikai jellemzésére az energia-áramsűrűséget használjuk. Ez természetesen szintén hullámhosszfüggő mennyiség. Ha a sugárzásban egy és 
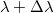közé eső hullámhossztartományban a sugárzás haladási irányára merőleges 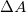nagyságú felületen idő alatt egy 
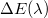energia halad át, akkor az adott hullámhosszra vonatkozó energia-áramsűrűség
![\[ I(\lambda) = \frac{\Delta E(\lambda)}{\Delta A \Delta t \Delta \lambda}. \]](/images/math/4/2/7/427b954c4a38d85ba5666f2200e9eae5.png)
Ezt a mennyiséget a hullámhosszú sugárzás intenzitásának nevezzük. Ha a sugárzásban terjedő összes energiát akarjuk jellemezni, akkor a különböző hullámhosszakra vonatkozó intenzitások összegzésével kapható teljes intenzitást kell megadnunk:
![\[ I_o = \int_0^\infty I(\lambda) \mathrm{d} \lambda. \]](/images/math/0/0/e/00e395f8e6cd0c843d07ae244c70f6dd.png)
Az integrált emisszióképességhez hasonlóan, a sugárzási intenzitás is definiálható meghatározott hullámhossztartományra .
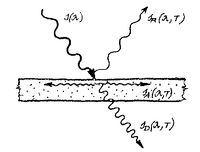
Ha egy testet sugárzás ér, akkor a testtel való kölcsönhatás következtében a sugárzás (és a szállított energia) több részre bomlik (1. ábra). A sugárzás egy része abszorbeálódik (elnyelődik) a testben. Az intenzitás abszorbeált részének jelölésére az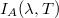 
szimbólumot használjuk. A sugárzás másik része a test felületéről reflektálódik (visszaverődik): 
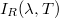, a sugárzás fennmaradó részét pedig a test átereszti: 
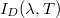. A fenti szimbólumokban a testet érő sugárzás hullámhossza, pedig a sugárzásnak kitett test hőmérséklete, a tapasztalat szerint ugyanis egy test elnyelési, visszaverési és áteresztési tulajdonságai általában függnek ezektől a mennyiségektől.
A sugárzásnak a test által elnyelt hányadát, vagyis az
![\[ a(\lambda,T) = \frac{I_A(\lambda,T) }{I(\lambda)} \]](/images/math/b/2/c/b2c83eb483d831d555207298172c0ef8.png)
hányadost a hőmérsékletű test hullámhosszú sugárzásra vonatkozó abszorpcióképességének nevezik.
Hasonló módon definiálható a hőmérsékletű test hullámhosszú sugárzásra vonatkozó reflexióképessége és áteresztő képesége
![\[ r(\lambda, T) = \frac{I_R(\lambda,T)}{I(\lambda)} \]](/images/math/5/2/f/52ffcdc0e854322d49c8ace288de20a9.png)
![\[ d(\lambda, T) = \frac{I_D(\lambda,T)}{I(\lambda)} \]](/images/math/f/9/3/f93661f71e20eddf6ee83ca5a6be1dfb.png)
Ha a testnek csak az összes beérkező sugárzással kapcsolatos viselkedése érdekel bennünket, akkor a fenti hullámhossztól függő (spektrális) jellemzők helyett integrált jellemzőket használunk. A test integrált abszorpcióképessége ennek megfelelően
![\[ a(T) = \frac{\int_0^\infty I_A (\lambda,T) \, \mathrm{d} \lambda}{\int_0^\infty I (\lambda) \, \mathrm{d} \lambda} = \frac{I_A(T)}{I}. \]](/images/math/f/6/2/f629e94d4c24f8e0b4167d4079a70159.png)
Hasonlóan kapható az integrált reflexióképesség
![\[ r(T) = \frac{\int_0^\infty I_R (\lambda,T) \, \mathrm{d} \lambda}{\int_0^\infty I (\lambda) \, \mathrm{d} \lambda} = \frac{I_R(T)}{I}, \]](/images/math/1/1/1/1113ba18bac896cfc38bb59901c1b69e.png)
és az integrált áteresztő képesség
![\[ d(T) = \frac{\int_0^\infty I_D (\lambda,T) \, \mathrm{d} \lambda}{\int_0^\infty I (\lambda) \, \mathrm{d} \lambda} = \frac{I_D(T)}{I}. \]](/images/math/2/a/a/2aa15b94bd4d4f72dd3f043d1bf9008e.png)
A fenti jellemzőket - az integrált emisszióképességhez és a sugárzás intenzitásához hasonlóan - szintén lehet definiálni egy véges hullámhossztartományra is. Az energiamegmaradás tételéből következik, hogy a fenti jellemzőkre fennállnak az alábbi összefüggések:
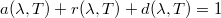, illetve
![\[a(T)+r(T)+d(T)=1. \]](/images/math/c/c/0/cc0668101969b0c029120d7bf6bdee79.png)
A testek sugárzási tulajdonságainak vizsgálatánál igen fontos szerepet játszik az a speciális test, amely a hőmérsékletétől és a ráeső sugárzás spektrális eloszlásától függetlenül az összes ráeső sugárzást elnyeli. Az ilyen testet abszolút fekete testnek, vagy rövidebben fekete testnek nevezzük, és definíciójának megfelelően, abszorpcióképességére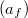 
fennáll, hogy
![\[a_f(\lambda,T)=a_f(T)=a_f=1. \]](/images/math/9/c/0/9c0342e3065d083caa4f4e3fa5895efe.png)
(A fekete testre vonatkozó mennyiségeket 
indexszel jelöljük.)
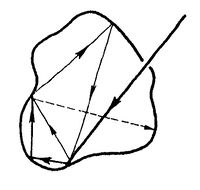
Jó közelítéssel fekete testnek tekinthető egy üreges test falán lévő kis nyílás (2. ábra), mivel a nyíláson bejutó sugárzásnak az üregből való kijövetele igen kis valószínűségű a nyílás kis mérete miatt. A fekete test jelentős szerepet játszik a sugárzások tanulmányozásánál, mivel a rá vonatkozó törvények elméletileg levezethetőek, és a nem fekete testek esetén is hasznosíthatók.
A fekete test sugárzása
A fekete test által kisugárzott energia elméleti úton meghatározható. Az emisszióképesség hullámhossztól és a test hőmérsékletétől való függésére a kísérleti eredményekkel egyező összefüggést Max Planck vezette le itt nem részletezett meggondolások alapján (ekkor vezette be a foton fogalmát). Az összefüggés egyik gyakran használt alakja a következő:
![\[ \varepsilon_f(\lambda,T)=\frac{c_1\lambda^{-5} }{exp \left(\frac{c_2}{\lambda T} \right) -1}. \]](/images/math/d/7/6/d76f83e9f27cbe66a29f39858c56e678.png)
Ez a Planck-féle sugárzási törvény (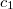
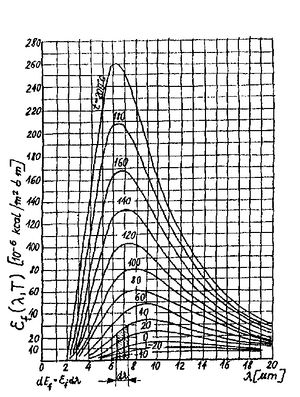
és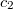 
állandók). Az emisszióképesség hullámhosszfüggése néhány hőmérsékleten a 3. ábrán látható. Adott hőmérsékleten a fekete test emisszióképessége maximumot mutat. A maximumnak megfelelő hullámhossz növekvő hőmérséklettel csökken.
Az ábrán feltüntetett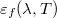 
mennyiség a fekete test által az egységnyi hullámhossz intervallumban (egységnyi felületről) kisugárzott teljesítményt adja meg. Ennek megfelelően a 
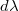intervallumhoz tartozó teljesítmény
![\[ \mathrm{d}E_f=\varepsilon_f (\lambda,T)\mathrm{d}\lambda =\frac{c_1\lambda^{-5} }{exp \left(\frac{c_2}{\lambda T} \right) -1} \mathrm{d}\lambda. \]](/images/math/2/6/9/269675702d18abe54804fb32c4b266bb.png)
Könnyen belátható, hogy ennek számértékét az ábrán a bevonalkázott terület adja meg. A hőmérsékletű fekete test egységnyi felületéről a teljes spektrumban kisugárzott teljesítmény (14) integrálásával kapható meg:
![\[ E_f (T)=\int_0^\infty \frac{c_1\lambda^{-5} }{exp \left(\frac{c_2}{\lambda T} \right) -1} \mathrm{d}\lambda. \]](/images/math/7/1/b/71b742d8fd2f6be6649fa317f9d341ba.png)
Az integrálás eredménye a következő:
![\[ E_f(T)=\sigma T^4. \]](/images/math/6/9/b/69ba5ddd2f1718dd3721578e94509d3f.png)
Ez a Stefan–Boltzmann-törvény, mely szerint a T hőmérsékletű fekete test egységnyi felülete által egységnyi idő alatt kisugárzott teljes energia arányos a test hőmérsékletének negyedik hatványával. A törvényben szereplő 
állandó értéke 
.
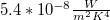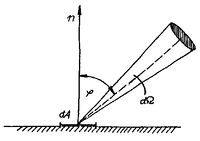
A Stefan–Boltzmann-törvény a fekete test által minden irányban kisugárzott összteljesítményt adja meg. A tapasztalat szerint azonban egy felületről ugyanolyan térszögbe kisugárzott energia függ a felülethez viszonyított iránytól. A sugárzás intenzitásának irányfüggését fekete test esetén a Lambert-törvény adja meg, amely szerint egységnyi felület által a felület n normálisával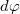 
szöget bezáró irányban a 
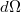térszögben egységnyi idő alatt kisugárzott energia (4. ábra):
![\[ \mathrm{d}E_\varphi (T) =\frac{\sigma}{\pi}T^4 \mathrm{d} \Omega cos\varphi \]](/images/math/4/0/9/4093864552a10e55ddf543ed0d4a2a23.png)
Nem fekete testek sugázása
A fekete test sugárzására érvényes törvényszerűségeknek a valódi (nem fekete) testekre való alkalmazásánál igen fontos szerepet játszik az emisszió- és abszorpcióképességek között fennálló alábbi tapasztalati törvény.
Különböző testek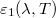 
, 
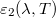, emisszióképességét és 
, 
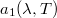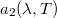, ... abszorpcióképességét megmérve, azt találjuk, hogy
![\[ \frac{\varepsilon_1(\lambda,T)}{a_1(\lambda,T)} = \frac{\varepsilon_2(\lambda,T)}{a_2(\lambda,T)} = const. \]](/images/math/a/3/5/a35506421cc8ebd184322e00f439729a.png)
Ez a hőmérsékleti sugárzásra vonatkozó Kirchhoff-törvény.
Mivel ez a törvény a fekete testre is érvényes, melyre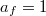 
, bármely test emisszió- és abszorpcióképességére teljesül, hogy
![\[ \frac{\varepsilon(\lambda,T)}{a(\lambda,T)} = \varepsilon_f(\lambda,T). \]](/images/math/d/9/8/d984556a417ba262778a926babd0907c.png)
Vagyis a fekete test emisszióképességének ismeretében bármely test emisszióképessége kiszámítható, ha ismerjük annak abszorpcióképességét is:
![\[ \varepsilon(\lambda,T) = a(\lambda,T)\varepsilon_f(\lambda,T). \]](/images/math/8/6/5/86569b161a22271ef29cd2e742e05e53.png)
Egy test hőmérsékleti sugárzásának jellemzésére gyakran használják a test ún. relatív emissziós tényezőjét (dimenzió nélküli, egynél nem nagyobb szám), vagy más néven feketeségi fokát, ami azt adja meg, hogy adott hőmérsékleten és hullámhosszon hogyan aránylik a test által kibocsátott teljesítmény a fekete test teljesítményéhez:
![\[ e(\lambda,T) =\frac{\varepsilon(\lambda,T)}{\varepsilon_f(\lambda,T)}. \]](/images/math/7/8/2/782f178cbeefde5109ada827f52b9f93.png)
A (19) és (21) egyenletek összevetéséből kiderül, hogy a test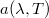 
abszorpcióképessége megegyezik az 
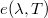relatív emissziós tényezővel:
![\[ e(\lambda,T) = a(\lambda,T). \]](/images/math/4/e/2/4e207f9b489ed575a50aea6205aeff7c.png)
Az integrált emisszióképességet a (20) egyenlet integrálásával kapjuk meg:
![\[ E(T) = \int_0^\infty \varepsilon(\lambda,T)\mathrm{d}\lambda = \int_0^\infty a(\lambda,T) \varepsilon_f(\lambda,T)\mathrm{d}\lambda. \]](/images/math/d/0/5/d0529ea16d02ba0f0bbc6831289be001.png)
Kiszámításához ismerni kell az 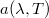függvényt, ami a feladatot eléggé megnehezíti. Szerencsére nem túl magas hőmérsékletű testek sugárzása esetén a legtöbb esetben a feladat egyszerűsíthető, mert a relatív emissziós tényező gyakorlatilag nem függ a hullámhossztól, azaz 
= 
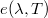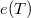. Azokat a testeket, amelyekre ez az összefüggés fennáll, szürke testeknek nevezik. Tovább egyszerűsíti a helyzetet, hogy az általunk vizsgált hőmérsékleteken a szürke testek relatív emissziós tényezője gyakorlatilag független a hőmérséklettől, így 
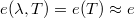. Ez a (20) egyenlet értelmében egyben azt is jelenti, hogy alacsony hőmérsékletű szürke testek esetén az abszorpcióképességre is igaz mindaz, ami a relatív emissziós tényezőre, és érvényes az
![\[ a=e \]](/images/math/5/1/f/51fadb811c89aaf78f73bfa26f426af5.png)
összefüggés is. A (23) és (24) összefüggés felhasználásával a test integrált emisszióképessége:
![\[ E(T) = a\int_0^\infty \varepsilon_f(\lambda,T)\mathrm{d}\lambda=aE_f(T)=eE_f(T). \]](/images/math/0/1/f/01f4b735028c937f8778e22c954c6918.png)
Behelyettesítve ide a fekete test ismert integrált emisszióképességét (Stefan–Boltzmann-törvény; (16) egyenlet), azt kapjuk, hogy
![\[ E(T) = e\sigma T^4. \]](/images/math/b/5/5/b55636a657bf78d50dc431d911657f83.png)
Alacsony hőmérsékletű szürke test integrált emisszióképessége tehát csak egy konstans szorzóban különbözik a fekete testétől.
A kísérlet során alkalmazott eszközök.
A sugárforrások
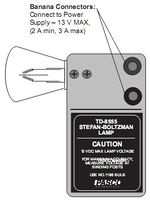
- A. Az alacsony hőmérsékletű sugárforrás egy alumíniumkocka, négy különböző minőségű felülettel (feketére festett, matt alumínium, fehérre festett és polírozott alumínium), melynek hőmérséklete szobahőmérséklettől kb. 120ºC - ig változtatható (5. ábra). A kocka belsejében egy 100 W-os izzólámpa helyezkedik el, melynek teljesítményét egy forgatógomb segítségével változtatni tudjuk. A kocka hőmérsékletét egy beépített termisztor méri. A termisztor ellenállás hőmérséklet függését az 2. táblázat tartalmazza (ld. Függelék).
 |
 |
 |
 |
| Figyelem: mérés közben a kocka felülete forró lehet, érintésétől tartózkodjunk! |
- B. A magas hőmérsékletű sugárzó egy izzólámpa - az ún. “Stefan–Boltzmann-izzó” (6. ábra) amelynek hőmérséklete a rákapcsolt feszültség segítségével változtatható.
| Figyelem: az izzóra maximum 12 V feszültséget kapcsoljon! |
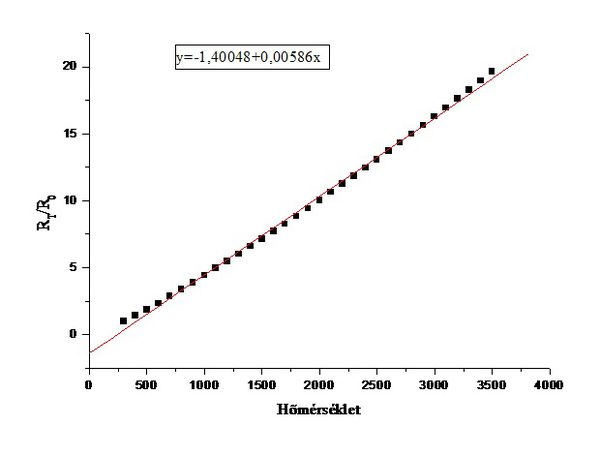
A sugárzó hőmérsékletét az 1. grafikon vagy a 1. táblázat segítségével határozhatjuk meg (ld. Függelék). Ehhez mérjük meg az izzó ellenállását szobahőmérsékleten négypontos ellenállásméréssel. Az aktuális hőmérsékleten mutatott ellenállásértéket az izzón eső feszültség és az átfolyó áram értékéből számítsuk ki.
A sugárzásérzékelő
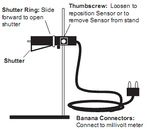
A sugárzás érzékelésére egy termoelem szolgál, amelynek feszültsége arányos a reá érkező sugárzás intenzitásával (7. ábra). Spektrális érzékenysége egyenletes az infravörös tartományban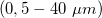 
, és feszültsége néhány 
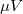és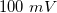 
között változik.
A termoelemet fényzár védi; melyet csak a mérés idejére, lehetőleg rövid időre szabad kinyitni. Ez akadályozza meg a termoelem referenciapontjának hőmérsékletváltozását. Az érzékelő habszivacs lapkával is árnyékolható. Az érzékelő optimális helyzete egy állvány segítségével állítható be.
A magas hőmérsékletű sugárzó és a sugárzásérzékelő egy fából készült tartószerkezeten helyezkedik el. Az érzékelőt egy erre a célra készített hasábbal lehet pontosan az izzólámpával szembe beállítani. Az érzékelő helyzete állandó, az izzót egy horonyban tolva lehet különböző távolságokra állítani.
 |
 |
Az abszorpciómérő
Az abszorpciómérő négy különböző felületű résszel rendelkezik: feketére festett, matt alumínium, fehérre festett és polírozott alumínium (8. ábra). A felületek hőmérsékletét egy-egy beépített termisztor méri. (A termisztor karakterisztikáját az 2. táblázat adja meg.) A vizsgálandó felületek termikusan jól szigeteltek, így a hőmérsékletük változását elsősorban a hőmérsékleti sugárzásból elnyelt energia határozza meg. A szerkezet hátoldalán levő tolókapcsolóval lehet a kiválasztott szegmens termisztorát a kimeneti csatlakozókra kapcsolni.
| Figyelem: az abszorpciómérőt ne melegítse 60ºC fölé! |
 |
Mérési feladatok
- 1. Mérje meg szobahőmérsékleten a „Stefan–Boltzmann-izzó” és az alacsony hőmérsékletű sugárforrás érzékelő termisztorának „hideg” ellenállását! (Ezekre az adatokra később szüksége lesz.) Az izzó ellenállását négypontos ellenállásmérővel, a termisztor ellenállását multiméterrel mérje!
- 2. Ellenőrizze a Stefan–Boltzmann-törvényt magas hőmérsékletű sugárforrás esetén! Mérőeszközök: Stefan–Boltzmann-izzó, tápegység (Ohmeg ST 255, 25V, 5A), 3 db multiméter, sugárzásdetektor állvánnyal, fa tartószerkezet.
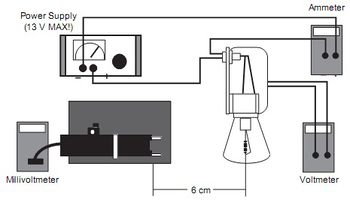
- A. Állítsa össze a 9. ábra szerinti mérési elrendezést. A mérés során az izzón 2 A-nél nagyobb áram fog folyni, ezért az áramot mérő mutiméteren a 20 A-es méréshatárt használja! (Üzemmód: Shift 20A, bemenetek: fekete és az alsó kék.) A sugárzásérzékelő jelét mérő multiméter a 200 mV-os méréshatárban (Shift DC mV) használja. Az érzékelő és a sugárforrás közötti távolság legyen 6 cm. Az izzó üzemi hőmérsékletét az átfolyó áram és a rajta eső feszültségből számított üzemi ellenállás, valamint a volfrám ellenállásának hőmérsékletfüggéséből számítjuk ki.
- B. Kapcsolja be a lámpa tápegységét, majd a feszültséget fokozatosan 1 V-os lépésekben emelje 12 V- ig. Mérje meg az izzón átfolyó áramot és a rajta eső feszültséget, valamint a sugárzásdetektor feszültségét! Ohm törvénye alapján számítsa az aktuális ellenállást és az izzó “hideg” ellenállásának ismeretében a 1. táblázat alapján határozza meg a hőmérsékletet! Vonja le a detektorfeszültségből a detektor sötétáramához tartozó feszültséget, így a sugárzással arányos
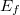kimenőjelet kap. Ábrázolja 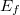-et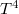 
függvényében! A sugárzásdetektorral ~ 1 s-ig mérjen és a két mérés közti szünetben gondosan árnyékolja le, hogy elkerülje az érzékelő felmelegedését!
| Ügyeljen arra, hogy az izzó ne kapjon 12 V-nál nagyobb feszültséget. |
 |
 |
- 3. Határozza meg a pontszerű forrás sugárzási intenzitásának távolságfüggését! Mérőeszközök: Stefan–Boltzmann-izzó, tápegység (Ohmeg ST 255, 25V, 5A), 3 db multiméter, sugárzásdetektor állvánnyal, fa tartószerkezet.
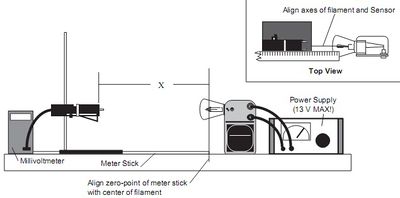
- Állítsa össze a 10. ábra szerinti mérési elrendezést.
- Az előző mérésnél elért maximális üzemi feszültséget (12 V) hagyja az izzón változatlanul bekapcsolva. Távolítsa az izzót a detektortól centiméterenként a lehetséges legtávolabbi pontig, mérje meg minden beállított távolságnál a sugárzásdetektor feszültségét. [Vonja le a detektorfeszültség értékéből a detektor sötétáramához tartozó feszültséget, így a sugárzással arányos kimenőjelet
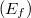kap.] Ábrázolja 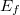-et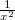 
függvényében!
- 4. Ellenőrizze a Stefan–Boltzmann-törvényt alacsony hőmérsékletű sugárforrás esetén! Határozza meg a sugárforrás felületeit jellemző abszorpciós és emissziós tényezőket! Mérőeszközök: Alacsonyhőmérsékletű sugárforrás, sugárzásérzékelő + állvány, 2 db multiméter, stopper.
- Állítsa össze a 11. ábrán látható elrendezést! A sugárzásérzékelő mérőfeje a sugárforrás lapjainak közepénél, attól kb. 3 - 4 cm távolságban legyen! A fűtés bekapcsolása előtt határozzuk meg a termisztor ellenállása alapján a környezet hőmérsékletét
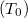! Kapcsolja a sugárforrás fűtését HIGH-állásba! 1 perc eltelte után olvassa le a fekete oldallal szembe állított detektor feszültségét (nyitott és zárt ablakkal), valamint a sugárforrás termisztorának ellenállását! Fél perc múlva ismételje meg a mérést a szomszédos felületen! Fél percenként váltogatva a vizsgált felületet folytassa a vizsgálatot kb. fél órán keresztül! (Az egyes felületek 2 percenként kerülnek sorra.) A méréssorozat végére a sugárforrás eléri a véghőmérsékletet. A fűtést még ne kapcsolja ki!
- Állítsa össze a 11. ábrán látható elrendezést! A sugárzásérzékelő mérőfeje a sugárforrás lapjainak közepénél, attól kb. 3 - 4 cm távolságban legyen! A fűtés bekapcsolása előtt határozzuk meg a termisztor ellenállása alapján a környezet hőmérsékletét
 |
 |
- Ábrázolja az egyes felületekre külön-külön 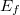-et
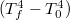függvényében! Határozza meg a felületek relatív emissziós tényezőit! Értékelje ki a fekete felületen mért adatokból a detektor 
együtthatóját (ld. alább)!
- Megjegyzések: A detektor hőmérsékletét a ráeső sugárzási teljesítmény és a leadott sugárzási teljesítmény különbsége határozza meg. Az előbbi a forrás hőmérsékletének
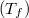negyedik hatványával arányos, míg az utóbbi a detektorhőmérséklet 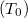negyedik hatványával. Így a kimenőjel 
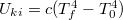, ahol c állandó. [A 2. és 3. feladatoknál, ahol a forrás hőmérséklete 1000 - 3000 K között változott a detektor által kibocsátott sugárzást elhanyagolhattuk. Most azonban, a sugárforrás hőmérséklete 120ºC alatt van, így ez nem tehető meg.] Feltesszük, hogy az érzékelő szobahőmérsékleten van, aminek értékét az 1. pontban mért termisztor ellenállásból határozhatjuk meg. A sugárforrás hőmérséklete az alumíniumkockában levő izzó áramával szabályozható. A skálával ellátott forgatógomb 5; 6,5; 8 és “HIGH” állásaihoz tartozó állandósult hőmérsékletek rendre ~ 80, 90, 100 és 110ºC.
- Ábrázolja az egyes felületekre külön-külön
- 5. Határozza meg az abszorpciómérő szegmenseit jellemző abszorpciós tényezőket!
- Megjegyzések: Távolítsa el a korábban használt sugárzásdetektort és cserélje fel az abszorpciómérő egységgel! Az abszorpciómérő állványát úgy állítsa be, hogy a mérőfej a sugárforrás középmagasságában legyen! Helyezze a mérőfejet a fekete felülettől 3 - 4 cm távolságba, majd a négy szegmenst 15 másodpercenként váltva kb. 10 percen át mérje a szegmensek hőmérsékletét mérő termisztorok ellenállását! Ábrázolja az egyes felületek hőmérsékletét az idő függvényében! Határozza meg a felületek (relatív) abszorpciós tényezőit! (Lásd 4. feladat.)
 |
PDF formátum
A pdf formátumú leírás nem frissül tovább. Nyomtatáshoz használja az oldalsó menüsoron az Eszközök csoport Nyomtatható változat pontját.
Függelék
A volfram fajlagos ellenállásának a hőmérsékletfüggése
|
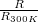
Hőm (K) |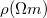 
|
|---|---|---|
| 1.00 | 300 | 5.65E-8 |
| 1.43 | 400 | 8.06E-8 |
| 1.87 | 500 | 10.56E-8 |
| 2.34 | 600 | 13.23E-8 |
| 2.85 | 700 | 16.09E-8 |
| 3.36 | 800 | 19.00E-8 |
| 3.88 | 900 | 21.94E-8 |
| 4.41 | 1000 | 24.93E-8 |
| 4.95 | 1100 | 27.94E-8 |
| 5.48 | 1200 | 30.96E-8 |
| 6.03 | 1300 | 34.08E-8 |
| 6.58 | 1400 | 37.19E-8 |
| 7.14 | 1500 | 40.36E-8 |
| 7.71 | 1600 | 43.55E-8 |
| 8.28 | 1700 | 46.78E-8 |
| 8.86 | 1800 | 50.05E-8 |
| 9.44 | 1900 | 53.35E-8 |
| 10 | 2000 | 56.67E-8 |
| 10.6 | 2100 | 60.06E-8 |
| 11.2 | 2200 | 63.48E-8 |
| 11.8 | 2300 | 66.91E-8 |
| 12.5 | 2400 | 70.39E-8 |
| 13.1 | 2500 | 73.91E-8 |
| 13.7 | 2600 | 77.49E-8 |
| 14.3 | 2700 | 81.04E-8 |
| 15 | 2800 | 84.70E-8 |
| 15.6 | 2900 | 88.33E-8 |
| 16.3 | 3000 | 92.04E-8 |
| 17 | 3100 | 95.76E-8 |
| 17.6 | 3200 | 99.54E-8 |
| 18.3 | 3300 | 103.3E-8 |
| 19 | 3400 | 107.2E-8 |
| 19.7 | 3500 | 111.1E-8 |
| 20.4 | 3600 | 115.0E-8 |
Az alacsony hőmérsékletű sugárforrásban és az abszorpciómérőben levő termisztor ellenállásának hőmérsékletfüggése
| Hőmérséklet (ºC) | Ellenállás ( )
|
|---|---|
| 6 | 255 380 |
| 7 | 242 460 |
| 8 | 230 260 |
| 9 | 218 730 |
| 10 | 207 850 |
| 11 | 197 560 |
| 12 | 187 840 |
| 13 | 178 650 |
| 14 | 169 950 |
| 15 | 161 730 |
| 16 | 153 950 |
| 17 | 148 580 |
| 18 | 139 610 |
| 19 | 133 000 |
| 20 | 126 740 |
| 21 | 120 810 |
| 22 | 115 190 |
| 23 | 109 850 |
| 24 | 104 800 |
| 25 | 100 000 |
| 26 | 95 447 |
| 27 | 91 126 |
| 28 | 87 022 |
| 29 | 83 124 |
| 30 | 79 422 |
| 31 | 75 903 |
| 32 | 72 560 |
| 33 | 69 380 |
| 34 | 66 356 |
| 35 | 63 480 |
| 36 | 60 743 |
| 37 | 58 138 |
| 38 | 55 658 |
| 39 | 53 297 |
| 40 | 51 048 |
| 41 | 48 905 |
| 42 | 46 863 |
| 43 | 44 917 |
| 44 | 43 062 |
| 45 | 41 292 |
| 46 | 39 605 |
| 47 | 37 995 |
| 48 | 36 458 |
| 49 | 34 991 |
| 50 | 33 591 |
| 51 | 32 253 |
| 52 | 30 976 |
| 53 | 29 756 |
| 54 | 28 590 |
| 55 | 27 475 |
| 56 | 26 409 |
| 57 | 25 390 |
| 58 | 24 415 |
| 59 | 23 483 |
| 60 | 22 590 |
| 61 | 21 736 |
| 62 | 20 919 |
| 63 | 20 136 |
| 64 | 19 386 |
| 65 | 18 668 |
| 66 | 17 980 |
| 67 | 17 321 |
| 68 | 16 689 |
| 69 | 16 083 |
| 70 | 15 502 |
| 71 | 14 945 |
| 72 | 14 410 |
| 73 | 13 897 |
| 74 | 13 405 |
| 75 | 12 932 |
| 76 | 12 479 |
| 77 | 12 043 |
| 78 | 11 625 |
| 79 | 11 223 |
| 80 | 10 837 |
| 82 | 10 100 |
| 84 | 9 437.7 |
| 86 | 8 816.0 |
| 88 | 8 240.6 |
| 90 | 7 707.7 |
| 92 | 7 214.0 |
| 94 | 6 755.9 |
| 96 | 6 330.8 |
| 98 | 5 936.1 |
| 100 | 5 569.3 |
| 102 | 5 228.1 |
| 104 | 4 910.7 |
| 106 | 4 615.1 |
| 108 | 4 339.7 |
| 110 | 4 082.9 |
| 112 | 3 843.4 |
| 114 | 3 619.8 |
| 116 | 3 411.0 |
| 118 | 3 215.8 |
| 120 | 3 033.3 |
| 122 | 2 862.5 |
| 124 | 2 702.7 |
| 126 | 2 553.0 |
| 128 | 2 412.6 |
| 130 | 2 281.0 |
| 132 | 2 157.6 |
| 134 | 2 041.7 |
