„RLC körök mérése” változatai közötti eltérés

A Fizipedia wikiből
(Visszavontam Balogh (vita | szerkesztései) szerkesztését (oldid: 28300))
 
(3 szerkesztő 47 közbeeső változata nincs mutatva)
35. sor: 35. sor:
 
$$u(t)=R i(t)$$
 
$$u(t)=R i(t)$$
  
−
összefüggés írja le. Szinuszos gerjesztés [$i(t)=I_0\sin\omega t$] esetén
+
összefüggés írja le. Szinuszos gerjesztés [$i(t)=I\cos\omega t$] esetén
  
−
$$u(t) = R I_0 \sin\omega t,$$
+
$$u(t) = R I \cos\omega t,$$
  
 
azaz az ohmos ellenálláson a feszültség és az áram azonos fázisban van.
 
azaz az ohmos ellenálláson a feszültség és az áram azonos fázisban van.
47. sor: 47. sor:
 
$$u(t) = L \frac{{\rm d}i(t)}{{\rm d}t}$$
 
$$u(t) = L \frac{{\rm d}i(t)}{{\rm d}t}$$
  
−
egyenlet írja le. Szinuszos gerjesztés [$i(t)=I_0\sin\omega t$] esetén
+
egyenlet írja le. Szinuszos gerjesztés [$i(t)=I\cos\omega t$] esetén
  
−
$$u(t) = L \omega I_0 \cos\omega t = L \omega I_0 \sin( \omega t + 90^\circ),$$
+
$$u(t) = -L \omega I \sin\omega t = L \omega I \cos( \omega t + 90^\circ),$$
  
 
tehát a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest.
 
tehát a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest.
59. sor: 59. sor:
 
$$i(t) = C \frac{{\rm d}u(t)}{{\rm d}t}.$$
 
$$i(t) = C \frac{{\rm d}u(t)}{{\rm d}t}.$$
  
−
Szinuszos gerjesztés [$i(t)=I_0\sin\omega t$] esetén:
+
Szinuszos gerjesztés [$i(t)=I\cos\omega t$] esetén:
  
−
$$u(t) = -\frac{I_0}{C\omega}\cos\omega t = \frac{I_0}{C\omega}\sin(\omega t - 90^\circ),$$
+
$$u(t) = \frac{I}{C\omega}\sin\omega t = \frac{I}{C\omega}\cos(\omega t - 90^\circ),$$
  
 
azaz a kondenzátor feszültsége 90°-kal késik az áramhoz képest.
 
azaz a kondenzátor feszültsége 90°-kal késik az áramhoz képest.
67. sor: 67. sor:
 
===Komplex jelölés===
 
===Komplex jelölés===
  
−
Színuszos gerjesztés esetén, állandósult állapotban minden áram- és feszültségfüggvény azonos $\omega$ körfrekvenciával változik. Az egymáshoz képesti fáziskülönbségeket ilyenkor fazorábrával szemléltethetjük. Az 1. ábrán egy soros RLC-kör (részletesen lásd később) fazorábrája látható. Az áram - a soros kapcsolás miatt - mindhárom elemen ugyanakkora, a feszültségek pedig ehhez viszonyítva sietnek, fázisban vannak, illetve késnek.
+
[[Fájl:Fazor.png|bélyegkép|150px|1. ábra]]
 +
Szinuszos gerjesztés esetén, állandósult állapotban minden áram- és feszültségfüggvény azonos $\omega$ körfrekvenciával változik. Az egymáshoz képesti fáziskülönbségeket ilyenkor fazorábrával szemléltethetjük. Az 1. ábrán egy soros RLC-kör (részletesen lásd később) fazorábrája látható. Az áram - a soros kapcsolás miatt - mindhárom elemen ugyanakkora, a feszültségek pedig ehhez viszonyítva sietnek, fázisban vannak, illetve késnek.
  
 
Az áramkörre kapcsolt feszültség a három, sorbakapcsolt feszültséget jelölő ''fazor'' vektori eredője.
 
Az áramkörre kapcsolt feszültség a három, sorbakapcsolt feszültséget jelölő ''fazor'' vektori eredője.
  
−
{| cellpadding="2" style="border: 0px solid darkgray;" align="center"
+
A fazorokat felfoghatjuk komlex számokként is. Így az egyes áram és feszültségjeleket egy-egy komplex szám jelöli. A fazorokhoz hasonlóan a komplex szám abszolút értéke a jel nagyságát (csúcsértékét), a komplex szám arkusza pedig a jel (a kiválasztott fázishelyzethez viszonyított) fázisát adja meg.
−
|- border="0"
+
 
−
|- align="center"
+
'''Figyelem!''' Mivel a villamos hálózatoknál $i$ az áram pillanatértékét jelöli, a komplex egység szokásos jelölése itt $j$ !
−
| [[Fájl:Fazor.jpg|bélyegkép|100px|1. ábra]]
+
−
| [[Fájl:Komplex.jpg|bélyegkép|100px|2. ábra]]
+
−
|- align="center"
+
−
|}
+
  
−
A fazorokat felfoghatjuk komlex számokként is. Így az egyes áram és feszültségjeleket egy-egy komplex szám jelöli. A fazorokhoz hasonlóan a kompex szám abszolút értéke a jel nagyságát, a komplex szám arkusza pedig a jel (a kiválasztott fázishelyzethez viszonyított) fázisát. Az 1. ábrán látható fazorábrán szereplő jeleknek megfelelő komlex mennyiségek:
+
Az 1. ábrán látható fazorábrán szereplő jeleknek megfelelő komplex mennyiségek:
 
$$\mathbf{I}=I$$
 
$$\mathbf{I}=I$$
 
$$\mathbf{U_{\rm R}}=U_{\rm R}=RI$$
 
$$\mathbf{U_{\rm R}}=U_{\rm R}=RI$$
86. sor: 83. sor:
  
 
Ekkor az eredő (komplex) feszültséget nem csak megszerkeszthetjük, hanem egyszerű komplex algebrával ki is számolhatjuk:
 
Ekkor az eredő (komplex) feszültséget nem csak megszerkeszthetjük, hanem egyszerű komplex algebrával ki is számolhatjuk:
−
$$\mathbf{U} = \mathbf{U_{\rm R}}+\mathbf{U_{\rm L}}+\mathbf{U_{\rm C}}= U_R + j\omega L + 1/j\omega C$$
+
$$\mathbf{U} = \mathbf{U_{\rm R}}+\mathbf{U_{\rm L}}+\mathbf{U_{\rm C}}= RI + j\omega LI + I/j\omega C$$
  
 +
Az eredő feszültség nagysága (csúcsértéke) a komplex érték abszolút értéke:
 +
$$U=|\mathbf{U}|=\sqrt{R^2+(\omega L-1/\omega C)^2}I=ZI,$$
 +
ahol $Z$ az eredő ellenállás.
 +
 +
Az eredő feszültség fázisa a komplex feszültség arkusza:
 +
$$\varphi=\arccos\frac{R}{Z}.$$
 +
 +
A komplex áram és feszültség alapján azonban közvetlenül is fel tudjuk írni az áram és a feszültség időfüggvényét:
 +
$$i(t)=\rm{Re}\left(\mathbf{I}e^{j\omega t}\right)=I\cos \omega t$$
 +
$$u(t)=\rm{Re}\left(\mathbf{U}e^{j\omega t}\right)=U\cos(\omega t+\varphi)=ZI\cos(\omega t+\varphi)$$
 +
 +
[[Fájl:Komplex.png|bélyegkép|120px|2. ábra]]
 +
Ha az 1. ábrán látható fazorokat leíró komplex feszültségeket elosztjuk az áramerősség nagyságával, akkor ellenállás dimenziójú komplex mennyiségeket kapunk:
 +
$$\frac{\mathbf{U_{\rm R}}}{I}=\mathbf{R}=R$$
 +
$$\frac{\mathbf{U_{\rm L}}}{I}=\mathbf{X_{\rm L}}=j\omega L$$
 +
$$\frac{\mathbf{U_{\rm C}}}{I}=\mathbf{X_{\rm C}}=1/j\omega C$$
 +
$$\frac{\mathbf{U}}{I}=\mathbf{Z}$$
 +
A komplex ellenállásokkal ugyanúgy számolhatunk egy váltóáramú körben, mint az ohmos ellenállásokkal egyenáramú hálózatok esetében.
 +
 +
A mi esetünkben a soros kapcsolás miatt az eredő (komplex) ellenállás az egyes (komplex) ellenállások összege:
 +
$$\mathbf{Z}=\mathbf{R}+\mathbf{X_{\rm L}}+\mathbf{X_{\rm C}}.$$
 +
 +
A komplex jelölésmóddal bármely áramköri elem leírása olyan, mintha egy ohmos ellenállás lenne:
 +
$$\mathbf{U_{\rm R}}=\mathbf{R}\mathbf{I}$$
 +
$$\mathbf{U_{\rm L}}=\mathbf{X_{\rm L}}\mathbf{I}$$
 +
$$\mathbf{U_{\rm C}}=\mathbf{X_{\rm C}}\mathbf{I}$$
 +
$$\mathbf{U}=\mathbf{Z}\mathbf{I}$$
 +
 +
A komplex ellenállás abszolút értéke a skalár ellenállás értéket adja, míg arkusza azt mutatja meg, hogy az adott áramköri elem mennyivel tolja el a fázist.
  
 
===Szűrő áramkörök===
 
===Szűrő áramkörök===
95. sor: 121. sor:
 
'''Aluláteresztő szűrők'''
 
'''Aluláteresztő szűrők'''
  
−
A 3/a és 3/b ábrákon látható kapcsolások kimenő feszültségeit a komplexjelölésmód segítségével könnyen felírhatjuk. (Egyszerűen az egyenáramú áramkörökben jól ismert feszültségosztó képletet használjuk, de itt komplex ellenállásokkal.) A vastag betűs mennyiségek komplex változók, $j$ a képzetes egység. Ugyanakkor mérni csak valós mennyiségeket lehet, azaz a komplex mennyiségek abszolút értékét!
+
A 3/a és 3/b ábrákon látható kapcsolások kimenő feszültségeit a komplex jelölésmód segítségével könnyen felírhatjuk. (Egyszerűen az egyenáramú áramkörökben jól ismert $U_1=UR_1/(R_1+R_2)$ feszültségosztó képletet használjuk, de itt komplex ellenállásokkal.) A vastag betűs mennyiségek komplex változók, $j$ a képzetes egység. Ugyanakkor mérni csak valós mennyiségeket lehet, azaz a komplex mennyiségek abszolút értékét!
  
 
{| cellpadding="2" style="border: 0px solid darkgray;" align="center"
 
{| cellpadding="2" style="border: 0px solid darkgray;" align="center"
136. sor: 162. sor:
 
Az eddig ismertetett szűrőkapcsolások passzív elemekből állnak, jellemzőjük, hogy a kimeneti jel az áteresztési tartományokban sem nagyobb a bemenetinél. Aktív eszközökkel (pl. [http://en.wikipedia.org/wiki/Operational_amplifier műveleti erősítő]) készíthető olyan szűrő, amelyik egyben a jel erősítését is elvégzi az áteresztési tartományban.
 
Az eddig ismertetett szűrőkapcsolások passzív elemekből állnak, jellemzőjük, hogy a kimeneti jel az áteresztési tartományokban sem nagyobb a bemenetinél. Aktív eszközökkel (pl. [http://en.wikipedia.org/wiki/Operational_amplifier műveleti erősítő]) készíthető olyan szűrő, amelyik egyben a jel erősítését is elvégzi az áteresztési tartományban.
  
−
[[Fájl:Soros_RLC.jpg|bélyegkép|200px|4. ábra]]
+
[[Fájl:Soros_RLC.jpg|bélyegkép|250px|6. ábra]]
 
===Soros rezgőkör===
 
===Soros rezgőkör===
  
−
Kondenzátor és tekercs soros kapcsolását (a veszteségeket soros ellenállással figyelembe véve) soros rezgőkörnek nevezik (4. ábra).
+
Kondenzátor és tekercs soros kapcsolását (a veszteségeket soros ellenállással figyelembe véve) soros rezgőkörnek nevezik (6. ábra).
  
−
A hálózat eredő impedanciája:
+
Ez az áramkör a [[A kényszerrezgés vizsgálata|kényszerrezgés]] elektromos megfelelője.
  
−
$$\mathbf{Z}(\omega) = R + j\omega L + 1/j\omega C$$
+
Ha a kondenzátort feltöltenénk, majd a bemenetet rövidre zárnánk, akkor egy csillapodó rezgést figyelhetnénk meg. A nagy frekvencia és a gyors csillapodás miatt azonban ezt nehezebb megfigyelni, mint egy kitérített, és magára hagyott mechanikai rezgő rendszert.
 +
 
 +
Ha a bemenetre szinuszos gerjesztő feszültséget kapcsolunk, akkor viszont a kényszerrezgéssel teljesen analóg viselkedést figyelhetünk meg.
 +
 
 +
Ha a rezgőkörre kapcsolt feszültség $u_0(t)=U_0\sin\omega t$, és a kondenzátor töltését az idő függvényében $q(t)$ írja le, akkor
 +
$$u_{\rm C}=q(t)/C$$
 +
$$i(t)=\dot{q}(t)$$
 +
$$u_{\rm R}=Ri(t)=R\dot{q}(t)$$
 +
$$u_{\rm L}=L\dot{i}(t)=L\ddot{q}(t)$$
 +
$$L\ddot{q}(t)+R\dot{q}(t)+q(t)/C=U_0\sin\omega t$$
 +
$$\ddot{q}(t)+\frac{R}{L}\dot{q}(t)+\frac{1}{LC}q(t)=\frac{U_0}{L}\sin\omega t.$$
 +
Ez a differenciálegyenlet $R/L=2\beta$ és $1/LC=\omega_0^2$ jelöléssel a kényszerrezgést leíró differenciálegyenlettel teljesen analóg egyenletet eredményez. Ennek következtében az általános megoldás is teljesen analóg: traniens és állandósult tagokat tartalmaz.
 +
 
 +
Esetünkben a tranziens tag hamar elhal, és az állandósult tagot tanulmányozhatjuk. Az amplitúdó itt a kondenzátor töltése, de számunkra sokkal érdekesebb ennek deriváltja, a körben folyó áramerősség. Ez tehát az analógia alapján a mechanikai rezgés sebességrezonanciájával egyezik meg:
 +
$$I(\omega)=\frac{U_0}{L\sqrt{\left(\omega^2-\omega_0^2\right)^2+4\beta^2\omega^2}}.$$
 +
Ha behelyettesítjük $\beta$ és $\omega_0$ értékét, akkor
 +
$$I(\omega)=\frac{U_0}{\sqrt{(\omega L-1/\omega C)^2+R^2}}.$$
 +
 
 +
 
 +
Ezt az eredményt azonban sokkal egyszerűbben megkapjuk a fentebb ismertetett komplex ellenállások felhasználásával. (Természetesen csak az állandósult állapotot vizsgálhatjuk így, a tranzienseket nem.)
 +
 
 +
A hálózat eredő impedanciája:
 +
$$\mathbf{Z}(\omega) = j\omega L + 1/j\omega C + R$$
  
−
[[Fájl:Z_I.jpg|bélyegkép|250px|5. ábra]]
 
 
Az impedancia abszolút értéke és fázisszöge:
 
Az impedancia abszolút értéke és fázisszöge:
  
−
$$Z(\omega) = \sqrt{R^2 + (\omega L-1/\omega C)^2}$$
+
$$Z(\omega) = \sqrt{(\omega L-1/\omega C)^2+R^2}$$
−
$$\tan\varphi = \frac{\omega L - 1/\omega C}{R}$$
+
$$\varphi = \arccos\frac{R}{Z}$$
  
 +
[[Fájl:Z_I.jpg|bélyegkép|350px|7. ábra]]
 
A körben folyó áram:
 
A körben folyó áram:
  
−
$$I(\omega) = \frac{U_{be}}{\sqrt{R^2 + (\omega L-1/\omega C)^2}}$$
+
$$I(\omega) = \frac{U_0}{Z}=\frac{U_0}{\sqrt{(\omega L-1/\omega C)^2+R^2}}$$
  
−
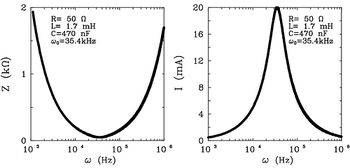
A $Z(\omega)$ és $I(\omega)$ függvényeket ábrázolva a kapcsolás jellegzetes tulajdonságaira derül fény (5. ábra).
+
A $Z(\omega)$ és $I(\omega)$ függvényeket ábrázolva a kapcsolás jellegzetes tulajdonságaira derül fény (7. ábra).
  
 
Látható, hogy az eredő impedanciának $\omega L = 1/\omega C$ esetén az
 
Látható, hogy az eredő impedanciának $\omega L = 1/\omega C$ esetén az
161. sor: 209. sor:
 
$$\omega_0 = \frac{1}{\sqrt{LC}}$$
 
$$\omega_0 = \frac{1}{\sqrt{LC}}$$
  
−
körfrekvencián minimuma van, értéke valós, a veszteségi ellenállással egyezik meg. A jelenséget rezonanciának, $\omega_0$-t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián a körben folyó áram értéke maximális, úgynevezett áramrezonancia alakul ki. A bemeneti feszültség és a körben folyó áram közötti fázisszög az impedancia fázisszöge, ebben az esetben nulla.  
+
körfrekvencián minimuma van, értéke valós, az ohmos (veszteségi) ellenállással egyezik meg. A jelenséget rezonanciának, $\omega_0$-t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián a körben folyó áram értéke maximális, ''áramrezonancia'' alakul ki. A bemeneti feszültség és a körben folyó áram közötti fázisszög az impedancia fázisszöge, ebben az esetben nulla.  
−
Ez az áram – kis veszteségi ellenállást feltételezve – igen nagy feszültségeket hozhat létre a kondenzátoron és a tekercsen. Azonban ezek a feszültségek egymással 180°-os szöget zárnak be, abszolút értékük megegyezik, hiszen azonos áram folyik át rajtuk (6. ábra).
+
Ez az áram – kis veszteségi ellenállást feltételezve – igen nagy feszültségeket hozhat létre a kondenzátoron és a tekercsen. Azonban ezek a feszültségek egymáshoz viszonyítva 180°-os fázisban vannak, abszolút értékük pedig megegyezik (hiszen azonos áram folyik át rajtuk), így egymást kiegyenlítik.
 +
 
 +
''Megjegyzés:'' A kondenzátoron és a tekercsen eső feszültségnek nem pontosan az $\omega_0$ rezonanciafrekvencián van maximuma - hasonlóan a mechanikai kényszerrezgés amplitúdórezonanciájához.
  
 
==Mérési feladatok==
 
==Mérési feladatok==
171. sor: 221. sor:
  
 
{{figN|RLC.png|figN:7|7. ábra|500}}
 
{{figN|RLC.png|figN:7|7. ábra|500}}
 +
{{figN|RLC panel.png|figN:8|8. ábra|500}}
  
 
* '' Általános megjegyzések:''
 
* '' Általános megjegyzések:''
177. sor: 228. sor:
 
** ''Az oszcilloszkópot csak esetleges ellenőrzésre használja, a frekvenciákat és a feszültségeket a digitális műszerekkel kell mérni.''
 
** ''Az oszcilloszkópot csak esetleges ellenőrzésre használja, a frekvenciákat és a feszültségeket a digitális műszerekkel kell mérni.''
  
−
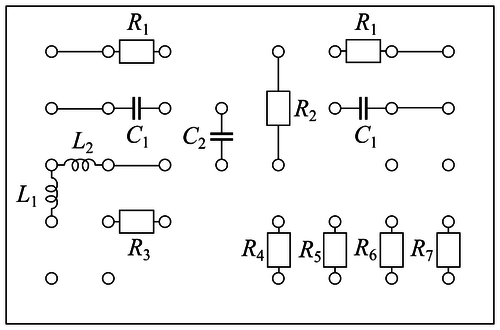
'''1.''' Mérje meg a dobozban található ellenállások értékét valamint a tekercsek ohmos ellenállását multiméterrel!
+
'''1.''' Mérje meg a dobozban (7. és 8. ábra) található $R_1\dots R_7$ ellenállások értékét valamint a tekercsek $R_{L1}$ és $R_{L2}$ ohmos ellenállását multiméterrel!
 
* ''Az ellenállásmérést csak hálózatba be nem kötött elemeken szabad végezni!''
 
* ''Az ellenállásmérést csak hálózatba be nem kötött elemeken szabad végezni!''
 +
 +
A kondenzátorok és tekercsek körülbelüli kapacitása és induktivitása (az áramkörök tervezéséhez): $C_1\approx 500 \rm{nF}$, $C_2=2C_1\approx 1000 \rm{nF}$, $L_1\approx 2 \rm{mH}$, $L_2\approx 100\rm{mH}$.
  
 
'''2.''' Állítson össze aluláteresztő szűrőt kondenzátor felhasználásával! Mérje meg a kimenő feszültséget $\omega$ függvényében! Ábrázolja a $20\lg(U_{ki}/U_{be})$ – $\lg\omega$ függvényt! Illesszen a mért adatokra az elméletnek megfelelő görbét! Az illesztésből határozza meg a szűrőre jellemző $\omega_0 = 1/RC$ körfrekvenciát, majd ebből az ellenállás ismeretében a kondenzátor (mért) $C$ kapacitását! ($U_{be} \approx 1{\rm V}$ legyen!)
 
'''2.''' Állítson össze aluláteresztő szűrőt kondenzátor felhasználásával! Mérje meg a kimenő feszültséget $\omega$ függvényében! Ábrázolja a $20\lg(U_{ki}/U_{be})$ – $\lg\omega$ függvényt! Illesszen a mért adatokra az elméletnek megfelelő görbét! Az illesztésből határozza meg a szűrőre jellemző $\omega_0 = 1/RC$ körfrekvenciát, majd ebből az ellenállás ismeretében a kondenzátor (mért) $C$ kapacitását! ($U_{be} \approx 1{\rm V}$ legyen!)
192. sor: 245. sor:
 
* ''Az illesztésnél vegye figyelembe a tekercs (korábban megmért) ohmos ellenállását is!
 
* ''Az illesztésnél vegye figyelembe a tekercs (korábban megmért) ohmos ellenállását is!
  
−
'''5.''' Végezze el az előző mérést egy nagyobb sorbakötött ellenállással is! Végezze el most is az illesztést! Ábrázolja a két mérésnél kapott $I(\omega)$ rezonanciagörbéket közös garfikonban!
+
'''5.''' Végezze el az előző mérést egy nagyobb sorba kötött ellenállással is! Végezze el most is az illesztést! Ábrázolja a két mérésnél kapott $I(\omega)$ rezonanciagörbéket közös grafikonban!
  
−
'''FONTOS!''' Ebből a mérésból és a [[A kényszerrezgés vizsgálata|kényszerrezgés vizsgálata]] mérésből '''közös jegyzőkönyvet''' kell készítenie a második mérést követő héten. A jegyzőkönyvben térjen ki a két mérés közös vonásaira, mutasson rá az egymásnak megfelelő, egymással analóg jelenségekre - és a méréstechnikai vagy más különbségekre is!
+
'''FONTOS!''' Ebből a mérésből és a [[A kényszerrezgés vizsgálata|kényszerrezgés vizsgálata]] mérésből '''közös jegyzőkönyvet''' kell készítenie a második mérést követő héten. A jegyzőkönyvben térjen ki a két mérés közös vonásaira, mutasson rá az egymásnak megfelelő, egymással analóg jelenségekre - és a méréstechnikai vagy más különbségekre is!
  
  

A lap jelenlegi, 2022. szeptember 8., 20:56-kori változata


A harmonikus rezgés alapvető fizikai jelenség. Vibrációk, oszcillációk harmonikus rezgéssel modellezhetők, ha az amplitúdók elég kicsinyek. A harmonikus mozgás differenciálegyenlete nem csupán a klasszikus fizikában (mechanika, villamosságtan), de a kvantumfizikában, a szilárdtestfizikában és az optikában is gyakran előfordul.

Ebben a mérésben elektromos rezgőköröket (és frekvenciafüggő áramköri elemeken alapuló szűrőket) fog tanulmányozni. Az ezzel teljesen analóg módon leírható mechanikai rezgéseket a kényszerrezgés vizsgálata mérésében tanulmányozza. A két mérésből közös jegyzőkönyvet kell készítenie.


Tartalomjegyzék


Elméleti összefoglaló

A felhasznált áramköri elemek:

Ohmos ellenállás

Az ellenálláson eső feszültséget az

\[u(t)=R i(t)\]

összefüggés írja le. Szinuszos gerjesztés [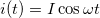\setbox0\hbox{$i(t)=I\cos\omega t$}% \message{//depth:\the\dp0//}% \box0%] esetén

\[u(t) = R I \cos\omega t,\]

azaz az ohmos ellenálláson a feszültség és az áram azonos fázisban van.

Tekercs

A tekercsben indukálódó feszültséget az

\[u(t) = L \frac{{\rm d}i(t)}{{\rm d}t}\]

egyenlet írja le. Szinuszos gerjesztés [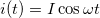\setbox0\hbox{$i(t)=I\cos\omega t$}% \message{//depth:\the\dp0//}% \box0%] esetén

\[u(t) = -L \omega I \sin\omega t = L \omega I \cos( \omega t + 90^\circ),\]

tehát a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest.

Kondenzátor

A kondenzátoron átfolyó áram időfüggését az alábbi egyenlet írja le:

\[i(t) = C \frac{{\rm d}u(t)}{{\rm d}t}.\]

Szinuszos gerjesztés [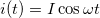\setbox0\hbox{$i(t)=I\cos\omega t$}% \message{//depth:\the\dp0//}% \box0%] esetén:

\[u(t) = \frac{I}{C\omega}\sin\omega t = \frac{I}{C\omega}\cos(\omega t - 90^\circ),\]

azaz a kondenzátor feszültsége 90°-kal késik az áramhoz képest.

Komplex jelölés

1. ábra

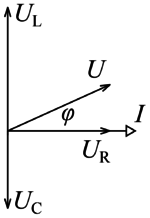
Szinuszos gerjesztés esetén, állandósult állapotban minden áram- és feszültségfüggvény azonos \setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0% körfrekvenciával változik. Az egymáshoz képesti fáziskülönbségeket ilyenkor fazorábrával szemléltethetjük. Az 1. ábrán egy soros RLC-kör (részletesen lásd később) fazorábrája látható. Az áram - a soros kapcsolás miatt - mindhárom elemen ugyanakkora, a feszültségek pedig ehhez viszonyítva sietnek, fázisban vannak, illetve késnek.

Az áramkörre kapcsolt feszültség a három, sorbakapcsolt feszültséget jelölő fazor vektori eredője.

A fazorokat felfoghatjuk komlex számokként is. Így az egyes áram és feszültségjeleket egy-egy komplex szám jelöli. A fazorokhoz hasonlóan a komplex szám abszolút értéke a jel nagyságát (csúcsértékét), a komplex szám arkusza pedig a jel (a kiválasztott fázishelyzethez viszonyított) fázisát adja meg.

Figyelem! Mivel a villamos hálózatoknál 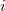\setbox0\hbox{$i$}% \message{//depth:\the\dp0//}% \box0% az áram pillanatértékét jelöli, a komplex egység szokásos jelölése itt \setbox0\hbox{$j$}% \message{//depth:\the\dp0//}% \box0% !

Az 1. ábrán látható fazorábrán szereplő jeleknek megfelelő komplex mennyiségek:

\[\mathbf{I}=I\]
\[\mathbf{U_{\rm R}}=U_{\rm R}=RI\]
\[\mathbf{U_{\rm L}}=jU_{\rm L}=j\omega LI\]
\[\mathbf{U_{\rm C}}=-jU_{\rm C}=I/j\omega C\]

Ekkor az eredő (komplex) feszültséget nem csak megszerkeszthetjük, hanem egyszerű komplex algebrával ki is számolhatjuk:

\[\mathbf{U} = \mathbf{U_{\rm R}}+\mathbf{U_{\rm L}}+\mathbf{U_{\rm C}}= RI + j\omega LI + I/j\omega C\]

Az eredő feszültség nagysága (csúcsértéke) a komplex érték abszolút értéke:

\[U=|\mathbf{U}|=\sqrt{R^2+(\omega L-1/\omega C)^2}I=ZI,\]

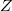ahol \setbox0\hbox{$Z$}% \message{//depth:\the\dp0//}% \box0% az eredő ellenállás.

Az eredő feszültség fázisa a komplex feszültség arkusza:

\[\varphi=\arccos\frac{R}{Z}.\]

A komplex áram és feszültség alapján azonban közvetlenül is fel tudjuk írni az áram és a feszültség időfüggvényét:

\[i(t)=\rm{Re}\left(\mathbf{I}e^{j\omega t}\right)=I\cos \omega t\]
\[u(t)=\rm{Re}\left(\mathbf{U}e^{j\omega t}\right)=U\cos(\omega t+\varphi)=ZI\cos(\omega t+\varphi)\]
2. ábra

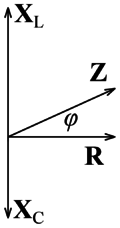
Ha az 1. ábrán látható fazorokat leíró komplex feszültségeket elosztjuk az áramerősség nagyságával, akkor ellenállás dimenziójú komplex mennyiségeket kapunk:

\[\frac{\mathbf{U_{\rm R}}}{I}=\mathbf{R}=R\]
\[\frac{\mathbf{U_{\rm L}}}{I}=\mathbf{X_{\rm L}}=j\omega L\]
\[\frac{\mathbf{U_{\rm C}}}{I}=\mathbf{X_{\rm C}}=1/j\omega C\]
\[\frac{\mathbf{U}}{I}=\mathbf{Z}\]

A komplex ellenállásokkal ugyanúgy számolhatunk egy váltóáramú körben, mint az ohmos ellenállásokkal egyenáramú hálózatok esetében.

A mi esetünkben a soros kapcsolás miatt az eredő (komplex) ellenállás az egyes (komplex) ellenállások összege:

\[\mathbf{Z}=\mathbf{R}+\mathbf{X_{\rm L}}+\mathbf{X_{\rm C}}.\]

A komplex jelölésmóddal bármely áramköri elem leírása olyan, mintha egy ohmos ellenállás lenne:

\[\mathbf{U_{\rm R}}=\mathbf{R}\mathbf{I}\]
\[\mathbf{U_{\rm L}}=\mathbf{X_{\rm L}}\mathbf{I}\]
\[\mathbf{U_{\rm C}}=\mathbf{X_{\rm C}}\mathbf{I}\]
\[\mathbf{U}=\mathbf{Z}\mathbf{I}\]

A komplex ellenállás abszolút értéke a skalár ellenállás értéket adja, míg arkusza azt mutatja meg, hogy az adott áramköri elem mennyivel tolja el a fázist.

Szűrő áramkörök

Szűrők segítségével egy különböző frekvenciájú rezgésekből álló elektromos jelből ki lehet szűrni bizonyos frekvenciatartományokat. Ezen a mérésen csak RC alul- és felüláteresztő szűrőket fog mérni, de itt néhány más kapcsolást is bemutatunk.

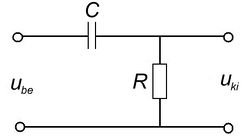
Aluláteresztő szűrők

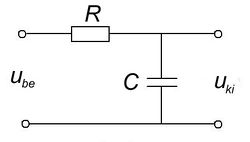
A 3/a és 3/b ábrákon látható kapcsolások kimenő feszültségeit a komplex jelölésmód segítségével könnyen felírhatjuk. (Egyszerűen az egyenáramú áramkörökben jól ismert 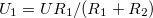\setbox0\hbox{$U_1=UR_1/(R_1+R_2)$}% \message{//depth:\the\dp0//}% \box0% feszültségosztó képletet használjuk, de itt komplex ellenállásokkal.) A vastag betűs mennyiségek komplex változók, \setbox0\hbox{$j$}% \message{//depth:\the\dp0//}% \box0% a képzetes egység. Ugyanakkor mérni csak valós mennyiségeket lehet, azaz a komplex mennyiségek abszolút értékét!

3/a ábra
3/b ábra
\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{1/j\omega C}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega RC} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega RC}\right|=\frac{1}{\sqrt{1+(\omega RC)^2}} \end{array} \]
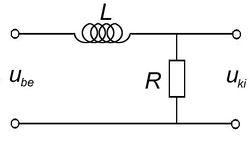
\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{R}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega L/R} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega L/R}\right|=\frac{1}{\sqrt{1+(\omega L/R)^2}} \end{array} \]

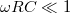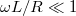A kimeneti és bemeneti feszültségek hányadosa, a hálózatra jellemző, frekvenciafüggő kifejezés. A két kifejezés formailag azonos, tehát a két kapcsolás azonos jellegű viselkedést mutat. 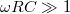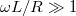Ameddig \setbox0\hbox{$\omega RC \ll 1$}% \message{//depth:\the\dp0//}% \box0% vagy \setbox0\hbox{$\omega L/R \ll 1$}% \message{//depth:\the\dp0//}% \box0%, a kifejezések értéke 1; ha \setbox0\hbox{$\omega RC \gg 1$}% \message{//depth:\the\dp0//}% \box0% vagy \setbox0\hbox{$\omega L/R \gg 1$}% \message{//depth:\the\dp0//}% \box0%, a hányados értéke 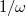\setbox0\hbox{$1/\omega$}% \message{//depth:\the\dp0//}% \box0% szerint csökken. Ez azt jelenti, hogy adott \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$C$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$L$}% \message{//depth:\the\dp0//}% \box0% esetén az alacsony frekvenciájú jelek csillapítás nélkül jelennek meg a kimeneten, míg magasabb frekvenciákon a kimenő feszültség egyre kisebb. Ezeket a kapcsolásokat aluláteresztő szűrőknek nevezik.

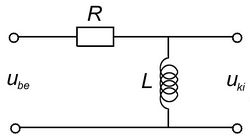
Felüláteresztő szűrő

A 4/a és a 4/b ábrákon látható kapcsolásokat leíró egyenletek az előző pontban követett eljárás alapján az alábbiak szerint alakulnak.

4/a ábra
4/b ábra
\[ \begin{array}{rcl} \mathbf{U}_{{\rm ki}} & = & \mathbf{U}_{{\rm be}} \frac{R}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{{\rm ki}}}{\mathbf{U}_{{\rm be}}} & = & \frac{1}{1 + 1/j\omega RC} \\ \\ \frac{U_{{\rm ki}}}{U_{{\rm be}}} & = & \left|\frac{1}{1 + 1/j\omega RC}\right|=\frac{1}{\sqrt{1+(1/\omega RC)^2}} \end{array} \]
\[ \begin{array}{rcl} \mathbf{U}_{{\rm ki}} & = & \mathbf{U}_{{\rm be}} \frac{j\omega L}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{{\rm ki}}}{\mathbf{U}_{{\rm be}}} & = & \frac{1}{1 + R/j\omega L} \\ \\ \frac{U_{{\rm ki}}}{U_{{\rm be}}} & = & \left|\frac{1}{1 + R/j\omega L}\right|=\frac{1}{\sqrt{1+(R/\omega L)^2}} \end{array} \]

A kifejezésekből jól látszik, hogy a kapcsolások a kisfrekvenciás jeleket nem engedik a kimenetre, míg a nagyfrekvenciás jelek csillapítás nélkül jelennek meg a kimeneti pontokon. Ezek felüláteresztő szűrők.

5. ábra

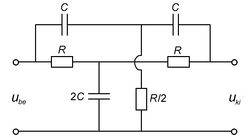
Sávzáró és sáváteresztő szűrő

Alul és felüláteresztő szűrők egymás után kapcsolásával és az áteresztési tartományok helyes megválasztásával előállítható olyan szűrő, amelyik csak egy meghatározott tartományban csillapítja a jelet. Az ilyen kapcsolást nevezik sávzáró szűrőnek. Ennek egy realizálása a 5. ábrán látható kettős T szűrő.

A kapcsolás részletes elemzése nélkül is megállapítható, hogy alacsony frekvenciákon a hosszági ellenállásokon, magas frekvenciákon a hosszági kondenzátorokon jut jel a kimenetre.

Ehhez hasonlóan alul- és felüláteresztő szűrőkből összeállítható olyan kapcsolás is, amely csak egy meghatározott tartományban engedi át a jeleket. Ezek a sáváteresztő szűrők.

Az eddig ismertetett szűrőkapcsolások passzív elemekből állnak, jellemzőjük, hogy a kimeneti jel az áteresztési tartományokban sem nagyobb a bemenetinél. Aktív eszközökkel (pl. műveleti erősítő) készíthető olyan szűrő, amelyik egyben a jel erősítését is elvégzi az áteresztési tartományban.

6. ábra

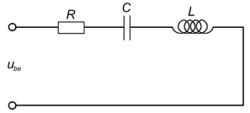
Soros rezgőkör

Kondenzátor és tekercs soros kapcsolását (a veszteségeket soros ellenállással figyelembe véve) soros rezgőkörnek nevezik (6. ábra).

Ez az áramkör a kényszerrezgés elektromos megfelelője.

Ha a kondenzátort feltöltenénk, majd a bemenetet rövidre zárnánk, akkor egy csillapodó rezgést figyelhetnénk meg. A nagy frekvencia és a gyors csillapodás miatt azonban ezt nehezebb megfigyelni, mint egy kitérített, és magára hagyott mechanikai rezgő rendszert.

Ha a bemenetre szinuszos gerjesztő feszültséget kapcsolunk, akkor viszont a kényszerrezgéssel teljesen analóg viselkedést figyelhetünk meg.

Ha a rezgőkörre kapcsolt feszültség 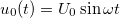\setbox0\hbox{$u_0(t)=U_0\sin\omega t$}% \message{//depth:\the\dp0//}% \box0%, és a kondenzátor töltését az idő függvényében 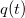\setbox0\hbox{$q(t)$}% \message{//depth:\the\dp0//}% \box0% írja le, akkor

\[u_{\rm C}=q(t)/C\]
\[i(t)=\dot{q}(t)\]
\[u_{\rm R}=Ri(t)=R\dot{q}(t)\]
\[u_{\rm L}=L\dot{i}(t)=L\ddot{q}(t)\]
\[L\ddot{q}(t)+R\dot{q}(t)+q(t)/C=U_0\sin\omega t\]
\[\ddot{q}(t)+\frac{R}{L}\dot{q}(t)+\frac{1}{LC}q(t)=\frac{U_0}{L}\sin\omega t.\]

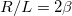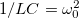Ez a differenciálegyenlet \setbox0\hbox{$R/L=2\beta$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$1/LC=\omega_0^2$}% \message{//depth:\the\dp0//}% \box0% jelöléssel a kényszerrezgést leíró differenciálegyenlettel teljesen analóg egyenletet eredményez. Ennek következtében az általános megoldás is teljesen analóg: traniens és állandósult tagokat tartalmaz.

Esetünkben a tranziens tag hamar elhal, és az állandósult tagot tanulmányozhatjuk. Az amplitúdó itt a kondenzátor töltése, de számunkra sokkal érdekesebb ennek deriváltja, a körben folyó áramerősség. Ez tehát az analógia alapján a mechanikai rezgés sebességrezonanciájával egyezik meg:

\[I(\omega)=\frac{U_0}{L\sqrt{\left(\omega^2-\omega_0^2\right)^2+4\beta^2\omega^2}}.\]

Ha behelyettesítjük \setbox0\hbox{$\beta$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0% értékét, akkor

\[I(\omega)=\frac{U_0}{\sqrt{(\omega L-1/\omega C)^2+R^2}}.\]


Ezt az eredményt azonban sokkal egyszerűbben megkapjuk a fentebb ismertetett komplex ellenállások felhasználásával. (Természetesen csak az állandósult állapotot vizsgálhatjuk így, a tranzienseket nem.)

A hálózat eredő impedanciája:

\[\mathbf{Z}(\omega) = j\omega L + 1/j\omega C + R\]

Az impedancia abszolút értéke és fázisszöge:

\[Z(\omega) = \sqrt{(\omega L-1/\omega C)^2+R^2}\]
\[\varphi = \arccos\frac{R}{Z}\]
7. ábra

A körben folyó áram:

\[I(\omega) = \frac{U_0}{Z}=\frac{U_0}{\sqrt{(\omega L-1/\omega C)^2+R^2}}\]

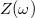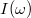A \setbox0\hbox{$Z(\omega)$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$I(\omega)$}% \message{//depth:\the\dp0//}% \box0% függvényeket ábrázolva a kapcsolás jellegzetes tulajdonságaira derül fény (7. ábra).

Látható, hogy az eredő impedanciának 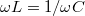\setbox0\hbox{$\omega L = 1/\omega C$}% \message{//depth:\the\dp0//}% \box0% esetén az

\[\omega_0 = \frac{1}{\sqrt{LC}}\]

körfrekvencián minimuma van, értéke valós, az ohmos (veszteségi) ellenállással egyezik meg. A jelenséget rezonanciának, \setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0%-t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián a körben folyó áram értéke maximális, áramrezonancia alakul ki. A bemeneti feszültség és a körben folyó áram közötti fázisszög az impedancia fázisszöge, ebben az esetben nulla. Ez az áram – kis veszteségi ellenállást feltételezve – igen nagy feszültségeket hozhat létre a kondenzátoron és a tekercsen. Azonban ezek a feszültségek egymáshoz viszonyítva 180°-os fázisban vannak, abszolút értékük pedig megegyezik (hiszen azonos áram folyik át rajtuk), így egymást kiegyenlítik.

Megjegyzés: A kondenzátoron és a tekercsen eső feszültségnek nem pontosan az \setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0% rezonanciafrekvencián van maximuma - hasonlóan a mechanikai kényszerrezgés amplitúdórezonanciájához.

Mérési feladatok

A méréshez rendelkezésre álló eszközök

  • A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
7. ábra
8. ábra
  • Általános megjegyzések:
    • A méréshez szükséges alkatrészek egy átlátszó plexidobozban találhatók, banánhüvelyes kivezetésekkel. Az alkatrészek körülbelüli értékei a dobozról leolvashatók, illetve a mellékelt lapon is megtalálhatók.
    • Az egyes mérési feladatok elvégzésekor azokban a frekvenciatartományokban, ahol jelentős a kimenő jel változása, sűrűbben vegyen fel mérési pontokat!
    • Az oszcilloszkópot csak esetleges ellenőrzésre használja, a frekvenciákat és a feszültségeket a digitális műszerekkel kell mérni.

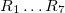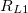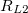1. Mérje meg a dobozban (7. és 8. ábra) található \setbox0\hbox{$R_1\dots R_7$}% \message{//depth:\the\dp0//}% \box0% ellenállások értékét valamint a tekercsek \setbox0\hbox{$R_{L1}$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$R_{L2}$}% \message{//depth:\the\dp0//}% \box0% ohmos ellenállását multiméterrel!

  • Az ellenállásmérést csak hálózatba be nem kötött elemeken szabad végezni!

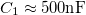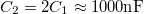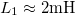A kondenzátorok és tekercsek körülbelüli kapacitása és induktivitása (az áramkörök tervezéséhez): \setbox0\hbox{$C_1\approx 500 \rm{nF}$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$C_2=2C_1\approx 1000 \rm{nF}$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$L_1\approx 2 \rm{mH}$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$L_2\approx 100\rm{mH}$}% \message{//depth:\the\dp0//}% \box0%.

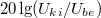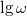2. Állítson össze aluláteresztő szűrőt kondenzátor felhasználásával! Mérje meg a kimenő feszültséget \setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0% függvényében! Ábrázolja a \setbox0\hbox{$20\lg(U_{ki}/U_{be})$}% \message{//depth:\the\dp0//}% \box0% – \setbox0\hbox{$\lg\omega$}% \message{//depth:\the\dp0//}% \box0% függvényt! Illesszen a mért adatokra az elméletnek megfelelő görbét! Az illesztésből határozza meg a szűrőre jellemző 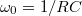\setbox0\hbox{$\omega_0 = 1/RC$}% \message{//depth:\the\dp0//}% \box0% körfrekvenciát, majd ebből az ellenállás ismeretében a kondenzátor (mért) \setbox0\hbox{$C$}% \message{//depth:\the\dp0//}% \box0% kapacitását! 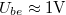(\setbox0\hbox{$U_{be} \approx 1{\rm V}$}% \message{//depth:\the\dp0//}% \box0% legyen!)

  • A multiméterekkel mérhető frekvenciatartomány: 5 Hz – 100 kHz. Az \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0% és (névleges) \setbox0\hbox{$C$}% \message{//depth:\the\dp0//}% \box0% értékeket úgy kell kiválasztani a panelen lévők közül, hogy \setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0% lehetőleg ennek a tartománynak a közepe táján (0,5-1 kHz körül) legyen. Figyelem! A képletekből \setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%-t számolunk, de a műszerek \setbox0\hbox{$f$}% \message{//depth:\the\dp0//}% \box0%-et mérnek!
  • A mérési naplóban írja le, hogy milyen elemeket használt fel a kapcsolás összeállításához! Válaszát számítással indokolja.
  • Mivel az eredményeket logaritmikus skálán fogja ábrázolni, érdemes nagyjából logaritmikusan egyenletes sűrűséggel felvenni az adatokat. Pl.: 5 Hz, 10 Hz, 20 Hz, 50 Hz, 100 Hz, ...

3. Állítson össze felüláteresztő szűrőt kondenzátor felhasználásával! A feladatokat az 2. pont szerint végezze el!

  • Vegye észre, hogy az alul- és felüláteresztő szűrő ugyanaz a kapcsolás, csak az egyiknél az ellenálláson, a másiknál a kondenzátoron mérjük a kimenő feszültséget. Mivel három műszer van, az egyikkel a bemenő feszültséget ellenőrizze, a másik kettővel pedig egyszerre lehet mérni az ellenálláson és kondenzátoron eső feszültséget, így a két karakterisztika egyszerre felvehető.

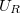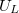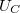4. Állítson össze soros rezgőkört! \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0% külön elemként legyen bekötve, mert a kör áramát az ellenálláson eső feszültségből fogja meghatározni! A frekvencia függvényében mérje meg \setbox0\hbox{$U_R$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$U_L$}% \message{//depth:\the\dp0//}% \box0%, és \setbox0\hbox{$U_C$}% \message{//depth:\the\dp0//}% \box0% értékeit! 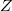Számítsa ki és ábrázolja a körben folyó \setbox0\hbox{$I$}% \message{//depth:\the\dp0//}% \box0% áramot és a \setbox0\hbox{$Z$}% \message{//depth:\the\dp0//}% \box0% eredő impedanciát \setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0% függvényében. A mért adatokra illesszen megfelelő függvényeket, és az illesztésből határozza meg \setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0%-t. 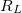Az eredmény (és a korábban megmért \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$R_L$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$C$}% \message{//depth:\the\dp0//}% \box0% értékek) alapján határozza meg a tekercs \setbox0\hbox{$L$}% \message{//depth:\the\dp0//}% \box0% induktivitását!

  • Melyik ellenállást célszerű választani az RLC-kör összeállításához, ha azt szeretné, hogy a rezonanciagörbe minél élesebb legyen? Válaszát indokolja!
  • Az illesztésnél vegye figyelembe a tekercs (korábban megmért) ohmos ellenállását is!

5. Végezze el az előző mérést egy nagyobb sorba kötött ellenállással is! Végezze el most is az illesztést! Ábrázolja a két mérésnél kapott 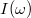\setbox0\hbox{$I(\omega)$}% \message{//depth:\the\dp0//}% \box0% rezonanciagörbéket közös grafikonban!

FONTOS! Ebből a mérésből és a kényszerrezgés vizsgálata mérésből közös jegyzőkönyvet kell készítenie a második mérést követő héten. A jegyzőkönyvben térjen ki a két mérés közös vonásaira, mutasson rá az egymásnak megfelelő, egymással analóg jelenségekre - és a méréstechnikai vagy más különbségekre is!


Vissza a Fizika laboratórium 1. tárgyoldalára.


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=RLC_körök_mérése&oldid=28304”