„Mérések interferométerrel” változatai közötti eltérés

A Fizipedia wikiből
a (Balogh átnevezte a(z) Empty2 lapot a következő névre: Mérések interferométerrel)
 
(2 szerkesztő 39 közbeeső változata nincs mutatva)
22. sor: 22. sor:
  
 
''Ennek érdekében:''
 
''Ennek érdekében:''
−
* áttekintjük a diffrakció és az interferencia elméletét,
+
* áttekintjük az interferencia elméletét,
 
* megmérjük a lézerfény koherenciahosszát,
 
* megmérjük a lézerfény koherenciahosszát,
 
* méréseket végzünk interferométerrel,
 
* méréseket végzünk interferométerrel,
−
* diffrakciós méréseket végzünk.
+
 
  
  
59. sor: 59. sor:
 
|}
 
|}
  
−
{{fig|Opt_2_kep_1.JPG|fig:2|2. ábra}}
+
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
|{{figN|Michelson2.png|fig:2|2. ábra|450}}
 +
|-
 +
|}
 +
 
  
−
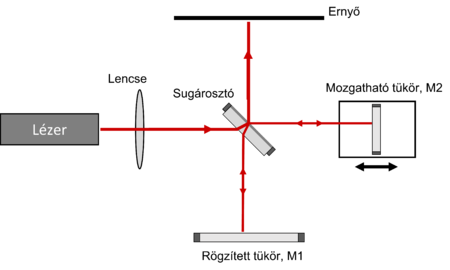
A [[#fig:2|2. ábrán]] a Michelson-féle interferométer vázlata látható. A lézer sugárnyalábja sugárosztóra esik, amely a beeső fény 50 %-át visszaveri, és másik 50 %-át átengedi. A beeső fény így két nyalábra oszlik. Az egyik a mozgatható tükörre ($M_1$) esik, a másik a rögzített tükörre ($M_2$) verődik. Mindkét tükör a sugárosztóra veri vissza a fényt.
+
A [[#fig:2|2. ábrán]] a Michelson-féle interferométer vázlata látható. A lézer sugárnyalábja sugárosztóra esik, amely a beeső fény 50 %-át visszaveri, és másik 50 %-át átengedi. A beeső fény így két nyalábra oszlik. Az egyik a rögzített tükörre ($M_1$) verődik vissza, a másik a mozgatható tükörre ($M_2$) esik. Mindkét tükör a sugárosztóra veri vissza a fényt.
  
 
A mozgatható tükörről visszavert fény egyik fele most a megfigyelő ernyőre esik be, és a rögzített tükörről visszaverődő fény fele a sugárosztón áthaladva szintén a megfigyelő ernyőre esik.
 
A mozgatható tükörről visszavert fény egyik fele most a megfigyelő ernyőre esik be, és a rögzített tükörről visszaverődő fény fele a sugárosztón áthaladva szintén a megfigyelő ernyőre esik.
  
−
{{fig2|Opt_2_kep_2.JPG|fig:3|3. ábra}}
+
{{figN|Opt_2_kep_2.JPG|fig:3|3. ábra|200}}
  
 
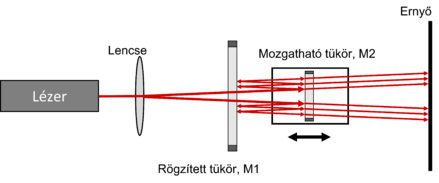
Ily módon az eredeti sugárnyaláb először kettéosztódik, majd a keletkezett nyalábok egy része visszafelé egyesül egymással. Mivel a nyalábok ugyanabból a fényforrásból származnak, fázisuk erősen korrelált. Így, amikor lencsét helyezünk a lézer fényforrás és a sugárosztó közé, a fénynyaláb kitágul és a megfigyelő ernyőn sötét és világos gyűrűkből álló kép jelenik meg ([[#fig:3|3. ábra]]).
 
Ily módon az eredeti sugárnyaláb először kettéosztódik, majd a keletkezett nyalábok egy része visszafelé egyesül egymással. Mivel a nyalábok ugyanabból a fényforrásból származnak, fázisuk erősen korrelált. Így, amikor lencsét helyezünk a lézer fényforrás és a sugárosztó közé, a fénynyaláb kitágul és a megfigyelő ernyőn sötét és világos gyűrűkből álló kép jelenik meg ([[#fig:3|3. ábra]]).
71. sor: 76. sor:
 
Mivel a két interferáló nyaláb ugyanabból a forrásból származik, fázisuk eredetileg azonos volt. Relatív fázisuk, amikor a megfigyelő ernyő bármely pontjában találkoznak, attól az optikai úthossztól függ, amelyet ezen pont eléréséig megtettek.
 
Mivel a két interferáló nyaláb ugyanabból a forrásból származik, fázisuk eredetileg azonos volt. Relatív fázisuk, amikor a megfigyelő ernyő bármely pontjában találkoznak, attól az optikai úthossztól függ, amelyet ezen pont eléréséig megtettek.
  
−
$M_1$ mozgatásával az egyik nyaláb úthossza változtatható. Mivel a nyaláb az $M_1$ és a sugárosztó közötti utat kétszer teszi meg, $M_1$-et 1/4 hullámhossznyival közelítve a sugárosztóhoz, a nyaláb úthossza 1/2 hullámhossznyival csökken. Eközben megváltozik az interferenciakép. A maximumok sugara oly módon csökken, hogy a korábbi minimumok helyét foglalják el. Ha $M_1$-et tovább mozgatjuk 1/4 hullámhossznyival a sugárosztó felé, a maximumok sugara tovább csökken úgy, hogy a maximumok és a minimumok ismét helyet cserélnek, és az új elrendezés megkülönböztethetetlen lesz az eredeti képtől.
+
$M_2$ mozgatásával az egyik nyaláb úthossza változtatható. Mivel a nyaláb az $M_2$ és a sugárosztó közötti utat kétszer teszi meg, $M_2$-et 1/4 hullámhossznyival közelítve a sugárosztóhoz, a nyaláb úthossza 1/2 hullámhossznyival csökken. Eközben megváltozik az interferenciakép. A maximumok sugara oly módon csökken, hogy a korábbi minimumok helyét foglalják el. Ha $M_2$-et tovább mozgatjuk 1/4 hullámhossznyival a sugárosztó felé, a maximumok sugara tovább csökken úgy, hogy a maximumok és a minimumok ismét helyet cserélnek, és az új elrendezés megkülönböztethetetlen lesz az eredeti képtől.
  
 
Lassan mozgatva a tükröt egy meghatározott $d_N$ távolságon, és közben leszámolva $N$-et, annak számát, hányszor jutott a gyűrűkép az eredeti állapotába, meghatározható a fény hullámhossza:
 
Lassan mozgatva a tükröt egy meghatározott $d_N$ távolságon, és közben leszámolva $N$-et, annak számát, hányszor jutott a gyűrűkép az eredeti állapotába, meghatározható a fény hullámhossza:
79. sor: 84. sor:
 
Ha a fény hullámhossza ismert, ugyanígy mérhető a $d_N$ távolság.
 
Ha a fény hullámhossza ismert, ugyanígy mérhető a $d_N$ távolság.
  
−
===Diffrakciós kép vizsgálata===
+
===Fabry--Pérot-interferométer felépítése===
 +
''Megjegyzés: A berendezés átépíthető úgy, hogy Fabry--Pérot interferométerként funkcionáljon, de technikai okok miatt a mérések során nem végezzük el az átépítést. De a Fabry--Pérot interferométer működés elvét érdemes megismerni.''
  
−
A tapasztalat szerint egy akadály mellett elhaladó fénysugár az akadályoknál részben elhajlik, behatol az árnyéktérbe is. Ez a diffrakció (fényelhajlás) jelensége. A jelenséget a "Huygens-Fresnel-elv" segítségével lehet meg-magyarázni: a Huygens-Fresnel-elv alapján a hullámfelület minden pontja elemi hullámforrásnak tekintendő, és ezeknek az egymással koherens elemi gömbhullámoknak az interferenciája szabja meg a tér egy pontjában a fényhatást.
+
A [[#fig:4|4. ábrán]] a Faby--Pérot-interferométer vázlata látható. Itt a lézerből bejövő nyaláb a lencse után széttartóvá válik és így éri el a rögzített, féligáteresztő tükröt ($M_1$). A széttartó nyalábok ezután a szintén féligáteresztő tükörre ($M_2$) jutnak, ahol részben visszaverődnek és részben továbbhaladnak. A visszaverődött nyalábok a rögzített tükörről újra visszaverődnek, így a két tükör között többszörös visszaverődés révén egy optikai üregrezonátor alakul ki. Mivel a rezonátorból kilépő transzmittált nyalábok egy közös bejövő nyalábból származnak, a fázisuk eredetileg azonos volt, az üregből kilépés után pedig a relatív fázisuk a széttartás szögétől és a két tükör távolságától függ. Ha a lencse rögzített, akkor a fáziskülönbség a mozgatható tükör mozgatásával változtatható. A Michelson-féle interferométernél leírtakhoz hasonlóan, ha az $M_2$ tükröt 1/2 hullámhossznyival mozdítjuk el, az új és a kiindulási gyűrűkép egyformának adódik. Így a Fabry--Pérot-interferométer is hasonlóan a gyűrűátmenetek számolásával használható a távolság mérésére, ha ismert hullámhosszú fényt használunk, vagy a hullámhossz meghatározására, ha ismerjük az elmozdulást.
  
−
{{fig2|Opt_2_kep_3.JPG|fig:4|4. ábra}}
+
A Fabry--Pérot-elrenedzés elviekben a Michelson-féle interferométernél látott gyűrűképhez képest fényesebb, vékonyabb és egymástól távolabb elhelyezkedő gyűrűkből álló képet ad.
  
−
Példaképp vizsgáljuk meg az optikai rés esetét. A rés egy átlátszatlan felületen kialakított keskeny, a fény hullámhosszával összemérhető szélességű, hosszú nyílás. Világítsuk meg a rést egy koherens, párhuzamos fénynyalábbal (legegyszerűbben egy lézer fényével). A fény a résen áthaladva elhajlik. A réstől távol elhelyezett ernyőn a résből kiinduló elemi hullámok interferenciája alakítja ki a diffrakciós képet. A diffrakciós képet – az intenzitást a hely függvényében - egy fotodióda mozgatásával könnyen meg lehet mérni ([[#fig:4|4. ábra]]).
+
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
|{{figN|Fabry.png|fig:4|4. ábra|439}}
 +
|-
 +
|}
  
−
A '''''k''''' hullámszámvektor irányában a relatív intenzitást a Fourier-integrál segítségével lehet kiszámítani. Az intenzitás arányos az integrál abszolút értékének négyzetével:
+
==Mérési feladatok==
  
−
$$ I(\pmb{k}) = \left \lvert \int_{-\infty}^{\infty} e^{\pmb{kx}i}f(\pmb{x})d\pmb{x} \right \rvert^2. $$
+
[[A méréshez rendelkezésre álló eszközök: Mérések Michelson-interferométerrel|A méréshez rendelkezésre álló eszközök]]
  
−
A kifejezésben
+
*''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
  
−
$$|\pmb{k}| = k = \frac{2\pi}{\lambda},$$
+
'''FELADATOK ELSŐ ALKALOMMAL'''
  
−
$$\pmb{kx} = kx \sin \theta \approx kx\theta  \;  (\theta\ll1), $$
+
===1. Piros félvezető lézer hullámhosszának mérése Michelson-féle interferométerrel===
  
−
$$ f(x) = \begin{cases} \frac{1}{d} \; \mathrm{ha} \; x \in \left[-\frac{d}{2};\frac{d}{2}\right] \\ 0\; \mathrm{ha} \; x \notin \left[-\frac{d}{2};\frac{d}{2}\right]. \end{cases} $$
+
'''a)''' Állítsuk össze a Michelson-féle interferométer elrendezést a leiratban ismertetett módon a piros félvezető lézer lézert használva!
  
−
Felhasználva, hogy
+
'''b)''' Állítsuk a mikrométert középállásba (közelítőleg 500 µm)!
  
−
$$ y = D \mathrm{tg} \theta \approx D\theta \; (\theta<<1), $$
+
* ''Ebben a helyzetben a leginkább lineáris az összefüggés a mikrométeren leolvasott érték és a tükör elmozdulása között.''
  
−
és elvégezve az integrálást
+
'''c)''' Forgassuk el a mikrométer gombját egy teljes fordulattal az óra járásával ellenkező irányban addig, amíg a nulla helyzet egybe nem esik a jelzéssel! Jegyezzük fel a leolvasott mikrométer értéket!
  
−
$$ I(y) = \left( \frac{\lambda D}{\pi yd} \right)^2\sin^2\left( \frac{\pi yd}{\lambda D} \right).$$
+
* ''Ha a mikrométer gomb forgatásának irányát megváltoztatjuk, a tükör nem indul meg azonnal. Ezt nevezzük kotyogásnak, amely minden mechanikai rendszernél előfordul mozgásirány megváltoztatásakor. A fenti módon a kotyogásból eredő hiba kiküszöbölhető.''
  
−
{{fig|Opt_2_kep_4.JPG|fig:5|5. ábra}}
+
'''d)''' A megfigyelő ernyőt állítsuk be úgy, hogy a milliméter skála egyik jele essék egybe az interferenciakép egyik gyűrűjével!
 +
* ''Könnyebb lesz a gyűrűk számlálása, ha a referencia jel a kép közepétől számított első vagy második gyűrűre esik.''
  
−
A diffrakciós kép az [[#fig:5|5. ábrán]] látható. A vízszintes tengely $\frac{yd}{\lambda D}$ egységekben van skálázva. Az intenzitás az $y_z=\pm\frac{\lambda D}{d}$ helyen válik először zérussá. Az két zérushely közti távolság ($2y_z$) és a $D$ távolság mérésével a $\lambda$ hullámhossz ismeretében a $d$ résszélesség, $d$ ismeretében pedig a $\lambda$ hullámhossz meghatározható.
+
'''e)''' Forgassuk tovább a mikrométer gombját az óramutató járásával ellenkező irányba és számoljuk meg a referencia jelen áthaladó gyűrűket! Legalább 20 gyűrűátmenetet számoljunk le, de a felbontás javítása érdekében érdemes lehet akár 50 átmenetig is elmenni! A gyűrűátmenetek leszámlálása után a gyűrűknek ugyanabban a helyzetben kell lenniük, mint a számlálás megkezdésekor. Jegyezzük fel a mikrométer tárcsán leolvasott értéket!
  
−
Meglepő módon a rés „inverzének”, egy vékony akadálynak (pl. hajszál) a diffrakciós képe ugyanilyen, így ezzel a módszerrel vékony drótok, hajszálak, stb. átmérője is mérhető.
+
* '' A mérést elvégezheti úgy is, hogy 15-20 gyűrűátmenetenként megáll és leolvassa az elmozdulás értékét, majd ezt megismétli 4-5-ször. A kapott tükörelmozdulás - gyűrűátmenet értékpárokat grafikonon ábrázolva a hullámhossz egyenesillesztéssel is meghatározható.''
−
Bonyolultabb optikai struktúrák (például két vagy több párhuzamos rés) esetén a diffrakciós kép hasonlóan kiszámítható, csak $f(x)$ kifejezését kell ennek megfelelően módosítani.
+
  
−
A diffrakciós kép alapján következtetni lehet az optikai struktúrára. Ha az intenzitás kifejezésében ismernénk az abszolútértékjelen belüli kifejezést, akkor inverz Fourier-transzformációval meg lehetne határozni a diffrakciós képet létrehozó struktúrát.  A mérés alapján azonban csak az intenzitást (az abszolút érték négyzetét) ismerjük, így nem teljesen egyértelmű a számítás.
+
'''f)''' Jegyezzük fel a leszámlált gyűrű átmenetek számát!
  
−
A másik lehetőség az, hogy a diffrakciós kép alapján megsejtjük (vagy más információk alapján tudjuk), hogy körülbelül milyen optikai struktúra hozta létre a diffrakciós képet (például néhány egyforma, párhuzamos rés); majd paraméteresen kiszámítjuk a feltételezett struktúra diffrakciós képét, végül a paramétereket addig változtatjuk, amíg a számított és a mért diffrakciós kép a legjobban egyezik egymással.
+
'''g)''' Határozzuk meg a lézer fényforrás hullámhosszát, annak figyelembe vételével, hogy a mikrométeren egy kis osztás egy µm ($10^{-6}$ m) tükör elmozdulásnak felel meg!
  
−
==Mérési feladatok==
+
'''h)''' Többször ismételjük meg a ''3 - 7. lépéseket''!
  
−
[[A méréshez rendelkezésre álló eszközök: Mérések Michelson-interferométerrel|A méréshez rendelkezésre álló eszközök]]
+
===2. A levegő törésmutatójának meghatározása Michelson-féle interferométerrel===
  
−
*''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
+
'''a)''' Állítsuk össze a Michelson-féle interferométert a piros félvezető lézer használatával!
  
−
'''Mérések Michelson-féle interferométerrel'''
+
'''b)''' Helyezzük az elemtartót a rögzített tükör és a sugárosztó közé, és helyezzük fel ennek mágneses hátoldalára a vákuum-kamrát és húzzuk a vákuumkamra levegőző csonkjára a kézi vákuumszivattyú csövét!
  
−
===Félvezető lézer koherencia hosszának mérése===
+
* ''Szükség szerint állítsuk be a rögzített tükröt úgy, hogy az interferenciakép közepe jól látható legyen a megfigyelő ernyőn!''
  
−
'''1.''' Állítsuk össze a Michelson-féle interferométert!  
+
'''c)''' A kézi vákuumszivattyún lévő billenőkapcsoló segítségével engedjünk levegőt a vákuumkamrába, és győződjünk meg arról, hogy a vákuumkamrában atmoszférikus nyomás uralkodik! Ez lesz a $P_\text i$ kezdeti nyomás.
  
−
* ''Tolómérő segítségével úgy állítsuk be a tükröket, hogy a kettéválasztott fénynyalábok optikai úthossza minél pontosabban megegyezzen.''
+
'''d)''' Lassan szivattyúzzuk ki a levegőt a vákuumkamrából, miközben számoljuk meg a bekövetkező gyűrű átmeneteket! Jegyezzük fel a manométerről leolvasott $P_\text f$ nyomás végértéket és a gyűrűátmenetek $N$ számát!
  
−
'''2.''' Állítsuk be a félvezető mutatólézert úgy, hogy a lézer nyaláb pontosan merőleges legyen a mozgatható tükörre.
+
* ''A manométer a nyomást az atmoszférikus nyomáshoz képest méri (pl. a 34 Hgcm állás az atmoszférikusnál 34 Hgcm-rel kisebb nyomást jelent). Ebben az esetben az abszolút nyomást a következőképpen kell számítani:''
  
−
* ''Ennek pontos beállításához egy papírlapba fúrt kis lyukon eresszük át a lézernyalábot, és addig állítsuk a lézer szögét, amíg a lézernyaláb pontosan a kis lyukba érkezik vissza. ''
+
$$ P_\text{abs} = P_\text{atm} - P_\text{m\'ert} $$
  
−
* ''A lézernyaláb beállítása közben a féligáteresztő tükröt fordítsuk oldalra, hogy ne legyen a lézer útjában.''
+
'''e)''' A mérési eredmények alapján határozzuk meg a törésmutató ($n$) - nyomás ($P$) grafikon meredekségét levegőre és a levegő törésmutatóját atmoszférikus nyomáson.
  
−
'''3.''' Helyezzük el a sugárosztót a lézernyalábbal $45^\circ$-os szöget bezárólag a jelzések közé úgy, hogy a nyaláb az álló tükörre verődjék!
+
A Michelson-féle interferométernél a gyűrűkép jellemzőit a két interferáló nyaláb fázisviszonyai határozzák meg. A fázisviszonyok kétféle módon változhatnak meg. Az egyik az egyes nyalábok által megtett utak változása (például, a mozgatható tükör mozgatása révén). A másik a közeg megváltozása, amelyben az egyik vagy mindkét nyaláb áthalad.
  
−
* ''A sugárosztó szögét úgy kell beállítani, hogy a visszavert nyaláb a rögzített tükör közepére essék!''
+
Adott frekvenciájú fény esetén a hullámhossz a következő formula szerint változik:
  
−
* ''Ekkor két fényes pontsorozatot kell látnunk a megfigyelő ernyőn. Az egyik pontsorozat a rögzített tükörről, a másik a mozgatható tükörről jön létre. Mindegyik pontsorozat egy fényes pontot és két vagy több kevésbé fényes pontot tartalmaz (a többszörös visszaverődés miatt).''
+
$$ \lambda = \lambda_0/n $$
 +
 +
ahol $\lambda_0$ a fény hullámhossza vákuumban, és $n$ a közeg törésmutatója, amelyben a fény halad. Megfelelően alacsony nyomásokon egy gáz törésmutatója lineárisan változik a gáz nyomásával. Vákuum esetén, ahol a nyomás zérus, a törésmutató pontosan 1. Ennek alapján kísérletileg meghatározva a törésmutató – nyomás grafikon meredekségét, kiszámíthatjuk a gáz törésmutatóját különböző nyomásokon.
  
−
'''4.''' Állítsuk a sugárosztó szögét addig, amíg a két pontsorozat a lehető legközelebb kerül egymáshoz, majd rögzítsük a sugárosztó helyzetét!
+
A lézer nyaláb oda és vissza megtéve az utat a sugárosztó és a mozgatható tükör között, kétszer halad át a vákuumkamrán. A kamrán kívül a két nyaláb optikai úthossza nem változik a kísérlet során. A kamrán belül azonban a fény hullámhossza megnövekszik a nyomás csökkenésével.
  
−
'''5.''' A rögzített tükör hátoldalán lévő csavarokkal állítsuk be annak hajlásszögét úgy, hogy a két pontsorozat a megfigyelő ernyőn egybeessék!
+
Feltételezve, hogy a kamra $d$ hossza eredetileg 10 hullámhossznyi volt (a valóságban természetesen sokkal hosszabb) és a kamra leszívása közben, a hullámhossz növekedése folytán 9 1/2 hullámhossznyi lesz, a kétszeri áthaladás miatt a kamrán, a fény eggyel kevesebb rezgést végez a kamrán belül. Ennek hatása az interferenciaképre ugyanolyan, mint amikor a mozgatható tükröt 1/2 hullámhossznyival közelebb hozzuk a sugárosztóhoz. Ezért egyetlen gyűrű átmenetet fogunk megfigyelni.
  
−
'''6.''' Helyezzünk egy 18 mm fókusztávolságú lencsét a lézer előtti elemtartó mágneses oldalára, és állítsuk be úgy, hogy a széttartó nyaláb a sugárosztóra koncentrálódjék!
+
Fentieknek megfelelően (a kétszeri fényáthaladást figyelembe véve) a kamra belseje eredetileg $N_\text i=2d/\lambda_\text i$ fényhullámhossznyi hosszúságú volt. A végnyomáson pedig  $N_\text f=2d/\lambda_\text f$ hullámhossznyi fért el a kamrában. Ezen két érték közötti különbség, $N=N_\text i-N_\text f$ , éppen a kamra leszívása közben leszámlált gyűrűátmenetek száma. Ezért $N=2d/\lambda_\text i-2d/\lambda_\text f$. Azonban $\lambda_\text i=\lambda_0/n_\text i$ és $\lambda_\text f=\lambda_0/n_\text f$, ahol $n_\text i$ és $n_\text f$ a kamrában lévő levegő törésmutatójának kezdeti és végértéke. Ezért $N=2d(n_\text i-n_\text f)/\lambda_0$, úgyhogy $n_\text i-n_\text f=N\lambda_0/2d$. A törésmutató-nyomás grafikon meredeksége pedig:
  
−
'''7.''' A mikrométercsavar segítségével mozgassuk az egyik tükröt addig, míg a koncentrikus gyűrűk megjelennek a képen. Állapítsuk meg, hogy milyen elmozdulás-tartományban láthatók a gyűrűk. Ez alapján becsüljük meg a mutatólézer koherenciahosszát.
+
$$ \frac{n_\text i-n_\text f}{P_\text i-P_\text f} = \frac{N\lambda_0}{2d(P_\text i-P_\text f)},$$
  
−
* ''Ha nem sikerül interferenciagyűrűket észlelni, akkor rossz a beállításunk, pl. nem eléggé kiegyenlítettek az optikai úthosszak.''
+
ahol $P_\text i$ a levegő kezdeti nyomása, $P_\text f$ a levegő végső nyomása, $n_\text i$ a levegő törésmutatója $P_\text i$ nyomáson, $n_\text f$ a levegő törésmutatója $P_\text f$  nyomáson, $N$ a leszívás során megfigyelt gyűrűátmenetek száma, $\lambda_0$ a lézerfény hullámhossza vákuumban és $d$ a vákuumkamra hossza (3 cm).
  
−
===He-Ne lézer hullámhosszának meghatározása===
+
===3. Üveg törésmutatójának meghatározása Michelson-féle interferométerrel===
  
−
'''1.''' Állítsunk össze Michelson-féle interferométert az előző feladatban leírtaknak megfelelően He-Ne lézert használva!
+
'''a)''' Továbbra is a Michelson-féle interferométer elrendezést használjuk, a mérés elején ellenőrizze, hogy megfelelően van-e beállítva a fényút.
  
−
'''2.''' Állítsuk a mikrométert középállásba (közelítőleg 500 µm)!  
+
'''b)''' Helyezzük a forgatható mutatót az elemtartóval a sugárosztó és a mozgatható tükör közé, és rögzítsük az üveglemezt az elemtartó mágneses hátlapjára!
  
−
* ''Ebben a helyzetben a leginkább lineáris az összefüggés a mikrométeren leolvasott érték és a tükör elmozdulása között.''
+
'''c)''' Úgy állítsuk be a mutatót, hogy finom skálájának "0"-ja az interferométer alapon lévő fokosztás nullpontjával essen egybe!
  
−
'''3.''' Forgassuk el a mikrométer gombját egy teljes fordulattal az óra járásával ellenkező irányban addig, amíg a nulla helyzet egybe nem esik a jelzéssel! Jegyezzük fel a leolvasott mikrométer értéket!
+
'''d)''' Vegyük el a lencsét a lézer elől! Tartsuk a megfigyelő ernyőt a sugárosztó és a mozgatható tükör között! Ha egy fényes pont és néhány másodlagos pont látható a megfigyelő ernyőn, addig állítsuk az elemtartó szögét a forgatható mutatóhoz képest, amíg egy fényes pont látható. Ezután ismét igazítsuk a forgatható mutatót a skálaosztás nullpontjához! Ekkor az üveglemez merőleges az optikai útra.
  
−
* ''Ha a mikrométer gomb forgatásának irányát megváltoztatjuk, a tükör nem indul meg azonnal. Ezt nevezzük kotyogásnak, amely minden mechanikai rendszernél előfordul mozgásirány megváltoztatásakor. A fenti módon a kotyogásból eredő hiba kiküszöbölhető.''
+
'''e)''' Helyezzük vissza a lencsét és a megfigyelő ernyőt, és végezzük el a szükséges tükör beállításokat, hogy tiszta gyűrűképet kapjunk!
  
−
'''4.''' A megfigyelő ernyőt állítsuk be úgy, hogy a milliméter skála egyik jele essék egybe az interferenciakép egyik gyűrűjével!  
+
'''f)''' Lassan forgassuk el a forgatható mutatót 0°-tól $\theta$ szögig (legalább 10 fokot), és eközben számoljuk le a megfigyelt gyűrűátmenetek számát!
−
* ''Könnyebb lesz a gyűrűk számlálása, ha a referencia jel a kép közepétől számított első vagy második gyűrűre esik.''
+
  
−
'''5.''' Forgassuk tovább a mikrométer gombját az óramutató járásával ellenkező irányba és számoljuk meg a referencia jelen áthaladó gyűrűket! Legalább húsz gyűrűátmenetet számoljunk le! A gyűrűátmenetek leszámlálása után a gyűrűknek ugyanabban a helyzetben kell lenniük, mint a számlálás megkezdésekor. Jegyezzük fel a mikrométer tárcsán leolvasott értéket!
+
'''g)''' A mérési eredmények alapján határozzuk meg az üveglemez törésmutatóját az alábbi összefüggés szerint:
  
−
'''6.''' Jegyezzük fel a leszámlált gyűrű átmenetek számát!
+
$$ n_g = \frac{(2t-N\lambda)(1-\cos\theta)}{2t(1-\cos\theta)-N\lambda} $$
  
−
'''7.''' Határozzuk meg a lézer fényforrás hullámhosszát, annak figyelembe vételével, hogy a mikrométeren egy kis osztás egy µm ($10^{-6}$ m) tükör elmozdulásnak felel meg!
+
ahol $t$ az üveglemez vastagsága.
  
−
'''8.''' Többször ismételjük meg a ''3 - 7. lépéseket''!
+
<!--===4. He-Ne lézer hullámhosszának meghatározása Fabry--Pérot-interferométerrel===
  
−
===A levegő törésmutatójának meghatározása===
+
* ''Mivel csak egy He-Ne lézer van, ha a másik mérőpár már elkezdte ezt a mérést, akkor ugorjon a "Félvezető lézer koherencia hosszának mérésére" és utána térjen vissza erre a feladatra.''
  
−
'''1.''' Állítsunk össze Michelson-féle interferométert!
+
* ''Ha az első alkalom végén, vagy a második alkalom során marad ideje, akkor próbálja meg meghatározni a piros és akár a zöld lézer hullámhosszát is ezzel a módszerrel és így összevetheti a különböző módon mért hullámhosszakat''
  
−
'''2.''' Helyezzük az elemtartót a rögzített tükör és a sugárosztó közé, és helyezzük fel ennek mágneses hátoldalára a vákuum-kamrát és húzzuk a vákuumkamra levegőző csonkjára a kézi vákuumszivattyú csövét!  
+
'''a)''' Állítsuk össze a Fabry--Pérot-interferométert a He-N lézerrel!  
  
−
* ''Szükség szerint állítsuk be a rögzített tükröt úgy, hogy az interferenciakép közepe jól látható legyen a megfigyelő ernyőn!''
+
'''b)''' Határozzuk meg a He-Ne lézer hullámhosszát, a gyűrűátmenetek számából és a tükör elmozdulásából. A mérést ismételje meg legalább 3 alkalommal és számoljon le alkalmanként legalább 30 gyűrűátmenetet!-->
  
−
'''3.''' A kézi vákuumszivattyún lévő billenőkapcsoló segítségével engedjünk levegőt a vákuumkamrába, és győződjünk meg arról, hogy a vákuumkamrában atmoszférikus nyomás uralkodik! Ez lesz a $P_i$ kezdeti nyomás.
+
===4. Kis koherenciahosszú félvezető lézer koherenciahosszának mérése===
  
−
'''4.''' Lassan szivattyúzzuk ki a levegőt a vákuumkamrából, miközben számoljuk meg a bekövetkező gyűrű átmeneteket! Jegyezzük fel a manométerről leolvasott $P_f$ nyomás végértéket és a gyűrűátmenetek $N$ számát!
+
'''a)''' Állítsuk össze a Michelson-féle interferométert a kis koherenciahosszú (mutató) félvezető lézerrel!  
  
−
* ''A manométer a nyomást az atmoszférikus nyomáshoz képest méri (pl. a 34 Hgcm állás az atmoszférikusnál 34 Hgcm-rel kisebb nyomást jelent). Ebben az esetben az abszolút nyomást a következőképpen kell számítani:''
+
* ''Ügyeljen arra, hogy a kettéválasztott fénynyalábok optikai úthossza minél pontosabban megegyezzen. Ehhez (jól beállított interferométer esetén) a mozgatható tükör középállásban ($500\,\mu m$) az interferométeren található fehér jelzéssel egyvonalba kell legyen.''
  
−
$$ P_{abs} = P_{atm} - P_{mert} $$
+
* ''Ne feledje el beépíteni a kompenzátort, hogy az optikai úthossz valóban egyezzen!''
  
−
'''5.''' A mérési eredmények alapján határozzuk meg a törésmutató ($n$) - nyomás ($P$) grafikon meredekségét levegőre és a levegő törésmutatóját atmoszférikus nyomáson.
+
'''b)''' Állítsuk be a félvezető mutatólézert úgy, hogy a lézer nyaláb pontosan merőleges legyen a mozgatható tükörre.  
  
−
A Michelson-féle interferométernél a gyűrűkép jellemzőit a két interferáló nyaláb fázisviszonyai határozzák meg. A fázisviszonyok kétféle módon változhatnak meg. Az egyik az egyes nyalábok által megtett utak változása (például, a mozgatható tükör mozgatása révén). A másik a közeg megváltozása, amelyben az egyik vagy mindkét nyaláb áthalad.
+
* ''Ennek pontos beállításához egy papírlapba fúrt kis lyukon eresszük át a lézernyalábot, és addig állítsuk a lézer szögét, amíg a lézernyaláb pontosan a kis lyukba érkezik vissza. ''
  
−
Adott frekvenciájú fény esetén a hullámhossz a következő formula szerint változik:
+
* ''A lézernyaláb beállítása közben a féligáteresztő tükröt fordítsuk oldalra, hogy ne legyen a lézer útjában.''
  
−
$$ \lambda = \lambda_0/n $$
+
'''c)''' Helyezzük el a sugárosztót a lézernyalábbal $45^\circ$-os szöget bezárólag a jelzések közé úgy, hogy a nyaláb az álló tükörre verődjék!
−
+
−
ahol $\lambda_0$ a fény hullámhossza vákuumban, és $n$ a közeg törésmutatója, amelyben a fény halad. Megfelelően alacsony nyomásokon egy gáz törésmutatója lineárisan változik a gáz nyomásával. Vákuum esetén, ahol a nyomás zérus, a törésmutató pontosan 1. Ennek alapján kísérletileg meghatározva a törésmutató – nyomás grafikon meredekségét, kiszámíthatjuk a gáz törésmutatóját különböző nyomásokon.
+
  
−
A lézer nyaláb oda és vissza megtéve az utat a sugárosztó és a mozgatható tükör között, kétszer halad át a vákuumkamrán. A kamrán kívül a két nyaláb optikai úthossza nem változik a kísérlet során. A kamrán belül azonban a fény hullámhossza megnövekszik a nyomás csökkenésével.
+
* ''A sugárosztó szögét úgy kell beállítani, hogy a visszavert nyaláb a rögzített tükör közepére essék!''
  
−
Feltételezve, hogy a kamra $d$ hossza eredetileg 10 hullámhossznyi volt (a valóságban természetesen sokkal hosszabb) és a kamra leszívása közben, a hullámhossz növekedése folytán 9 1/2 hullámhossznyi lesz, a kétszeri áthaladás miatt a kamrán, a fény eggyel kevesebb rezgést végez a kamrán belül. Ennek hatása az interferenciaképre ugyanolyan, mint amikor a mozgatható tükröt 1/2 hullámhossznyival közelebb hozzuk a sugárosztóhoz. Ezért egyetlen gyűrű átmenetet fogunk megfigyelni.  
+
* ''Ekkor két fényes pontsorozatot kell látnunk a megfigyelő ernyőn. Az egyik pontsorozat a rögzített tükörről, a másik a mozgatható tükörről jön létre. Mindegyik pontsorozat egy fényes pontot és két vagy több kevésbé fényes pontot tartalmaz (a többszörös visszaverődés miatt).''
  
−
Fentieknek megfelelően (a kétszeri fényáthaladást figyelembe véve) a kamra belseje eredetileg $N_i=2d/\lambda_i$ fényhullámhossznyi hosszúságú volt. A végnyomáson pedig  $N_f=2d/\lambda_f$ hullámhossznyi fért el a kamrában. Ezen két érték közötti különbség, $N=N_i-N_f$ , éppen a kamra leszívása közben leszámlált gyűrűátmenetek száma. Ezért $N=2d/\lambda_i-2d/\lambda_f$. Azonban $\lambda_i=\lambda_0/n_i$ és $\lambda_f=\lambda_0/n_f$, ahol $n_i$ és $n_f$ a kamrában lévő levegő törésmutatójának kezdeti és végértéke. Ezért $N=2d(n_i-n_f)/\lambda_0$, úgyhogy $n_i-n_f=N\lambda_0/2d$. A törésmutató-nyomás grafikon meredeksége pedig:
+
'''d)''' Állítsuk a sugárosztó szögét addig, amíg a két pontsorozat a lehető legközelebb kerül egymáshoz, majd rögzítsük a sugárosztó helyzetét!
  
−
$$ \frac{n_i-n_f}{P_i-P_f} = \frac{N\lambda_0}{2d(P_i-P_f)},$$
+
'''e)''' A rögzített tükör hátoldalán lévő csavarokkal állítsuk be annak hajlásszögét úgy, hogy a két pontsorozat a megfigyelő ernyőn egybeessék!
  
−
ahol $P_i$ a levegő kezdeti nyomása, $P_f$ a levegő végső nyomása, $n_i$ a levegő törésmutatója $P_i$ nyomáson, $n_f$ a levegő törésmutatója $P_f$  nyomáson, $N$ a leszívás során megfigyelt gyűrűátmenetek száma, $\lambda_0$ a lézerfény hullámhossza vákuumban és $d$ a vákuumkamra hossza (3 cm).
+
'''f)''' Helyezzünk egy 18 mm fókusztávolságú lencsét a lézer előtti elemtartó mágneses oldalára, és állítsuk be úgy, hogy a széttartó nyaláb a sugárosztóra koncentrálódjék!
  
−
===Üveg törésmutatójának meghatározása===
+
'''g)''' A mikrométercsavar segítségével mozgassuk az egyik tükröt addig, míg a koncentrikus gyűrűk megjelennek a képen. Állapítsuk meg, hogy milyen elmozdulás-tartományban láthatók a gyűrűk. Ez alapján becsüljük meg a mutatólézer koherenciahosszát.
  
−
'''1.''' Állítsunk össze Michelson-féle interferométert!
+
* ''Ha nem sikerül interferenciagyűrűket észlelni, akkor rossz a beállításunk, pl. nem eléggé kiegyenlítettek az optikai úthosszak.''
  
−
'''2.''' Helyezzük a forgatható mutatót az elemtartóval a sugárosztó és a mozgatható tükör közé, és rögzítsük az üveglemezt az elemtartó mágneses hátlapjára!
+
'''FIGYELEM!''' A második alkalomra az eddigi feladatok előzetes kiértékelését el kell végezni és meg kell mutatni a mérésvezetőnek.
  
−
'''3.''' Úgy állítsuk be a mutatót, hogy finom skálájának "0"-ja az interferométer alapon lévő fokosztás nullpontjával essen egybe!
+
'''FELADATOK MÁSODIK ALKALOMMAL'''
  
−
'''4.''' Vegyük el a lencsét a lézer elől! Tartsuk a megfigyelő ernyőt a sugárosztó és a mozgatható tükör között! Ha egy fényes pont és néhány másodlagos pont látható a megfigyelő ernyőn, addig állítsuk az elemtartó szögét a forgatható mutatóhoz képest, amíg egy fényes pont látható. Ezután ismét igazítsuk a forgatható mutatót a skálaosztás nullpontjához! Ekkor az üveglemez merőleges az optikai útra.
+
''' Ha az első mérési alkalommal elvégzett feladatok kiértékelése során probléma adódott a mért adatok helytelensége miatt, akkor elsőként ezeket a mérési feladatokat végezze el újra.'''
  
−
'''5.''' Helyezzük vissza a lencsét és a megfigyelő ernyőt, és végezzük el a szükséges tükör beállításokat, hogy tiszta gyűrűképet kapjunk!
+
===5. Piezomozgató kalibrálása ismert hullámhosszú lézerrel Michelson-féle elrendezésben===
  
−
'''6.''' Lassan forgassuk el a forgatható mutatót 0°-tól $\theta$ szögig (legalább 10 fokot), és eközben számoljuk le a megfigyelt gyűrűátmenetek számát!
+
A korábbi feladatokban a tükör mozgatásának mértékét ismertük és ebből határoztuk meg a hullámhosszat. Ebben a feladatban a kapott hullámhosszat felhasználva egy piezomozgató kalibrációját végezzük el, azaz meghatározzuk, hogy adott feszültség hatására mekkora a piezokristály megnyúlása.
  
−
'''5.''' A mérési eredmények alapján határozzuk meg az üveglemez törésmutatóját az alábbi összefüggés szerint:
+
'''a)''' Állítsuk össze a Michelson-féle interferométert a piros lézer használatával úgy, hogy a mozgatható tükör helyére a tükörrel ellátott piezomozgatót helyezzük!
  
−
$$ n_g = \frac{(2t-N\lambda)(1-\cos\theta)}{2t(1-\cos\theta)-N\lambda} $$
+
* ''Ügyeljen arra, hogy a kettéválasztott fénynyalábok optikai úthossza minél pontosabban megegyezzen. Ehhez (jól beállított interferométer esetén) a mozgatható tükör középállásban ($500\,\mu m$) az interferométeren található fehér jelzéssel egyvonalba kell legyen.''
  
−
ahol $t$ az üveglemez vastagsága.
+
* ''Ne feledje el beépíteni a kompenzátort, hogy az optikai úthossz valóban egyezzen!''
 +
 
 +
'''b)''' Állítsuk be úgy a piezoerősítőt, hogy a -3-3 V bemeneti jelre -30 V és 30 V közötti kimenetet adjon ki!
 +
 
 +
* ''Ha ehhez a feladathoz ért, szóljon a mérésvezetőnek, aki megmutatja az eszközök működését!
 +
* ''A piezomozgató meghajtásához egy speciális erősítőt használunk, amit egy függvénygenerátorral (oszcilloszkópba beépített) vezérlünk. Az erősítő offset-je és erősítése állítható, a maximális tartomány -30 V és 150 V, de a mérés során balesetvédelmi okokból csak kisebb tartományon használjuk.''
 +
* '''FIGYELEM! Nem tudhatjuk, hogy korábban ki "tekergette" az erősítőt és rossz beállítás esetén akár 150V-ot is kiadhat, ezért ne érjen a kimeneti kábel és a piezokristály kivezetéseihez!'''
 +
* ''Először 0 V bemenet mellett állítsa be az erősítőt a rajta található "OFFSET" tekerőgomb segítségével, hogy 0 V-ot mutasson a kijelzője! Utána a kösse rá a bemenetet a függvénygenerátorra, melyen 1 V kimeneti feszültséget állít be! Az erősítőn található "AMPL" tekerőgombbal állítsa be az erősítést úgy, hogy a kijelzőn 10 V legyen látható! Ha ez megtörtént, emelje fel a tápegység kimeneti feszültségét 3 V-ra és ellenőrizze a kijelzőn megjelenő értéket! Ha nem 30 V-ot lát, akkor óvatosan finomhangolja az erősítést az "AMPL" tekerőgombbal!''
 +
* '''FIGYELEM! A tekerőgombok könnyen elállítódhatnak, így amikor a gombok körül szerel, különösen figyeljen oda, hogy ne érjen a gombokhoz!'''
 +
 
 +
'''c)''' A piezomozgatóra adott feszültség változtatása közben számoljuk le a gyűrűátmeneteket először 0-30 V, majd 30-(-30 V) és végül -30-0 V tartományokban!
 +
 
 +
* ''A mérést érdemes úgy végezni, hogy minden gyűrűátmenet után felírjuk a feszültséget. Mivel a lézer hullámhossza ismert, az átmenetek számát könnyen távolságra tudjuk váltani és így megkapjuk az elmozdulás - feszültség grafikont.''
 +
 
 +
'''d)''' Ismételjük meg az előző feladatot!
 +
 
 +
* '' A piezoelektromos effektus esetén egy hiszterézist tapasztalhatunk, ami azt jelenti, hogy a pontos elmozdulás függhet attól, hogy milyen irányba mozgunk és milyen sebességgel. A pontosabb kép érdekében így érdemes legalább két teljes ciklust lemérni kalibrációként.''
 +
 
 +
'''e)''' Cseréljük le az ernyőt egy fotodetektorra, melynek jelét vezessük az oszcilloszkóp egyik csatornájába! A függvénygenerátor jelét szintén kössük be az oszcilloszkópba egy T-elosztó segítségével! A függvénygenerátoron állítsunk be egy -3-3V-os 1Hz körüli háromszögjelet, ekkor a piezoerősítő kimenete -30-30 V között kell változzon.
 +
 
 +
* '' A háromszögjel rákapcsolása után figyelje meg a gyűrűképet! Mit tapasztal?''
 +
 
 +
* '' Érdemes a detektort úgy beállítani, hogy a gyűrűmintázaton olyan helyre essen, ahol nem túl sűrű a gyűrűk elhelyezkedése. Ez a középtől számított kb. 3-6 gyűrű környéke.''
 +
 
 +
* '''FIGYELEM! Az erősítő kimenetét semmi esetre se kösse rá az oszcilloszkópra, mert rossz beállítás esetén nagy feszültséget is kiadhat, ami károsíthatja az eszközt!'''
 +
 
 +
'''f)''' Ábrázoljuk együtt az oszcilloszkópon a meghajtó jelet és a detektor jelét, majd mentsük el egy pendrive-ra az oszcilloszkóppal mért értékeket!
 +
 
 +
* '' Ezzel a módszerrel "automatizáltuk" a gyűrűátmenetek számlálását. A detektor jele periodikusan változik, egy-egy periódus egy-egy gyűrűátmenethez tartozik. A mért jelből így kinyerhető a gyűrűátmenetek száma, a meghajtójelből pedig a piezomozgatóra kapcsolt feszültség és ebből megkapjuk a kalibrációt.''
 +
 
 +
* '' Ez a módszer a teljes hiszterézis kimérésére kevésbé alkalmas, bár megfelelő beállítás mellett ez is megkapható. Egy monoton módon változó fel, vagy lemenő feszültségágban viszont megkaphatjuk a kalibrációt, az "automatizálásnak" köszönhetően pedig könnyen végezhetünk több mérést is.''
 +
 
 +
'''g)''' Határozzuk meg a piezomozgató kalibrációját az előző pontban ismertetett módszerrel 0,5-1-2-3 Hz-es háromszögjelek használatával!
 +
 
 +
===6. Zöld lézer hullámhosszának meghatározása===
 +
 
 +
'''a)''' Az előző elrendezésben használt piros lézert cseréljük ki a zöld lézerre, majd állítsuk be a fényutat!
 +
 
 +
'''b)''' Határozzuk meg a zöld lézer hullámhosszát az oszcilloszkóppal mért jelek és a piezomozgató kalibrációjának felhasználásával!
 +
 
 +
''' Ha minden feladatot megoldott és minden szükséges mennyiséget kiszámolt és még maradt ideje a mérés végén, akkor megismételheti kombinálva a feladatokat. Például megmérheti a zöld lézer hullámhosszát Michelson-féle elrendezésben, vagy a He-Ne lézer hullámhosszát automatizált módon.'''
  
 
</wlatex>
 
</wlatex>

A lap jelenlegi, 2024. október 16., 12:07-kori változata


A mérés célja:

  • koherens optikai jelenségek tanulmányozása.

Ennek érdekében:

  • áttekintjük az interferencia elméletét,
  • megmérjük a lézerfény koherenciahosszát,
  • méréseket végzünk interferométerrel,



Tartalomjegyzék


Elméleti összefoglaló

Koherencia fogalma

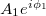A koherencia fogalmát a következő egyszerű képen keresztül definiálhatjuk. Tételezzük fel, hogy egy hullám egy \setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0% kiindulási pontból két úton keresztül juthat el a \setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0% pontba. Az 1. és 2. 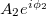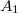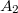úton a \setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0% pontba érkező nyalábokat \setbox0\hbox{$A_1e^{i\phi_1}$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$A_2e^{i\phi_2}$}% \message{//depth:\the\dp0//}% \box0% komplex számokkal jellemezhetjük, ahol \setbox0\hbox{$A_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$A_2$}% \message{//depth:\the\dp0//}% \box0% a nyalábok amplitúdóit, 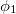\setbox0\hbox{$\phi_1$}% \message{//depth:\the\dp0//}% \box0% és \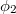setbox0\hbox{$\phi_2$}% \message{//depth:\the\dp0//}% \box0% pedig a fázisukat adják meg. B pontban a két nyaláb a szuperpozíció elve alapján összeadódik, így az eredő komplex amplitúdó 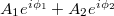\setbox0\hbox{$A_1e^{i\phi_1}+A_2e^{i\phi_2}$}% \message{//depth:\the\dp0//}% \box0% lesz. Detektoraink viszont nem a komplex amplitúdót, hanem annak az abszolút érték négyzetét, az intenzitást érzékelik, mely egyszerű számolás alapján:

\[ I_B = A_1^2 + A_2^2 + 2A_1A_2\cos(\phi_1- \phi_2). \]

Látszik, hogy a két nyaláb intenzitásának összege mellett megjelenik az úgynevezett interferencia tag is: ha a két nyaláb azonos fázisban érkezik a \setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0% pontba, akkor erősítést, ha ellentétes fázisban érkeznek, akkor kioltást kapunk. Persze interferenciát csak akkor tapasztalunk, ha a két nyaláb fáziskülönbsége időben állandó, ekkor beszélünk koherens nyalábokról. Ellenkező esetben az interferenciatag időben kiátlagolódik, így nem látunk erősítéseket, ill. kioltásokat.

Fény esetében az interferencia tag eltűnésének a leggyakoribb oka, hogy maga az \setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0% pontban elhelyezett fényforrás sem koherens. Ha az 1. és 2. nyaláb által megtett optikai úthossz különbözik, akkor a \setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0% pontban találkozó nyalábok különböző időpontban indultak el az \setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0% pontból. 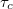Koherencia időnek hívjuk azt a maximális \setbox0\hbox{$\tau_c$}% \message{//depth:\the\dp0//}% \box0% időkülönbséget, melyre a fényforrásból a \setbox0\hbox{$T_0$}% \message{//depth:\the\dp0//}% \box0% ill. 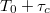\setbox0\hbox{$T_0+\tau_c$}% \message{//depth:\the\dp0//}% \box0% időpontban kibocsátott fotonok fázisai között korreláció tapasztalható. Ha az 1. és 2. nyaláb optikai úthosszainak különbsége nagyobb a fény által 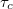\setbox0\hbox{$\tau_c$}% \message{//depth:\the\dp0//}% \box0% idő alatt megtett útnál, 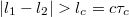\setbox0\hbox{$|l_1-l_2|>l_c=c\tau_c$}% \message{//depth:\the\dp0//}% \box0%, akkor az interferencia tag eltűnik. Az ennek megfelelő 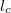\setbox0\hbox{$l_c$}% \message{//depth:\the\dp0//}% \box0% úthosszat koherenciahossznak nevezzük.

Az első koherens optikai kísérletet Thomas Young végezte úgy, hogy keskeny fénynyalábot irányított két szorosan egymás mellett elrendezett résre. A résekkel szemben elhelyezett ernyőn a réseken keresztül ráeső fényből szabályos, sötét és világos sávokból álló interferenciakép jött létre. Young kísérlete fontos bizonyítéka volt a fény hullámtermészetének. 1881-ben, 78 évvel Young után, A. A. Michelson hasonló elven működő interferométert épített. Michelson kísérletében a fényhullámot egy félig áteresztő tükör segítségével választotta két részre, melyek különböző utak megtétele után (lásd később) egy detektáló ernyőn újra találkozva alkotnak interferenciaképet. Michelson eredetileg az éternek, az elektromágneses sugárzások – így a fénynek is – terjedését biztosító feltételezett közegnek a kimutatására szerkesztette meg interferométerét. Részben az ő erőfeszítéseinek is köszönhetően az éter feltételezését ma nem tekintjük életképes hipotézisnek. Ezen túlmenően azonban a Michelson-féle interferométer széleskörűen elterjedt a fény hullámhosszának mérésére illetve ismert hullámhosszúságú fényforrás alkalmazásával rendkívül kis távolságok mérésére és optikai közegek vizsgálatára.

A fenti kísérletek elvégzése hagyományos fényforrásokkal rendkívül nehéz feladat a rövid koherenciaidő, illetve a különböző frekvenciájú fénykomponensek keveredése miatt. A lézerek feltalálása óta lényegesen könnyebb interferencia-jelenségeket vizsgálni, egy vékony résen történő diffrakciót akár otthon is kipróbálhatjuk egy mutatólézer segítségével.

A lézer működési elvénél fogva egy nagy koherencia-hosszal rendelkező, jól meghatározott irányban terjedő monokromatikus fénynyalábot biztosít. A lézerben egy aktív közeg jól meghatározott frekvenciájú fotonokat emittál, melyek egy rezonátorban „oda-vissza pattognak”. A stimulált emisszió jelenségének köszönhetően az emittált fotonok a rezonátorban már jelenlévő fotonokkal azonos állapotúak lesznek, azaz a már jelenlévő fotonokkal azonos fázisú és terjedési irányú fotonok emittálódnak. A rezonátor egyik oldalán a fény egy részét kicsatolva egy irányított, koherens nyalábot kapunk. A mérésen is használt He-Ne lézerben a fényemissziót a gázkeverék bizonyos atomi átmenetei biztosítják, míg a rezonátort két szembeállított tükör alkotja, melyek egyike a fény kb. 1 %-át kiengedi. Mivel a rezonátor szélessége 10-20 cm is lehet, illetve a fotonok a kilépés előtt sokszor körbejárják a rezonátort, így a He-Ne lézer koherenciahossza több méter is lehet.

A napjainkban tömegesen alkalmazott félvezető lézerekben a fény elektronok és lyukak rekombinációjának köszönhetően emittálódik. A rezonátort maga a félvezető nanoszerkezet biztosítja, így kisebb koherenciahosszat várunk.

Michelson-féle interferométer felépítése

1. ábra
2. ábra


A 2. ábrán a Michelson-féle interferométer vázlata látható. A lézer sugárnyalábja sugárosztóra esik, amely a beeső fény 50 %-át visszaveri, és másik 50 %-át átengedi. A beeső fény így két nyalábra oszlik. Az egyik a rögzített tükörre (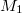\setbox0\hbox{$M_1$}% \message{//depth:\the\dp0//}% \box0%) verődik vissza, a másik a mozgatható tükörre (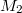\setbox0\hbox{$M_2$}% \message{//depth:\the\dp0//}% \box0%) esik. Mindkét tükör a sugárosztóra veri vissza a fényt.

A mozgatható tükörről visszavert fény egyik fele most a megfigyelő ernyőre esik be, és a rögzített tükörről visszaverődő fény fele a sugárosztón áthaladva szintén a megfigyelő ernyőre esik.

3. ábra

Ily módon az eredeti sugárnyaláb először kettéosztódik, majd a keletkezett nyalábok egy része visszafelé egyesül egymással. Mivel a nyalábok ugyanabból a fényforrásból származnak, fázisuk erősen korrelált. Így, amikor lencsét helyezünk a lézer fényforrás és a sugárosztó közé, a fénynyaláb kitágul és a megfigyelő ernyőn sötét és világos gyűrűkből álló kép jelenik meg (3. ábra).

Mivel a két interferáló nyaláb ugyanabból a forrásból származik, fázisuk eredetileg azonos volt. Relatív fázisuk, amikor a megfigyelő ernyő bármely pontjában találkoznak, attól az optikai úthossztól függ, amelyet ezen pont eléréséig megtettek.

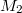\setbox0\hbox{$M_2$}% \message{//depth:\the\dp0//}% \box0% mozgatásával az egyik nyaláb úthossza változtatható. Mivel a nyaláb az 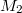\setbox0\hbox{$M_2$}% \message{//depth:\the\dp0//}% \box0% és a sugárosztó közötti utat kétszer teszi meg, 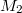\setbox0\hbox{$M_2$}% \message{//depth:\the\dp0//}% \box0%-et 1/4 hullámhossznyival közelítve a sugárosztóhoz, a nyaláb úthossza 1/2 hullámhossznyival csökken. Eközben megváltozik az interferenciakép. A maximumok sugara oly módon csökken, hogy a korábbi minimumok helyét foglalják el. Ha 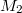\setbox0\hbox{$M_2$}% \message{//depth:\the\dp0//}% \box0%-et tovább mozgatjuk 1/4 hullámhossznyival a sugárosztó felé, a maximumok sugara tovább csökken úgy, hogy a maximumok és a minimumok ismét helyet cserélnek, és az új elrendezés megkülönböztethetetlen lesz az eredeti képtől.

Lassan mozgatva a tükröt egy meghatározott 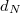\setbox0\hbox{$d_N$}% \message{//depth:\the\dp0//}% \box0% távolságon, és közben leszámolva \setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0%-et, annak számát, hányszor jutott a gyűrűkép az eredeti állapotába, meghatározható a fény hullámhossza:

\[ \lambda = \frac{2d_N}{N}. \]

Ha a fény hullámhossza ismert, ugyanígy mérhető a 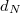\setbox0\hbox{$d_N$}% \message{//depth:\the\dp0//}% \box0% távolság.

Fabry--Pérot-interferométer felépítése

Megjegyzés: A berendezés átépíthető úgy, hogy Fabry--Pérot interferométerként funkcionáljon, de technikai okok miatt a mérések során nem végezzük el az átépítést. De a Fabry--Pérot interferométer működés elvét érdemes megismerni.

A 4. ábrán a Faby--Pérot-interferométer vázlata látható. Itt a lézerből bejövő nyaláb a lencse után széttartóvá válik és így éri el a rögzített, féligáteresztő tükröt (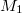\setbox0\hbox{$M_1$}% \message{//depth:\the\dp0//}% \box0%). A széttartó nyalábok ezután a szintén féligáteresztő tükörre (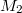\setbox0\hbox{$M_2$}% \message{//depth:\the\dp0//}% \box0%) jutnak, ahol részben visszaverődnek és részben továbbhaladnak. A visszaverődött nyalábok a rögzített tükörről újra visszaverődnek, így a két tükör között többszörös visszaverődés révén egy optikai üregrezonátor alakul ki. Mivel a rezonátorból kilépő transzmittált nyalábok egy közös bejövő nyalábból származnak, a fázisuk eredetileg azonos volt, az üregből kilépés után pedig a relatív fázisuk a széttartás szögétől és a két tükör távolságától függ. Ha a lencse rögzített, akkor a fáziskülönbség a mozgatható tükör mozgatásával változtatható. A Michelson-féle interferométernél leírtakhoz hasonlóan, ha az 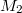\setbox0\hbox{$M_2$}% \message{//depth:\the\dp0//}% \box0% tükröt 1/2 hullámhossznyival mozdítjuk el, az új és a kiindulási gyűrűkép egyformának adódik. Így a Fabry--Pérot-interferométer is hasonlóan a gyűrűátmenetek számolásával használható a távolság mérésére, ha ismert hullámhosszú fényt használunk, vagy a hullámhossz meghatározására, ha ismerjük az elmozdulást.

A Fabry--Pérot-elrenedzés elviekben a Michelson-féle interferométernél látott gyűrűképhez képest fényesebb, vékonyabb és egymástól távolabb elhelyezkedő gyűrűkből álló képet ad.

4. ábra

Mérési feladatok

A méréshez rendelkezésre álló eszközök

  • A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.

FELADATOK ELSŐ ALKALOMMAL

1. Piros félvezető lézer hullámhosszának mérése Michelson-féle interferométerrel

a) Állítsuk össze a Michelson-féle interferométer elrendezést a leiratban ismertetett módon a piros félvezető lézer lézert használva!

b) Állítsuk a mikrométert középállásba (közelítőleg 500 µm)!

  • Ebben a helyzetben a leginkább lineáris az összefüggés a mikrométeren leolvasott érték és a tükör elmozdulása között.

c) Forgassuk el a mikrométer gombját egy teljes fordulattal az óra járásával ellenkező irányban addig, amíg a nulla helyzet egybe nem esik a jelzéssel! Jegyezzük fel a leolvasott mikrométer értéket!

  • Ha a mikrométer gomb forgatásának irányát megváltoztatjuk, a tükör nem indul meg azonnal. Ezt nevezzük kotyogásnak, amely minden mechanikai rendszernél előfordul mozgásirány megváltoztatásakor. A fenti módon a kotyogásból eredő hiba kiküszöbölhető.

d) A megfigyelő ernyőt állítsuk be úgy, hogy a milliméter skála egyik jele essék egybe az interferenciakép egyik gyűrűjével!

  • Könnyebb lesz a gyűrűk számlálása, ha a referencia jel a kép közepétől számított első vagy második gyűrűre esik.

e) Forgassuk tovább a mikrométer gombját az óramutató járásával ellenkező irányba és számoljuk meg a referencia jelen áthaladó gyűrűket! Legalább 20 gyűrűátmenetet számoljunk le, de a felbontás javítása érdekében érdemes lehet akár 50 átmenetig is elmenni! A gyűrűátmenetek leszámlálása után a gyűrűknek ugyanabban a helyzetben kell lenniük, mint a számlálás megkezdésekor. Jegyezzük fel a mikrométer tárcsán leolvasott értéket!

  • A mérést elvégezheti úgy is, hogy 15-20 gyűrűátmenetenként megáll és leolvassa az elmozdulás értékét, majd ezt megismétli 4-5-ször. A kapott tükörelmozdulás - gyűrűátmenet értékpárokat grafikonon ábrázolva a hullámhossz egyenesillesztéssel is meghatározható.

f) Jegyezzük fel a leszámlált gyűrű átmenetek számát!

g) Határozzuk meg a lézer fényforrás hullámhosszát, annak figyelembe vételével, hogy a mikrométeren egy kis osztás egy µm (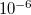\setbox0\hbox{$10^{-6}$}% \message{//depth:\the\dp0//}% \box0% m) tükör elmozdulásnak felel meg!

h) Többször ismételjük meg a 3 - 7. lépéseket!

2. A levegő törésmutatójának meghatározása Michelson-féle interferométerrel

a) Állítsuk össze a Michelson-féle interferométert a piros félvezető lézer használatával!

b) Helyezzük az elemtartót a rögzített tükör és a sugárosztó közé, és helyezzük fel ennek mágneses hátoldalára a vákuum-kamrát és húzzuk a vákuumkamra levegőző csonkjára a kézi vákuumszivattyú csövét!

  • Szükség szerint állítsuk be a rögzített tükröt úgy, hogy az interferenciakép közepe jól látható legyen a megfigyelő ernyőn!

c) A kézi vákuumszivattyún lévő billenőkapcsoló segítségével engedjünk levegőt a vákuumkamrába, és győződjünk meg arról, hogy a vákuumkamrában atmoszférikus nyomás uralkodik! Ez lesz a 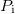\setbox0\hbox{$P_\text i$}% \message{//depth:\the\dp0//}% \box0% kezdeti nyomás.

d) Lassan szivattyúzzuk ki a levegőt a vákuumkamrából, miközben számoljuk meg a bekövetkező gyűrű átmeneteket! Jegyezzük fel a manométerről leolvasott 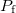\setbox0\hbox{$P_\text f$}% \message{//depth:\the\dp0//}% \box0% nyomás végértéket és a gyűrűátmenetek \setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0% számát!

  • A manométer a nyomást az atmoszférikus nyomáshoz képest méri (pl. a 34 Hgcm állás az atmoszférikusnál 34 Hgcm-rel kisebb nyomást jelent). Ebben az esetben az abszolút nyomást a következőképpen kell számítani:
\[ P_\text{abs} = P_\text{atm} - P_\text{m\'ert} \]

e) A mérési eredmények alapján határozzuk meg a törésmutató (\setbox0\hbox{$n$}% \message{//depth:\the\dp0//}% \box0%) - nyomás (\setbox0\hbox{$P$}% \message{//depth:\the\dp0//}% \box0%) grafikon meredekségét levegőre és a levegő törésmutatóját atmoszférikus nyomáson.

A Michelson-féle interferométernél a gyűrűkép jellemzőit a két interferáló nyaláb fázisviszonyai határozzák meg. A fázisviszonyok kétféle módon változhatnak meg. Az egyik az egyes nyalábok által megtett utak változása (például, a mozgatható tükör mozgatása révén). A másik a közeg megváltozása, amelyben az egyik vagy mindkét nyaláb áthalad.

Adott frekvenciájú fény esetén a hullámhossz a következő formula szerint változik:

\[ \lambda = \lambda_0/n \]

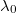ahol \setbox0\hbox{$\lambda_0$}% \message{//depth:\the\dp0//}% \box0% a fény hullámhossza vákuumban, és \setbox0\hbox{$n$}% \message{//depth:\the\dp0//}% \box0% a közeg törésmutatója, amelyben a fény halad. Megfelelően alacsony nyomásokon egy gáz törésmutatója lineárisan változik a gáz nyomásával. Vákuum esetén, ahol a nyomás zérus, a törésmutató pontosan 1. Ennek alapján kísérletileg meghatározva a törésmutató – nyomás grafikon meredekségét, kiszámíthatjuk a gáz törésmutatóját különböző nyomásokon.

A lézer nyaláb oda és vissza megtéve az utat a sugárosztó és a mozgatható tükör között, kétszer halad át a vákuumkamrán. A kamrán kívül a két nyaláb optikai úthossza nem változik a kísérlet során. A kamrán belül azonban a fény hullámhossza megnövekszik a nyomás csökkenésével.

Feltételezve, hogy a kamra \setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0% hossza eredetileg 10 hullámhossznyi volt (a valóságban természetesen sokkal hosszabb) és a kamra leszívása közben, a hullámhossz növekedése folytán 9 1/2 hullámhossznyi lesz, a kétszeri áthaladás miatt a kamrán, a fény eggyel kevesebb rezgést végez a kamrán belül. Ennek hatása az interferenciaképre ugyanolyan, mint amikor a mozgatható tükröt 1/2 hullámhossznyival közelebb hozzuk a sugárosztóhoz. Ezért egyetlen gyűrű átmenetet fogunk megfigyelni.

Fentieknek megfelelően (a kétszeri fényáthaladást figyelembe véve) a kamra belseje eredetileg 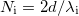\setbox0\hbox{$N_\text i=2d/\lambda_\text i$}% \message{//depth:\the\dp0//}% \box0% fényhullámhossznyi hosszúságú volt. A végnyomáson pedig 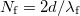\setbox0\hbox{$N_\text f=2d/\lambda_\text f$}% \message{//depth:\the\dp0//}% \box0% hullámhossznyi fért el a kamrában. Ezen két érték közötti különbség, 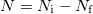\setbox0\hbox{$N=N_\text i-N_\text f$}% \message{//depth:\the\dp0//}% \box0% , éppen a kamra leszívása közben leszámlált gyűrűátmenetek száma. Ezért 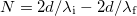\setbox0\hbox{$N=2d/\lambda_\text i-2d/\lambda_\text f$}% \message{//depth:\the\dp0//}% \box0%. 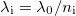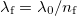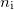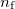Azonban \setbox0\hbox{$\lambda_\text i=\lambda_0/n_\text i$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\lambda_\text f=\lambda_0/n_\text f$}% \message{//depth:\the\dp0//}% \box0%, ahol \setbox0\hbox{$n_\text i$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$n_\text f$}% \message{//depth:\the\dp0//}% \box0% a kamrában lévő levegő törésmutatójának kezdeti és végértéke. Ezért 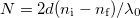\setbox0\hbox{$N=2d(n_\text i-n_\text f)/\lambda_0$}% \message{//depth:\the\dp0//}% \box0%, úgyhogy 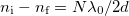\setbox0\hbox{$n_\text i-n_\text f=N\lambda_0/2d$}% \message{//depth:\the\dp0//}% \box0%. A törésmutató-nyomás grafikon meredeksége pedig:

\[ \frac{n_\text i-n_\text f}{P_\text i-P_\text f} = \frac{N\lambda_0}{2d(P_\text i-P_\text f)},\]

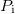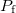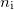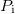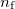ahol \setbox0\hbox{$P_\text i$}% \message{//depth:\the\dp0//}% \box0% a levegő kezdeti nyomása, \setbox0\hbox{$P_\text f$}% \message{//depth:\the\dp0//}% \box0% a levegő végső nyomása, \setbox0\hbox{$n_\text i$}% \message{//depth:\the\dp0//}% \box0% a levegő törésmutatója \setbox0\hbox{$P_\text i$}% \message{//depth:\the\dp0//}% \box0% nyomáson, \setbox0\hbox{$n_\text f$}% \message{//depth:\the\dp0//}% \box0% a levegő törésmutatója \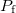setbox0\hbox{$P_\text f$}% \message{//depth:\the\dp0//}% \box0% nyomáson, \setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0% a leszívás során megfigyelt gyűrűátmenetek száma, \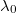setbox0\hbox{$\lambda_0$}% \message{//depth:\the\dp0//}% \box0% a lézerfény hullámhossza vákuumban és \setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0% a vákuumkamra hossza (3 cm).

3. Üveg törésmutatójának meghatározása Michelson-féle interferométerrel

a) Továbbra is a Michelson-féle interferométer elrendezést használjuk, a mérés elején ellenőrizze, hogy megfelelően van-e beállítva a fényút.

b) Helyezzük a forgatható mutatót az elemtartóval a sugárosztó és a mozgatható tükör közé, és rögzítsük az üveglemezt az elemtartó mágneses hátlapjára!

c) Úgy állítsuk be a mutatót, hogy finom skálájának "0"-ja az interferométer alapon lévő fokosztás nullpontjával essen egybe!

d) Vegyük el a lencsét a lézer elől! Tartsuk a megfigyelő ernyőt a sugárosztó és a mozgatható tükör között! Ha egy fényes pont és néhány másodlagos pont látható a megfigyelő ernyőn, addig állítsuk az elemtartó szögét a forgatható mutatóhoz képest, amíg egy fényes pont látható. Ezután ismét igazítsuk a forgatható mutatót a skálaosztás nullpontjához! Ekkor az üveglemez merőleges az optikai útra.

e) Helyezzük vissza a lencsét és a megfigyelő ernyőt, és végezzük el a szükséges tükör beállításokat, hogy tiszta gyűrűképet kapjunk!

f) Lassan forgassuk el a forgatható mutatót 0°-tól \setbox0\hbox{$\theta$}% \message{//depth:\the\dp0//}% \box0% szögig (legalább 10 fokot), és eközben számoljuk le a megfigyelt gyűrűátmenetek számát!

g) A mérési eredmények alapján határozzuk meg az üveglemez törésmutatóját az alábbi összefüggés szerint:

\[ n_g = \frac{(2t-N\lambda)(1-\cos\theta)}{2t(1-\cos\theta)-N\lambda} \]

ahol \setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0% az üveglemez vastagsága.


4. Kis koherenciahosszú félvezető lézer koherenciahosszának mérése

a) Állítsuk össze a Michelson-féle interferométert a kis koherenciahosszú (mutató) félvezető lézerrel!

  • Ügyeljen arra, hogy a kettéválasztott fénynyalábok optikai úthossza minél pontosabban megegyezzen. Ehhez (jól beállított interferométer esetén) a mozgatható tükör középállásban (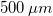\setbox0\hbox{$500\,\mu m$}% \message{//depth:\the\dp0//}% \box0%) az interferométeren található fehér jelzéssel egyvonalba kell legyen.
  • Ne feledje el beépíteni a kompenzátort, hogy az optikai úthossz valóban egyezzen!

b) Állítsuk be a félvezető mutatólézert úgy, hogy a lézer nyaláb pontosan merőleges legyen a mozgatható tükörre.

  • Ennek pontos beállításához egy papírlapba fúrt kis lyukon eresszük át a lézernyalábot, és addig állítsuk a lézer szögét, amíg a lézernyaláb pontosan a kis lyukba érkezik vissza.
  • A lézernyaláb beállítása közben a féligáteresztő tükröt fordítsuk oldalra, hogy ne legyen a lézer útjában.

c) Helyezzük el a sugárosztót a lézernyalábbal 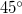\setbox0\hbox{$45^\circ$}% \message{//depth:\the\dp0//}% \box0%-os szöget bezárólag a jelzések közé úgy, hogy a nyaláb az álló tükörre verődjék!

  • A sugárosztó szögét úgy kell beállítani, hogy a visszavert nyaláb a rögzített tükör közepére essék!
  • Ekkor két fényes pontsorozatot kell látnunk a megfigyelő ernyőn. Az egyik pontsorozat a rögzített tükörről, a másik a mozgatható tükörről jön létre. Mindegyik pontsorozat egy fényes pontot és két vagy több kevésbé fényes pontot tartalmaz (a többszörös visszaverődés miatt).

d) Állítsuk a sugárosztó szögét addig, amíg a két pontsorozat a lehető legközelebb kerül egymáshoz, majd rögzítsük a sugárosztó helyzetét!

e) A rögzített tükör hátoldalán lévő csavarokkal állítsuk be annak hajlásszögét úgy, hogy a két pontsorozat a megfigyelő ernyőn egybeessék!

f) Helyezzünk egy 18 mm fókusztávolságú lencsét a lézer előtti elemtartó mágneses oldalára, és állítsuk be úgy, hogy a széttartó nyaláb a sugárosztóra koncentrálódjék!

g) A mikrométercsavar segítségével mozgassuk az egyik tükröt addig, míg a koncentrikus gyűrűk megjelennek a képen. Állapítsuk meg, hogy milyen elmozdulás-tartományban láthatók a gyűrűk. Ez alapján becsüljük meg a mutatólézer koherenciahosszát.

  • Ha nem sikerül interferenciagyűrűket észlelni, akkor rossz a beállításunk, pl. nem eléggé kiegyenlítettek az optikai úthosszak.

FIGYELEM! A második alkalomra az eddigi feladatok előzetes kiértékelését el kell végezni és meg kell mutatni a mérésvezetőnek.

FELADATOK MÁSODIK ALKALOMMAL

Ha az első mérési alkalommal elvégzett feladatok kiértékelése során probléma adódott a mért adatok helytelensége miatt, akkor elsőként ezeket a mérési feladatokat végezze el újra.

5. Piezomozgató kalibrálása ismert hullámhosszú lézerrel Michelson-féle elrendezésben

A korábbi feladatokban a tükör mozgatásának mértékét ismertük és ebből határoztuk meg a hullámhosszat. Ebben a feladatban a kapott hullámhosszat felhasználva egy piezomozgató kalibrációját végezzük el, azaz meghatározzuk, hogy adott feszültség hatására mekkora a piezokristály megnyúlása.

a) Állítsuk össze a Michelson-féle interferométert a piros lézer használatával úgy, hogy a mozgatható tükör helyére a tükörrel ellátott piezomozgatót helyezzük!

  • Ügyeljen arra, hogy a kettéválasztott fénynyalábok optikai úthossza minél pontosabban megegyezzen. Ehhez (jól beállított interferométer esetén) a mozgatható tükör középállásban (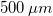\setbox0\hbox{$500\,\mu m$}% \message{//depth:\the\dp0//}% \box0%) az interferométeren található fehér jelzéssel egyvonalba kell legyen.
  • Ne feledje el beépíteni a kompenzátort, hogy az optikai úthossz valóban egyezzen!

b) Állítsuk be úgy a piezoerősítőt, hogy a -3-3 V bemeneti jelre -30 V és 30 V közötti kimenetet adjon ki!

  • Ha ehhez a feladathoz ért, szóljon a mérésvezetőnek, aki megmutatja az eszközök működését!
  • A piezomozgató meghajtásához egy speciális erősítőt használunk, amit egy függvénygenerátorral (oszcilloszkópba beépített) vezérlünk. Az erősítő offset-je és erősítése állítható, a maximális tartomány -30 V és 150 V, de a mérés során balesetvédelmi okokból csak kisebb tartományon használjuk.
  • FIGYELEM! Nem tudhatjuk, hogy korábban ki "tekergette" az erősítőt és rossz beállítás esetén akár 150V-ot is kiadhat, ezért ne érjen a kimeneti kábel és a piezokristály kivezetéseihez!
  • Először 0 V bemenet mellett állítsa be az erősítőt a rajta található "OFFSET" tekerőgomb segítségével, hogy 0 V-ot mutasson a kijelzője! Utána a kösse rá a bemenetet a függvénygenerátorra, melyen 1 V kimeneti feszültséget állít be! Az erősítőn található "AMPL" tekerőgombbal állítsa be az erősítést úgy, hogy a kijelzőn 10 V legyen látható! Ha ez megtörtént, emelje fel a tápegység kimeneti feszültségét 3 V-ra és ellenőrizze a kijelzőn megjelenő értéket! Ha nem 30 V-ot lát, akkor óvatosan finomhangolja az erősítést az "AMPL" tekerőgombbal!
  • FIGYELEM! A tekerőgombok könnyen elállítódhatnak, így amikor a gombok körül szerel, különösen figyeljen oda, hogy ne érjen a gombokhoz!

c) A piezomozgatóra adott feszültség változtatása közben számoljuk le a gyűrűátmeneteket először 0-30 V, majd 30-(-30 V) és végül -30-0 V tartományokban!

  • A mérést érdemes úgy végezni, hogy minden gyűrűátmenet után felírjuk a feszültséget. Mivel a lézer hullámhossza ismert, az átmenetek számát könnyen távolságra tudjuk váltani és így megkapjuk az elmozdulás - feszültség grafikont.

d) Ismételjük meg az előző feladatot!

  • A piezoelektromos effektus esetén egy hiszterézist tapasztalhatunk, ami azt jelenti, hogy a pontos elmozdulás függhet attól, hogy milyen irányba mozgunk és milyen sebességgel. A pontosabb kép érdekében így érdemes legalább két teljes ciklust lemérni kalibrációként.

e) Cseréljük le az ernyőt egy fotodetektorra, melynek jelét vezessük az oszcilloszkóp egyik csatornájába! A függvénygenerátor jelét szintén kössük be az oszcilloszkópba egy T-elosztó segítségével! A függvénygenerátoron állítsunk be egy -3-3V-os 1Hz körüli háromszögjelet, ekkor a piezoerősítő kimenete -30-30 V között kell változzon.

  • A háromszögjel rákapcsolása után figyelje meg a gyűrűképet! Mit tapasztal?
  • Érdemes a detektort úgy beállítani, hogy a gyűrűmintázaton olyan helyre essen, ahol nem túl sűrű a gyűrűk elhelyezkedése. Ez a középtől számított kb. 3-6 gyűrű környéke.
  • FIGYELEM! Az erősítő kimenetét semmi esetre se kösse rá az oszcilloszkópra, mert rossz beállítás esetén nagy feszültséget is kiadhat, ami károsíthatja az eszközt!

f) Ábrázoljuk együtt az oszcilloszkópon a meghajtó jelet és a detektor jelét, majd mentsük el egy pendrive-ra az oszcilloszkóppal mért értékeket!

  • Ezzel a módszerrel "automatizáltuk" a gyűrűátmenetek számlálását. A detektor jele periodikusan változik, egy-egy periódus egy-egy gyűrűátmenethez tartozik. A mért jelből így kinyerhető a gyűrűátmenetek száma, a meghajtójelből pedig a piezomozgatóra kapcsolt feszültség és ebből megkapjuk a kalibrációt.
  • Ez a módszer a teljes hiszterézis kimérésére kevésbé alkalmas, bár megfelelő beállítás mellett ez is megkapható. Egy monoton módon változó fel, vagy lemenő feszültségágban viszont megkaphatjuk a kalibrációt, az "automatizálásnak" köszönhetően pedig könnyen végezhetünk több mérést is.

g) Határozzuk meg a piezomozgató kalibrációját az előző pontban ismertetett módszerrel 0,5-1-2-3 Hz-es háromszögjelek használatával!

6. Zöld lézer hullámhosszának meghatározása

a) Az előző elrendezésben használt piros lézert cseréljük ki a zöld lézerre, majd állítsuk be a fényutat!

b) Határozzuk meg a zöld lézer hullámhosszát az oszcilloszkóppal mért jelek és a piezomozgató kalibrációjának felhasználásával!

Ha minden feladatot megoldott és minden szükséges mennyiséget kiszámolt és még maradt ideje a mérés végén, akkor megismételheti kombinálva a feladatokat. Például megmérheti a zöld lézer hullámhosszát Michelson-féle elrendezésben, vagy a He-Ne lézer hullámhosszát automatizált módon.


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Mérések_interferométerrel&oldid=29419”